Đề chọn học sinh giỏi Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Long – Bình Phước

UBND THỊ XÃ BÌNH LONG
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024-2025
Môn: Toán – Lớp 9
(Đề thi gồm có 02 trang)
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1. (5 điểm) Cho A= x +3 x +1 x + 7     + +  : 1 x −  
(với x ≥ 0, x ≠1, x ≠ 9). x 1 3
x x 4 x 3   x 1 − − − + +    
1. Rút gọn biểu thức A.
2. Tính giá giá trị của biểu thức A khi x = 7 − 4 3 .
3. Tìm giá trị nhỏ nhất của biểu thức 1 . A Câu 2. (5 điểm)
1. Giải phương trình và hệ phương trình: 2 2
a) x − 2x + 3 = 2 2x − 4x + 3
xy + x + 2y =14 b)  3 2
x + 6x +12x − y = 7 −
2. Một giáo viên đến nhà sách để mua một số sách và tập để làm phần thưởng cho học
sinh. Nhà sách đã niêm yết giá một quyển sách là 30000 đồng và giá một quyển tập là
10000 đồng. Biết giáo viên muốn mua tất cả 30 quyển sách và tập. Khi ra quầy thu ngân
để thanh toán tiền, nhà sách thông báo hôm nay được giảm giá 10% trên tổng số tiền,
nên giáo viên chỉ phải trả 450000 đồng. Hỏi giáo viên đã mua bao nhiêu quyển sách và bao nhiêu quyển tập?
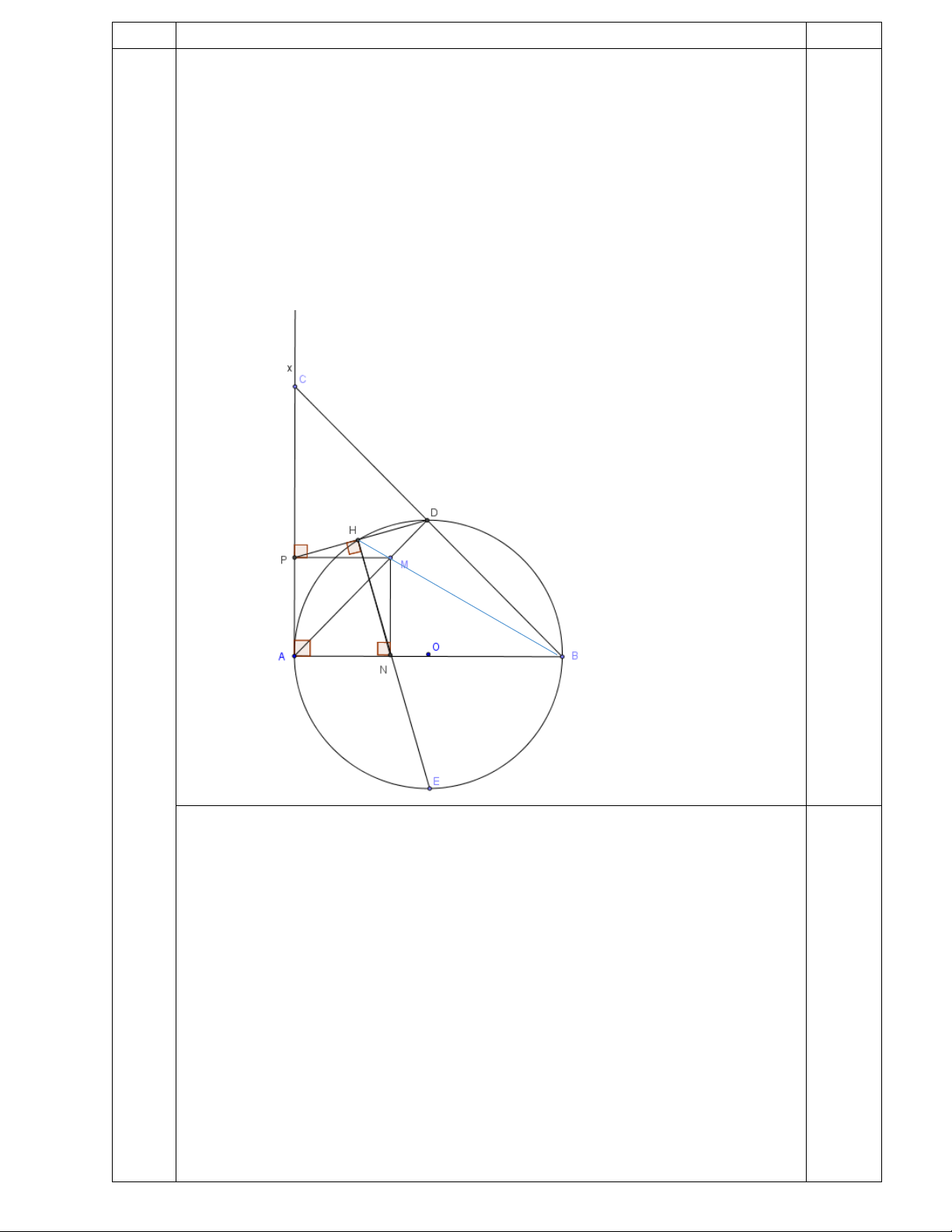
Câu 3. (5 điểm) Cho đường tròn (O), đường kính AB. Trên tia tiếp tuyến Ax với (O) lấy
điểm C sao cho AC=AB. Đường thẳng BC cắt (O) tại D, M là điểm thay đổi trên đoạn AD.
Gọi N, P lần lượt là chân đường vuông góc hạ từ M xuống AB, AC; H là chân đường vuông
góc hạ từ N xuống PD. Chứng minh:
1. 5 điểm A, N, M, P, H cùng thuộc một đường tròn. 2. H, M, B thẳng hàng.
3. HN luôn đi qua một điểm cố định khi M thay đổi. Câu 4. (2 điểm)
1. Một bể cá dạng hình hộp chữ nhật có chiều dài 80cm, chiều rộng 60cm, đang chứa
240 000cm3 nước. Người ta bỏ vào bể 6 viên đá dạng hình chóp tứ giác đều có cạnh
đáy 12 cm, chiều cao 15 cm và một số viên đá dạng hình chóp tam giác đều có diện
tích mặt đáy là 110cm2, chiều cao 18 cm. Tính số viên đá dạng hình chóp tam giác
đều đã bỏ vào bể cá, biết sau khi bỏ các viên đá vào thì mực nước trong bể cao 52 cm.
2. Cho 1 hộp gồm các thẻ đánh số 1;2;3;4;5;6;7;8. Mỗi thẻ khác nhau đánh các số khác
nhau. Lấy ngẫu nhiên 2 thẻ trong hộp. Tính xác suất của biến cố “Tích của 2 thẻ được
lấy ra là một số chẵn”.
Câu 5. (3 điểm)
1. Tìm nghiệm nguyên của phương trình: 2 2 2 2
(x +1)(x + y ) = 4x y . 2. Chứng minh : 3 3
x y − xy 6 (với x, y ∈ Z ). 3 3 x + y − ( 2 2 ( ) x + y )
3. Cho x, y >1.Chứng minh: ( ≥ . x − ) 8 1 (y −1)
========== HẾT ==========
• Thí sinh không được sử dụng tài liệu.
• Giám thị coi thi không giải thích gì thêm.
UBND THỊ XÃ BÌNH LONG
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM MÔN TOÁN 9 NĂM HỌC 2024 – 2025 CÂU ĐÁP ÁN ĐIỂM 1  x + 3 x +1 x + 7   x  a)A =  + +  : 1−      − − − + +  x 1 3
x x 4 x 3   x 1
( x +3)( x −3)−( x + )1( x − )1+ x +7 1 =
( x − )1( x −3) : x +1 0,5
x − 9 − x +1+ x + 7 = . x +1 0,5
( x − )1( x −3) ( ) x −1 = . x +1 0,5
( x − )1( x −3) ( ) x +1 0,5 = x −3 b x = − = ( − )2 ) 7 4 3 2 3 ⇒ x = 2 − 3 0,5
Thay x = 2 − 3 vào A, ta được 2 3 1 A − + = 2 − 3 − 3 3− 3 0,5 = 1 − − 3 = 3− 2 3 0,5 1 x − 3 4 c) = =1− A x +1 x +1 0,5 Vì: 4 1
x ≥ 0 ⇒ x +1≥1⇒ ≤ 4 ⇒ ≥1− 4 = 3 − x +1 A 0,5
Dấu “ =” xảy ra ⇔ x +1=1⇔ x = 0(TM ) 0,25 Vậy 1 min = 3 − khi x = 0 A 0,25 2 2 2
a) x − 2x + 3 = 2 2x − 4x + 3(1) Ta có: 2
2x − 4x + 3 = 2(x − )2 1 +1≥1
⇒ phương trình có nghĩa với mọi x thuộc R 0,25 2 2
(1) ⇔ 2x − 4x + 6 = 4 2x − 4x + 3 0,25 2 2
⇔ 2x − 4x + 3− 4 2x − 4x + 3 + 3 = 0 Đặt 2
y = 2x − 4x + 3 (y ≥1) Ta được pt: 2
y − 4y + 3 = 0 0,25 y =1 ⇔  0,25  y = 3 0,25 2 2
* y =1⇒ 2x − 4x + 3 =1 ⇔ 2x − 4x + 3 =1 ⇔ x =1 x = 1 − 0,25 2 2
* y = 3 ⇒ 2x − 4x + 3 = 3 ⇔ 2x − 4x + 3 = 9 ⇔ x =3 Vậy S ={1; 1; − 3 }
xy + x + 2y = 14
y(x + 2) + 2 + x =16 0,5 b) ⇔ 3 2  3 2
x + 6x +12x − y = 7 − 
x + 6x +12x + 8 = y +1 (  x + 2  )( y + )1 =16 ( )1 ⇔ (x+2 0,25  )3 = y +1 (2) Thế (2) vào (1) được (x + )4 2 =16 ⇔ x + 2 = 2 ± 0,25
x = 0 ⇒ y = 7 ⇔  0,25 x = 4 − ⇒ y = 9 −
Vậy nghiệm của hệ phương trình là (0;7);(−4;−9). 0,25
2. Gọi số quyển sách và số quyển tập giáo viên đã mua lần lượt là x, y 0,25 ( *
x, y∈ N )
Vì giáo viên đã mua mua tất cả 30 cuốn sách và tập 0,25
Ta có pt: x + y = 30
Khi giảm giá 10% trên tổng số tiền giáo viên chỉ phải trả 450000 đồng, ta có pt 0,5 90
(30000x +10000y). = 450000 . 100 x + y = 30
Do đó ta được hệ pt:  90 0,25
(30000x +10000y). =  450000  100 x + y = 30 3   x + y = 50 x =10  (TM) 0,5 y = 20
Vậy giáo viên mua 10 quyển sách và 20 quyển vở 0,25 3 - Vẽ đúng hình 0,25 a) Ta có:  +  0 0 0 PAN PHN = 90 + 90 =180
Nên tứ giác APHN nội tiếp (1) 0,5 Ta có: A
∆ BC cân tại A (AB= AC) nên AD vừa là đường cao vừa là
trung trực vừa là phân giác ( 2) Xét tứ giác APMN có:  =  =  0 PAN MNA MPA = 90
⇒ Tứ giác APMN là hình chữ nhật (3) Từ (2) và (3) 0,5
⇒ tứ giác APMN là hình vuông nên nội tiếp (4)
Từ (1) và (4) ta có 5 điểm A, N,M,P,H cùng thuộc môt đường tròn. 0,25
b) Ta có: Tứ giác MPCD nội tiếp nên  = 
MPD MCD ( cùng chắn  MD ) 0,25
mà: AD vừa là đường cao vừa là trung trực vừa là phân giác của A ∆ BC
⇒ MB = MC ⇒ MB ∆ C cân tại M ⇒  =  ⇒  =  MCD MBD MPD MBD 0,5 Ta lại có: 
AMB là góc ngoài của MB ∆ D tại M 0,25  =  +  =  0 AMB MBD MDB MBD + 90  =  +  0 = + 
APH APM MPH 90 MPD Do đó:  =  APH AMB Mà:  +  0
APH AMH =180 ( tứ giác APHM nội tiếp) 0,5 Nên:  +  0 AMB AMH =180
Do đó: H, M, B thẳng hàng 0,5
c) Ta có : H, M, B thẳng hàng nên  0 AHB = 90
Gọi E là giao điểm thứ hai của HN với (O) 0,5 Ta có:  =  0 =  0 = ⇒  0
AHN APN 45 , AHB 90 NHB = 45
Do đó HN là tia phân giác của  AHB 0,5
⇒ E là điểm chính giữa của 
AB nên điểm E cố định.
Vậy khi M di động trên đoạn AD thì HN luôn đi qua điểm E cố định 0,5
là điểm chính giữa của cung AB của (O) 4
1. Thể tích của nước và đá trong bể là: 80.60.52 = 249600(cm3)
Thể tích của đá bỏ vào bể là: 249600-240000 = 9600 (cm3) 0,25
Thể tích của 6 viên đá dạng hình chóp tam giác đều là: 1 2 3
6.( .12 .15) = 4320(cm ) 3
Thể tích của số viên đá dạng hình chóp tam giác đều là: 0,25 9600 – 4320=5280(cm3)
Số viên đá dạng hình chóp tam giác đều đã bỏ vào bể là: 5280: 1 ( .110.18) =8 (viên) 0,5 3
2. Cho 1 hộp gồm các thẻ đánh số 1;2;3;4;5;6;7;8. Mỗi thẻ khác nhau
đánh các số khác nhau. Lấy ngẫu nhiên 2 thẻ trong hộp. Tính xác suất
của biến cố “Tích của 2 thẻ được lấy ra là một số chẵn”
Trong hộp có 4 thẻ ghi số lẻ, 4 thẻ ghi số chẵn
Lấy ngẫu nhiên hai thẻ ở trong hộp, sau đó tính tích hai số được đánh
ở hai tấm thẻ đó nên ta có các khả năng sau:
Trường hợp 1: Thẻ số ban đầu lấy ra ghi số lẻ, như vậy thẻ ban đầu có 4 khả năng là 1;3;5;7
Khi đó thẻ sau có thể 7 khả năng xảy ra, trong đó có 4 khả năng sẽ là
số chẵn, như vậy có 4 tích là số chẵn
Vậy trường hợp này có số biến cố xảy ra là 4.7 = 28 (biến cố)
Số biến cố mà tích là số chẵn là 4.4 = 16 (biến cố) 0,25
Trường hợp 2: Thẻ số ban đầu lấy ra ghi số chẵn, như vậy thẻ ban đầu có 4 khả năng là 2;4;6;8
Khi đó thẻ sau có thể 7 khả năng xảy ra, và tích đều là số chẵn
Vậy trường hợp này có số biến cố xảy ra là 4.7 = 28 (biến cố)
Số biến cố mà tích là số chẵn là 4.7 = 28 (biến cố) 0,25 Như vậy:
Tổng số biến cố xảy ra là 28 + 28 = 56 (biến cố)
Số biến cố mà tích là số chẵn là 16 + 28 = 44 (biến cố) 0,25
Xác suất của biến cố “ Tích của 2 thẻ được lấy ra là một số chẵn” là 44 11 = 56 14 0,25 5 a) 2 2 2 2
(x +1)(x + y ) = 4x y 4 2 2 2 2 2
⇔ x + x y + x + y − 4x y = 0 4 2 2 2 2 2 2
⇔ (x − 2x y + y ) + (x y − 2x y + x ) = 0 0,25 2 2 2 2
⇔ (x − y) + x (y −1) = 0 2
x − y = 0  2 x = 0 ⇔  2 x − y =  0   y −1 = 0 x = 0  y = 0 ⇔ x = 1±  0,5 y =1
Vậy nghiệm nguyên của phương trình là (0;0), (1;1), (-1;1) 0,25 b) Chứng minh : 3 3
x y − xy 6 (với x, y ∈ Z ) 3 3 3 3
x y − xy = x y − xy + xy − xy 0,25 2 2
= xy(x −1) − xy(y −1) = (x −1). .
x (x +1)y − (y −1)y(y +1)x 0,25
Vì: x −1, x, x +1 là 3 số nguyên liên tiếp nên có một số chia hết cho 2, một số chia hết cho 3
⇒ (x −1)x( x +1)6 ⇒ (x −1)x( x +1)y6 0,25
Tương tự: (y −1)y( y +1)x6
Do đó : (x −1) .x(x +1)y −(y −1)y(y +1)x6 Vậy: 3 3 x y − xy 6 0,25 3 3 x + y − ( 2 2 ( ) x + y )
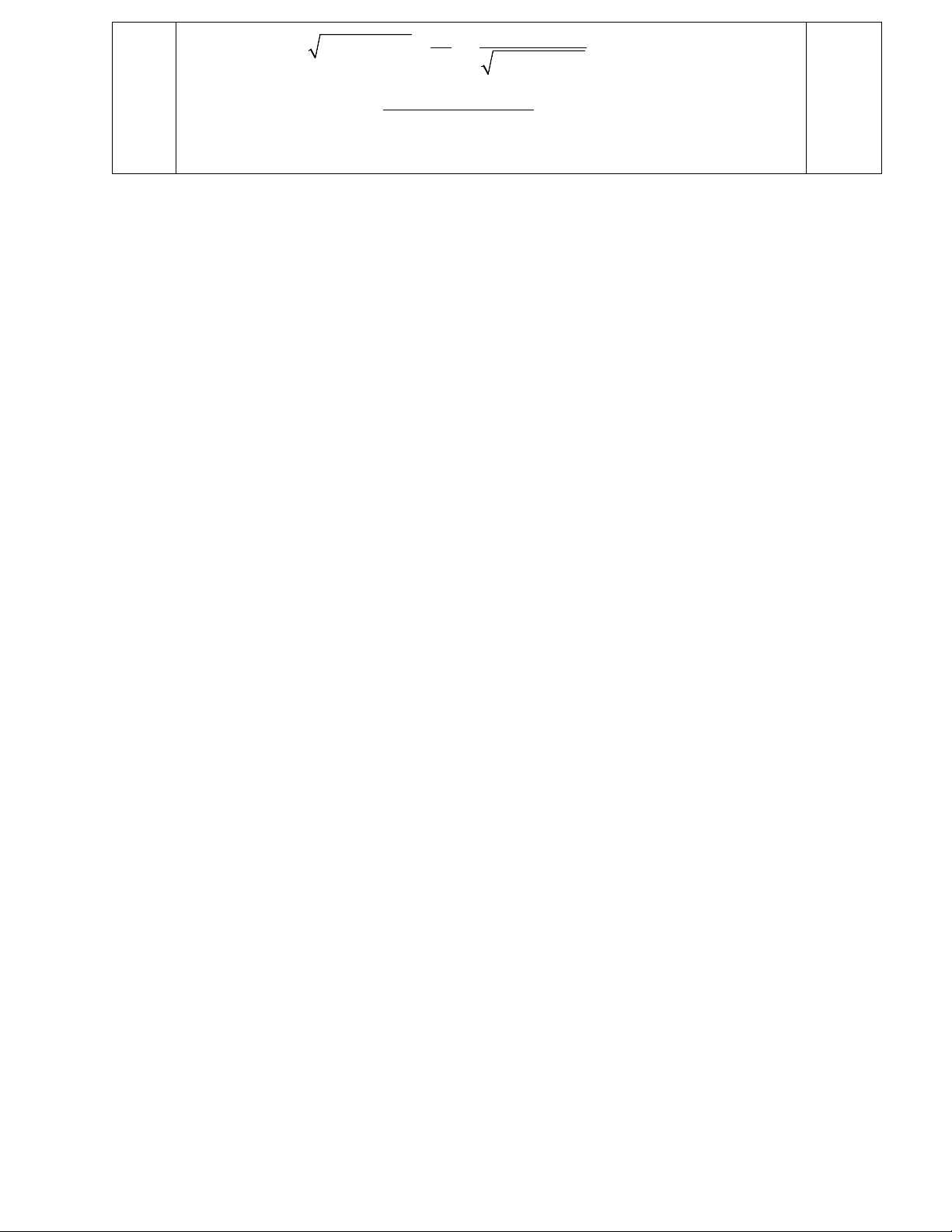
c) Cho x, y >1.Chứng minh ( ≥ x − ) 8 1 (y −1) Ta có: 3 3 (x + y ) − ( 2 2 x + y ) 3 2 3 2
(x − x ) + (y − y ) ( = x − ) 1 (y −1)
(x − )1(y −1) 2 2 2 2
x (x −1) + y (y −1) x y 0,25 = ( = + x − ) 1 (y −1) y −1 x −1 2 2 x y 2 ≥ 2 . xy = (1) 0,25 y −1 x −1 (y −1)(x −1)
Mà: x, y >1⇒ x −1> 0, y −1> 0 . Theo bất đẳng thức Côsi ta có: 1+ x −1 −1 = ( −1).1 x x x ≤ = 2 2 1+ y −1 −1 = ( −1).1 y y y ≤ = 2 2 0,25 Do đó: xy 2 ( −1)( −1) xy x y ≤ ⇔ ≥ 8 (2) 4 (x −1)(y −1) 3 3 x + y − ( 2 2 ( ) x + y ) Từ (1) và (2) ⇒ ( ≥ x − ) 8 1 (y −1) 0,25
Xem thêm: ĐỀ THI HSG TOÁN 9
https://thcs.toanmath.com/de-thi-hsg-toan-9
Document Outline

• ĐỀ TOÁN 9 CHÍNH THỨC THỊ XÃ 24-25
• New Microsoft Word Document