Đề chọn học sinh giỏi Toán 9 năm 2024 – 2025 phòng GD&ĐT Đồng Xoài – Bình Phước

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THÀNH PHỐ THÀNH PHỐ ĐỒNG XOÀI
LỚP 9 NĂM HỌC 2024-2025 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 26/11/2024
(Đề thi có 02 trang) Câu 1: (5,0 điểm) 3 x 2 x 9x x 1 3 x 1 1. Cho biểu thức P : , x 0,x 1 . x 1 3x 2 x 3x x 2 7x 7 x
a) Rút gọn biểu thức P .
b) Tìm x sao cho P nhận giá trị là một số nguyên. 2. Cho các số thực ,
x y, z thỏa mãn x + y + z = 3 và 2 2 2
x + y + z = xy + yz + zx . Tính giá trị của biểu thức 2024 2024 2024 B = x + y + z + xyz . Câu 2: (5,0 điểm)
1. Giải phương trình: ( x + ) 2 2 4
10 − x = x + 2x − 8 2 x − 3y = 2  ( )1
2. Giải hệ phương trình:  2 9  y −8x = 8  (2)
3. Cho hàm số y = mx − 2m −1(m  0). Gọi ,
A B lần lượt là giao điểm của đồ thị hàm số với trục O ,
x Oy . Xác định m để diện tích tam giác AOB bằng 4 (đvdt).
Câu 3: (5,0 điểm) Cho tam giác ABC nhọn nội tiếp (O) . Gọi điểm I là tâm đường tròn nội tiếp
tam giác ABC , tia AI cắt đường tròn (O) tại M (điểm M khác điểm A ).
a) Chứng minh: Các tam giác IMB và IMC là các tam giác cân.
b) Đường thẳng MO cắt đường tròn tại điểm N (N khác điểm M ) và cắt cạnh BC tại điểm BAC IP
P . Chứng minh rằng: sin = . 2 IN
c) Gọi các điểm D, E lần lượt là hình chiếu của điểm I trên các cạnh AB, AC . Gọi các điểm
H , K lần lượt đối xứng với các điểm D, E qua điểm I . Biết rằng AB + AC = 3BC , chứng
minh các điểm B,C, H , K cùng thuộc một đường tròn. Câu 4: (2,0 điểm)
1) Đội văn nghệ của lớp 9A có 3 bạn nam và 3 bạn nữ. Cô giáo phụ trách đội chọn ngẫu nhiên
hai bạn để hát song ca. Tính xác suất của biến cố T: “Trong hai bạn được chọn ra, có một bạn nam và một bạn nữ”.
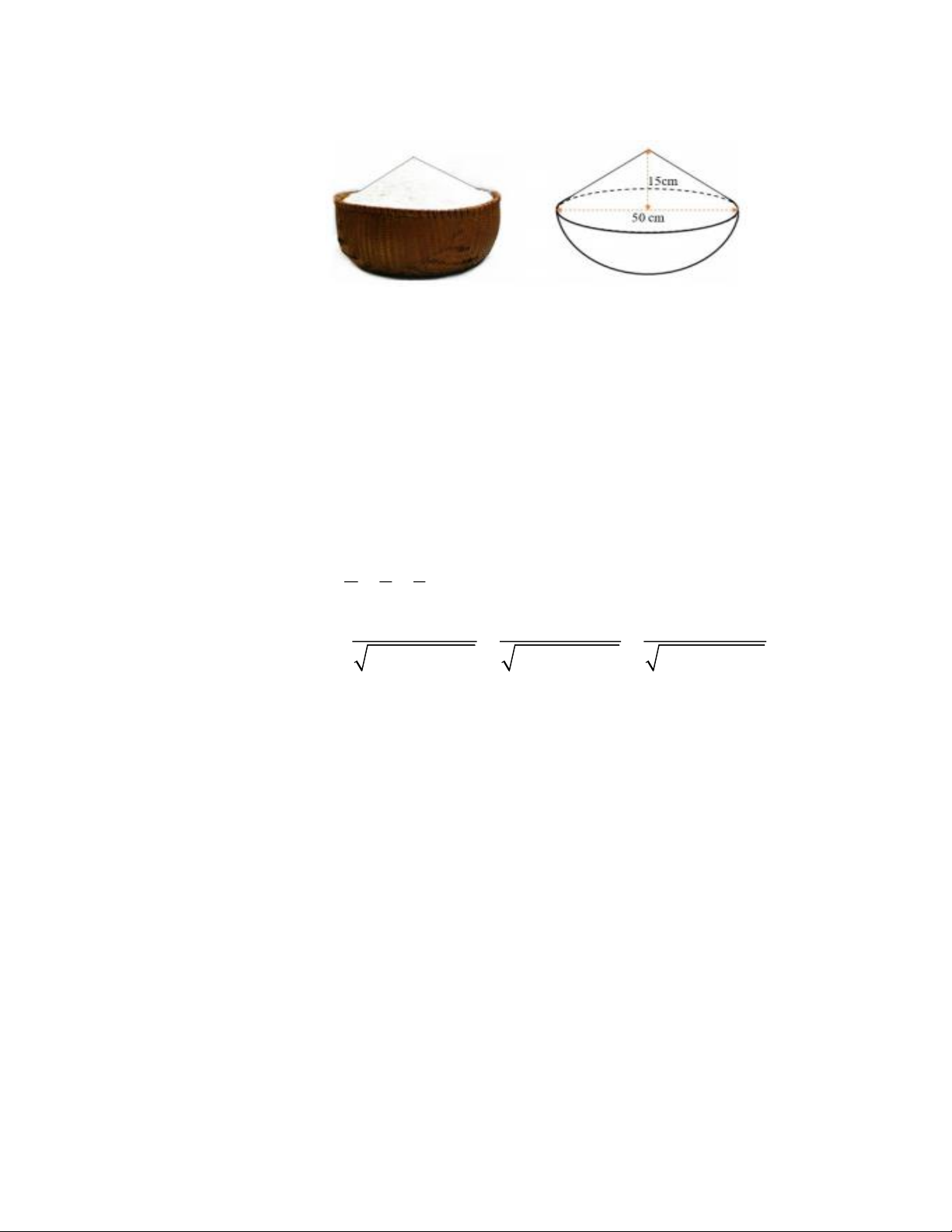
2) Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính 50 , cm
phần gạo vun lên có dạng hình nón cao 15cm .
a) Tính thể tích phần gạo trong thúng.
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm , chiều cao 15cm ) để
đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm
90% thể tích lon. Hỏi với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu
ngày? (làm tròn đến dạng 0,1). Câu 5: (3,0 điểm) 1) Tìm các số nguyên ( ;
x y ) thỏa mãn: ( y + ) 2 2
2 x − y − 2 y −1 = 0 1 1 1 2) Cho a, , b c  0 thỏa mãn + + = 3. a b c 1 1 1
Tìm giá trị lớn nhất của: P = + +  2 2 2 2 2 2
a − ab + b
b − bc + c
c − ca + a
…..……….HẾT……………
• Thí sinh không được sử dụng tài liệu, máy tính • Giám thị không giải thích gì thêm.
PHÒNG GD & ĐT THÀNH PHỐ HƯỚNG DẪN CHẤM ĐỒNG XOÀI
KỲ THI CHỌN HỌC SINH GIỎI CẤP THÀNH PHỐ
LỚP 9 NĂM HỌC 2024-2025 MÔN: TOÁN
Hướng dẫn chấm gồm 06 trang
Lưu ý: Điểm toàn bài lấy điểm lẻ đến 0,125; thí sinh làm cách khác đúng vẫn cho điểm tối đa. Câu Nội dung Điểm 3 x 2 x 9x x 1 3 x 1 1. Cho biểu thức P : , x 1 3x 2 x 3x x 2 7x 7 x 5,0 Câu x 0,x 1 . 1
a) Rút gọn biểu thức P . b) Tìm x sao cho P nhận giá trị là một số nguyên. 2. Cho các số thực ,
x y, z thỏa mãn x + y + z = 3 và 2 2 2
x + y + z = xy + yz + zx .
Tính giá trị của biểu thức 2024 2024 2024 B = x + y + z + xyz . 3 x 2 9x x 1 3 x 1 P : x 1 3 x 2 x 1 3 x 2 7x 7 x 1a 3 x 3 x 2 2 x 1 9x x 1 7 x x 1 . 0,5 x 1 3 x 2 3 x 1 3 x 1 7 x 7 x . 1,0 3 x 2 3 x 1 3 x 2 7 x x 0,x 1 x 0 0,25 P 0 3 x 2 7 x 7 14 7 P 3 x 2 3 3 3 3 x 2 0,25 1b
P nhận giá trị là một số nguyên P 1;2 0,25 1 1 0,25 P 1 x x (tmđk) 2 4 0,25 P 2 x 4 x 16 (tmđk) 1 Vậy x
;16 thì P nhận giá trị là một số nguyên. 0,25 4
Ta có: x + y + z = xy + yz + zx  (x − y)2 + ( y − z)2 + (z − x)2 2 2 2
= 0  x = y = z 1,0 1.2 Mà 0,5
x + y + z = 3 nên x = y = z = 1 do đó 2024 2024 2024 0,5 B = 1 +1 +1 +1 = 4
1. Giải phương trình: ( x + ) 2 2 4
10 − x = x + 2x − 8 2 x − 3y = 2  ( )1 5,0
Câu 2 2. Giải hệ phương trình  2 9  y −8x = 8  (2)
3. Cho hàm số y = mx − 2m −1(m  0). Gọi ,
A B lần lượt là giao điểm của đồ thị
hàm số với trục O ,
x Oy . Xác định m để diện tích tam giác AOB bằng 4 (đvdt).
Điều kiện: − 10  x  10 0,25 Ta có: ( x + 4) 2 2
10 − x = x + 2x − 8  ( x + 4) 2
10 − x = ( x + 4)( x − 2)  ( 0,25 x + 4)( 2
10 − x − x + 2) = 0 2.1 x = 4 − (ktm) x + 4 = 0  x  2 x = 3     x − 2  0      0,75 2 2
 10 − x = x − 2 
2x − 4x − 6 = 0 x = 1 −  (L) 10  − x =  (x − 2)2 2
Vậy phương trình có nghiệm x = 3 0,25 2 2
x −3y = 2
4x −12y = 8
Ta có hệ phương trình    2 2 2 9
 y −8x = 8
4x −12y −9y +8x = 0 2 x − 3y = 2  ( )1   2 2
4x − 9y + 8x −12y = 0  (2) 0,25 Giải phương trình (2):
(2)  (2x −3y)(2x +3y)+ 4(2x −3y) = 0  (2x −3y)(2x +3y + 4) = 0 0,25 2.2
+) TH1: 2x − 3y = 0  3y = 2x  2(1+ 3)  y =  0,5  ( ) x = 1+ 3  2 3
1 : x − 2x − 2 = 0     x =1− 3 2  (1− 3) y =  3
+) TH2: x + y + =  y = − − x  ( ) 2 2 3 4 0 3 4 2
1  x + 2x + 2 = 0 ( ptvn) 0,25  +   −  2  (1 3) 2(1 3 )  Vậy HPT có hai nghiệm ( ; x y)   1 3; , 1 3;   + −   0,25 3   3        
Theo bài ra ta có tọa độ của hai điểm , A B lần lượt là  2m +1  A ; 0 ; B (0; 2 − m −   )1 0,5  m 
Diện tích tam giác OAB : 2.3 1 1 2m +1 ( m + )2 2 1 S = O . A OB = . 2 − m −1 = 4  = 8 OAB 2 2 m m 1,0 1 6 − + 4 2 6 − − 4 2   m   ; ; . 2 4 4   0,5
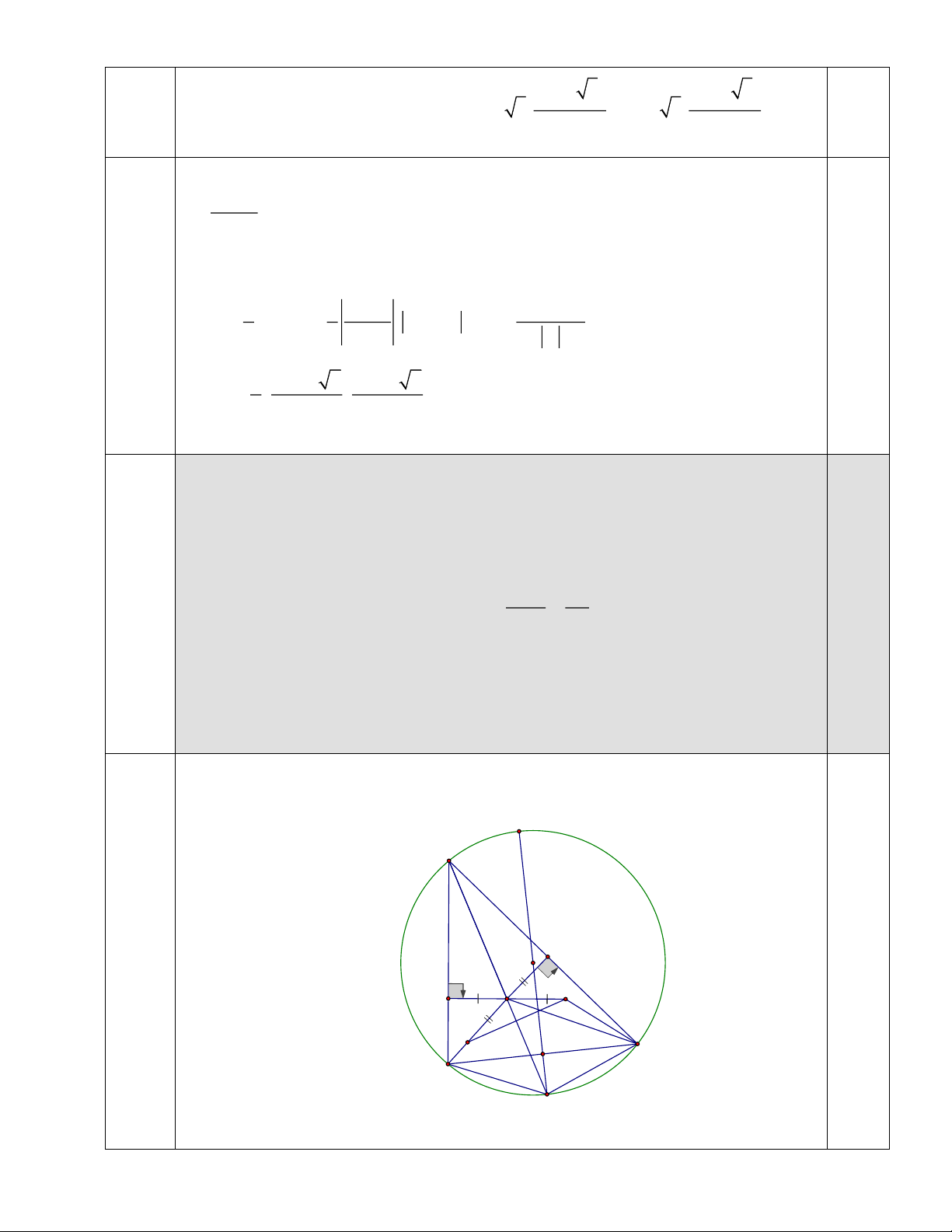
Cho tam giác ABC nhọn nội tiếp (O) . Gọi điểm I là tâm đường tròn nội tiếp
tam giác ABC , tia AI cắt đường tròn (O) tại M (điểm M khác điểm A ).
a) Chứng minh các tam giác IMB và IMC là các tam giác cân.
b) Đường thẳng MO cắt đường tròn tại điểm N (N khác điểm M ) và cắt cạnh 5,0 Câu 3 BC BAC IP
tại điểm P . Chứng minh rằng: sin = . 2 IN
c) Gọi các điểm D, E lần lượt là hình chiếu của điểm I trên các cạnh AB, AC
. Gọi các điểm H , K lần lượt đối xứng với các điểm D, E qua điểm I . Biết
rằng AB + AC = 3BC , chứng minh các điểm B,C, H , K cùng thuộc một đường tròn.
Hình vẽ đúng đạt 0,5đ N A 0,5 E O D I H K C P B M Ta có ABC  BAC   =  +  = + 3a IBM IBC CBM ; 2 2 0,25 ABC  BAC  BI  M = I
 AB + IBA = + . 0,25 2 2 Suy ra I  BM = B  IM  I
 BM cân tại M . 0,25
Tương tự, tam giác MIC cân tại M. 0,75  Ta có BAC MP MP sin = sin B  CM = =
(1) (do MP ⊥ BC và 0,5 2 MC MI MI = MC) 3b
MBN vuông tại B, có MP MI 2 2
MP  MN = MB = MI  =
(2)  MPI ~ MIN ( c.g.c ) MI MN 0,5 MI IP  = (3) 0,5 MN IN
Ta có AB + AC = 3BC AB + AC − 
BC = BC  AE = BC 2 MP CP 1 I  AE ~ M
 CP(g.g)  = =  IE = 2MP 0,25 IE AE 2
Gọi F là trung điểm của IK , M  CP = M  IF( . c g.c) do MC = MI ; P  MC = E  IA = M  IF ; 3c 1 MP = IF = IE  I  FM = M  PC = 90 2 0,5 Suy ra I
 MK cân tại M nên MK = MI .
Tương tự MH = MI . 0,5
Suy ra MB = MC = MH = MK = MI .
Vậy B,C, H , K cùng thuộc một đường tròn. 0,25
1) Đội văn nghệ của lớp 9A có 3 bạn nam và 3 bạn nữ. Cô giáo phụ trách đội
chọn ngẫu nhiên hai bạn để hát song ca. Tính xác suất của biến cố T: “Trong
hai bạn được chọn ra, có một bạn nam và một bạn nữ”.
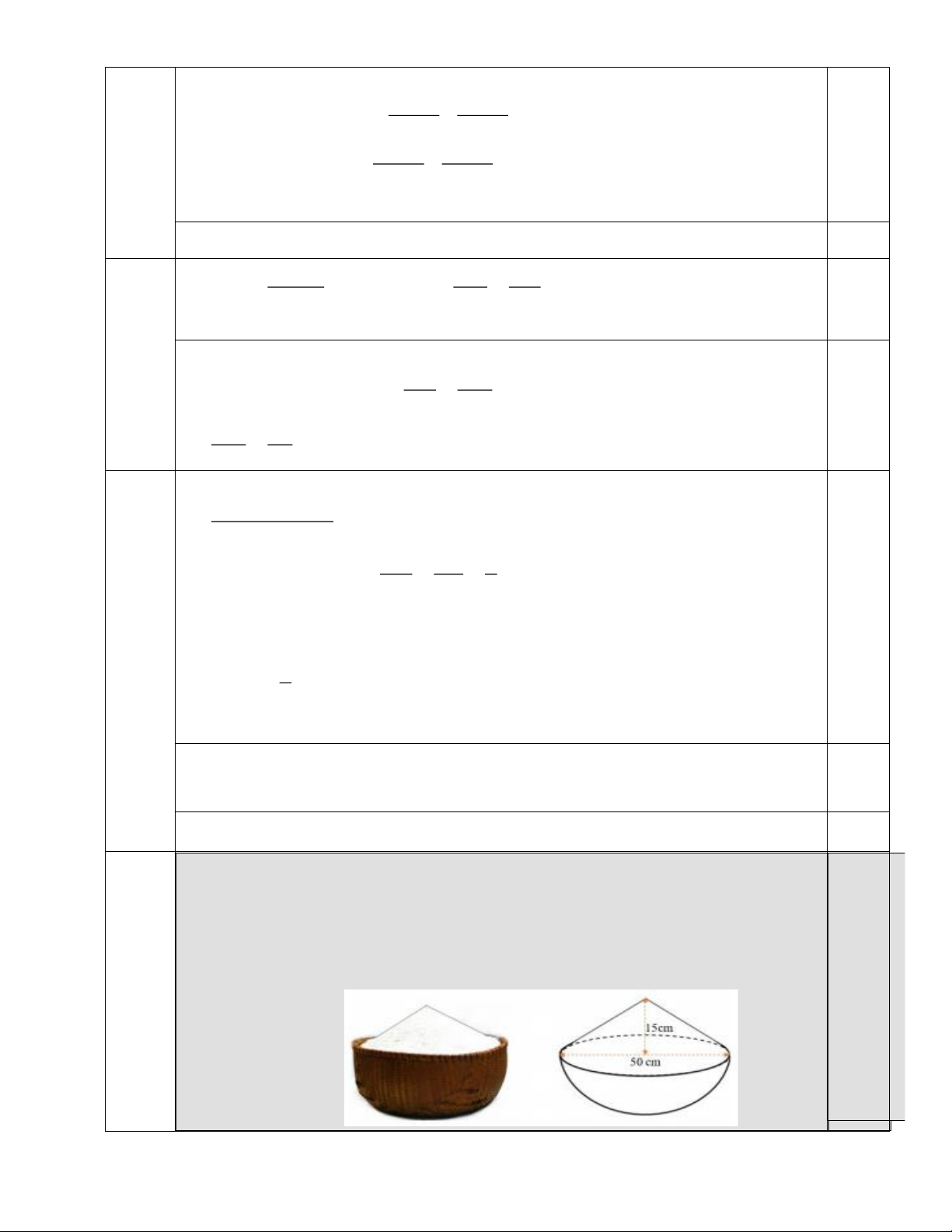
2) Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với
Câu 4 đường kính 50 ,
cm phần gạo vun lên có dạng hình nón cao 15cm . 1,0 1,0 2,0
a) Tính thể tích phần gạo trong thúng.
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm ,
chiều cao 15cm ) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo
và mỗi lần đong thì lượng gạo chiếm 90% thể tích lon. Hỏi với lượng gạo ở
thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày? (làm tròn đến dạng 0,1).
Gọi 3 bạn nam lần lượt là1,2,3 .
3 bạn nữ lần lượt là A, B, C.
Kết quả có thể của phép thử là cặp (a,b) sao cho a  b . Vì lấy đồng thời
hai bạn nên loại trừ các trường hợp trùng nhau. Ta có  = (
{ 1, 2);(1,3);(1, A); (1, B); (1,C );(2,3); (2, A); (2, B);(2, C ); 0,25
(3, A) ;(3, B); (3, C );( , A B);( ,
A C ); ( B,C )} 4.1
Tập  gồm 15 phần tử. 0,25
Vì chọn ngẫu nhiên nên các kết quả có thể là đồng khả năng.
Có 9 kết quả thuận lợi cho biến cố T: “Trong hai bạn được chọn ra, có một
bạn nam và một bạn nữ” là (
{ 1, A); (1, B); (1,C );(2, A); (2, B);(2, C );(3, A) ;(3, B); (3, C )} 0,25
nên xác suất của biến cố T là: 9 3 P(T ) = = . 15 5 0,25
Bán kính hình cầu là: 50:2 = 25(cm)
Thể tích gạo trong thúng là: 4.2a 1 1 1 4 0,25 2 3 V = V + V
=  R h + .  R gao non h.cau 2 3 2 3 1 1 4 40625 2 3 =  25 .15 + . .25 =   42542,4( 3 cm ) 0,25 3 2 3 3
Thể tích gạo 1 lần đong là: 675 2 2
90% R h = 0, 9. .5 .15 =  ( 3 cm ) 2
Thể tích gạo 1 ngày nhà Danh ăn là 675 3375 0,25 : 5.  =  ( 3 cm ) 4.2b 2 2
Với lượng gạo trong thúng số ngày nhiều nhất nhà Danh có thể ăn được là: 40625  3375   :   8   ngày 0,25 3  2  1) Tìm các số nguyên ( ;
x y ) thỏa mãn ( y + ) 2 2
2 x − y − 2 y −1 = 0 1 1 1 2) Cho a, , b c  0 thỏa mãn + + = 3 . 1,25 1,25 Câu 5 a b c 3,0 Tìm giá trị 1 1 1
lớn nhất của: P = + +  2 2 2 2 2 2
a − ab + b
b − bc + c
c − ca + a Ta có: ( y + ) 2 2
x − y − y − =  ( y + ) 2 x − ( 2
y + y ) − =  ( y + )( 2 2 2 1 0 2 2 1 0 2 x − y ) = 1 0,5 y + 2 =1 y = 1 −   5.1 2 2
x − y = 1 x = 0 y = 1 −       0,75 2 y + 2 = 1 − y = 3 − x = 0     (loai) 2 2
x − y = −1 x = −4
Vậy nghiệm của phương trình là: ( ; x y) = (0; − ) 1 0,25 Ta có: 2 2 (a + b) 3(a − b) a + b 2 2
a − ab + b = +  0,25 4 4 2 1 2 1  1 1     +   2 2 − + a + b 2  a b a ab b  0,25 5.2
Chứng minh tương tự ta được: 1 1  1 1  1 1  1 1   + ;  +     . 2 2 2 2 − + 2  b c  − + 2  a c b bc c c ac a  0,5 1   1 1 1   P  2 + + = 3    0,25 2   a b c 
Đẳng thức xảy ra khi a = b = c . 0,25