Đề chọn học sinh giỏi Toán 9 năm 2024 – 2025 phòng GD&ĐT Từ Sơn – Bắc Ninh

UBND THÀNH PHỐ TỪ SƠN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẤP THÀNH PHỐ NĂM HỌC 2024-2025 Môn: Toán ĐỀ CHÍ NH THỨC
Thời gian làm bài: 150 phút (Không kể thời gian giao đề)
(Đề gồm có 01 trang) Ngày thi 03/01/2025
Câu 1: (4 điểm)
 3x + 16x − 7 x +1 x + 7   x 
1) Cho biểu thức A =  − −  : 2 −    
 với x 1, x  4, x  0 x + 2 x − 3 x + 3 x −1 x −1     x 2 27 + 7 5
a) Rút gọn A . b) Tính giá trị của A khi x thoả mãn = 16 10 + 7 2
2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d ) 1 : y =
x − 3 cắt hai trục tọa độ Ox , Oy lần 2 lượt tại ,
A B . Tìm tọa độ các điểm A , B và viết phương trình đường thẳng () đi qua M (2; −2)
thỏa mãn cắt đoạn thẳng OA tại C sao cho diện tích tam giác AMC bằng 5 . Câu 2: (4 điểm) 1) Giải phương trình: 2
3x +13 = 6 2x +1 + 4x 2
x (x −3y) = 1 − 6
2) Giải hệ phương trình  3 2
y +16 = 3xy Câu 3: (4 điểm)
1) Một chiếc hộp đựng 51 tấm thẻ như nhau được ghi các số tự nhiên từ 10 đến 60. Rút ngẫu
nhiên một tấm thẻ trong hộp. Tính xác suất để rút được tấm thẻ mà tổng các chữ số ghi trên
tấm thẻ là một số chẵn.
2) Tìm các số nguyên x, y thỏa mãn: 2 2 2 2
x + y + 5x y + 60 = 37xy Câu 4: (6.0 điểm).
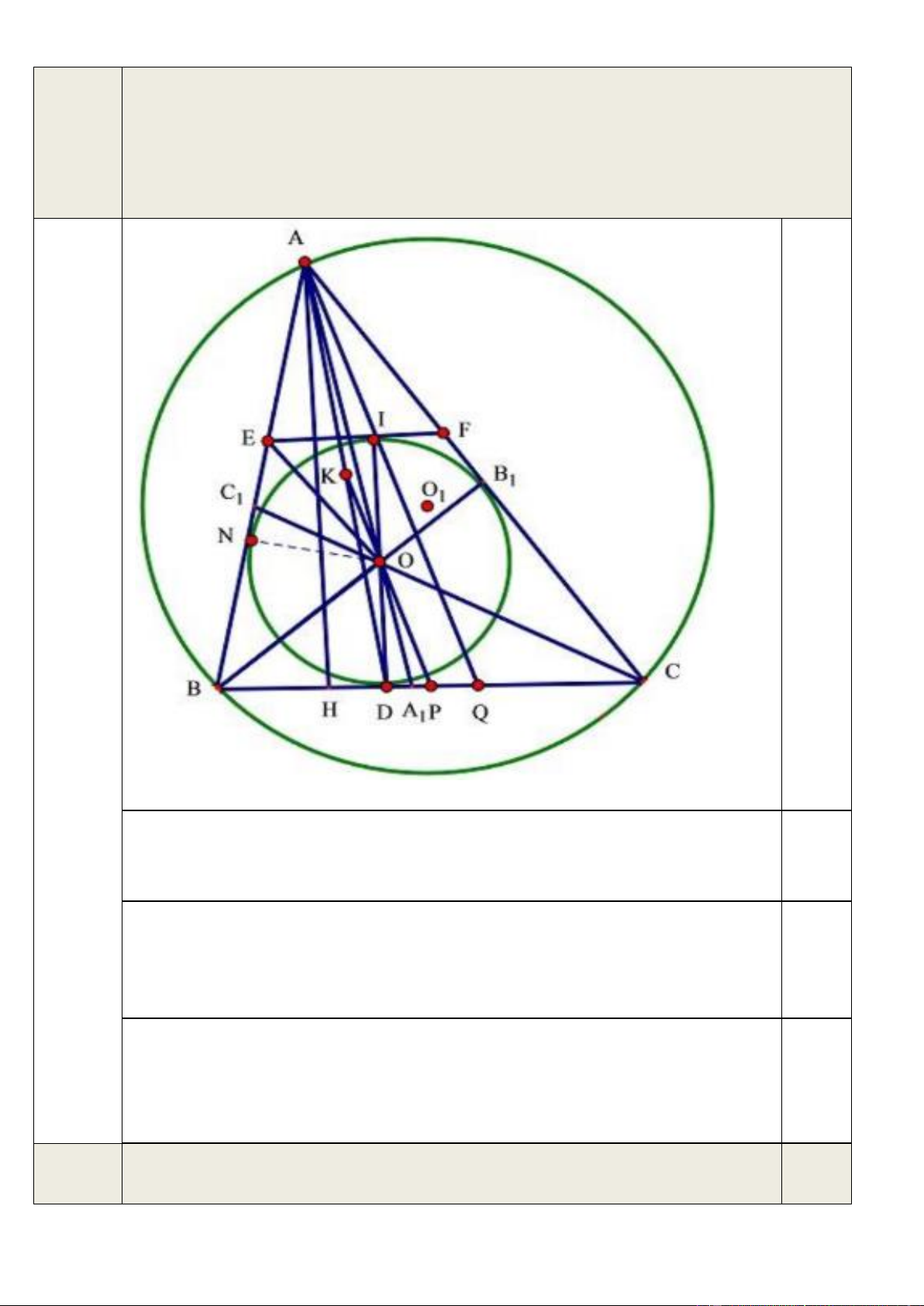
Cho tam giác ABC với AB  AC . Đường tròn (O; R) tiếp xúc với các cạnh của tam giác ABC .
Gọi D, N lần lượt là các tiếp điểm của (O; R) với BC và AB , kẻ đường kính DI của đường tròn
(O;R). Tiếp tuyến đường tròn (O;R) tại I cắt các cạnh AB, AC lần lượt tại E và F.
1) Chứng minh  BOE vuông và 2
EI.BD = FI.CD = R . 2) Gọi ,
P K lần lượt là trung điểm các đoạn thẳng BC, AD. Q là giao điểm của BC và AI. Chứng minh AQ = 2K . P
3) Gọi A là giao điểm của AO với cạnh BC, B là giao điểm của BO với cạnh AC, C là giao 1 1 1
điểm của CO với cạnh AB và (O ; R là đường tròn ngoại tiếp  ABC. Chứng minh 1 1 ) 1 1 1 2 + +  . AA BB CC R − OO 1 1 1 1 1 Câu 5: (2.0 điểm). 1 1 1) Cho ,
a b  0 thỏa mãn a + b = 1. Chứng minh rằng: +  6 . 2 2 ab a + b
2) Trong tuần, mỗi ngày bạn Nam chơi một môn thể thao. Nam chạy 3 ngày một tuần nhưng
không bao giờ Nam chạy 2 ngày liên tiếp. Vào ngày thứ hai, Nam chơi bóng bàn và 2 ngày sau đó
Nam chơi bóng đá. Nam còn đi bơi và chơi cầu lông nhưng không bao giờ Nam chơi cầu lông sau
ngày Nam chạy hoặc bơi. Hỏi Nam chơi cầu lông vào thứ mấy trong tuần?
---------- HẾT ----------
Họ và tên thí sinh:………………………………….. Số báo danh:………………………………… UBND THÀNH PHỐ TỪ SƠN HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
CẤP THÀNH PHỐ NĂM HỌC 2024 - 2025 Môn: Toán Ngày thi 03/01/2025 Câu Đáp án Điểm
 3x + 16x − 7 x +1 x + 7   x 
Cho biểu thức A =  − −  : 2 −      x + 2 x − 3 x + 3 x −1 x −1        Câu 1.1 với x 1, x 4, x 0 2,5 điểm a) Rút gọn A . x 2 27 + 7 5
b) Tính giá trị của biểu thức A khi x thoả mãn = 16 10 + 7 2
 3x + 16x − 7 x +1 x + 7   x  A =  − −  : 2 −    
 với x 1, x  4, x  0 x + 2 x − 3 x + 3 x −1 x −1    
 3x + 16x − 7 ( x +1)( x −1)
( x + 7)( x + 3)   2( x −1) − x  =  − −  :      1,0
( x + 3)( x −1)
( x + 3)( x −1)
( x + 3)( x −1) x −1     x − 6 x − 27 x − 2 = :
( x −1)( x + 3) x −1
( x + 3)( x − 9) x −1 = .
( x −1)( x + 3) x − 2 x − 9 = 0,5 x − 2 x − 9 Vậy A =
Khi x  1, x  4, x  0 x − 2 2 x 2 27 + 7 5 2 54 +14 5 2. ( 5 + 7) b. Có = = = =1 16 10 + 7 2 2( 5 + 7) 2( 5 + 7) 0,5 Suy ra x =16 (t/m đk) −
Thay x =16 vào biểu thức A ta được kết quả 5 A = 2 0,5 Kết luận
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d ) 1 : y =
x − 3 cắt hai trục tọa độ Ox , 2
Câu 1.2 Oy lần lượt tại ,
A B . Tìm tọa độ các điểm A , B và viết phương trình đường thẳng ()
1,5 điểm đi qua M (2;−2) thỏa mãn cắt đoạn thẳng OA tại C sao cho diện tích tam giác AMC bằng 5 . Tìm tọa độ của , A B .
Xét x = 0  y = 3 −  B (0; 3 − ) 0,5
Xét y = 0  x = 6  A(6;0)
Gọi H là chân đường cao kẻ từ M trong A
 MC , suy ra MH = 2. 1 Ta có S
= MH.AC = 5, suy ra AC = 5. A  MC 2 0,5
Vì C thuộc đoạn OA nên C (1;0) .
Giả sử () : y = ax + b , khi đó ( )
 đi qua M(2; -2) và C(1; 0) nên ta có a + b = 0 a = 2 −    2a + b = 2 − b  = 2 0,5 Suy ra () : y = 2 − x + 2 .
Câu 2.1 Giải phương trình: 2
3x +13 = 6 2x +1 + 4x 2,0 điểm − 2
3x +13 = 6 2x +1 + 4x ( ĐK: 1 x  ) 2 0,5 2
3x − 4x +13 − 6 2x +1 = 0 2
3(x − 2x +1) + (2x +1) − 2.3 2x +1 + 9 = 0   2 2
3(x −1) + ( 2x +1 − 3) = 0 0,5 Chỉ ra được  x −1 = 0    2x +1 −3 = 0 0,5  x = 1    2x +1 = 3  x = 1  (vô lí) x = 4 0,5
Vậy phương trình vô nghiệm 2
x (x −3y) = 1 − 6
Câu 2.2 Giải hệ phương trình  2,0 điểm 3 2
y +16 = 3xy 2
x (x −3y) = 1 − 6 (1)  3 2
y +16 = 3xy (2) Từ pt (2) suy ra 2 3
16 = 3xy − y thay vào phương trình (1) ta có 1 2
x ( x − y) = − ( 2 3 xy − y ) 3 2 2 3 3 3
 x − 3x y + 3xy − y = 0
 (x − y)3 = 0  x = y .
Với x = y thay vào phương trình (2) ta có: 3 3 y +16 = 3y 3 2 y = 16 1 y = 2 .
Với y = 2  x = 2 Vậy hệ có nghiệm ( ; x y) = (2; 2)
Một chiếc hộp đựng 51 tấm thẻ như nhau được ghi các số tự nhiên từ 10 đến 60. Rút
Câu 3.1 ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất để rút được tấm thẻ mà tổng các chữ
2,0 điểm số ghi trên tấm thẻ là một số chẵn.
Gọi biến cố B : “số được ghi trên thẻ là số có tổng các chữ số là một số chẵn”.
Giả sử rút được thẻ ghi số ab với , a b 
và 1 a  5,0  b  9 và số 60 .
Ta có a + b là số chẵn có ba khả năng xảy ra: + TH1: đó là số 60. 1 + TH2: ,
a b cùng là số chẵn. Với mỗi chữ số chẵn a 2 ;  4 , tương ứng với
b 0 ; 2 ; 4 ; 6 ; 
8 nên trường hợp này có 2 . 5 = 10 (số). + TH3: ,
a b cùng lẻ thì với mỗi chữ số lẻ a 1; 3 ;  5 , tương ứng với
b 1; 3 ; 5 ; 7 ; 
9 nên trường hợp này có 3 . 5 = 15 (số).
Số các khả năng xảy ra biến cố là: 1 1+10 +15 = 26 . Do đó xác suấ 26
t của biến cố B là . 51
Tìm các số nguyên x, y thỏa mãn: 2 2 2 2
x + y + 5x y + 60 = 37xy Câu 3.2 2,0 điểm Ta có 2 2 2 2
x + y + 5x y + 60 = 37xy (x − y)2 2 2 = 5
− x y + 35xy − 60 0,5
(x − y)2 = 5(xy −3)(4 − xy)
Vì ( x − y)2  0 => 5( xy − 3)(4 − xy)  0 = 3  xy  4 . xy = 3 0,5 Do x, y nguyên nên .
x y Z =  xy  = 4 xy = 3  x = y Với: (   ( vô nghiệm) 0,5  x − y  )2 2 = 0 x = 3 xy = 4  x = y  x = y = 2 Với (      x − y  )2 2 = 0 x = 4 x = y = 2 − 0,5 Kết luận Câu 4 6,0 điểm
Câu 4.1 Cho tam giác ABC có AB  AC . Đường tròn (O; R) tiếp xúc với các cạnh của tam giác
3 điểm ABC . Gọi D, N lần lượt là các tiếp điểm của (O; R) với BC và AB , kẻ đường kính DI
của đường tròn (O; R). Tiếp tuyến đường tròn (O; R) tại I cắt các cạnh AB, AC lần lượt tại E và F.
1) Chứng minh  BOE vuông và 2
EI.BD = FI.CD = R . 0,5 Vẽ hình đủ làm câu a)
Áp dụng tính chất hai tiếp tuyến cắt nhau chỉ ra OE và OB lần lượt là phân
giác của các góc ION và NOD . 1  ⊥  
Mà ION và NOD là hai góc kề bù OE OB BOE vuông tại . O
Áp dụng hệ thức lượng trong tam giác vuông BOE, đường cao ON ta có 2 2
EN.BN = ON = R . 1
Mà EN = EI, BN = BD (tính chất hai tiếp tuyến cắt nhau) 2
EN = EI , BN = BD  EI.BD = R
Chứng minh tương tự ta có F
 OC vuông tại O và 2
FI.CD = R . 0,5 Vậy: 2
EI.BD = FI.CD = R . Câu 4.2 Gọi ,
P K lần lượt là trung điểm các đoạn thẳng BC, AD. Q là giao điểm của
1,5 điểm BC và AI. Chứng minh AQ = 2K . P IF AF FE
Ta có: EF //BC (⊥ ID) nên theo định lý Ta – lét có: = = ( )1 QC AC BC 0,75 FI EI FI + EI EF
Lại có: EI.BD = FI.CD (cmt )  = = = . (2) BD CD BD + CD BC FI FI Từ ( ) 1 và (2) suy ra: =  QC = B . D 0,25 QC BD
Mà: CP = CQ + Q ,
P BP = DB + D ,
P CP = PB  QP = P . D 0,25
Hay P là trung điểm của đoạn . QD Xét A
 DQ có P là trung điểm của QD (cmt) và K là trung điểm của AD (gt).
 PK là đường trung bình của A  Q . D 0,25 1
 PK = AQ hay AQ = 2PK (đpcm) 2
Gọi A là giao điểm của AO với cạnh BC, B là giao điểm của BO với cạnh 1 1 Câu 4.3
AC, C là giao điểm của CO với cạnh AB và (O ; R là đường tròn ngoại tiếp  1 1 ) 1 1,5 điểm 1 1 1 2 ABC. Chứng minh + +  . AA BB CC R − OO 1 1 1 1 1 A O OD S
+ Kẻ AH ⊥ BC tại H thì AH//OD, dẫn đến: 1 OBC  = = A A AH S 1 ABC  0,5 B O S C O S
+ Chứng minh tương tự, ta được: 1 OAC  = ; 1 O  AB = B B S C C S 1 ABC  1 ABC 
+ Do O là điểm thuộc miền trong ABC  nên ta có: A O B O C O S + S + S 1 1 1 O  BC O  AC O  AB + + = = 1 A A B B C C S 1 1 1 ABC  0,25  AO BO CO 1− +1− +1− = 1 A A B B C C 1 1 1 − − −  AO BO CO + + = AO O O BO O O CO O O 2  1 1 1 1 1 1 2 ≥ + + A A B B C C A A B B C C 1 1 1 1 1 1  1 1 1 2 + + ≤ 0,5
(*), (vì AO = BO = CO = R ; R  O O ) AA BB CC R − O O 1 1 1 1 1 1 1 1 1 1 1
+ Do AB < AC suy ra ABC 
không phải là tam giác đều nên dấu “=” trong (*) không thể xảy ra. 0,25 1 1 1 2 Vậy: + +  AA BB CC R − O O 1 1 1 1 1 1 1 Câu 5.1 Cho ,
a b  0 thỏa mãn a + b = 1. Chứng minh rằng: +  6 . 2 2 ab a + b 1,0 điểm 1 1 4
Học sinh chứng minh được với , x y  0 ta có +  (*) . x y x + y
Dấu “=” xảy ra khi x = y 0,5 1 1 4
Áp dụng bất đẳng thức (*) ta có +  = 4(1) 2 2 2ab a + b (a +b)2 Lại có 1
a + b  2 ab  1  4ab   2(2) 2ab 1 1 1 Từ (1) và (2)  + +  2 + 4 2 2 2ab 2ab a + b 0,5 1 1  +  6 2 2 ab a + b 1
Dấu “=” xảy ra khi a = b = 2
Trong tuần, mỗi ngày bạn Nam chơi một môn thể thao. Nam chạy 3 ngày một tuần
nhưng không bao giờ Nam chạy 2 ngày liên tiếp. Vào ngày thứ hai, Nam chơi bóng bàn
Câu 5.2 và 2ngày sau đó Nam chơi bóng đá. Nam còn đi bơi và chơi cầu lông nhưng không bao
1,0 điểm giờ Nam chơi cầu lông sau ngày Nam chạy hoặc bơi. Hỏi Nam chơi cầu lông vào thứ mấy trong tuần ?
Theo đề bài, Nam chơi bóng bàn vào thứ hai và bóng đá vào thứ tư.
Do Nam chạy 3 ngày một tuần nhưng không bao giờ Nam chạy 2 ngày liên
tiếp nên Nam chỉ có thể chạỵ vào thứ ba, thứ năm, thứ bẩy hoặc thứ ba, thứ
năm, chủ nhật hoặc thứ ba, thứ sáu, chủ nhật. TH1: Thứ hai Thứ ba Thứ tư T.năm Thứ sáu Thứ bẩy C.nhật 0,5 B.Bàn Chạy B.Đá Chạy Chạy
Nếu Nam chạy vào thứ ba, thứ năm, thứ bẩy thì Nam chỉ có thể chơi cầu lông
vào thứ sáu hoặc chủ nhật. Mà Nam không chơi cầu lông sau ngày Nam chạy
nên không thể xảy ra trường hợp này. TH2: Thứ hai Thứ ba Thứ tư T.năm Thứ sáu Thứ bẩy C.nhật B.Bàn Chạy B.Đá Chạy Chạy
Nếu Nam chạy vào thứ ba, thứ năm, chủ nhật thì Nam chỉ có thể chơi cầu lông
và bơi vào hai ngày thứ sáu và thứ bẩy. Mà theo đề bài, Nam không chơi cầu
lông sau ngày Nam chạy hoặc bơi nên không xảy ra trường hợp này. 0,5 TH3: Thứ hai Thứ ba Thứ tư T.năm Thứ sáu Thứ bẩy C.nhật B.Bàn Chạy B.Đá Chạy Chạy
Nếu Nam chạy vào thứ ba, thứ sáu, chủ nhật thì Sơn chỉ có thể chơi cầu lông
vào thứ năm hoặc thứ bẩy. Mà Nam không chơi cầu lông sau ngày Nam chạy
nên Nam chơi cầu lông vào thứ năm và bơi vào thứ bẩy.
Vậy Nam chơi cầu lông vào thứ năm.
Lưu ý: Học sinh làm cách khác nếu đúng cho điểm tối đa.