Đề chọn học sinh giỏi Toán THCS năm 2024 – 2025 phòng GD&ĐT Cai Lậy – Tiền Giang

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ CAI LẬY
TRUNG HỌC CƠ SỞ, NĂM HỌC 2024-2025 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian phát đề) Ngày thi: 17/02/2025
(Đề thi có 02 trang, gồm 05 bài)
--------------------------------------------------------------------------------------------------------
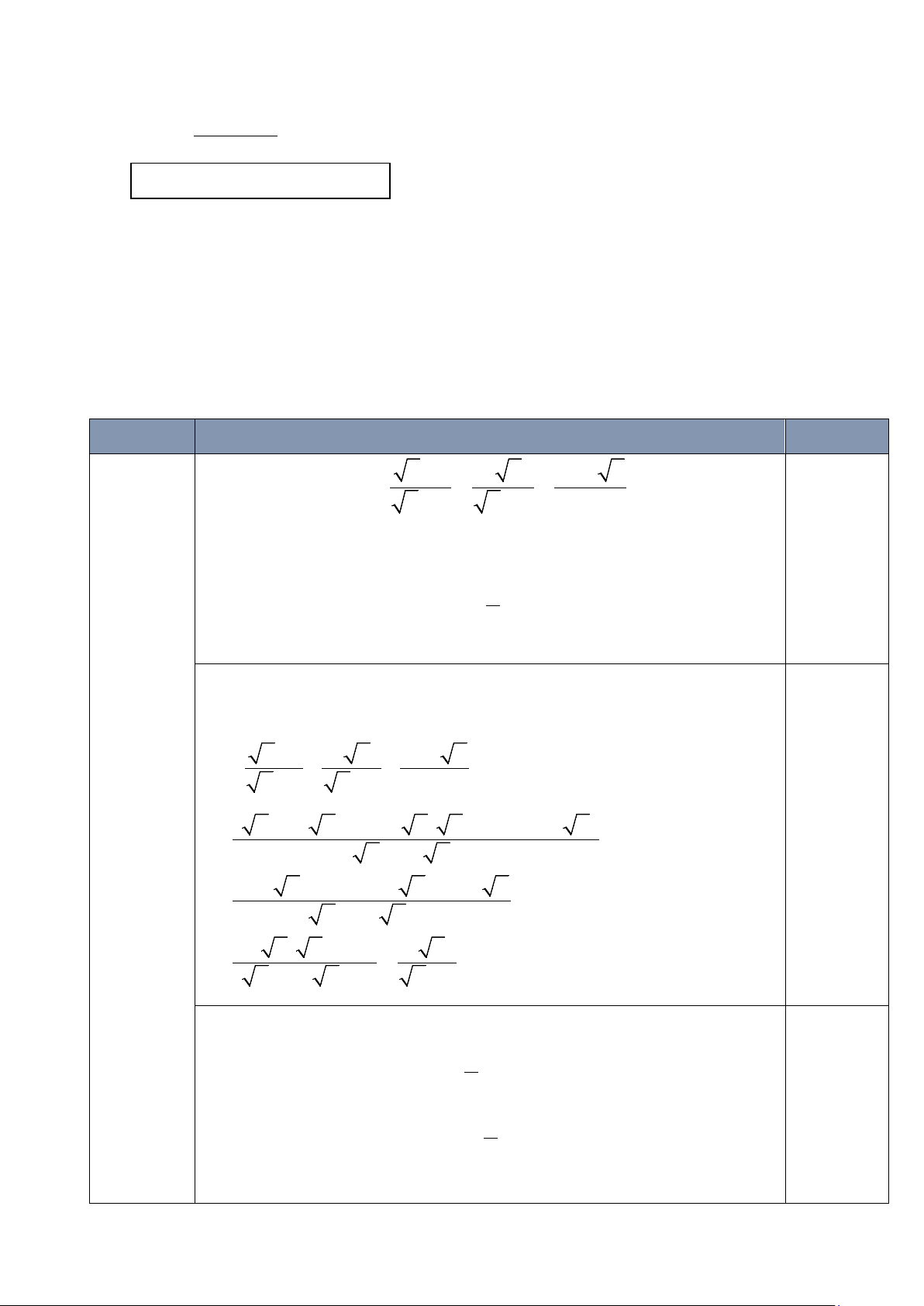
Bài 1: (4,0 điểm) Cho biểu thức x 1 2 x 2 5 x A + + = + +
với x ≥ 0 và x ≠ 4. x − 2 x + 2 4 − x 1. Rút gọn . A
2. Tính giá trị của A khi 4 x = . 9
3. Tìm giá trị của x để A có giá trị nguyên.
Bài 2: (4,0 điểm)
mx − 2y = 2
1. Cho hệ phương trình: 
(với m là tham số).
2x + my = 5
a. Giải hệ phương trình trên khi m = 6 .
b. Tìm 𝑚𝑚 để hệ phương trình đã cho có nghiệm ( ;x y) thỏa mãn: 2 2025 − m +14m −8102 x + y − 2024 = . 2 m + 4 2. Giải phương trình: 4 3 2
x − 5x + 8x − 5x + 1 = 0 .
Bài 3: (4,0 điểm)
1. Biết rằng a,b là các số thoả mãn a > b > 0 và . a b = 1. 2 2
Chứng minh: a +b ≥ 2 2 . a −b 2. Cho ba số a, ,
b c∈Z thoả mãn 2023
a +b + c = 2022 . Chứng minh: 3 3 3
a +b + c chia hết cho 6.
Ngày thi: 17/02/2025 Môn thi: Toán Trang 1/2
Bài 4: (2,0 điểm)
Nhà bạn An được ông nội cho một mảnh đất hình chữ nhật. Khi bạn
Bình đến nhà bạn An chơi, An đố Bình tìm ra kích thước của mảnh đất khi
cho biết: “Mảnh đất đó có chiều dài gấp bốn lần chiều rộng. Nếu giảm chiều
rộng đi 2m, tăng chiều dài lên gấp đôi thì diện tích mảnh đất đó sẽ tăng thêm 2
20m ”. Các em hãy giúp Bình tìm ra chiều dài và chiều rộng của mảnh đất nhà bạn An.
Bài 5: (6,0 điểm) 1. Cho góc nhọn α biết 5 cosα =
. Tính sinα và tanα . 13
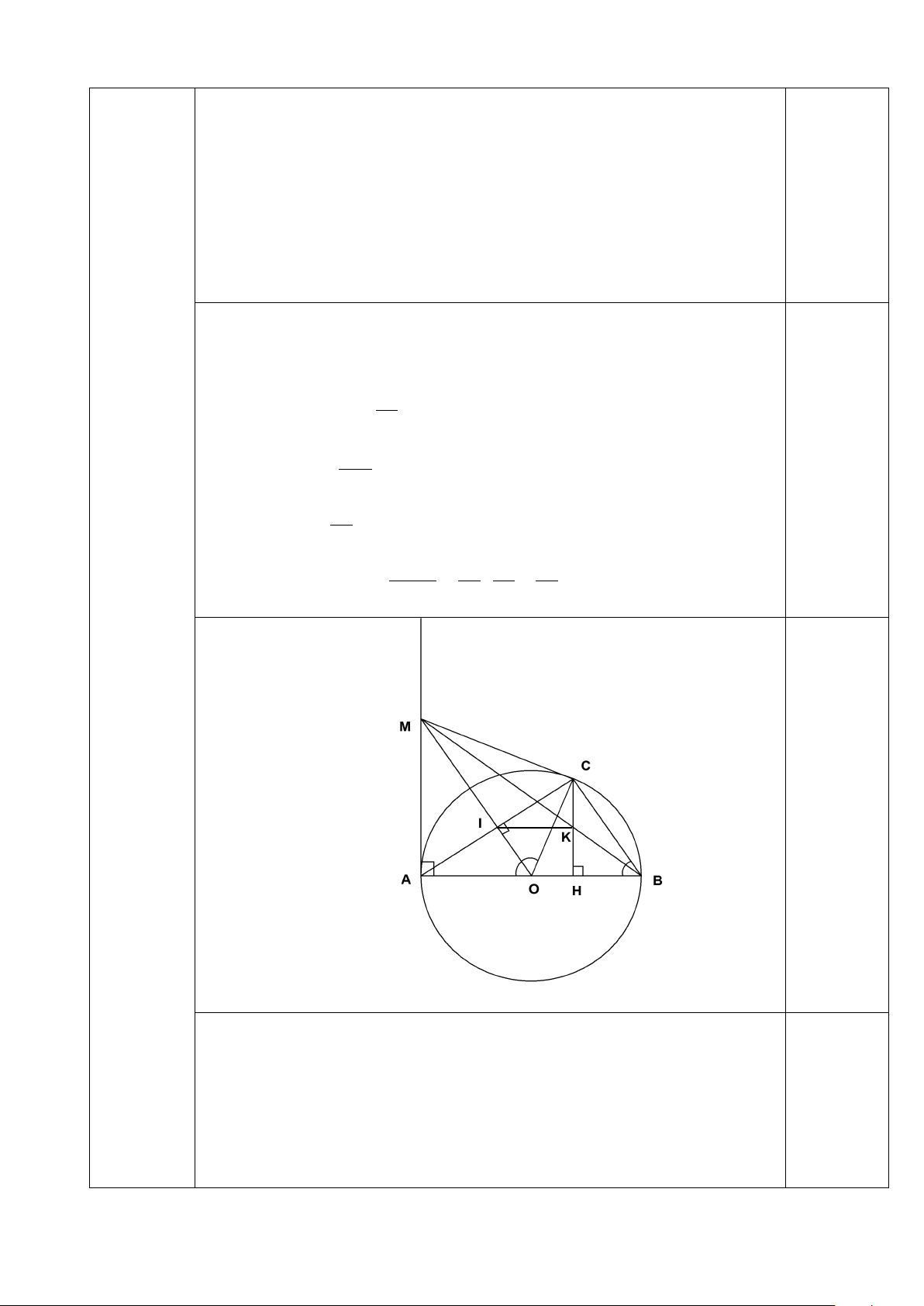
2. Cho đường tròn tâm O , bán kính R có đường kính AB cố định. C là một
điểm thay đổi trên đường tròn (C khác A và B ). Kẻ CH vuông góc AB ( H
thuộc AB ), I là trung điểm của AC . Đường thẳng OI cắt tiếp tuyến tại A của đường tròn ( ;
O R) tại M , đường thẳng MB cắt đường thẳng CH tại K .
a. Chứng minh MC là tiếp tuyến của ( ; O R).
b. Chứng minh IK song song với AB .
---------------------------------------- HẾT -------------------------------------------------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ........................................ Số báo danh: ......................................
Ngày thi: 17/02/2025 Môn thi: Toán Trang 2/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ CAI LẬY
TRUNG HỌC CƠ SỞ, NĂM HỌC 2024-2025 Môn thi: TOÁN
ĐÁP ÁN CHÍNH THỨC Ngày thi: 17/02/2025
(Đáp án gồm có 07 trang)
-------------------------------------------------------------------------------------------------------- I. Hướng dẫn chấm thi:
- Cán bộ chấm thi chấm 2 vòng độc lập.
- Cán bộ chấm thi không tự ý thay đổi thang điểm trong đáp án.
II. Đáp án và thang điểm: Bài Nội dung Điểm Bài 1: x x x (4,0 Cho biểu thức 1 2 2 5 A + + = + + với x ≥ 0 và x − 2 x + 2 4 − x điểm) x ≠ 4. 1. Rút gọn . A 4
2. Tính giá trị của A khi x = . 9
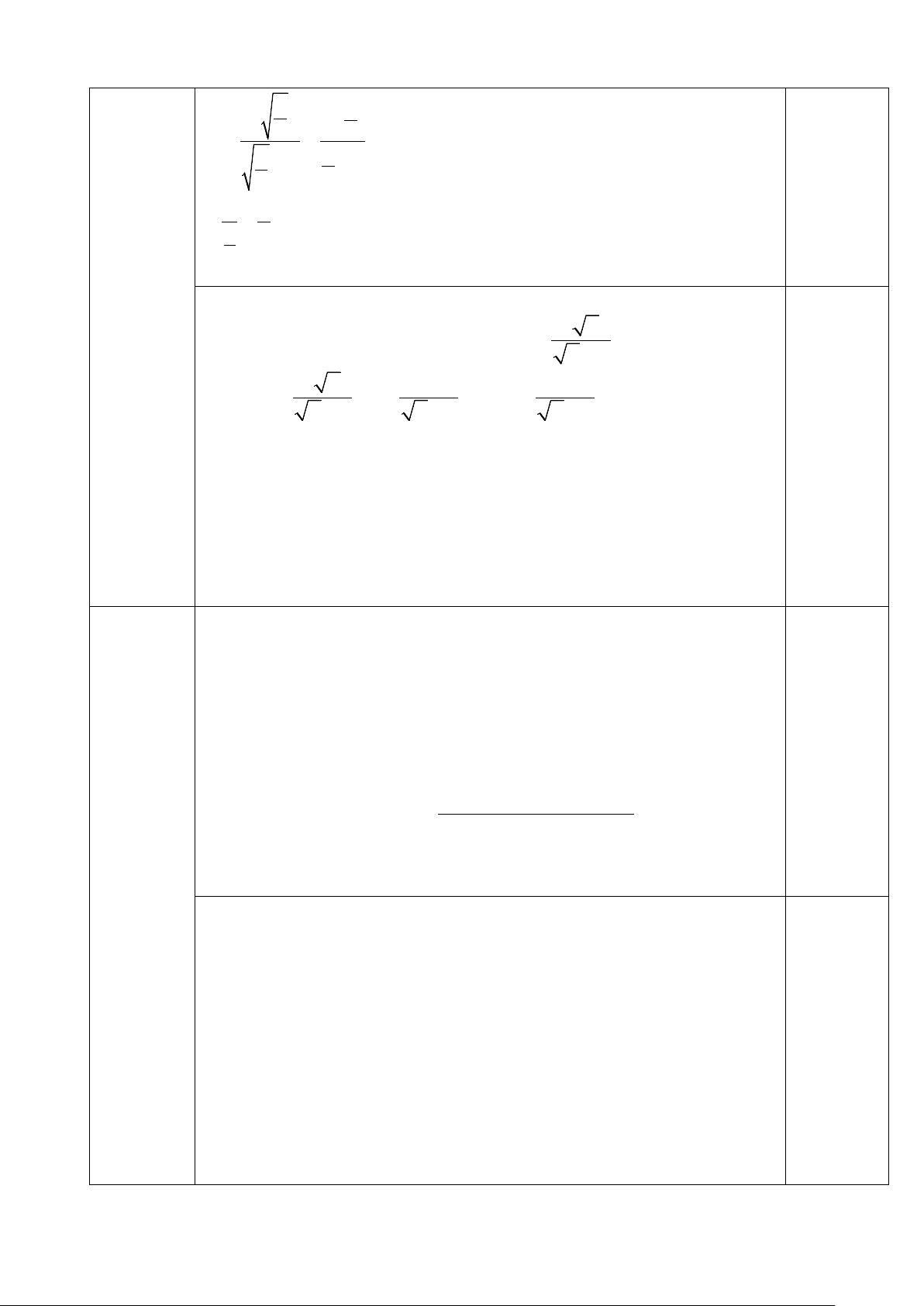
3. Tìm giá trị của x để A có giá trị nguyên. 1. Rút gọn A. A = x +1 2 x 2+5 x + + 0,5 x − 2 x + 2 4− x
( x +1)( x + 2)+ 2 x( x − 2)−(2+5 x) = 0,5
( x − 2)( x + 2)
x +3 x + 2+ 2x − 4 x − 2−5 x =
( x − 2)( x + 2) 0,5 3 x( x − 2) 3 x = =
( x − 2)( x + 2) x + 2
2. Tính giá trị của A khi 4 x = . 9
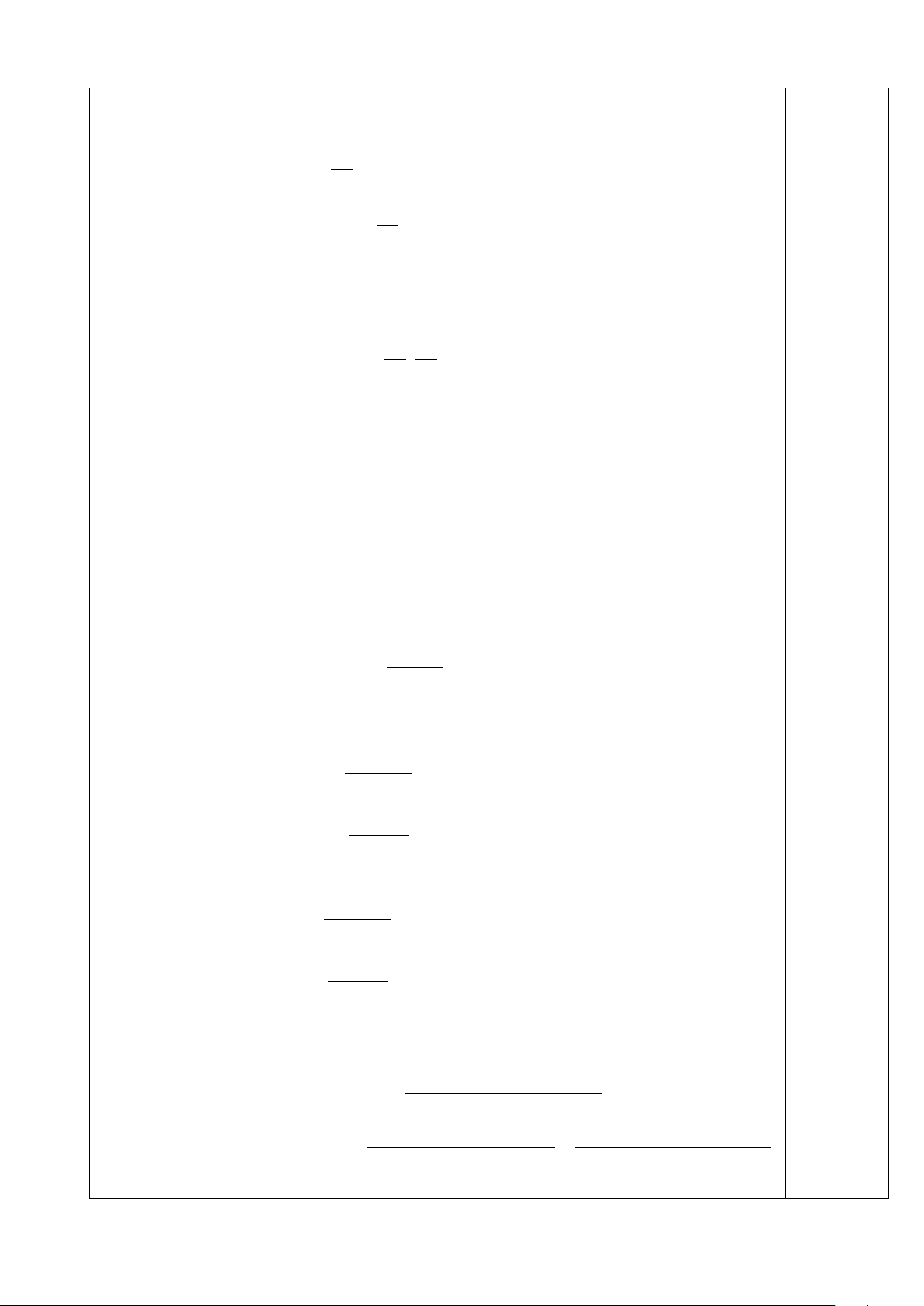
Với x ≥ 0 và x ≠ 4 , tại 4 x = ( t/m đk ) 9 0,25 Trang 1/7 4 2 3 3. 9 0,75 3 A = = 4 2 + 2 + 2 9 3 2 3 = = 8 4 0,5 3
3. Tìm giá trị của x để A có giá trị nguyên.
Với x ≥ 0 và x ≠ 4 ; A nguyên khi 3 x có giá trị nguyên. x + 2 0,25 Mặt khác 3 x 6 = 3− < 3 (vì 6 > 0) x + 2 x + 2 x + 2 0,25 Suy ra 0 ≤ A < 3
Vì A nguyên và 0 ≤
A < 3 nên A = 0;1; 2 A = 0 0,25
giải ra ta được x = 0 ( T/m đk )
A =1 giải ra ta được x = 1 ( T/m đk )
A = 2 giải ra ta được x = 1 6 ( T/m đk ) Vậy x = 0 ; 1 x = ; 1
x = 6 thì A có giá trị nguyên 0,25
mx − 2y = 2
1. Cho hệ phương trình: 
(với 𝑚𝑚 là tham số).
2x + my = 5
a. Giải hệ phương trình trên khi m = 6 .
b. Tìm 𝑚𝑚 để hệ phương trình đã cho có nghiệm ( ;x y) thỏa mãn: 2 2025 − m +14m −8102 x + y − 2024 = . 2 m + 4 Bài 2: 2. Giải phương trình: 4 3 2
x − 5x + 8x − 5x + 1 = 0 . (4,0 điểm)
1. Cho hệ phương trình: mx − 2y = 2 
(với m là tham số). 2x + my = 5
a. Thay m = 6 ta được hệ: 6x − 2y = 2  2x + 6y = 5 18   x − 6y = 6  0,25
 2x + 6y = 5  20x =11 
2x + 6y = 5 Trang 2/7  11 x = 0,25  20   11 2. + 6y = 5  20  11 x =  20  0,25  13 y  =  20
Vậy với m = 6 thì hệ phương trình có nghiệm duy nhất 0,25 là: (x y) 11 13 ; = ;   20 20   
b.mx − 2y = 2  2x + my = 5  mx − 2  y =  2  2x + my = 5  mx − 2  y =  2   mx − 2 2x + m = 5  2 0,25  mx − 2  y =  2   + ( 2 m 4)x = 2m+10  2m +10 x = 2  m + 4  , m ∀ ∈R  5m − 4 y  = 2  m + 4
Do đó hệ phương trình có nghiệm duy nhất là: 0,25  2m +10 x = 2  m + 4  , m ∀ ∈  5m − 4 y  = 2  m + 4 Thay 2m +10 x = và 5m − 4 y = vào hệ thức: 2 m + 4 2 m + 4 2 2025 − m +14m −8102 x + y − 2024 = 2 m + 4 2 2 Ta được: 2024 − m + 7m −8090 2025 − m +14m −8102 = 2 2 m + 4 m + 4 2 2 2024 −
m + 7m −8090 = 2025 − m +14m −8102 Trang 3/7 2 m −7m +12 = 0 0,25
(m−3)(m−4) = 0 m = 3  m = 4
Vậy để hệ phương trình đã cho có nghiệm ( ; x y) thỏa 2 mãn hệ thức: 2025 − m +14m −8102 x + y − 2024 = 2 m + 4
thì m = 3 hoặc m = 4 . 0,25 2. Giải phương trình: 4 3 2
x − 5x + 8x − 5x + 1 = 0 (1)
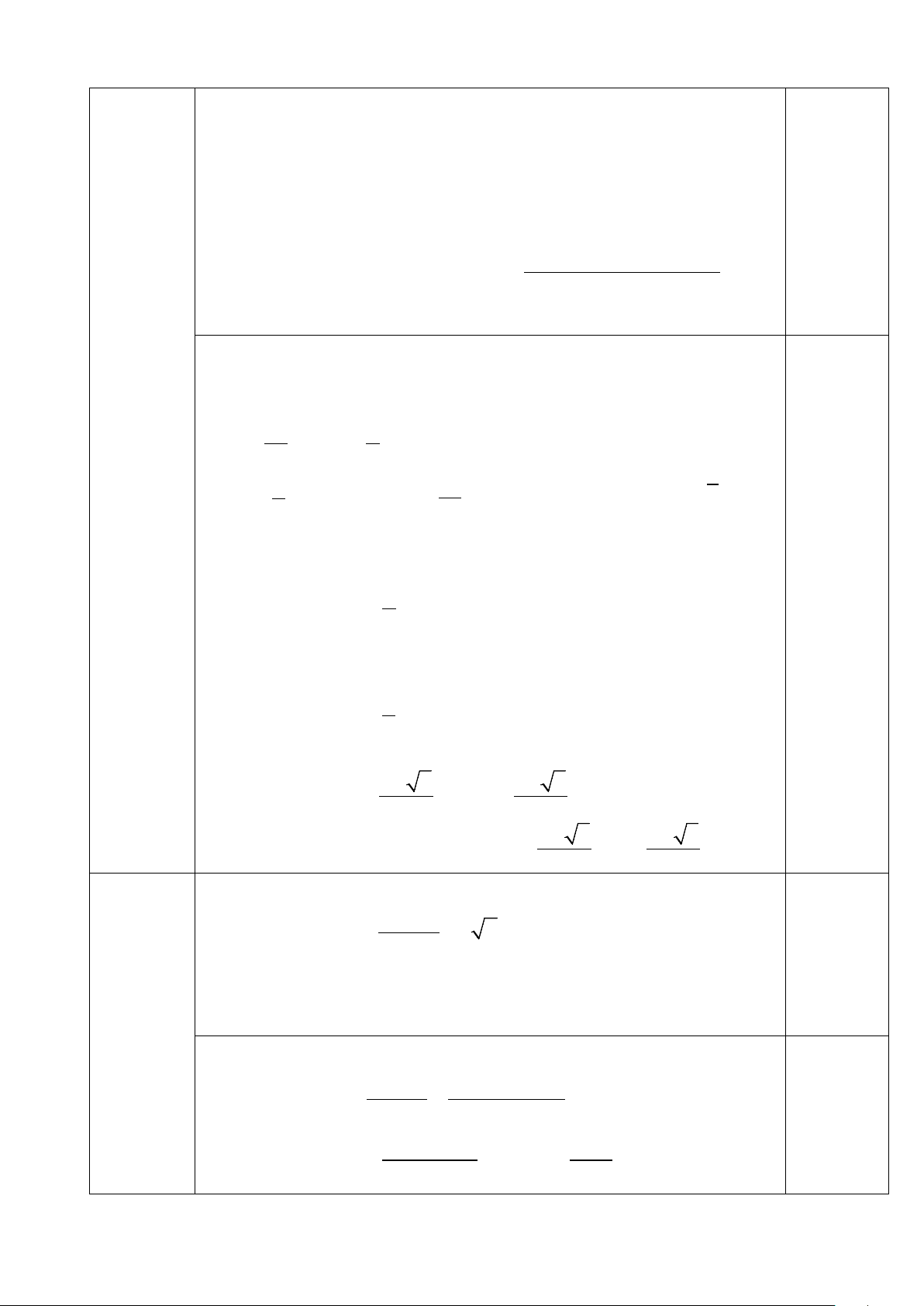
Vì x = 0 không là nghiệm của phương trình (1) nên chia hai vế cho x2 ta được  2 1   1 x + −5 x     +  + 8 = 0 (2) 2  x   x  Đặt 1
x + = t ta được 2 1 2 x + =
t − 2 điều kiện: x | 2 𝑡𝑡|> 0,5 x √2
Phương trình (2) trở thành 2
t – 5t + 6 = 0
Giải phương trình ta được t = 2 ,t = 3 ( thỏa điều kiện) 0,5 1 2
Với t = 2 ta có 1 x + = 2 1 x 2
x − 2x + 1 = 0 x =1 0,5
Với t = 3 ta có 1 x + = 3 2 x 2
x − 3x + 1 = 0 3 + 5 x = và 3 − 5 = 2 x 2 0,5
Vậy phương có 3 nghiệm x 1 = ; 3 + 5 x = ; 3 − 5 = 2 x 2 Bài 3:
1. Biết rằng a,b là các số thoả mãn a > b > 0 và . a b = 1. (4,0 2 2 a +b điểm) Chứng minh: ≥ 2 2 a . −b 2. Cho ba số a, ,
b c∈Z thoả mãn 2023
a +b + c = 2022 . Chứng minh: 3 3 3
a +b + c chia hết cho 6. 1. Vì . a b = 1 nên a +b (a −b)2 2 2 + 2ab = a −b a −b 0,5 ( a −b)2 + 2 = = (a −b) 2 + 0,5 a −b a −b Trang 4/7
- Do a > b > 0 nên áp dụng BĐT Cô Si cho 2 số dương Ta có : ( 0,5 a −b) 2 + ≥ (a −b) 2 2 ⋅ a −b a −b 2 2
Vậy a +b ≥ 2 2 0,5 a −b 2. Ta có: 3 3 3 + + = ( 3 − )+( 3 − )+( 3 a b c a a b b
c −c)+(a +b+c) 0,5 Mà 3
a − a = (a − ) 1 a(a + )
1 6 (tích ba số nguyên liên tiếp nên chia hết cho 6). Tương tự 3 3
(b −b)6, (c −c)6 0,75 và 2023
a +b + c = 2022 6 (vì 2022 6 ) 0,5 0,25 Vậy 3 3 3
(a + b + c )6
Bài 4: Nhà bạn An được ông nội cho một mảnh đất hình chữ nhật. (2,0
Khi bạn Bình đến nhà bạn An chơi, An đố Bình tìm ra kích thước điểm)
của mảnh đất khi cho biết: “Mảnh đất đó có chiều dài gấp bốn lần
chiều rộng. Nếu giảm chiều rộng đi 2m, tăng chiều dài lên gấp
đôi thì diện tích mảnh đất đó sẽ tăng thêm 2 20m ”. Các em hãy
giúp Bình tìm ra chiều dài và chiều rộng của mảnh đất nhà bạn An.
Gọi chiều rộng của mảnh đất là x(m) ( 2 x > )
Vậy chiều dài là: 4x(m)
Diện tích mảnh đất là: 2 ( 2 4x m ) 0,5
Diện tích mảnh đất sau khi giảm chiều rộng 2m và tăng chiều dài 0,5
lên gấp đôi là: 8x(x − 2) ( 2 m )
Theo bài ra ta có phương trình: 2
8x(x − 2) − 4x = 20 0,5
Giải phương trình ta được x = 5 (nhận) x = 1 − (loại)
Vậy chiều rộng của mảnh đất là 5(m); chiều dài của mảnh đất là 0,5 20(m) 5
1. Cho góc nhọn α biết cosα =
. Tính sinα và tanα . 13 Trang 5/7
2. Cho đường tròn tâm O , bán kính R có đường kính AB cố
định. C là một điểm thay đổi trên đường tròn (C khác A và B ).
Kẻ CH vuông góc AB ( H thuộc AB ), I là trung điểm của AC
Bài 5: . Đường thẳng OI cắt tiếp tuyến tại A của đường tròn ( ; O R) tại (6,0
M , đường thẳng MB cắt đường thẳng CH tại K . điểm)
a. Chứng minh MC là tiếp tuyến của ( ; O R).
b. Chứng minh IK song song với AB . 1. Ta có 2 2 sin α + cos α =1 2 2 sin α =1− cos α 0,25 2 2  5 sin 1  α = − 13   0,25 2 144 sin α = 169 12 sinα = 13 0,25 sinα 12 5 12 Suy ra tan α = = : = 0,25 cosα 13 13 5 2. 0,5
a. Chứng minh MC là tiếp tuyến của của (O; R )
Tam giác OAC cân tại O, có OI là đường trung tuyến nên OI là đường trung trực
Mà M ∈OI ⇒ MA = MC 0,5 Trang 6/7 OA  = OC Xét OA ∆ M và OC ∆ M có O   M chung MA = 1,0  MC Vậy OA ∆ M = OC ∆
M ( .c .cc) Nên  =  0 MAO MCO = 90 0,5
⇒ MC ⊥ CO tạiC , mà C ∈(O)
Vậy MC là tiếp tuyến của ( ; O R)
b. Chứng minh IK song song với AB . Ta có C  H ⊥ AB KH BH BH  ⇒ KH / /MA ⇒ = = (1) MA ⊥ AB MA AB 2R 0,5 Do  0
ACB = 90 ⇒ BC ⊥ AC ⇒ BC / /OM   = 
Xét hai tam giác BCH và OMA có BHC OAM    =  CBH MOA S Suy ra B ∆ CH O ∆ MA 0,5 Suy ra CH BH BH = = (2) MA OA R 0,5
Từ (1) và (2) suy ra CH = 2KH ⇒ K là trung điểm của CH 0,5  =
∆CAH có: IC IA 
⇒ IK là đường trung bình của C ∆ AH KC = KH
⇒ IK / / AH ⇒ IK / / AB 0,5 Chú ý:
- Học sinh làm cách khác đúng đều ghi nhận và cho điểm tương ứng theo từng phần.
- Học sinh không vẽ hình bài 5 câu 2 thì không chấm điểm.
------------------------------------------------- HẾT ------------------------------------------------ Trang 7/7
Document Outline

• DE CHINH THUC
• DAP AN CHINH THUC