Đề chọn HSG Toán 10 năm 2024 – 2025 trường THPT Phan Huy Chú – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHAN HUY CHÚ–QUỐC OAI
Môn : Toán – Khối: 10 Năm học : 2024-2025
Thời gian làm bài: 120 phút
Câu 1.(4,0 điểm)
a. Cho hai tập hợp A = ( 5;
− 3) và B = [2;+∞). Tìm A∩ B . b. Cho hai tập hợp 2
A = 7;m − m, B =(9;12  
] với A là tập hợp khác rỗng. Có bao nhiêu giá trị
nguyên của m thuộc [0;2024] để B ⊂ A .
Câu 2.(4,0 điểm)
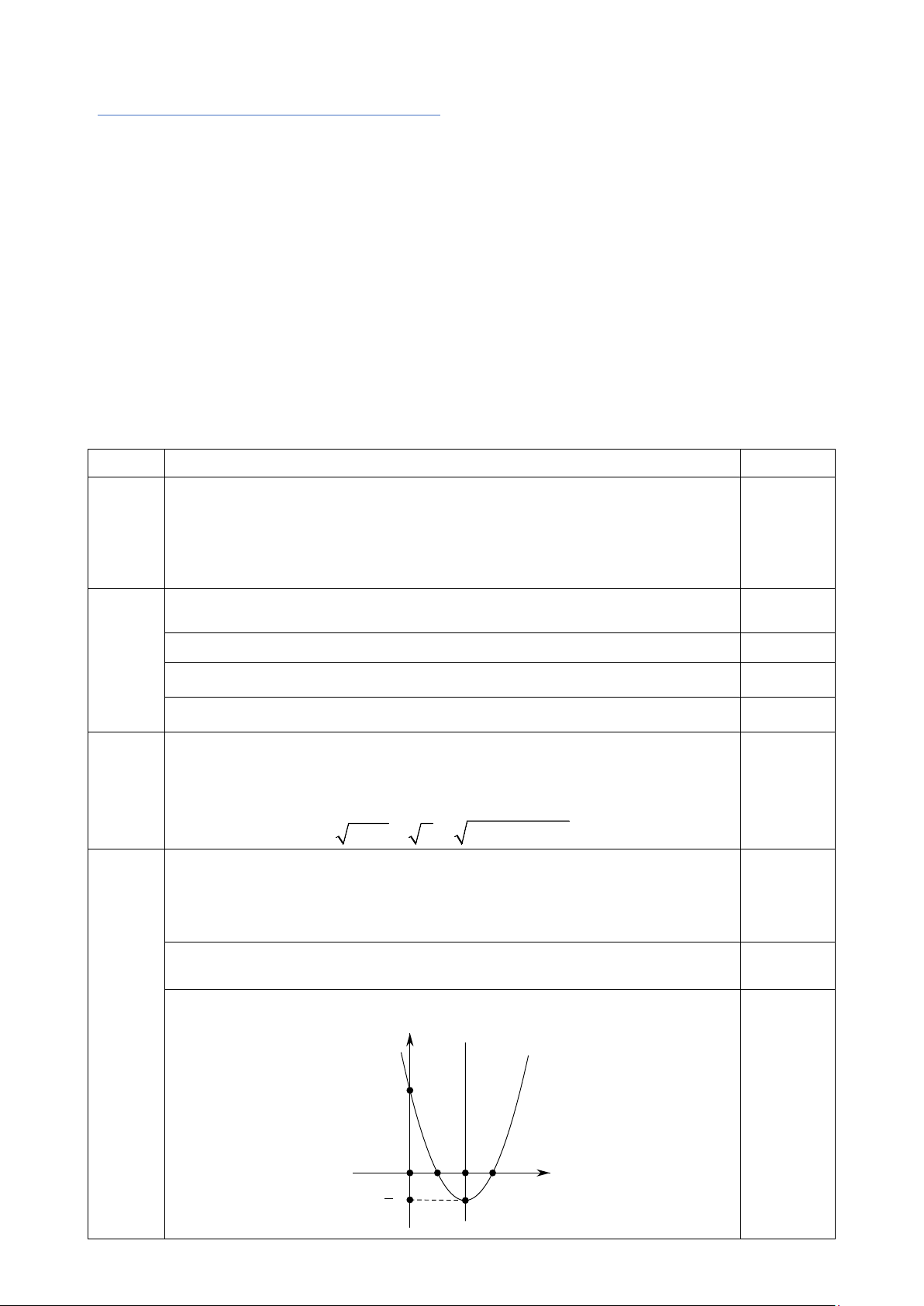
a. Vẽ đồ thị hàm số 2
y = x − 4x + 3.
b. Tìm tất cả các tham số m để phương trình sau có nghiệm thực 2
4 − x + x = 3m + 4x − x
Câu 3.(3,0 điểm)
Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và một máy chuyên
dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg nguyên liệu và máy làm việc trong
3 giờ. Để sản xuất được một kilôgam sản phẩm loại II cần 4kg nguyên liệu và máy làm việc
trong 1,5 giờ. Biết một kilôgam sản phẩm loại I lãi 300000 đồng, một kilôgam sản phẩm loại II
lãi 400000 đồng và máy chuyên dụng làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao
nhiêu kilôgam sản phẩm mỗi loại để tiền lãi lớn nhất.
Câu 4. (3,0 điểm)
Cho tam giác ABC thỏa mãn: .
AB AC =12 và sin B + sinC = sin A . Gọi M là trung điểm của cos B + cosC
cạnh BC và G là trọng tâm của tam giác ABC . Tìm diện tích tam giác BMG .
Câu 5.(4,0 điểm)
a. Cho hình bình hành ABCD . Trên đường chéo BD lấy các điểm G và H sao cho
DG = GH = HB . Gọi M là giao điểm của AH và BC ; N là giao điểm của AG và DC .   
Chứng minh: 2AM + 2AN = 3AC
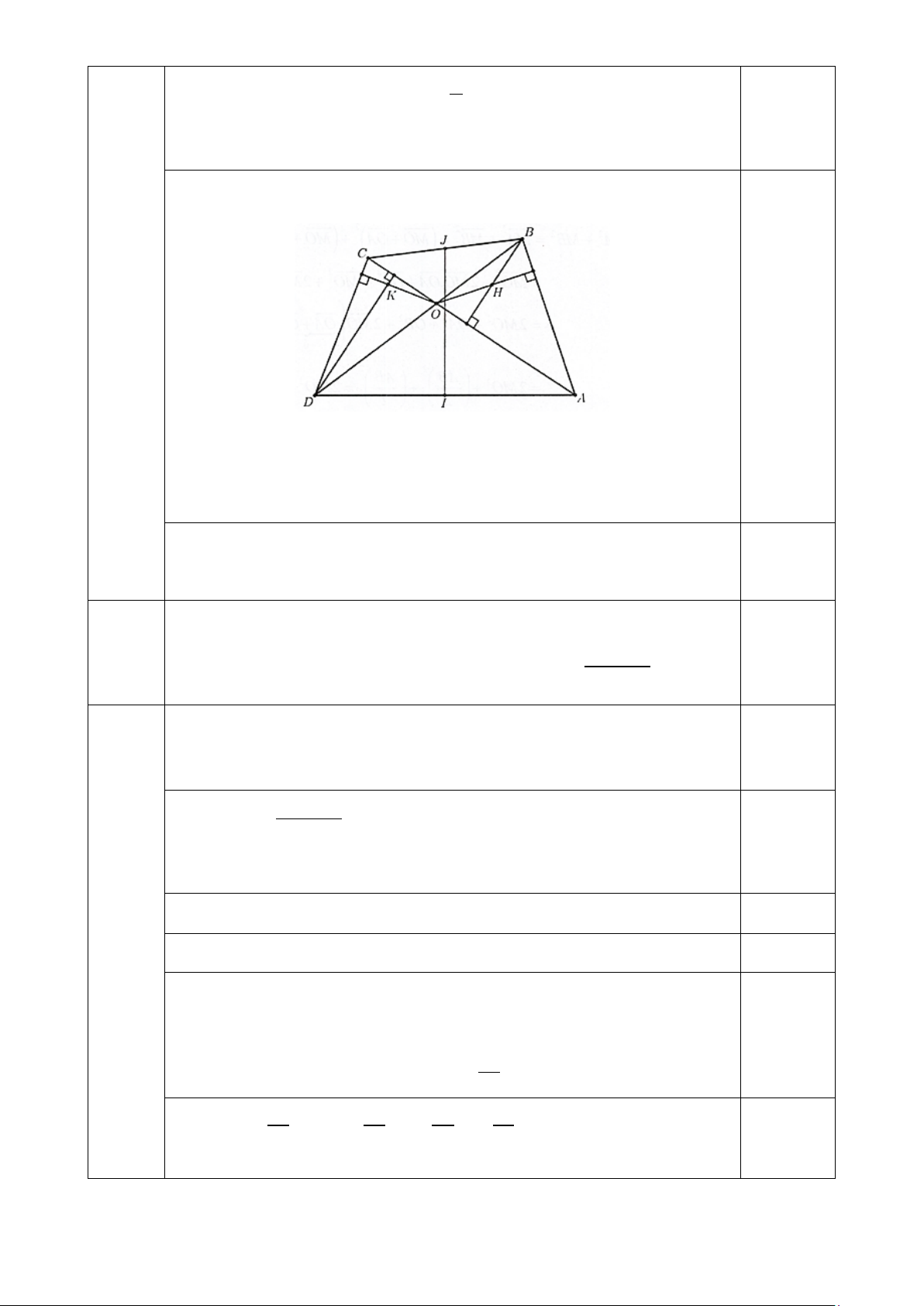
b. Cho tứ giác lồi ABCD , hai đường chéo AC và BD cắt nhau tại điểm O . Gọi điểm H , K
lần lượt là trực tâm các tam giác ABO và CDO . Gọi điểm I, J lần lượt là trung điểm của cạnh
AD và BC . Chứng minh rằng HK ⊥ JI . Câu 6. (2,0 điểm)
Cho các số thực x, y, z thỏa mãn 2 2 2
x + y + z = 9 và x + y − z = 3. Tìm giá trị lớn nhất và nhỏ + − nhất của biểu thức x z 1 P = . y + 4
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT PHAN HUY CHÚ–QUỐC OAI
Môn : Toán – Khối: 10 Năm học : 2024-2025
Thời gian làm bài: 120 phút HƯỚNG DẪN CHẤM
I. HƯỚNG DẪN CHUNG
o Hướng dẫn chấm chỉ trình bày sơ lược các bước giải, lời giải của học sinh cần lập luận
chặt chẽ, hợp logic. Nếu học sinh trình bày cách làm khác mà đúng thì vẫn được điểm
theo thang điểm tương ứng.
o Đối với bài toán hình học nếu học sinh chứng minh có sử dụng đến hình vẽ thì yêu cầu
phải vẽ hình, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không cho điểm phần tương ứng.
o Điểm toàn bài không làm tròn.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu Nội dung Điểm
a. Cho hai tập hợp A = ( 5;
− 3) và B = [2;+∞). Tìm A∩ B . 1 b. Cho hai tập hợp 2
A = 7;m − m, B =(9;12 (4,0  
] với A là tập hợp khác điểm)
rỗng. Có bao nhiêu giá trị nguyên của m thuộc [0;2024] để B ⊂ A .
a. A∩ B = [2;3) 2,0
b. Để B ⊂ A thì 2 m − m ≥12 1,0 ⇔ m ∈( ; −∞ − ] 3 ∪[4;+∞) 0,5
Vì m nguyên và thuộc [0;2024] nên có 2021 giá trị 0,5 a. Vẽ đồ thị hàm số 2
y = x − 4x + 3. 2
b. Tìm tất cả các tham số m để phương trình sau có nghiệm thực (4,0 điểm) 2
4 − x + x = 3m + 4x − x a. Vẽ đồ thị hàm số 2
y = x − 4x + 3.
Nêu được toạ độ đỉnh I (2;− ) 1 1,0
Nêu đúng phương trình trục đối xứng x = 2
Nhận xét được giao với các trục hoặc lập đúng bảng giá trị (tối thiểu là ba điểm) 0,5
Vẽ đúng đồ thị hàm số y 3 0,5 O 1 2 3 x 1
b. ĐKXĐ 0 ≤ x ≤ 4
Bình phương hai vế của PT ta được 2 2
4 + 2 4x − x = 3m − x + 4x 0,5 ⇔ −( 2 x − x ) 2 4
+ 2 4x − x + 4 = 3m (1) Đặt 2
4x − x = t , có 2
0 ≤ 4x − x = 4 − (x − 2)2 ≤ 2 x ∀ ∈[0;4] ⇒ t ∈[0;2] 0,5 PT (1) trở thành: 2t
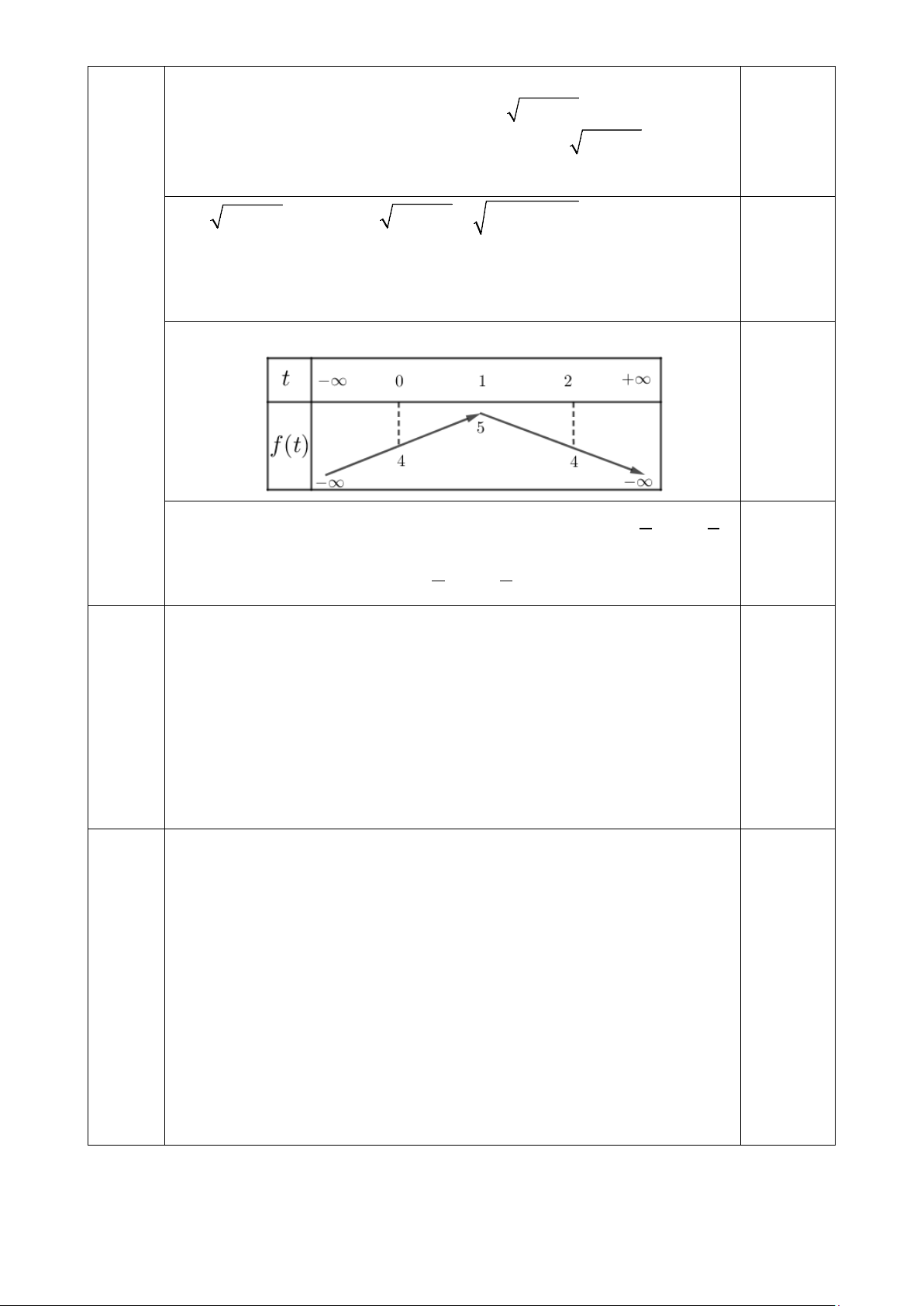
− + 2t + 4 = 3m (2) Ta có BBT của hàm số 2 f (t) = t − + 2t + 4 0,5
Dựa vào BBT suy ra PT (2) có nghiệm khi 4 5
4 ≤ 3m ≤ 5 ⇔ ≤ m ≤ 3 3 0,5
Vậy PT ban đầu có nghiệm khi 4 5 ≤ m ≤ . 3 3
Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên
liệu và một máy chuyên dụng. Để sản xuất được một kilôgam sản
phẩm loại I cần 2kg nguyên liệu và máy làm việc trong 3 giờ. Để sản 3
xuất được một kilôgam sản phẩm loại II cần 4kg nguyên liệu và máy (3,0
làm việc trong 1,5 giờ. Biết một kilôgam sản phẩm loại I lãi 300000 điểm)
đồng, một kilôgam sản phẩm loại II lãi 400000 đồng và máy chuyên
dụng làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao nhiêu
kilôgam sản phẩm mỗi loại để tiền lãi lớn nhất.
Giả sử sản xuất x(kg) sản phẩm loại I và y(kg) sản phẩm loại II.
Điều kiện x ≥ 0, y ≥ 0 và 2x + 4y ≤ 200 ⇔ x + 2y ≤100
Tổng số giờ máy làm việc: 3x +1,5y
Ta có 3x +1,5y ≤120
Số tiền lãi thu được là T = 300000x + 400000y (đồng). 1,0
x ≥ 0, y ≥ 0
Ta cần tìm x, y thoả mãn: x + 2y ≤100 (I) sao cho 3  x +1,5y ≤  120
T = 300000x + 400000y đạt giá trị lớn nhất.
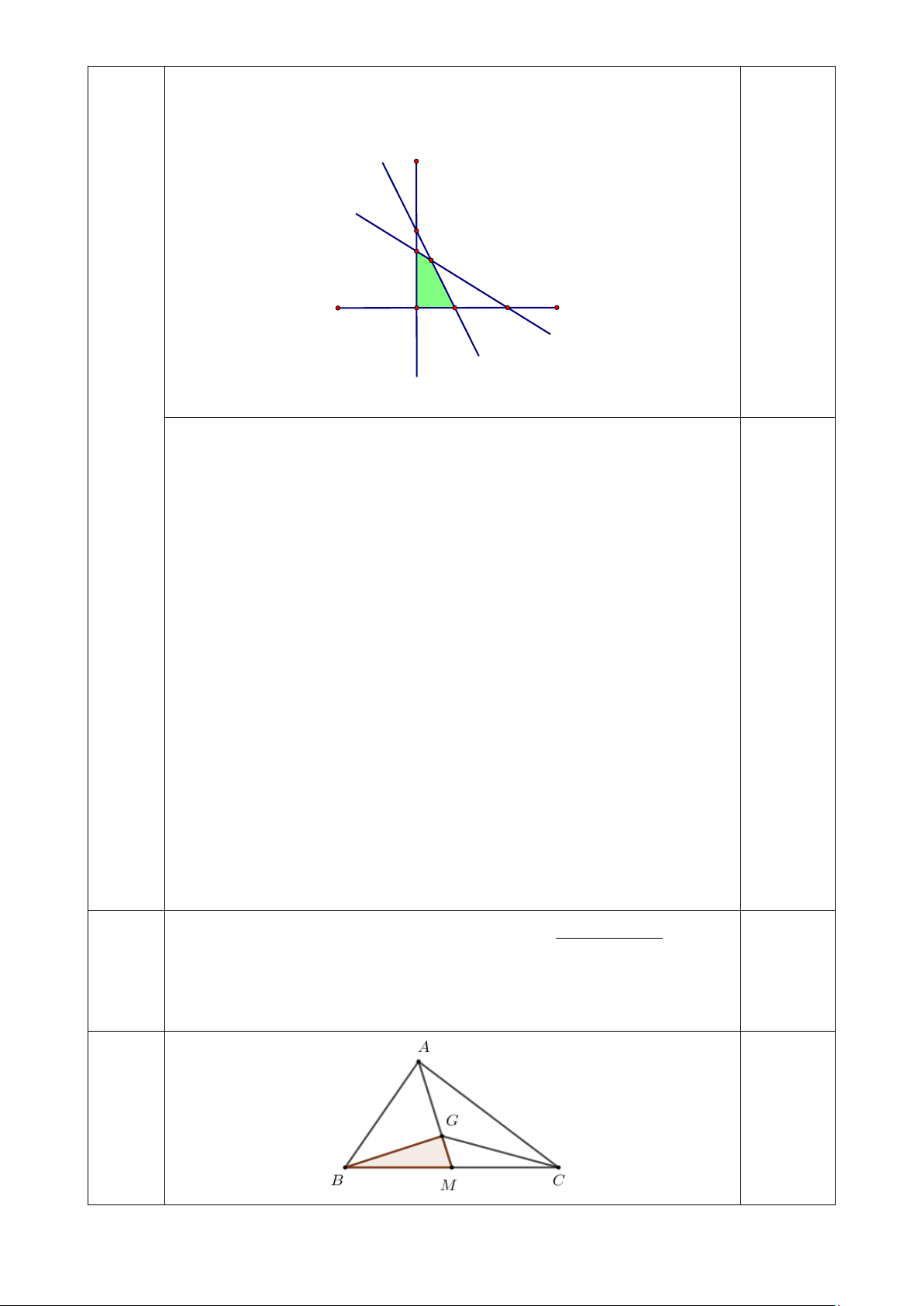
Trên mặt phẳng tọa độ Oxy vẽ các đường thẳng
d : x + 2y =100; d : 3x +1,5y =120 1 2 y D 1,0 B E x O C A
Đường thẳng d cắt trục hoành tại điểm (
A 100;0), cắt trục tung tại 1 điểm B(0;50) .
Đường thẳng d cắt trục hoành tại điểm C(40;0) , cắt trục tung tại 2 điểm D(0;80).
Đường thẳng d và d cắt nhau tại điểm E (20;40) . 1 2
Biểu diễn hình học tập nghiệm của hệ bất phương trình (I) là miền đa giác OBEC . 1,0 x = 0 x = 0  ⇒ T = 0;  ⇒ T = 20000000 ; y = 0 y = 50 x = 20 x = 40  ⇒ T = 22000000 ;  ⇒ T =12000000 y = 40 y = 0
Vậy để thu được tổng số tiền lãi nhiều nhất thì xưởng cần sản xuất
20kg sản phẩm loại I và 40kg sản phẩm loại II.
Cho tam giác ABC thỏa mãn: .
AB AC =12 và sin B + sinC = sin A . cos B + cosC 4 (3,0
Gọi M là trung điểm của cạnh BC và G là trọng tâm của tam giác điểm)
ABC . Tìm diện tích tam giác BMG .
Đặt BC =a,AC =b,AB =c. Áp dụng định lí sin cho ABC ∆ ta có: 0,5 a b c = = = 2 ⇒ sin a = ,sin b = ,sin c R A B C =
sin A sin B sinC 2R 2R 2R
Khi đó sin B + sinC = sin A ⇔ b + c = a(cos B + cosC) (*) cos B + cosC 0,5
Áp dụng định lí cosin cho ABC ∆ ta có: 2 2 2 2 2 2 cos
a + c − b = ,cos
a + b − c B C = 2ac 2ab nên (*) 2 2 2 2 2 2
 a + c − b
a + b − c 
⇔ b + c = a + 2ac 2ab    1,0 2 2 2 2 2 2
b + c − a
b + c − a ⇔ + = 0 2c 2b
⇔ (c + b)( 2 2 2
b + c − a ) = 0 2 2 2
⇒ b + c = a ⇒ tam giác ABC vuông tại A và . AB AC S = = 0,5 ABC ∆ 6 2 Ta có 1 1 S = = = . ∆ S∆ S GBM GBC ABC ∆ 1 2 6 0,5
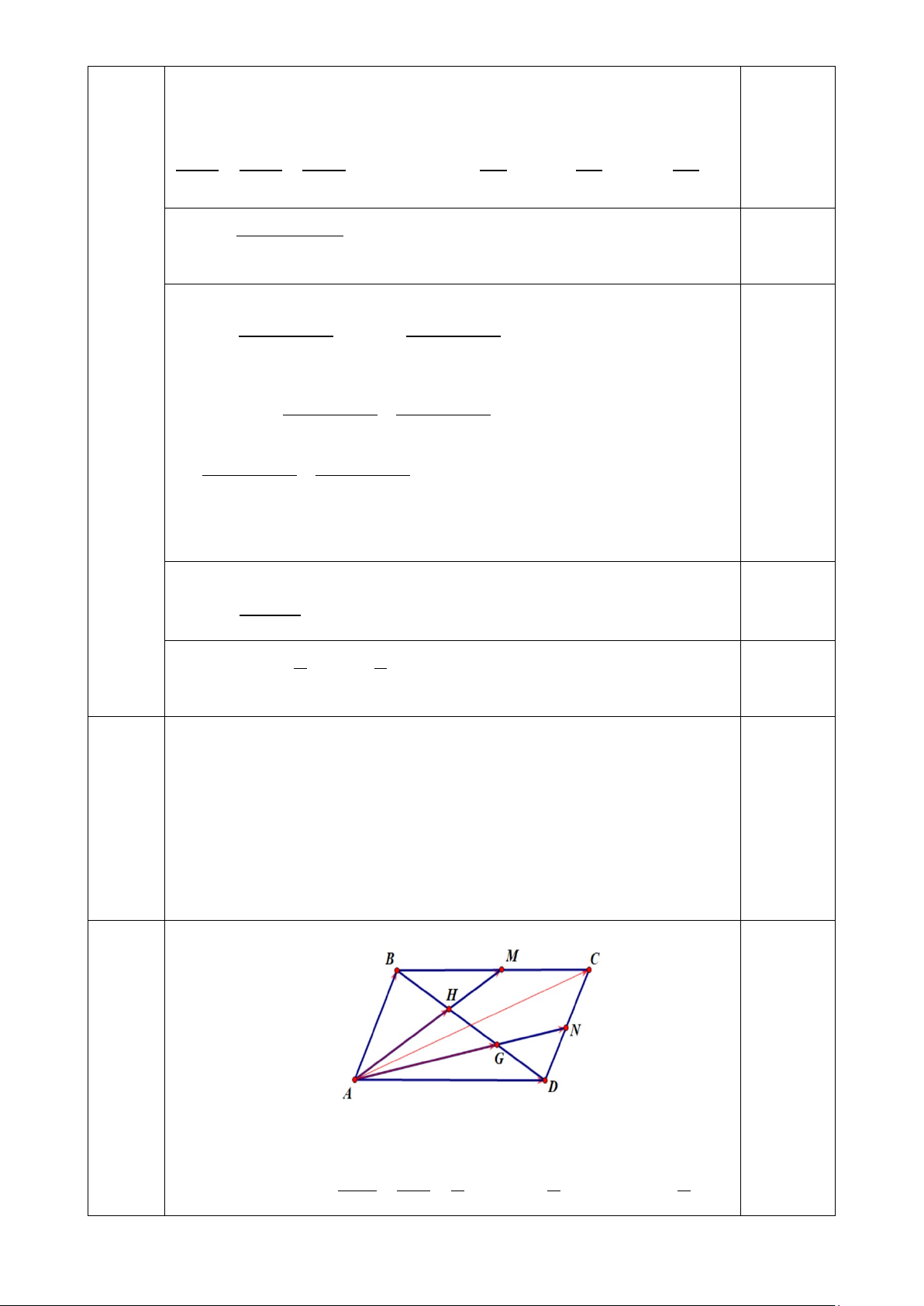
a. Cho hình bình hành ABCD. Trên đường chéo BD lấy các điểm G
và H sao cho DG = GH = HB. Gọi M là giao điểm của AH và BC; N   
là giao điểm của AG và DC. Chứng minh: 2AM + 2AN = 3AC 5 (4,0
b. Cho tứ giác lồi ABCD , hai đường chéo AC và BD cắt nhau tại điểm)
điểm O . Gọi điểm H , K lần lượt là trực tâm các tam giác ABO và
CDO . Gọi điểm I, J lần lượt là trung điểm của cạnh AD và BC .
Chứng minh rằng HK ⊥ JI . a.
Gọi O là tâm của hình bình hành ABCD. Từ gt suy ra O là trung điểm của HM 1,0  
Do BM / / AD nên HM BH 1 3 3 =
= ⇒ AM = AH ⇒ AM = AH AH HD 2 2 2  
Chứng minh tương tự ta có 3 AN = AG 2       1,0
2AM + 2AN = 3(AG + AH ) = 3.2AO = 3AC b.
   
IJ = IA + AC + CJ
   Ta có: 1,0
    ⇒ 2IJ = AC + DB .
IJ = ID + DB + BJ
    
   
Suy ra: HK.2IJ = HK(AC + DB) = HK.AC + HK.DB
            
= (HB + BD + DK)AC + (HA + AC + CK)DB = AC(BD + DB) = AC.0  
Vậy HK.IJ = 0 nên HK ⊥ JI . 1,0
Cho các số thực x, y, z thỏa mãn 2 2 2
x + y + z = 9 và x + y − z = 3. 6 ( 2,0 + −
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức x z 1 P = . điểm ) y + 4
Ta có: (x + z)2 = ( 2 2
2 x + z ) −(x − z)2 0,5 = ( 2
− y ) − ( − y)2 2 2 9 3 = 3 − y + 6y + 9 + − Khi đó: x z 1 P =
⇒ P( y + 4) +1 = x + z nên y + 4 0,25 P  ( y + ) 2 +  =  (x + z)2 4 1 2
⇒ P ( y + )2 + ( y + ) 2 4 2 4 P +1 = 3 − y + 6y + 9 0,25 ⇔ ( 2 P + ) 2 y + ( 2 P + P − ) 2 3 8 2
6 y +16P + 8P −8 = 0( ) 1 0,25 Phương trình ( ) 1 có nghiệm
⇔ ∆′ = ( P + P − )2 2 − ( 2 P + )( 2 4 3
3 16P + 8P −8) ≥ 0 0,5 2 11 ⇔ 63
− P − 30P + 33 ≥ 0 ⇔ 1 − ≤ P ≤ 21 Vậy 11 P = khi 8 y = , 56 7 x = , z = max 21 19 19 19 0,25 và P = 1
− khi y = 0 , x = 0, z = 3 − . min
Xem thêm: ĐỀ THI HSG TOÁN 10
https://toanmath.com/de-thi-hsg-toan-10
Document Outline

• Toán 10
• HSG 10