Đề chọn HSG Toán 10 vòng 1 năm 2020 – 2021 trường THPT Trần Nguyên Hãn – Hải Phòng

SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI PHÒNG
ĐỀ THI CHỌN HỌC SINH GIỎI VÒNG 1
TRƯỜNG THPT TRẦN NGUYÊN HÃN
LỚP 10 - NĂM HỌC 2020-2021 Môn: Toán ĐỀ THI CHÍNH THỨC (Đề thi có 01 trang)
Thời gian bàm bài: 180 phút, không kể thời gian phát đề
Họ, tên thí sinh: ……………………………………. Số báo danh: ……………….………… Câu I (4,0 điểm). 1. Cho hàm số 2
y  x  2x3 có đồ thị là parabol (P).
a. Khảo sát và vẽ đồ thị hàm số (P).
b. Dựa vào đồ thị (P) vừa vẽ trên hãy tìm tất cả các giá trị của m để phương trình 2
x  2x3  m  0 có 4 nghiệm phân biệt.
2. Tìm tất cả các giá trị của tham số m để hàm số 2
y  (2m 1)x  2mx  m  2 đồng biến trên khoảng (1;) . Câu II (2,0 điểm).  
Cho số thực a  0 và hai tập hợp A   a 16 ; 4 , B  ;  
 . Tìm tất cả các giá trị của a để  a  A B   . Câu III (4,0 điểm). x   2 4 x 3x   2  0 1) Giải phương trình . x m x2
2) Tìm tất cả các giá trị của tham số m để phương trình   2 vô nghiệm. x 1 x 1 Câu IV (2,0 điểm). x2y  4m
Tìm tất cả các giá trị của tham số m để hệ phương trình  có nghiệm thỏa 2 2 x  y  5 2x   y  3m3  .
Câu V (4,0 điểm). Cho tam giác ABC có điểm G là trọng tâm.   
1) Phân tích véctơ AG theo hai véctơ AB và AC .
      
2) Điểm N thỏa mãn NB  3NC  0 chứng minh đẳng thức : 6GN 5AB 7AC  0. PA
3) Gọi P là giao điểm của AC và GN , tính tỉ số . PC Câu VI (2,0 điểm).
Cho các số dương a,b,c thỏa mãn điều kiện abc 1. Tìm giá trị nhỏ nhất của biểu thức bc ca ab P    2 2 2 2 2 2
a b  a c b a b c c a c b
------------------ Hết ------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ tên, Chữ kí của cán bộ coi thi:…………………………………………………………………… ĐÁP ÁN - THANG ĐIỂM Câu I 1. Cho hàm số (P): 2 y  x  2x3 . 3,0
a. Khảo sát và vẽ đồ thị hàm số.
b. Dựa vào đồ thị vừa vẽ trên hãy tìm tất cả các giá trị của m để phương trình 2
x  2x3  m  0 có 4 nghiệm phân biệt.  Ta có : 0,5
 b = 1 và   = 4. 2a 4a
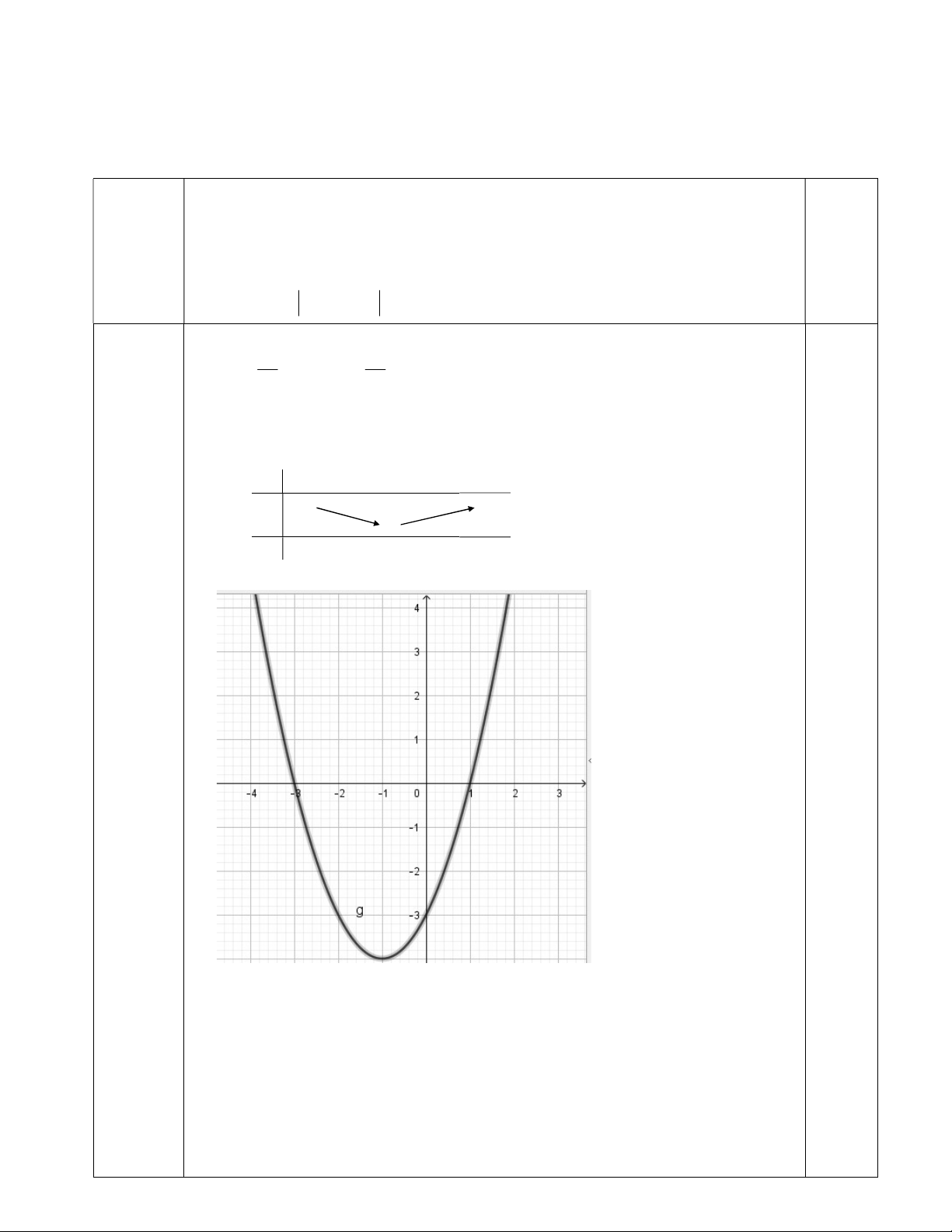
 Vậy, đồ thị hàm số là một parabol có đỉnh S(1; 4), nhận đường thẳng 0,5
x = 1 làm trục đối xứng và hướng bề lõm lên trên.  Bảng biến thiên: x  1 + 0,5 + 4 + y
 Đồ thị: Đồ thị đi qua 2 điểm A(3; 0), B(1; 0). 0,5 c.   Ta có   y  f x f x ; f x 0  
. Từ đó suy ra cách vẽ đồ thị hàm số   f  x ; f x 0 
C từ đồ thị hàm số y  f x như sau: 0,25 
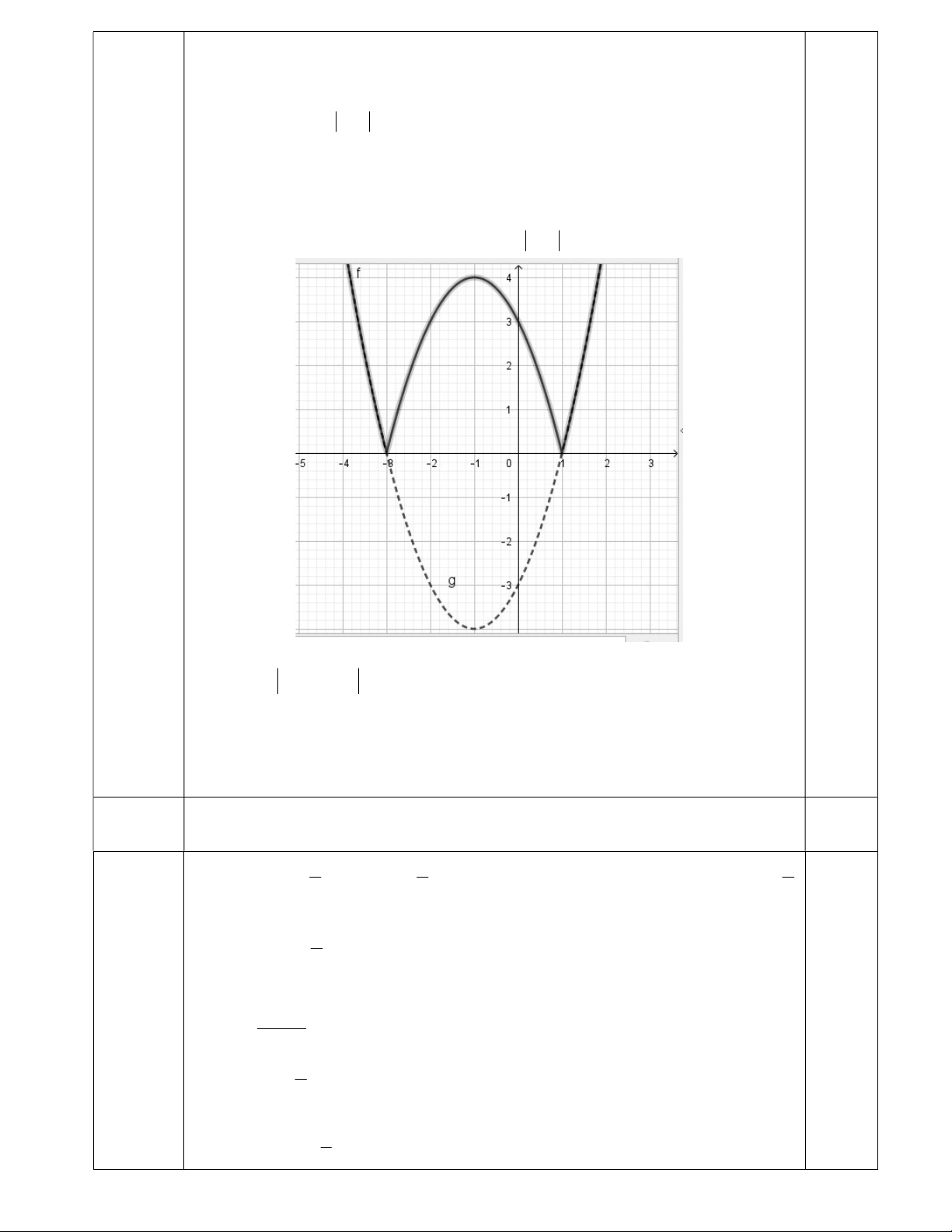
Giữ nguyên đồ thị y  f x phía trên trục hoành. Lấy đối xứng phần đồ
thị y  f x phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
Kết hợp hai phần ta được đồ thị hàm số y  f x như hình vẽ. 0,25
 Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số 2
y  x  2x3 (phần đường đậm) và đường thẳng (d): y =- m là đường
thẳng song song hoặc trùng với trục hoành cắt trục tung tại tung độ -m . 0,25
 Vậy phương trình có 4 nghiệm khi và chỉ khi -4 0,25 2. Tìm m để hàm số 2
y  (2m 1)x  2mx  m  2 đông biến trên khoảng (1;) 1,0 . 1 5 1 0,25
 Với m   y  x  . Hàm số nghịch biến trên  . Do đó m  2 2 2 không thỏa mãn. 0,25  1
Với m  . Hàm số đồng biến trên khoảng 1; khi và chỉ kh 2 2m 1  0   m  0,25 1 2m 1 1 0,25  m  2  Vậy 1 m  2 Câu 2 2,0 Cho số thực  
a  0 và hai tập hợp A   a 16 ; 4 , B  ;  
 . Tìm a để A B    a 
Ta có : A B  khi và chỉ khi 16  4a a 0,5 2 16  4a   0 a 0,25 2
 16  4a  0 (Vì a  0 ) 2  a  4 0,25 a  2 0,25   0,25 a  2 
Kết hợp với a  0 thì a  2  0,25
Kết luận với a  (; 2  ) thì A B  . 0,25 Câu 3 4,0 x   2 4 x 3x   2  0 2,0 1)Giải phương trình (1) Điều kiện 0,5 x  4  x4  0 Ta có   1   0,5 2 x 3x2 0  x  4   x 1 0,5   x  2  0,25  x  4vì x  4.
Kết luận: Phương trình có một nghiệm x = 4. 0,25
2)Tìm m để phương trình sau vô nghiệm: 2,0 x m x2   2 (1) x 1 x 1
 Điều kiện: x  1. 0,5
Ta có (1) suy ra (m + 2)x = 4  m. (2) 0,25 
Trường hợp 1: Nếu m + 2 = 0  m = 2 thì 0,5
(2)  0x = 6, mâu thuẫn  phương trình vô nghiệm.
 Trường hợp 2: Nếu m  2  0  m  2 thì: (2)  x = 4  m . m  2 0,5
Do đó (1) vô nghiệm khi và chỉ khi 4  m 4  m 1 hoÆc  1  m  2 m  2 GPT tìm được m = 1.
 Vậy với m = 2 hoặc m = 1 phương trình (1) vô nghiệm. 0,25 Câu 4 2,0 x2y  4m
Cho hệ phương trình  2x  y  3m 3 
Tìm m để hệ có nghiệm thỏa 2 2 x  y  5 Nhận xét : 1 2 
nên hệ có nghiệm với mọi m 0,5 2 1 0,5 x  m2
Giải hệ có nghiệm  y  1m  0,5 Tính 2 2 2 x  y  2m  2m 5 0,25 Ta có 2 2m  2m 5  5 m  0 0,25   m  1   Câu 5
Cho tam giác ABC có trọng tâm G 4,0   
1) Phân tích véctơ AG theo hai véctơ AB và AC .
  
2) Điểm N thỏa mãn NB  3NC  0 chứng minh đẳng thức:     6GN  5AB 7AC  0 PA
3) Gọi P là giao điểm của AC và GN , tính tỉ số . PC
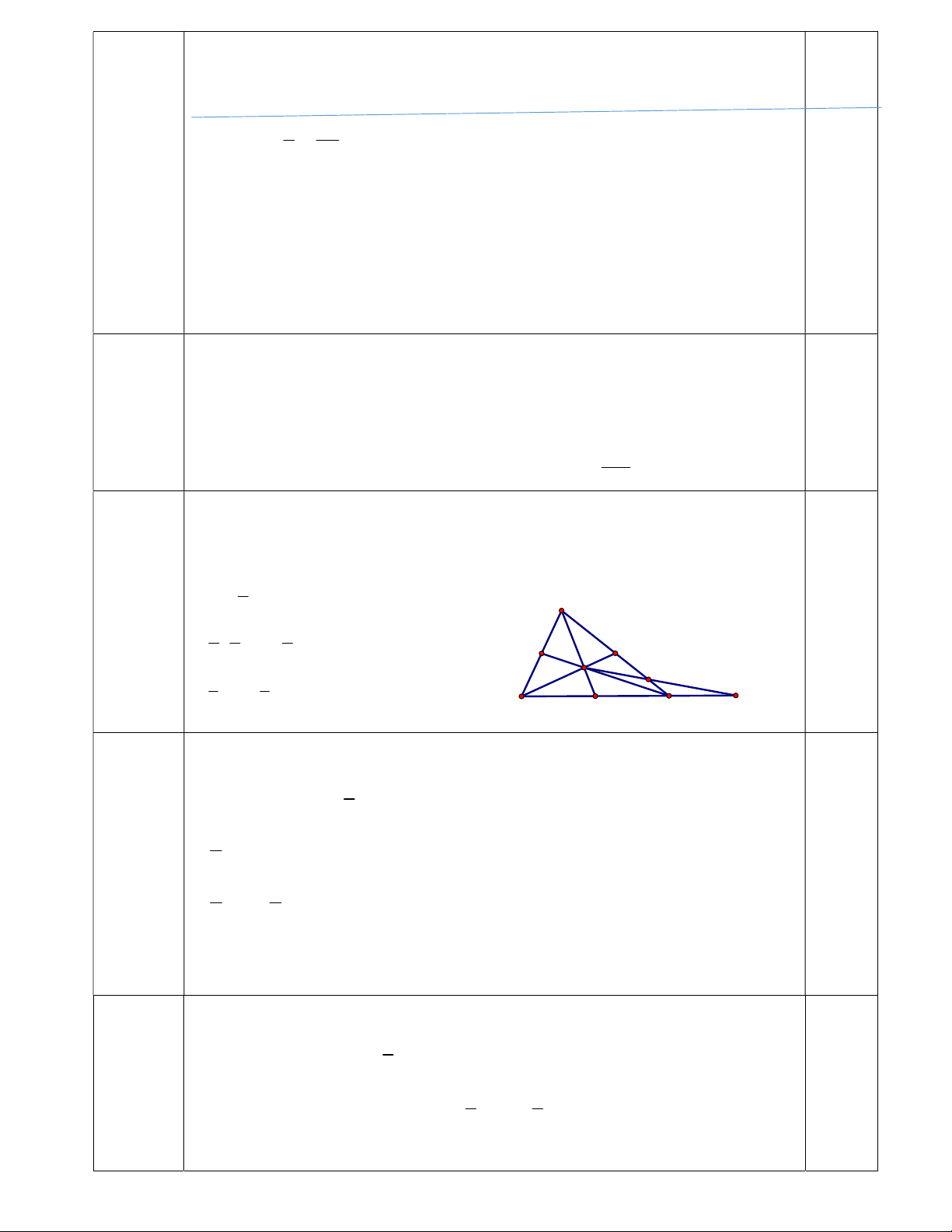
Gọi M là trung điểm của BC 1) Ta có :  0,5 2  AG  AM 3 A
2  1  1   AB AC    0,5 3  2 2  G 1  1  P  AB  AC 3 3 N B M C 0,5 1) Ta có
   1   GN  GM  MN  AM  BC 0,5 3 1    
 AB  AC  AC  AB 0,25 6 7  5   AC  AB 0,25 6 6      6GN  5AB  7AC  O 0,5   2) Đặt AP  k AC .
    1  
GP  AP  AG  k AC   AB  AC 3 0,25 
1   1   k  AC  AB   .  3  3 0,25  5  7 
Theo 2) có GN   AB  AC 6 6  
Ba điểm G, P, N thẳng hàng nên hai vectơ GP,GN cùng phương 0,25 1 1 1 k   k  2 1 7 4  4 3 3 3      k    k   AP  AC 7 5 7 5 3 15 5 5  6 6 6 4 PA  0,25 AP  AC   4 5 PC Câu 6
Cho các số dương a,b,c thỏa mãn điều kiện abc = 1. Tìm giá trị nhỏ nhất của 2,0 biểu thức bc ca ab P    2 2 2 2 2 2
a b  a c b a b c c a c b 1 1 1 1 1 1 bc ca ab P    = 2 2 2 a b c 2 2 2   = a b c   2 2 2 2 2 2
a b  a c b a b c c a  c b b  c a  c a b 1 1 1 1 1 1 0,5    bc ac ab b c c a a b Đặt 1 1 1 x  , y  , z  . a b c
Do abc = 1  xyz = 1 và a,b,c dương suy ra x,y,z dương. Ta có 0,5 2 2 2 x y z P    y  z z  x x  y
Áp dụng bất đẳng thức Côsi, ta có 2 x y  z 2 y z  x 2 z x  y   x ,   y ,   z y  z 4 z  x 4 x  y 4 0,5 x  y  z    x y z 3 3 P   x  y  z 3  P   xyz  2 2 2 2
Dấu “=” xảy ra khi x = y = z = 1 hay a = b = c = 1. Vậy 3 P  khi x = y = z = 1 min 0,5 2