Đề cuối học kì 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Chí Linh – Hải Dương

UBND THÀNH PHỐ CHÍ LINH
ĐỀ KIỂM TRA CUỐI HỌC KÌ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2023– 2024 Môn: Toán 9
Đề gồm 05 câu – 1 trang
Thời gian làm bài: 90 phút
Câu 1 (2.0 điểm): 1) Thực hiện phép tính: 1 A = 20 − 45 + 5 3 2) Rút gọn biểu thức: 2 − 9 2 +1 + 3 P = x x x + −
với x ≥ 0; x ≠ 4; x ≠ 9
( x − 3)( x − 2) x − 3 x − 2
Câu 2 (2.0 điểm): Giải phương trình: 2 1) x − 2x +1 = 3 1 2) 9x − 45 + 4x − 20 = 8 2
Câu 3 (2.0 điểm): Cho hàm số: y = (1 – 3m)x + 5m (d) (m là tham số).
1) Tìm m để hàm số trên nghịch biến trên R.
2) Tìm m để đường thẳng (d) cắt đường thẳng y = 4x +7m +6 (d') tại một điểm trên trục tung.
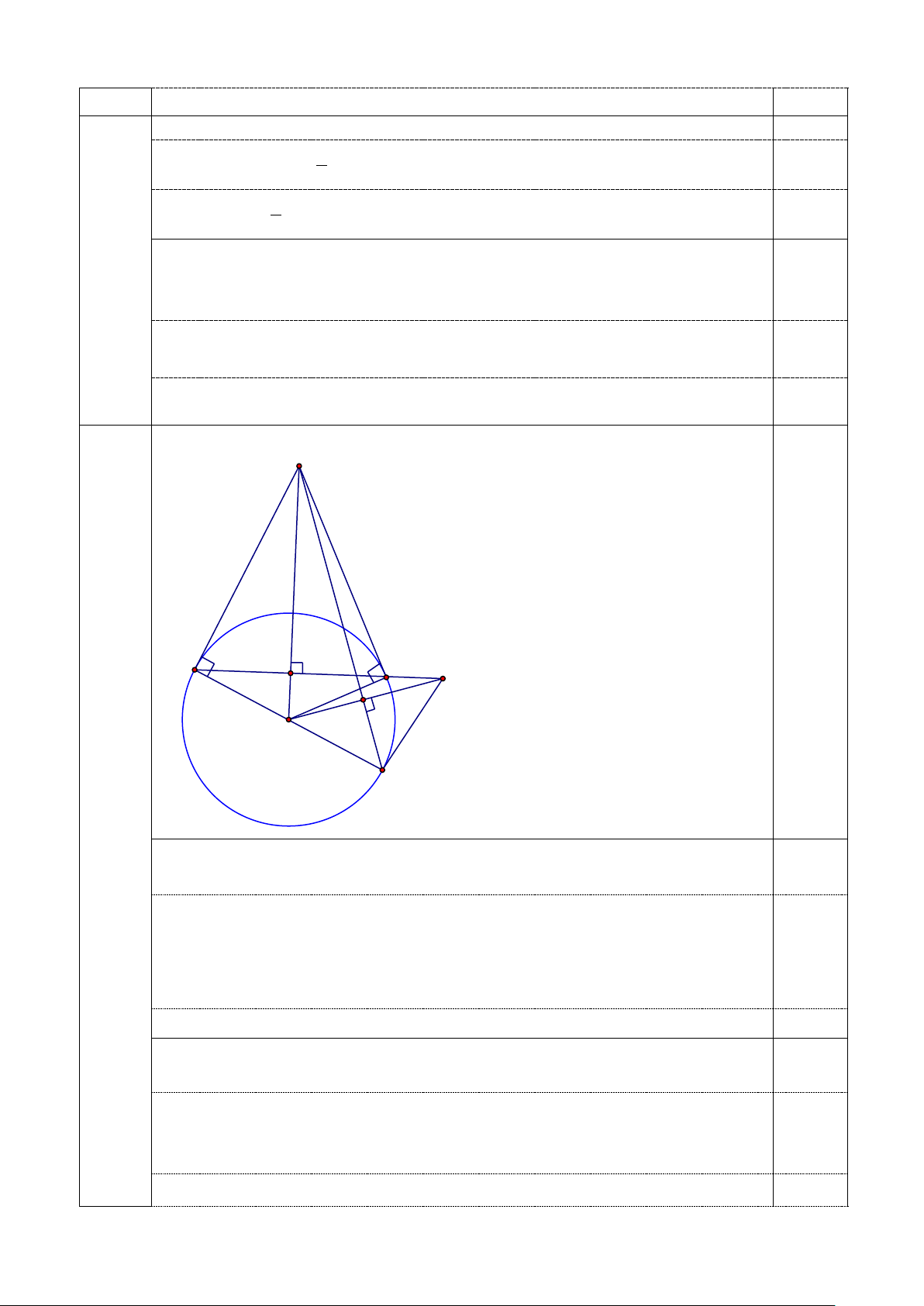
Câu 4 (3,0 điểm): Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn. Từ A kẻ hai
tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Gọi giao điểm của AO và BC là H. Kẻ đường kính BD.
a) Chứng minh: 4 điểm A, B, O, C cùng thuộc một đường tròn. 2 b) Chứng minh . BD OH OA = 4
c) Từ O kẻ OI ⊥ AD (I ∈ AD). Hai đường thẳng OI và BC cắt nhau tại M.
Chứng minh MD là tiếp tuyến của đường tròn (O). Câu 5 (1.0 điểm):
1) Tìm x để biểu thức A đạt giá trị lớn nhất: A = 1 3x − 2 6x + 5 2) Chứng minh: 1 1 2 + ≥ với x
∀ , y > 0 thỏa mãn xy ≥1.
1+ x 1+ y 1+ xy ----- Hết ----- UBND THÀNH PHỐ CHÍ LINH HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ I
Năm học 2023 – 2024 Môn: Toán 9 Câu Đáp án Điểm 1 A = 20 − 45 + 5 3 1 = 2 5 − .3 5 + 5 0,5 3 = 2 5 0,5 2 x − 9 2 x + 1 x + 3 P = + −
(x ≥ 0; x ≠ 4; x ≠ 9) ( x − 3)( x − 2) x − 3 x − 2 2 x − 9
(2 x + 1)( x − 2) ( x + 3)( x − 3) 1 P = + − 0,25 ( x − 3)( x − 2) ( x − 3)( x − 2) ( x − 3)( x − 2)
2 x − 9 + 2x − 3 x − 2 − x + 9 − − P = x x 2 P = ( x − 3)( x − 2) ( x − 3)( x − 2) 0,25 P ( x − 2)( x +1) P = ( x − 3)( x − 2) 0,25 x + 1 P = 0,25 x − 3
Vậy với x ≥ 0; x ≠ 4; x ≠ 9 thì x + 1 P = x − 3 2 1) x − 2x +1 = 3 2 ⇔ (x −1) = 3 ⇔ x −1 = 3 0,25
⇔ x −1 = 3hoặc x −1 = 3 − 0,25 ⇔ x = 4 hoặc x = -2 0,25
Vậy PT có 2 nghiệm: x = 4; x = -2 0,25 2 1 2) 9x − 45 +
4x − 20 = 8 (ĐK: x ≥ 5) 0,25 2 1
⇔ 3 x − 5 + .2 x − 5 = 8 2 ⇔ 4 x − 5 = 8 ⇔ x − 5 = 2 0,25 ⇔ x − 5 = 4 ⇔ x = 9(TM ) 0,25
Vậy phương trình có nghiệm x = 9 0,25
1) Để hàm số nghịch biến trên R thì 1−3m < 0 0,25 1 ⇔ 3 − m < 1 − ⇔ m > 3 0,5 3 Vậy với 1
m > thì hàm số đã cho nghịch biến trên R 3 0,25
2) Để (d) và (d’) cắt nhau tại một điểm trên trục tung thì 1  − 3m ≠ 4 0,25 5   m = 7m + 6  3 − m ≠ 3 m ≠ 1 − ⇔  ⇔  ⇔ m = 3 −  2 − m = 6 m = 3 − 0,5
Vậy với m = -3 thì hai đường thẳng (d )và (d’) cắt nhau tại một điểm 0,25 trên trục tung A 4 B H C 0,25 M I O D
a) Vì AB, AC là tiếp tuyến tại B và C của đường tròn (O) ⇒ AB ⊥ OB, AC ⊥ OC 0,25 Vì ∆ABO vuông tại B
⇒ A, B, O cùng thuộc đường tròn đường kính AO (1) 0,25 Vì ∆ACO vuông tại C
⇒ A, C, O cùng thuộc đường tròn đường kính AO (2)
Từ (1) và (2) ⇒ 4 điểm A, B, O, C cùng thuộc đường tròn đường kính AO 0,25
b) Vì AB, AC là 2 tiếp tuyến cắt nhau tại A của (O) ⇒ AB = AC 0,25 Mà OB = OC (= R)
⇒ OA là trung trực của BC ⇒ OA ⊥ BC tại H 0,25
Xét ∆ ABO vuông tại B có BH ⊥ OA ⇒ 2 OB = . OAOH 0,25 2 Mà BD OB = ⇒ . BD OH OA = 2 4 0,25 c)
Chứng minh ∆OHM ∽ ∆OIA (g-g) ⇒ OH.OA = OI.OM 0,25
Mà OH.OA = OB2 = OD2 ⇒ OI.OM = OD2 ⇒ OD OM =
⇒ ∆OID ∽ ∆ODM (c – g – c) OI OD 0,25 ⇒ góc OID = góc ODM = 900 ⇒ MD ⊥ OD 0,25
⇒ MD là tiếp tuyến tại D của đường tròn (O) 0,25 1) A = 1 ( ĐK: x ≥ 0 ) 3x − 2 6x + 5 1 = 3x − 2 3x. 2 + 2 + 3 = 1 0,25 ( 2 3x − 2 ) + 3 Do ( 2
3x − 2 ) + 3 ≥ 3 với mọi x ≥0 nên 1 1 2 ( ) ≤ − + 3 3x 2 3 1
⇒ GTLN của A là khi và chỉ khi ( 2 3x − 2 ) = 0 5 3 ⇔ 3x = 2 2 1 2
⇔ x = (TM). Vậy GTLN của A là khi x = . 0,25 3 3 3 2) Xét hiệu : 1 1 2 + −
1+ x 1+ y 1+ xy 1 1 1 1 xy − x xy − y = − + − = + 0,25
1+ x 1+ xy 1+ y 1+ xy (1+ x)(1+ xy) (1+ y)(1+ xy)
x ( y − x)
y ( y − x)  y − x    = − =  . x y  − 
(1+ x)(1+ xy) (1+ y)(1+ xy)  1+ 
xy  1 x 1 y  + +     −   + − − 
( y − x)2( xy y x x x y y x y − ) 1 =  .  = ≥   1+ xy     ( x)( y)  + +  (1+ xy ) 0 1 1 (1+ x)(1+ y)
(Vì x,y > 0; xy ≥1 nên xy ≥1 ⇒ ( − )2 y x ( xy − ) 1 ≥ 0
và(1+ xy )(1+ x)(1+ y) > 0) Vậy 1 1 2 + ≥
1+ x 1+ y 1+ xy 0,25