Đề cuối học kì 2 Toán 10 năm 2022 – 2023 trường THPT Thanh Bình – Đồng Nai

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra cuối học kì 2 môn Toán 10 năm học 2022 – 2023 trường THPT Thanh Bình, tỉnh Đồng Nai, mời bạn đọc đón xem

84 42 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

16 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/4 - Mã đề 111
SỞ GD VÀ ĐT ĐỒNG NAI
TRƯỜNG THPT THANH BÌNH
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút;
(35 câu trắc nghiệm - 03 bài tự luận)
Mã đề 111
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng tọa độ
Oxy
, cho
(
) ( )
2; 5 , 1; 0ab=−=−

. Khi đó, tích vô hướng
.
ab

là:
Ⓐ
.2
ab=

Ⓑ
Ⓒ
Ⓓ
.1ab=

Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất. Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai. Ⓓ Căn bậc hai của phương sai.
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
22
22
1 ( 0)
xy
ab
ab
+ = >>
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5
M −
và có vectơ chỉ phương
( )
1; 3u
= −
là
Ⓐ
( )
2
53
xt
t
yt
= −
∈
=−+
. Ⓑ
( )
23
5
xt
t
yt
= +
∈
=−−
.
Ⓒ
( )
12
35
xt
t
yt
=−+
∈
= −
. Ⓓ
( )
15
32
xt
t
yt
=−−
∈
= +
.
Câu 5: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10xy− + −=
.
Ⓐ Song song. Ⓑ Trùng nhau.
Ⓒ Vuông góc. Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm
( )
1; 2I −
, bán kính bằng
3
?
Ⓐ
( ) ( )
22
1 29xy− ++ =
. Ⓑ
( ) ( )
22
1 29xy+ ++ =
.
Ⓒ
( ) ( )
22
1 29xy− +− =
. Ⓓ
(
) ( )
22
1 29xy+ +− =
.
Trang 2/4 - Mã đề 111
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
2
2 ( 0)y px p= >
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số
1, 2, 3
có thể lập được bao nhiêu số tự nhiên có
3
chữ số:
Ⓐ
6
. Ⓑ
27
. Ⓒ
12
. Ⓓ
8
.
Câu 9: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là
Ⓐ
1
. Ⓑ
9!
. Ⓒ
9
. Ⓓ
9
9
.
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố
A
:
Ⓐ
()
() 1 .
()
nA
PA
n
= −
Ω
Ⓑ
()
() .
()
n
PA
nA
Ω
=
Ⓒ
()
() .
()
nA
PA
nB
=
Ⓓ
()
() .
()
nA
PA
n
=
Ω
Câu 11: Trong hệ tọa độ
,Oxy
cho
(
)
( )
5;2 , 10;8AB
. Tìm tọa độ của vectơ
?AB

Ⓐ
( )
15;10AB
=

. Ⓑ
( )
2;4AB =

. Ⓒ
( )
5;6AB
=

. Ⓓ
( )
50;16AB =

.
Câu 12: Một lớp học có 18 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là:
Ⓐ 20 Ⓑ 38 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm
5
chữ số khác nhau được lập từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
.
Ⓐ
20
số. Ⓑ
720
số. Ⓒ
90
số. Ⓓ
120
số.
Câu 14: Chiều cao của một tòa nhà là
34,13 0, 2h mm= ±
. Độ chính xác
d
của phép đo trên là
Ⓐ
34,13dm
=
. Ⓑ
0, 2dm=
. Ⓒ
34,93dm
=
. Ⓓ
34,33m
.
Câu 15: Tổ 1 của lớp 10A1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn.
Ⓐ
8
. Ⓑ
15
. Ⓒ
5
3
. Ⓓ
3
5
Câu 16: Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
3; 4M −
đến đường thẳng
:3 4 1 0xy∆ − −=
.
Ⓐ
8
5
. Ⓑ
24
5
. Ⓒ
12
5
. Ⓓ
24
5
−
.
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng
11
là:
Ⓐ
25
2
. Ⓑ
6
1
. Ⓒ
8
1
. Ⓓ
18
1
.
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả
như bảng sau.
Tìm mốt của mẫu số liệu trên
Ⓐ
7
. Ⓑ
4
. Ⓒ
6
. Ⓓ
5
.
Trang 3/4 - Mã đề 111
Câu 19: Trong mặt phẳng tọa độ
Oxy
cho
( )
3; 5A
,
( )
1; 3B
. Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
.
Ⓐ
( )
2;3I −
. Ⓑ
( )
4;7
I
. Ⓒ
( )
2; 4
I
. Ⓓ
(
)
2; 4I −
.
Câu 20: Gieo một đồng tiền liên tiếp
3
lần thì
()n
Ω
là bao nhiêu?
Ⓐ
16
. Ⓑ
4
. Ⓒ
6
. Ⓓ
8
.
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
Ⓐ
1
2
. Ⓑ
2
3
. Ⓒ
1
. Ⓓ
1
3
.
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ
123
150; 164; 178QQQ= = =
. Ⓑ
123
160; 168; 176QQQ= = =
.
Ⓒ
123
158; 166; 174QQQ= = =
. Ⓓ
123
158; 164; 174QQQ
= = =
.
Câu 23: Cho ba điểm
( ) ( ) ( )
2; 4 , 6;0 , ;4A B Cm−
. Định
m
để
,,
ABC
thẳng hàng?
Ⓐ
6m
= −
. Ⓑ
10m =
. Ⓒ
10
m = −
. Ⓓ
2m =
.
Câu 24: Cho hai vectơ
( )
1; 4a = −
;
( )
6;15b = −
. Tìm tọa độ vectơ
u
biết
uab+=

Ⓐ
( )
7; –19
. Ⓑ
( )
–7; –19
. Ⓒ
( )
–7;19
. Ⓓ
( )
7;19
.
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là
Ⓐ
1
. Ⓑ
2
. Ⓒ
3
. Ⓓ
0
.
Câu 26: Một nhóm học sinh có
10
người. Cần chọn
3
học sinh trong nhóm để làm
3
công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là
Ⓐ
3
10
A
. Ⓑ
3
10
C
. Ⓒ
3
10
. Ⓓ
30
.
Câu 27: Với đa giác lồi
10
cạnh thì số đường chéo là
Ⓐ
35.
Ⓑ
55
. Ⓒ
45.
Ⓓ
90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là:
Ⓐ 15 Ⓑ 20 Ⓒ 16 Ⓓ 18
Câu 29: Trong mặt phẳng
( )
Oxy
, cho elip
( )
E
có phương trình
22
1
36 16
xy
+=
. Tìm tiêu cự của
( )
E
.
Ⓐ
12
25FF =
Ⓑ
12
45FF =
Ⓒ
12
12FF =
Ⓓ
12
8FF =
Câu 30: Khai triển của nhị thức
( )
5
2x −
.
Ⓐ
54 3 2
5 10 40 80 80 32xx xx x 
. Ⓑ
54 32
10 40 80 80 32xx xxx 
.
Ⓒ
54 3 2
10 40 80 80 32xx xx x 
. Ⓓ
54 3 2
100 400 800 800 32xx xx x 
.
Trang 4/4 - Mã đề 111
Câu 31: Xác định
m
để
2
đường thẳng
: 2 30dx y− +=
và
: 30d x my
′
+ +=
vuông góc với nhau.
Ⓐ
2.m 
Ⓑ
1
.
2
m 
Ⓒ
2.m
Ⓓ
1
.
2
m
Câu 32: Tính bán kính đường tròn tâm
( )
1; 2I −
và tiếp xúc với đường thẳng
:3 4 26 0dx y−−=
.
Ⓐ
3
R =
Ⓑ
5
R =
Ⓒ
15R =
Ⓓ
3
5
R =
Câu 33: Trong mặt phẳng
,
Oxy
phương trình elip:
22
1
25 16
xy
+=
có một tiêu điểm là
Ⓐ
( )
0; 4
. Ⓑ
( )
0; 5
. Ⓒ
( )
5;0
−
. Ⓓ
( )
3; 0
.
Câu 34: Trong mặt phẳng tọa độ
,Oxy
cho đường thẳng
d
:
2 5y 1 0
+ +=x
. Phương trình đường thẳng
đi qua điểm
A( 1; 2)−
và vuông góc với d là
Ⓐ
5 2y 9 0− +=x
Ⓑ
2 5y 8 0+ −=x
Ⓒ
5 2y 1 0+ +=x
Ⓓ
5 2y 10 0−+=
x
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là
Ⓐ
3
14
. Ⓑ
3
5
. Ⓒ
3
7
. Ⓓ
3
11
.
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2022 0xy∆ ++ =
và điểm
(0;2022)M
.
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng
∆
.
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng, 8 bông hoa đỏ. Chọn ngẫu
nhiên ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3
bông hoa đỏ.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho
( ) (
)
22
: 2 2 1 10
m
C x y mx m y+ + − − +=
(m là tham số).
Tìm m để
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 122 0xy
∆ + ++ =
.
-----------------------------------------------
----------- HẾT ----------
Trang 1/4 - Mã đề 522
SỞ GD VÀ ĐT ĐỒNG NAI
TRƯỜNG THPT THANH BÌNH
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút;
(35 câu trắc nghiệm - 03 bài tự luận)
Mã đề 522
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng tọa độ
Oxy
, cho
( ) ( )
1; 5 , 1; 0ab=−− =−

. Khi đó, tích vô hướng
.
ab

là:
Ⓐ
.2
ab=

Ⓑ
Ⓒ
Ⓓ
.1
ab=

Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất. Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai. Ⓓ Căn bậc hai của phương sai.
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
22
22
1 ( 0)
xy
ab
ab
+ = >>
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5M −
và có vectơ chỉ phương
( )
3; 1u = −
là
Ⓐ
( )
2
53
xt
t
yt
= −
∈
=−+
. Ⓑ
( )
23
5
xt
t
yt
= +
∈
=−−
.
Ⓒ
( )
12
35
xt
t
yt
=−+
∈
= −
. Ⓓ
( )
15
32
xt
t
yt
=−−
∈
= +
.
Câu 5: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10
xy− +=
và
2
∆
:
4 6 20xy− + −=
.
Ⓐ Song song. Ⓑ Trùng nhau.
Ⓒ Vuông góc. Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm
( )
1; 2I −−
, bán kính bằng
3
?
Ⓐ
( )
( )
22
1 29xy− ++ =
. Ⓑ
(
)
(
)
22
1 29xy+ ++ =
.
Ⓒ
( ) ( )
22
1 29xy−+− =
. Ⓓ
( )
( )
22
1 29xy+ +− =
.
Trang 2/4 - Mã đề 522
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
2
2 ( 0)y px p= >
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số
1, 3
có thể lập được bao nhiêu số tự nhiên có
2
chữ số:
Ⓐ
6
. Ⓑ
27
. Ⓒ
12
. Ⓓ
4
.
Câu 9: Số cách sắp xếp 6 học sinh ngồi vào một dãy gồm 6 ghế là
Ⓐ
1
. Ⓑ
9!
. Ⓒ
6!
. Ⓓ
6
6
.
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố
A
:
Ⓐ
()
() 1 .
()
nA
PA
n
= −
Ω
Ⓑ
()
() .
()
n
PA
nA
Ω
=
Ⓒ
()
() .
()
nA
PA
nB
=
Ⓓ
()
() .
()
nA
PA
n
=
Ω
Câu 11: Trong hệ tọa độ
,Oxy
cho
( ) ( )
5;2 , 7;6AB
. Tìm tọa độ của vectơ
?AB

Ⓐ
( )
15;10AB =

. Ⓑ
( )
2;4AB =

. Ⓒ
( )
5;6AB =

. Ⓓ
( )
50;16AB =

.
Câu 12: Một lớp học có 19 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là:
Ⓐ 20 Ⓑ 380 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm
4
chữ số khác nhau được lập từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
.
Ⓐ
360
số. Ⓑ
720
số. Ⓒ
90
số. Ⓓ
120
số.
Câu 14: Chiều cao của một tòa nhà là
5,13 0, 2h mm= ±
. Độ chính xác
d
của phép đo trên là
Ⓐ
5,13
dm=
. Ⓑ
0, 2dm=
. Ⓒ
5,93dm=
. Ⓓ
5,33m
.
Câu 15: Tổ 1 của lớp 10A1 có 8 học sinh nam và 7 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn.
Ⓐ
8
. Ⓑ
15
. Ⓒ
5
3
. Ⓓ
3
5
Câu 16: Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
3; 4M −
đến đường thẳng
:3 4 1 0xy∆ + −=
.
Ⓐ
8
5
. Ⓑ
24
5
. Ⓒ
12
5
. Ⓓ
24
5
−
.
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng
11
là:
Ⓐ
25
2
. Ⓑ
6
1
. Ⓒ
18
1
. Ⓓ
8
1
.
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả
như bảng sau.
Tìm mốt của mẫu số liệu trên
Ⓐ
7
. Ⓑ
4
. Ⓒ
6
. Ⓓ
5
.
Trang 3/4 - Mã đề 522
Câu 19: Trong mặt phẳng tọa độ
Oxy
cho
( )
3; 5A
,
(
)
7;1
B
−
. Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
.
Ⓐ
. Ⓑ
(
)
4;7I
. Ⓒ
( )
2; 4I
. Ⓓ
( )
2; 4
I −
.
Câu 20: Gieo một đồng tiền liên tiếp
2
lần thì
()n Ω
là bao nhiêu?
Ⓐ
16
. Ⓑ
4
. Ⓒ
6
. Ⓓ
8
.
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là
Ⓐ
1
2
. Ⓑ
2
3
. Ⓒ
1
. Ⓓ
1
3
.
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ
123
150; 164; 178QQQ= = =
. Ⓑ
123
160; 168; 176QQQ= = =
.
Ⓒ
123
158; 166; 174QQ Q= = =
. Ⓓ
123
158; 164; 174QQ Q= = =
.
Câu 23: Cho ba điểm
(
) ( ) ( )
2; 2 , 4;0 , ;2A B Cm
−
. Định
m
để
,,ABC
thẳng hàng?
Ⓐ
6
m
=
. Ⓑ
10m =
. Ⓒ
10m = −
. Ⓓ
2m =
.
Câu 24: Cho hai vectơ
( )
1; 4a = −
;
( )
6;15b = −
. Tìm tọa độ vectơ
u
biết
uab−=

Ⓐ
( )
5;11−
. Ⓑ
( )
–7; –19
. Ⓒ
( )
–7;19
. Ⓓ
( )
5;11
.
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là
Ⓐ
1
. Ⓑ
2
. Ⓒ
3
. Ⓓ
0
.
Câu 26: Một nhóm học sinh có
11
người. Cần chọn
3
học sinh trong nhóm để làm
3
công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là
Ⓐ
3
11
A
. Ⓑ
3
11
C
. Ⓒ
3
11
. Ⓓ
33
.
Câu 27: Với đa giác lồi
12
cạnh thì số đường chéo là
Ⓐ
35.
Ⓑ
55
. Ⓒ
54.
Ⓓ
90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là:
Ⓐ 15 Ⓑ 16 Ⓒ 20 Ⓓ 18
Câu 29: Trong mặt phẳng
( )
Oxy
, cho elip
( )
E
có phương trình
22
1
25 16
xy
+=
. Tìm tiêu cự của
( )
E
.
Ⓐ
12
25FF =
Ⓑ
12
45FF =
Ⓒ
12
12FF =
Ⓓ
12
6FF =
Câu 30: Khai triển của nhị thức
( )
5
21x −
.
Ⓐ
5432
32 80 80 40 10 1xxxxx 
. Ⓑ
54 32
10 40 80 80 32xx xxx 
.
Ⓒ
54 3 2
32 10 40 80 80 1xx xx x 
. Ⓓ
54 3 2
100 400 800 800 32xx xx x 
.
Trang 4/4 - Mã đề 522
Câu 31: Xác định
m
để
2
đường thẳng
1
: 30
2
dx y− +=
và
: 30
d x my
′
+ +=
vuông góc với nhau.
Ⓐ
2.m = −
Ⓑ
1
.
2
m = −
Ⓒ
2.m =
Ⓓ
1
.
2
m =
Câu 32: Tính bán kính đường tròn tâm
( )
1; 2I −
và tiếp xúc với đường thẳng
:3 4 36 0dx y−−=
.
Ⓐ
3R =
. Ⓑ
5R =
. Ⓒ
15R =
. Ⓓ
3
5
R =
.
Câu 33: Trong mặt phẳng
,
Oxy
phương trình elip:
22
1
100 64
xy
+=
có một tiêu điểm là
Ⓐ
( )
0; 4
. Ⓑ
( )
0;3
. Ⓒ
( )
5;0−
. Ⓓ
( )
6;0
.
Câu 34: Trong mặt phẳng tọa độ
,Oxy
cho đường thẳng
d
:
2 5y 1 0+ +=x
. Phương trình đường thẳng
đi qua điểm
A( 1; 2)−
và vuông góc với d là
Ⓐ
5 2y 9 0− +=
x
Ⓑ
2 5y 8 0+ −=x
Ⓒ
5 2y 1 0+ +=x
Ⓓ
5 2y 10 0
−+=x
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là
Ⓐ
3
14
. Ⓑ
3
5
. Ⓒ
3
7
. Ⓓ
3
11
.
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2023 0
xy
∆ ++ =
và điểm
(0;2023)M
.
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng
∆
.
Bài 2: Cửa hàng nhà An có 7 bông hoa vàng, 8 bông hoa đỏ, 5 bông hoa trắng. Chọn ngẫu
nhiên ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông
hoa trắng.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho
( ) ( )
22
: 4 22 1 1 0
m
C x y mx m y+ + − − +=
(m là tham số).
Tìm m để
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 122 0xy∆ + ++ =
.
----------- HẾT ----------
Trang 1/4 - Mã đề 111
SỞ GD VÀ ĐT ĐỒNG NAI
TRƯỜNG THPT THANH BÌNH
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút;
(35 câu trắc nghiệm - 03 bài tự luận)
Mã đề 939
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: .............................
Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng tọa độ
Oxy
, cho
( ) ( )
2; 5 , 1; 0ab=−=−

. Khi đó, tích vô hướng
.ab

là:
Ⓐ
.2
ab=

Ⓑ
.2ab= −

Ⓒ
.7ab= −

Ⓓ
.1ab=

Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất. Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai. Ⓓ Căn bậc hai của phương sai.
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
22
22
1 ( 0)
xy
ab
ab
+ = >>
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5M −
và có vectơ chỉ phương
( )
1; 3u = −
là
Ⓐ
( )
2
53
xt
t
yt
= −
∈
=−+
. Ⓑ
( )
23
5
xt
t
yt
= +
∈
=−−
.
Ⓒ
( )
12
35
xt
t
yt
=−+
∈
= −
. Ⓓ
( )
15
32
xt
t
yt
=−−
∈
= +
.
Câu 5: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10xy− + −=
.
Ⓐ Song song. Ⓑ Trùng nhau.
Ⓒ Vuông góc. Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm
( )
1; 2I −
, bán kính bằng
3
?
Ⓐ
( ) ( )
22
1 29xy− ++ =
. Ⓑ
( ) ( )
22
1 29xy+ ++ =
.
Ⓒ
( ) ( )
22
1 29xy− +− =
. Ⓓ
(
) ( )
22
1 29xy+ +− =
.
Trang 2/4 - Mã đề 111
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc
dạng:
2
2 ( 0)y px p= >
?
Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số
1, 2, 3
có thể lập được bao nhiêu số tự nhiên có
3
chữ số:
Ⓐ
6
. Ⓑ
27
. Ⓒ
12
. Ⓓ
8
.
Câu 9: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là
Ⓐ
1
. Ⓑ
9!
. Ⓒ
9
. Ⓓ
9
9
.
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố
A
:
Ⓐ
()
() 1 .
()
nA
PA
n
= −
Ω
Ⓑ
()
() .
()
n
PA
nA
Ω
=
Ⓒ
()
() .
()
nA
PA
nB
=
Ⓓ
()
() .
()
nA
PA
n
=
Ω
Câu 11: Trong hệ tọa độ
,Oxy
cho
(
) ( )
5;2 , 10;8AB
. Tìm tọa độ của vectơ
?AB

Ⓐ
( )
15;10AB
=

. Ⓑ
(
)
2;4
AB =

. Ⓒ
(
)
5;6AB =

. Ⓓ
( )
50;16AB =

.
Câu 12: Một lớp học có 18 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là:
Ⓐ 20 Ⓑ 38 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm
5
chữ số khác nhau được lập từ các chữ số
1
,
2
,
3
,
4
,
5
,
6
.
Ⓐ
20
số. Ⓑ
720
số. Ⓒ
90
số. Ⓓ
120
số.
Câu 14: Chiều cao của một tòa nhà là
34,13 0, 2h mm= ±
. Độ chính xác
d
của phép đo trên là
Ⓐ
34,13dm=
. Ⓑ
0, 2dm=
. Ⓒ
34,93dm=
. Ⓓ
34,33m
.
Câu 15: Tổ 1 của lớp 10A1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn.
Ⓐ
8
. Ⓑ
15
. Ⓒ
5
3
. Ⓓ
3
5
Câu 16: Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
3; 4M −
đến đường thẳng
:3 4 1 0
xy∆ − −=
.
Ⓐ
8
5
. Ⓑ
24
5
. Ⓒ
12
5
. Ⓓ
24
5
−
.
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng
11
là:
Ⓐ
25
2
. Ⓑ
6
1
. Ⓒ
8
1
. Ⓓ
18
1
.
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả
như bảng sau.
Tìm mốt của mẫu số liệu trên
Ⓐ
7
. Ⓑ
4
. Ⓒ
6
. Ⓓ
5
.
Trang 3/4 - Mã đề 111
Câu 19: Trong mặt phẳng tọa độ
Oxy
cho
( )
3; 5A
,
( )
1; 3
B
. Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
.
Ⓐ
( )
2;3
I
−
. Ⓑ
( )
4;7I
. Ⓒ
( )
2; 4I
. Ⓓ
( )
2; 4
I −
.
Câu 20: Gieo một đồng tiền liên tiếp
3
lần thì
()
n Ω
là bao nhiêu?
Ⓐ
16
. Ⓑ
4
. Ⓒ
6
. Ⓓ
8
.
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là
Ⓐ
1
2
. Ⓑ
2
3
. Ⓒ
1
. Ⓓ
1
3
.
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ
123
150; 164; 178QQQ= = =
. Ⓑ
123
160; 168; 176
QQQ
= = =
.
Ⓒ
123
158; 166; 174QQ Q= = =
. Ⓓ
123
158; 164; 174QQ Q= = =
.
Câu 23: Cho ba điểm
( )
( ) ( )
2; 2 , 4;0 , ;2A B Cm−
. Định
m
để
,,ABC
thẳng hàng?
Ⓐ
6m =
. Ⓑ
10m
=
. Ⓒ
10m = −
. Ⓓ
2m =
.
Câu 24: Cho hai vectơ
( )
1; 4a = −
;
( )
6;15b = −
. Tìm tọa độ vectơ
u
biết
uab−=

Ⓐ
( )
5;11−
. Ⓑ
(
)
–7; –19
. Ⓒ
(
)
–7;19
. Ⓓ
( )
5;11
.
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là
Ⓐ
1
. Ⓑ
2
. Ⓒ
3
. Ⓓ
0
.
Câu 26: Một nhóm học sinh có
11
người. Cần chọn
3
học sinh trong nhóm để làm
3
công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là
Ⓐ
3
11
A
. Ⓑ
3
11
C
. Ⓒ
3
11
. Ⓓ
33
.
Câu 27: Với đa giác lồi
12
cạnh thì số đường chéo là
Ⓐ
35.
Ⓑ
55
. Ⓒ
54.
Ⓓ
90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là:
Ⓐ 15 Ⓑ 16 Ⓒ 20 Ⓓ 18
Câu 29: Trong mặt phẳng
( )
Oxy
, cho elip
( )
E
có phương trình
22
1
25 16
xy
+=
. Tìm tiêu cự của
( )
E
.
Ⓐ
12
25FF =
Ⓑ
12
45FF =
Ⓒ
12
12FF =
Ⓓ
12
6FF =
Câu 30: Khai triển của nhị thức
(
)
5
21x −
.
Ⓐ
5432
32 80 80 40 10 1xxxxx 
. Ⓑ
54 32
10 40 80 80 32xx xxx 
.
Ⓒ
54 3 2
32 10 40 80 80 1
xx xx x 
. Ⓓ
54 3 2
100 400 800 800 32xx xx x 
.
Trang 4/4 - Mã đề 111
Câu 31: Xác định
m
để
2
đường thẳng
1
: 30
2
dx y− +=
và
: 30d x my
′
+ +=
vuông góc với nhau.
Ⓐ
2.m = −
Ⓑ
1
.
2
m
= −
Ⓒ
2.m =
Ⓓ
1
.
2
m =
Câu 32: Tính bán kính đường tròn tâm
( )
1; 2I −
và tiếp xúc với đường thẳng
:3 4 36 0dx y−−=
.
Ⓐ
3
R
=
. Ⓑ
5R =
. Ⓒ
15R =
. Ⓓ
3
5
R =
.
Câu 33: Trong mặt phẳng
,Oxy
phương trình elip:
22
1
100 64
xy
+=
có một tiêu điểm là
Ⓐ
( )
0; 4
. Ⓑ
(
)
0;3
. Ⓒ
(
)
5;0
−
. Ⓓ
(
)
6;0
.
Câu 34: Trong mặt phẳng tọa độ
,Oxy
cho đường thẳng
d
:
2 5y 1 0+ +=x
. Phương trình đường thẳng
đi qua điểm
A( 1; 2)−
và vuông góc với d là
Ⓐ
5 2y 9 0− +=x
Ⓑ
2 5y 8 0+ −=x
Ⓒ
5 2y 1 0+ +=x
Ⓓ
5 2y 10 0
−+=x
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là
Ⓐ
3
14
. Ⓑ
3
5
. Ⓒ
3
7
. Ⓓ
3
11
.
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2023 2022 0xy∆+ + =
và điểm
(0;1)M
.
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng
∆
.
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng. Chọn ngẫu nhiên ra 3 bông
hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho phương trình đường tròn
( ) ( )
22
: 2 2 1 10
m
C x y mx m y+ + − − +=
(m là tham số). Tìm m để
( )
m
C
tiếp xúc với đường thẳng
: 122 0xy∆ + ++ =
.
-----------------------------------------------
----------- HẾT ----------
ĐÁP ÁN
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 – MÔN TOÁN 10 - 2023
ĐÁP ÁN ĐỀ THI TRẮC NGHIỆM - (7 điểm)
Mã đề [111]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
D
D
A
A
D
A
B
B
D
C
C
B
B
A
B
D
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
C
D
A
C
B
C
C
A
A
B
B
C
D
A
D
A
D
Mã đề [213]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
A
D
A
C
D
A
A
C
A
C
C
D
B
A
B
D
B
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
C
D
D
C
B
D
A
C
D
A
C
B
B
A
B
B
Mã đề [315]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
D
B
A
A
C
A
D
D
A
B
A
C
B
D
C
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
B
A
B
B
C
B
B
C
A
D
C
D
C
B
B
B
Mã đề [417]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
B
D
C
A
A
C
A
A
D
D
C
D
C
A
D
A
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
B
D
C
B
C
D
C
C
B
C
D
A
C
B
B
A
Mã đề [522]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
D
D
B
B
B
A
D
C
D
B
B
A
B
B
A
C
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
B
A
C
A
C
C
A
C
C
D
A
C
B
D
A
D
Mã đề [624]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
D
A
A
B
B
A
A
D
B
B
D
B
B
A
C
A
A
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
C
D
D
C
C
C
D
A
C
A
B
C
B
D
A
D
C
Mã đề [726]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
A
B
C
D
B
A
C
D
B
D
C
D
C
B
D
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
A
A
A
B
D
A
B
B
C
D
D
A
C
B
C
A
Mã đề [828]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
C
C
A
A
B
B
A
C
D
A
B
D
A
C
C
A
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
A
A
B
B
C
C
C
B
C
B
D
D
D
D
B
C
Mã đề [939]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
D
D
A
A
D
A
B
B
D
C
C
B
B
A
B
D
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
C
D
A
C
A
C
C
A
C
C
D
A
C
B
D
A
D
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [111]-[213]-[315]-[417]
Bài
Ý
Nội dung
Điểm
1
1 điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2022 0xy∆ ++ =
và điểm
(0;2022)M
. Viết phương trình tổng quát của đường thẳng đi qua M và song song
với đường thẳng
∆
.
∑
1,0đ
Giả sử
'
∆
là đường thẳng song song với đường thẳng
:2 2022 0xy∆ ++ =
có dạng :
2 0 ( 2022).xym m++ = ≠
0,25
Vì
(0;2022) 'M ∈∆
nên
2022 0 2022mm+=⇔=−
(nhận)
0,5
Vậy PTTQ của
'∆
:
2 2022 0.xy+− =
0,25
2
1 điểm
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng, 8 bông hoa đỏ. Chọn ngẫu nhiên
ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3 bông
hoa đỏ.
∑
1,0đ
Số phần tử của không gian mẫu:
( )
6
20
38760
nC
Ω= =
.
0,25
Gọi A là biến cố: “chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3 bông hoa đỏ”.
( )
123
578
. . 5880nA CCC= =
cách.
0,25
Vậy xác suất cần tìm là
( )
( )
( )
5880 49
38760 323
nA
pA
n
= = =
Ω
.
0,5
3
1 điểm
Bài 3: Trong mặt phẳng tọa độ Oxy, cho
( ) ( )
22
: 2 2 1 10
m
C x y mx m y+ + − − +=
(m là tham
số). Tìm m để
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 1 22 0xy
∆ + ++ =
∑
1,0đ
Ta có:
, 1, 1a mb m c=− =−=
( )
m
C
là đường tròn tâm
( )
;1I mm−−
và bán kính
2
22R mm= −
khi
22
0abc+ −>
0,25
22 2
1
( 1) 1 0 2 2 0
0
m
mm m m
m
>
⇔ + − −>⇔ − >⇔
<
0,25
Do
(
)
m
C
tiếp xúc với
( )
2
: 1 22 0 ;
1
m
x y dI R
m
=
∆ + ++ = ⇔ ∆= ⇔
= −
(thỏa mãn )
0,25
Vậy
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 1 22 0
xy∆ + ++ =
khi
{ }
1; 2m = −
0,25
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [522]-[624]-[726]-[828]
Bài
Ý
Nội dung
Điểm
1
1 điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2023 0xy∆ ++ =
và điểm
(0;2023)M
.
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng
∆
.
∑
1,0đ
Giả sử
'∆
là đường thẳng song song với đường thẳng
:2 2023 0xy
∆ ++ =
có dạng :
2 0 ( 2023).
xym m++ = ≠
0,25
Vì
(0;2023) 'M ∈∆
nên
2023 0 2023
mm+=⇔=−
(nhận)
0,5
Vậy PTTQ của
'∆
:
2 2023 0.xy+− =
0,25
2
1 điểm
Bài 2: Cửa hàng nhà An 7 bông hoa vàng, 8 bông hoa đỏ, có 5 bông hoa trắng. Chọn ngẫu nhiên
ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa
trắng.
∑
1,0đ
Số phần tử của không gian mẫu:
( )
6
20
38760nC
Ω= =
.
0,25
Gọi A là biến cố: “chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng”.
( )
123
78 5
. . 1960nA CCC= =
cách.
0,25
Vậy xác suất cần tìm là
( )
( )
( )
1960 49
38760 969
nA
pA
n
= = =
Ω
.
0,5
3
1 điểm
Bài 3:
Trong mặt phẳng tọa độ Oxy, cho
( ) ( )
22
: 4 22 1 1 0
m
C x y mx m y+ + − − +=
(m là tham
số). Tìm m để
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 1 22 0xy∆ + ++ =
∑
1,0đ
Ta có:
2 , 2 1, 1a mb m c=− =−=
(
)
m
C
là đường tròn tâm
(
)
2 ;2 1I mm
−−
và bán kính
2
84R mm= −
khi
22
0abc+ −>
0,25
22 2
1
4 (2 1) 1 0 8 4 0
2
0
m
m m mm
m
>
⇔ + − −>⇔ − >⇔
<
0,25
Do
( )
m
C
tiếp xúc với
(
)
1
: 1 22 0 ;
1
2
m
x y dI R
m
=
∆ + ++ = ⇔ ∆= ⇔
−
=
(thỏa mãn )
0,25
Vậy
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 1 22 0xy∆ + ++ =
khi
1
;1
2
m
−

=


0,25
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [939]
Bài
Ý
Nội dung
Điểm
1
1 điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:2 2023 2022 0xy∆+ + =
và điểm
(0;1)M
. Viết phương trình tổng quát của đường thẳng đi qua M và song song với
đường thẳng
∆
.
∑
1,0đ
Giả sử
'
∆
là đường thẳng song song với đường thẳng
:2 2023 2022 0xy∆+ + =
có dạng :
2 2023 0 ( 2022).x ym m+ += ≠
0,25
Vì
(0;1) 'M ∈∆
nên
2023 0 2023mm+=⇔=−
(nhận)
0,5
Vậy PTTQ của
'
∆
:
2 2023 2023 0.
xy+ −=
0,25
2
1 điểm
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng. Chọn ngẫu nhiên ra 3 bông
hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng.
∑
1,0đ
Số phần tử của không gian mẫu:
( )
3
12
220nCΩ= =
.
0,25
Gọi A là biến cố: “chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng”.
( )
12
57
. 105nA CC= =
cách.
0,25
Vậy xác suất cần tìm là
( )
( )
( )
105 21
220 44
nA
pA
n
= = =
Ω
.
0,5
3
1 điểm
Bài 3: Trong mặt phẳng tọa độ O xy, cho phương trình đường tròn
( ) ( )
22
: 2 2 1 10
m
C x y mx m y+ + − − +=
(m là tham số). Tìm m để
( )
m
C
tiếp xúc với
đường thẳng
: 1 22 0
xy∆ + ++ =
.
∑
1,0đ
Ta có:
, 1, 1
a mb m c
=− =−=
Đường tròn
( )
m
C
có tâm
(
)
;1I mm−−
và bán kính
2
22R mm
= −
0,25
Do
( )
m
C
tiếp xúc với
( )
2
: 1 22 0 ;
1
m
x y dI R
m
=
∆ + ++ = ⇔ ∆= ⇔
= −
(thỏa mãn )
0,5
Vậy
( )
m
C
là đường tròn và tiếp xúc với đường thẳng
: 1 22 0
xy∆ + ++ =
khi
{ }
1; 2m = −
0,25
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD VÀ ĐT ĐỒNG NAI
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
TRƯỜNG THPT THANH BÌNH
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(35 câu trắc nghiệm - 03 bài tự luận) Mã đề 111
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: ............................. Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).  
Câu 1: Trong mặt phẳng tọa độ  
Oxy , cho a = (2; 5 − ),b = ( 1;
− 0) . Khi đó, tích vô hướng . a b là:         Ⓐ . a b = 2 Ⓑ . a b = 2 − Ⓒ . a b = 7 − Ⓓ . a b = 1
Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất.
Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai.
Ⓓ Căn bậc hai của phương sai.
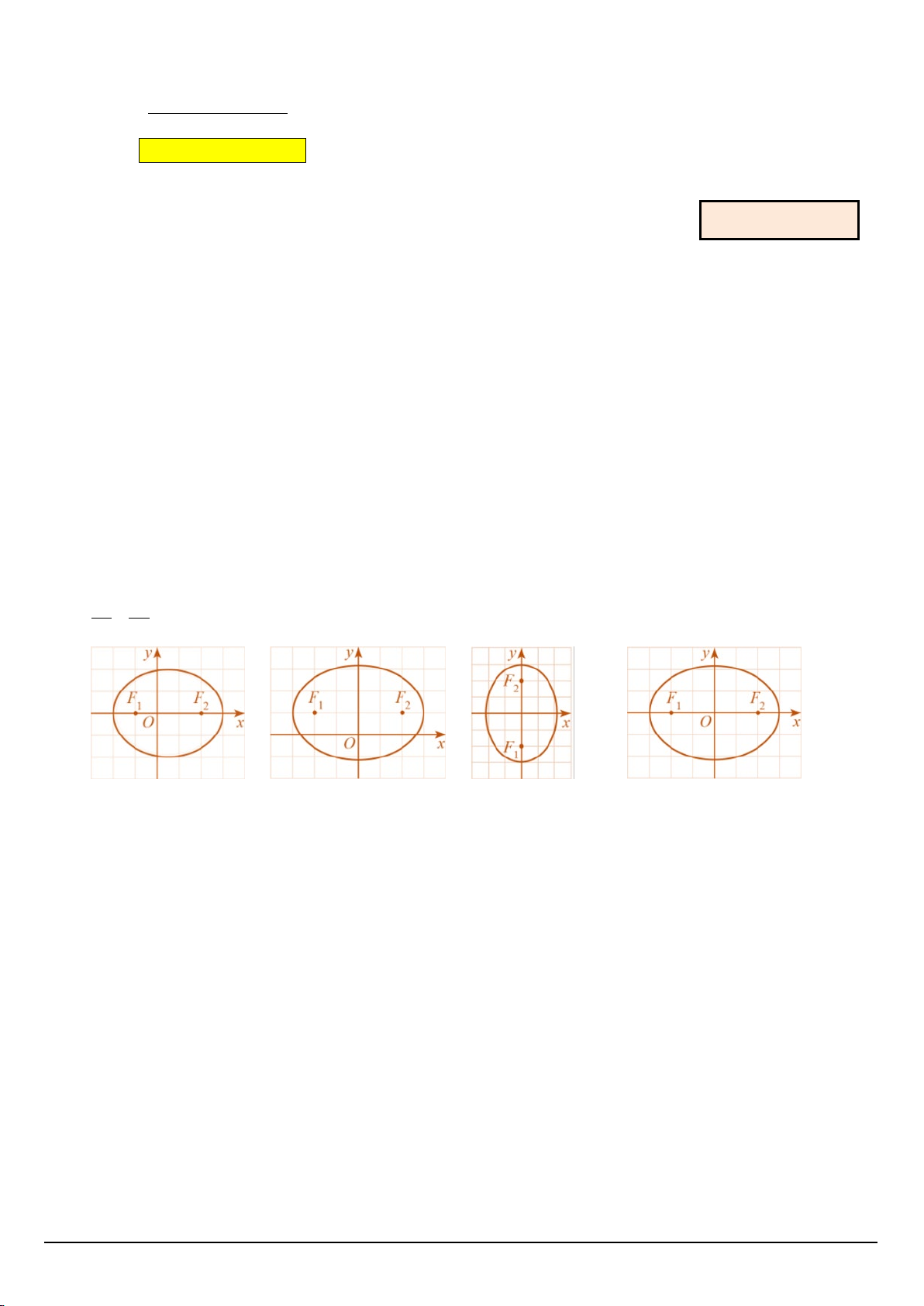
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc 2 2 dạng: x y +
= 1 (a > b > 0) ? 2 2 a b Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u =( 1; − 3) là x = 2 − tx = 2 + 3t Ⓐ  (t ∈). Ⓑ  (t ∈) . y = 5 − + 3ty = 5 − − tx = 1 − + 2tx = 1 − − 5t Ⓒ  (t ∈) . Ⓓ  (t ∈) . y = 3− 5ty = 3+ 2t
Câu 5: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ : và ∆ : .
1 2x − 3y +1 = 0 2 4
− x + 6y −1 = 0 Ⓐ Song song. Ⓑ Trùng nhau. Ⓒ Vuông góc.
Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm I ( 1; − 2), bán kính bằng 3?
Ⓐ ( x − )2 + ( y + )2 1 2 = 9 .
Ⓑ ( x + )2 + ( y + )2 1 2 = 9 .
Ⓒ ( x − )2 + ( y − )2 1 2 = 9.
Ⓓ ( x + )2 + ( y − )2 1 2 = 9 . Trang 1/4 - Mã đề 111
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: 2
y = 2 px ( p > 0) ? Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số 1,2,3 có thể lập được bao nhiêu số tự nhiên có 3chữ số: Ⓐ 6 . Ⓑ 27 . Ⓒ 12. Ⓓ 8 .
Câu 9: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là Ⓐ 1. Ⓑ 9!. Ⓒ 9. Ⓓ 9 9 .
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố A : n A n Ω n A n A Ⓐ ( ) P( ) A =1− . Ⓑ ( ) P( ) A = . Ⓒ ( ) P( ) A = . Ⓓ ( ) P( ) A = . n(Ω) n( ) A n(B) n(Ω) 
Câu 11: Trong hệ tọa độ Oxy, cho A(5;2), B(10;8). Tìm tọa độ của vectơ AB?    
Ⓐ AB = (15;10) .
Ⓑ AB = (2;4) .
Ⓒ AB = (5;6) .
Ⓓ AB = (50;16) .
Câu 12: Một lớp học có 18 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là: Ⓐ 20 Ⓑ 38 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được lập từ các chữ số 1, 2 , 3, 4 , 5, 6 . Ⓐ 20 số. Ⓑ 720 số. Ⓒ 90 số. Ⓓ 120 số.
Câu 14: Chiều cao của một tòa nhà là h = 34,13m ± 0,2m . Độ chính xác d của phép đo trên là
Ⓐ d = 34,13m .
Ⓑ d = 0,2m .
Ⓒ d = 34,93m .
Ⓓ 34,33m .
Câu 15: Tổ 1 của lớp 10A1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn. Ⓐ 8 . Ⓑ 15 . Ⓒ 5 3 . Ⓓ 3 5
Câu 16: Trong mặt phẳng Oxy , khoảng cách từ điểm M (3;− 4) đến đường thẳng ∆ :3x − 4y −1= 0 . Ⓐ 8 . Ⓑ 24 . Ⓒ 12 . Ⓓ 24 − . 5 5 5 5
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng 11 là: Ⓐ 2 . Ⓑ 1 . Ⓒ 1 . Ⓓ 1 . 25 6 8 18
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả như bảng sau.
Tìm mốt của mẫu số liệu trên Ⓐ 7 . Ⓑ 4 . Ⓒ 6 . Ⓓ 5. Trang 2/4 - Mã đề 111
Câu 19: Trong mặt phẳng tọa độ Oxy cho A(3;5), B(1;3) . Tìm tọa độ trung điểm I của đoạn thẳng AB . Ⓐ I ( 2; − 3). Ⓑ I (4;7). Ⓒ I (2;4). Ⓓ I ( 2; − 4) .
Câu 20: Gieo một đồng tiền liên tiếp 3 lần thì n(Ω) là bao nhiêu? Ⓐ 16. Ⓑ 4 . Ⓒ 6 . Ⓓ 8 .
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là Ⓐ 1 . Ⓑ 2 . Ⓒ 1. Ⓓ 1 . 2 3 3
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ Q =150;Q =164;Q =178 .
Ⓑ Q =160;Q =168;Q =176 . 1 2 3 1 2 3
Ⓒ Q =158;Q =166;Q =174 .
Ⓓ Q =158;Q =164;Q =174 . 1 2 3 1 2 3
Câu 23: Cho ba điểm A(2 ; 4
− ), B(6 ; 0),C (m ; 4) . Định m để ,
A B,C thẳng hàng? Ⓐ m = 6 − .
Ⓑ m =10 . Ⓒ m = 10 − .
Ⓓ m = 2 .      
Câu 24: Cho hai vectơ a = (1; 4 − ) ; b = ( 6;
− 15) . Tìm tọa độ vectơ u biết u + a = b Ⓐ (7; –19) . Ⓑ (–7; –19) . Ⓒ (–7;19) . Ⓓ (7;19) .
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là Ⓐ 1. Ⓑ 2 . Ⓒ 3. Ⓓ 0 .
Câu 26: Một nhóm học sinh có 10 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là Ⓐ 3 A . Ⓑ 3 C . Ⓒ 3 10 . Ⓓ 30. 10 10
Câu 27: Với đa giác lồi 10 cạnh thì số đường chéo là Ⓐ 35. Ⓑ 55. Ⓒ 45. Ⓓ 90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là: Ⓐ 15 Ⓑ 20 Ⓒ 16 Ⓓ 18 2 2
Câu 29: Trong mặt phẳng (Oxy), cho elip (E) có phương trình x y +
=1. Tìm tiêu cự của (E). 36 16 Ⓐ F F = 2 5 Ⓑ F F = 4 5 Ⓒ F F =12 Ⓓ F F =8 1 2 1 2 1 2 1 2
Câu 30: Khai triển của nhị thức (x − )5 2 . Ⓐ 5 4 3 2
5x 10x  40x 80x 80x32. Ⓑ 5 4 3 2
x 10x  40x 80x 80x 32 . Ⓒ 5 4 3 2
x 10x  40x 80x 80x32 . Ⓓ 5 4 3 2
x 100x  400x 800x 800x32 . Trang 3/4 - Mã đề 111
Câu 31: Xác định m để 2 đường thẳng d : x − 2y + 3 = 0 và d′: x + my + 3 = 0 vuông góc với nhau. Ⓐ m  2. Ⓑ 1 m   . Ⓒ m  2. Ⓓ 1 m  . 2 2
Câu 32: Tính bán kính đường tròn tâm I (1; 2
− ) và tiếp xúc với đường thẳng d :3x − 4y − 26 = 0 . Ⓐ R = 3 Ⓑ R = 5 Ⓒ R =15 Ⓓ 3 R = 5 2 2
Câu 33: Trong mặt phẳng x y
Oxy, phương trình elip: + =1 25 16
có một tiêu điểm là Ⓐ (0;4) . Ⓑ (0; 5). Ⓒ (− 5;0). Ⓓ (3;0) .
Câu 34: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d :2x +5y +1 = 0. Phương trình đường thẳng đi qua điểm A( 1
− ; 2) và vuông góc với d là
Ⓐ 5x − 2y + 9 = 0
Ⓑ 2x + 5y − 8 = 0
Ⓒ 5x + 2y +1 = 0
Ⓓ 5x − 2y +10 = 0
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là Ⓐ 3 . Ⓑ 3 . Ⓒ 3 . Ⓓ 3 . 14 5 7 11
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + y + 2022 = 0 và điểm M (0;2022).
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng ∆ .
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng, 8 bông hoa đỏ. Chọn ngẫu
nhiên ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3 bông hoa đỏ.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho (C
x + y + mx − m − y + = (m là tham số). m ) 2 2 : 2 2( )1 1 0
Tìm m để (C là đường tròn và tiếp xúc với đường thẳng ∆ : x + y +1+ 2 2 = 0. m )
----------------------------------------------- ----------- HẾT ---------- Trang 4/4 - Mã đề 111 SỞ GD VÀ ĐT ĐỒNG NAI
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
TRƯỜNG THPT THANH BÌNH
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(35 câu trắc nghiệm - 03 bài tự luận) Mã đề 522
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: ............................. Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).  
Câu 1: Trong mặt phẳng tọa độ  
Oxy , cho a = ( 1; − 5 − ),b = ( 1;
− 0) . Khi đó, tích vô hướng . a b là:         Ⓐ . a b = 2 Ⓑ . a b = 2 − Ⓒ . a b = 7 − Ⓓ . a b = 1
Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất.
Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai.
Ⓓ Căn bậc hai của phương sai.
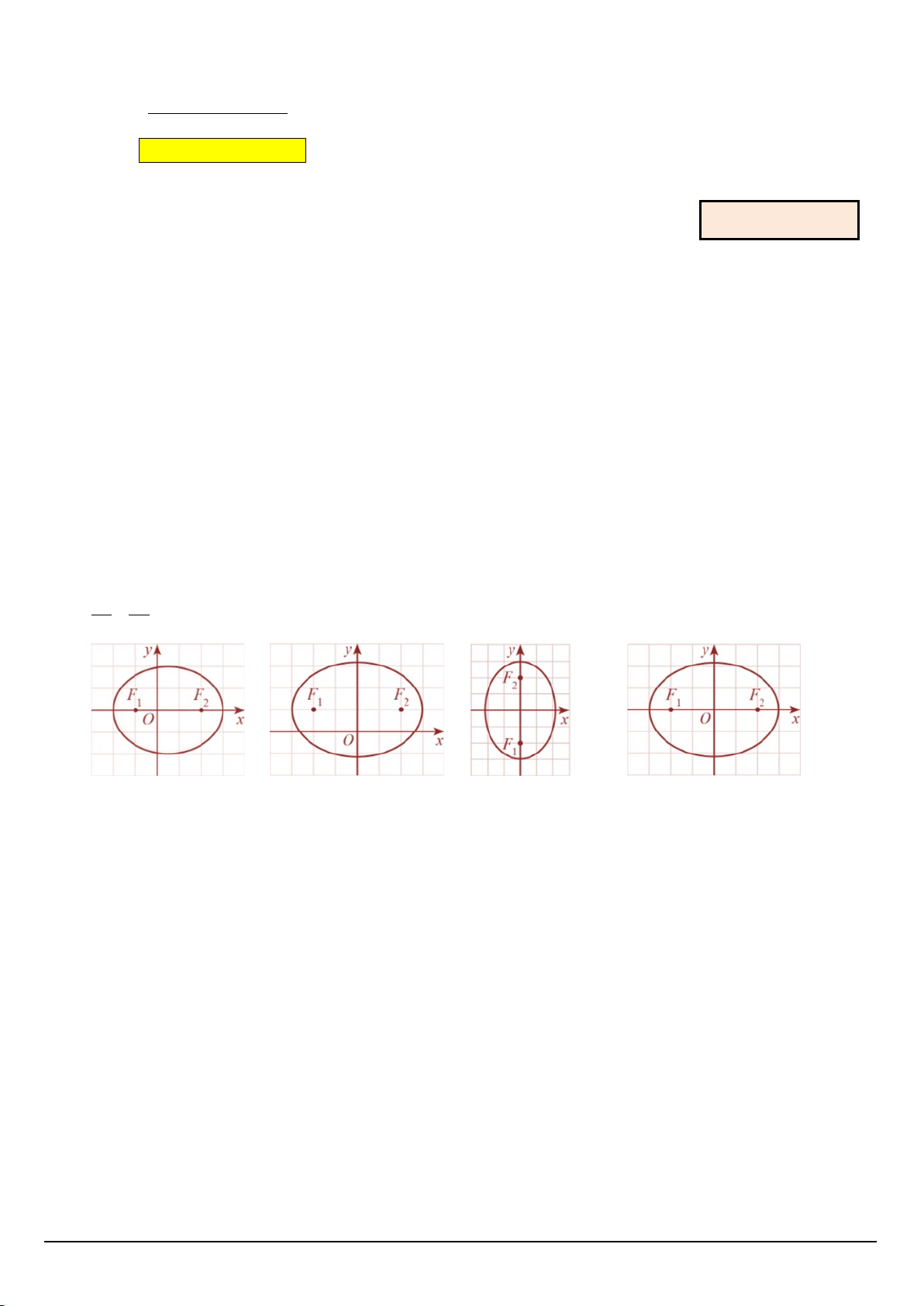
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc 2 2 dạng: x y +
=1 (a > b > 0) ? 2 2 a b Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u =(3;− )1 là x = 2 − tx = 2 + 3t Ⓐ  (t ∈). Ⓑ  (t ∈) . y = 5 − + 3ty = 5 − − tx = 1 − + 2tx = 1 − − 5t Ⓒ  (t ∈) . Ⓓ  (t ∈) . y = 3− 5ty = 3 + 2t
Câu 5: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ : và ∆ : − + − = .
1 2x − 3y +1 = 0 2 4x 6y 2 0 Ⓐ Song song. Ⓑ Trùng nhau. Ⓒ Vuông góc.
Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm I ( 1; − 2 − ) , bán kính bằng 3?
Ⓐ ( x − )2 + ( y + )2 1 2 = 9 .
Ⓑ ( x + )2 + ( y + )2 1 2 = 9 .
Ⓒ ( x − )2 + ( y − )2 1 2 = 9.
Ⓓ ( x + )2 + ( y − )2 1 2 = 9 . Trang 1/4 - Mã đề 522
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: 2
y = 2 px ( p > 0) ? Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số 1,3 có thể lập được bao nhiêu số tự nhiên có 2 chữ số: Ⓐ 6 . Ⓑ 27 . Ⓒ 12. Ⓓ 4 .
Câu 9: Số cách sắp xếp 6 học sinh ngồi vào một dãy gồm 6 ghế là Ⓐ 1. Ⓑ 9!. Ⓒ 6!. Ⓓ 6 6 .
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố A : n A n Ω n A n A Ⓐ ( ) P( ) A =1− . Ⓑ ( ) P( ) A = . Ⓒ ( ) P( ) A = . Ⓓ ( ) P( ) A = . n(Ω) n( ) A n(B) n(Ω) 
Câu 11: Trong hệ tọa độ Oxy, cho A(5;2), B(7;6). Tìm tọa độ của vectơ AB?    
Ⓐ AB = (15;10) .
Ⓑ AB = (2;4) .
Ⓒ AB = (5;6) .
Ⓓ AB = (50;16) .
Câu 12: Một lớp học có 19 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là: Ⓐ 20 Ⓑ 380 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lập từ các chữ số 1, 2 , 3, 4 , 5, 6 . Ⓐ 360 số. Ⓑ 720 số. Ⓒ 90 số. Ⓓ 120 số.
Câu 14: Chiều cao của một tòa nhà là h = 5,13m ± 0,2m . Độ chính xác d của phép đo trên là
Ⓐ d = 5,13m .
Ⓑ d = 0,2m .
Ⓒ d = 5,93m .
Ⓓ 5,33m .
Câu 15: Tổ 1 của lớp 10A1 có 8 học sinh nam và 7 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn. Ⓐ 8 . Ⓑ 15 . Ⓒ 5 3 . Ⓓ 3 5
Câu 16: Trong mặt phẳng Oxy , khoảng cách từ điểm M (3;− 4) đến đường thẳng ∆ :3x + 4y −1= 0 . Ⓐ 8 . Ⓑ 24 . Ⓒ 12 . Ⓓ 24 − . 5 5 5 5
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng 11 là: Ⓐ 2 . Ⓑ 1 . Ⓒ 1 . Ⓓ 1 . 25 6 18 8
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả như bảng sau.
Tìm mốt của mẫu số liệu trên Ⓐ 7 . Ⓑ 4 . Ⓒ 6 . Ⓓ 5. Trang 2/4 - Mã đề 522
Câu 19: Trong mặt phẳng tọa độ Oxy cho A(3;5), B( 7; − )
1 . Tìm tọa độ trung điểm I của đoạn thẳng AB . Ⓐ I ( 2; − 3). Ⓑ I (4;7). Ⓒ I (2;4). Ⓓ I ( 2; − 4) .
Câu 20: Gieo một đồng tiền liên tiếp 2 lần thì n(Ω) là bao nhiêu? Ⓐ 16. Ⓑ 4 . Ⓒ 6 . Ⓓ 8 .
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là Ⓐ 1 . Ⓑ 2 . Ⓒ 1. Ⓓ 1 . 2 3 3
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ Q =150;Q =164;Q =178 .
Ⓑ Q =160;Q =168;Q =176 . 1 2 3 1 2 3
Ⓒ Q =158;Q =166;Q =174 .
Ⓓ Q =158;Q =164;Q =174 . 1 2 3 1 2 3
Câu 23: Cho ba điểm A(2 ; 2
− ), B(4 ; 0),C (m ; 2) . Định m để ,
A B,C thẳng hàng?
Ⓐ m = 6 .
Ⓑ m =10 . Ⓒ m = 10 − .
Ⓓ m = 2 .      
Câu 24: Cho hai vectơ a = (1; 4 − ) ; b = ( 6;
− 15) . Tìm tọa độ vectơ u biết u − a = b Ⓐ ( 5; − 1 ) 1 . Ⓑ (–7; –19) . Ⓒ (–7;19) . Ⓓ (5;1 ) 1 .
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là Ⓐ 1. Ⓑ 2 . Ⓒ 3. Ⓓ 0 .
Câu 26: Một nhóm học sinh có 11 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là Ⓐ 3 A . Ⓑ 3 C . Ⓒ 3 11 . Ⓓ 33. 11 11
Câu 27: Với đa giác lồi 12 cạnh thì số đường chéo là Ⓐ 35. Ⓑ 55. Ⓒ 54. Ⓓ 90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là: Ⓐ 15 Ⓑ 16 Ⓒ 20 Ⓓ 18 2 2
Câu 29: Trong mặt phẳng (Oxy), cho elip (E) có phương trình x y +
= 1. Tìm tiêu cự của (E). 25 16 Ⓐ F F = 2 5 Ⓑ F F = 4 5 Ⓒ F F =12 Ⓓ F F =6 1 2 1 2 1 2 1 2
Câu 30: Khai triển của nhị thức ( x − )5 2 1 . Ⓐ 5 4 3 2
32x 80x 80x 40x 10x1. Ⓑ 5 4 3 2
x 10x  40x 80x 80x 32 . Ⓒ 5 4 3 2
32x 10x  40x 80x 80x1. Ⓓ 5 4 3 2
x 100x  400x 800x 800x32 . Trang 3/4 - Mã đề 522
Câu 31: Xác định m để 2 đường thẳng 1
d : x − y + 3 = 0 và d′: x + my + 3 = 0 vuông góc với nhau. 2 Ⓐ m = 2. − Ⓑ 1 m = − . Ⓒ m = 2. Ⓓ 1 m = . 2 2
Câu 32: Tính bán kính đường tròn tâm I (1; 2
− ) và tiếp xúc với đường thẳng d :3x − 4y − 36 = 0 . Ⓐ R = 3. Ⓑ R = 5. Ⓒ R =15. Ⓓ 3 R = . 5 2 2
Câu 33: Trong mặt phẳng Oxy, phương trình elip: x y + =1 100 64
có một tiêu điểm là Ⓐ (0;4) . Ⓑ (0;3) . Ⓒ (− 5;0). Ⓓ (6;0) .
Câu 34: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d :2x +5y +1 = 0. Phương trình đường thẳng đi qua điểm A( 1
− ; 2) và vuông góc với d là
Ⓐ 5x − 2y + 9 = 0
Ⓑ 2x + 5y − 8 = 0
Ⓒ 5x + 2y +1 = 0
Ⓓ 5x − 2y +10 = 0
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là Ⓐ 3 . Ⓑ 3 . Ⓒ 3 . Ⓓ 3 . 14 5 7 11
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + y + 2023 = 0và điểm M (0;2023) .
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng ∆ .
Bài 2: Cửa hàng nhà An có 7 bông hoa vàng, 8 bông hoa đỏ, 5 bông hoa trắng. Chọn ngẫu
nhiên ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho (C
x + y + mx −
m − y + = (m là tham số). m ) 2 2 : 4 2(2 )1 1 0
Tìm m để (C là đường tròn và tiếp xúc với đường thẳng ∆ : x + y +1+ 2 2 = 0 m ) . ----------- HẾT ---------- Trang 4/4 - Mã đề 522 SỞ GD VÀ ĐT ĐỒNG NAI
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
TRƯỜNG THPT THANH BÌNH
MÔN TOÁN 10_Năm học: 2022-2023
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(35 câu trắc nghiệm - 03 bài tự luận) Mã đề 939
(Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm)
Họ, tên thí sinh:..................................................................... Số báo danh: ............................. Lớp:.................
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).  
Câu 1: Trong mặt phẳng tọa độ  
Oxy , cho a = (2; 5 − ),b = ( 1;
− 0) . Khi đó, tích vô hướng . a b là:         Ⓐ . a b = 2 Ⓑ . a b = 2 − Ⓒ . a b = 7 − Ⓓ . a b = 1
Câu 2: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
Ⓐ Hiệu của số lớn nhất và số nhỏ nhất.
Ⓑ Một nửa của phương sai.
Ⓒ Bình phương của phương sai.
Ⓓ Căn bậc hai của phương sai.
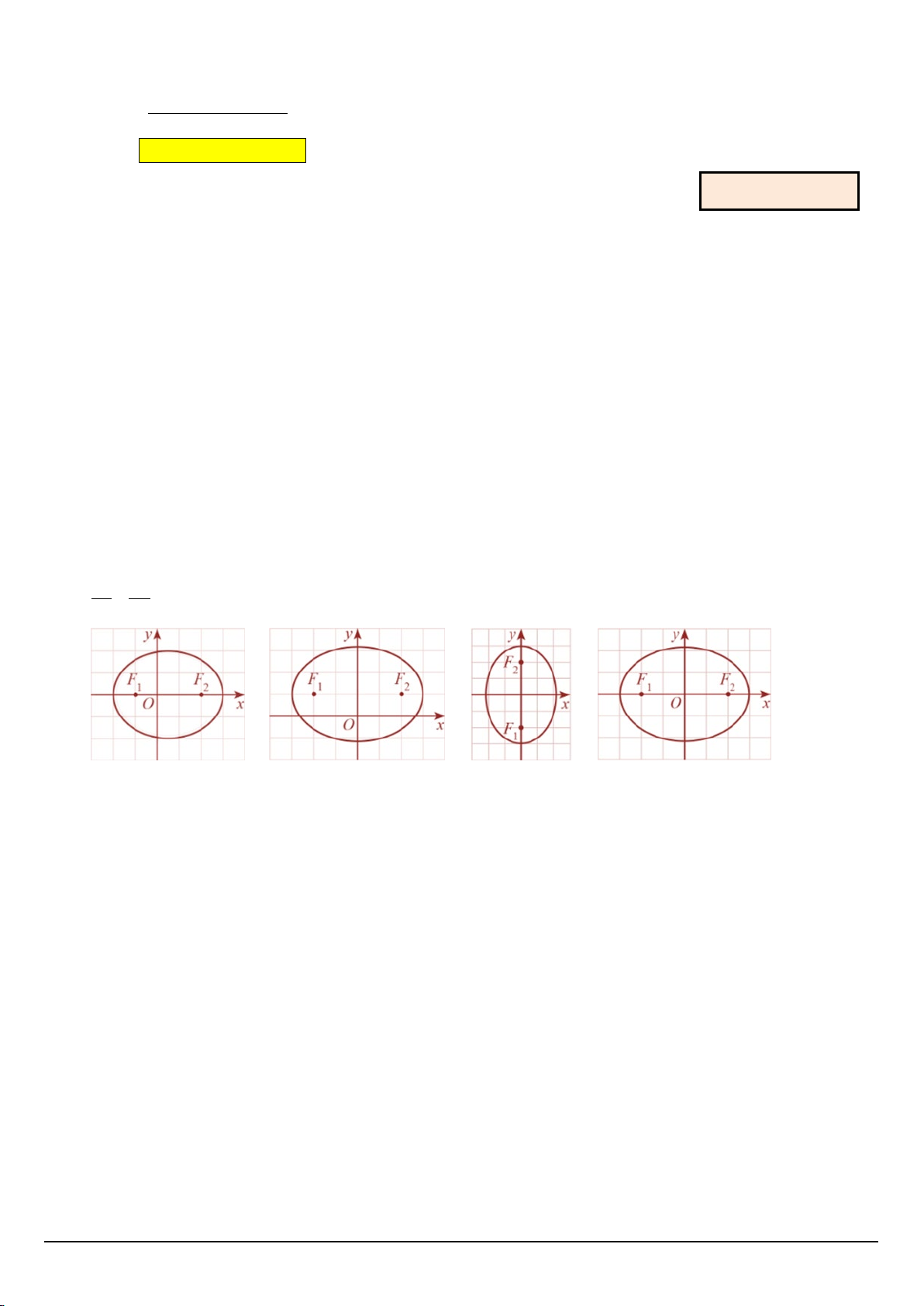
Câu 3: Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc 2 2 dạng: x y +
= 1 (a > b > 0) ? 2 2 a b Ⓐ Ⓑ Ⓒ Ⓓ
Câu 4: Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u =( 1; − 3) là x = 2 − tx = 2 + 3t Ⓐ  (t ∈). Ⓑ  (t ∈) . y = 5 − + 3ty = 5 − − tx = 1 − + 2tx = 1 − − 5t Ⓒ  (t ∈) . Ⓓ  (t ∈) . y = 3− 5ty = 3+ 2t
Câu 5: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ : và ∆ : .
1 2x − 3y +1 = 0 2 4
− x + 6y −1 = 0 Ⓐ Song song. Ⓑ Trùng nhau. Ⓒ Vuông góc.
Ⓓ Cắt nhau nhưng không vuông góc nhau.
Câu 6: Phương trình nào sau đây là phương trình của đường tròn tâm I ( 1; − 2) , bán kính bằng 3?
Ⓐ ( x − )2 + ( y + )2 1 2 = 9 .
Ⓑ ( x + )2 + ( y + )2 1 2 = 9 .
Ⓒ ( x − )2 + ( y − )2 1 2 = 9.
Ⓓ ( x + )2 + ( y − )2 1 2 = 9 . Trang 1/4 - Mã đề 111
Câu 7: Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: 2
y = 2 px ( p > 0) ? Ⓐ Ⓑ Ⓒ Ⓓ
Câu 8: Từ các số 1,2,3 có thể lập được bao nhiêu số tự nhiên có 3chữ số: Ⓐ 6 . Ⓑ 27 . Ⓒ 12. Ⓓ 8 .
Câu 9: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là Ⓐ 1. Ⓑ 9!. Ⓒ 9. Ⓓ 9 9 .
Câu 10: Công thức nào sau đây dùng để tính xác suất của biến cố A : n A n Ω n A n A Ⓐ ( ) P( ) A =1− . Ⓑ ( ) P( ) A = . Ⓒ ( ) P( ) A = . Ⓓ ( ) P( ) A = . n(Ω) n( ) A n(B) n(Ω) 
Câu 11: Trong hệ tọa độ Oxy, cho A(5;2), B(10;8). Tìm tọa độ của vectơ AB?    
Ⓐ AB = (15;10) .
Ⓑ AB = (2;4) .
Ⓒ AB = (5;6) .
Ⓓ AB = (50;16) .
Câu 12: Một lớp học có 18 học sinh nam và 20 học sinh nữ. Nếu muốn chọn một học sinh nam và một
học sinh nữ đi dự một cuộc thi nào đó thì số cách chọn là: Ⓐ 20 Ⓑ 38 Ⓒ 360 Ⓓ 18
Câu 13: Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được lập từ các chữ số 1, 2 , 3, 4 , 5, 6 . Ⓐ 20 số. Ⓑ 720 số. Ⓒ 90 số. Ⓓ 120 số.
Câu 14: Chiều cao của một tòa nhà là h = 34,13m ± 0,2m . Độ chính xác d của phép đo trên là
Ⓐ d = 34,13m .
Ⓑ d = 0,2m .
Ⓒ d = 34,93m .
Ⓓ 34,33m .
Câu 15: Tổ 1 của lớp 10A1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1
bạn học sinh của tổ 1 đi tham gia ngày hội Toán học. Hỏi có bao nhiêu cách chọn. Ⓐ 8 . Ⓑ 15 . Ⓒ 5 3 . Ⓓ 3 5
Câu 16: Trong mặt phẳng Oxy , khoảng cách từ điểm M (3;− 4) đến đường thẳng ∆ :3x − 4y −1= 0 . Ⓐ 8 . Ⓑ 24 . Ⓒ 12 . Ⓓ 24 − . 5 5 5 5
Câu 17: Gieo hai con súc sắc cân đối đồng chất. Xác suất để tổng số chấm trên hai mặt bằng 11 là: Ⓐ 2 . Ⓑ 1 . Ⓒ 1 . Ⓓ 1 . 25 6 8 18
Câu 18: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả như bảng sau.
Tìm mốt của mẫu số liệu trên Ⓐ 7 . Ⓑ 4 . Ⓒ 6 . Ⓓ 5. Trang 2/4 - Mã đề 111
Câu 19: Trong mặt phẳng tọa độ Oxy cho A(3;5), B(1;3) . Tìm tọa độ trung điểm I của đoạn thẳng AB . Ⓐ I ( 2; − 3). Ⓑ I (4;7). Ⓒ I (2;4). Ⓓ I ( 2; − 4) .
Câu 20: Gieo một đồng tiền liên tiếp 3 lần thì n(Ω) là bao nhiêu? Ⓐ 16. Ⓑ 4 . Ⓒ 6 . Ⓓ 8 .
Câu 21: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là Ⓐ 1 . Ⓑ 2 . Ⓒ 1. Ⓓ 1 . 2 3 3
Câu 22: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
Các tứ phân vị của mẫu số liệu là
Ⓐ Q =150;Q =164;Q =178 .
Ⓑ Q =160;Q =168;Q =176 . 1 2 3 1 2 3
Ⓒ Q =158;Q =166;Q =174 .
Ⓓ Q =158;Q =164;Q =174 . 1 2 3 1 2 3
Câu 23: Cho ba điểm A(2 ; 2
− ), B(4 ; 0),C (m ; 2) . Định m để ,
A B,C thẳng hàng?
Ⓐ m = 6 .
Ⓑ m =10 . Ⓒ m = 10 − .
Ⓓ m = 2 .      
Câu 24: Cho hai vectơ a = (1; 4 − ) ; b = ( 6;
− 15) . Tìm tọa độ vectơ u biết u − a = b Ⓐ ( 5; − 1 ) 1 . Ⓑ (–7; –19) . Ⓒ (–7;19) . Ⓓ (5;1 ) 1 .
Câu 25: Điểm thi HK1năm học 2022 – 2023 của học sinh lớp 10 như sau:
Khoảng biến thiên của mẫu số liệu là Ⓐ 1. Ⓑ 2 . Ⓒ 3. Ⓓ 0 .
Câu 26: Một nhóm học sinh có 11 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việc. Số cách chọn là Ⓐ 3 A . Ⓑ 3 C . Ⓒ 3 11 . Ⓓ 33. 11 11
Câu 27: Với đa giác lồi 12 cạnh thì số đường chéo là Ⓐ 35. Ⓑ 55. Ⓒ 54. Ⓓ 90.
Câu 28: Số các chữ số tự nhiên có hai chữ số mà hai chữ số đó đều là hai số chẵn là: Ⓐ 15 Ⓑ 16 Ⓒ 20 Ⓓ 18 2 2
Câu 29: Trong mặt phẳng (Oxy), cho elip (E) có phương trình x y +
=1. Tìm tiêu cự của (E). 25 16 Ⓐ F F = 2 5 Ⓑ F F = 4 5 Ⓒ F F =12 Ⓓ F F =6 1 2 1 2 1 2 1 2
Câu 30: Khai triển của nhị thức ( x − )5 2 1 . Ⓐ 5 4 3 2
32x 80x 80x 40x 10x1. Ⓑ 5 4 3 2
x 10x  40x 80x 80x 32 . Ⓒ 5 4 3 2
32x 10x  40x 80x 80x1. Ⓓ 5 4 3 2
x 100x  400x 800x 800x32 . Trang 3/4 - Mã đề 111
Câu 31: Xác định m để 2 đường thẳng 1
d : x − y + 3 = 0 và d′: x + my + 3 = 0 vuông góc với nhau. 2 Ⓐ m = 2. − Ⓑ 1 m = − . Ⓒ m = 2. Ⓓ 1 m = . 2 2
Câu 32: Tính bán kính đường tròn tâm I (1; 2
− ) và tiếp xúc với đường thẳng d :3x − 4y − 36 = 0 . Ⓐ R = 3. Ⓑ R = 5. Ⓒ R =15. Ⓓ 3 R = . 5 2 2
Câu 33: Trong mặt phẳng Oxy, phương trình elip: x y + =1 100 64
có một tiêu điểm là Ⓐ (0;4) . Ⓑ (0;3) . Ⓒ (− 5;0). Ⓓ (6;0) .
Câu 34: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d :2x +5y +1 = 0. Phương trình đường thẳng đi qua điểm A( 1
− ; 2) và vuông góc với d là
Ⓐ 5x − 2y + 9 = 0
Ⓑ 2x + 5y − 8 = 0
Ⓒ 5x + 2y +1 = 0
Ⓓ 5x − 2y +10 = 0
Câu 35: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu.
Xác suất để được 3 quả cầu khác màu là Ⓐ 3 . Ⓑ 3 . Ⓒ 3 . Ⓓ 3 . 14 5 7 11
II. TỰ LUẬN (03 câu – 3,0 điểm)
Bài 1:Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + 2023y + 2022 = 0 và điểm M (0;1).
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng ∆ .
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng. Chọn ngẫu nhiên ra 3 bông
hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng.
Bài 3:Trong mặt phẳng tọa độ Oxy, cho phương trình đường tròn
(C x + y + mx − m − y + = (m là tham số). Tìm m để (C tiếp xúc với đường thẳng m ) m ) 2 2 : 2 2( )1 1 0
∆ : x + y +1+ 2 2 = 0.
----------------------------------------------- ----------- HẾT ---------- Trang 4/4 - Mã đề 111 ĐÁP ÁN
ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 – MÔN TOÁN 10 - 2023
ĐÁP ÁN ĐỀ THI TRẮC NGHIỆM - (7 điểm) Mã đề [111] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B D D A A D A B B D C C B B A B D C
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D A C B C C A A B B C D A D A D Mã đề [213] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 A D A C D A A C A C C D B A B D B C
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D C D D C B D A C D A C B B A B B Mã đề [315] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 D D B A A C A D D A B A C B D C A C
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D B A B B C B B C A D C D C B B B Mã đề [417] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B A B D C A A C A A D D C D C A D A
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B B D C B C D C C B C D A C B B A Mã đề [522] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 D D D B B B A D C D B B A B B A C D
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A B A C A C C A C C D A C B D A D Mã đề [624] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 C D A A B B A A D B B D B B A C A A
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D D C C C D A C A B C B D A D C Mã đề [726] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 C A B C D B A C D B D C D C B D A C
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A A A A B D A B B C D D A C B C A Mã đề [828] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 C C C A A B B A C D A B D A C C A D
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D A A B B C C C B C B D D D D B C Mã đề [939] 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 B D D A A D A B B D C C B B A B D C
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C D A C A C C A C C D A C B D A D
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [111]-[213]-[315]-[417] Bài Ý Nội dung Điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + y + 2022 = 0 và điểm ∑
M (0;2022). Viết phương trình tổng quát của đường thẳng đi qua M và song song 1,0đ với đường thẳng ∆ . 1
Giả sử ∆ ' là đường thẳng song song với đường thẳng ∆ :2x + y + 2022 = 0 có dạng : 1 điểm
2x + y + m = 0 (m ≠ 2022). 0,25
Vì M (0;2022)∈∆ ' nên 2022 + m = 0⇔ m = 2022 − (nhận) 0,5
Vậy PTTQ của ∆ ' : 2x + y − 2022 = 0. 0,25
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng, 8 bông hoa đỏ. Chọn ngẫu nhiên ∑
ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3 bông hoa đỏ. 1,0đ
Số phần tử của không gian mẫu: n(Ω) 6 = C = 38760. 0,25 2 20 1 điểm
Gọi A là biến cố: “chọn ra 1 bông hoa trắng, 2 bông hoa vàng, 3 bông hoa đỏ”. n( A) 1 2 3
= C .C .C = 5880 5 7 8 cách. 0,25 n A 5880 49
Vậy xác suất cần tìm là p( A) ( ) = = = . n(Ω) 38760 323 0,5
Bài 3: Trong mặt phẳng tọa độ Oxy, cho (C
x + y + mx − m − y + = m ) 2 2 : 2 2( )1 1 0 (m là tham ∑
số). Tìm m để (C ∆ + + + = 1,0đ
m ) là đường tròn và tiếp xúc với đường thẳng : x y 1 2 2 0 Ta có: a = − ,
m b = m −1, c =1
(C là đường tròn tâm I (− ; m m − ) 1 và bán kính 2
R = 2m − 2m khi 0,25 m ) 3 1 điểm 2 2
a + b − c > 0 m >1 2 2 2
⇔ m + (m −1) −1 > 0 ⇔ 2m − 2m > 0 ⇔  0,25 m < 0 m =
Do (C tiếp xúc với ∆ x + y + + = ⇔ d (I ∆) 2 : 1 2 2 0 ; = R ⇔ (thỏa mãn ) m )  0,25 m = 1 −
Vậy(C là đường tròn và tiếp xúc với đường thẳng ∆ : x + y +1+ 2 2 = 0khi m = { 1; − } 2 m ) 0,25
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [522]-[624]-[726]-[828] Bài Ý Nội dung Điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + y + 2023 = 0và điểm M (0;2023) . ∑
Viết phương trình tổng quát của đường thẳng đi qua M và song song với đường thẳng ∆ . 1,0đ 1
Giả sử ∆ ' là đường thẳng song song với đường thẳng ∆ :2x + y + 2023 = 0có dạng : 1 điểm
2x + y + m = 0 (m ≠ 2023). 0,25
Vì M (0;2023)∈∆ 'nên 2023+ m = 0⇔ m = 2023 − (nhận) 0,5
Vậy PTTQ của ∆ ' : 2x + y − 2023 = 0. 0,25
Bài 2: Cửa hàng nhà An 7 bông hoa vàng, 8 bông hoa đỏ, có 5 bông hoa trắng. Chọn ngẫu nhiên ∑
ra 6 bông hoa để bán. Tính xác suất để chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng. 1,0đ
Số phần tử của không gian mẫu: n(Ω) 6 = C = 38760. 0,25 2 20 1 điểm
Gọi A là biến cố: “chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng”. n( A) 1 2 3
= C .C .C =1960 7 8 5 cách. 0,25 n A 1960 49
Vậy xác suất cần tìm là p( A) ( ) = = = . n(Ω) 38760 969 0,5
Bài 3: Trong mặt phẳng tọa độ Oxy, cho (C
x + y + mx − m − y + = m ) 2 2 : 4 2(2 )1 1 0 (m là tham ∑
số). Tìm m để (C ∆ + + + = 1,0đ
m ) là đường tròn và tiếp xúc với đường thẳng : x y 1 2 2 0 Ta có: a = 2 − ,
m b = 2m −1, c =1
(C là đường tròn tâm I ( 2 − ;2 m m − ) 1 và bán kính 2
R = 8m − 4m khi 0,25 m ) 2 2
a + b − c > 0 3  1 1 điểm m > 2 2 2 4m (2m 1) 1 0 8m 4m 0  ⇔ + − − > ⇔ − > ⇔ 2  0,25 m < 0 m =1
Do (C tiếp xúc với : x y 1 2 2 0 d (I; ) R  ∆ + + + = ⇔ ∆ = ⇔ (thỏa mãn ) m ) 1 0,25 m −  =  2  1
Vậy (C là đường tròn và tiếp xúc với đường thẳng ∆ : x + y +1+ 2 2 = 0khi m −  ;1 = m ) 0,25 2   
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
ĐÁP ÁN ĐỀ THI TỰ LUẬN – 3 CÂU (3 điểm) [939] Bài Ý Nội dung Điểm
Bài 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ :2x + 2023y + 2022 = 0 và điểm
M (0;1) . Viết phương trình tổng quát của đường thẳng đi qua M và song song với ∑ 1,0đ 1 đường thẳng ∆ . 1 điểm
Giả sử ∆ ' là đường thẳng song song với đường thẳng ∆ :2x + 2023y + 2022 = 0 có dạng :
2x + 2023y + m = 0 (m ≠ 2022). 0,25
Vì M (0;1)∈∆ ' nên 2023+ m = 0⇔ m = 2023 − (nhận) 0,5
Vậy PTTQ của ∆ ' : 2x + 2023y − 2023 = 0. 0,25
Bài 2: Cửa hàng nhà An có 5 bông hoa trắng, 7 bông hoa vàng. Chọn ngẫu nhiên ra 3 bông ∑
hoa để bán. Tính xác suất để chọn ra 1 bông hoa trắng, 2 bông hoa vàng. 1,0đ
Số phần tử của không gian mẫu: n(Ω) 3 = C = 220 . 0,25 2 12 1 điểm
Gọi A là biến cố: “chọn ra 1 bông hoa vàng, 2 bông hoa đỏ, 3 bông hoa trắng”. n( A) 1 2 = C .C =105 5 7 cách. 0,25 n A 105 21
Vậy xác suất cần tìm là p( A) ( ) = = = . n( 0,5 Ω) 220 44
Bài 3: Trong mặt phẳng tọa độ Oxy, cho phương trình đường tròn
(C x + y + mx − m − y + = (m là tham số). Tìm m để (C tiếp xúc với ∑ m ) m ) 2 2 : 2 2( )1 1 0 1,0đ
đường thẳng ∆ : x + y +1+ 2 2 = 0. Ta có: 3 a = − ,
m b = m −1, c =1 0,25 1 điểm
Đường tròn (C có tâm I (− ; m m − ) 1 và bán kính 2
R = 2m − 2m m ) m =
Do (C tiếp xúc với ∆ x + y + + = ⇔ d (I ∆) 2 : 1 2 2 0 ; = R ⇔ (thỏa mãn ) m )  0,5 m = 1 −
Vậy(C là đường tròn và tiếp xúc với đường thẳng ∆ : x + y +1+ 2 2 = 0khi m = { 1; − } 2 m ) 0,25
**Ghi chú: Nếu học sinh giải bằng cách khác mà vẫn đúng thì cho điểm tối đa theo từng phần đó.
Document Outline

  • HKII-2023_CUỐI HKII - ĐỀ 101_111
  • HKII-2023_CUỐI HK2 - ĐỀ 102_522
  • HKII-2023_CUỐI HKII - ĐỀ 103_939
  • ĐÁP ÁN ĐỀ TOÁN 10 - HKII-2023