Đề cuối học kỳ 1 Toán 10 năm 2022 – 2023 trường Nguyễn Thái Bình – Quảng Nam

TRƯỜNG THPT NGUYỄN THÁI BÌNH
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2022-2023 TỔ TOÁN
Môn: TOÁN – Lớp 10 ( ĐỀ CHÍNH THỨC)
Thời gian: 60 phút (không kể thời gian giao đề)
Họ và tên học sinh:…………………………………………………. SBD:………………. Mã đề: 201
I. PHẦN TRẮC NGHIỆM( 5.0 điểm)  
Câu 1. Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC .        
A. AB + AC = a 2 .
B. AB + AC = a .
C. AB + AC = 2a . D. a 2 AB + AC = . 2
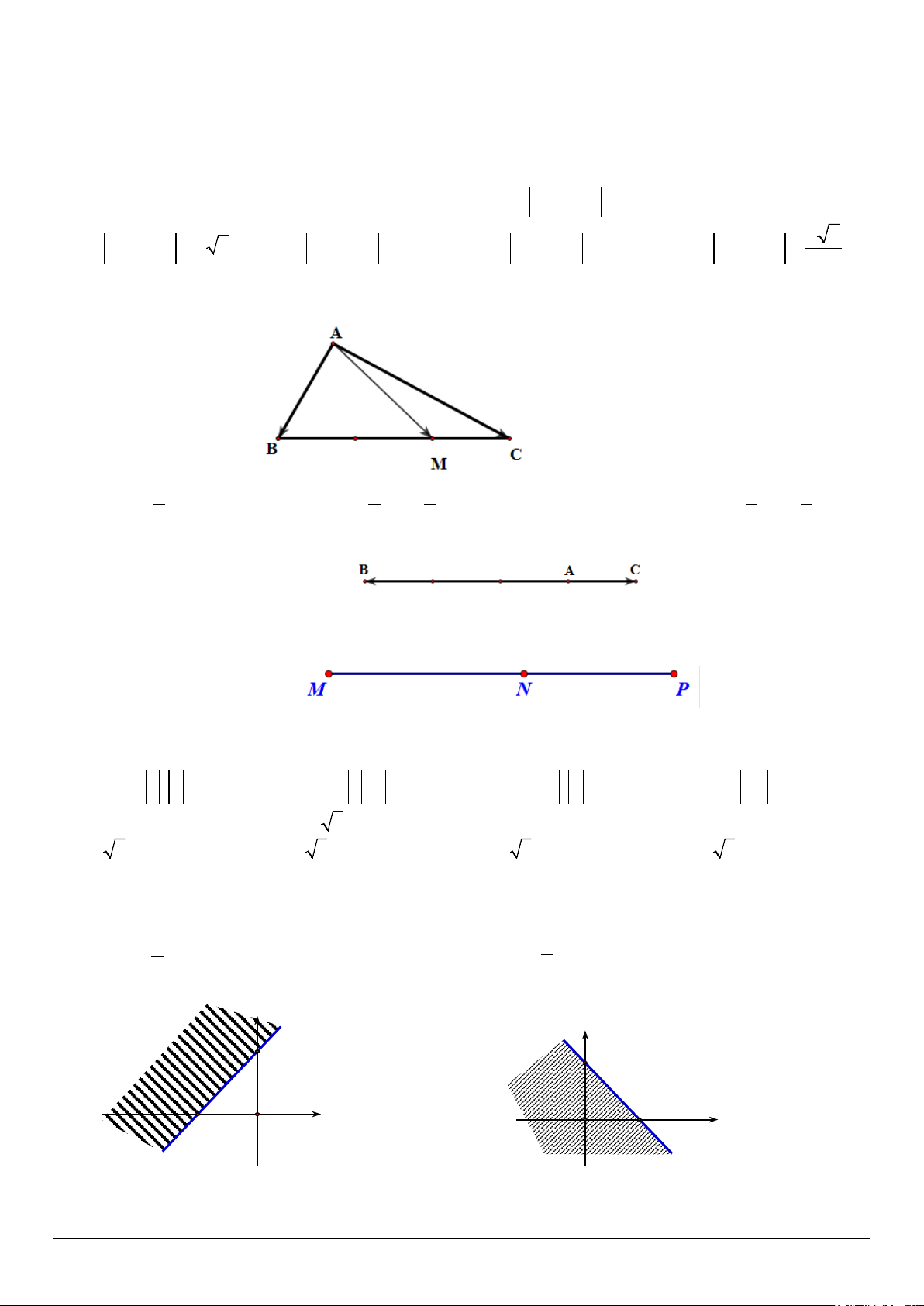
Câu 2. Cho tam giác ABC . Gọi M là một điểm trên cạnh BC sao cho MB = 2MC . Khi đó đẳng thức nào sau đây đúng?
 1    1  3  
    
A. AM = (AB + AC) 1 2
. B. AM = − AB + AC . C. AM = 3AB + 2AC . D. AM = AB + AC . 2 2 2 3 3  
Câu 3. Cho ba điểm phân biệt ,
A B,C . Nếu AB = 3
− AC ( hình vẽ) thì đẳng thức nào dưới đây đúng?         A. BC = 2 − AC .
B. BC = 4AC .
C. BC = 2AC . D. BC = 4 − AC .
Câu 4. Cho ba điểm M , N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P . Khi đó các cặp vectơ
nào sau đây ngược hướng?        
A. MP và NP .
B. NM và PN .
C. MN và PN .
D. MP và MN .   
Câu 5. Cho hai véctơ x và y đều khác véctơ 0 . Khẳng định nào sau đây đúng?                         A. .
x y = x . y .sin (x, y). B. .xy = x . y .cot(x, y). C. .xy = x . y .cos(x, y). D. .xy = .xy .cos(x, y) .
Câu 6. Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ?
A. 5 ∉Q .
B. 5 ⊄ Q .
C. 5 ⊂ Q . D. 5 ≠ Q .  
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy , cho hai vectơ a = (m;2m − ) 1 và b = (4 )
;1 . Tìm m để vectơ  
a vuông góc với b . A. 1 m = − .
B. m = 6. C. 1 m = . D. 1 m = . 2 2 6
Câu 8. Miền nghiệm ( miền không gạch chéo) của bất phương trình 3x − 2y ≥ 6 − là y y 3 3 2 x 2 − O x O A. B. Mã đề 201 Trang 1/2 y y 2 − O x 3 2 − 3 O x C. D.
Câu 9. Cho số gần đúng a = 2 841 277 với độ chính xác d = 400. Số quy tròn của số a là A. 2 841 000 . B. 2 841 300. C. 2 841 780. D. 2 841 200.
Câu 10. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? 3 3  x + y < 0 x + 2y < 0
x − y < 1 3
−x + y < 4 A.  . B.  . C.  . D.  . x + y > 3 2 y + 3 < 0 x + 2y ≥ 0 x + 2y <1
Câu 11. Cho tam giác ABC.Khẳng định nào sau đây đúng?
  
  
  
  
A. AB + CA = CB .
B. AB + AC = BC .
C. CA + BA = CB .
D. AA + BB = AB .
Câu 12. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin(180° −α) = −sinα
B. cos(180° −α ) = −cosα .
C. cos(180° −α ) = cosα
D. tan (180° −α ) = tanα .
Câu 13. Trong tam giác ABC , hệ thức nào sau đây sai? A. a = 2R csin A a . B. sin C = C. sin A = .
D. bsin B = 2R . sin A a 2R
Câu 14. Trong các câu sau, câu nào là mệnh đề?
A. Bạn học trường nào?
B. Trung Quốc là nước đông dân nhất thế giới.
C. Không được làm việc riêng trong giờ học. D. Đi ngủ đi.
Câu 15. Trong mặt phẳng toạ độ Oxy cho hai điểm A(1;5) và B(3;4) . Khi đó:    
A. AB = (4;9) . B. AB = (2;− ) 1 . C. AB = ( 2; − ) 1 . D. AB = (1;2) .
II. PHẦN TỰ LUẬN( 5.0 điểm)
Câu 1: (1,0 điểm) Cho hai tập hợp A = {1;2;5; } 7 , B = {2;3;4;5; }
6 . Xác định các tập hợp A∪ B, A∩ B .
Câu 2: (1,0 điểm) Cho hình chữ nhật ABCD tâm O có AB = 3; BC = 6 .
    
a) Chứng minh rằng: OA + OB + OC + OD = 0 .   
b) Tính độ dài của vectơ u = AB + AD .
Câu 3: (2,0 điểm) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(4;4), B( 1; − − ) 1 và C ( 4; − − ) 1 .   a) Tính B .
A BC và suy ra số đo góc  ABC .
b) Tìm giá trị của t để điểm E(t;2) thỏa mãn đường thẳng BE song song với đường thẳng AC .
Câu 4: (1,0 điểm) Bạn Nam muốn làm một cái chuông gió bằng tấm bìa hình thoi. Nam mắc 4 chuông gió có
khối lượng lần lượt là 20gr;20gr,10gr,10gr vào các đỉnh ,
A B,C, D của hình thoi. Nam tìm một vị trí cân 
   
bằng trên tấm bìa để móc chuông lên, bằng cách xác định điểm M sao cho 2MA + 2MB + MC + MD = 0 .
a) Em hãy giúp Nam xác định điểm M . 
  
b) Từ đó tìm vị trí điểm K trên các cạnh hình thoi sao cho 2KA + 2KB + KC + KD đạt giá trị nhỏ nhất.
Biết ABCD là hình thoi có cạnh bằng a và  0 ABC = 60 .
------ HẾT ------ Mã đề 201 Trang 2/2 Đề\câu 000 201 203 205 207 1 A A D A B 2 A D A D D 3 A B D D D 4 A C A A B 5 A C D B B 6 A A B C D 7 A D D D D 8 A A B D D 9 A A C A C 10 A C C C A 11 A A B C B 12 A B C A D 13 A D C B D 14 A B D D A 15 A B C C A
Xem thêm: ĐỀ THI HK1 TOÁN 10
https://toanmath.com/de-thi-hk1-toan-10
TRƯỜNG THPT NGUYỄN THÁI BÌNH
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2022-2023 TỔ TOÁN
Môn: TOÁN – Lớp 10 ( ĐỀ CHÍNH THỨC)
Thời gian: 60 phút (không kể thời gian giao đề)
ĐÁP ÁN ĐỀ 201, 203, 205, 207 Bài Đáp án Thang điểm 1
Cho hai tập hợp A  1;2;5; 
7 , B  2;3; 4;5; 
6 . Xác định các tập hợp A  B, (1,0 điểm) A  B .
A  B  1;2;3, 4,5;6;  7 0,5
A  B  2;  5 0,5 2
Cho hình chữ nhật ABCD tâm O có AB  3; BC  6 . (1,0 điểm)
a) Chứng minh rằng: OA  OB  OC  OD  0.
b) Tính độ dài của vectơ u  AB  AD .
OA  OC  0  0,5
  OA OB  OC  OD  0
OB  OD  0  2 2
u  AB  AD  AC  u  AC  3  6  3 5 0,5 3
Trong mặt phẳng tọa độ Oxy, cho ba điểm A4;4, B 1  ;  1 và C  4  ;  1 . 2,0 điểm a) Tính B .
A BC và suy ra số đo góc ABC .
b) Tìm giá trị của t để điểm E(t; 2) thỏa mãn đường thẳng BE song song với
đường thẳng AC .
BA  5;5; BC   3  ;0  B . A BC  1  5 0,5 1  5 1
BA  5 2; BC  3  cos ABC     ABC 135 0,5 15 2 2
E(t; 2); B  1  ; 
1  BE  t 1;3 0,25
A4; 4;C  4  ;  1  AC   8  ; 5   0,25
BE / / AC  BE cp AC 0,25 t 1 3 19    0,25 t  8  5  5 4
Bạn Nam muốn làm một cái chuông gió bằng tấm bìa hình thoi. Nam mắc 4 1,0
chuông gió có khối lượng lần lượt là 20gr;20gr,10gr,10gr vào các đỉnh điểm , A ,
B C, D của hình thoi. Nam tìm một vị trí cân bằng trên tấm bìa để móc chuông
lên, bằng cách xác định điểm M sao cho 2MA 2MB  MC  MD  0.
a) Em hãy giúp Nam xác định điểm M . Trang 1/4
b)Từ đó tìm vị trí điểm K trên các cạnh hình thoi sao cho 2KA  2KB  KC  KD
đạt giá trị nhỏ nhất.
Biết ABCD là hình thoi có cạnh bằng a và ABC  60 .
a) Em hãy giúp Nam xác định điểm M .
Gọi I, J lần lượt là trung điểm A , B CD .
2MA  2MB  MC  MD  0  2MA  MB  MC  MD  0
 2.2MI  2MJ  0 O,25đ  2MI  MJ  0  3MI  IJ  0  0,25đ 3MI  JI
( M là trọng tâm tam giác JAB )
b)Từ đó tìm vị trí điểm K trên các cạnh hình thoi sao cho 2KA  2KB  KC  KD
đạt giá trị nhỏ nhất. 0,25đ
Đưa về 2KA 2KB  KC  KD  6KM 0,25đ
KM ngắn nhất khi K là hình chiếu của M lên AB .
(Trong các đoạn vuông góc hạ từ M lên các cạnh thì đoạn vuông góc hạ từ M
lên AB là ngắn nhất).
Lưu ý: Học sinh không cần tính độ dài KM( tính KM sai vẫn cho điểm tối đa)
ĐÁP ÁN 202, 204, 206, 208 Bài Đáp án Thang điểm 1
Cho hai tập hợp A  0;1;3; 
6 , B  2;3; 4;5; 
6 . Xác định các tập hợp A  B, (1,0 điểm) A  B .
A  B  0;1;2;3, 4,5;  6 0,5
A  B  3;  6 0,5 2
Cho hình chữ nhật ABCD tâm I có AD  5; DC  3 . (1,0 điểm)
a) Chứng minh rằng: IA  IB  IC  ID  0.
b) Tính độ dài của vectơ v  AB  AD .
IA  IC  0  0,5
  IA  IB  IC  ID  0
IB  ID  0  Trang 2/4 2 2
u  AB  AD  AC  u  AC  5  3  34 0,5 3
Trong mặt phẳng tọa độ Oxy, cho ba điểm A 2
 ;2, B1;3 và C 1;  1 . 2,0 điểm a) Tính C .
ACB và suy ra số đo góc ACB .
b) Tìm giá trị của t để điểm E( 1
 ;t) thỏa mãn đường thẳng CE song song với
đường thẳng AB . CA   3
 ;3;CB  0;4  B . A BC  12 0,5 12 1
CA  3 2; CB  4  cos ACB    ABC  45 12 2 2 0,5 E( 1
 ;t);C 1;  1  CE   2  ;t   1 0,25 A 2
 ;2; B1;3  AB  3  ;1 0,25
CE / / AB  BE cp AB 0,25 t 1 2  5    0,25 t   1 3 3 4
Bạn Nam muốn làm một cái chuông gió bằng tấm bìa hình thoi. Nam mắc 4 1,0
chuông gió có khối lượng lần lượt là 10gr,10gr, 20gr;20gr vào các đỉnh điểm , A ,
B C, D của hình thoi. Nam tìm một vị trí cân bằng trên tấm bìa để móc chuông
lên, bằng cách xác định điểm M sao cho MA MB  2MC  2MD  0.
a) Em hãy giúp Nam xác định điểm M .
b) Từ đó tìm vị trí điểm K trên các cạnh hình thoi sao cho
KA  KB  2KC  2KD đạt giá trị nhỏ nhất.
Biết ABCD là hình thoi có cạnh bằng a và ABC  60 .
a) Em hãy giúp Nam xác định điểm M .
Gọi I, J lần lượt là trung điểm A , B CD .
MA  MB  2MC  2MD  0  MA  MB  2MC  MD  0
 2MI  2.2MJ  0 O,25đ  MI  2MJ  0  3MJ  JI  0  0,25đ 3MJ  IJ
( M là trọng tâm tam giác ICD ).
b)Từ đó tìm vị trí điểm K trên các cạnh hình thoi sao cho KA  KB  2KC  2KD
đạt giá trị nhỏ nhất. 0,25đ
Đưa về KA KB  2KC  2KD  6KM 0,25đ
KM ngắn nhất khi K là hình chiếu của M lên CD . Trang 3/4
(Trong các đoạn vuông góc hạ từ M lên các cạnh thì đoạn vuông góc hạ từ M
lên CD là ngắn nhất). Trang 4/4
Document Outline

• Ma_de_201 MOI
• DAP AN DE LE
  • Sheet1
• DAP AN TU LUAN 10