Đề cuối học kỳ 2 Toán 7 năm 2023 – 2024 phòng GD&ĐT Kinh Môn – Hải Dương

UBND THỊ XÃ KINH MÔN
ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI HỌC KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
MÔN: TOÁN – LỚP 7 ĐỀ CHÍ NH THỨC
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề gồm 02 trang)
I. TRẮC NGHIỆM (3,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau:
Câu 1. Cho 3a = 4b và a,b≠0. Khẳng định nào sau đây sai? A. a b = . B . a 3 = . C. 3 b = . D. a 4 = . 4 3 b 4 4 a b 3
Câu 2. Bậc của đa thức 3 2
x − x + 7x − 9 là A. 1. B . 2. C. 9 − . D. 3.
Câu 3. Cho đa thức một biến P(x) 2 3
= x + 3x − 5 + 2x . Cách biểu diễn nào sau đây là sắp
xếp theo lũy thừa giảm dần của biến? A. P(x) 2 3
= x + 3x + 2x − 5. B. P(x) 3 2
= 2x + 3x + x − 5. C. P(x) 2 3 = 5
− + x + 3x + 2x . D. P(x) 3 2 = 5
− + x + 2x + 3x .
Câu 4. Trong các số 1
− ; 0; 1; 3 thì số nào là nghiệm của đa thức: P(x) 2 = 2x + 3x − 5 A. 1 − B. 0 C. 1 D. 3
Câu 5. Gieo một con xúc xắc được chế tạo cân đối, đồng chất. Biến cố “Số chấm
xuất hiện trên con xúc xắc là 7” là biến cố A. Chắc chắn B. Ngẫu nhiên C . Không thể D. Không chắc chắn Câu 6.
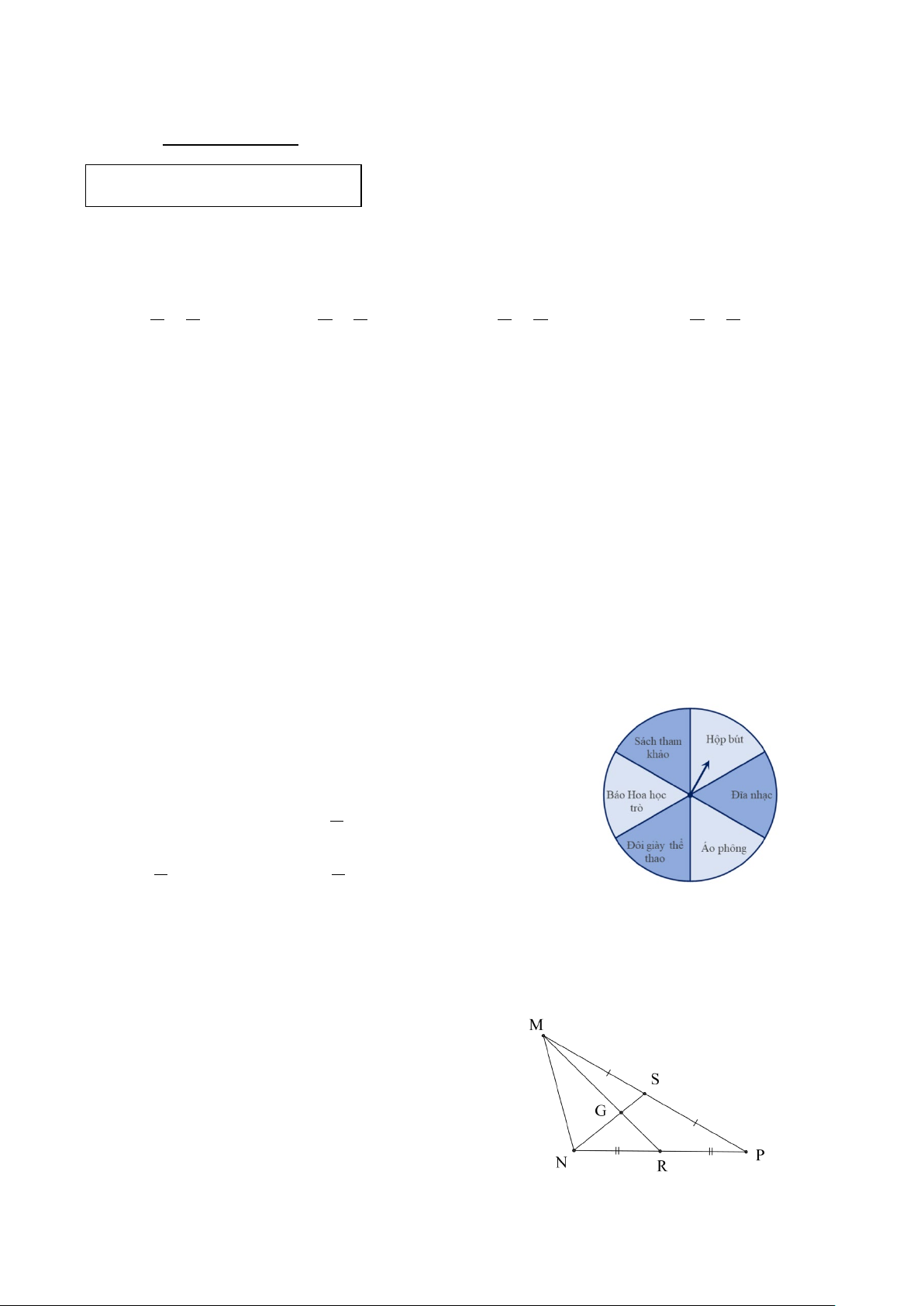
Một lớp học tổ chức trò chơi “Vòng quay
may mắn” bằng cách quay vòng quay như hình
bên. Xác suất để bạn An chọn được phần thưởng “Sách tham khảo” là A. 0. B. 1 . 2 C. 1 . D. 1 . 4 6
Câu 7. Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng? A.    B > A > C B.    C > A > B C.    A > B > C D.    A < B < C
Câu 8. Cho ∆MNP vuông tại M, khi đó: A. MN > NP B. MN > MP C. MP > MN D. NP > MN
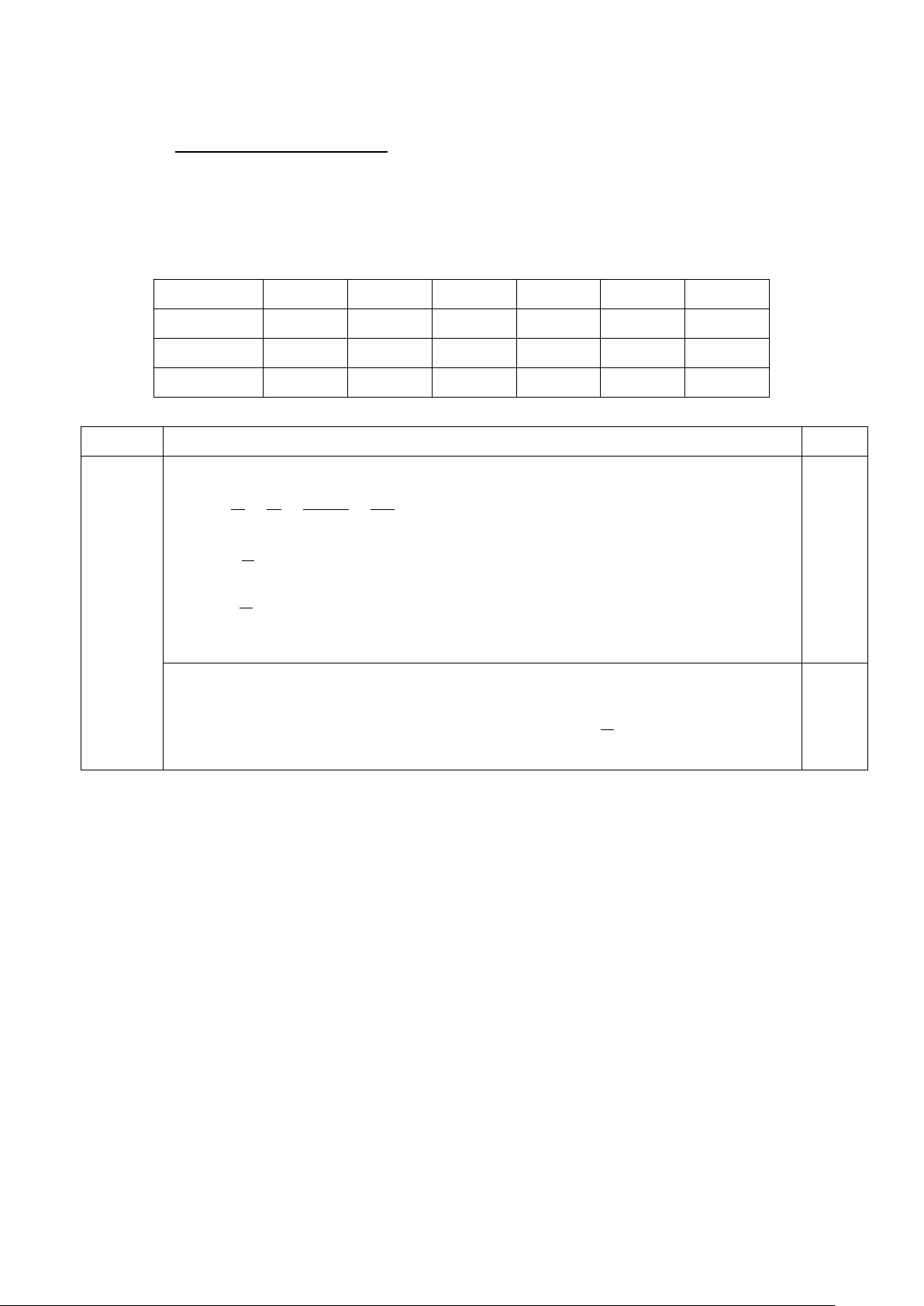
Câu 9. Cho hình vẽ sau.
Biết MR = 9cm. Độ dài đoạn thẳng MG bằng: A. 6 cm B. 4,5 cm C. 3 cm D. 9 cm 2
Câu 10. Trong các công thức sau, công thức nào cho biết: Đại lượng y tỉ lệ thuận với
đại lượng x theo hệ số tỉ lệ 2? A. y = x + 2 . B. 2 y = . C. y = 2x . D. 2 y = x . x
Câu 11. Số mặt của hình hộp chữ nhật là A. 6. B. 8. C.12 . D. 4 .
Câu 12. Mặt đáy của một hình lăng trụ đứng tam giác là A. hình chữ nhật. B. hình tam giác. C. hình vuông. D. hình thoi.
II. TỰ LUẬN (7,0 điểm)
Câu 13. (2,0 điểm)
a) Tìm hai số x và y, biết: x y
= và x + y = 26 . 9 4
b) Đội múa có 1 bạn nam và 5 bạn nữ, chọn ngẫu nhiên 1 bạn để phỏng vấn (biết
khả năng được chọn của mỗi bạn là như nhau). Hãy tính xác suất của biến cố bạn được chọn là nam.
c) Ba lớp 7A; 7B; 7C được phân công chăm sóc cây xanh trong sân trường. Biết
số cây các lớp 7A; 7B; 7C cần chăm sóc tỉ lệ lần lượt với các số 3; 4; 5 và số cây lớp
7C chăm sóc nhiều hơn số cây lớp 7A chăm sóc là 6 cây. Hỏi mỗi lớp chăm sóc bao nhiêu cây xanh?
Câu 14. (1,5 điểm) Cho hai đa thức 3 2 (
A x) = 2x − 3x + 4x + 3 và 2 3
B(x) = 2x + 3x − 6 .
a) Xác định bậc, hệ số cao nhất của đa thức ( A x). b) Tính (
A x) + B(x) và (
A x) − B(x) .
c) Tìm đa thức C(x) biết (2x + ) 1 .C(x) = ( A x).
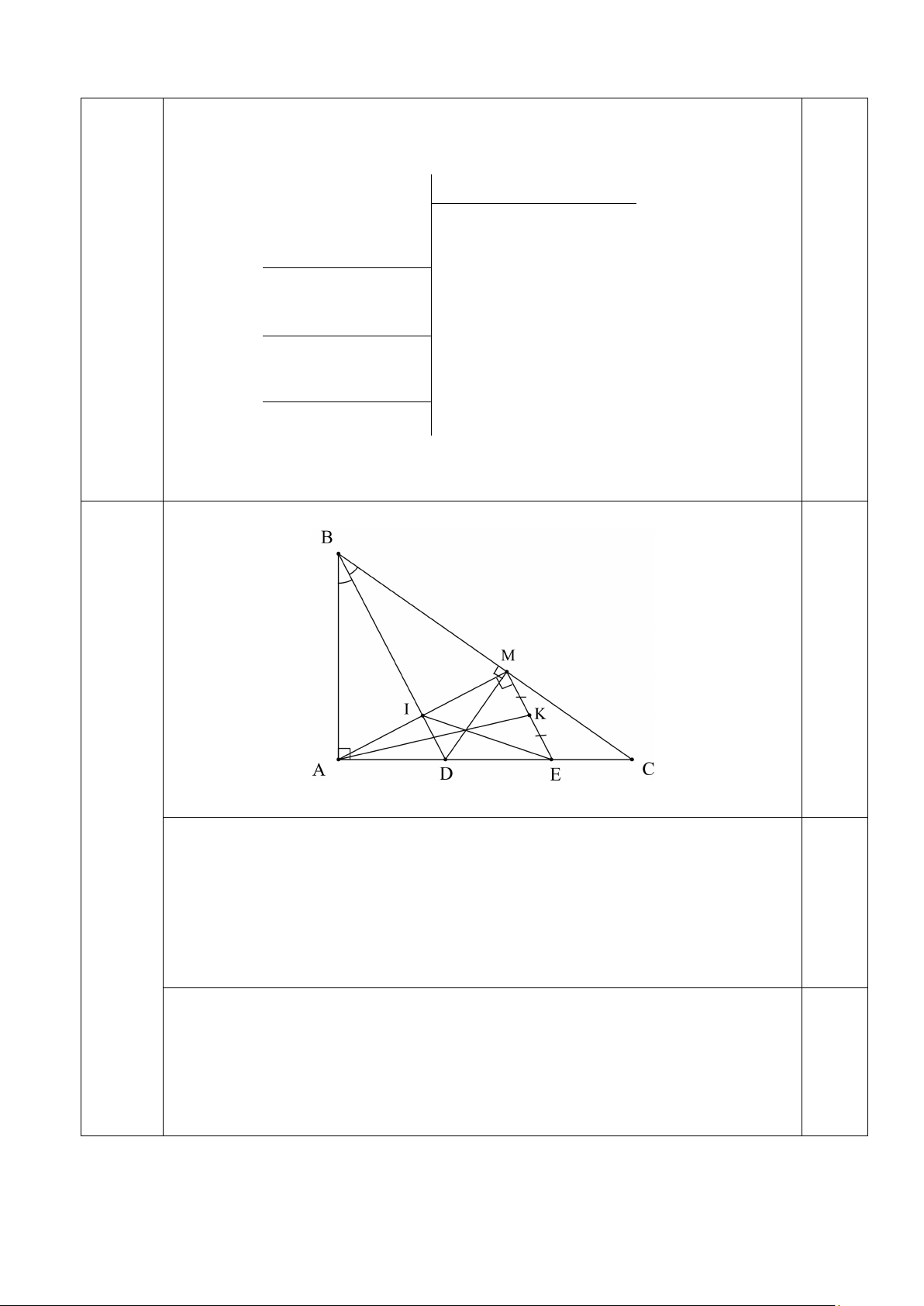
Câu 15. (2,5 điểm) Cho A
∆ BC vuông tại A có AB < AC , kẻ đường phân giác BD của 
ABC,(D∈ AC). Kẻ DM vuông góc với BC tại M . a) Chứng minh DA ∆ B = DM ∆ B. b) Chứng minh AD < DC .
c) Từ M kẻ đường thẳng vuông góc với AM cắt AC tại E . Gọi K là trung
điểm của ME . Gọi I là giao điểm của BD và AM . Chứng minh ba đường thẳng
AK , EI và MD đồng quy. Câu 16. (1,0 điểm)
Tìm các cặp số nguyên ( ; + +
x y) để biểu thức xy x 1 M =
có giá trị là số nguyên. xy + x + 2
–––––––– Hết ––––––––
Họ và tên học sinh:……………………………………Số báo danh:………………
Giám thị 1:…………………………………. Giám thị 2:……………………………… 3 UBND THỊ XÃ KINH MÔN
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC: 2023 – 2024 Môn: TOÁN 7 (HDC gồm 04 trang)
I. TRẮC NGHIỆM (3 điểm). Mỗi câu đúng được 0,25 điểm. Câu 1 2 3 4 5 6 Đáp án B D B C C D Câu 7 8 9 10 11 12 Đáp án A D A C A B
II. TỰ LUẬN (7,0 điểm). Câu Nội dung Điểm
a) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: x y x + y 26 = = = = 2 0.25 9 4 9 + 4 13
Suy ra: x = 2 ⇒ x =18; 0.25 9y 13 = 2 ⇒ y = 8 4
(2,0đ) Vậy x =18; y = 8.
b) Tổng số học sinh trong đội múa là 1 + 5 = 6 (học sinh) 0.25
Xác suất của biến cố “Bạn được chọn là nam” là 1 0.25 6 4
c) Gọi số cây xanh các lớp 7A; 7B; 7C cần chăm sóc là x, y, z cây ( *
x, y, z ∈ )
Vì số cây các lớp 7A; 7B; 7C cần chăm sóc tỉ lệ lần lượt với các số 3; 4; 5 nên ta có x y z = = 3 4 5
Do số cây lớp 7C chăm sóc nhiều hơn số cây lớp 7A chăm sóc là 6 cây
nên ta có z − x = 6 . 0,25
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: x y z z − x 6 = = = = = 3 3 4 5 5 − 3 2 0,25 Khi đó x = 3.3 = 9 y = 4.3 =12 0,25 z = 5.3 =15
Vậy mỗi lớp 7A; 7B; 7C chăm sóc lần lượt là 9; 12; 15 cây xanh. 0,25
a) Xác định bậc, hệ số cao nhất của đa thức ( A x) . Đa thức ( A x) có bậc là 3; 0.25
có hệ số cao nhất là 2. 0,25 b) Ta có: 3 2 2 3 (
A x) + B(x) = (2x −3x + 4x + 3) + (2x + 3x − 6) 3 2 2 3
= 2x − 3x + 4x + 3+ 2x + 3x − 6 3 3 2 2
= 2x + 3x − 3x + 2x + 4x + 3− 6 3 3 2 2
= (2x + 3x ) − (3x − 2x ) + 4x + (3− 6) 14 3 2
= 5x − x + 4x − 3 0.25 (1,5đ)
A x − B x = ( 3 2
x − x + x + ) −( 2 3 ( ) ( ) 2 3 4 3 2x + 3x − 6) 3 2 2 3
= 2x − 3x + 4x + 3− 2x − 3x + 6 3 3 2 2
= (2x − 3x ) − (3x + 2x ) + 4x + (3+ 6) 3 2
= −x − 5x + 4x + 9 Vậy 3 2 (
A x) + B(x) = 5x − x + 4x − 3 0,25 3 2 (
A x) − B(x) = −x − 5x + 4x + 9 5 c) Từ (2x + ) 1 .C(x) = (
A x) suy ra C(x) = ( A x) :(2x + ) 1 3 2
C(x) = 2x − 3x + 4x + 3 : 2x +1 ( ) ( ) 3 2
2x − 3x + 4x + 32x +1 − 3 2 2x + x 2 x − 2x + 3 2 4 − x + 4x + 3 − 2 4 − x − 2x 6x + 3 − 6x + 3 0,5 0 Vậy 2
C(x) = x − 2x + 3 HS vẽ hình đúng 15 0,25 (2,5đ)
a) X ét ∆𝐷𝐷𝐷𝐷𝐷𝐷 và ∆𝐷𝐷𝐷𝐷𝐷𝐷 có:  =  0 BAD BMD = 90  = 
ABD MBD (BD là tia phân giác góc ABD) 0,25 Cạnh BD chung 0,25 Vậỵ DA ∆ B = DM ∆
B (cạnh huyền – góc nhọn) 0,25
b) Từ phần a ta có: DA ∆ B = DM ∆ B nên
AD = MD ( Hai cạnh tương ứng bằng nhau ) (1) 0,25 Vì D
∆ MC vuông tại M nên DC > DM . (2) 0,25
Từ (1) và (2) suy ra DC > AD.
Vậy AD < DC . 0,25 6
c) Ta có BA = MB (do DA ∆ B = DM ∆ B).
Nên tam giác ABM cân tại B
mà có BI là đường phân giác nên BI cũng là đường trung tuyến
⇒ I là trung điểm của AM (3) Ta có DA = DM (do DA ∆ B = DM ∆ B). 0.25
⇒ Tam giác ADM cân tại D ⇒  =  DAM DMA Vì  +  =  +  o
DAM DEM DMA DME(= 90 ) nên suy ra  =  DEM DME ⇒ D
∆ ME cân tại D ⇒ DM = DE.
Mà DA = DM (theo chứng minh trên) ⇒DA = DE
⇒ D là trung điểm của AE (4) 0.25
Xét tam giác AME có I, D lần lượt là trung điểm của các cạnh AM, AE
(theo chứng minh (3),(4)), và K là trung điểm của cạnh ME (theo GT)
Nên AK, EI và MD là ba đường trung tuyến của tam giác AME. Do
đó, ba đường thẳng AK, EI và MD đồng quy. 0.25 Ta có
xy + x +1 xy + x + 2 −1 1 M = = =1− xy + x + 2 xy + x + 2 xy + x + 2
Để biểu thức M có giá trị là số nguyên thì 1 nhận giá trị là số xy + x + 2 nguyên. 0,25
Do x, y ∈ Z nên xy + x + 2 là số nguyên và là ước của 1
Suy ra xy + x + 2 ∈ {-1 ; 1}
+ Nếu xy + x + 2 =1 ⇒ x( y + ) 1 = 1 −
Vì x, y là các số nguyên nên x và y + 1 cũng là các số nguyên. Ta có bảng giá trị x -1 1 16 y +1 1 -1 y 0 -2 0,25 KL Thỏa mãn Thỏa mãn
+ Nếu xy + x + 2 = 1 − ⇒ x( y + ) 1 = 3 −
Vì x, y là các số nguyên nên x và y + 1 cũng là các số nguyên. ta có bảng giá trị x -1 1 -3 3 y +1 3 -3 1 -1 y 2 -4 0 -2 0,25 KL
Thỏa mãn Thỏa mãn Thỏa mãn Thỏa mãn
Vậy các cặp số nguyên (x, y) cần tìm là
(-1; 0) ; (1; -2) ; (-1; 2) ; (1 ; -4) ; (-3 ; 0) ; (3 ; -2) 0,25
Ghi chú: Mọi cách giải khác đúng, phù hợp với chương trình đều chấm điểm tối đa. 7
Document Outline

• Câu 1. Cho và . Khẳng định nào sau đây sai?
• Câu 5. Gieo một con xúc xắc được chế tạo cân đối, đồng chất. Biến cố “Số chấm xuất hiện trên con xúc xắc là 7” là biến cố
• Câu 6.