Đề cuối kỳ 1 Toán 9 năm 2023 – 2024 phòng GD&ĐT Thanh Oai – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra cuối học kỳ 1 môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo UBND huyện Thanh Oai, thành phố Hà Nội; kỳ thi được diễn ra vào thứ Ba ngày 26 tháng 12 năm 2023; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem.
Preview text:
UBND HUYỆN THANH OAI
ĐỀ KIỂM TRA HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024 Môn: Toán 9 Thời gian: 90 phút Bài 1 (2,0 điểm)
1. Tính giá trị các biểu thức sau: 2
a) A = 5 72 −12 8 + 4 18 + 3 9 b) B = − + ( + )2 21 7 2 7 − 2 7 3 −1 2. Giải phương trình: x +1
3 4x + 4 − 9x + 9 −8 = 5 16 Bài 2 (2,0 điểm) Cho biểu thức − = x A và x 2 x 10 x + 2 B = − :
(x ≥ 0; x ≠ 25; x ≠ 4) x + 2
x +5 x 25 − x + 5
1. Tính giá trị của biểu thức A khi x = 9 2. Rút gọn B 3. Đặt = A P
. Tìm x để P = P B Bài 3 (2,5 điểm)
1. Cho đường thẳng (d): y = (m−2)x −3 với m ≠ 2.
a) Vẽ đường thẳng (d) trên mặt phẳng tọa độ Oxy khi m = 5;
b) Tìm m để đường thẳng (d) song song với đường thẳng (d’): y = -5x + 2;
c) Gọi giao điểm của đường thẳng (d) với hai trục
tọa độ là A và B. Tìm m để tam giác OAB vuông cân tại O.
2. Để chuyển đồ lên xe hàng, người ta dùng băng
chuyền CB dài 4,5m. Biết góc hợp bởi băng chuyền và
mặt đất là 280. Tính khoảng cách BA từ khoang của xe
hàng đến mặt đất? (Kết quả làm tròn đến chữ số thập
phân thứ nhất). (Xem hình vẽ mô tả). Bài 4 (3,0 điểm)
Từ điểm A nằm ngoài đường tròn (O; R) vẽ tiếp tuyến AB với đường tròn (O) (B
là tiếp điểm). Vẽ dây cung BC của đường tròn (O) vuông góc với OA tại H (H ∈ OA) .
a) Chứng minh H là trung điểm của BC và AC là tiếp tuyến của đường tròn (O);
b) Cho OA = 2R. Chứng minh: AH. AO = AB2 = 3R2 và ∆ABC đều;
c) Trên tia đối của tia BC lấy điểm Q bất kì. Từ điểm Q vẽ hai tiếp tuyến QD, QE với
đường tròn (O) (D, E là các tiếp điểm). Chứng minh ba điểm A, E, D thẳng hàng. Bài 5 (0,5 điểm) Chứng minh rằng: a + b 1
≥ , với a,b là các số dương.
a(3a + b) + b(3b + a) 2
........ Hết ........
(Giám thị coi thi không giải thích gì thêm)
ĐÁP ÁN – HƯỚNG DẪN CHẤM ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 9 NĂM HỌC 2023 - 2024 BÀI Ý ĐÁP ÁN ĐIỂM Bài 1 1a 2 0,75 (2,0 điểm)
A = 5 72 −12 8 + 4 18 + 3
= 30 2 − 24 2 +12 2 + 2 =19 2 9 1b 0,25 B = − − + ( + )2 21 7 2
7 − 2 7 = 7( 3 1) + 2 + 7 − 2 7 3 −1 3 −1
= 7 + 2+ 7 − 2 7 = 2 0,5
2 6 x +1−3 x +1− 2 x +1 = 5 ⇔ x +1 = 5 (Điều kiện: x ≥ 1 − ) 0,25
Giải pt tìm được: x = 24 và kết luận 0,25
a Thay x = 9 (TMĐK) vào biểu thức Bài 2 A 0,25 (2,0 điểm) Tính được 3 A = kết luận 0,25 5 b 2. x
( x −5) x +2 B
(x ≥ 0; x ≠ 25; x ≠ 4) 0,25 ( = − x + 5) ( x +5).( x − 5) : x + 5 x − 2 x + 5 B = . 0,25 x + 5 x + 2 x − 2 B = 0,25 x + 2 Vậy x − 2 B =
với x ≥ 0; x ≠ 25; x ≠ 4 x + 2 0,25 c Ta có: A x x − 2 P = = : B x + 2 x + 2 x x + 2 P = . x + 2 x − 2 = x P x − 2 0,25
Để P = P ⇔ P ≥ 0 ⇔ x ≥ 0 x − 2
Lập luận xét hai trường hợp tìm được x = 0 (thỏa mãn ĐKXĐ) 0,25 Bài 3
1a Khi m = 5, đường thẳng (d) có dạng: y = 3x – 3 0,25 (2,5 điểm)
Xác định được giao điểm của đường thẳng (d) với hai trục tọa độ 0,25
Vẽ đúng đường thẳng (d) 0,25
1b Đường thẳng (d’) song song với (d) ⇔ m – 2 = -5 và – 3 ≠ 2 0,5 Tìm được m = -3 0,25
1c Xác định được giao điểm của đường thẳng (d) với hai trục tọa độ là
A(0; -3) và B( 3 ;0). Suy ra OA = 3 3 − = 3;OB = 0,25 m − 2 m − 2 ∆OAB vuông cân 3 0,25 ⇔ OA = OB ⇔
= 3. Từ đó tìm được m = 1 hoặc m − 2 m = 3
2 AB = BC. sin28o = 4,5.sin28o B 0,25 4,5 28° C A
Tính được AB ≈ 2,1(m) và kết luận. 0,25 Bài 4
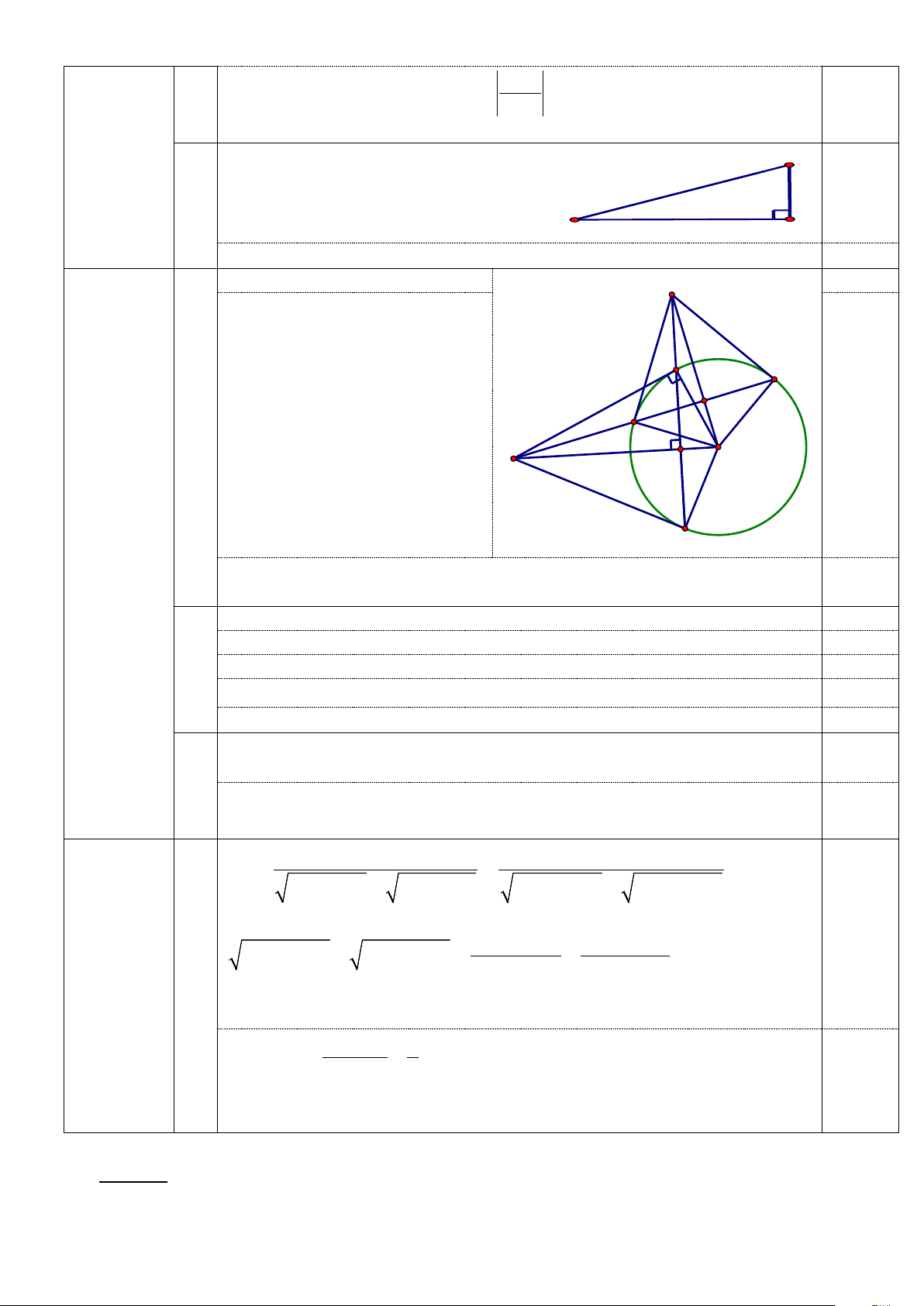
a Vẽ hình đúng đến câu a Q 0,25 (3,0 điểm)
Chứng minh được H là trung điểm BC. 0,5 B E K D O H A C
Chứng minh được ∆OAB = ∆OAC (c.g.c). Từ đó chứng minh được AC 0,5 là tiếp tuyến của (O).
b Chứng minh được AH.AO = AB2 0,25
Chứng minh được AB2 = AO2 – OB2 0,25 Suy ra được AH. AO = 3R2 0,25 Tính được 0
BAO = 30 . Từ đó suy ra 0 BAC = 60 0,25
Chứng minh được ∆ABC đều 0,25
c Gọi K là giao điểm của OQ và DE 0,25
Chứng minh được: A ∆ OK ∽ QOH ∆ ( . c g.c)
Chứng minh được: = 0
AKO QHO = 90 ⇒ AK ⊥ OQ mà DE ⊥ OQ tại K 0,25 nên A, D, E thẳng hàng. Bài 5 a + b 2.(a + b) (0,5 điểm) VT = = .
a(3a + b) + b(3b + a)
4a(3a + b) + 4b(3b + a)
Áp dụng bất đẳng thức Cô – Si, ta có: 0,25 ( + ) +
( + ) 4a + 3a + b 4b + 3 4 3 4 3 b + a a a b b b a ≤ +
= 4(a + b) > 0 , 2 2
với a,b là các số dương. 2(a + b) 0,25 Suy ra 1 VT ≥ = . 4(a + b) 2
Dấu “=” xảy ra khi a = b . Lưu ý :
- Điểm toàn bài làm tròn đến chữ số thập phân thứ nhất.
- Học sinh làm cách khác đúng cho điểm tương đương.
Document Outline
- Bài 1 (2,0 điểm)
- 1. Tính giá trị các biểu thức sau:
- a)
- b) B =
- 2. Giải phương trình:
- Bài 2 (2,0 điểm)
- Bài 3 (2,5 điểm)
- 1. Cho đường thẳng (d): với m ≠ 2.
- a) Vẽ đường thẳng (d) trên mặt phẳng tọa độ Oxy khi m = 5;
- b) Tìm m để đường thẳng (d) song song với đường thẳng (d’): y = -5x + 2;
- c) Gọi giao điểm của đường thẳng (d) với hai trục tọa độ là A và B. Tìm m để tam giác OAB vuông cân tại O.
- 2. Để chuyển đồ lên xe hàng, người ta dùng băng chuyền CB dài 4,5m. Biết góc hợp bởi băng chuyền và mặt đất là 280. Tính khoảng cách BA từ khoang của xe hàng đến mặt đất? (Kết quả làm tròn đến chữ số thập phân thứ nhất). (Xem hình vẽ mô tả).
- Bài 4 (3,0 điểm)
- Từ điểm A nằm ngoài đường tròn (O; R) vẽ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Vẽ dây cung BC của đường tròn (O) vuông góc với OA tại H (H ( OA) .
- a) Chứng minh H là trung điểm của BC và AC là tiếp tuyến của đường tròn (O);
- b) Cho OA = 2R. Chứng minh: AH. AO = AB2 = 3R2 và (ABC đều;
- c) Trên tia đối của tia BC lấy điểm Q bất kì. Từ điểm Q vẽ hai tiếp tuyến QD, QE với đường tròn (O) (D, E là các tiếp điểm). Chứng minh ba điểm A, E, D thẳng hàng.
- Bài 5 (0,5 điểm)
- ĐÁP ÁN – HƯỚNG DẪN CHẤM ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 9
- NĂM HỌC 2023 - 2024
- Lưu ý :
- - Điểm toàn bài làm tròn đến chữ số thập phân thứ nhất.
- - Học sinh làm cách khác đúng cho điểm tương đương.