Đề cuối kỳ 2 Toán 10 năm 2021 – 2022 trường THPT Phan Đăng Lưu – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ KIỂM TRA, ĐÁNH GIÁ CUỐI KỲ II THÀNH PHỐ HỒ CHÍ MINH
LỚP 10 - NĂM HỌC 2021 - 2022
TRƯỜNG TRUNG HỌC PHỔ THÔNG Môn thi:TOÁN PHAN ĐĂNG LƯU
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) ĐỀ CHÍNH THỨC (Đề thi có 1 trang) ĐỀ A
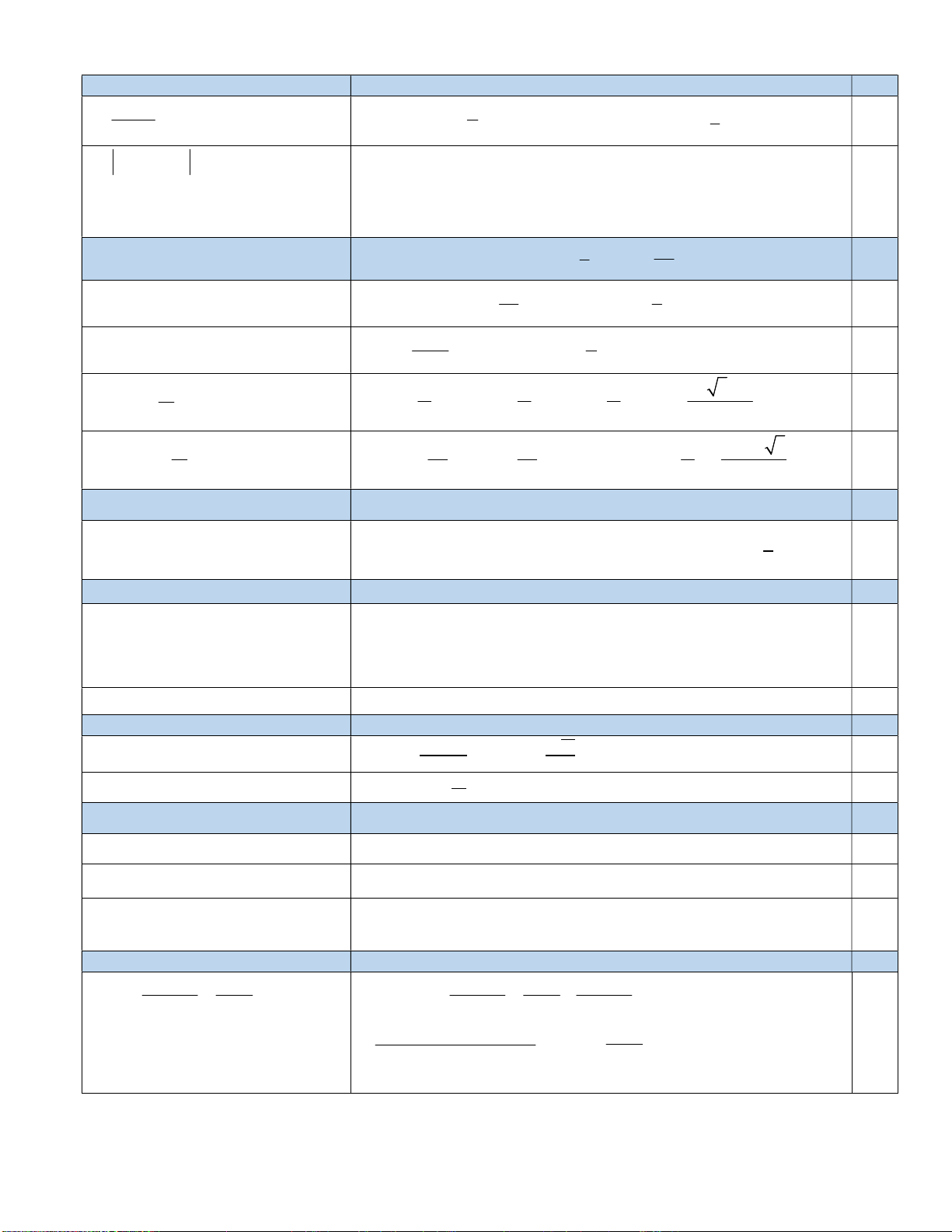
Câu 1. (2 điểm) Giải các bất phương trình 3x 1 a)  0 ; b) 2 x  2x  4  4 x 1 3 
Câu 2. (2 điểm) Cho sin x  biết  x   . 5 2       Tính cos ; x tan ; x cos x  ,sin 2x      .  3   6 
Câu 3. (1 điểm) Tìm m để phương trình 2 2x  2m  
3 x  2  0 có hai nghiệm phân biệt.
Câu 4 (1 điểm) Trong mặt phẳng tọa độ Oxy, cho ( A 4  ;5);B(2;1). 
a) Viết phương trình tham số đường thẳng qua A nhận AB làm vecto chỉ phương.
b) Viết phương trình tổng quát đường trung trực của đoạn AB.
Câu 5 (1 điểm) Trong mặt phẳng tọa độ Oxy. Cho đường thẳng 𝑑: 2𝑥 − 𝑦 + 5 = 0 và đường thẳng 𝛥: 3𝑥 + 4𝑦 + 1 = 0
a) Gọi 𝜑 là góc giữa đường thẳng d và đường thẳng  .Tính 𝑐𝑜𝑠𝜑.
b) Tính khoảng cách từ điểm 𝑀(0 ; 1) đến đường thẳng  .
Câu 6 (2 điểm) Cho đường tròn C 2 2
: x  y  8x 12y 16  0 :
a) Tìm tâm và bán kính của đường tròn.
b) Viết phương trình đường tròn đường kính AB với A1;5, B( 5  ; 3  ) .
c) Viết phương trình tiếp tuyến của C  tại điểm M trên C  có tung độ bằng 0.
Câu 7 (1 điểm) Chứng minh rằng sin x 1 cot x  
với x  k , k   . 1 cos x sin x ------- Hết -------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: …………………………………………… Số báo danh: ……………….....
Họ và tên giám thị: ….……………………………………… Chữ ký: …………………………..
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ KIỂM TRA, ĐÁNH GIÁ CUỐI KỲ II THÀNH PHỐ HỒ CHÍ MINH
LỚP 10 - NĂM HỌC 2021 - 2022
TRƯỜNG TRUNG HỌC PHỔ THÔNG Môn thi:TOÁN PHAN ĐĂNG LƯU
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) ĐỀ CHÍNH THỨC (Đề thi có 1 trang) ĐỀ B
Câu 1. (2 điểm) Giải các bất phương trình 2x  3 a)  0 ; b) 2 x  3x  2  2 x  2 4 3
Câu 2. (2 điểm) Cho cos x   , biết   x  . 5 2       Tính sin x;cot ; x sin x  ;cos 2x       6   3 
Câu 3. (1 điểm) Tìm m để phương trình 2
x  3m  5 x  4  0 vô nghiệm.
Câu 4 (1 điểm) Trong mặt phẳng tọa độ Oxy, cho ( A 3;2);B(1;6) . 
a) Viết phương trình tham số đường thẳng qua B nhận AB làm vecto chỉ phương.
b) Viết phương trình tổng quát đường trung trực của đoạn AB.
Câu 5 (1 điểm) Trong mặt phẳng tọa độ Oxy. Cho đường thẳng 𝑑: 3𝑥 + 2𝑦 + 7 = 0 và đường thẳng 𝛥: 4𝑥 − 3𝑦 + 5 = 0
a) Gọi 𝜑 là góc giữa đường thẳng d và đường thẳng  .Tính 𝑐𝑜𝑠𝜑.
b) Tính khoảng cách từ điểm 𝑀(1; −1) đến đường thẳng  .
Câu 6 (2 điểm) Cho đường tròn C 2 2
: x  y 14x 10y  25  0 :
a) Tìm tâm và bán kính của đường tròn.
b) Viết phương trình đường tròn có tâm I 4; 2   và đi qua A 2  ;6 .
c) Viết phương trình tiếp tuyến của C  tại điểm M trên C  có hoành độ bằng 0. 
Câu 7 (1 điểm) Chứng minh rằng cos x 1 tan x   vói x   k , k   . 1 sin x cos x 2 ------- Hết -------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: …………………………………………… Số báo danh: ……………….....
Họ và tên giám thị: ….……………………………………… Chữ ký: ………………………….. ĐÁP ÁN TOÁN 10 ĐỀ A Câu 1. (2 điểm) Bài giải TĐ 3x 1 1  1  1 đ a)  0
x  1 và x  (0.25) BXD đúng (0.5) => x  1  ; (0.25đ) x 1   3  3  b) 2 x  2x  4  4 2 x  2x  4  4 x    4  ; 2 1đ   (0.25)   (0.5) 2 x   2x  4  4  x    ;  2  0;  x  4
 ;20;2 (0.25) Câu 2. (2 điểm) Cho 3  sin x  ;  x   . 5 2 cos x 0.5 2 2 16 4 cos x 1 sin x 
(0.25) => cos x   (x  (II )) (0.25) 25 5 tan x sin x 3 0.5 tan x  (0.25)   (0.25) cos x 4    0.5 cos x       4   3 3   cos x 
 cos xcos  sin xsin (0.25) = (0.25)  3     3  3 3 10       24 3  7 0.5 sin 2x  24 7   sin 2x   ;cos2x  (0.25)  sin 2x     (0.25)  6  25 25  6  50 Câu 3. (1 điểm)
Tìm m để phương trình có 2 nghiệm phân biệt 2 2x  2m   3 x  2  0 a  0 7 1 1đ  (0,25)  2
4m 12m  7  0 (0,5)  m  ; m  (0,25).   0 2 2 Câu 4. (1 điểm) ( A 4  ;5);B(2;1) a)PTTS đường thẳng AB  x  4   6t 0.5
AB  (6;4) (0.25) PTTS:  (t  ) (0.25) y  5  4t b)PTTQ trung trực AB I là tđiểm AB  I ( 1
 ;3) (0.25) PTTQ: 6x  4 y 18  0 (0.25) 0.5 Câu 5. (1 điểm)
𝜟: 𝟑𝒙 + 𝟒𝒚 + 𝟏 = 𝟎; 𝒅: 𝟐𝒙 − 𝒚 + 𝟓 = 𝟎 a)cos góc tạo bởi 2 đt | ⃗. ⃗| 𝑐𝑜𝑠𝜑 =
(𝟎. 𝟐𝟓) = √ (0.25đ) 0.5 | ⃗|.| ⃗| b)Kc 𝑀(0 ; 1) đến 𝛥 𝑑[𝑀, (∆)] = 1 (0.5đ) 0.5 Câu 6. (2 điểm) C 2 2
: x  y  8x 12y 16  0 a)Tâm, bán kinh (C)
Tâm I 4;6 (0,25), bán kính R  6 (0,25) 0.5
b)Đt đường kinh A1;5,B( 5  ; 3
 ) . Tâm I(-2;1), R  IA  5(0,25);PTĐT x  2   y  2 2 1  25 (0,25). 0.75
c) M trên C  có tung độ
y  0  x  4  M ( 4  ;0) (0.25) 0.75  bằng 0.
Tiếp tuyến có VTPT MI  0;6(0.25) =>PTTT y  0 (0.25) Câu 7. (1 điểm) Chứng minh sin x 1 sin x cos x sin x 1 cot x   VT  cot x    (0.25) 1 cos x sin x 1 cos x sin x 1 cos x x   x 2 cos 1 cos  sin x 1 cos x   1 (0.5)   VP (0.25) sin x 1 cos x sin x 1 cos x sin x ĐÁP ÁN TOÁN 10 ĐỀ B Câu 1. 2 điểm Bài giải TĐ x  3 1 đ a) 2 3  0
x  2 và x   (0.25) BXD đúng (0.5)  3  x   ;    2;    (0.25đ) x  2 2  2  b) 2 x  3x  2  2 2 x 3x  2  2 x    1  ; 4 1đ   (0.25)   (0.5) 2 x 3x  2  2  x  
;03;  x  1  ;03;4 (0.25) Câu 2. 2 điểm 4  cos x   ; 3   x  . 5 2 sin x 9 3 0.5 2 2 sin x  1 cos x 
(0.25)  sin x   (vì x (III ) ) (0.25) 25 5 cot x cos x 4 0.5 cot x  (0.25)  (0.25) sin x 3         3  3  4 0.5 sin x    sin x   sin x cos  cos xsin   (0.25) = (0.25)  6   6  6 6 10        cos 2x  24 7 7 24 3   sin 2x  ;cos 2x  (0.25)  cos 2x     (0.25)  3  25 25  3  50 Câu 3. 1 điểm 2
x  3m  5 x  4  0 vô nghiệm a  0 1 1  (0,25)  2
9m  30m  9  0 (0,5)  3   m   (0,25).   0 3 Câu 4. 1 điểm ( A 3  ;2);B(1;6) a)Tham số AB  x 1 4t 0.5
VTCP AB  (4;4) (0.25)=>PTTS:  (t  ) (0.25)  y  6  4t b)Trung trực AB
I là trung điểm AB  I (1;4) (0.25) PTTQ: x  y  3  0 (0.25) 0.5 Câu 5. 1 điểm
𝜟: 𝟒𝒙 − 𝟑𝒚 + 𝟓 = 𝟎; 𝒅: 𝟑𝒙 + 𝟐𝒚 + 𝟕 = 𝟎
a)Tính cos góc 2 đường thẳng | ⃗. ⃗| 𝑐𝑜𝑠𝜑 =
(𝟎. 𝟐𝟓) = √ (0,25đ) 0.5 | ⃗|.| ⃗|
b)Khoảng cách 𝑀(1 ; −1) đến 𝛥 𝑑[𝑀, (∆)] = (0,5đ) 0.5 Câu 6. 2 điểm C 2 2
: x  y 14x 10y  25  0 a)Tâm, bán kinh
Tâm I 7;5 (0,25), bán kính R  7 (0,25). 0.5 b) tâm I 4; 2   qua A 2  ;6
R  IA  10 (0,25) PTĐT: x  2   y  2 4 2  100 (0,5) 0.75 
c) M trên C  có hoành
x  0  y  5 (0.25) tiếp tuyến có VTPT MI  7;0 (0.25) 0.75 độ bằng 0.
Phương trình tiếp tuyến 7  x  0 (0.25) Câu 7. 1 điểm cos x 1 cos x sin x cos x 1 tan x   VT  tan x    (0.25) 1 sin x cos x 1 sin x cos x 1 sin x x   x 2 sin 1 sin  cos x  1 (0.25)   VP (0.5) cos x 1 sin x cos x