
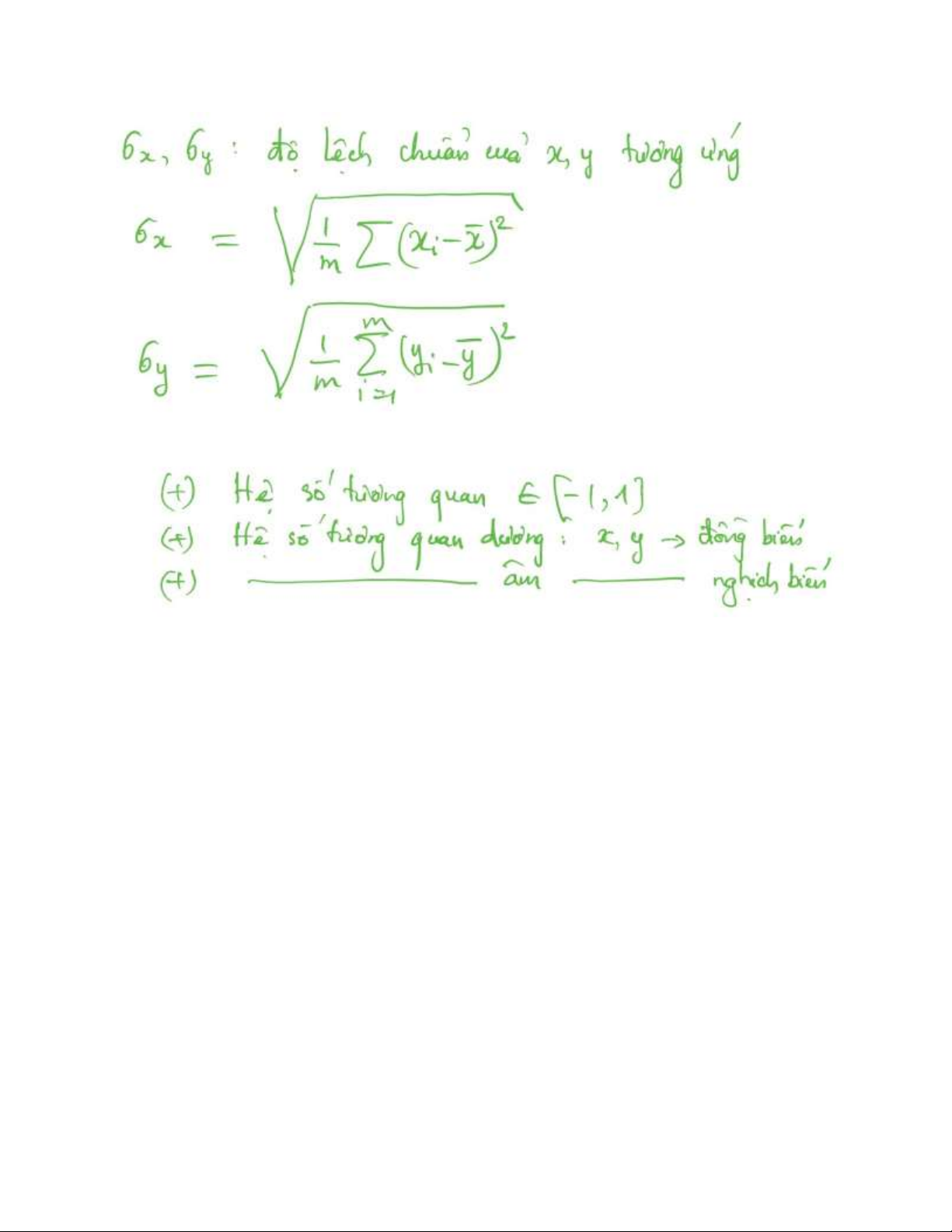
Preview text:
lOMoAR cPSD| 59561309 Phần 1.
Lý thuyết về trí tuệ nhân tạo và khoa học dữ liệu đọc hết các slide đã dạy Phần 2. Tính toán
Các bạn có thể xem thêm file DeCuong.xlsx về các công thức tính II.1 Phân lớp
Tính về Entropy và Information Gain Ví dụ:
Đối tượng A B C D Phân lớp 1 1 0 1 0 yes 2 1 0 1 1 no lOMoAR cPSD| 59561309 3 0 1 1 0 yes 4 0 1 0 1 no 5 1 0 1 0 yes 6 1 1 0 0 no 7 0 1 0 1 yes 8 1 0 1 1 no 9 0 1 1 0 yes 10 0 0 1 0 no
1. Tính entropy của tập dữ liệu ban đầu: Entropy ban đầu E(S)
Nhận thấy dataset có 2 class là Yes và no
Vậy ta có S(yes) có 5 đối tượng (1,3,5,7,9) , S(no) có 5 đối tượng (2,4,6,8,10)
Vậy |S(yes)| =5; và|S(no)| =5;
Như vậy E(S) = -5/10 * log2(5/10) + - 5/10*log2(5/10) = 1;
2.Tính Information Gain cho Đặc trưng A.
Trước hết tính giá trị Entropy của từng giá trị đặc trưng A mang.
Đặc trưng A mang hai giá trị là 1 và 0;
Giá trị 1; gồm các đối tượng 1, 2 ,5, 6, 8
Giá trị 0; gồm các đối tượng 3, 4,7, 9, 10
Xét tiếp có bao nhiêu class và Yes/No khi Đặc trưng A mang giá trị 1 ( A=1)
A = 1 ; đối tượng 1 (yes); 2(no); 5 (yes) ; 6 (no); 8(no)
A= 0; đối tượng 3 (yes); 4 (no) ; 7(yes); 9(yes); 10 (no)
Vậy Entropy (A=1) = -2/5 * log2(2/5) + - 3/5 *log2(3/5) lOMoAR cPSD| 59561309
Entropy (A=0) = -3/5*log2(3/5) + - 2/5*log2(2/5)
Vậy Information gain của S khi chọn A để chia
IG(S,A) = E(S) - ( 5/10 * Entropy (A=1) + 5/10 * Entropy (A=0) );
II.2 Mô hình hồi quy
II.2.1 Phương trình hồi quy
1) Cho bộ dữ liệu X và Y = {(1 ; 2); (2; 3); (3 ; 5) ; (4;6)}; Tìm phương trình hồi quy.
Phương trình hồi quy được viết dưới dạng Y = aX + b;
Để tìm a và b; áp dụng các công thức sau:
Bước 1. Xác định được các Ymean (Y trung bình) và Xmean (X trung bình) n n yi xi y= i=1 x= i=1 n n Bước 2. Tính SSxy n
SSxy = (xi −x)(yi −y) i=1 Bước 3 Tính SSx n
SSx = (xi −x)2 i=1 𝑺𝑺𝒙𝒚
Bước 4. Hệ số a = 𝑺𝑺𝒙
Hệ số b = Ymean - a* Xmean lOMoAR cPSD| 59561309
Tìm a và b cho phương trình với bộ dữ liệu như trên;
Xác định được n =4; Xmean = 2.5; Ymean = 4;
SSx = 5; Ssxy = 7; a = 1.4; b = 0.5;
Vậy phương trình hồi quy là Y = 0.5 +1.4X;
II.2.2 Các hệ số sai số
Các hệ số sai số cơ bản
1) Tổng lỗi bình phương. SSE ( Sum of the Squared Errors) 2) MSE 3. RMSE lOMoAR cPSD| 59561309 4. MAE
5. R2-score (R squared) hay R2 lOMoAR cPSD| 59561309
Ví dụ: Cho phương trình dự đoán Y = aX +b; sau khi thành lập được phương trình; có các giá trị Y dự
đoán (Y^) như sau: Y_pred = 4; 3; 3; 5; 5;
Trong khi đó giá trị thật là Y = 3; 4; 5; 6; 7
Tính các giá trị MAE, SSE, MSE, RMSE và R2-score; III. Thống kê
III.1 Mode (số yếu vị): Là giá trị của phần tử có số lần xuất hiện nhiều nhất trong danh sách hoặc tập mẫu.
Ví dụ 1, yếu vị của {1, 3, 6, 6, 6, 7, 7, 12, 12, 17} là 6
Ví dụ 2, Mode của {1, 1, 2, 2, ,3, 5} là 1 và 2;
Ví dụ 3, {1, 2 , 3 , 4, 5} không có mode, vì các phần tử đều xuất hiện 1 lần
III.2 Median và Tứ phân vị
Median là phần tử ở giữa dãy số được xác định như sau.
Cho dãy số có 5 phần tử {1 , 5, 2 , 4, 9}
Sắp xếp lại dãy số theo thứ tự tăng dần: {1, 2, 4, 5, 9}
Lúc này Median của dãy số là phần tử thứ 3, có giá trị là 4.
Tuy nhiên với dãy số chẵn : {1 , 5, 2 , 4, 9, 7} lOMoAR cPSD| 59561309
Sắp xếp lại dãy số theo thứ tự tăng dần: {1, 2, 4, 5, 7, 9}
Lúc này Median là giá trị trung bình của hai phần tử ở giữa dãy số: phần tử số 3 và phần tử số 4: median = (4+5)/2 = 4.5
Xác định khoảng Tứ phân vị như sau IQR
Vẫn cho dãy : {1 , 5, 2 , 4, 9, 7} , ta đã biết Median của dãy số là 4.5
Dãy số chia làm 2 dãy con là 1 2 4 | 4 7 9
Xác định Q1 là median của dãy con 1 2 4 -> Q1 = 2
Q3 là median của dãy con 4 7 9 -> Q3 = 7 Vậy IQR = Q3-Q1 = 7-2 =5
Làm ví dụ sau: Cho dãy con {1, 5, 6, 3, 4, 6, 7, 8} xác định Median của dãy và IQR
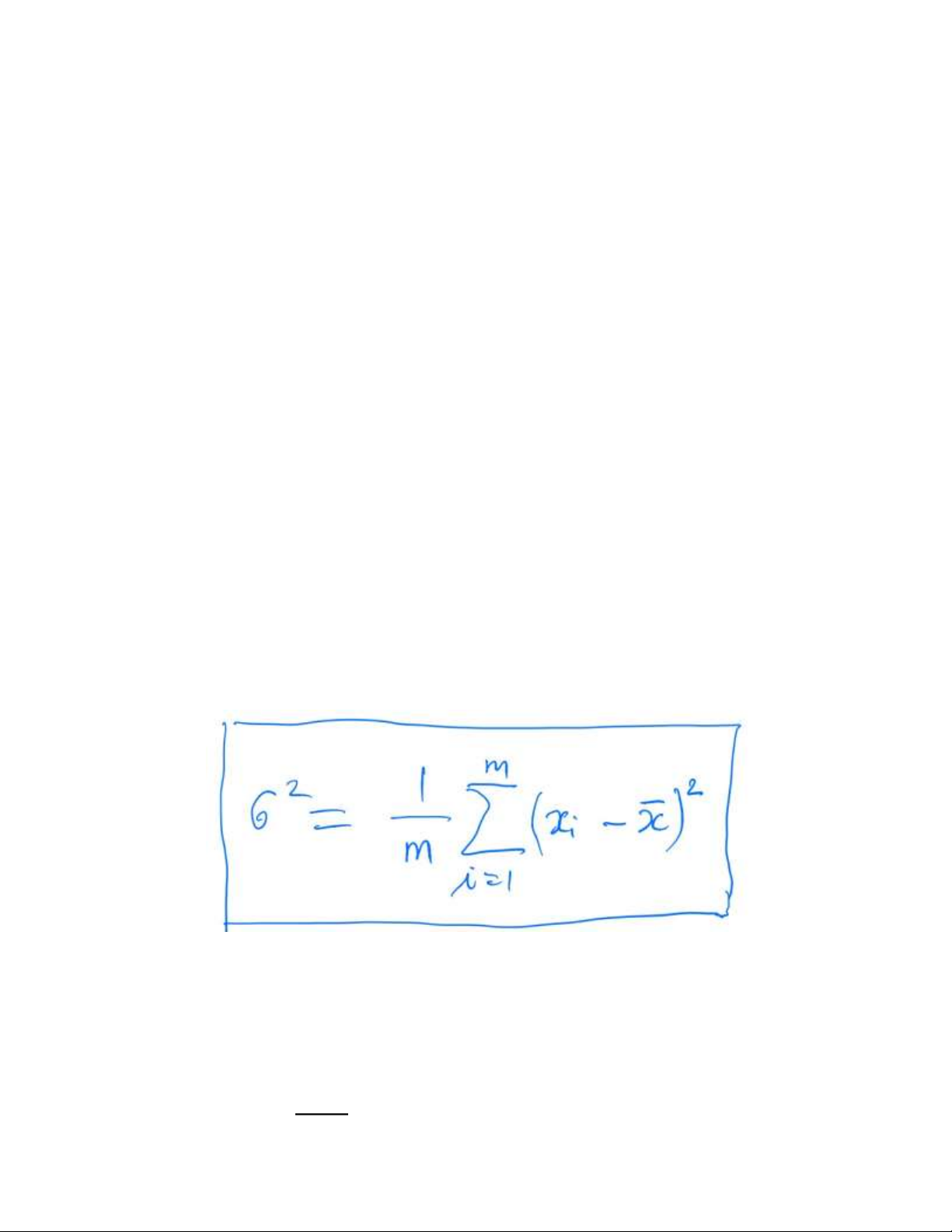
III.3 Tính phương sai
Đại lượng đặc trưng cho độ phân tán (sai số của 1 phép đo) của tập dữ liệu quanh giá trị trung bình
Giá trị của Phương sai (Variance) được tính như sau
III.4 Tính độ lệch chuẩn (Std: standard deviatiбon}
Độ lệch chuẩn cho ta biết được độ phân tán của giá trị thống kê so với giá trị trung bình, ở từng thời điểm khác nhau. lOMoAR cPSD| 59561309
Б = √ б𝟐
Như vậy độ lệch chuẩn mà Căn bậc hai của Phương Sai
III.5 Tính độ tương quan
Trong đấy COV (x,y) gọi là Hiệp phương sai. lOMoAR cPSD| 59561309
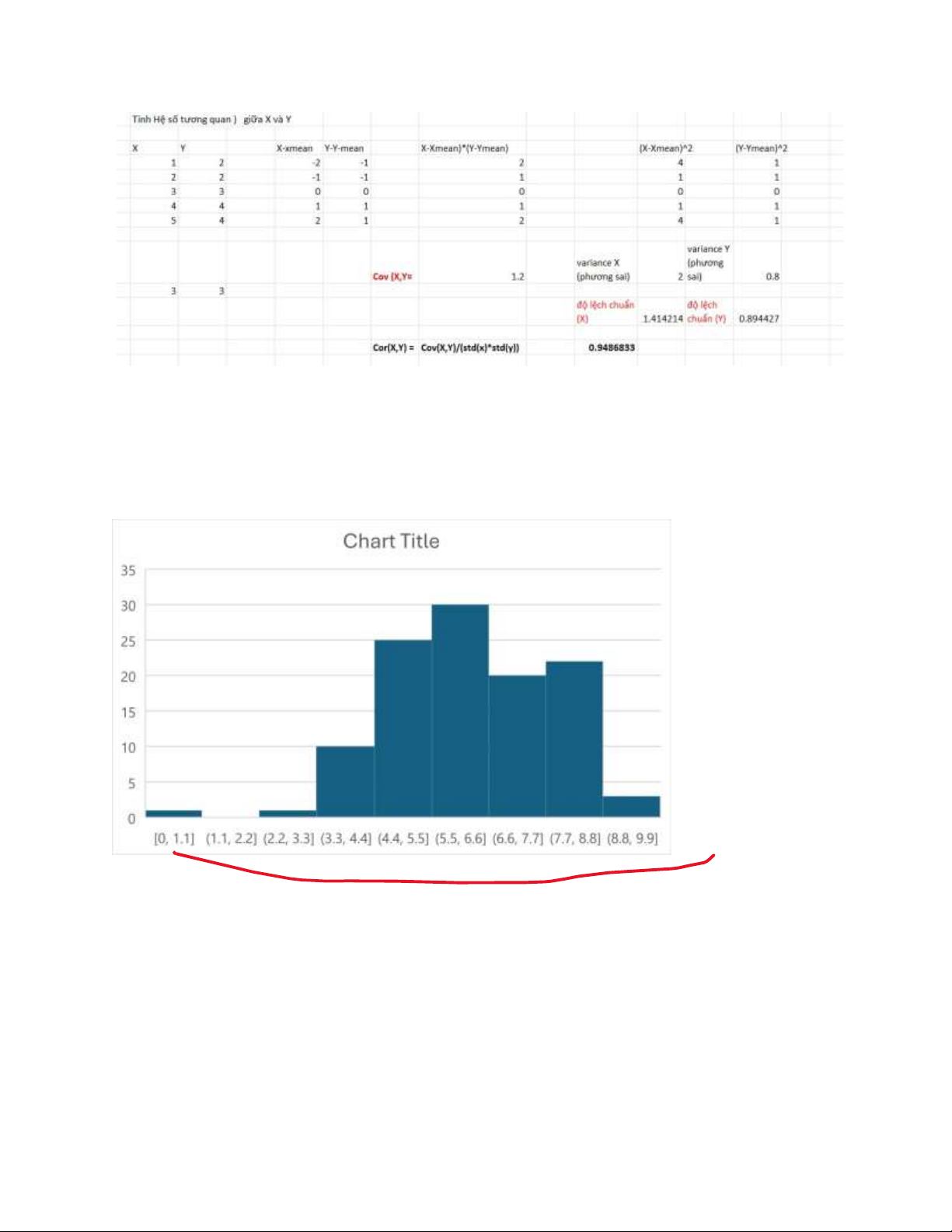
Cho ví dụ như sau:
Tính độ tương quan của hai dãy số X { 1, 2, 3, 4, 5} và Y { 2, 2, 3, 4 , 4}
Bước 1 Tính độ lệch chuẩn (std) của từng dãy số X và Y ;
Bước 2. Tính Hiệu phương sai COV(X,y)
BƯớc 3. Corr = COV(X,y)/ (std(X)* std(Y) lOMoAR cPSD| 59561309 IV. Trực quan hóa Biểu đồ histogram lOMoAR cPSD| 59561309
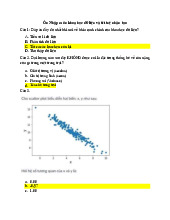
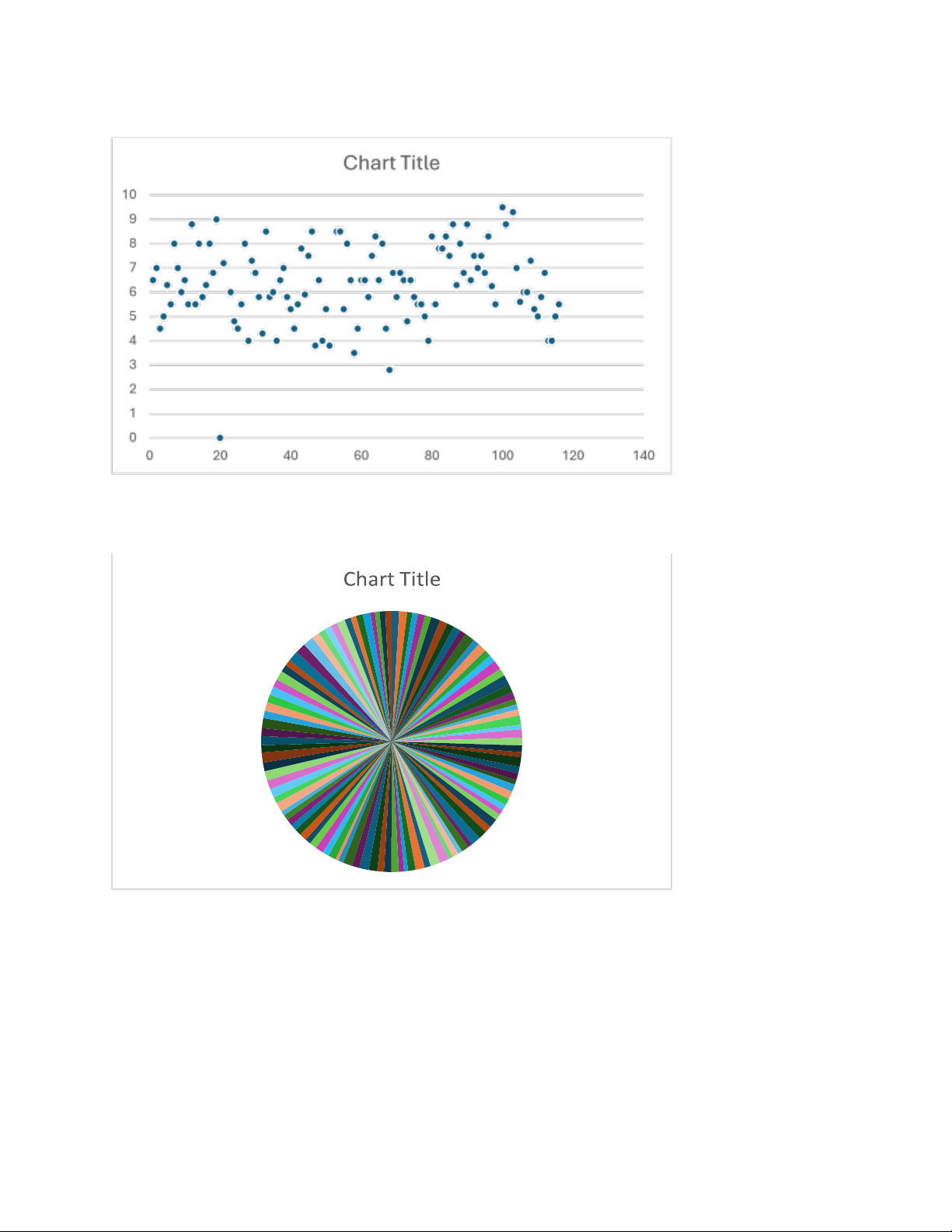
Biểu đồ phân tán (scatter)
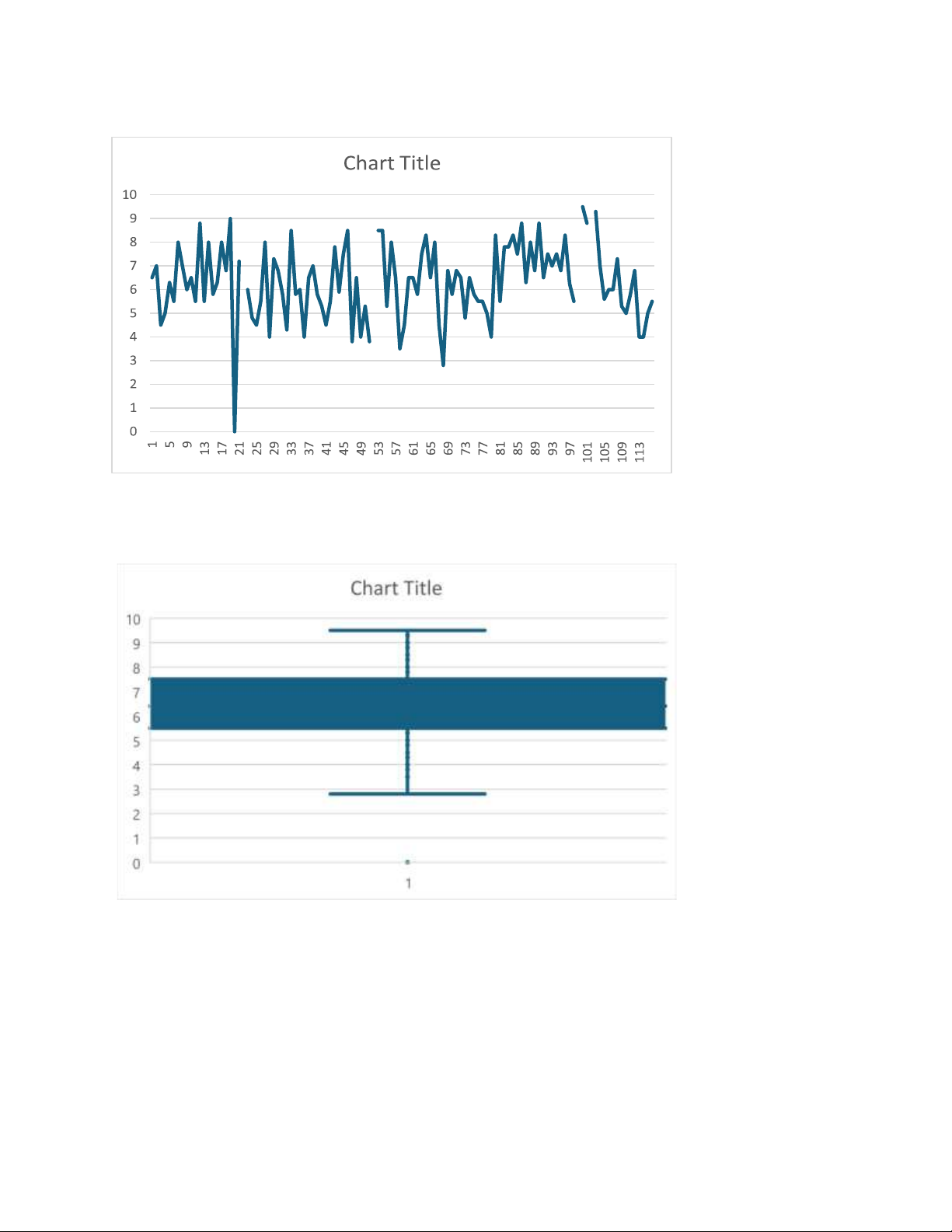
Biểu đồ tròn (pie) lOMoAR cPSD| 59561309 Biểu đồ đường Biểu đồ hộp lOMoAR cPSD| 59561309
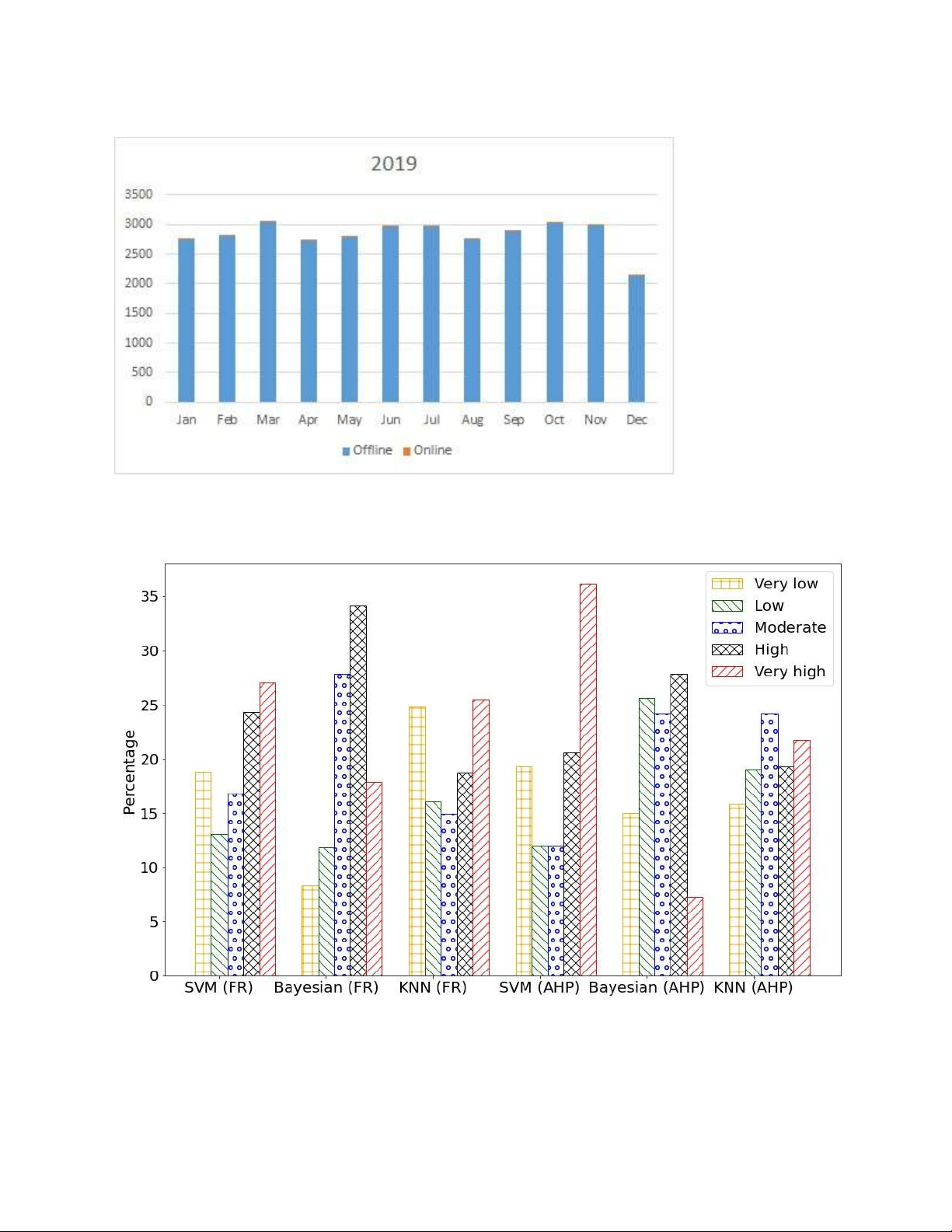
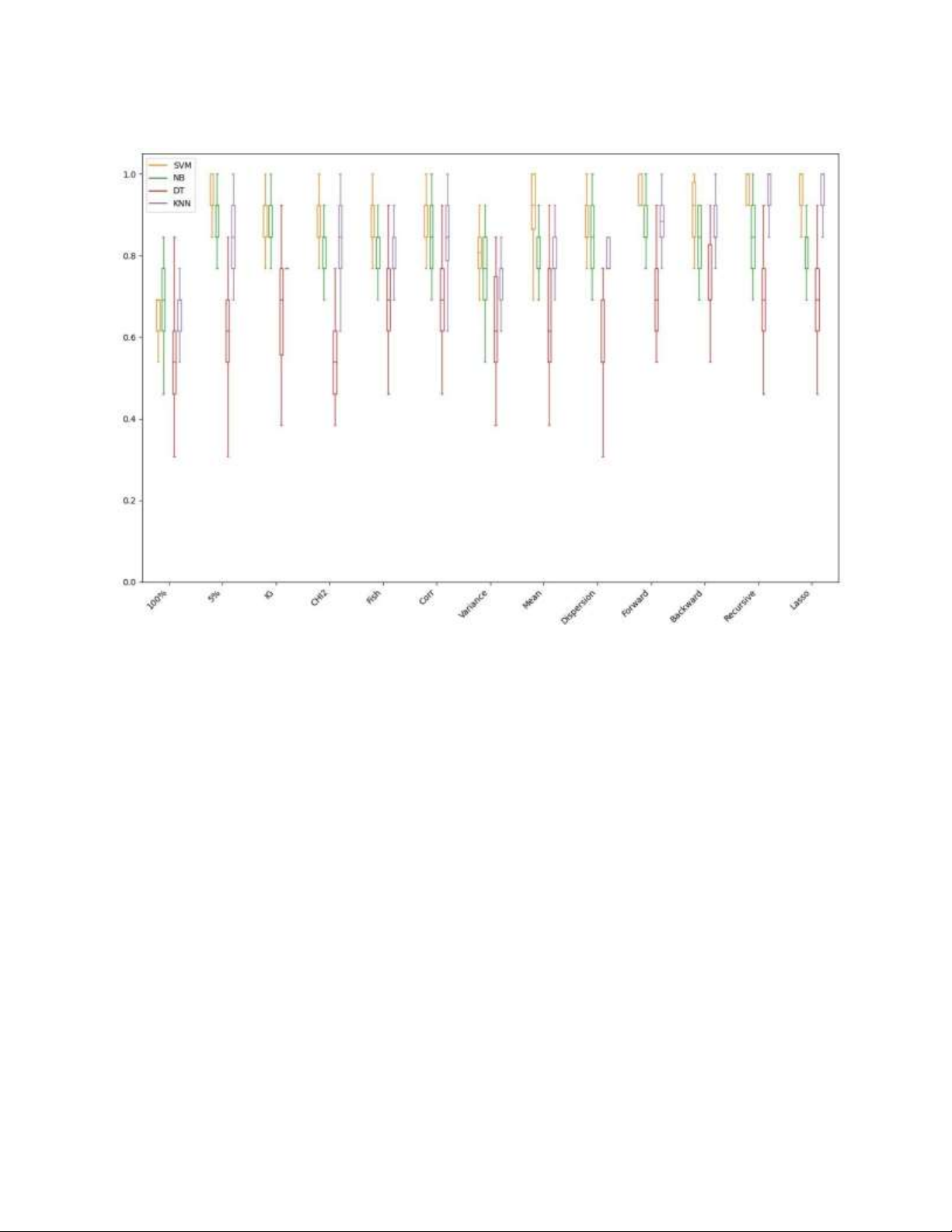
Biểu đồ cột (bar) Biểu đồ groupBar lOMoAR cPSD| 59561309 Group Box