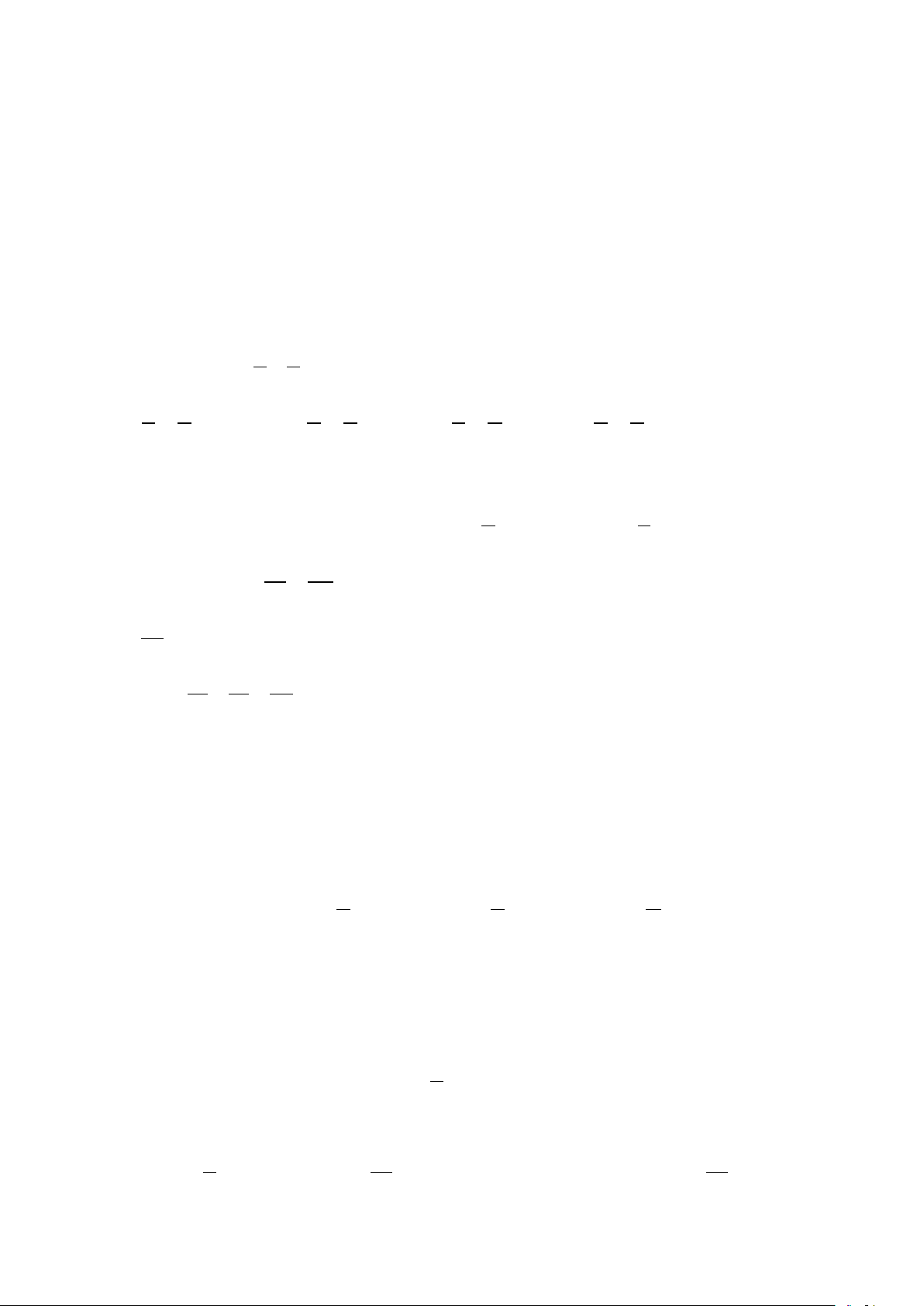




Preview text:
TRƯỜNG THCS ĐA TỐN
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA KÌ II NHÓM : TOÁN 7 NĂM HỌC 2024 -2025 A/ LÍ THUYẾT
1. Tỉ lệ thức, tính chất dãy tỉ số bằng nhau.
2. Đại lượng tỉ lệ thuận, đại lượng tỉ lệ nghịch.
3. Đa thức 1 biến, cộng trừ đa thức 1 biến.
4. Quan hệ giữa góc và cạnh đối diện trong tam giác.
5. Quan hệ giữa đường vuông góc và đường xiên.
6. Quan hệ giữa ba cạnh trong tam giác B/ BÀI TẬP
I. Trắc nghiệm khách quan: Chọn đáp án đúng nhất a c
Câu 1: Từ tỉ lệ thức = (a,b,c,d ≠ 0) b d ta suy ra: a d c a a b d b A. = = = = c b B. b d C. c d D. a c
Câu 2: Cho đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ -2. Công thức liên hệ giữa y và x là: 1 1
A. y = −2x B. y = 2x C. y = x y = − x 2 D. 2 x −4
Câu 3: Cho tỉ lệ thức = 15
5 thì giá trị của x là: −4 A. 3 B. 4 C. -12 D. – 10 a b c Câu 4: Cho = = + − = − 11 15 22 và a b c
8 thì giá trị của a, b, c lần lượt là:
A. a = −22;b = −30;c = −60 B. a = 22;b = 30;c = 60
C. a = −22;b = −30;c = −44 D. a = 22;b = 30;c = 44
Câu 5: Biết rằng x : y = 7 : 6 và 2x − y = 120. Giá trị của x và y bằng:
A. x = 105;y = 90 B. x = 103;y = 86 C. x = 110;y = 100 D. x = 98;y = 84
Câu 6: Cho y và x là hai đại lượng tỉ lệ nghịch, biết rằng khi x = 2 thì y = - 2. Công thức liên hệ giữa y và x là: 4 2 4 A. y = 2x B. y = − y = − y = x C. x D. x
Câu 7: Khi có xy = a với a là hằng số khác 0, ta nói:
A. y tỉ lệ nghịch với x B. y tỉ lệ nghịch với x theo hệ số tỉ lệ a
C. y tỉ lệ thuận với x D. x tỉ lệ thuận với y theo hệ số tỉ lệ a
Câu 8: Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là: 1 A. 3 B. 75 C. 3 D. 10
Câu 9: Cho x và y là hai đại lượng tỉ lệ nghịch. Khi x 6 thì y 7 . Tìm y khi x 3 7 20 18 A. y B. y C. y 14 D. y 2 7 7
Câu 10: Đa thức nào dưới đây là đa thức một biến? 1
A. x2 + y + 1 B. x3 - 2x2 + 3 C. xy + x2 – 3 D. xyz - yz + 3
Câu 11: Sắp xếp 6.x3 + 5x4 - 8x6 - 3x2 + 4 theo lũy thừa giảm dần của biến ta được
A. -8x6 + 5x4 + 6x3 - 3x2 + 4 B. -8x6 - 5x4 + 6x3 - 3x2 + 4
C. 8x6 + 5x4 + 6x3 - 3x2 + 4 D. 8x6 + 5x4 + 6x3 + 3x2 + 4
Câu 12: Đa thức 7x12 - 8x10 + x11 - x5 + 6x6 + x - 10 được sắp xếp theo lũy thừa tăng dần của biến ta được:
A. -10 + x + x5 + 6x6 - 8x10 + x11 + 7x12 B. 10 + x + x5 + 6x6 - 8x10 + x11 + 7x12
C. 10 + x - x5 + 6x6 - 8x10 + x11 + 7x12 D. -10 + x - x5 + 6x6 - 8x10 + x11 + 7x12
Câu 13: Hệ số tự do của đa thức x2 + 7x - 2 là: A. 2 B. 7 C. – 2 D. 9
Câu 14: Hệ số cao nhất của đa thức 5x6 + 6x5 + x4 - 3x2 + 7 là: A. 6 B. 7 C. 4 D. 5
Câu 15: Cho đa thức A = x4 - 4x3 + x - 3x2 + 1. Tính giá trị của A tại x = -2
A. A = -35 B. A = 53 C. A = 33 D. A = 35
Câu 16: Cho đa thức p(x) = −3x 1
7 + x5 + 8x + 2. Câu nào sau đây là sai: 2 A. Bậc của p(x) là 7
B. Hệ số cao nhất của p(x) là 8
C. Hệ số tự do của p(x) là 2
D. Hệ số của các lũy thừa bậc 6, bậc 4, bậc 3, bậc 2 bằng 0
Câu 17: Viết một đa thức một biết có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là -1
A. −x2 + 5 B. 5x2 – x C. 5x3 – 1 D. A, B, C đều sai
Câu 18: Cho đa thức p(x) = x2−16x+64.Tính giá trị của p(x) tại x=8. Câu nào sau đây đúng:
A. p(x)=0 B. p(x)=64 C. p(x)=128 D. Một kết quả khác A,B,C 1
Câu 19. Bậc của đơn thức 2 3
x x là: A. 1 B. 3 C. 4 D. 5. 3 15 7 Câu 20. Tính tổng 3 3 1 3
3x 5x x A. 3 x B. 3 15x C. 3 x D. 3 7x 2 2 2
Câu 21: Ba canh của tam giác có độ dài 6cm, 7cm, 8cm. Góc lớn nhất là góc:
A.Đối diện với cạnh có độ dài 6cm C. Đối diện với cạnh có độ dài 7cm
B.Đối diện với cạnh có độ dài 8cm D. Ba góc có độ lớn bằng nhau.
Câu 22: Cho tam giác ABC có 0 = 0
B 60 ,C = 50 . Câu nào sau đây đúng:
A. AB > AC B. AC < BC C. AB > BC D. Một đáp án khác Câu 23: Cho A BC có B tù,
A C khẳng định nào sau đây là đúng:
A. AC AB BC
B. BC AB AC
C. AB AC BC
D.AC BC AB
Câu 24: Cho tam giác ABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng? A.
A > B > C B. C > A > B C. C < A < B D. A < B < C 2
Câu 25 : Cho ba điểm ,
A B,C thẳng hàng, B nằm giữa A và C . Trên đường thẳng vuông góc với
AC tại B ta lấy điểm H . Khi đó
A. AH BH .
B. AH AB .
C. AH BH .
D. AH BH .
Câu 26: Cho tam giác ABC có cạnh AB = 1cm và cạnh BC = 4cm, độ dài cạnh AC là một số
nguyên. Độ dài cạnh AC có thể là số nào sau đây: A. 1 cm B. 2cm C. 3cm D. 4cm II. Tự luận
Dạng 1: Bài tập về tỉ lệ thức, tính chất dãy tỉ số bằng nhau Bài 1: Tìm x biết a) x 3 = b) x 15 = c) x − 2 4 = d) x + 3 5 = 25 5 16 − 20 3 5 4 − 20 x 8 x − 2 −3
e) 2x + 3 4x −1 − + = f) x 1 x 3 = g) = h) = 7 15 3 5 2 x −27 x − 2
Bài 2: Tìm x, y biết: x y x y x y a) = và x +y=14
b) = và x –y =30 c) = và 3x -2y =44 3 4 7 4 5 2 x y x y
d) = và 2x +5y =32 e) 2x = 3y và x +y=10 f) = và 2 2 x + y =100 3 2 3 4 x y x y x y g) = và x.y=12 h) = và 3 3 x + y = 91 i) = và 2 x y =100 4 3 3 4 5 4
Bài 3: Tìm x, y, z biết: x y z x y z a) = = và x + y + z = 90
− b) = = và 2x + 3y − 5z = 21 − 2 3 5 2 3 4 x y z
c) = = và 4x − 3y + 2z = 36 d) 2x = 5y = 3z và x + y − z = 44 − 1 2 3 x y z x y y z
e) = = và x.y.z = 648 f) = ; = và x + y − z = 69 2 3 4 5 6 8 7
Dạng 2: Bài toán đại lượng tỉ lệ thuận, bài toán tỉ lệ nghịch
Bài 1: Ba đơn vị góp vốn kinh doanh theo tỉ lệ 3; 5;7. Hỏi mỗi đơn vị góp bao nhiêu tiền, biết
tổng số vốn góp được là 300 triệu đồng.
Bài 2: Học sinh của ba lớp 7 cần trồng và chăm sóc 24 cây xanh. Lớp 7A có 32 học sinh, lớp 7B
có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh?
Biết số cây xanh mỗi lớp trồng tỉ lệ với số học sinh lớp đó.
Bài 3. Cuối học kì I, tổng số học sinh khối 7 đạt loại giỏi và khá nhiều hơn số học sinh đạt trung
bình là 45 em. Biết rằng số học sinh đạt loại giỏi, khá, trung bình tỉ lệ với 2;5;6 . Tính số học sinh
giỏi, khá, trung bình của khối 7.
Dạng 3: Bài tập đa thức một biến
Bài 1 : Cho đa thức: Q(x) 3 2 = 6
− x − 2x + 3− 2x + x − 2
a) Thu gọn đa thức Q(x). b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thứcQ(x) . 3
Bài 2: Tìm nghiệm của các đa thức sau: a) x −10; b) 2x + 8; c) 3x + 8; d) − 2 16 x ; e) 2 4x − 9; f) 2 2x − 6; g) 2 3x + 6x; h) 3 4x + 9 . x
Bài 3: Cho hai đa thức M(x) = 3 2 5
2x − 5x + x − 4 N(x) = 3 2 5 2
− x + x − x + 8 7 7
a) Tính A(x) = M(x) + N(x) ; B(x) = M(x) – N(x) b) Tìm nghiệm của A(x)
Bài 4.Cho 2 đa thức: A(x) = 6x2 + 7x – 5 + 2x3 - 4 x2 - 1 – 3x ;
B (x) = x3 – 2x2 + 2x + 3x2 - 3x3 + 6
a)Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b) Tính A(x) + B (x); A(x) - B (x)
c) Tìm nghiệm của đa thức A(x) + B (x)
d) Tìm bậc của A(x) và hệ số cao nhất của B(x) e) Tính A (2); B(-3)
Bài 5.Cho 2 đa thức: C(x) = 2x3 -x + 7 - x3 + 3x2 - 1 ; D(x) = - x3 - 8- x2 + 2x - x2 + 2
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b) Tìm bậc của C(x) và hệ số tự do của D(x) c) Tính C (2); D(- 1)
d) Tính C(x) + D(x); C(x) - D (x)
e) Tìm x biết C(x) = - D (x)
Bài 6.Cho A(x) = 9 - x5 + 2x - 2x4 - 2x3 - 2x2 - 5x4 ; B(x) = x5 - 3 + x2 + 7x4 + 2x3 + x2 - 4x
a) Sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
b) Tìm đa thức H(x) sao cho: H(x) - B(x) = A(x)
c) Tìm đa thức Q(x) sao cho: Q(x) + B(x) = A(x)
Bài 7.Cho các đa thức : A(x) = 2x3 - x + 2 + x3 + 3x2 - 1 ; B(x) = -x2 + 4x- 2 + x3 + 4x2 -x + 1
a)Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm của biến
b)Tính A(x) + B(x) ; A(x) - B(x)
Bài 8.Cho hai đa thức: M(x) = 5x2 + 7x - 5 + 2x3 - x2 - 1 - 3x ; N(x) = x3 - x2 + 2x - 3x2 -3x3 + 3
a) Sắp xếp mỗi hạng tử của mỗi đa thức theo luỹ thừa tăng dần của biến. b) Tính M(-1); N(-2)
c) Tính M(x) + N(x); M(x) - N(x)
Bài 9.Cho đa thức : A(x) = 1 + 5x3 + 9x - 2x4 - 3x3 - 2x2 + 3x4- 9x +2x2 - 3x3
a) Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa tăng dần của biến.
b) Xác định bậc hệ số cao nhất hệ số tự do của đa thức. c) Tính M(-2); M(3)
Bài 10.Cho hai đa thức : A(x) = 2x3 - x + 10 - 5x3 +3x2 - 1 ;
B(x) = x2 + 6x - 4 + 3x3 - 4x2 - 2x + 1
a)Thu gọn và sắp xếp theo lũy thừa giảm dần của biến trong mỗi đa thức.
b)Tính A(x) + B(x) , A(x) - B(x)
Dạng 4: Hình học
Bài 1: Cho tam giác ABC cân tại A. Từ Akẻ AH vuông góc với BC tại H , trên đoạn thẳng
AH lấy điểm M tùy ý ( M khác A và H ). Chứng minh rằng: a) AB ∆ H = AC ∆ H
b) H là trung điểm của BC.
c) MB = MC và MH là tia phân giác của góc BMC. d) MB < AB.
Bài 2: Cho ∆ ABC vuông tại A. Kẻ đường phân giác BE (E∈AC), kẻ EH vuông góc với BC (H ∈BC).
a) Chứng minh ∆ AEB = ∆ HEB.
b) Chứng minh BE là đường trung trực của AH
c) Gọi K là giao điểm của BA và EH. So sánh EK với HE;
d) Chứng minh BE vuông góc với KC. 4 Bài 3: Cho AB ∆ C vuông tại C có 0
A = 60 . Trên cạnh AB lấy điểm K sao cho AK = AC. Từ K kẻ
đường thẳng vuông góc với AB, cắt BC tại E. a) Chứng minh AC ∆ E = AK ∆
E và AE là tia phân giác của CAB . b) Chứng minh EC < EB.
c) Chứng minh K là trung điểm của AB và AB = 2AC. d) Chứng minh EB > AC. Bài 4: Cho AB ∆
C cân tại C. Gọi D, E lần lượt là trung điểm của AC, BC. Các đường thẳng AE,
BD cắt nhau tại M. các đường thẳng CM và AB cắt nhau tại I.
a) Chứng minh AE = BD b) Chứng minh DE // AB
c) Chứng minh IM ⊥ AB d) Chứng minh AB + 2BC > CI + 2AE Bài 5: Cho DEF ∆
có I là trung điểm của EF. Kẻ EH vuông góc DI tại H, kẻ FK vuông góc DI tại K. a) Chứng minh EHI ∆ = F ∆ KI và IH = IK.
b) Chứng minh HF = EK và HF // EK
c) Chứng minh DE + DF > 2DI. Bài 6: Cho AB ∆
C có AC > AB. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. a) Chứng minh AB ∆ M = D
∆ CM . b) Chứng minh AC // BD. c) So sánh MAB và MAC
Bài 7: Cho tam giác ABC vuông tại A(ABđiểm E sao cho BE = BA a)Chứng minh rằng A ∆ BD = E
∆ BD b)Chứng minh 0
DEB = 90 c)Chứng minh DC > DA BÀI TẬP NÂNG CAO
Bài 1. Cho tỉ lệ thức a c = . Chứng minh: b d a) 2a + b 2c + d 2 2 2 2 = b) a + b c + d = 3a b – 3c – d a2 – b2 c2 – d2
Bài 2. Cho các số a, b, c, d thỏa mãn a + b + c ≠ 0 và a + b – c a + c b – b + c – a = = . c b a
Tính giá trị biểu thức: M = (a + b)(b + c)(c + a) . abc ĐỀ THAM KHẢO
I. PHẦN TRẮC NGHIỆM
Câu 1 . Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức? A. 10 : 16 và 5 8 : B. – 20 : 30 và 2 − 3 : − 3 3 3 7 . C.2 : 3 và 2 − 3 : D. – 10 : 15 và 2 3 : 7 7 7 7
Câu 2 . Nếu 3 c = thì: 2 d A.3c = 2d. B.3d = 2c. C. 3 : d = 2 : c D.cd = 6.
Câu 3 .Cho đẳng thức 8.6 = 4.12 ta lập được tỉ lệ thức là 5 A.12 6 = B. 8 12 = C. 4 8 = D. 4 12 = 4 8 4 6 12 6 8 6 x 2
Câu 4 . Từ tỉ lệ thức = suy ra: y 5 x x + 2 x x + 5 x x + 2 A. = . B. = . C. = x y y y + 5 y y + 2 y y −5 . D. = 5 2 .
Câu 5 .Cho ba số a; b; c tỉ lệ với 2;5;3 ta có dãy tỉ số A.𝑎𝑎 = b = c B.𝑎𝑎 = b = c C.𝑎𝑎 = b = c D.𝑎𝑎 = b = c 2 3 5 5 3 2 3 5 2 2 5 3
Câu 6 . Từ tỉ lệ thức 2 3 = , suy ra: x 5 A. 2.3 x = B. 2.5 x = C. 3 x = D. 5 x = 5 3 2.5 2.3
Câu 7 . Hệ số cao nhất của đa thức 5x6 + 6x5 + x4 - 3x2 + 7 là: A. 6 B. 7 C. 4 D. 5 1
Câu 8 . Bậc của đơn thức 2 3 x x là: 3 A. 1 B. 3 C. 4 D. 5.
Câu 9 . Tam giác có hai cạnh bằng nhau có thêm điều kiện nào thì trở thành tam giác đều
A. có ba góc nhọn. B. có một góc bằng 60º.
C. có hai góc bằng nhau. D. có một góc vuông.
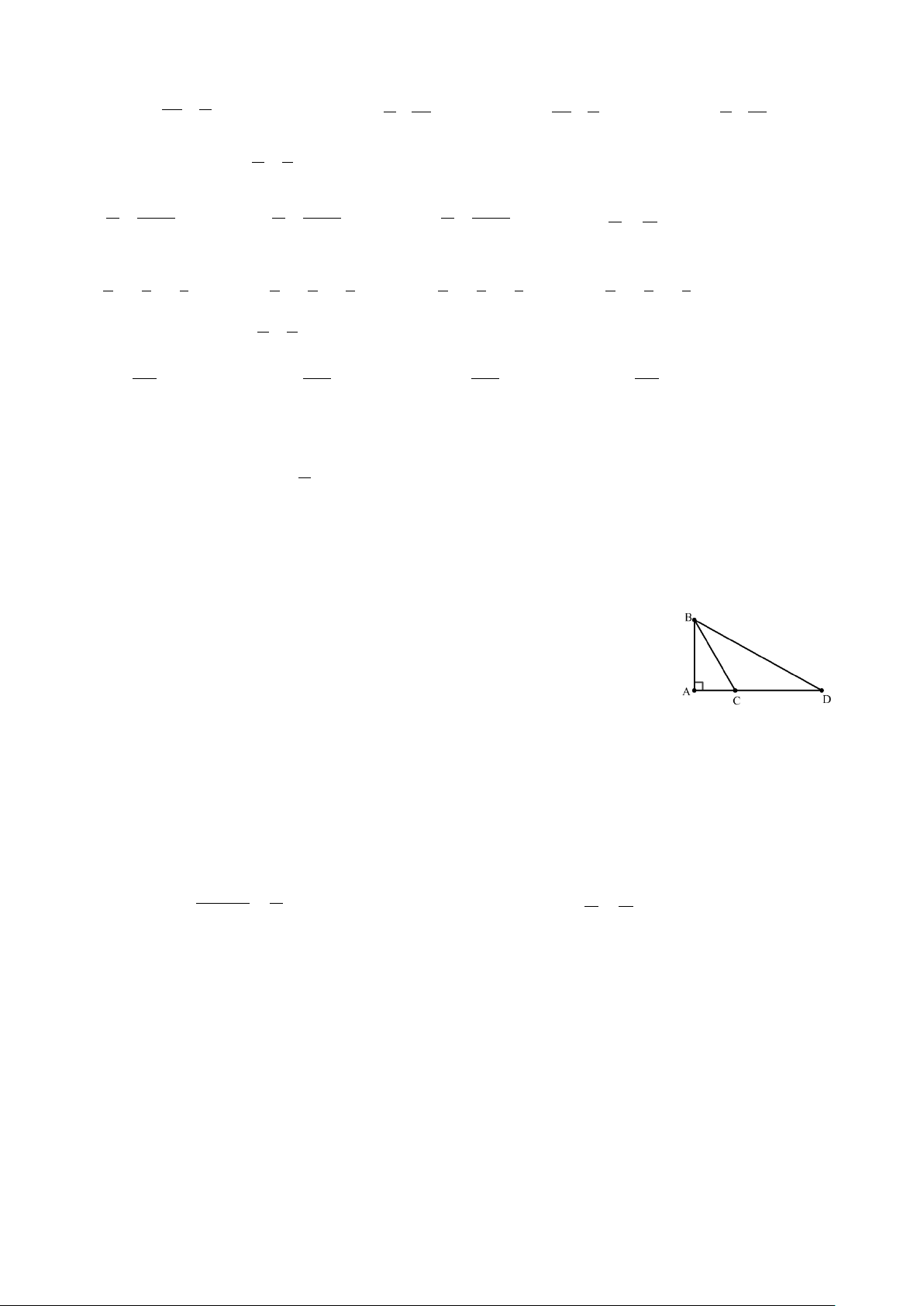
Câu 10 . Cho hình vẽ bên. So sánh AB, BC, BD ta được:
A. AB > BC > BD. B. AB < BC < BD. C. BC > BD > AB. D. BD < AB < CB.
Câu 11 . Một tam giác cân có số đo góc ở đỉnh bằng 500 thì số đo các góc đáy là: A. 1300. B. 1000. C. 500. D. 650.
Câu 12 . Độ dài hai canh của một tam giác là 1cm và 8cm. Trong các số đo sau, số đo nào sau đây
là độ dài cạnh thứ 3 của tam giác: A. 8 cm. B. 9cm. C. 6cm. D. 7cm. II. PHẦN TỰ LUẬN
Câu 1 . (1,0 điểm) 2x − 7 4 a) Tìm x biết
= b)Tìm hai số x, y biết: x y x − y = − 6 3 = và 2 2 3 9
Câu 2 . (1,5 điểm).Hưởng ứng phong trào “Chia sẻ khó khăn với học sinh vùng cao”, Liên đội một
trường THSC đã phát động các lớp ủng hộ vở viết. Ba lớp 7A; 7B; 7C đã ủng hộ được 600 quyển
vở. Biết số vở của mỗi lớp ủng hộ tỉ lệ với 3; 4; 5. Tìm số vở mỗi lớp đã ủng hộ?
Câu 3 . (1,5 điểm) Cho các đa thức :
A(x) = 2x2 + 5x3 + 9 – x; D(x) = 3x – 5 + 2x2 + 5x3
a) Sắp xếp các đa thức trên theo lũy thừa giảm dần của biến
b) Tính A(x) + D(x); A(x) - D(x)
c) Tìm nghiệm của đa thức A(x) - D(x)
Câu 4 (2,5 điểm) Cho ∆ ABC vuông tại A. Kẻ đường phân giác BE (E∈AC), kẻ EH vuông góc với BC (H∈BC).
a) Chứng minh ∆ AEB = ∆ HEB.
b) Chứng minh BE là đường trung trực của AH 6
c) Gọi K là giao điểm của BA và EH. So sánh EK với HE;
d) Chứng minh BE vuông góc với KC.
Câu 5 . (0,5 điểm)Cho a, b, c là ba số khác 0 thỏa mãn: ab bc ca = =
(với giả thiết các tỉ số
a + b b + c c + a
đều có nghĩa) .Tính giá trị của biểu thức M = ab + bc + ca 2 2 2 a + b + c 7
Xem thêm: ĐỀ CƯƠNG ÔN TẬP TOÁN 7
https://thcs.toanmath.com/de-cuong-on-tap-toan-7
Document Outline
- ĐA TỐN - ĐC ÔN TẬP GIỮA KÌ II TOÁN 7 ( 24- 25 ) doc
- Bài 5.Cho 2 đa thức: C(x) = 2x3 -x + 7 - x3 + 3x2 - 1 ; D(x) = - x3 - 8- x2 + 2x - x2 + 2
- Câu 5 . (0,5 điểm)Cho a, b, c là ba số khác 0 thỏa mãn: (với giả thiết các tỉ số đều có nghĩa) .Tính giá trị của biểu thức M =
- DE CUONG 7





