
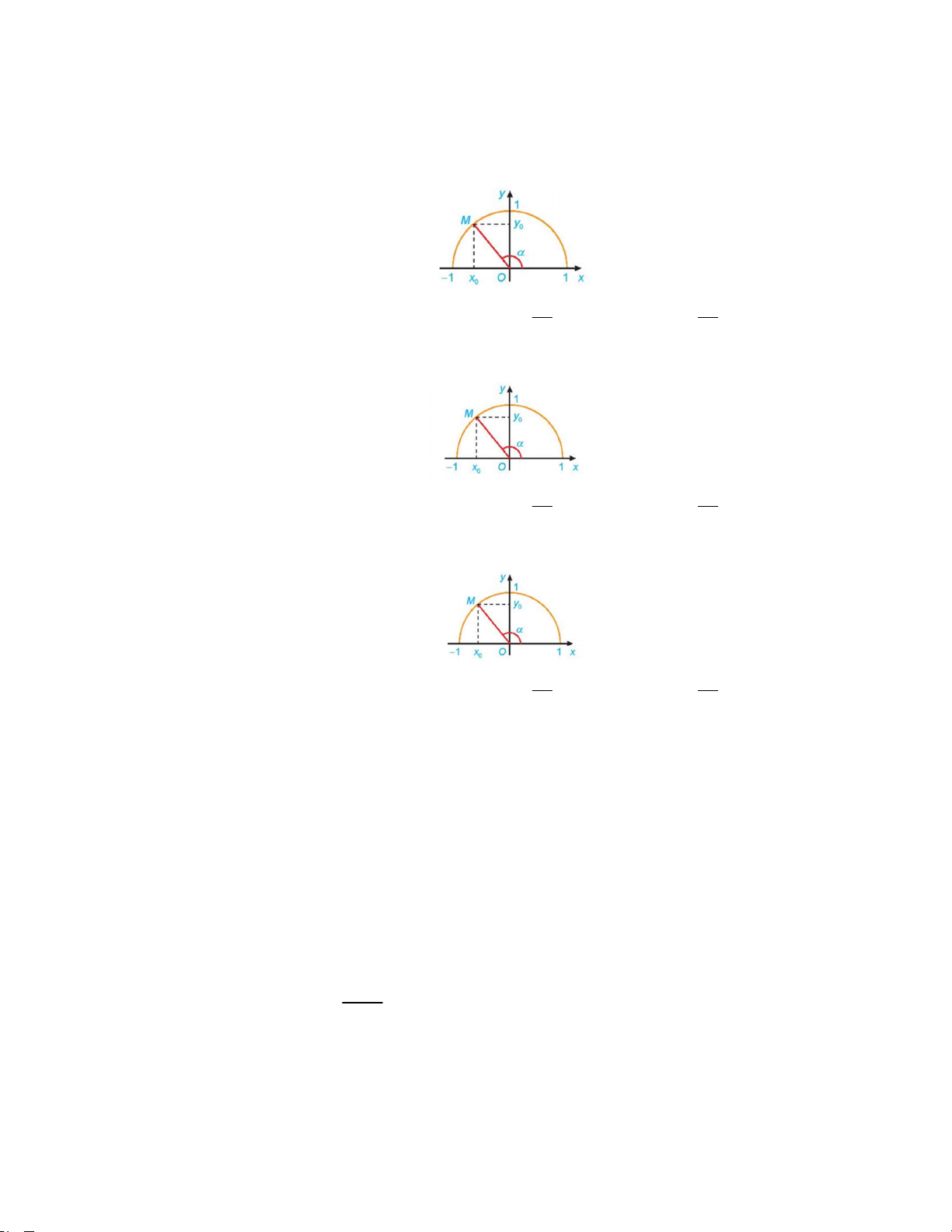








Preview text:
HỘI ĐỒNG MÔN TOÁN TỈNH QUẢNG TRỊ
TỔ TOÁN – TRƯỜNG THPT HƯỚNG HÓA
I. MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ 1 - NĂM HỌC 2025 - 2026
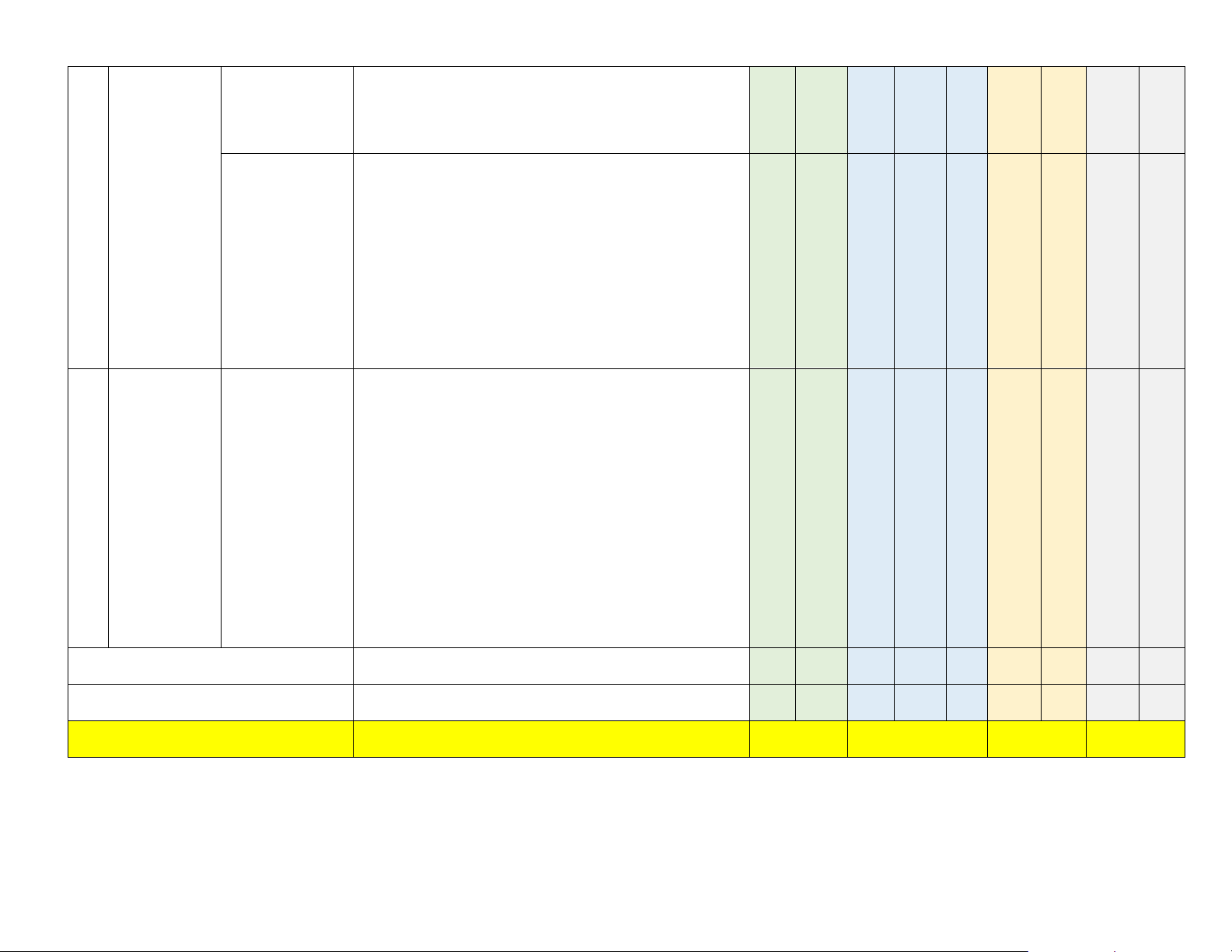
MÔN TOÁN – LỚP 11 (Thời gian: 90 phút) Mức độ đáng giá Chương/ Tổng Tỉ lệ TT Nội dung DT1 DT2 DT3 Tự tuận Chủ đề Biết Hiểu Biết Hiểu VD Hiểu VD Hiểu VD Biết Hiểu VD Góc lượng giác. Số đo của góc lượng giác.
Đường tròn lượng giác.
Giá trị lượng giác của C1a C1 C1 C3* 3 1 góc lượng giác, quan C1b hệ giữa các giá trị lượng giác Hàm số (3 tiết) lượng giác Các phép biến đổi và phương lượng giác (công thức 1 3 50% trình lượng cộng; công thức nhân C3 giác (10
đôi; công thức biến đổi C6 C2 C2 2 0 tiết) tích thành tổng; công thức biến đổi tổng thành tích) (2 tiết) Hàm số lượng giác C3 C1c C3* C1 1 2 (2 tiết) Phương trình lượng C4 C1d C3* 2 giác cơ bản (2 tiết) C5 Dãy số (2 tiết) C11 2 1 7,5% Dãy số. cấp C6 số cộng và 2 Cấp số cộng. Số hạng cấp số nhân C2a tổng quát của cấp số C2b (7 tiết) C2d C4 3 1 1 15% cộng. Tổng của n số C2c
hạng đầu tiên của cấp số cộng (2 tiết) Cấp số nhân. Số hạng tổng quát của cấp số C7 nhân. Tổng của n số C12 C4 2 1 1 12,5% C8
hạng đầu tiên của cấp số nhân (2 tiết) Các số đặc trưng đo xu thế trung tâm Các số đặc trưng của C9 3 của mẫu mẫu số liệu ghép nhóm C2 C5 2 1 1 15% C10 số liệu ghép nhóm (4 tiết) Tổng số lệnh hỏi 10 2 6 2 2 2 2 4 16 8 6 Tổng điểm 2,5 0,5 1,5 0,5 1,0 1,0 1,0 2,0 4,0 3,0 3,0 10 Tỉ lệ % 30 20 20 30 70 30 100
Lưu ý: DT1 (Trắc nghiệm bốn lựa chọn): 0,25 điểm/câu; DT2 (Trắc nghiệm Đúng/Sai): 0,25 điểm/ý; DT3 (Trắc nghiệm trả lời ngắn): 0,5
điểm/câu; Tự luận: 0,5 điểm/câu.
II. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I MÔN TOÁN - LỚP 11
Số câu hỏi ở các mức độ đáng giá T Chương/ Nội dung Yêu cầu cần đạt DT1 DT2 DT3 Tự luận T Chủ đề
Biết Hiểu Biết Hiểu VD Hiểu VD Hiểu VD Góc lượng Nhận biết: Hàm số
giác. Số đo của – Nhận biết được các khái niệm cơ bản về góc lượng giác 1 góc lượng
lượng giác: khái niệm góc lượng giác; số đo của và phương giác. Đường
góc lượng giác; hệ thức Chasles cho các góc 1 2 1 1* trình lượng C3 tròn lượng
lượng giác; đường tròn lượng giác. giác (10 C6 giác.
– Nhận biết được khái niệm giá trị lượng giác của tiết) Giá trị lượng một góc lượng giác. giác của góc
Thông hiểu: Mô tả được bảng giá trị lượng giác lượng giác,
của một số góc lượng giác thường gặp; hệ thức cơ quan hệ giữa
bản giữa các giá trị lượng giác của một góc lượng các giá trị
giác; quan hệ giữa các giá trị lượng giác của các lượng giác.
góc lượng giác có liên quan đặc biệt: bù nhau, phụ
nhau, đối nhau, hơn kém nhau .
Vận dụng: Sử dụng được máy tính cầm tay để tính
giá trị lượng giác của một góc lượng giác khi biết số đo của góc đó.
Vận dụng cao: Giải quyết được một số vấn đề thực
tiễn gắn với giá trị lượng giác của góc lượng giác. Nhận biết: Các phép biến
– Mô tả được các phép biến đổi lượng giác cơ
đổi lượng giác bản: công thức cộng; công thức góc nhân đôi; (công thức
công thức biến đổi tích thành tổng và công thức cộng; công
biến đổi tổng thành tích.
thức nhân đôi; Thông hiểu: Mô tả được các phép biến đổi lượng 1 1
công thức biến giác cơ bản: công thức cộng; công thức góc nhân đổi tích thành
đôi; công thức biến đổi tích thành tổng và công tổng; tổng
thức biến đổi tổng thành tích. thành tích)
Vận dụng cao: Giải quyết được một số vấn đề
thực tiễn gắn với các phép biến đổi lượng giác. Nhận biết:
– Nhận biết được các khái niệm về hàm số chẵn,
hàm số lẻ, hàm số tuần hoàn.
– Nhận biết được các đặc trưng hình học của đồ
thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
– Nhận biết được định nghĩa các hàm lượng giác y Hàm số lượng = sin x, giác và đồ thị
y = cos x, y = tan x, y = cot x thông qua đường tròn 1 1 1* 1 lượng giác Thông hiểu:
– Mô tả được bảng giá trị của các hàm lượng giác y = sin x,
y = cos x, y = tan x, y = cot x trên một chu kì.
– Giải thích được: tập xác định; tập giá trị; tính
chất chẵn, lẻ; tính tuần hoàn; chu kì; khoảng đồng
biến, nghịch biến của các hàm số y = sin x, y = cos
x, y = tan x, y = cot x dựa vào đồ thị.
Vận dụng: Vẽ được đồ thị các hàm số y = sin x, y = cos x, y = tan x, y = cot x.
Vận dụng cao: Giải quyết được một số vấn đề thực
tiễn gắn với hàm số lượng giác (ví dụ: một số bài
toán có liên quan đến dao động điều hoà trong Vật lí,...). Nhận biết:
– Nhận biết được công thức nghiệm của phương
trình lượng giác cơ bản: sin x = m; cos x = m; tan x
= m; cot x = m bằng cách vận dụng đồ thị hàm số lượng giác tương ứng. Vận dụng:
– Tính được nghiệm gần đúng của phương trình Phương trình
lượng giác cơ bản bằng máy tính cầm tay. lượng giác cơ 1 1 1*
– Giải được phương trình lượng giác ở dạng vận bản
dụng trực tiếp phương trình lượng giác cơ bản (ví
dụ: giải phương trình lượng giác dạng sin 2x = sin 3x, sin x = cos 3x).
Vận dụng cao: Giải quyết được một số vấn đề thực
tiễn gắn với phương trình lượng giác (ví dụ: một số
bài toán liên quan đến dao động điều hòa trong Vật lí,...). Nhận biết:
– Nhận biết được dãy số hữu hạn, dãy số vô hạn.
Dãy số. Dãy số – Nhận biết được tính chất tăng, giảm, bị chặn của tăng, dãy số
dãy số trong những trường hợp đơn giản. 2 1 giảm
Thông hiểu: Thể hiện được cách cho dãy số bằng Dãy số. cấp 2
liệt kê các số hạng; bằng công thức tổng quát; số cộng và
bằng hệ thức truy hồi; bằng cách mô tả. cấp số nhân (7 tiết) Cấp số cộng.
Nhận biết: Nhận biết được một dãy số là cấp số Số hạng tổng cộng. quát của cấp
Thông hiểu: Giải thích được công thức xác định số 3 1 số cộng. Tổng
hạng tổng quát của cấp số cộng. 1 của n số hạng
Vận dụng: Tính được tổng của n số hạng đầu tiên đầu tiên của của cấp số cộng. cấp số cộng.
Vận dụng cao: Giải quyết được một số vấn đề thực
tiễn gắn với cấp số cộng để giải một số bài toán
liên quan đến thực tiễn (ví dụ: một số vấn đề trong
Sinh học, trong Giáo dục dân số,...).
Nhận biết: Nhận biết được một dãy số là cấp số nhân. Cấp số nhân.
Thông hiểu: Giải thích được công thức xác định số Số hạng tổng
hạng tổng quát của cấp số nhân. quát của cấp
Vận dụng: Tính được tổng của n số hạng đầu tiên số nhân. Tổng 2 1 1 của cấp số nhân. của n số hạng
Vận dụng cao: Giải quyết được một số vấn đề thực đầu tiên của
tiễn gắn với cấp số nhân để giải một số bài toán cấp số nhân
liên quan đến thực tiễn (ví dụ: một số vấn đề trong
Sinh học, trong Giáo dục dân số,...).
Nhận biết: Nhận biết được mối liên hệ giữa thống
kê với những kiến thức của các môn học khác
trong Chương trình lớp 11 và trong thực tiễn.
Thông hiểu: Hiểu được ý nghĩa và vai trò của các Các số đặc Các số đặc
số đặc trưng nói trên của mẫu số liệu trong thực
trưng đo xu trưng của mẫu tiễn. thế trung số liệu ghép
Vận dụng: Tính được các số đặc trưng đo xu thế 2 1 1 tâm của nhóm
trung tâm cho mẫu số liệu ghép nhóm: số trung 3 mẫu số liệu
bình cộng (hay số trung bình), trung vị (median), ghép nhóm
tứ phân vị (quartiles), mốt (mode). (4 tiết)
Vận dụng cao: Rút ra được kết luận nhờ ý nghĩa
của các số đặc trưng nói trên của mẫu số liệu trong trường hợp đơn giản. Tổng số lệnh hỏi 10 2 6 2 2 2 2 4 Tổng điểm 2,5 0,5 1,5 0,5 1,0 1,0 1,0 2,0 Tỉ lệ % 30 20 20 30
ĐỀ MINH HỌA GIỮA KỲ I – KHỐI 11 NĂM HỌC 2025 – 2026
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu
12. Mỗi câu hỏi thí sinh chọn một phương án đúng.
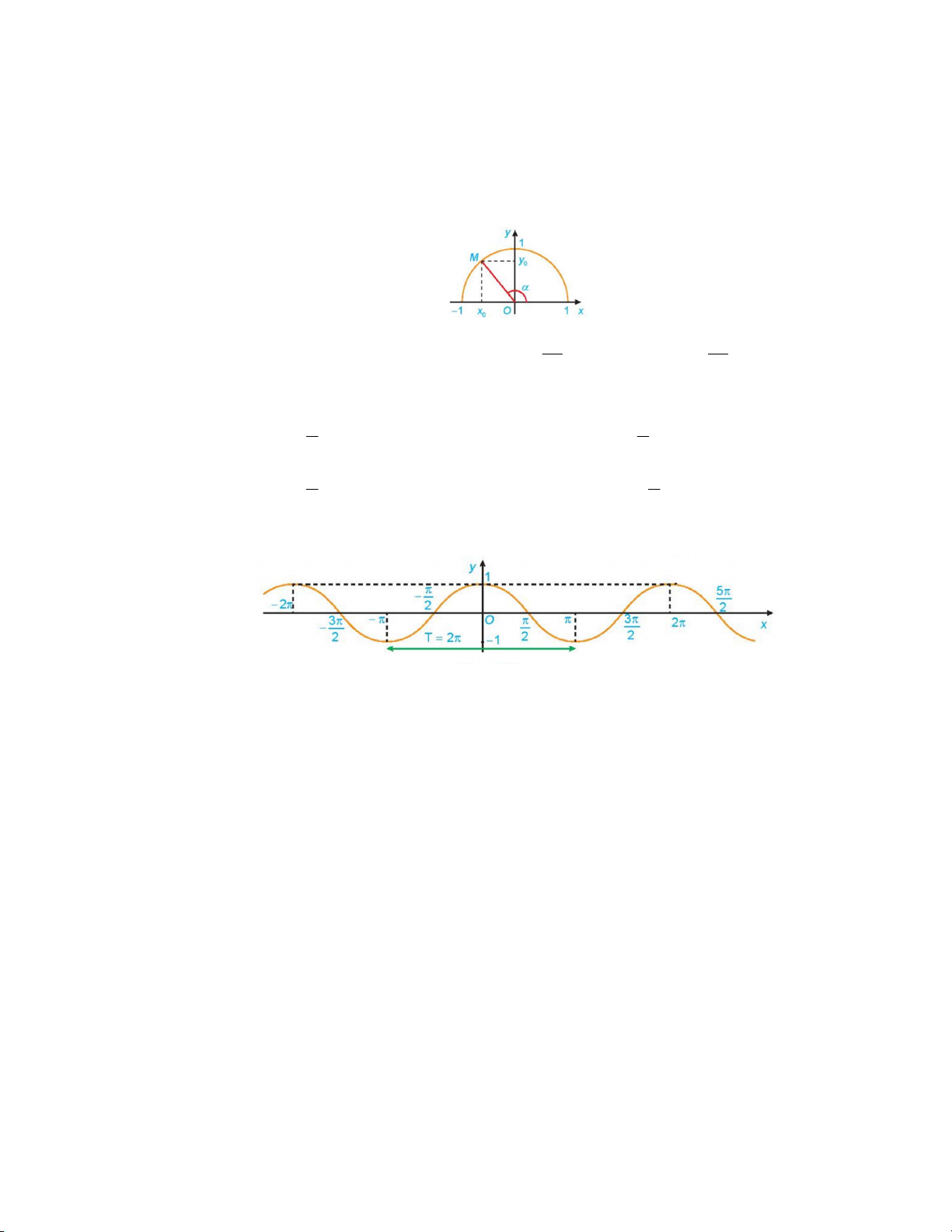
Câu 1: Dựa vào hình vẽ, giá trị lượng giác cos bằng y x A. x . B. y . C. 0 . D. 0 . 0 0 x y 0 0
Câu 2: Chọn công thức đúng trong các công thức sau: 1 1 A. sin . a sin b cos
a b cosa b. sin .asinb cos a b cos a b . 2 B. 2 1 1 C. sin . a sin b sin
a b cosa b. sin .asinb cos a b sin a b . 2 D. 2
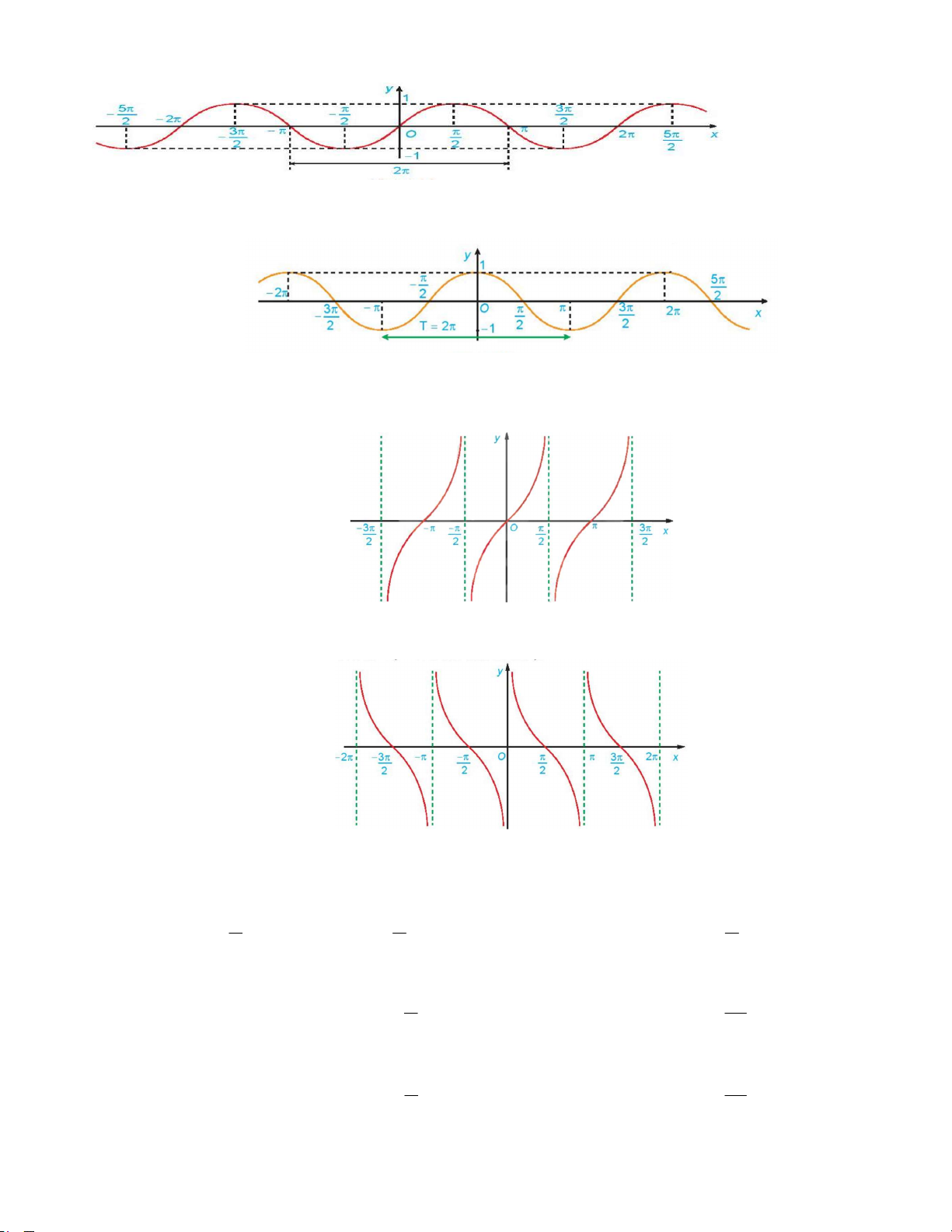
Câu 3: Dựa vào hình dạng đồ thị sau, hãy cho biết đây là đồ thị của hàm số nào? A. y sin x B. y cosx C. y tan x D. y cot x .
Câu 4: Phương trình sinx sin có nghiệm là x k2 x k A. ;k B. ;k . x k2 x k x k2 x k C. ;k . D. ;k . x k2 x k
Câu 5: Dãy số nào sau đây là dãy số hữu hạn? A. 1;2;3;4 . B. 2;4;6;8;.... C. 1;3;5;7.... D. 1;4;9;16;....
Câu 6: Dãy số nào sau đây là dãy số tăng? A. 1;2;3;4;5. B. 1;3;2;5;6. C. -1;-2;-3;-4;-5. D. 1;1;1;1;1.
Câu 7: Cho dãy số u có dạng: 0; 1; 2; 3; 4;…. Số hạng tổng quát của dãy số u là n n A. u n 1. B. u n . C. u n 1. D. u 2n 2 . n n n n
Câu 8: Trong các dãy số hữu hạn sau, dãy số nào là cấp số nhân? A. 1;2;3;4 . B. 2;4;8;16 . C. 1;3;5;7 . D. 8;6;4;2 .
Câu 9: Cho cấp số nhân (u ) có 4;24;144;..... Số hạng thứ 7 của (u ) là n n A. 2 4576. B. 6 718464. C. 1 86624 . D. 1119744 .
Câu 10: Cho dãy số u , biết u n 1. Năm số hạng đầu tiên của dãy số đó lần lượt là n n A. 0; 1; 2; 3; 4. B. 1;0;1;2;3 . C. 1; 2; 3; 4; 5. D. 2; 3; 4; 5; 6.
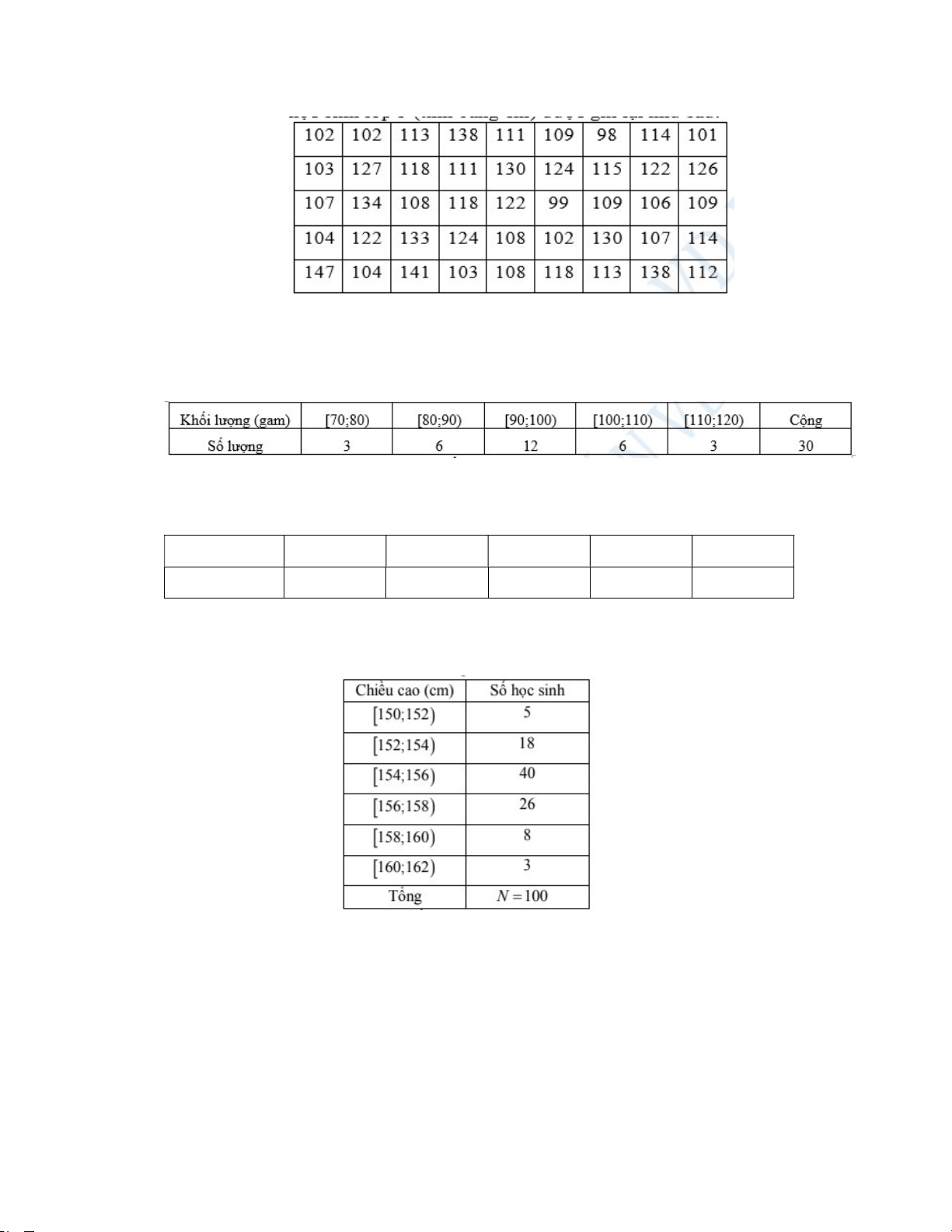
Câu 11: Cho bảng khảo sát về khối lượng của 30 củ khoai tây thu hoạch ở một nông trường như sau:
Độ dài các nhóm của mẫu số liệu bằng A. 5 . B. 10. C. 15. D. 20 .
Câu 12: Tìm hểu thời gian xem tivi trong tuần trước của một số học sinh thu được kết quả sau: Thòi gian [0; 5) [5; 10) [10; 15) [15; 20) [20; 25) Số học sinh 8 16 4 2 2
Số học sinh có thời gian xem tivi từ 10h trở lên là A. 7. B. 8. C. 22. D. 28.
PHẦN II. Trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b),
c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 3 a) rad 135 . 4
b) Điểm biểu diễn các góc 36 k360
, k trên đường tròn lượng giác là điểm M thuộc góc phần tư thứ II . x k2
c) Phương trình cos x cos k . x k2
d) Tập xác định của hàm số 2
f (x) sin x cos x 1 là .
Câu 2: Cho cấp số cộng u có số hạng thứ hai u 3, số hạng thứ năm u 3 . n 2 5
a) Công thức số hạng tổng quát của cấp số cộng u là u 7 2 . n . n n
b) Số 13 là một số hạng của cấp số cộng u . n
c) Công sai của cấp số cộng u là d 2. n
d) Số hạng đầu của cấp số cộng u là u 5. n 1
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4. 1 3
Câu 1: Biết cos . Khi đó giá trị sin bằng bao nhiêu? 2 2 1 Câu 2: Biết: sin và
. Khi đó giá trị cos bằng bao nhiêu? 4 2 3 x
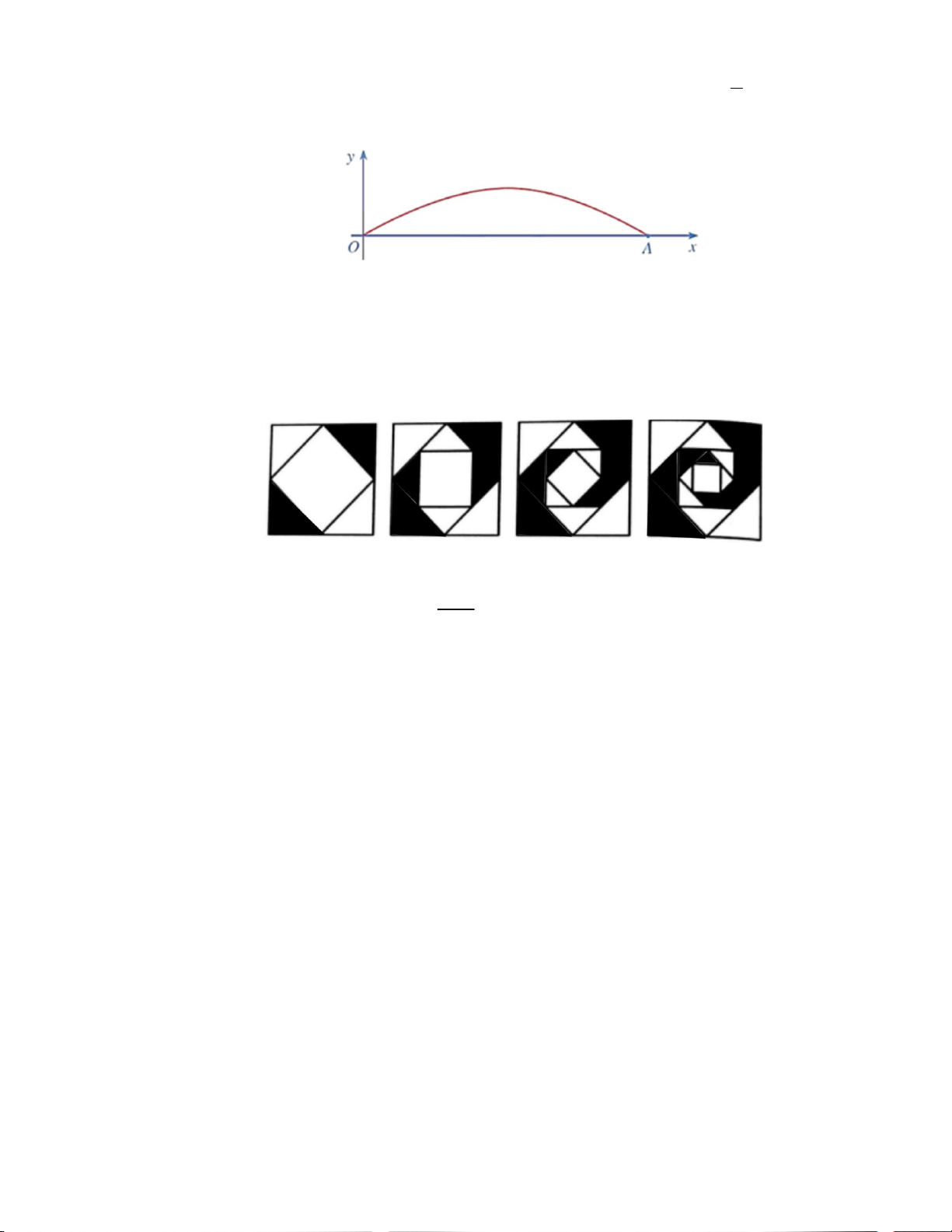
Câu 3: Một cây cầu có dạng cung OA là một phần của đồ thị hàm số y 4,8.sin và được mô tả 9
trong hệ trục tọa độ với đơn vị trục là mét như hình dưới.
Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tính chiều rộng đó.
Câu 4: Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành
bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình
tam giác kết quả được tô màu. Nếu quá trình này được lặp lại năm lần nữa, hãy xác định
tổng diện tích của vuông được tô màu. PHẦN IV. Tự luận 1
Câu 1: Tìm tập xác định của hàm số: y . sin x
Câu 2: Giải phương trình 2sin x 1 0.
Câu 3: Khi kí kết hợp đồng lao động với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:
Phương án 1: Năm thứ nhất, tiền lương là 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi
năm tiền lương được tăng 18 triệu đồng.
Phương án 2: Quý thứ nhất, tiền lương là 24 triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý
tiền lương được tăng 1,8 triệu đồng.
Nếu là người được tuyển dụng vào doanh nghiệp trên, em nên chọn phương án nào khi:
a) Kí hợp đồng lao động 3 năm?
b) Kí hợp đồng lao động 10 năm?
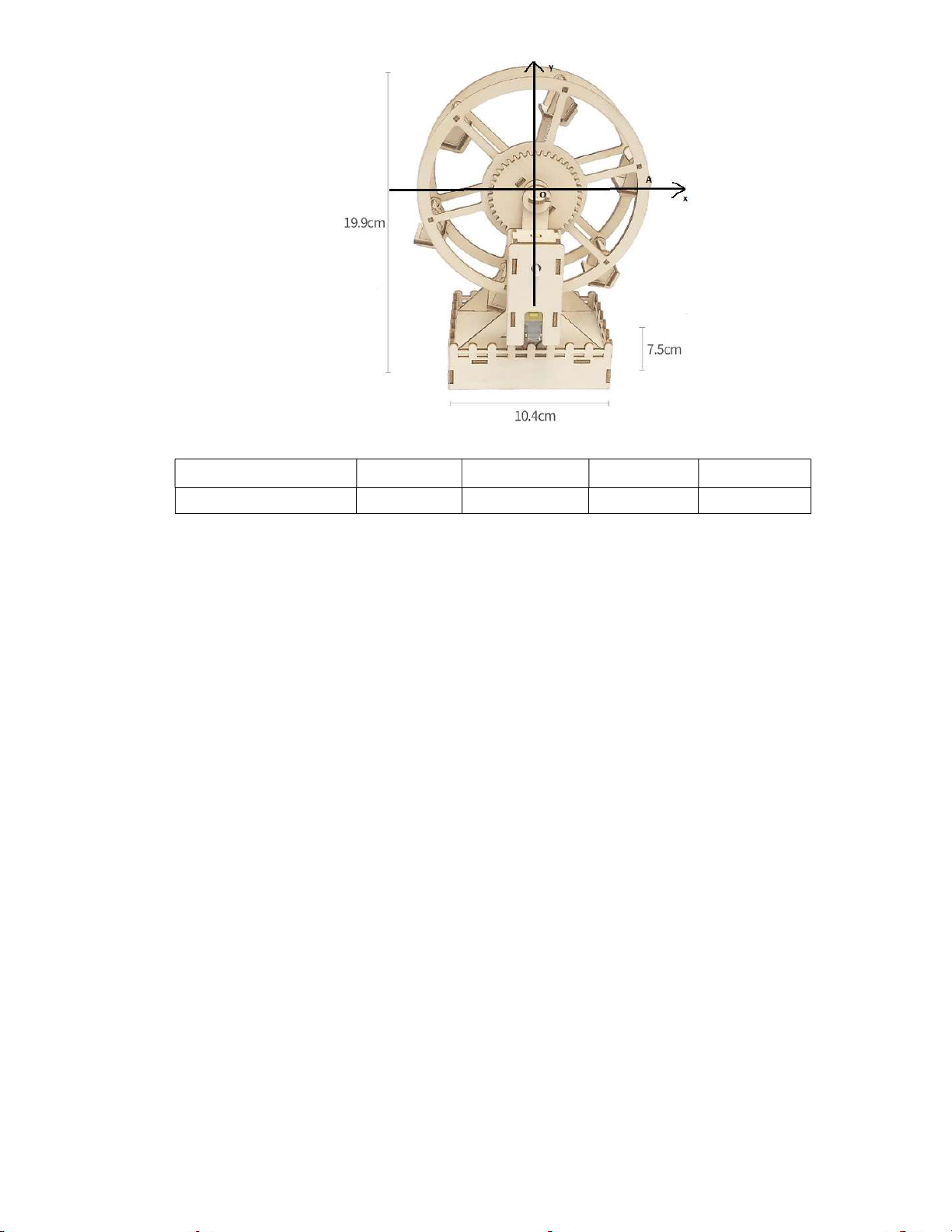
Câu 4: Mô hình vòng quay mặt trời chạy bằng pin chuyển động đều theo chiều kim đồng hồ với
vận tốc góc không đổi là 13rad/s . Vị trí điểm A được đánh dấu như hình vẽ bên dưới. Hỏi
sau một phút di chuyển, khoảng cách từ vị trí điểm A đến mặt bàn là bao nhiêu. Kết quả
làm tròn đến hàng phần mười.
Câu 5: Tổng hợp tiền lương tháng của một số nhân viên văn phòng được ghi lại như sau: Lương tháng [6;8) [8;10) [10;12) [12;14) Số nhân viên 3 6 8 7
a) Xác định giá trị đại diện của mẫu số liệu ghép nhóm?
b) Hãy tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên?
NGÂN HÀNG ĐỀ GKI MÔN TOÁN 11 NĂM HỌC 2025 - 2026
A. TRẮC NGHIỆM 4 LỰA CHỌN
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 1: Dựa vào hình vẽ, giá trị lượng giác sin bằng y x A. x . B. y . C. 0 . D. 0 . 0 0 x y 0 0
Câu 2: Dựa vào hình vẽ, giá trị lượng giác cos bằng y x A. x . B. y . C. 0 . D. 0 . 0 0 x y 0 0
Câu 3: Dựa vào hình vẽ, giá trị lượng giác tan bằng y x A. x . B. y . C. 0 . D. 0 . 0 0 x y 0 0
Câu 4: Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là thuộc góc phần
tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
A. sin 0; cos 0. B. sin 0; cos 0. C. sin 0; cos 0. D. sin 0; cos 0.
Câu 5: Điểm P trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là thuộc góc phần
tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai ? A. sin 0. B. cos 0. C. tan 0. D. cot 0.
Câu 6: Trên đường tròn lượng giác, điểm M ; x
y biểu diễn góc lượng giác có số đo . Khẳng định nào sau đây sai?
A. Hoành độ x của điểm được gọi là côsin của , kí hiệu là cos.
B. Tung độ y của điểm được gọi là sin của , kí hiệu là sin . cos
C. Nếu sin 0 , tỉ số
được gọi là tang của , kí hiệu tan. sin
D. Các giá trị cos, sin , tan và cotđược gọi là các giá trị lượng giác của góc .
Câu 7: Công thức nào sau đây sai?
A. cosa b sin asinb cosacos . b
B. cosa b sin asinb cosacos . b 1
C. sina b sin acosb cos asin . b
D. sina b sin acosb cosasin . b
Câu 8: Khẳng định nào sai trong các khẳng định sau? 1 cos 2x 1 cos 2x A. 2 sin x . B. 2 cos x . 2 2 x x 1 cos 2x C. sin x 2sin cos . D. 2 sin x . 2 2 2
Câu 9: Khẳng định nào đúng trong các khẳng định sau? A.
sin a cos a 2 sin a .
B. sin a cos a 2 sin a . 4 4 C.
sin a cos a 2 sin a .
D. sin a cos a 2 sin a . 4 4
Câu 10: Đẳng thức nào sau đây đúng? sin b a 1 A. cot a cot b . B. 2 cos a 1 cos 2a. sin . a sin b 2 1 sin a b
C. sin a b sin 2a b. D. tan a b . 2 cos . a cosb
Câu 11: Chọn công thức đúng trong các công thức sau: 1 1 A. sin . a sin b cos
a bcosa b. sin .
a sin b cos a b cos a b . 2 B. 2 1 1 C. sin . a sin b sin
a b cosa b. sin .
a sin b cos a b sin a b . 2 D. 2
Câu 12: Công thức nào sau đây đúng?
A. cosa b sin acosb cosasin . b
B. cosa b sin asinb cosacos . b
C. sina b sin asinb cosacos . b
D. sina b sin acosb cosasin . b
Câu 13: Khẳng định nào sai trong các khẳng định sau? 1 cos 2x 1 cos 2x A. 2 sin x . B. 2 cos x . 2 2 x x 1 cos 2x C. sin x 2sin cos . D. 2 co s x . 2 2 2
Câu 14: Khẳng định nào đúng trong các khẳng định sau? 1 cos 2x 1 cos x A. 2 sin x . B. 2 cos x . 2 2 1 cos 2x C. sin x 2sin xcos . x D. 2 co s x . 2
Câu 15: Khẳng định nào đúng trong các khẳng định sau? 1 cos x 1 cos x A. 2 sin x . B. 2 cos x . 2 2 1 cos 2x C. sin 2x 2sin xcos . x D. 2 co s x . 2
Câu 16: Chọn công thức đúng trong các công thức sau: 2 a b a b a b a b A. sin a sin b 2sin .cos . B. sin a sin b 2cos .cos . 2 2 2 2 a b a b a b a b C. sin a sin b 2sin .sin . D. sin a sin b 2cos .cos . 2 2 2 2
Câu 17: Chọn công thức đúng trong các công thức sau: a b a b a b a b A. sin a sin b 2cos .sin . B. sin a sin b 2cos .cos . 2 2 2 2 a b a b a b a b C. sin a sin b 2sin .sin . D. sin a sin b 2cos .sin . 2 2 2 2
Câu 18: Chọn công thức đúng trong các công thức sau: a b a b a b a b A. cos a cosb 2cos .sin . B. cos a cosb 2sin .sin . 2 2 2 2 a b a b a b a b C. cos a cosb 2cos .sin . D. cos a cosb 2cos .cos . 2 2 2 2
Câu 19: Chọn công thức đúng trong các công thức sau: 2 tan a tan a A. tan 2a . B. tan 2a . 2 1 tan a 1 tan a 2 tan a tan a C. tan 2a . D. tan 2a . 1 tan a 2 1 tan a
Câu 20: Chọn công thức sai trong các công thức sau: A. 2 2 cos 2a sin a cos a. B. 2 2 cos 2a cos a sin a. C. 2 cos 2a 2 cos a 1. D. 2 cos 2a 1 2 sin a.
Câu 21: Trong các hàm số sau, hàm số nào là hàm số lẻ? A. y sin x. B. y cos x. C. y cos 2 . x D. y o c s3 . x
Câu 22: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y sin x. B. y cos 2x. C. y tan x. D. y cot . x
Câu 23: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y sin x. B. y cos 3x. C. y tan x. D. y cot . x
Câu 24: Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2 y sin . x B. y cos x. C. y tan x. D. y cos 2 . x
Câu 5 . Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y sin x. B. y cos x. C. y tan x. D. y cot . x
Câu 25: Mệnh đề nào sau đây là sai?
A. Hàm số y sin x tuần hoàn với chu kì 2.
B. Hàm số y cos x tuần hoàn với chu kì 2.
C. Hàm số y cot x tuần hoàn với chu kì 2.
D. Hàm số y tan x tuần hoàn với chu kì .
Câu 26: Dựa vào hình dạng đồ thị sau, hãy cho biết đây là đồ thị của hàm số nào? 3 A. y sin x B. y cosx C. y tan x D. y cot x .
Câu 27: Dựa vào hình dạng đồ thị sau, hãy cho biết đây là đồ thị của hàm số nào? A. y sin x B. y cosx C. y tan x D. y cot x .
Câu 28: Dựa vào hình dạng đồ thị sau, hãy cho biết đây là đồ thị của hàm số nào? A. y sin x B. y cosx C. y tan x D. y cot x .
Câu 29: Dựa vào hình dạng đồ thị sau, hãy cho biết đây là đồ thị của hàm số nào? A. y sin x B. y cosx C. y tan x D. y cot x .
Câu 30: Nghiệm của phương trình sin x 1 là A. x k2 . B. x k . C. x k . D. x k2 . 2 2 2
Câu 31: Nghiệm của phương trình cos x 1 là 3 A. x k . B. x k2 . C. x k2 . D. x k . 2 2
Câu 32: Nghiệm của phương trình cos x 1,5 là 3 A. x k2 . B. x k . C. Vô nghiệm. D. x k . 2 2
Câu 33: Phương trình sinx sin có nghiệm là 4 x k2 x k A. ; k B. ;k . x k2 x k x k2 x k C. ;k . D. ;k . x k2 x k
Câu 34: Phương trình co t x co t có nghiệm là A. x k2 , k .
B. x k , k .
C. x k2 ,k . D. x k , k .
Câu 35: Phương trình cos x m vô nghiệm khi và chỉ khi A. m ; 1 1; . B. m (; 1). C. m 1; . D. m ( ; 1][1; ).
Câu 36: Phương trình cos x 0 có nghiệm là A. x k k .
B. x k 2 k . 2
C. x k k . D. x k2 k . 2
Câu 37: Nghiệm của phương trình sin x 1 là: 3
A. x k2 ,k . B. x k ,k . 2 2 C. x k , k .
D. x k ,k . 2
Câu 38: Chọn khẳng định đúng trong các khẳng định sau? x y k2 x y k A. cos x cos y k . B. cos x cos y k . x y k2 x y k x y k C. cos x cos y k . D. x y k x y k2 cos x cos y k . x y k2
Câu 39: Phương trình tan x tan có nghiệm là A. x k2 , k .
B. x k , k .
C. x k2 ,k . D. x k , k .
CHƯƠNG II. DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
Câu 40: Dãy số nào sau đây là dãy số hữu hạn? A. 1; 2;3; 4 . B. 2;4;6;8;... . C. 1;3;5;7.... D. 1; 4;9;16;... .
Câu 41: Dãy số nào sau đây là dãy số hữu hạn? A. 1;3;5;7 . B. 1; 2;3; 4.... C. 3;2;1;0;... . D. 0; 2; 4;6;....
Câu 42: Dãy số nào sau đây là dãy số vô hạn? A. 1; 2;3; 4;... . B. 10;9;8;7 . C. 1;1;1;1 . D. 1; 4;7;10 .
Câu 43: Dãy số nào sau đây là dãy số vô hạn? A. 2;4;6;8;... . B. 3;6;9;12 . C. 5;4;3;2 . D. 1; 1;11.
Câu 44: Dãy số nào sau đây là dãy số vô hạn? 5 A. 2; 2; 2; 2;... . B. 0;3; 6;9 . C. 4;3; 2;1 . D. 1;5;9;13 . Câu 12
Câu 45: Dãy số nào sau đây là dãy số tăng? A. 1;2;3;4;5. B. 1;3;2;5;6. C. -1;-2;-3;-4;-5. D. 1;1;1;1;1.
Câu 46: Dãy số nào sau đây là dãy số tăng? 1 1 1 1 A. 1;2;3;4;5. B. 1; ; ; ; . C. 1;-1;1;-1;1. D. 2;2;2;2;2. 2 3 4 5
Câu 47: Dãy số nào sau đây là dãy số giảm? A. 9;7;5;3;1. B. 4;6;8;10;12. C. 3;4;5;2;7. D. 0;1;0;1;0.
Câu 48: Dãy số nào sau đây là dãy số giảm? A. 8;6;4;2;0. B. 1;2;3;4;5. C. 1;2;1;3;1;4. D. 3;3;3;3;3.
Câu 49: Dãy số nào sau đây là dãy số giảm? A. -2;-4;-6;-8;-10. B. 1;2;3;5;7. C. 8;7;9;10;11. D. 7;7;7;7;7. Câu 17
Câu 50: Cho dãy số u có dạng: 0; 2; 4; 6; 8;…. Số hạng tổng quát của dãy số u là n n A. u 2n 2 . B. u 2n . C. u n 1. D. u 2n 1. n n n n
Câu 51: Cho dãy số u có dạng: 0; 1; 2; 3; 4;…. Số hạng tổng quát của dãy số u là n n A. u n 1. B. u n . C. u n 1. D. u 2n 2 . n n n n
Câu 52: Cho dãy số u có dạng: 1; 3; 5; 7; 9…. Số hạng tổng quát của dãy số u là n n A. u 2n 1. B. u n . C. u n 1. D. u n 1. n n n n
Câu 53: Cho dãy số u , biết u 2n . Năm số hạng đầu tiên của dãy số đó lần lượt là n n A. 2; 4; 6; 8; 10. B. 0; 2; 4; 6; 8. C. 2; 3; 4; 5; 6. D. 0; 1; 2; 3; 4.
Câu 54: Cho dãy số u , biết u n 1. Năm số hạng đầu tiên của dãy số đó lần lượt là n n A. 0; 1; 2; 3; 4. B. 1;0;1; 2;3. C. 1; 2; 3; 4; 5. D. 2; 3; 4; 5; 6.
Câu 55: Trong các dãy số hữu hạn sau, dãy số nào là cấp số nhân? A. 1; 2;3; 4 . B. 2; 4;8;16 . C. 1;3;5;7 . D. 8;6; 4;2 .
Câu 56: Trong các dãy số hữu hạn sau, dãy số nào là cấp số nhân? A. 2;4;6;8 . B. 1;3;9; 27 . C. 1;3;5;7 . D. 1; 4;7;10 .
Câu 57: Trong các dãy số hữu hạn sau, dãy số nào là cấp số nhân? A. 3;6;12;24 . B. 1; 2; 4; 6 . C. 2; 4;6;8 . D. 2;3; 4;5 .
Câu 58: Trong các dãy số hữu hạn sau, dãy số nào không phải là cấp số nhân? A. 2;2;2;2 . B. 1; 2; 4;8 . C. 1;3;5;7 . D. 1;3;9;27 .
Câu 59: Trong các dãy số hữu hạn sau, dãy số nào không phải là cấp số nhân? A. 1; 1; 1; 1. B. 1;3;9; 27 . C. 1; 2;3; 4 . D. 2; 4; 8;16 . Câu 18
Câu 60: Cho cấp số nhân (u ) có số hạng đầu u 23 và công bội q 5 . Số hạng thứ 9 của (u ) là n 1 n 6 A. 44921875 . B. 224609375 . C. 391554926405. D. 8984375 .
Câu 61: Cho cấp số nhân (u ) có số hạng đầu u 28 và công bội q 5
. Số hạng thứ 11 của (u ) n 1 n là A. 1 480983833477120. B. 273437500 . C. 1 367187500. D. 6835937500 .
Câu 62: Cho cấp số nhân (u ) có số hạng đầu u 3 và công bội q 5 . Số hạng thứ 11 của (u ) là n 1 n A. 732421875. B. 146484375. C. 29296875 . D. 295245 .
Câu 63: Cho cấp số nhân (u ) có 7; 21; 63;..... Số hạng thứ 11 của (u ) là n n A. 3 720087. B. 4 13343. C. 1 240029. D. 847425747.
Câu 64: Cho cấp số nhân (u ) có 4; 24; 144;..... Số hạng thứ 7 của (u ) là n n A. 2 4576. B. 6 718464. C. 1 86624. D. 1119744.
CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM
Câu 65: Điều tra về chiều cao của 100 học sinh lớp 10 của một trường THPT, ta được kết quả:
Chiều cao 150;152 152;154 154;156 156;158 158;160 160;162 162;168 Số học 5 18 40 25 8 3 1 sinh
Mẫu số liệu trên có bao nhiêu nhóm A. 7. B. 6. C. 5. D. 8.
Câu 66: Cho bảng khảo sát về khối lượng của 30 củ khoai tây thu hoạch ở một nông trường như sau:
Độ dài các nhóm của mẫu số liệu bằng A. 5. B. 10. C. 15. D. 20 .
Câu 67: Bảng thống kê sau cho biết tốc độ của một số xe máy khi đi qua vị trí có cảnh sát giao
thông đang làm nhiệm vụ. Tốc độ
20;35 35;50 50;60 60;70 70;85 85;100 Số phương tiện 27 70 8 3 1 1 giao thông
Vị trí đo tốc độ trên đường trong khu dân cư, tốc độ tối đa theo quy định là 50 . Có bao nhiêu xe vi
phạm quy định về an toàn giao thông? A. 13. B. 5. C. 97. D. 2.
Câu 68: Điều tra về chiều cao của 100 học sinh lớp 10 của một trường THPT, ta được kết quả:
Chiều cao 150;152 152;154 154;156 156;158 158;160 160;162 162;168 Số học 5 18 40 25 8 3 1 sinh
Số học sinh có chiều cao từ 156 cm trở lên là A. 37. B. 77. C. 12. D. 25. 7
Câu 69: Chiều cao của 45 học sinh lớp 5 được ghi lại như sau:
Chiều cao 115 cm thuộc nhóm nào sau đây? A. 98;103 B. 118;123 C. 103;108 D. 113;118
Câu 70: Cho bảng khảo sát về khối lượng của 30 củ khoai tây thu hoạch ở một nông trường như sau:
Số lượng củ khoai tây có khối lượng từ 100 gam đến dưới 110 gam là A. 3. B. 6 . C. 12. D. 30 .
Câu 71: Tìm hểu thời gian xem tivi trong tuần trước của một số học sinh thu được kết quả sau: Thòi gian [0; 5) [5; 10) [10; 15) [15; 20) [20; 25) Số học sinh 8 16 4 2 2
Số học sinh có thời gian xem tivi từ 10h trở lên là A. 7. B. 8. C. 22. D. 28.
Câu 72: Điều tra về chiều cao của học sinh khối 11 ta có mẫu số liệu sau
Mẫu số liệu này có bao nhiêu nhóm ? A.5. B. 6. C. 7. D.12 .
Câu 73: Điều tra về chiều cao của học sinh khối 11 ta có mẫu số liệu sau 8
Giá trị đại diện của nhóm thứ tư là ? A.156,5 . B.157 . C.157,5. D.158.
Câu 74: Điều tra về thời gian truy cập mạng của học sinh khối 11 ta có mẫu số liệu sau
Có bao nhiêu học sinh truy cập mạng có thời gian từ 21,5 phút trở lên ? A.3. B. 2. C.12 . D.15 .
Câu 75: Độ dài của mỗi nhóm trong mẫu số liệu ghép nhóm có dạng a;b được tính như thế nào ? A. a b. B. . a b . C. a b . D. b a.
Câu 76: Đo chiều cao của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao 150;154 154;158 158;162 162;166 166;170 Số học sinh 25 50 200 175 50
Giá trị đại diện của nhóm 162;166 là A. 162. B. 164. C. 166. D. 4.
Câu 77: Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau: Thời gian
9,5;12,5 12,5;15,5 15,5;18,5 18,5;21,5 21,5;24,5 Số học sinh 3 12 15 24 2
Có bao nhiêu học sinh truy cập Internet mỗi buổi tối có thời gian từ 18,5 phút đến dưới 21,5 phút? A. 24 . B. 15 . C. 2. D. 20 .
Câu 78: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40;60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 79: Cho mẫu số liệu về số tiền điện phải trả của 50 gia đình trong một tháng ở một khu phố . Giá trị
375;450 450;525 525;600 600;675 675;750 750;825 9 Số lượng 6 15 10 6 9 4 gia đình
Số gia đình trong một tháng có số tiền điện từ 525 nghìn đồng đến dưới 750 nghìn đồng là A. 30 . B. 29 . C. 44 . D. 25 . B: TRẮC NGHIỆM ĐÚNG SAI
Câu 80: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
a) Điểm biểu diễn góc 125 trên đường tròn lượng giác thuộc góc phần tư thứ II. x k2
b) Phương trình sin x sin k . x k2
c) Tập xác định của hàm số f (x) tan x 1 là . d) 3 sin k2 (k ) 3 2
Câu 81: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 3 a) rad 135 . 4
b) Điểm biểu diễn các góc 36 k360
, k trên đường tròn lượng giác là điểm M thuộc góc phần tư thứ II . x k2
c) Phương trình cos x cos k . x k2
d) Tập xác định của hàm số 2
f (x) sin x cos x 1 là .
Câu 82: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. a) Cho 0 90 . Khi đó B 0 cos 90 0. b) 3 108 rad. 5
c) Hàm số y 3sin x có tập giá trị là T [3;3] . x k
d) Phương trình cos x cos k . x k
Câu 83: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. a) Cho 0
. Khi đó A cos( ) 0 . 2 19
b) Điểm biểu diễn góc 3 trên đường tròn lượng giác thuộc góc phần tư thứ II. 0 x a k2 c) Phương trình 0 cos x cos a k . 0 x a k2
d) Giá trị lớn nhất của hàm số f (x) sin x 2 bằng 2
Câu 84: Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. a) 2 150 rad. 3
b) Độ dài của cung tròn có số đo 1,5 rad của đường đường tròn bán kính 20 cm bằng 30cm . 10
c) Phương trình sin x m có nghiệm khi và chỉ khi 1 m 1. 1sin x
d) Tập xác định của hàm số y
D \ 2k , k . cos x 1 là
Câu 85: Cho cấp số cộng u có số hạng đầu u 5, công sai d 3. n 1
a) Số hạng thứ 4 của cấp số cộng u là u 17. n 4
b) Số 20 là số hạng thứ 6 của cấp số cộng u . n
c) Công thức số hạng tổng quát của cấp số cộng u là u 5 3n . n n
d) Tổng 10 số hạng đầu của cấp số cộng u bằng 180. n
Câu 86: Cho cấp số cộng u có số hạng đầu u 2 , số hạng thứ hai u 5. n 1 2
a) Công thức số hạng tổng quát của cấp số cộng u là u 3n 1. n n
b) Số 18 là số hạng thứ 5 của cấp số cộng u . n
c) Công sai của cấp số cộng u là d 2. n
d) Số hạng thứ 3 của cấp số cộng u là u 8. n 3
Câu 87: Cho cấp số cộng u viết dưới dạng liệt kê như sau 2;0;2;4;.... n
a) Công thức số hạng tổng quát của cấp số cộng u là u 2n 2. n n
b) Số 18 là một số hạng của cấp số cộng u . n
c) Công sai của cấp số cộng u là d 2. n
d) Số hạng thứ 5 của cấp số cộng u là u 8. n 5
Câu 88: Cho cấp số cộng u có số hạng đầu u 1
, số hạng thứ ba u 5. n 1 3
a) Công thức số hạng tổng quát của cấp số cộng u là u 3n 1. n n
b) Số 49 là một số hạng của cấp số cộng u . n
c) Công sai của cấp số cộng u là d 6. n
d) Số hạng thứ 2 của cấp số cộng u là u 2. n 2
Câu 89: Cho cấp số cộng u có số hạng thứ hai u 3 , số hạng thứ năm u 3 . n 2 5
a) Công thức số hạng tổng quát của cấp số cộng u là u 7 2 . n . n n
b) Số 13 là một số hạng của cấp số cộng u . n
c) Công sai của cấp số cộng u là d 2. n
d) Số hạng đầu của cấp số cộng u là u 5. n 1
C: TRẮC NGHIỆM TRẢ LỜI NGẮN Câu 90: Biết 3
sin . Khi đó giá trị sin 5 bằng bao nhiêu? 5 Câu 91: Biết 1
cos . Khi đó giá trị 3 sin bằng bao nhiêu? 2 2 11




