Đề cương giữa kì 1 Toán 7 năm 2023 – 2024 trường THCS Nguyễn Gia Thiều – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề cương ôn tập giữa học kì 1 môn Toán 7 năm học 2023 – 2024 trường THCS Nguyễn Gia Thiều, quận Long Biên, thành phố Hà Nội.
Preview text:
ĐỀ CƯƠNG ÔN TẬP GIỮA KÌ I
THCS NGUYỄN GIA THIỀU- 2023-2024 PHẦN I. TRẮC NGHIỆM
Câu 1. Nhà trường quét vôi bên trong một phòng học (gồm 4 bức tường và trần nhà) có dạng hình hộp chữ
nhật dài 15 m, rộng 8 m và cao 2,7 m. Biết diện tích các cửa chiếm 8,5 m2, diện tích cần quét vôi là A. 120 m2. B. 235,7 m2. C. 252,7 m2. D. 244,2 m2.
Câu 2. Thể tích của hình lăng trụ đứng có đáy là hình thoi có hai đường chéo lần lượt dài 6 cm, 8 cm,
chiều cao của lăng trụ là 5 cm. Thể tích lăng trụ đó là A. 240 cm3. B. 60 cm3. C. 120 cm3. D. 140 cm3.
Câu 3. Cho hình hộp chữ nhật có chiều dài 4 cm, chiều rộng 3 cm và chiều cao 5 cm. Thể tích của hình
hộp chữ nhật đã cho bằng: A. 40 cm3. B. 60 cm3. C. 20 cm3. D. 12 cm3. Câu 4.
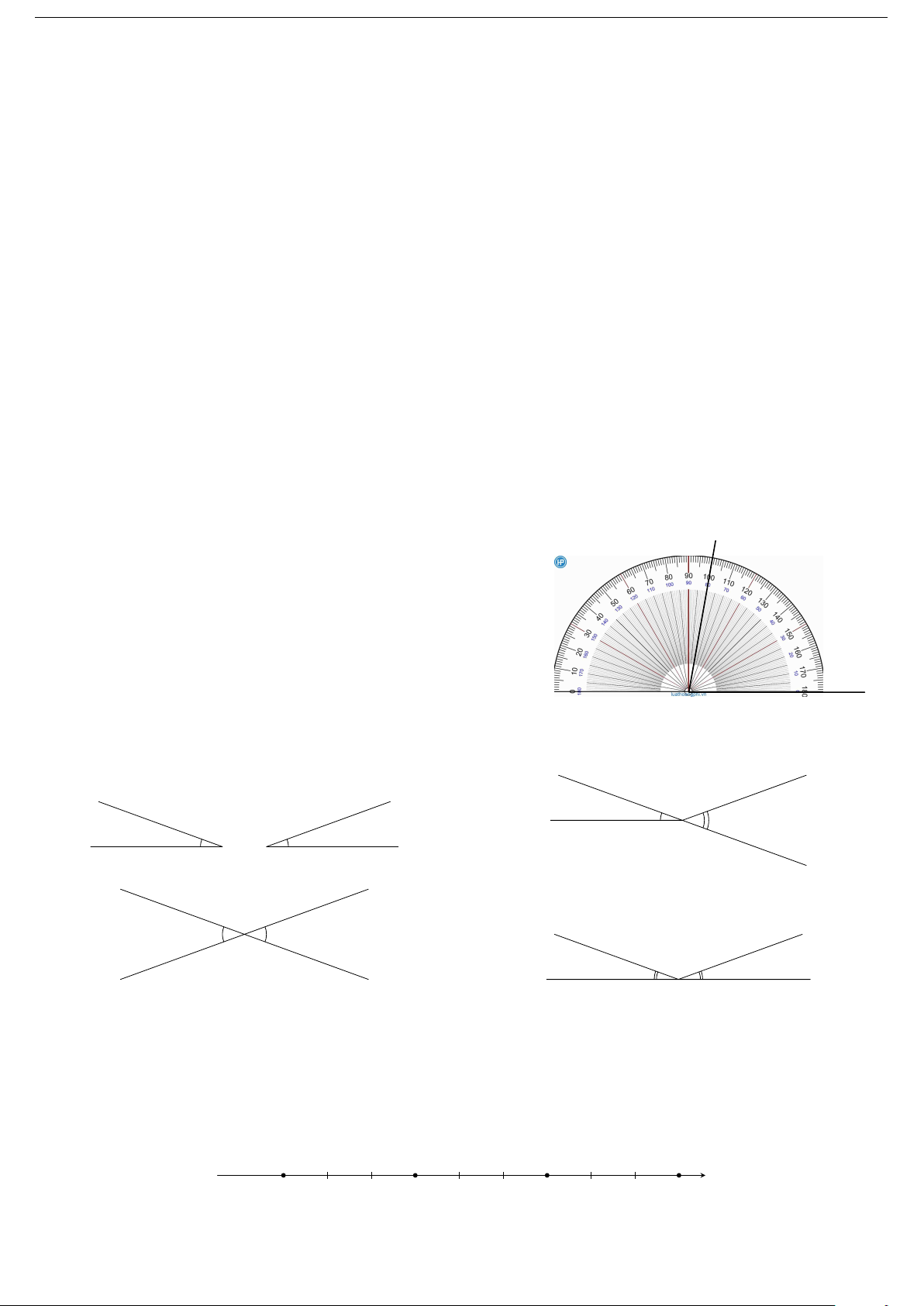
Góc mOn dưới đây có số đo là n A. 80◦. B. 100◦. C. 90◦. D. 70◦. m O
Câu 5. Cho các hình vẽ sau: Hình a Hình b Hình c Hình d
Số hình không có cặp góc đối đỉnh là A. 2. B. 3. C. 1. D. 4. Câu 6. Cho hình vẽ sau: M N −1 0 1 2 1
Trên trục số, điểm M , N lần lượt biểu diễn các số hữu tỉ 2 1 2 1 1 2 −1 2 A. ; . B. ; − . C. ; − . D. ; . 3 3 3 3 3 3 3 3
Câu 7. Cho xOy = 76◦, Om là tia đối của tia Ox, On là tia đối của tia Oy. Số đo góc xOn A. 104◦. B. 76◦. C. 114◦. D. 180◦.
Câu 8. Kết quả của phép tính 65 : 25 viết dưới dạng lũy thừa là A. 45. B. 35. C. 31. D. 25.
Câu 9. Khẳng định đúng là
A. Hai góc kề nhau thì có tổng số đo bằng 180◦.
B. Hai góc bằng nhau thì đối đỉnh.
C. Hai góc đối đỉnh thì bằng nhau.
D. Hai góc phụ nhau thì có tổng số đo bằng 180◦. Å 25 ã4 Câu 10. Lũy thừa bằng: 49 Å 5 ã16 Å 5 ã4 Å 5 ã6 Å 5 ã8 A. . B. . C. . D. . 7 7 7 7 Å 1 ã2 3 Câu 11. Cho 1 − x + =
. Giá trị của x thỏa mãn đẳng thức đã cho là 3 4 ß 5 1 ™ 1 A. x ∈ − ; . B. x ∈ ∅. C. x = . D. x = −. 6 6 6
Câu 12. Viết biểu thức 68 · 125 dưới dạng 2a · 3b thì giá trị của a + b =? A. 30. B. 18. C. 13. D. 31.
Câu 13. Cho (x − 1)2 = 54 Giá trị của x là A. x ∈ {6; −4}. B. x = 26. C. x ∈ {26; −24}. D. x = −24. Å 4 ã2 Å 2 ã6 Å −8 ã3
Câu 14. Kết quả của phép tính · : là 25 5 125 −2 2 4 A. . B. . C. . D. −1. 5 5 25 15 2 7 2 8 17
Câu 15. Kết quả của phép tính · − · + · là 19 3 19 3 3 19 17 19 8 A. . B. . C. . D. −1. 19 3 3 PHẦN II. TỰ LUẬN Dạng 1
Thực hiện phép tính
Bài 1. Thực hiện phép tính 1 5 1 Å −2 ã2 1 5 Å 2 ã 3 1 − 0,4 · + + − (−0,5)3 2 3 − − − 6 8 2 3 6 8 5 10 −5 1 4545 Å 1 ã 1 1 33 −1 1 4 0,2 + − (−0,8) 5 − + − − 6 0,5 + + 0,4 − − + 13 2 2020 3 6 3 20 6 4 8 4 1 Å −1 ã2 5 5 Å 2 1 ã 7 0,3 − : · + 1 8 − : (0,5)3 − · (−6) 9 2 + 4 : − · (−2,25) 3 3 5 2 8 3 3 6 Å 5 4 ã Å 1 1 ã Å 2 1 ã Å 4 3 ã2 10 2 + 1 : 10 − 9 11 1 − − · − 6 9 12 2 3 4 5 4 2 ß ï 7 Å 5 5 ãò™ 12 0,8 : 0,2 − 8 · + − 48 24 16
Bài 2. Thực hiện phép tính (tính hợp lý nếu có thể): 4 Å 5 3 5 ã Å 9 8 ã 5 7 7 Å −10 8 1 ã 4 1 A = − − + + − 2 B = + − + + + − 3 3 4 18 4 3 18 15 21 36 15 3 9 Å 2 1 ã Å 5 3 ã Å 7 5 ã −6 7 3 C = 6 − + − 5 + − − 3 − + 4 D = 3,7 · − 6,3 − 3,7 · 3 2 3 2 3 2 13 13 2 Å 9 125 −27 ã Å 2 3 ã Å 2 4 ã 5 4 + 25 · : : 6 − + : + + 2 15 16 64 8 5 10 −5 3 7 Å 2 1 ã 7 Å 1 5 ã 7 : − : : − 8 9 18 8 36 12
Bài 3. Các phân số nào sau đây viết được dưới dạng số thập phân hữu hạn; vô hạn tuần hoàn? 1 8 11 5 12 43 −7 12 −36 −153 63 ; ; ; ; ; ; ; ; ; ; 6 25 40 44 9 125 8 75 52 120 210
Bài 4. Viết các số thập phân sau đây dưới dạng phân số tối giản 0, (1) 0, (01) 1, (8) 0, (27) Dạng 2 Tìm x Bài 1. Tìm x, biết 1 2 Å 1 ã 3 1 Å 3 ã Å 2 1 ã 3 1 x + = − − 2 − x = − − 3 x − − = 3 5 3 7 4 5 21 3 7 2 Å 1 ã 5 11 Å 2 ã 2 1 2 Å 1 ã 4 − − x = 5 − + x = 6 x − = − − 9 3 6 12 5 3 3 5 2 Å 3 ã 5 5 1 5 2 7 x · − = 8 3x − = x − 9 + : x = 1 7 21 3 4 7 7 1 1 2 1 2 3 1 3 10 x − = 3 : 11 x + (x − 1) = 0 12 + : x = 2 2 7 3 5 7 7 14
Bài 2. Tìm các số nguyên n, m biết: 1 5n + 5n+2 = 650 2 2n + 2n+3 = 144 8n : 2n = 162011 3 1 Å 1 ã2n−1 1 1 · 34 · 3n = 37 4 5 = · 2n+4 · 2n = 25 6 9 2 8 2 Dạng 3 Toán thực tế
Bài 1. Trên bản đồ có tỉ lệ 1 : 1000000, một cánh đồng lúa có dạng hình vuông với độ dài cạnh 0,8 cm.
Diện tích thực tế theo đơn vị mét vuông của cánh đồng lúa đó là (viết kết quả dạng a.10n với 1 ≤ a < 10 ).
Bài 2. Mẹ bạn Ngân gửi vào ngân hàng 20 triệu đồng với kì hạn 1 năm, lãi suất 7, 8%/năm, kì hạn 1 năm, 3 mẹ bạn Ngân rút ra
số tiền (cả gốc và lãi) để mua một chiếc xe đạp thưởng bạn Ngân vì kết quả học tập 40
đạt mức Tốt. Hỏi số tiền để mua chiếc xe đạp là bao nhiêu?
Bài 3. Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh 17,5 m và 12,5 m. Dọc các cạnh của 3
mảnh vườn, người ta trồng các cây, cứ
m trồng một cây. Tính số cây cần trồng 2 3 Dạng 4 Hình học
Bài 1. Hình sau biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng tam giác hình vẽ
1 Tính thể tích lưỡi rìu.
2 Tính khối lượng của lưỡi rìu, biết khối lượng riêng của sắt là 7,874 kg/dm3 (phần cán: trong lưỡi rìu là không đáng kể).
Bài 2. Các kích thước của một bể bơi được cho dựa trên hình vẽ (mặt nước có dạng hình chữ nhật). Hãy
tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước. Bài 3.
Một ngôi nhà có kích thước như hình vẽ.
1 Tính thể tích của ngôi nhà.
2 Biết rằng 1 lít sơn bao phủ được 4 m2 tường. Hỏi phải cần ít
nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi
nhà? (không sơn cửa)? Biết tổng diện tích các cửa là 9 m2.
Bài 4. Một khuôn đúc bê tông có kích thước như hình vẽ. Bể dày các mặt bên của khuôn là 1,2 cm. Bề dày
mặt đáy của khuôn là 1,9 cm. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăng-ti-mét khối? 4 Bài 5.
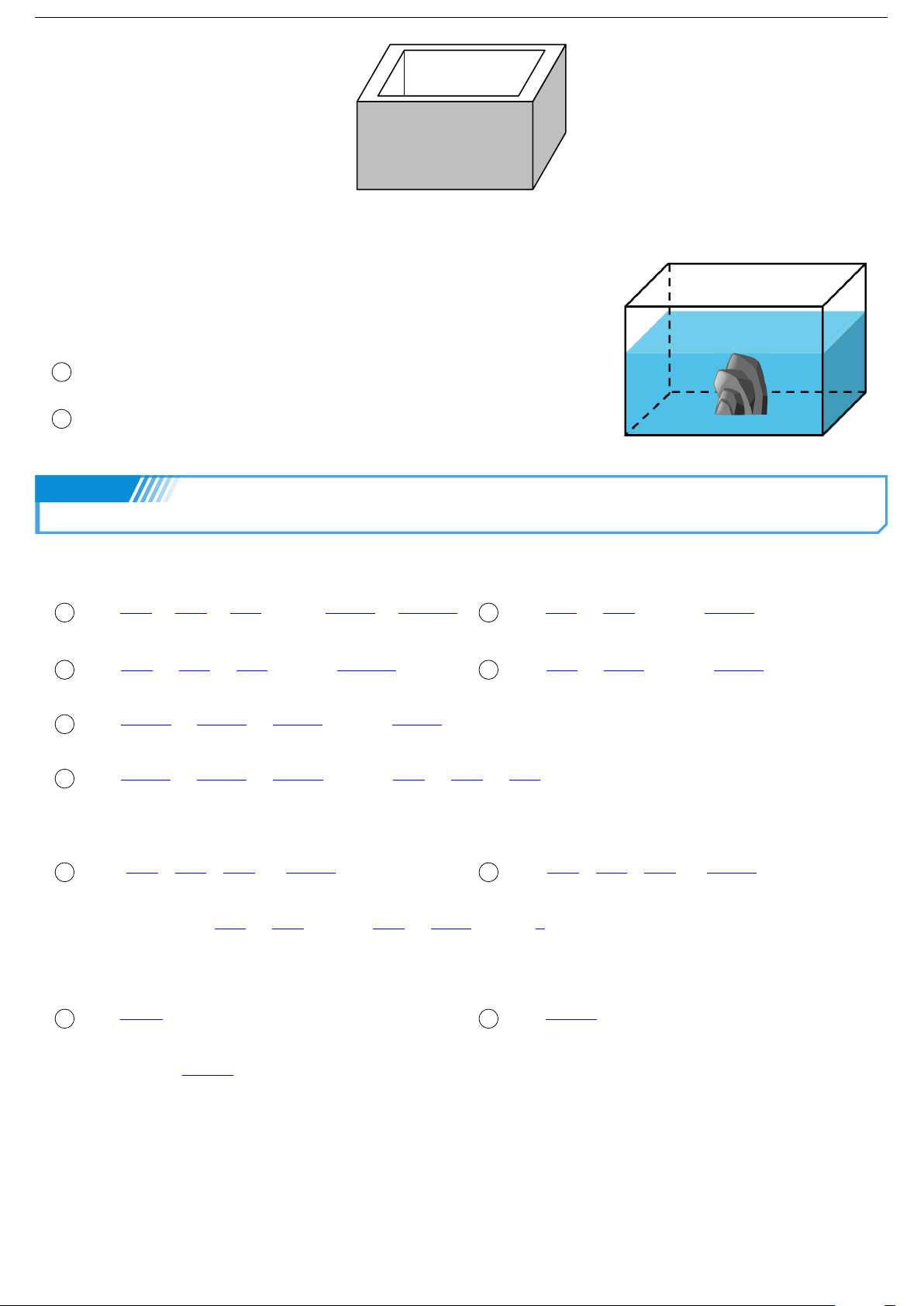
Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có
chiều dài 80 cm, chiều rộng 50 cm, chiều cao 45 cm. Mực nước ban đầu trong bể cao 35 cm.
1 Tính diện tích kính dùng để làm bể cá đó.
2 Người ta cho vào bể một hòn đá có thể tích 10 dm3. Hỏi mực
nước trong bể lúc này cao bao nhiêu xăng-ti-mét? Dạng 5 Toán nâng cao
Bài 1. Tính nhanh tổng sau: 1 1 1 1 1 1 1 1 1 A = + + + . . . + + 2 B = + + . . . + 1 · 2 2 · 3 3 · 4 98 · 99 99 · 100 5 · 6 6 · 7 24 · 25 2 2 2 2 52 52 52 3 C = + + + . . . + 4 D = + + . . . + 1 · 3 3 · 5 5 · 7 99 · 101 1 · 6 6 · 11 26 · 31 4 4 4 4 5 E = + + + . . . + 11 · 16 16 · 21 21 · 26 61 · 66 −5 5 5 5 5 5 6 Q = − − − . . . − − − 99 · 97 97 · 95 95 · 93 7 · 5 5 · 3 3 · 1 Bài 2. Tính tích 22 32 42 202 12 22 32 102 1 M = · · . . . 2 N = · · . . . 1 · 3 2 · 4 3 · 5 19 · 21 1 · 2 2 · 3 3 · 4 10 · 11 Å 1 1 1 1 ã 1 Bài 3. Tìm x, biết: + + . . . + + · x = 2 · 3 3 · 4 8 · 9 9 · 10 5
Bài 4. Tìm x ∈ Z để A, B ∈ Z và tìm giá trị đó x + 3 1 − 2x 1 A = 2 B = x − 2 x + 3 42 − x Bài 5. Cho M =
. Tìm số nguyên x để M đạt giá trị nhỏ nhất. x − 15 5
Document Outline
- violetDạng 0.0.1. Thực hiện phép tính
- violetDạng 0.0.2. Tìm x
- violetDạng 0.0.3. Toán thực tế
- violetDạng 0.0.4. Hình học
- violetDạng 0.0.5. Toán nâng cao