Đề cương HK1 Toán 10 năm 2021 – 2022 trường Lương Ngọc Quyến – Thái Nguyên

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề cương ôn tập cuối học kỳ 1 môn Toán lớp 10 năm học 2021 – 2022 trường THPT Lương Ngọc Quyến, tỉnh Thái Nguyên.

HÌNH THỨC KIỂM TRA: Kiểm tra 90 phút: Trắc nghiệm 35 câu – 7 điểm + Tự luận – 3 điểm.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
MÔN: 10
 2022
I. TRC NGHIM KHÁCH QUAN
Câu 1 :
 th ca hàm s
cbxaxy
2
là mm
)6;1(A
,
)4;1(B
,
)12;2(C
.

cba 32
bng :
A.
11
B.
C.
7
D.
7
Câu 2 :
Tng các nghim c
04234
2
xxx
bng :
A.
7
B.
C.
6
D.
3
Câu 3 :
Cho hàm s
42
3
1
2
xxy
. M nào  ?
A.
Hàm s t giá tr nh nht bng 3 khi
1x
B.
Hàm s t giá tr nh nht bng 1 khi
3x
C.
Hàm s ng bin trên khong
)3;(
và nghch bin trên khong
);3( 
D.
Hàm s ng bin trên khong
);1( 
và nghch bin trên khong
)1;(
Câu 4 :
Hàm s
)(xfy
nh trên tp có  th i. M 
là sai ?
A.
Hàm s
)(xfy
ng bin trên các khong
)1;( 
và
);3( 
B.
Hàm s
)(xfy
là hàm s l
C.
Hàm s
)(xfy
nghch bin trên khong
)3;1(
D.
Hàm s
)(xfy
nhn giá tr bng
4
khi
3x
Câu 5 :
Bit h 
594
32
yx
yx
có mt nghim
);(
00
yx

00
yx
bng :
A.
6
1
B.
6
1
C.
6
5
D.
6
5
Câu 6 :
Cho hai na khong
)3;4[],6;(  mmBA

BA
là mt khong ?
A.
103 m
B.
103 m
C.
3m
D.
10m
Câu 7 :
Tp xnh ca hàm s
2
2
xx
x
y
là :
A.
}2{\]0;( 
B.
}1{\);0[ 
C.
)1;2(
D.
}1;2{\
Câu 8 :
S nghim c
3611 xx
bng :
A.
2
B.
C.
3
D.
0
0
S GIÁO DO THÁI NGUYÊN
C QUYN
2
Câu 9 :
Cho hai tp hp
]3;0[),2;5( BA
p
BA
là :
A.
x{
}20| x
B.
x{
}05| x
C.
x{
}35| x
D.
x{
}32| x
Câu 10 :
Tìm tt c các giá tr ca tham s  h 
323
1
mmymx
myx
có nghim .
A.
3
0
m
m
B.
3m
C.
3
0
m
m
D.
0m
Câu 11 :
ng thng
baxyd :)(
m
)1;6(),2;3( NM
ng thng (d)
ct trc hoành t bng :
A.
1
B.
C.
1
D.
3
Câu 12 :
c hai
0
2
cbxax
có hai nghim âm phân bit
21
,xx

sai ?
A.
Parabol
cbxaxy
2
ct trc hoành tm phân bit
B.

0
2
abxcx
có hai nghim phân bit
21
1
,
1
xx
C.
nh ca parabol
cbxaxy
2
nm phía bên phi trc tung
D.
Biu thc
cbxax
2
có th vii dng
))((
21
xxxxa
Câu 13 :
n x có dng
0bax
có vô s nghing hp nào ?
A.
0
0
b
a
B.
0
0
b
a
C.
0
0
b
a
D.
0
0
b
a
Câu 14 :
n x có dng
0
24
cbxax
có hai nghim phân bing hp
nào ?
A.
0
0
4
0
0
2
ac
ab
acb
a
ac
B.
0
4
0
0
0
2
ab
acb
ac
bc
a
C.
0
4
0
0
0
2
ab
acb
ac
bc
a
D.
04
0
2
acb
a
Câu 15 :
 th ca hàm s n trc tung làm tri xng ?
A.
13
24
xxy
B.
2 xy
C.
12 xy
D.
xxy
3
2
Câu 16 :
 .
A.
B.
C.
D.
Câu 17 :

0


A.
3a
B.
2
3
a
C.
5
3
a
D.
5a
Câu 18 :

i, Hai vect


-
SAI:
A.
ii,
B.
C.
i,
D.
iv,
Câu 19 :
 theo
.
3
A.
B.
C.
D.
Câu 20 :
 ) và B( ) và C( 

A.
B.
C.
D.
( )
Câu 21 :
 ) và B( 
AB là:
A.
B.
C.
D.
( )
Câu 22 :

A.
B.
C.
D.
Câu 23 :
?
A.
B.
C.
D.
Câu 24 :
SAI?
A.
B.
C.
D.
Câu 25 :
Cho hìn
SAI?
A.
B.
C.
D.
Câu 26: Trong các câu sau, có bao nhiêu câu là m?
a. Hu là mt thành ph ca Vit Nam.
b. y ngang qua thành ph Hu.
c. Hãy tr li câu hi này!
d.
5 19 24
.
e.
6 81 25
.
f. Bn có ri ti nay không?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 27: M
2
" , 3"xx
khnh
A. a mi s thc bng
3
.
B. có ít nht mt s tha nó bng
3
.
C. ch có mt s thng
3
.
D. nu
x
là s thc thì
2
3x
.
Câu 28: M sai?
A. T giác
ABCD
là hình ch nht
t giác
ABCD
có ba góc vuông.
B. Tam giác
ABC
u
60A 
.
C. Tam giác
ABC
cân ti
A
AB AC
.
D. T giác
ABCD
ni ting tròn tâm
O
OA OB OC OD
.
C©u 29 :
.
A.
OA OB OC OD
B.
0OA OB OC OD
C.
0OA OB OC OD
D.
OA OB AB
C©u 30 :
 
,a AM b AN
.
4
A.
22
33
AC a b
B.
12
33
AC a b
C.
2
4
3
AC a b
D.
3AC a b
C©u 31 :

SAI ?
A.
AB AC a
B.
3AB AC a
C.
0GA GB GC
D.
GB GC a
C©u 32 :

c ABC.
A.
2GA GI
B.
0AG BG CG
C.
2GB GC GI
D.
1
3
GI AI
C©u 33 :
-1;4),
B(
A.
2;12
B.
1;12
C.
3;1
D.
1;12
C©u 34 :
-

A.
2;5
B.
11 1
;
22



C.
13; 3
D.
11; 1
C©u 35 :
y cho
2;1 , 3;0 , 1;2a b c

c ma nb


A.
2; 1mn
B.
2; 1mn
C.
2; 1mn
D.
2; 1mn
C©u 36 :

.BA BC

A.
2
4a
B.
2
4a
C.
2
2a
D.
2
a
C©u 37 :


A.
.2AM DB 
B.
.2AM DB
C.
1
.
2
AM DB 
D.
1
.
8
AM DB 
C©u 38 :


.AB AC AM

A.
2
3
2
a
B.
2
9
2
a
C.
2
9a
D.
2
27
2
a
C©u 39 :

A.
2
,9 1xx
B.
2
,2xx
C.
2
,n n n
D.
2
,3 10 3 0x x x
C©u 40 :

2 3, 2 3ab
SAI ?
A.
22
\ab
B.
.ab
C.
22
ab
D.
ab
C©u 41 :
Cho
12;3 , B= 1;4A

AB

A.
1;3
B.
1;3
C.
1;3
D.
1; 3
C©u 42 :
Cho
4;7 , N= ; 2 3;M  

MN

A.
4; 2
B.
3;7
C.
4; 2 3;7
D.
4; 2 3;7
C©u 43 :

5
A.
4;1 4 1xx
B.
4;1 4 1xx
C.
4;1 4 1xx
D.
4;1 4 1xx
C©u 44 :

2
4
1
2
x
yx
x

A.
\2
B.
1; 
C.
1;2 2; 
D.
\ 1;2
C©u 45 :

M 1; 3 , N 2;1 

A.
4
3
B.
3
4
C.
1
2
D.
2
C©u 46 :

A 2; 2 , B 1;4 

A.
2yx
B.
21yx
C.
21yx
D.
2yx
C©u 47 :
Cho Parabol (P):
2
2 6 3y x x

A.
33
;
22
I



B.
33
;
22
I




C.
33
;
22
I



D.
33
;
22
I



C©u 48 :
Cho Parabol (P):
2
2y x bx c
 Parabol (P) 

A.
2
2 4 4y x x
B.
2
2 4 4y x x
C.
2
2 4 4y x x
D.
2
2 4 4y x x
C©u 49:
Parabol (P):
2
y ax bx c

0; 1 , 1;4 , 2;13A B C

a b c

A.
0
B.
C.
3
D.
-2
C©u 50 :
Cho Parabol (P):
2
2 3 2y x x

:4d y x


A.
1; 3
B.
1; 5
C.
1; 5
D.
1;3
C©u 51 :
Cho 
2
y x bx c
-
A.
2, 0bc
B.
2, 4bc
C.
0, 2bc
D.
1, 3bc
C©u 52 :
 p
2
11
2
11
xx
xx


A.
0
B.
C.
2
D.

C©u 53 :

7 3 5x x x

A.
0
B.
C.
2
D.
3
C©u 54 :

3 2 5 1xx

A.
19
8
B.
31
8
C.
21
16
D.


C©u 55 :
Khi
2
1 2 3 0x m x m
hai
12
,xx

12
,xx

A.
1 2 1 2
25x x x x
B.
1 2 1 2
25x x x x
C.
1 2 1 2
25x x x x
D.
1 2 1 2
25x x x x
C©u 56 :

2
2 1 1xx

A.
23
B.
C.
2
D.
23
6
C©u 57 :

1
21
3
5
32
2
xy
xy


A.
19 1
;
36 6



B.
19 1
;
36 6



C.
11
;
36 6



D.
11
;
36 6



C©u 58 :

3 2 9
2 3 2 3
4 3 11
x y z
x y z
x y z
A.
11 1 8
;;
3 3 3



B.
11 1 8
;;
3 3 3




C.
11 1 8
;;
3 3 3




D.
11 1 8
;;
3 3 3



Câu 59: 
y x x
?
A.
2;6
. B.
1; 1
. C.
2; 10
. D.
0; 4
.
Câu 60: 
, 0
1
()
1
, 0
1
x
x
x
fx
x
x

0 , 2 , 2f f f
là
A.
2
(0) 0; (2) , ( 2) 2
3
f f f
. B.
21
(0) 0; (2) , ( 2)
33
f f f
.
C.
1
(0) 0; (2) 1, ( 2)
3
f f f
. D.
0 0; 2 1; 2 2f f f
.
Câu 6: Cho
4
cos
5
vi
0 180
oo

. Tính
sin
A.
1
sin
5
B.
3
sin
5
C.
1
sin
5

D.
3
sin
5

Câu 62: M ph nh ca m
2
: 2 2 0x x x

A.
2
: 2 2 0x x x
B.
2
: 2 2 0x x x
;
C.
2
: 2 2 0x x x
; D.
2
: 2 2 0x x x
Câu 63:  th hàm s m A(0; 3) và B(1; 5) khi a và b có giá tr là:
A. a = 2; b = 3 B. a = 2; b = 3 C. a = 2; b = 3 D. a = 2; b = 3
Câu 64: 
1; 2 , 0;3 , 3;4 , 1;8A B C D


A.
,,A B C
. B.
,,B C D
. C.
,,A B D
. D.
,,A C D
.
Câu 65: g
;,O i j

36a i j
và
8 4 .b i j

A.
. 0.ab
B.
ab
. C.
.0ab
. D.
.0ab
.
Câu 66: Hàm s nào trong các hàm s sau không phi là hàm s chn?
A. y = |2x + 1| + |2x 1| B. y = 3x - 2|x| + x²
C. y =
24
11xx
D. y = 1 + |x³ 3x|
Câu 67: Cho tam giác ABC có
(5;5); (6; 2); ( 2;4).A B C
Tìm t  t giác ABCD là
hình bình hành.
A.
( 3;11)D
B.
( 1; 3)D 
C.
( 3; 1)D 
D.
(3;11)D
Câu 68: Hàm s t giá tr ln nht ti
3
?
4
x
7
A.
2
4 3 1y x x
B.
2
3
1
2
y x x
C.
2
2 3 1y x x
D.
2
3
1
2
y x x
Câu 69: 
9MA MB MC
là
A. ng thng qua G song song vi AB B. ng tròn tâm G có bán kính bng 2
C. ng tròn tâm G có bán kính bng 6 D. ng tròn tâm G có bán kính bng 3
Câu 70:      m M thu n thng AC vi AC = 3AM. Bit rng
1
( ) ( , ).
3
BM mBA nBC m n
Tính tích m.n
A. 5 B. 3 C. 2 D.
2
3
Câu 71: Tnh ca hàm s y =
25
4
x
x

là:
A.
( ; ) \{4}D  
B.
[4; )D 
C.
(5; )D 
; D.
[5; )D 
Câu 72: Cho tam giác ABC vuông tng tròn ngoi ti
kính bng :
A. 2 cm B.
2
cm C. 1cm D. 5 cm
Câu 73: . m trái du ?
A.
2
(1 3) 3 1 0xx
B. 4x
2
+ x 15 = 0
C.
2
2 3 5 1 0xx
D.
2
(1 2) 3 2 0xx
Câu 74: Hãy cho bit cng tht nhau ?
A.
1
1
2
yx
và
2
1
2
yx




B.
1
1
2
yx
và
23yx
;
C.
1
2
yx
và
2
1
2
yx
; D.
21yx
và
27yx
.
Câu 75:   th hàm s y = x
2
+ 3x m ct trc hoành tm phân bit ?
A. m <
9
4
. B.
9
4
m 
; C. m >
9
4
; D. m <
9
4
;
Câu 76: c hai có hai nghim
53
và
53
là
A. x
2
- 2
5
x + 3 = 0. B. x
2
- 2
2
x + 3 = 0. C. x
2
- 2
5
x + 2 = 0. D. x
2
+ 2
2
x - 3 = 0.
Câu 77:  hàm s
2
21
2
x
y
x x m

có tnh là
A.
2m
B.
m 
C.
m 
D.
1m 
Câu 78: S nghim c
5
5
5
x
xx
x
là
A. 2 B. 0 C. 3 D. 1
Câu 79:  th hàm s y = x + 2m +1 to vi các trc t mt tam giác có din tích bng
18
.
Giá tr ca m là
A.
5
2
m
B.
7
2
m
C.
57
;
22
mm

D. m = 2; m = 2
Câu 80: ng thng y = ax + b vuông góc vng thng
: 2 5d y x
m M(-4;1)

A.
27yx
B.
1
3
2
yx
C.
1
3
2
yx
D.
1
3
2
yx
8
Câu 81: Cho tam giác ABC vuông cân ti A vi
2.AB AC a
Tính
22AB AC
A.
22 2 2AB AC a
B.
22AB AC a
C.
2 2 4 2AB AC a
D.
2 2 0AB AC
Câu 82: Cho tam giác ABC có A(10; 5), B(3; 2), C(6; -5). Tìm m 
A. Tam giác ABC vuông ti A B. Tam giác ABC vuông ti B
C. Tam giác ABC vuông ti C D. Tam giác ABC không phi là tam giác vuông
Câu 83: Cho
3;3 , 5;5 , 6;9A B C
. Tìm t D sao cho A là trng tâm tam giác BCD
A.
( 2; 5)D 
B.
( 2; 4)D 
C.
( 1; 5)D 
D.
(2;5)D
Câu 84:  dài cnh bng
.a
m M và N lm ca
ng
.AM AN
A.
2
2a
B.
2
a
C.
2
1
2
a
D.
2
1
2
a
Câu 85: Cho mt tam giác vuông v dài các c là
cm
. N
cnh góc vuông lên
2cm
và
3cm
thì din       
2
50 .cm
Nu gim c hai
c
2cm
thì diu gi
2
32 .cm
Tích hai cnh góc vuông ca
u là
A.
2
208cm
B.
2
36cm
C.
2
32cm
D.
2
34cm
Câu 86: M  sai?
A.
()A B B
B.
()A B A
C.
()A B A A
D.
()A B A B
Câu 87: u kinh c
2
11
1
x
x
x
x

là
A.
và1 0x x
. B.
và 01 xx
. C.
và 01 xx
. D.
và 01 xx
.
Câu 88: Cho tp hp
{ | 21 chia hevà t cho 3}.A x x x
Hãy chn kh
A.
A
có 8 phn t. B.
A
có 7 phn t. C.
A
có 2 phn t. D.
A
có 6 phn t.
Câu 89: Ph nh ca m 
2
0x bx c
có 2 nghim phân bin
nào?
A. 
2
0x bx c
có nghim kép.
B. B
2
0x bx c
có 2 nghim phân bit.
C. 
2
0x bx c
vô nghim.
D. 
2
0x bx c
không có 2 nghim phân bit.
Câu 90: Cho Parabol
2
y ax bx c
 th hình bên ca hàm s nào?
4
2
y
x
5
3
1
4
3
2
O
1
A.
2
2 4 4y x x
B.
2
2 12 19y x x
C.
2
4 8 3y x x
D.
2
2 12 19y x x
Câu 92:  2m = 2x + 3. Chn kt lu
A. p nghim R khi m = 0
9
B.  có tm
C. t 1 nghim
D. m duy nht
Câu 93:m C nm trên trc Ox. Khng

A.
0
A C B
x x x
B. 
AB
 khác 0
C.  bng 0 D.  khác nhau
Câu 94: Chn khnh sai trong các khnh sau
A. Hàm s
2
10 9y x x
nh I( 5; 3)
B. Hàm s
2
10 9y x x
ng bin trên khong
5; 
C. ng thng
15
22
yx
m N=(1; 2)
D. Hàm s
3
yx
là hàm s l
Câu 95: Cho hàm s
2
y x mx n
 th là parabol (P).  nh là
S(-1; -3)
A. m= -2;n=3 B. m = 2; n = 3 C. m = 2; n = 1 D. m = 2; n = 2
Câu 96: Cho
;ab

0
. Kh
A.
..a b a b
B.
.1ab
C.
..a b a b
D.
.0ab
Câu 97: Cho các m sau, chn kh
A. 
B. ng nhau thì chúng trùng nhau
C. 
D. i nhau
Câu 98: Cho
3; 2 ; 1;6uv
. Kh
A.
2uv
và
v
 B.
;uv

C.
uv
và
4; 4a
ng D.
uv
và
6; 24b 
ng
Câu 99:  
3x m 2x m 1
có nghim kép?
A.
9
3
m 
B.
3
5
m
C.
5
2
m
D.
3
5
m
Câu 100: Cho hàm s
2
a 0 0y x bx c a
 th (P). T nh ca (P) là :
A.
;
24
b
I
aa




B.
;
24
b
I
aa




C.
;
4
b
I
aa



D.
;
24
b
I
aa



.
Câu 101: Cho hai tp hp
và{1;2;3;5} {2;6; 1}MN
. Xét các kh
{2} ; \ {1;3;5} ; {1;2;3;5;6; 1}M N N M M N
Có bao nhiêu khnh nêu trên ?
A. 1 B. 2 C. 4 D. 3
Câu 102: Cho hàm s
2
23y x x
. Chn kh ?
A. Hàm s ng bin trên
1; 
B.  th hàm s không ct trc Ox
C. Hàm s nghch bin trên
;0
D. Hàm s t giá tr nh nht là - 4 ti x = -1
10
Câu 103: Cho hình bình hành ABCD. Tính tng
S AB AC AD
A.
2S AC
B.
0S
C.
2
3
S AC
D.
2
3
S AC
Câu 104: S nghim c 5|x 1| = 1 là?
A. 4 B. 1 C. 3 D. 2
Câu 105:
-m G(2; -1) là trng tâm c
A. Tam giác ABD B. Tam giác ACD C. Tam giác ABC D. Tam giác BCD
Câu 106: Cho hình bình hành ABCD tâm O, Hãy tìm khng thc sau?
A.
0OA OB OC OD
B.
OA OB OC OD
C.
0OA OB OC OD
D.
OA OB AB
Câu 107: 
22
(2 3) 2 0x m x m m
. Vi giá tr nào ca m 
có nghim
A.
9
5
m
B.
9
4
m
C.
9
3
m
D.
9
2
m
Câu 108:-2), B(0;
3), C(-5;-1).m G 
A. (5; 2) B. (0; 11) C. (10; 0) D. (0; 0)
Câu 109: M sai ?
A.
\ ;3 3; 
. B.
1;4 2;3 2;3
;
C.
3
1;3 3; 3;3
2



; D.
\ 2; ; 2 
;
Câu 110: Trong mt phng cho
1;1 ; 1;3 ;C 1; 1AB
. Kh

A. u nhn B. Tam giác ABC có ba cnh bng nhau
C. Tam giác ABC vuông cân ti A D. Tam giác ABC cân ti B
Câu 111: Cho tp hp
{ | 1 0}.X x x
Hãy chn kh
A.
( 1;0)X 
. B.
(0;1)X
. C.
(1; )X 
. D.
(0; )X 
.
Câu 112: 
2y x x
. Chn kt lu
A.  th hàm s m ( 1; 2) B.  th hàm s không ct trc Ox
C. Hàm s nghch bin trên
;0
D. Hàm s ng bin trên toàn trc s
Câu 113: m M tha mãn
2 MA CA AC AB CB
A. n BC
B. M thung kính BC
C. m B
D. M thung tròn tâm C bán kính BC
Câu 114:  h 
3x 2y 9
mx 2y 2


vô nghim ?
A. vi mi m B. m = 0 C. m = - 3 D. m = - 3; m = 1
Câu 115: Cho hàm s
2y
. Chn kt lu
A.  th hàm s không ct trc Ox B.  th hàm s m ( 1;
2
)
C. Hàm s ng bin trên toàn trc s D. Hàm s nghch bin trên
;0
Câu 116:  2| = x + 1. Chn kt lun sai
11
A. nh có nghi B. m nguyên
C. nh vi mi x D. m duy nht
Câu 117: Có my giá tr ca tham s
m

22
( ) 3 2m m x m m
vô nghim ?
A. 1. B. 2. C. 0. D. 3.
Câu 118: Trong các m sau, m 
A. Nu a
b thì
22
ba
B. Nu
22
ba
thì a
b
C. Nu a chia ht cho 9 thì a chia ht cho 3. D. Nu a chia ht cho 3 thì a chia ht cho 9.
Câu 119ng thm A(2;3), B(-1;-3) song song vng th
A. y = -2x+2 B. y= - x+1 C. y= x-1 D. y= 2x+2
Câu 120: S các tp hp con có hai phn t ca tp hp A =
fedcba ;;;;;
là
A.15 B.16 C. 22 D. 25
Câu 121: Hàm s  chn?
A.
3
21y x x
B.
2
1
x
y
x
C.
3
2y x x
D.
2yx
Câu 122: Cho hai tp hp hp A \ B là
A. {2; 4; 5} B. {1; 7} C. (2; 5) D. [1; 7]
Câu 123: Cho hàm s:
x
x
x
y
3
)3(
2
. Tnh ca hàm s này là
A.
2;1
B.
3;1
C.
3;2
D.
3;2
Câu 124: Trong mt phng Oxy, cho
(1;3), ( 2;2)ab
. T c
bau 23
là
A.
(7;5)u
B.
( 7; 5)u
C.
(7; 5)u 
D.
( 7;5)u 
Câu 125: Tìm m ph nh ca m
"012,"
2
nnNn
.
A.
2
,2 1 0n N n n
B.
2
,2 1 0n N n n
C.
2
,2 1 0n N n n
D.
2
,2 1 0n N n n
Câu 126: T nh ca parabol (P):
342
2
xxy
là
A. ( 1 ; -1) B. (1; 1) C. ( -1; 1) D. ( -1; -1)
Câu 127: Hàm s nào trong các hàm s  th ?
A.
2
3 2 1y x x
B.
2
21y x x
C.
2
3 2 1y x x
D.
2
21y x x
x
y
O
1
1
Câu 128: S nghim c 3|x| + 2 = 0 là
A. 0 B. 2 C. 3 D. 4
Câu 129: nh a, b, c bit parabol
2
y ax bx c
m A(0;1); B(1;-1); C(-1;1).
A.
1; 1a c b
B.
1; 1a b c
C.
1abc
D.
1; 1a b c
Câu 130: Cho hai tp hp A=
7;4
và B=
 ;32;
p hp
BA
là
A.
2;4
B.
7;3
C.
7;32;4
D.
4; 2 3;7
12
Câu 131: Cho lu ABCDEF có tâm O. S 
0
i
OE
có
m cunh lc giác bng :
A. 4 B. 6 C. 7 D. 8
Câu132: Tp nghim c
0532
24
xx
là
A.
2
5
S
B.
2
5
S
C.
5
2
S
D.
5
1;
2
S




Câu 133:  ?
A.
0
sin sin(180 )

B.
0
cos cos(180 )

C.
0
tan tan(180 )


D.
0
cot cot(180 )


Câu 134: Nghim ca h 
2 2 1
2 3 4
3 3 5
x y z
x y z
x y z
là
A.
7
16
;
7
3
;2
B.
7
16
;
7
3
;2
C.
7
16
;
7
3
;2
D.
7
16
;
7
3
;2
Câu 135: T m ca parabol
2
2y x x
vng thng
1yx
là
A.(1;3) B. (1;0), (1;2) C. (1;2) D. (0;-1)
Câu 136:  2(m 1)x + m² 3m = 0. Tìm giá tr c 
nghim phân bit x
1
, x
2
tha mãn x
1
² + x
2
² = 8.
A. m = 0, m = 1 B. m = 1, m = 2 C. m = 2 D. m = 1, m = 2
Câu 137: Vi giá tr nào c
234)1(
2
mxxm
nghim i mi x ?
A. m = 1 B. m = -1 C. m=2 D. m=-2
Câu 138: Cho bm phân bing th
A.
CBADBDAC
B.
DBACCDAB
C.
CBADCDAB
D.
CBADCDBA
Câu 139: u cnh 2a. Gm c
AB BH
bng A.
3a
B.
2
2
a
C.
2
3
a
D.
2a
Câu 140: Cho hàm s:
22
2
xxy
. Tìm câu tr l
Ang bin trên
1;
và nghch bin trên
 ;1
B. ng bin trên
 ;1
và nghch bin trên
1;
Cng bin trên
1;
và nghch bin trên
;1
Dng bin trên
;1
và nghch bin trên
1;
.
Câu 141: Cho tam giác ABC có A(- 4, 0), B(4, 6), C(- ng
BC.AC
bng
A. -7 B. 7 C. -23 D. 23
Câu 142: Cho tam giác ABC có A(1; 1), B(3; 2), C(5; 5). T ng tròn ngoi tip tam
giác ABC là
A.
47 13
( ; )
10 10
B.
47 13
( ; )
10 10

C.
47 13
( ; )
10 10
D.
47 13
( ; )
10 10
Câu 145: Trong mt phm M(2; 3), N(0;-4), P( -1; 6) lm các
cnh BC, CA, AB ca tam giác ABC. T nh A ca tam giác là
A.(-3 ;-1) B. (1; 5) C. (-2; -7) D. (1 ; -10)
13
Câu 146: Trong mt phng Oxy, c m A, B, C
thng hàng.
A. m = -2 B. m =
5
2
C. m = 1 D. m = 4
Câu147: Cho hàm s y = f(x)=
2
12
12
x khi x
x khi x


m A(0;-1), B(-2;3), C(1;2), D(3;8), E(-m thu th f(x) ?
A. 2 B. 3 C. 4 D. 5
Câu 148-2; 7), C = (-3; 1].
A. [-2; 1] B.(-4; 7) C. (4; -3] U [5; 7) D. [3; -2) U [1; 5]
Câu 149: Cho tp hp A = [m;m + 2] và B = [-
AB

khi và ch khi
A.
1m 
B. m
3
C. 0
m3
D. -3
0m
Câu 150: Tnh ca hàm s y =
2
x1
(x 3) x 1


là
A. (   D. (
Câu 151: Cho hai hàm s f(x) = x³ 3x và g(x) = x³ + 1. Kh
u là hàm s l. B. f(x) là hàm s l, g(x) là hàm s chn.
C. f(x) là hàm s chn, g(x) là hàm s l. D. Ch có f(x) là hàm s l.
Câu 152: Vix+b cng thm A(3; 1), B(2; 6).
A. y = x + 4 B. y = 2x + 7 C. y = 2x + 2 D. y = 2x 5
Câu 153: S nghim ca h 
22
xy 2x 2y 8
x 3xy y 1
là
A. 0 B. 1 C. 2 D. 4
Câu 154: Trong mt phng Oxy, c𝐴𝐵𝐶 i 𝐻 là trc tâm ca
tam giác. T cm 𝐻 là
A.
54
( ; )
43
H
B.
51
( ; )
24 6
H
C.
51
( ; )
24 6
H
D.
51
( ; )
24 6
H
Câu 155: Tp nghim c
1
3
1
3
2
x
x
x
x
là
A.
2
3
S
B.
2
3
S
C.
2S
D. Vô nghim
Câu 156: Tri xng ca parabol y = x² + 3x + 3 là
A.
3
2
x 
B.
3
2
x
C. x = 3 D. x = 3
II. T LUN
Câu 1: Gi
a)
1262
2
xxx
b)
2
x 2x 6 2x 1
Câu 2: Gi
32
2
2 3 11 8 10 8
3 4 1 1
x x x x
x x x
Câu 3: Trong mt phng Oxy , cho tam giác ABC có A(1;2), B(-2;6), C(9;8).
a) Tính chu vi và din tích tam giác ABC.
b) ng tròn ni tip tam giác ABC.
Câu 4 
2
43y x x
.
14
a) Kho sát s bi
b) Tìm giá tr c
2
43x x m
có 4 nghim phân
bit.
Câu 5: Trong h trc t Oxy, cho tam giác ABC có A = (-1; 2), B = (3; 4),
C = (-4; 8)
a) Tính côsin ca góc gi
,AB AC
b) Tìm t ng tròn ngoi tip tam giác ABC
Câu 6: Tìm tt c các giá tr ca tham s
m
 
22
4 4 5 4 2 1x x x x m
có bn
nghim phân bit.
Câu 7: V  th và lp bng bin thiên ca hàm s
32
2
xxy
.
Câu 8: Gii và bin lu m:
1)14()3(
2
xmxm
.
Câu 9: Tìm các giá tr ca tham s m sao cho tm c
042)3(
2
xxm
bng 4.
Câu 10:  ), B( ), C( )
 .
b, 
Câu 11: 
 .
Câu 12: Kho sát s bin thiên và v  th hàm s
2
4 3.y x x
Câu 13: Gia)
3 5 4xx
. b)
2
4 3 2 x x x
Câu 14: Cho tam giác ABC có A(1; 2), B(-2; 6), C(9; 8). Tính din tích tam giác ABC.
Câu 15: Cho tam giác ABC. Gi D, I lnh bi
30BD BC
và
0.IA ID
Gm tha mãn
( ).AM xAC x
a. Biu th
BI
theo
BA
và
;BC
 m B, I, M thng hàng.
Câu 16: 
2
43y x x
.

o:
2
4 3 0x x k
.
Câu 17: Cho
2 0, 2 0, 0.MB MC NA NC PA PB

, theo vecto , .PM PN AB AC
Câu 18: 
3; 1 , B 2;3 .A 
a) 
, , OA OB AB

b) 
Câu 19: Kho sát s bin thiên và v  th hàm s
2
4 3.y x x
Câu 20: Gi
14 2 3xx
Câu 21: Trong mt phm A(2;3) ; B(4; 1) ; C(7; 4).
a) Tính din tích tam giác ABC.
b) Tính
.AB BC
c) Tìm t m M thuc trm C.
Câu 22: Cho tam giác ABC. Gi D, I lt là các nh bi
40BD BC
và
0.IA ID
Gm tha mãn
( ).MA xAC x
15
a. Biu th
BI
theo
BA
và
;BC
 m B, I, M thng hàng.
Câu 23.  th ca hàm s bc hai
2
4. y ax x c
a) Tìm hàm s
p bng bi
2
4 y ax x c
vc trên.
Câu 24.
2 2 2
) 3 3 2 3. ) 2 8 12 2 . a x x x b x x x x
Câu 25

2
6 8 2m m x m x m
theo tham s m.
b) Mt quán ph có bán ba mt hàng là ph bò, ph gà và quy. Ngày th nht quán ph c 23
bát ph bò, 25 bát ph y thu v  c 28 bát ph bò,
30 bát ph y thu v  c 25 bát ph bò, 22 bát ph gà
a mi mt hàng trên.
Câu 26. i h t m
A 6; 2 ,B 4;4 ,C 2;6 .
m A, B, C to thành m
c tâm ca tam giác ABC.
Câu 27. 
    
1
2
AM AB
      
20KM KN

minh r
1
3
AK AB AC
.
Câu 28. 
1
33
1
28
x x y
y
xy
y
------------------------------------Ht--------------------------------
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀ O TẠO THÁI NGUYÊN
TRƯỜNG THPT Ư ƠNG NGỌC QUYẾN
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA HỌC KỲ I, MÔN TO N, : 10
NĂM HỌC 2021 – 2022
I. TRẮC NGHIỆM KHÁCH QUAN
Câu 1 : Đồ thị của hàm số y ax2  bx c là một parabol đi qua ba điểm ( A  ) 6 ; 1 , ) 4 ; 1 ( B , C( ) 12 ; 2 . Khi đó a b 2  c 3 bằng : A. 11 B. 11 C.  7 D. 7
Câu 2 : Tổng các nghiệm của phương trình 2
x  4x  3 2  x  4  0 bằng : A. 7 B. 1 C. 6 D. 3 Câu 3 : 1 Cho hàm số 2 y
x  2x  4 . Mệnh đề nào sau đây là đúng ? 3
A. Hàm số đạt giá trị nhỏ nhất bằng 3 khi x  1
B. Hàm số đạt giá trị nhỏ nhất bằng 1 khi x  3
C. Hàm số đồng biến trên khoảng ( ) 3 ;
và nghịch biến trên khoảng ; 3 ( ) 
D. Hàm số đồng biến trên khoảng ; 1 ( )
 và nghịch biến trên khoảng ( ) 1 ;
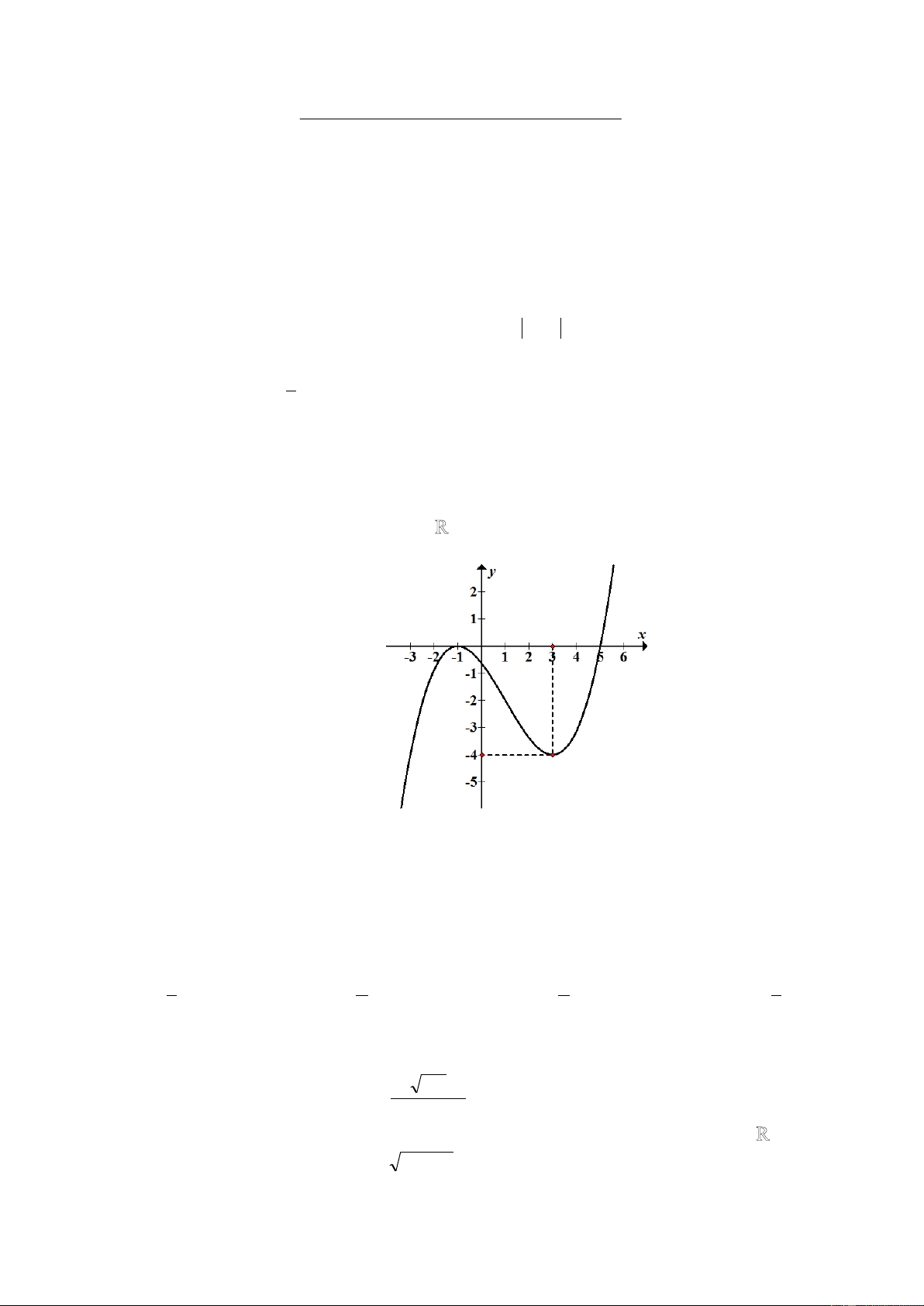
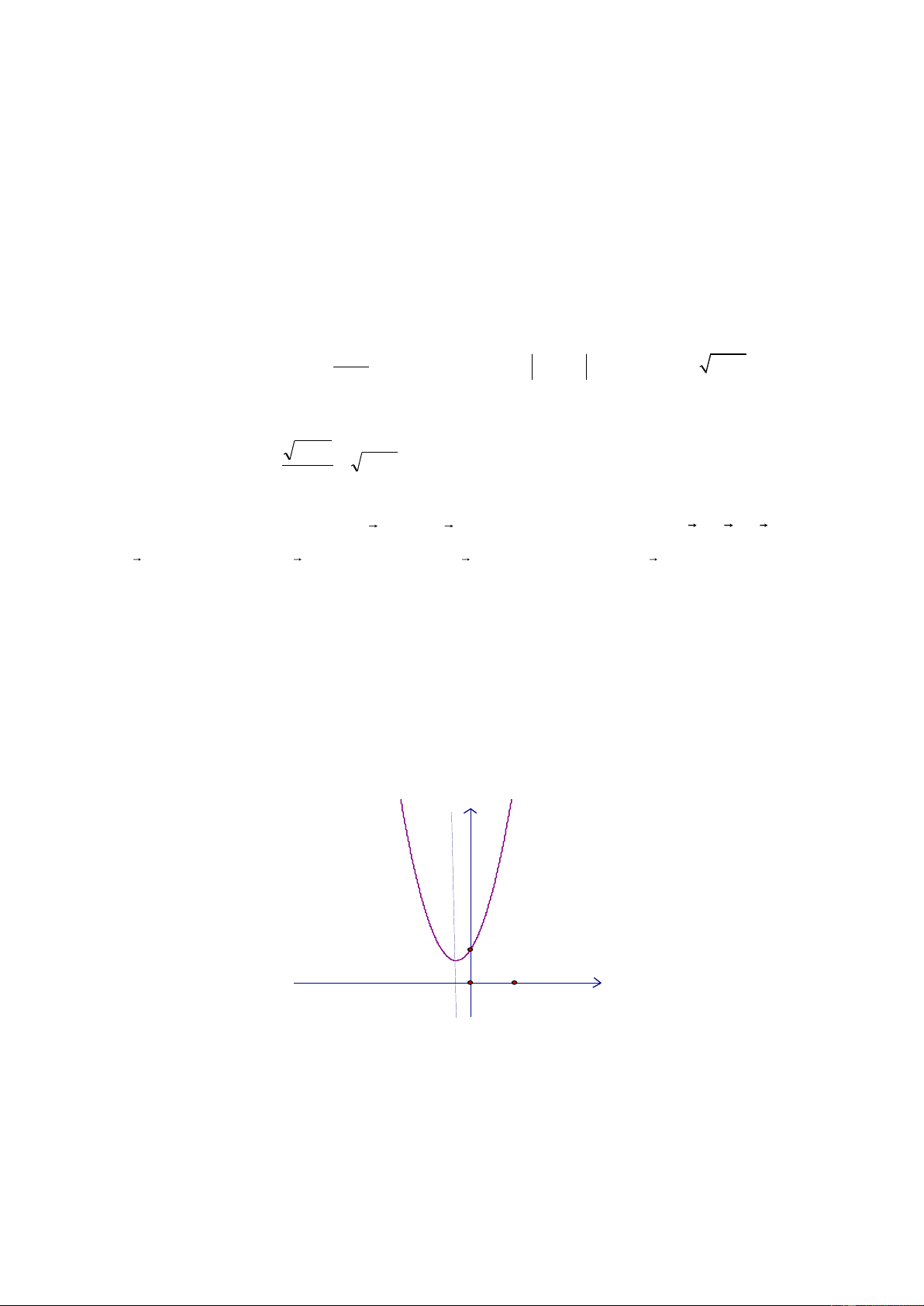
Câu 4 : Hàm số y f (x) xác định trên tập
có đồ thị như trong hình dưới. Mệnh đề nào sau đây là sai ? 0
A. Hàm số y f (x) đồng biến trên các khoảng ( ;   ) 1 và ; 3 ( ) 
B. Hàm số y f (x) là hàm số lẻ
C. Hàm số y f (x) nghịch biến trên khoảng ( ) 3 ; 1
D. Hàm số y f (x) nhận giá trị bằng  4 khi x  3 Câu 5 : 2x  3y
Biết hệ phương trình 
có một nghiệm (x ; y ) . Khi đó x y bằng :
4x  9y  5 0 0 0 0 1 1 5 5 A. B. C. D.  6 6 6 6
Câu 6 : Cho hai nửa khoảng A  ( ], 6 ; B  [m  ; 4 m  )
3 . Tìm m để AB là một khoảng ?
A. 3  m  10
B. 3  m 10 C. m  3 D. m 10 Câu 7 : x
Tập xác định của hàm số y  là : 2 x x  2 A. ( ] 0 ; \ { } 2 B. ; 0 [ )  \ } 1 { C. ( ) 1 ; 2 D. \ { } 1 ; 2
Câu 8 : Số nghiệm của phương trình 11 6x x  3 bằng : A. 2 B. 1 C. 3 D. 0 1
Câu 9 : Cho hai tập hợp A  ( ), 2 ; 5 B  ] 3 ; 0 [
. Khi đó tập AB là : A. x {  | 0  x  } 2 B. x {  | 5   x  } 0 C. x {  | 5   x  } 3 D. x {  | 2  x  } 3 Câu 10 : x my 1
Tìm tất cả các giá trị của tham số m để hệ phương trình  có nghiệm .
mx  3my  2m  3 m  0 m  0 A. m C. D. m  0  B. 3  m  3 m  3
Câu 11 : Đường thẳng (d) : y ax b đi qua hai điểm M ( ), 2 ; 3 N ; 6 (  )
1 . Khi đó đường thẳng (d)
cắt trục hoành tại điểm có hoành độ bằng : A. 1 B. 3 C. 1 D.  3
Câu 12 : Phương trình bậc hai 2
ax bx c  0 có hai nghiệm âm phân biệt x , x . Khi đó mệnh đề 1 2 nào sau đây sai ?
A. Parabol y ax2  bx c cắt trục hoành tại hai điểm phân biệt 2 1 1
B. Phương trình cx bx a  0 có hai nghiệm phân biệt , x x 1 2
C. Đỉnh của parabol y ax2  bx c nằm ở phía bên phải trục tung
D. Biểu thức ax2  bx c có thể viết dưới dạng a(x x )(x x ) 1 2
Câu 13 : Phương trình ẩn x có dạng ax b  0 có vô số nghiệm trong trường hợp nào ? a  0 a  0 a  0 a  0 A.   C.    B. D. b  0 b  0 b  0 b  0
Câu 14 : Phương trình ẩn x có dạng 4 2
ax bx c  0 có hai nghiệm phân biệt trong trường hợp nào ? ac  0 a  0 a  0    a  0 bc  0 bc  0    a  0 A.  2 b ac  0 ac  0  4ac C.      2 b  4ac  0 ab  0 B.  2 b  4ac  2 b  4ac D.    ac  0 ab  0 ab  0
Câu 15 : Đồ thị của hàm số nào sau đây nhận trục tung làm trục đối xứng ? A. 4 y x  3 2 x 1
B. y x  2
C. y  2x 1
D. y   x3 2  x
Câu 16 : Cho hình bình hành ABCD. Tính tổng . A. B. C. D.
Câu 17 : Cho tam giác ABC vuông tại A biết AB = a và góc B bằng 300. Độ dài vectơ bằng: 2a 5a A. 3a B. C. D. 5a 3 3
Câu 18 : Cho các mệnh đề sau đây:
i, Hai vectơ bằng nhau thì cùng phương
ii, Hai vectơ cùng hướng thì bằng nhau
iii, Hai vectơ bằng nhau thì cùng hướng
iv, Vectơ-không cùng hướng với mọi vectơ
Chọn mệnh đề SAI: A. ii, B. iii, C. i, D. iv,
Câu 19 : Cho tam giác ABCcó trọng tâm G. Gọi D là điểm đối xứng với A qua C. Tính theo . 2 A. B. D. C.
Câu 20 : Trong mặt phẳng tọa độ Oxy cho điểm A( ) và B( ) và C( ). Tìm tọa độ điểm
D để tứ giác ABCD là hình bình hành. A. ( ) B. ( ) C. ( ) D. ( )
Câu 21 : Trong mặt phẳng tọa độ Oxy cho điểm A( ) và B(
). Tọa độ trung điểm M của AB là: A. ( ) B. ( ) C. ( ) D. ( )
Câu 22 : Nếu G là trọng tâm của tam giác ABC thì: A. B. C. D.
Câu 23 : Cho hình bình hành ABCD. Đẳng thức nào sau đây ĐÚNG? A. B. C. D.
Câu 24 : Trong các đẳng thức sau đây, đẳng thức nào SAI? A. B. C. D.
Câu 25 : Cho hình bình hành ABCD và điểm M bất kì, hai đường chéo cắt nhau tại O. Đẳng thức nào sau đây SAI? A. B. C. D.
Câu 26: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a. Huế là một thành phố của Việt Nam.
b. Sông Hương chảy ngang qua thành phố Huế.
c. Hãy trả lời câu hỏi này! d. 5 19  24 . e. 6  81  25 .
f. Bạn có rỗi tối nay không? A. 1. B. 2 . C. 3 . D. 4 . Câu 27: Mệnh đề 2 " x
  , x  3" khẳng định
A. bình phương của mỗi số thực bằng 3 .
B. có ít nhất một số thực mà bình phương của nó bằng 3 .
C. chỉ có một số thực có bình phương bằng 3 .
D. nếu x là số thực thì 2 x  3.
Câu 28: Mệnh đề nào sau đây sai?
A. Tứ giác ABCD là hình chữ nhật  tứ giác ABCD có ba góc vuông.
B. Tam giác ABC là tam giác đều  A  60 .
C. Tam giác ABC cân tại A AB AC .
D. Tứ giác ABCD nội tiếp đường tròn tâm O OA OB OC OD .
C©u 29 : Cho hình bình hành ABCD tâm O. H y tìm đẳng thức đúng trong các đẳng thức sau.
A. OAOB OC OD
B. OAOB OC OD  0
C. OAOB OC OD  0
D. OAOB AB
C©u 30 : Cho hình bình hành ABCD. Gọi M, N l n lượt là trung điểm của BC và CD. Đặt
a AM , b AN H y tìm đẳng thức đúng trong các đẳng thức sau. 3 2 2 1 2 2 A. AC a b
B. AC a b C. AC a  4b
D. AC a  3b 3 3 3 3 3
C©u 31 : Cho tam giác ABC đều cạnh a. Gọi G là trọng tâm tam giác ABC. Đẳng thức nào dưới đây SAI ? A.
AB AC a B.
AB AC a 3
C. GA GB GC  0
D. GB GC a
C©u 32 : Cho tam giác ABC và I là trung điểm của cạnh BC. Điểm G có tính chất nào sau đây thì
G là trọng tâm của tam giác ABC. 1
A. GA  2GI
B. AG BG CG  0
C. GB GC  2GI D. GIAI 3
C©u 33 : Trong mặt phẳng tọa độ Oxy cho tam giác ABC với trọng tâm G. Biết rằng A(-1;4),
B( ), G(0 ). Hỏi tọa độ đỉnh C là cặp số nào A. 2;12 B. 1;12 C. 3;  1 D. 1;12
C©u 34 : Trong mặt phẳng tọa độ Oxy cho hai điểm M( - ), N(3 ). Nếu P là điểm đối xứng với
điểm M qua điểm N thì tọa độ điểm P là cặp số nào 11 1  A. 2;5 B. ;   13; 3 11; 1  C.   D.   2 2 
C©u 35 : Trong mặt phẳng tọa độ Oxy cho a  2 
;1 , b  3;0, c  1; 2 . Cho biết c ma nb . Khi đó:
A. m  2; n  1  B. m  2  ; n  1 
C. m  2; n 1 D. m  2  ; n 1
C©u 36 : Cho tam giác ABC vuông cân tại A, AB= a. Ta tính được giá trị của B . A BC là: A. 2 4  a B. 2 4a C. 2 2a D. 2 a
C©u 37 : Cho hình vuông ABCD cạnh bằng , tâm O. Gọi M là trung điểm của AB. Chọn khẳng
định đúng trong các khẳng định sau: 1 1
A. AM.DB   2
B. AM.DB  2
C. AM .DB  
D. AM .DB   2 8
C©u 38 : Cho tam giác đều ABC cạnh bằng 3a. Gọi H là trung điểm của BC, M là điểm thuộc
đoạn BC và độ dài đoạn BM=a . Khi đó giá trị của  AB AC.AM là: 2 3a 2 9a 2 27a A. B. C. 2 9a D. 2 2 2
C©u 39 : Chọn mệnh đề đúng trong các mệnh đề sau: 2 x   ,9x 1 B. 2 x   , x  2 A. C. 2 n
  ,n n D. 2 x
  ,3x 10x 3  0
C©u 40 : Cho số a  2  3,b  2  3 . Khẳng định nào sau đây là SAI ? A. 2 2 a b  \ B. . a b C. 2 2 a b
D. a b
C©u 41 : Cho A   12  ;3, B= 1
 ;4 . Khi đó AB là: A. 1;  3 B. 1;3 C. 1;3 D. 1; 3
C©u 42 : Cho M  4;7, N=  ;
 2 3; . Khi đó M N là: A. 4; 2 B. 3; 7 C.  4  ; 2   3;7 D.  4  ; 2   3;7
C©u 43 : Chọn mệnh đề đúng trong các mệnh đề sau: 4 A. x  4  ;  1  4   x  1 B. x  4  ;  1  4   x  1 C. x  4  ;  1  4   x  1 D. x  4  ;  1  4   x  1 C©u 44 : 2 x  4 Cho hàm số y
x 1 . Tập xác định của hàm số này là: x  2 A. \   2 B. 1; 
C. 1; 2  2;  D. \ 1;  2
C©u 45 : Đường thẳng đi qua hai điểm M 1; 3  , N 2  ; 
1 có hệ số góc là bao nhi u 4 3 1 A. B. C. D. 2 3 4 2
C©u 46 : Đường thẳng đi qua hai điểm A 2; 2  , B 1
 ;4 song song với đường thẳng nào dưới đây
A. y x  2 B. y  2  x 1
C. y  2x 1
D. y  x  2
C©u 47 : Cho Parabol (P): 2
y  2x  6x  3 . Tọa độ đỉnh của (P) là:  3 3   3 3   3 3   3 3  A. I ;    I  ;    I  ;   I ;    B. C. D. 2 2   2 2   2 2   2 2 
C©u 48 : Cho Parabol (P): 2
y  2x bx c , biết rằng Parabol (P) có trục đối xứng là đường thẳng
x= và cắt trục tung tại điểm M(0 ). Phương trình của Parabol (P) là: A. 2
y  2x  4x  4 B. 2
y  2x  4x  4 C. 2
y  2x  4x  4 D. 2
y  2x  4x  4 C©u 49: Parabol (P): 2
y ax bx c đi qua ba điểm A0;  
1 , B 1; 4, C 2;13 khi đó giá trị của
a b c là: A. 0 B. 2 C. 3 D. -2
C©u 50 : Cho Parabol (P): 2
y  2x  3x  2 và đường thẳng d  : y  x  4 . Tọa độ giao điểm của (P) và (d) là: A. 1; 3 B. 1; 5 C. 1; 5 D. 1;3
C©u 51 : Cho hàm số 2
y x bx c . Biết hàm số đạt giá trị nhỏ nhất bằng - khi x= . Tìm b và c A. b  2  , c  0
B. b  2, c  4 
C. b  0, c  2 
D. b 1, c  3  C©u 52 : 1 1
Số nghiệm của phương trình 2 2x   x  là: x 1 x 1 A. 0 B. 1 C. 2 D. Vô số
C©u 53 : Số nghiệm nguy n của phương trình 7  x x x 3  5 là: 3 0 B. 1 C. 2 D. A.
C©u 54 : Cho phương trình 3x  2  5 x 1 . Khi đó tổng các nghiệm của phương trình là: 19 31 21 Một giá trị A. B. C. D. 8 8 16 khác
C©u 55 : Khi phương trình 2
x  m  
1 x  2m  3  0 có hai nghiệm x , x . Tìm hệ thức giữa x , x độc 1 2 1 2 lập đối với m.
A. 2x x x x  5
x x  2 x x  5
x x  2 x x  5
2x x x x  5 1 2  1 2  1 2  1 2  1 2  1 2  B. C. D. 1 2  1 2 
C©u 56 : Cho phương trình 2
2x 1  x 1. Khi đó tổng các nghiệm của phương trình là: A. 2 3 B. -2 C. 2 D. 2 3 5  1 2x y  1 
Tìm nghiệm của hệ phương trình: 3 C©u 57 :  5 3
x y  2  2  19 1   19 1   1 1   1 1  A. ;    ;   ;    ;    B. C. D. 36 6   36 6   36 6   36 6   3
x  2y z  9 C©u 58 :
Tìm nghiệm của hệ phương trình: 2x  3y  2z  3  
4x  3y z  1  1 11 1 8   11 1 8   11 1 8   11 1 8  A. ; ;    B.  ; ;    C.  ;  ;   D.  ; ;    3 3 3   3 3 3   3 3 3   3 3 3 
Câu 59: Điểm nào sau đây thuộc đồ thị hàm số y x –  3 x  ? A. 2;6 . B. 1;   1 . C.  2  ; 10   . D. 0;  4 .  x , x  0  x 1
Câu 60: Cho hàm số: f (x)  
. Giá trị f 0, f 2, f  2   là 1  , x  0  x 1 2 2 1
A. f (0)  0; f (2)  , f ( 2)   2.
B. f (0)  0; f (2)  , f ( 2  )   . 3 3 3 1
C. f (0)  0; f (2)  1, f ( 2  )   .
D. f 0  0; f 2  1; f  2    2 . 3 4 Câu 6: Cho cos  với 0o   180o  . Tính sin 5 1 3 1 3 A. sin   B. sin   C. sin   D. sin   5 5 5 5
Câu 62: Mệnh đề phủ định của mệnh đề “ 2
x  : x  2x  2  0 ” là A. 2 x
  : x  2x  2  0 B. 2 x
  : x  2x  2  0 ; C. 2 x
  : x  2x  2  0 ; D. 2
x  : x  2x  2  0
Câu 63: Đồ thị hàm số y = ax + b đi qua điểm A(0; 3) và B(–1; 5) khi a và b có giá trị là: A. a = –2; b = 3 B. a = 2; b = 3 C. a = –2; b = –3 D. a = 2; b = –3
Câu 64: Trong mặt phẳng Oxy, cho điểm A1; 2
 , B0;3,C  3  ;4, D 1
 ;8 . Ba điểm nào trong
điểm đ cho thẳng hàng A. , A , B C . B. , B C, D . C. , A , B D . D. , A C, D .
Câu 65: Trong mặt phẳng O;i, j cho vectơ a  3i  6 j và b  8i  4 j. Kết luận nào sau đây sai A. . a b  0.
B. a b .
C. a . b  0 . D. . a b  0 .
Câu 66: Hàm số nào trong các hàm số sau không phải là hàm số chẵn?
A. y = |2x + 1| + |2x – 1| B. y = 3x - 2|x| + x² C. y = 2 4
x 1  x 1
D. y = 1 + |x³ – 3x|
Câu 67: Cho tam giác ABC có ( A 5;5); B(6; 2  ); C( 2
 ;4). Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành. A. D(3;11) B. ( D 1  ; 3  ) C. ( D 3  ; 1  ) D. D(3;11) 3
Câu 68: Hàm số nào sau đây đạt giá trị lớn nhất tại x  ? 4 6 3 3 A. 2 y  4
x 3x 1 B. 2 y  x x 1 C. 2 y  2
x 3x 1 D. 2 y x x 1 2 2
Câu 69: Cho tam giác ABC có trọng tâm G, tập hợp các điểm M sao cho
MA MB MC  9 là
A. Đường thẳng qua G song song với AB
B. Đường tròn tâm G có bán kính bằng 2
C. Đường tròn tâm G có bán kính bằng 6
D. Đường tròn tâm G có bán kính bằng 3
Câu 70: Cho tam giác ABC và điểm M thuộc đoạn thẳng AC với AC = 3AM. Biết rằng 1 BM
(mBA nBC) ( , m n  ). Tính tích m.n 3 2 A. 5 B. 3 C. 2 D. 3 2  x  5
Câu 71: Tập xác định của hàm số y = là: x  4 A. D  ( ;
 ) \{4} B. D  [4;)
C. D  (5; ) ;
D. D  [5; )
Câu 72: Cho tam giác ABC vuông tại A có BC = 0cm. Đường tròn ngoại tiếp tam giác đó có bán kính bằng : A. 2 cm B. 2 cm C. 1cm D. 5 cm
Câu 73: . Phương trình nào sau đây có nghiệm trái dấu ? A. 2
(1 3)x  3x 1  0
B. – 4x2 + x – 15 = 0 C. 2
2 3x  5x 1  0 D. 2
(1 2)x  3x  2  0
Câu 74: Hãy cho biết cặp đường thẳng nào sau đây cắt nhau ?  2  A. 1 y  
x 1 và y    x 1 B. 1 y
x 1 và y  2x  3 ; 2   2   2 2 C. 1 y x và y x 1 ;
D. y  2x 1 và y  2x  7 . 2 2
Câu 75: Tìm m để đồ thị hàm số y = x2 + 3x – m cắt trục hoành tại hai điểm phân biệt ? 9 9 9 9 A. m < . B. m   ; C. m >  ; D. m <  ; 4 4 4 4
Câu 76: Phương trình bậc hai có hai nghiệm 5  3 và 5  3 là
A. x2 - 2 5 x + 3 = 0. B. x2 - 2 2 x + 3 = 0. C. x2 - 2 5 x + 2 = 0. D. x2 + 2 2 x - 3 = 0. x 2 1
Câu 77: Tìm m để hàm số y  có tập xác định là 2
x  2x m A. m  2 B. m   C. m   D. m  1   x
Câu 78: Số nghiệm của phương trình 5
x x  5 là x  5 A. 2 B. 0 C. 3 D. 1
Câu 79: Đồ thị hàm số y = –x + 2m +1 tạo với các trục tọa độ một tam giác có diện tích bằng 18 . Giá trị của m là 5 7  5 7  A. m B. m C. m  ; m D. m = –2; m = 2 2 2 2 2
Câu 80: Đường thẳng y = ax + b vuông góc với đường thẳng d : y  2
x  5 và đi qua điểm M(-4;1) có phương trình 1 1 1 A. y  2  x  7 B. y x  3
C. y   x  3 D. y x  3 2 2 2 7
Câu 81: Cho tam giác ABC vuông cân tại A với AB AC  2 .
a Tính 2 AB  2 AC
A. 2 AB  2 AC  2a 2
B. 2 AB  2 AC a
C. 2 AB  2 AC  4a 2
D. 2 AB  2 AC  0
Câu 82: Cho tam giác ABC có A(10; 5), B(3; 2), C(6; -5). Tìm mệnh đề đúng
A. Tam giác ABC vuông tại A
B. Tam giác ABC vuông tại B
C. Tam giác ABC vuông tại C
D. Tam giác ABC không phải là tam giác vuông
Câu 83: Cho A3;3, B 5;5, C 6;9 . Tìm tọa độ D sao cho A là trọng tâm tam giác BCD A. D( 2  ; 5  ) B. D( 2  ; 4)  C. ( D 1  ; 5  ) D. D(2;5)
Câu 84: Cho hình vuông ABCD có độ dài cạnh bằng .
a Hai điểm M và N l n lượt là trung điểm của
BC và CD. Tính tích vô hướng AM.AN 1 1 A. 2 2a B. 2 a C. 2 a D. 2  a 2 2
Câu 85: Cho một tam giác vuông với độ dài các cạnh được tính theo đơn vị là cm . Nếu tăng các
cạnh góc vuông lên 2cm và 3cm thì diện tích tam giác ban đ u tăng l n 2
50cm . Nếu giảm cả hai
cạnh góc vuông đi 2cm thì diện tích tam giác ban đ u giảm đi 2
32cm . Tích hai cạnh góc vuông của tam giác ban đ u là A. 2 208cm B. 2 36cm C. 2 32cm D. 2 34cm
Câu 86: Mệnh đề nào sau đây là mệnh đề sai?
A. ( A B)  B
B. ( A B)  A C. ( A  )
B A A D. (A  )
B A B 1 x 1
Câu 87: Điều kiện xác định của phương trình x   là 2 1 x x A. x  và 1 x  0 . B. x   v 1 à x  0 . C. x   v 1 à x  0 . D. x   v 1 à x  0 .
Câu 88: Cho tập hợp A  {x  | x  21
và x chia het cho 3}. Hãy chọn khẳng định đúng.
A. A có 8 ph n tử.
B. A có 7 ph n tử.
C. A có 2 ph n tử.
D. A có 6 ph n tử.
Câu 89: Phủ định của mệnh đề “Phương trình 2
x bx c  0 có 2 nghiệm phân biệt” là mệnh đề nào? A. Phương trình 2
x bx c  0 có nghiệm kép.
B. Bất phương trình 2
x bx c  0 có 2 nghiệm phân biệt. C. Phương trình 2
x bx c  0 vô nghiệm. D. Phương trình 2
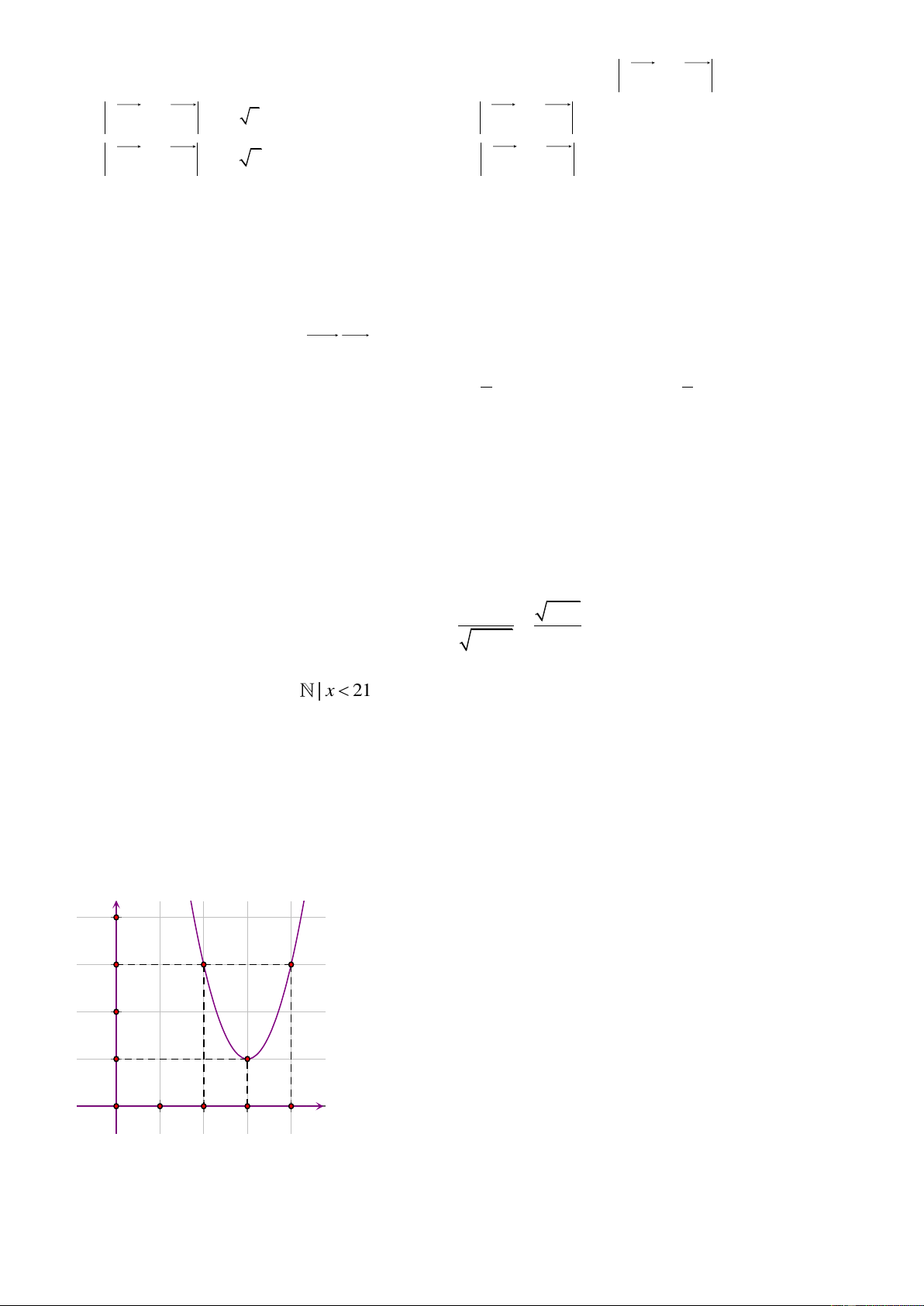
x bx c  0 không có 2 nghiệm phân biệt. Câu 90 5 : Cho Parabol 2
y ax bx c có đồ thị hình bên của hàm số nào? 4 y 3 2 1 x O 1 2 3 4 A. 2
y  2x  4x  4 B. 2
y  2x 12x 19 C. 2
y  4x 8x  3 D. 2
y  2x 12x 19
Câu 92: Cho phương trình (m² + )x – 2m = 2x + 3. Chọn kết luận đúng
A. Phương trình có tập nghiệm R khi m = 0 8
B. Phương trình chỉ có tối đa nghiệm
C. Phương trình luôn có ít nhất 1 nghiệm
D. Phương trình luôn có nghiệm duy nhất
Câu 93: Trong mặt phẳng tọa độ Oxy cho hình bình hành OABC, điểm C nằm trên trục Ox. Khẳng
định nào sau đây là đúng
A. x x x  0
B. Véc tơ AB có tung độ khác 0 A C B
C. Điểm C có hoành độ bằng 0
D. Điểm A và B có tung độ khác nhau
Câu 94: Chọn khẳng định sai trong các khẳng định sau A. Hàm số 2
y x 10x  9 có đỉnh I( 5; 3) B. Hàm số 2
y x  10x  9 đồng biến trên khoảng  5;   1 5 y   x C. Đường thẳng 2 2 đi qua điểm N=(1; 2) D. Hàm số 3
y x là hàm số lẻ Câu 95: Cho hàm số 2
y x mx n có đồ thị là parabol (P). Tìm m, n để parabol có đỉnh là S(-1; -3) A. m= -2;n=3 B. m = –2; n = –3 C. m = 2; n = 1 D. m = 2; n = –2
Câu 96: Cho a; b là véc tơ cùng hướng và đều khác véc tơ Cho 0 . Khẳng định nào sau đây là đúng A. .
a b   a . b . a b  1  C. .
a b a . b D. . a b  0 B.
Câu 97: Cho các mệnh đề sau, chọn khẳng định đúng
A. Hai véc tơ bằng nhau thì không cùng phương
B. Hai véc tơ bằng nhau thì chúng trùng nhau
C. Hai véc tơ đối nhau thì cùng phương
D. Hai véc tơ cùng phương thì đối nhau
Câu 98: Cho u  3; 2
 ; v  1;6 . Khẳng định nào sau đây là đúng
A. 2u v và v cùng phương
B. u; v là véc tơ cùng phương
C. u v và a  4; 4 ngược hướng
D. u v và b  6; 2  4 cùng hướng
Câu 99: Tìm m để phương trình 3x  m  2x  m  có nghiệm kép? 1 9 3 5 3 m   m m m A. 3 C. D. B. 5 2 5
Câu 100: Cho hàm số 2
y  ax bx c  0a  0 có đồ thị (P). Tọa độ đỉnh của (P) là :  b     b    b     b    A. I ;   B. I ;   C. I ;   D. I ;   .  2a 4a   2a 4a   a 4a   2a 4a
Câu 101: Cho hai tập hợp M  {1;2;3;5} và N  {2;6; 1
 }. Xét các khẳng định sau đây:
M N  {2} ; N \ M  {1;3;5} ; M N  {1; 2;3;5;6; 1  }
Có bao nhiêu khẳng định đúng trong ba khẳng định nêu trên ? A. 1 B. 2 C. 4 D. 3
Câu 102: Cho hàm số 2
y x  2x  3 . Chọn khẳng định đúng ?
A. Hàm số đồng biến trên 1;
B. Đồ thị hàm số không cắt trục Ox
C. Hàm số nghịch biến trên  ;0  
D. Hàm số đạt giá trị nhỏ nhất là - 4 tại x = -1 9
Câu 103: Cho hình bình hành ABCD. Tính tổng S AB AC AD 2 2
A. S  2AC B. S  0 C. S AC D. S AC 3 3
Câu 104: Số nghiệm của phương trình x² – 5|x – 1| = 1 là? A. 4 B. 1 C. 3 D. 2
Câu 105: Trong mặt phẳng tọa độ Oxy cho tam giác ABC với trọng tâm G. Biết rằng A(3 ), B(
),C( ), D( - ). Hỏi tọa độ điểm G(2; -1) là trọng tâm của tam giác nào sau đây A. Tam giác ABD B. Tam giác ACD C. Tam giác ABC D. Tam giác BCD
Câu 106: Cho hình bình hành ABCD tâm O, Hãy tìm khẳng định đúng trong các đẳng thức sau?
A. OA OB OC OD  0
B. OA OB OC OD
C. OA OB OC OD  0
D. OA OB AB
Câu 107: Cho phương trình 2 2
x  (2m  3)x m  2m  0 . Với giá trị nào của m thì phương trình có nghiệm 9 9 9 9 m m m m A. 5 C. D. B. 4 3 2
Câu 108: Trong mặt phẳng tọa độ Oxy cho tam giác ABC với trọng tâm G. Biết rằng A( -2), B(0;
3), C(-5;-1). Hỏi tọa độ điểm G là cặp số nào A. (5; 2) B. (0; 11) C. (10; 0) D. (0; 0)
Câu 109: Mệnh đề nào sau đây sai ? A. \  ;  3   3  ;. B.  1
 ;42;3  2;3;  3  C. 1;  3  3  ;     3  ;3; D. \  2  ;   ;  2  ;  2 
Câu 110: Trong mặt phẳng tọa độ Oxy, cho A   1  ; 
1 ; B  1;3;C  1;  
1 . Khẳng định nào sau đây là đúng
A. Tam giác ABC có ba góc đều nhọn
B. Tam giác ABC có ba cạnh bằng nhau
C. Tam giác ABC vuông cân tại A
D. Tam giác ABC cân tại B
Câu 111: Cho tập hợp X  {x
| x 1  0}. Hãy chọn khẳng định đúng. A. X  ( 1  ;0) .
B. X  (0;1) .
C. X  (1;  ) .
D. X  (0;  ) .
Câu 112: Cho phương trình y x  2x . Chọn kết luận đúng
A. Đồ thị hàm số đi qua điểm ( 1; 2)
B. Đồ thị hàm số không cắt trục Ox
C. Hàm số nghịch biến trên  ;0  
D. Hàm số đồng biến trên toàn trục số
Câu 113: Cho tam giác ABC, điểm M thỏa mãn 2 MA CA AC AB CB
A. M là trung điểm đoạn BC
B. M thuộc đường tròn tâm C đường kính BC
C. Điểm M trùng điểm B
D. M thuộc đường tròn tâm C bán kính BC 3x   2y  9
Câu 114: Tìm m để hệ phương trình  vô nghiệm ? mx  2y  2 A. với mọi m B. m = 0 C. m = - 3 D. m = - 3; m = 1
Câu 115: Cho hàm số y  2 . Chọn kết luận đúng
A. Đồ thị hàm số không cắt trục Ox
B. Đồ thị hàm số đi qua điểm ( 1; 2 )
C. Hàm số đồng biến trên toàn trục số
D. Hàm số nghịch biến trên  ;0  
Câu 116: Cho phương trình |x – 2| = x + 1. Chọn kết luận sai 10
A. Phương trình có nghiệm dương
B. Phương trình có nghiệm nguyên
C. Phương trình xác định với mọi x
D. Phương trình có nghiệm duy nhất
Câu 117: Có mấy giá trị của tham số m thì phương trình 2 2 (m  )
m x m  3m  2 vô nghiệm ? A. 1. B. 2. C. 0. D. 3.
Câu 118: Trong các mệnh đề sau, mệnh đề nào đúng A. Nếu a  b thì 2 2 a b B. Nếu 2 2
a b thì a  b
C. Nếu a chia hết cho 9 thì a chia hết cho 3. D. Nếu a chia hết cho 3 thì a chia hết cho 9.
Câu 119: Đường thẳng đi qua hai điểm A(2;3), B(-1;-3) song song với đường thẳng nào dưới đây
A. y = -2x+2 B. y= - x+1 C. y= x-1 D. y= 2x+2
Câu 120: Số các tập hợp con có hai ph n tử của tập hợp A = a;b;c;d;e; f  là
A.15 B.16 C. 22 D. 25
Câu 121: Hàm số nào sau đây là hàm số chẵn? 2  x A. 3
y x  2x 1 B. y C. 3
y x  2x
D. y x  2 x 1
Câu 122: Cho hai tập hợp A = { } và B = ( ). Khi đó tập hợp A \ B là
A. {2; 4; 5} B. {1; 7} C. (2; 5) D. [1; 7] x  2
Câu 123: Cho hàm số: y
 3 x . Tập xác định của hàm số này là (x  ) 3 A.  2 ; 1 B.   3 ; 1 C.   3 ; 2 D.  3 ; 2
Câu 124: Trong mặt phẳng Oxy, cho a  (1;3), b  ( 2
 ;2) . Tọa độ của véctơ u a 3  b 2 là
A. u  (7;5) B. u  (7; 5) C. u  (7; 5
 ) D. u  ( 7  ;5)
Câu 125: Tìm mệnh đề phủ định của mệnh đề "nN,2 2
n n 1 " 0 . A. 2 n
  N,2n n 1 0 B. 2 n
  N,2n n 1 0 C. 2 n
  N,2n n 1 0 D. 2 n
  N,2n n 1 0
Câu 126: Tọa độ đỉnh của parabol (P): y  2 2
x  4x  3 là
A. ( 1 ; -1) B. (1; 1) C. ( -1; 1) D. ( -1; -1)
Câu 127: Hàm số nào trong các hàm số sau có đồ thị như hình vẽ? 2    2    2    2    A. y 3x 2x 1 B. y x
2x 1 C. y 3x 2x 1 D. y x 2x 1 y 1 x O 1
Câu 128: Số nghiệm của phương trình x² – 3|x| + 2 = 0 là A. 0 B. 2 C. 3 D. 4
Câu 129: Xác định a, b, c biết parabol 2
y ax bx c đi qua ba điể m A(0;1); B(1;-1); C(-1;1).
A. a c 1;b  1 
B. a  1
 ;b c 1 C. a b c 1 D.     a b 1;c 1
Câu 130: Cho hai tập hợp A=  7 ; 4  và B=    ; 2  ; 3
. Khi đó tập hợp AB là A.  ; 4   2 B.  7 ; 3  C.  ; 4   2   7 ; 3  D.  4  ;2 3;  7 11
Câu 131: Cho lục giác đều ABCDEF có tâm O. Số các véc tơ khác 0 cùng phương với OE có
điểm đ u và điểm cuối là đỉnh lục giác bằng :
A. 4 B. 6 C. 7 D. 8
Câu132: Tập nghiệm của phương trình 2 4 x  3 2 x  5  0 là  5   5   2   5  A. S    B. S  
C. S  
D. S   1  ;   2   2   5   2 
Câu 133: Điều khẳng định nào sau đây đúng ? A. 0 sin  sin(180 ) B. 0 cos  cos(180 ) C. 0 tan  tan(180 ) D. 0 cot  cot(180 )
2x y  2z 1 
Câu 134: Nghiệm của hệ phương trình x  2y  3z  4 là
3x 3y z  5    3 16   3 16   3 16   3 16  A.  ; 2 ;  B.  ; 2  ;  C.   ; 2 ;  D.  ; 2 ;   7 7   7 7   7 7   7 7 
Câu 135: Tọa độ giao điểm của parabol 2
y x x  2 với đường thẳng y x 1 là A.(1;3) B. (1;0), (1;2) C. (1;2) D. (0;-1)
Câu 136: Cho phương trình x² – 2(m – 1)x + m² – 3m = 0. Tìm giá trị của m để phương trình có
nghiệm phân biệt x1, x2 thỏa mãn x1² + x2² = 8.
A. m = 0, m = –1 B. m = –1, m = 2 C. m = 2 D. m = 1, m = 2
Câu 137: Với giá trị nào của m thì phương trình: 2 m (x  )
1  4x  3m  2 nghiệm đúng với mọi x ?
A. m = 1 B. m = -1 C. m=2 D. m=-2
Câu 138: Cho bốn điểm phân biệt A,B,C,D . Đẳng thức nào sau đây là đúng
A. AC BD AD CB
B. AB CD AC DB
C. AB CD AD CB D. BACD AD CB
Câu 139: Cho tam giác ABC đều cạnh 2a. Gọi H là trung điểm của BC. Khi đó giá trị AB BH 2 3 bằng A. a 3 B. a C. a D. 2 2 a 2
Câu 140: Cho hàm số: 2
y x  2x  2 . Tìm câu trả lời đúng.
A. Đồng biến trên  ;   
1 và nghịch biến trên   ; 1 
B. Đồng biến trên   ; 1
 và nghịch biến trên  ;    1
C. Đồng biến trên  1 ;
 và nghịch biến trên   ; 1 
D. Đồng biến trên   ; 1
 và nghịch biến trên  1 ;  .
Câu 141: Cho tam giác ABC có A(- 4, 0), B(4, 6), C(- , ). Khi đó tích vô hướng BC.AC bằng A. -7 B. 7 C. -23 D. 23
Câu 142: Cho tam giác ABC có A(1; –1), B(3; 2), C(5; –5). Tọa độ tâm đường tròn ngoại tiếp tam giác ABC là 47 13 47 13 47 13 47 13 ( ;  ) ( ;  ) ( ; ) ( ; ) A. 10 10 B. 10 10 C. 10 10 D. 10 10
Câu 145: Trong mặt phẳng Oxy, cho ba điểm M(2; 3), N(0;-4), P( -1; 6) l n lượt là trung điểm các
cạnh BC, CA, AB của tam giác ABC. Tọa độ đỉnh A của tam giác là
A.(-3 ;-1) B. (1; 5) C. (-2; -7) D. (1 ; -10) 12
Câu 146: Trong mặt phẳng Oxy, cho A(0 ), B(3 ), C(m + + m). Tìm m để 3 điểm A, B, C thẳng hàng. 5 A. m = -2 B. m = C. m = –1 D. m = 4 2 2
x 1khi x  2
Câu147: Cho hàm số y = f(x)= 
x 1khi x  2
Trong các điểm A(0;-1), B(-2;3), C(1;2), D(3;8), E(-3 ), có bao nhi u điểm thuộc đồ thị f(x) ? A. 2 B. 3 C. 4 D. 5
Câu 148: Tìm A ∩ B ∩ C, với A = (− ], B = [-2; 7), C = (-3; 1]. A. [-2; 1] B.(-4; 7) C. (–4; -3] U [5; 7) D. [–3; -2) U [1; 5]  
Câu 149: Cho tập hợp A = [m;m + 2] và B = [- 0]. Khi đó A B  khi và chỉ khi A. m  1  B. m  3  C. 0  m  3 D. -3  m  0 2
Câu 150: Tập xác định của hàm số y = x 1  là (x  3) x 1 A. (–∞ ) B. [ +∞) C. ( +∞) D. (–∞ ]
Câu 151: Cho hai hàm số f(x) = x³ – 3x và g(x) = –x³ + 1. Khẳng định nào sau đây là đúng
A. f(x) và g(x) đều là hàm số lẻ.
B. f(x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x) là hàm số chẵn, g(x) là hàm số lẻ. D. Chỉ có f(x) là hàm số lẻ.
Câu 152: Viết phương trình y=ax+b của đường thẳng đi qua hai điểm A(3; 1), B(–2; 6).
A. y = –x + 4 B. y = –2x + 7 C. y = –2x + 2 D. y = 2x – 5 xy  2x  2y  8
Câu 153: Số nghiệm của hệ phương trình  là 2 2 x  3xy  y  1  A. 0 B. 1 C. 2 D. 4
Câu 154: Trong mặt phẳng Oxy, cho ∆𝐴𝐵𝐶 có A( 3), B( − ), C(−3 − ). Gọi 𝐻 là trực tâm của
tam giác. Tọa độ của điểm 𝐻 là 5 4 5 1 5 1 5 1 A. H ( ;  ) B. H ( ;  ) C. H ( ; ) D. H ( ; ) 4 3 24 6 24 6 24 6 3 3x
Câu 155: Tập nghiệm của phương trình 2x   là x  1 x  1 3  3
A. S    B. S    C. S    2 D. Vô nghiệm 2  2
Câu 156: Trục đối xứng của parabol y = –x² + 3x + 3 là 3 3 x   x  A. 2 B. 2 C. x = –3 D. x = 3 II. TỰ LUẬN
Câu 1: Giải phương trình sau: a) 2
x  2x  6  2x 1 b) 2 x  2x  6  2x  1 3 2
2x  3x 11x  8 10x  8
Câu 2: Giải phương trình sau:  2 3x  4x 1 x 1
Câu 3: Trong mặt phẳng Oxy , cho tam giác ABC có A(1;2), B(-2;6), C(9;8).
a) Tính chu vi và diện tích tam giác ABC.
b) Tính bán kính đường tròn nội tiếp tam giác ABC. Câu 4 Cho hàm số 2
y  x  4x  3 . 13
a) Khảo sát sự biến thi n và vẽ đồ thị (P) của hàm số đ cho.
b) Tìm giá trị của tham số m số nghiệm của phương trình : 2
x  4x  3  m có 4 nghiệm phân biệt.
Câu 5: Trong hệ trục tọa độ Oxy, cho tam giác ABC có A = (-1; 2), B = (3; 4), C = (-4; 8)
a) Tính côsin của góc giữa hai véc tơ  AB, AC
b) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC
Câu 6: Tìm tất cả các giá trị của tham số m để phương trình 2 2
4 x  4x  5  x  4x  2m 1 có bốn nghiệm phân biệt.
Câu 7: Vẽ đồ thị và lập bảng biến thiên của hàm số 2
y x  2x  3 .
Câu 8: Giải và biện luận phương trình sau theo tham số m: ( 2 m  ) 3 x  ( m 4x  ) 1 1.
Câu 9: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình (m  ) 3 2
x  2x  4  0 bằng 4.
Câu 10: Trong mặt phẳng tọa độ Oxy cho điểm A( ), B( ), C( )
a, Tìm tọa độ điểm M sao cho .
b, Tìm tọa độ điểm D tr n trục tung sao cho A, B, D thẳng hàng.
Câu 11: Cho tam giác ABC có BC = a, AC = b, AB = c và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: . 2
Câu 12: Khảo sát sự biến thiên và vẽ đồ thị hàm số y x  4x  3.
Câu 13: Giải phương trình sau: a) x  3  5  4x . b) 2
x  4x  3  x  2
Câu 14: Cho tam giác ABC có A(1; 2), B(-2; 6), C(9; 8). Tính diện tích tam giác ABC.
Câu 15: Cho tam giác ABC. Gọi D, I l n lượt là các điểm xác định bởi
3BD BC  0 và IA ID  0. Gọi M là điểm thỏa mãn AM x AC (x  ).
a. Biểu thị BI theo BA và BC;
b. Tìm x để ba điểm B, I, M thẳng hàng. Câu 16: Cho hàm số 2
y  x  4x  3 .
a) Khảo sát sự biến thi n và vẽ đồ thị (P) của hàm số đ cho.
b) Dựa vào đồ thị, h y biện luận theo tham số k số nghiệm của phương trình : 2
x  4x 3 k  0.
Câu 17: Cho tam giác ABC, lấy các điểm M, N, P sao cho:
MB  2MC  0, NA  2NC  0, PA PB  0. H y biểu thị các vectơ PM , PN theo vecto AB, AC.
Câu 18: Trong mặt phẳng tọa độ Oxy cho hai điểm A3;   1 , B 2  ;3.
a) Tìm tọa độ các vectơ ,
OA OB, AB và tính chu vi tam giác OAB.
b) Tìm tọa độ điểm M tr n trục Ox, sao cho tam giác MAB vuông tại A. 2
Câu 19: Khảo sát sự biến thiên và vẽ đồ thị hàm số y  x  4x  3.
Câu 20: Giải phương trình sau: 14  2x x  3
Câu 21: Trong mặt phẳng Oxy, cho các điểm A(2;3) ; B(4; 1) ; C(7; 4).
a) Tính diện tích tam giác ABC. b) Tính A . B BC
c) Tìm tọa độ điểm M thuộc trục Oy sao cho M cách đều điểm B và điểm C.
Câu 22: Cho tam giác ABC. Gọi D, I l n lượt là các điểm xác định bởi
4BD BC  0 và IA ID  0. Gọi M là điểm thỏa mãn MA x AC (x  ). 14
a. Biểu thị BI theo BA và BC;
b. Tìm x để ba điểm B, I, M thẳng hàng.
Câu 23. Cho (P) là đồ thị của hàm số bậc hai 2
y ax  4x  . c
a) Tìm hàm số biết đồ thị (P) có trục đối xứng là đường thẳng x= và cắt trục hoành tại điểm M(3 0).
b) Vẽ đồ thị và lập bảng biến thi n của hàm số 2
y ax  4x c với a, c tìm được ở trên.
Câu 24. Giải các phương trình: 2 2 2
a) 3x  3  2x x  3. b) x x  2x  8  12  2 . x Câu 25
a) Giải và biện luận phương trình: mm   2 6 x m  8
x m  2 theo tham số m.
b) Một quán phở có bán ba mặt hàng là phở bò, phở gà và quẩy. Ngày thứ nhất quán phở bán được 23
bát phở bò, 25 bát phở gà và 0 đĩa quẩy thu về . .000đ, ngày thứ hai bán được 28 bát phở bò,
30 bát phở gà và đĩa quẩy thu về . .000đ, ngày thứ ba bán được 25 bát phở bò, 22 bát phở gà
và 0 đĩa quẩy thu được . 00.000đ. Tính giá của mỗi mặt hàng trên.
Câu 26. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A 6; 2  ,B4;4,C  2  ;6 .
a) Chứng minh rằng: ba điểm A, B, C tạo thành một tam giác cân tại B.
b) Tìm tọa độ trực tâm của tam giác ABC.
Câu 27. Cho tam giác ABC, gọi I là trung điểm của cạnh BC. Kéo dài cạnh CA một đoạn AN=AC,
kéo dài cạnh BA một đoạn 1 AM
AB . Gọi K là điểm thỏa m n hệ thức 2KM KN  0 . Chứng 2 1
minh rằng AK    AB AC . 3  1
x   x y  3  3  y
Câu 28. Giải hệ phương trình:   1
2x y  8   y
------------------------------------Hết-------------------------------- 15