












Preview text:
ĐỀ CƯƠNG HỌC KÌ I MÔN TOÁN LỚP 11- 2025-2026 I.
Trắc nghiệm nhiều lựa chọn
Câu 1: Nhận biết:
– Nhận biết được các khái niệm cơ bản về góc lượng giác: khái niệm góc lượng giác; số đo của góc
lượng giác; hệ thức Chasles cho các góc lượng giác; đường tròn lượng giác.
– Nhận biết được khái niệm giá trị lượng giác của một góc lượng giác.
Câu 2 – Mô tả được các phép biến đổi lượng giác cơ bản: công thức cộng; công thức góc nhân đôi;
công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích.
Câu 3 Nhận biết:
– Nhận biết được các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
– Nhận biết được các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
– Nhận biết được định nghĩa các hàm lượng giác y = sin x, y = cos x, y = tan x, y = cot x thông
qua đường tròn lượng giác.
Câu 4 Nhận biết:
– Nhận biết được công thức nghiệm của phương trình lượng giác cơ bản: sin x = m; cos x = m; tan x =
m; cot x = m bằng cách vận dụng đồ thị hàm số lượng giác tương ứng.
Câu 5 Nhận biết:
– Nhận biết được dãy số hữu hạn, dãy số vô hạn.
– Nhận biết được tính chất tăng, giảm, bị chặn của dãy số trong những trường hợp đơn giản.
Câu 6 Nhận biết:
– Nhận biết được một dãy số là cấp số cộng.
Câu 7 Nhận biết:
– Nhận biết được một dãy số là cấp số nhân. Câu 8 Thông hiểu:
– Hiểu được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn.
Câu 9, Thông hiểu:
– Mô tả được ba cách xác định mặt phẳng (qua ba điểm không thẳng hàng; qua một đường thẳng và
một điểm không thuộc đường thẳng đó; qua hai đường thẳng cắt nhau).
Câu 10: Thông hiểu:
– Giải thích được điều kiện để đường thẳng song song với mặt phẳng.
– Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng.
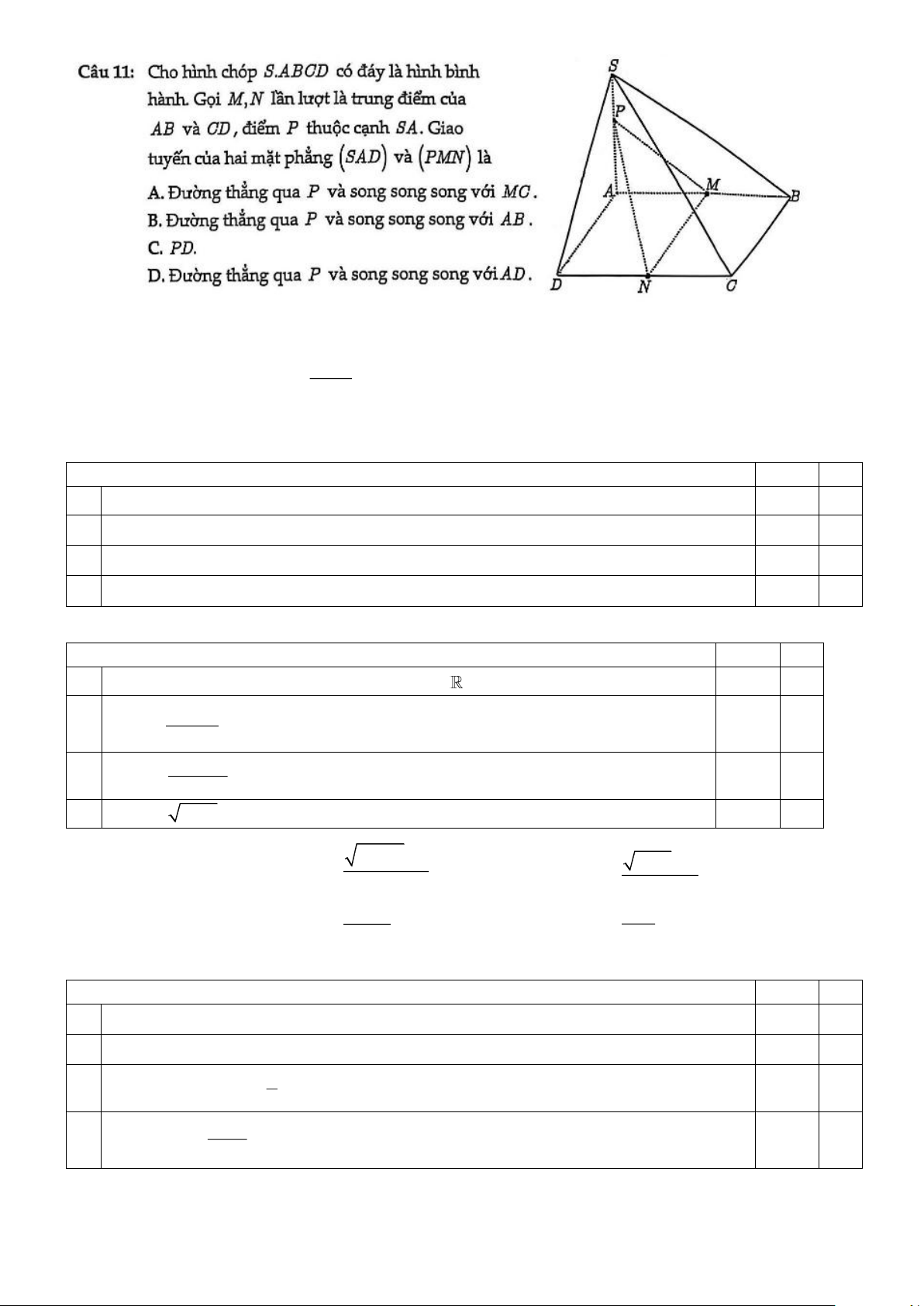
Câu 11 Nhận biết:
– Nhận biết được hai mặt phẳng song song trong không gian.
Câu 12: Nhận biết:
– Nhận biết được khái niệm và các tính chất cơ bản về phép chiếu song song. II. Đúng sai
Câu 13: a) Thông hiểu:
– Giải thích được tính chất cơ bản về hai đường thẳng song song trong không gian. b) Thông hiểu:
– Giải thích được điều kiện để đường thẳng song song với mặt phẳng.
– Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng.
c) d) Vận dụng:
– Xác định được ảnh của một điểm, một đoạn thẳng, một tam giác, một đường tròn qua một phép chiếu song song.
– Vẽ được hình biểu diễn của một số hình khối đơn giản.
Câu 14: Nhận biết:
– Nhận dạng được hàm số liên tục tại một điểm, hoặc trên một khoảng, hoặc trên một đoạn.
– Nhận dạng được tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục.
– Nhận biết được tính liên tục của một số hàm sơ cấp cơ bản (như hàm đa thức, hàm phân thức, hàm
căn thức, hàm lượng giác) trên tập xác định của chúng. III. Trả lời ngắn
Câu 15: 16:Thông hiểu:
– Giải thích được điều kiện để hai mặt phẳng song song.
– Giải thích được tính chất cơ bản về hai mặt phẳng song song.
– Giải thích được định lí Thalès trong không gian.
– Giải thích được tính chất cơ bản của lăng trụ và hình hộp.
Câu 17 Thông hiểu: 1
– Giải thích được một số giới hạn cơ bản như: lim = 0 (k *); lim n
q = 0 (| q | 1); →+ k n n n→+
lim c = c với c là hằng số. n→+
Câu 18: Vận dụng:
– Tính được một số giới hạn hàm số bằng cách vận dụng các phép toán trên giới hạn hàm số. IV. Tự luận Câu 19: a) Thông hiểu:
– Giải thích được tính chất cơ bản về hai đường thẳng song song trong không gian.
b) Vận dụng cao:
– Vận dụng được kiến thức về hai đường thẳng song song để mô tả một số hình ảnh trong thực tiễn. c) Thông hiểu:
– Giải thích được điều kiện để đường thẳng song song với mặt phẳng.
– Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng.
d) Vận dụng cao:
– Vận dụng được kiến thức về quan hệ song song để mô tả một số hình ảnh trong thực tiễn.
Câu 20: Vận dụng:
a) – Vận dụng được các phép toán giới hạn dãy số để tìm giới hạn của một số dãy số đơn giản (ví dụ: 2n +1 2 4n +1 lim ) lim . n→+ n n→+ n
b) Vận dụng:
– Tính được một số giới hạn hàm số bằng cách vận dụng các phép toán trên giới hạn hàm số. ĐỀ MINH HỌA I. TRẮC NGHIỆM
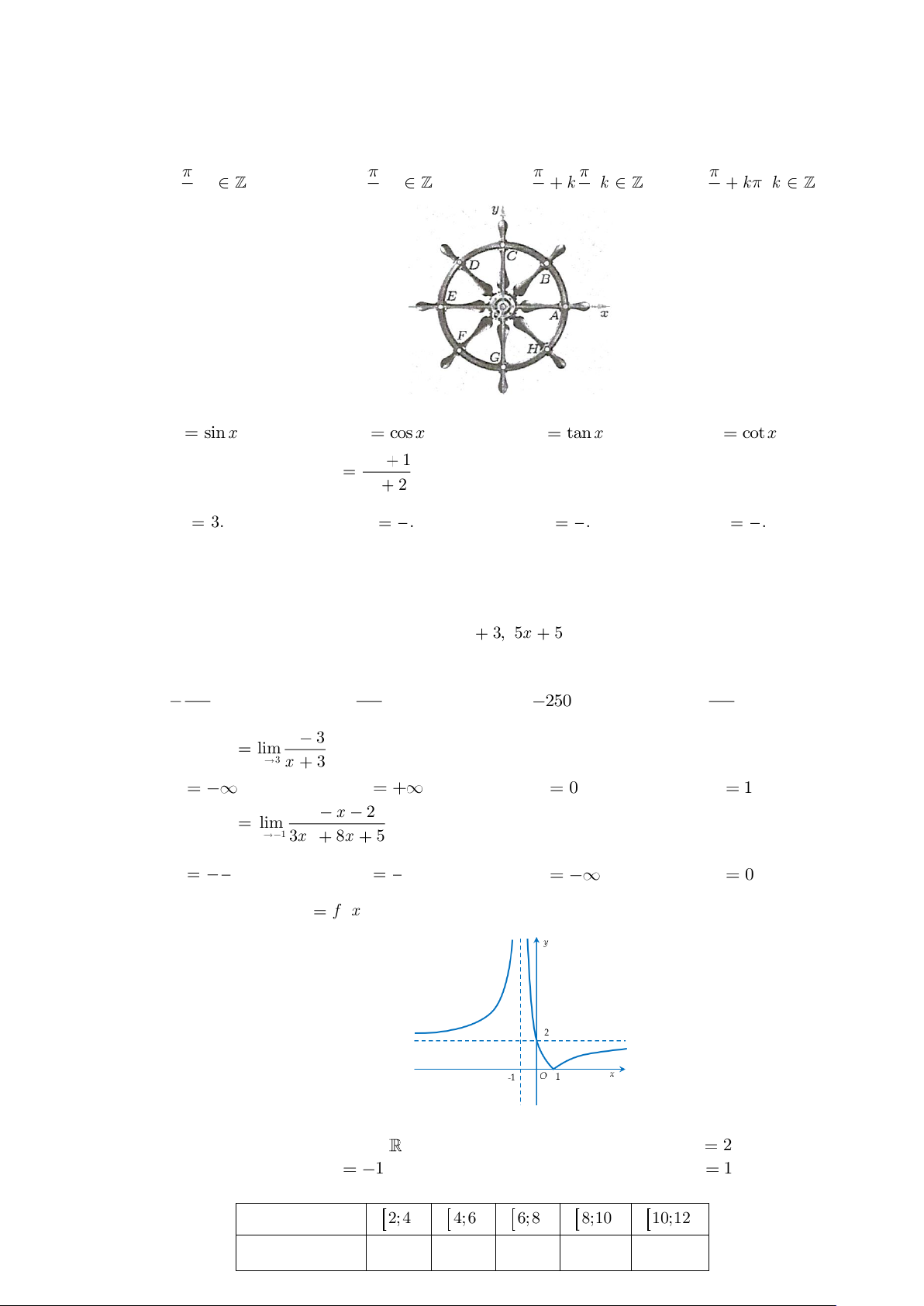
Câu 1: Trong hình vẽ bên dưới, ta xem hình ảnh đường tròn trên một bánh lái tàu thuỷ tương ứng
với một đường tròn lượng giác. Công thức tổng quát chỉ ra góc lượng giác tương ứng với
bốn điểm biểu diễn là , B ,
D F,H theo đơn vị radian là
A. k k .
B. k k . C. k k . D. k k . 3 4 4 2 4
Câu 2: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y sinx .
B. y cosx .
C. y tanx .
D. y cotx . Câu 3: Cho dãy số n u , biết 2 1 u . Số hạng u là n n n 2 4 A. 3 6 9 u 3. B. u . C. u . D. u . 4 4 2 4 9 4 4
Câu 4: Một nhà hát có n hàng ghế với hàng thứ nhất có 15 ghế, kể từ hàng thứ 2 trở đi hàng sau
nhiều hơn hàng liền trước nó 2 ghế. Số ghế của hàng thứ 3 trong nhà hát là A. 16. B. 17. C. 18. D. 19.
Câu 5: Với x là số nguyên dương, ba số 2x, 3x 3, 5x
5 theo thứ tự là ba số hạng liên tiếp của
một cấp số nhân. Số hạng tiếp theo của cấp số nhân đó là A. 250 . B. 250 . C. 250 . D. 250 . 3 3 3 Câu 6: Giới hạn x 3 L lim bằng x 3 x 3 A. L . B. L . C. L 0 . D. L 1. 2 Câu 7: Giới hạn x x 2 L lim bằng 2
x 1 3x 8x 5 A. 3 L . B. 1 L . C. L .
D. L 0 . 2 2
Câu 8: Cho đồ thị hàm số y f x như hình vẽ.
Khẳng định nào sau đây sai?
A. Hàm số không liên tục trên .
B. Hàm số liên tục tại x 2 .
C. Hàm số liên tục tại x 1.
D. Hàm số liên tục tại x 1.
Câu 9: Cho mẫu số liệu ghép nhóm dưới đây về điểm kiểm tra Toán của 30 bạn học sinh lớp 11A Điểm 2 ; 4 4 ;6 6 ; 8 8 ;10 1 0;12 Số học sinh 1 8 11 9 1
Số trung bình của mẫu số liệu ghép nhóm trên là A. 106 . B. 34 . C. 32 . D. 312 . 15 5 5 15
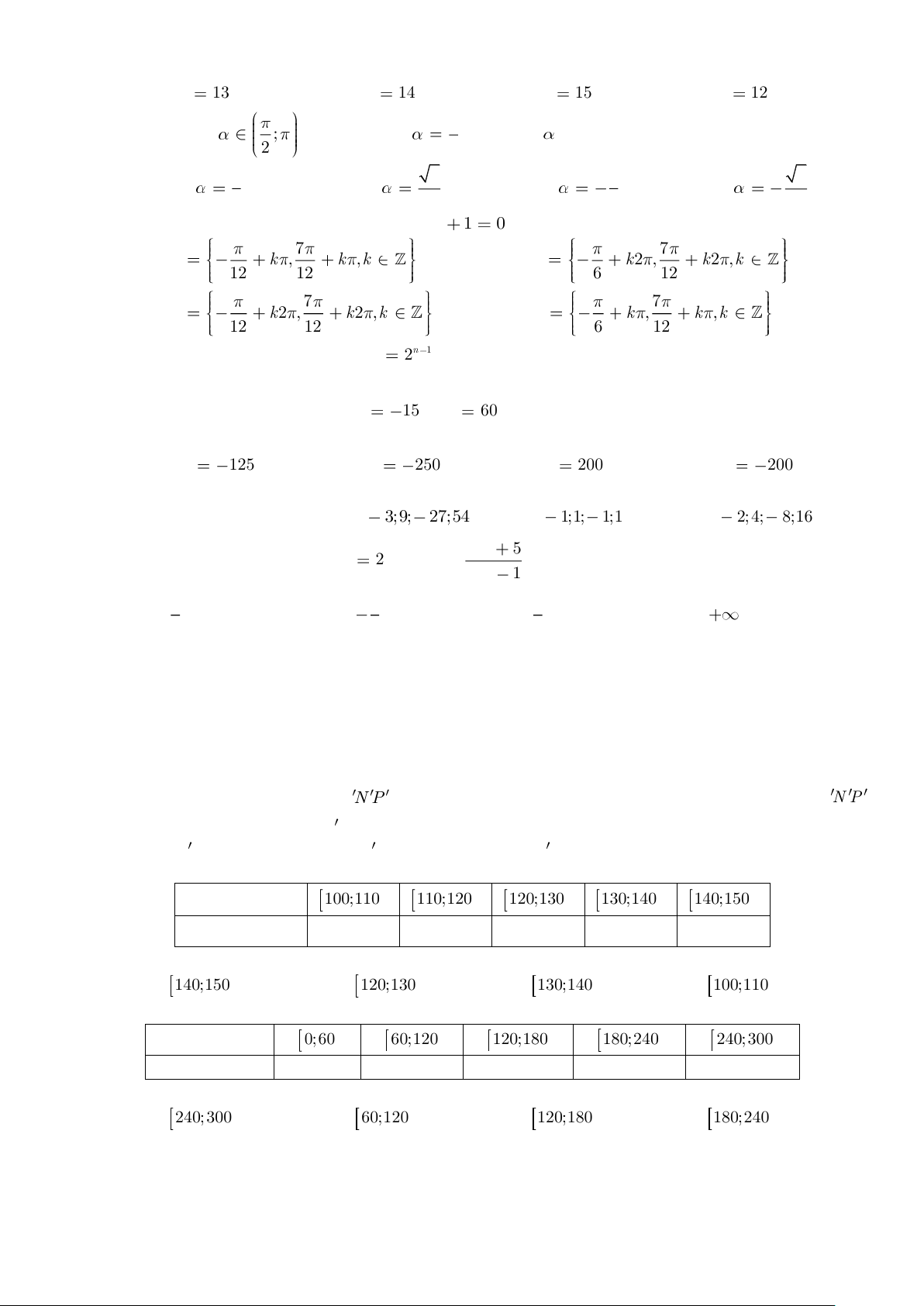
Câu 10: Hàm số f x có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu?
A. x 0.
B. x 1.
C. x 2. D. x 3.
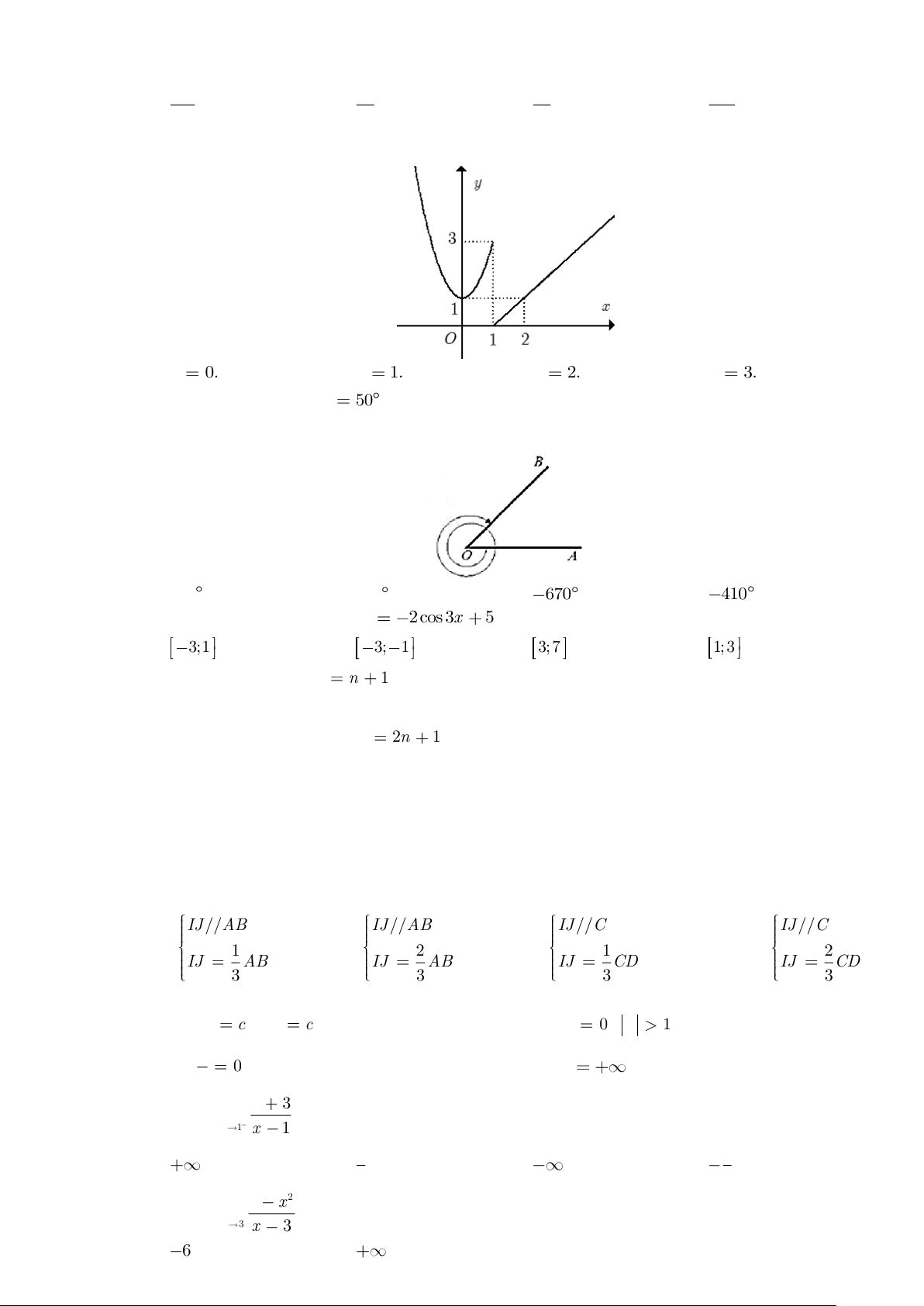
Câu 1: Cho góc hình học
AOB 50 . Số đo của góc lượng giác O ,
A OB trong hình vẽ bên dưới là bao nhiêu? A. 410. B. 670. C. 670 . D. 410 .
Câu 2: Tìm tập giá trị của hàm số y 2cos 3x 5 . A. 3;1 . B. 3 ; 1 . C. 3; 7 . D. 1; 3 .
Câu 3: Cho dãy số u có u n 1. Năm số hạng đầu tiên của dãy số đã cho là? n n
A. 1; 2; 3; 4; 5 .
B. 3;6;12;24;36;....
C. 2; 3; 4; 5; 6 . D. 2;4;6;8;....
Câu 4: Cho cấp số cộng u có u 2n 1. Số 1035 là số hạng thứ mấy của u ? n n n A. 7 . B. 2071 . C. 517 . D. 6 .
Câu 5: Có bao nhiêu mặt phẳng tạo bởi 3 điểm , A , B C thẳng hàng? A. 1. B. vô số. C. 2. D. 3.
Câu 6: Cho tứ diện ABCD . Gọi I, J lần lượt là trọng tâm các tam giác ABC, AB . D Mệnh đề nào sau đây đúng? IJ //AB IJ //AB IJ //CD IJ //CD A. . 1 B. . 2 C. . 1 D. . 2 IJ AB IJ AB IJ CD IJ CD 3 3 3 3
Câu 7: Phát biểu nào sau đây là sai?
A. limu c (u c là hằng số). B. lim n
q 0 q 1. n n C. 1 lim 0 .
D. limn . n
Câu 8: Giới hạn x 3 lim bằng x 1 x 1 A. . B. 1 . C. D. 1 . 2 2 2
Câu 9: Giới hạn 9 x lim bằng x 3 x 3 A. 6 . B. . C. 0 . D. 6 .
Câu 10: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:
Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7;9). B. [9;11). C. [11;13). D. [13;15) .
Câu 1: Đổi số đo của góc 3
rad sang đơn vị độ, phút, giây. 16 A. 0 33 45'. B. 0 29 30 '. C. 0 33 45 '. D. 0 32 55.
Câu 2: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. x y sin2x.
B. y x cosx.
C. y cosx.cotx. D. tan y . sin x Câu 3: Cho dãy số n
u , biết u
. Năm số hạng đầu tiên của dãy số đó là n n n 1 A. 1 2 3 4 5 ; ; ; ; . B. 2 3 4 5 6 ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 C. 1 2 3 4 5 ; ; ; ; . D. 2 3 4 5 6 ; ; ; ; . 2 3 4 5 6 3 4 5 6 7
Câu 4: Dãy số 1 2 3 4
0; ; ; ; ; . có số hạng tổng quát là 2 3 4 5 2 A. n 1 n n n n u . B. u . C. 1 u . D. u . n n n n 1 n n n n 1
Câu 5: Với x là số dương và ba số 2; x; 18 theo thứ tự lập thành cấp số nhân. Khi đó số hạng tiếp theo là: A. 72. B. 54 . C. 24 . D. 36 . Câu 6: Cho dãy số ( n
u ) có số hạng tổng quát 2 1 u
. Tính lim u ta được kết quả là: n n 3 n n A. 3 . B. 2 . C. 2 . D. 1 . 2 3 3
Câu 7: Giới hạn lim 2 3x 2 x 1 bằng: x 1 A. 2 . B. 4 . C. 10 . D. 16 . 2 x 3 x 2 a
Câu 8: Cho giới hạn lim
trong đó a là phân số tối giản. Tính 2 2 a b . 2 x 2 x 4 b b A. 5 . B. 4 . C. 17 . D. 25 . 3 x 1 Câu 9: Cho hàm số khi x 1
y f (x) x 1
. Giá trị của tham số m để hàm số liên tục tại 2m 7 khi x 1 điểm x 1 là: 0 A. 3 . B. 4 . C. m 5 . D. 25 .
Câu 10: Một hình chóp có đáy là tứ giác có tổng số mặt bên và mặt đáy là A. 5 . B. 4 . C. 8 . D. 6 .
Câu 11: Cho tứ diện ABCD , gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC . Mệnh đề nào dưới đây đúng?
A. GE và CD chéo nhau.
B. GE//CD .
C. GE và AD cắt nhau.
D. GE và CD cắt nhau.
Câu 12: Lớp 12E có 40 học sinh và mỗi học sinh phải trả lời 40 câu hỏi trong một bải kiểm tra. Kết
quả được thống kê ở bảng sau. Hãy ước lượng trung bình số câu trả lời đúng của các học sinh lớp 12E. A. 30 . B. 32 . C. 29. D. 31.
Câu 1: Tập nghiệm của phương trình sin2x sinx là A. S k2π; π k2π k . B. π S k 2π; k2π k . 3 C. π k2π S k 2π; k . D. π S k 2π; k2π k . 3 3 3
Câu 2: Dãy số gồm tất cả các số tự nhiên lẻ nhỏ hơn 20, theo thứ tự tăng dần là
A. 1,3,5,7,9,11,13,15,17,19 .
B. 19,17,15,13,11,9,7,5,3,1.
C. 1,3,5,7,... .
D. 1,2,5,7,9,11,13,15,17,19 .
Câu 3: Số hạng tổng quát của cấp số cộng u biết số hạng đầu u 5 , công sai d 2 là n 1 A. u 2 3n .
B. u 1 4n .
C. u 5n .
D. u 3 2n . n n n n
Câu 4: Cho cấp số nhân có u 4,q 2 khi đó u ? 1 2 A. 6 . B. 8 . C. 2 . D. 4 . Câu 5: Tìm 2025 lim n A. 0 . B. 1 . C. . D. Không tồn tại.
Câu 6: Biết lim f x 2 và lim f x 3
g x
5 . Tìm lim g x ? x 1 x 1 x 1 A. 1 . B. 1 . C. 0 . D. 2 .
Câu 7: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm phân biệt.
Câu 8: Cho tứ diện ABCD , G là trọng tâm ABD và M là điểm trên cạnh BC sao choBM 2MC
. Đường thẳng MG song song với mặt phẳng A. ACD . B. ABC . C. ABD . D. BCD .
Câu 9: Cho tam giác ABC nằm trong mp và phương l . Biết hình chiếu theo phương l của tam
giác ABC lên mặt phẳng P là một đoạn thẳng. Khẳng định nào sau đây đúng?
A. || P .
B. P .
C. || l hoặc l .D. A, B, C đều sai.
Câu 10: Điểm thi môn Toán của 60 thí sinh được cho trong bảng sau:
Mốt của mẫu số liệu trên bằng A. 45,5 . B. 46,5 . C. 45 . D. 47,5 .
Câu 11: Tìm hiểu thời gian hoàn thành một bài tập của một số học sinh thu được kết quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là A. Q 13 . B. Q 14 . C. Q 15 . D. Q 12 . 3 3 3 3 Câu 1: Cho góc ; thỏa mãn 2 sin . Tính cos . 2 3 A. 1 cos . B. 5 cos . C. 1 cos . D. 5 cos . 3 3 3 3
Câu 2: Tập nghiệm của phương trình 2sin2x 1 0 là A. 7 S k , k ,k . B. 7 S k2 , k2 ,k . 12 12 6 12 C. 7 S k2 , k2 ,k . D. 7 S k , k ,k . 12 12 6 12
Câu 3: Cho dãy số u thỏa mãn 1
u 2n . Tìm số hạng thứ 10 của dãy số đã cho. n n A. 11 2 . B. 9 2 . C. 10 2 . D. 8 2 .
Câu 4: Cho cấp số cộng u có u 15 , u 60 . Tổng của 10 số hạng đầu tiên của cấp số cộng n 5 20 này là
A. S 125 .
B. S 250 . C. S 200 .
D. S 200 . 10 10 10 10
Câu 5: Dãy số nào sau đây không phải là cấp số nhân? A. 1;2;4;8;16 . B. 1; 3 ;9; 27;54 . C. 1; 1 ;1; 1;1. D. 1; 2 ; 4; 8;16 . Câu 6: Cho dãy số u
u có lim u 2 . Tìm 2 5 lim n . n n 3u 1 n A. 2 . B. 1 . C. 9 . D. . 3 5 5
Câu 7: Cho hình chóp S.ABC . Gọi M là trung điểm của cạnh BC . Giao tuyến của hai mặt phẳng
SAM và SBC là A. SB . B. SM . C. SC . D. BC .
Câu 8: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b . A. 0 . B. 1 . C. 2 . D. Vô số.
Câu 9: Cho hình lăng trụ MNP.M N P
. Hình chiếu song song của điểm N trên mặt phẳng M N P
theo phương chiếu MMlà điểm A. M. B. N. C. P. D. M .
Câu 10: Kết quả khảo sát cân nặng của 20 quả cam được cho ở bảng sau Cân nặng 1 00;110 1 10;120 1 20;130 1 30;140 1 40;150 Số quả cam 1 4 5 4 6
Cân nặng trung bình của mỗi quả cam thuộc nhóm nào dưới đây? A. 1 40;150. B. 1 20;130 . C. 1 30;140 . D. 1 00;110 .
Câu 11: Thời gian sử dụng điện thoại trong một ngày của 30 sinh viên được ghi lại ở bảng sau Thời gian 0 ;60 6 0;120 1 20;180 180 ;240 240 ; 300 Số sinh viên 2 7 7 10 4
Trung vị của mẫu số liệu ghép nhóm trên thuộc nhóm nào dưới đây A. 240 ; 300. B. 6 0;120 . C. 1 20;180 . D. 180 ;240 .
Câu 1: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm phân biệt.
Câu 1: Cho hình hộp ABCD A B C D
. Mặt phẳng ( AB D
) song song với mă̆t phẳng A. ( ABCD). B. (BCC B ) . C. (BDA) . D. (BDC ') .
Câu 2: Phép chiếu song song theo phương l không song song với a hoặc b , mặt phẳng chiếu là
(P) , hai đường thẳng a và b biến thành a và b. Quan hệ nào giữa a và b không được
bảo toàn đối với phép chiếu song song? A. Cắt nhau B. Chéo nhau C. Song song D. Trùng nhau
Câu 3: Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau? A. Hình thang
B. Hình bình hành C. Hình chữ nhật D. Hình thoi
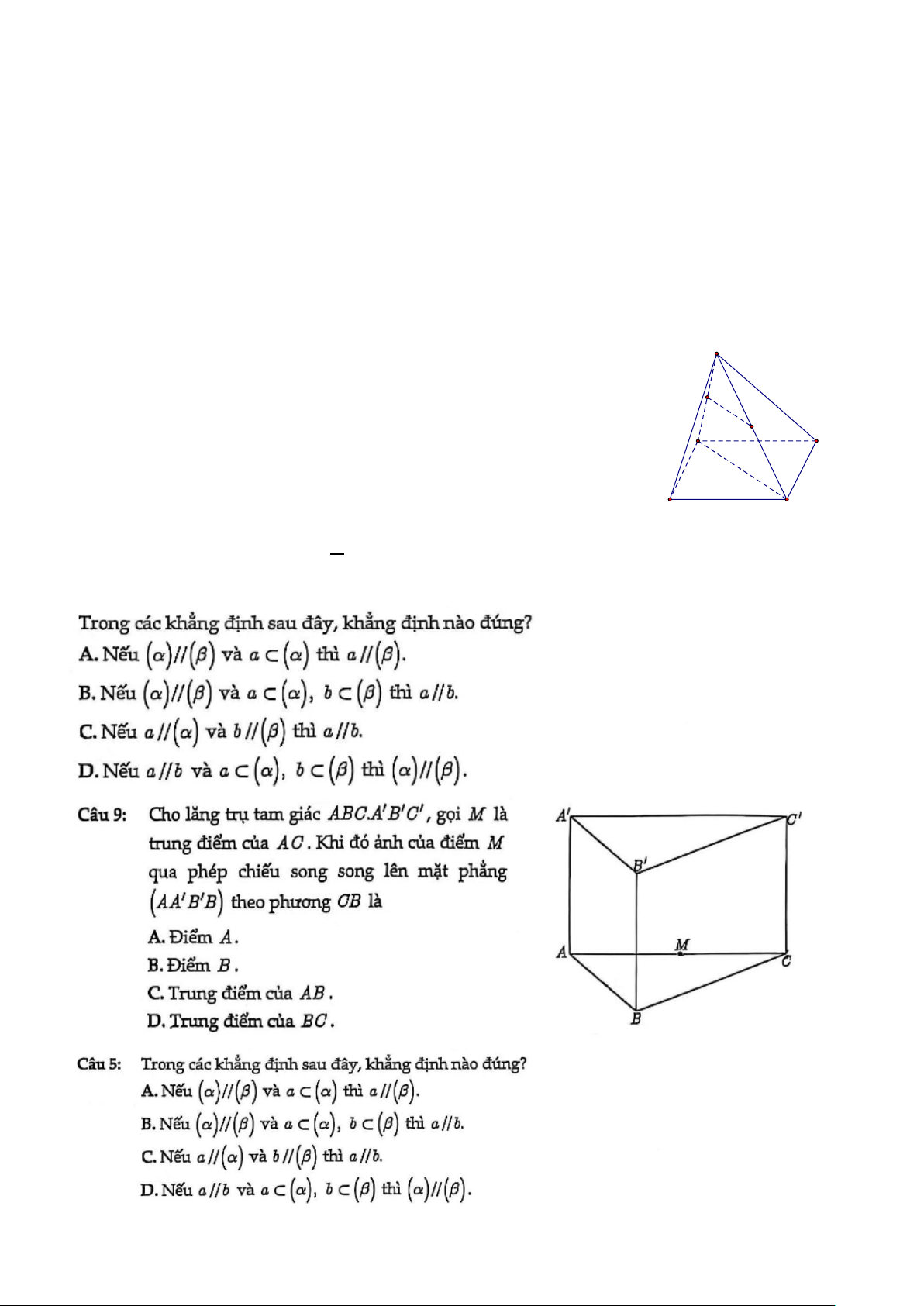
Cho hình chóp S.ABCD có đáy là hình bình hành, gọi M là trung S
điểm của cạnh SC (như hình vẽ). Hình chiếu song song của
điểm M theo phương AC lên mặt phẳng (SAD) là điểm M N nào sau đây? C B D
A. Trung điểm SB .
B. Trung điểm SD . A
C. Điểm D .
D. Trung điểm SA. II. ĐÚNG SAI 2 x −1 khi x 1
Câu 1. Cho hàm số f (x) = x −1 và g x = 2
( ) 4x − x +1 . Khi đó:
x +1 khi x =1
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Ta có f (1) = 2
b) Hàm số f ( x) liên tục tại điểm x =1 0
c) Hàm số g ( x) liên tục tại điểm x =1 0
d) Hàm số y = f (x) − g ( x) không liên tục tại điểm x =1 0
Câu 2. Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a) 3 2 f ( )
x = x − x +8x là hàm số liên tục trên . b) 2 x f (x) =
là hàm số liên tục trên khoảng (− ; + ) . 2 x − 3x c) sin x +1 f (x) =
là hàm số liên tục trên các khoảng (− ; 0),(0;+ ) . x +1
d) f (x) = x − 2 là hàm số liên tục trên nửa khoảng [2; ) + . 4x − 7 −1 khi x 2 x + 2 − 2 2 khi x 2
Câu 3. Cho các hàm số x − 4 f (x) = và 2 ( ) − x g x = . Khi đó: 5x − 9 khi x 2 1− x khi x 2 2 4
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số f ( x) liên tục tại điểm x = 2 . 0
b) Hàm số g ( x) gián đoạn tại điểm x = 2 . 0 c) Giới hạn 1
lim g(x) = . x 2+ → 4 d) f ( x) Hàm số y =
liên tục tại điểm x = 2 . g ( x) 0
− x khi x 1 Câu 4. Cho hàm số 2 f (x) = và 2
g(x) = x − 3x +1 . Khi đó: 2 x − 3x + 2 khi x 1 2 x −1
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Hàm số f (x) liên tục tại điểm x =1. 0
b) Hàm số g(x) liên tục tại điểm x =1. 0 c) Giới hạn 1
lim f (x) = . x 1+ → 2
d) Hàm số y = f (x) + g (x) liên tục tại điểm x =1. 0 2 x − 4 khi x 2
Câu 1. Cho các hàm số f (x) = x − 2 và 2 g(x) = . Khi đó: x −1 4,5 khi x = 2
a) Hàm số g(x) liên tục tại điểm x = 2 . 0
b) Giới hạn lim f (x) = 4 x→2
c) Hàm số f (x) liên tục tại điểm x = 2 . 0 f ( x) d) Hàm số y =
liên tục tại điểm x = 2 . g ( x) 0 4x − 7 −1 khi x 2 x + 2 − 2 2 khi x 2
Câu 2. Cho các hàm số x − 4 f (x) = và 2 ( ) − x g x = . Khi đó: 5x − 9 khi x 2 1− x khi x 2 2 4
a) Hàm số f ( x) liên tục tại điểm x = 2 . 0
b) Hàm số g ( x) gián đoạn tại điểm x = 2 . 0 c) Giới hạn 1 lim g(x) = . x 2+ → 4 f ( x) d) Hàm số y =
liên tục tại điểm x = 2 . g ( x) 0 2 x − 3x + 2 , x 1
Câu 3. Hàm số f (x) ( ) = x −1 . Khi đó: 1 − (x = ) 1
a) Liên tục tại điểm x = 1 − .
b) Liên tục tại điểm x =1.
c) Không liên tục tại điểm x =1.
d) không liên tục tại điểm x = 2 .
Câu Hình nào sau đây là hình biểu diễn của một lục giác đều? A. . B. . C. . D. .
Câu 4: Cho hình lăng trụ ABC ABC
; I và I lần lượt là trung điểm của đoạn AB và A B .
a) AI / /IB
b) Hình chiếu song song của
I trên mặt phẳng ( ABC ) phương A I là điểm C .
c) Trong mặt phẳng ( ABC ) , vẽ hình bình hành ACMI . Suy ra ACMI là hình bình hành.
d) M là hình chiếu song song của
C theo phương AI trên mặt phẳng ( A B C ) .
Câu 3: Cho hình lăng trụ ABC ABC .
a) AA / /CC
b) A hình chiếu của A trên mặt phẳng ( ABC ) qua phép chiếu song song theo phương CC .
c) Gọi M là một điểm trên đoạn thẳng AB . Hình chiếu của M trên mặt phẳng ( ABC ) qua phép
chiếu song song theo phương BB là điểm M AB d) Gọi
O là tâm của hình bình hành BCC B . Ảnh của O qua phép chiếu song song theo phương
AA trên mặt phẳng ( ABC ) là trung điểm của BC.
Câu 2: Trong mặt phẳng ( )
P , cho hình bình hành ABCD. Vẽ các nửa đường thẳng song song nhau,
nằm về một phía đối với mặt phẳng ( )
P và đi qua các điểm ,
A B , C, D . Một mặt phẳng ( ) Q cắt
bốn nửa đường thẳng nói trên tại A, B,C, D .
a) mp ( AA, BB ) song song với mp(CC, DD ).
b) AB / /CD
c) Tứ giác ABCD là hình thang d) Gọi
O và O lần lượt là giao điểm của hai đường chéo của ABCD và A B C D . Khi đó OO / / AA .
Câu 3: Cho lăng trụ tam giác ABC ABC
có I, K,G lần lượt là trọng tâm các tam giác
ABC, ABC, ACC . Gọi M , M lần lượt là trung điểm của BC, BC . Khi đó:
a) AMMA là hình bình hành b) AI AG 1 = = AM AN 3
c) (IKG) cắt (BCCB )
Câu 1. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng và có tâm
lần lượt là O và O. Gọi M, N lần lượt là hai điểm trên các cạnh AE, BD sao cho 1 AM = AE , 3 1
BN = BD . Khi đó: 3
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) OO song song với mặt phẳng (ADF)
b) OO cắt mặt phẳng (BCE) c) BN 2 = BD 3
d) MN song song với mặt phẳng (CDFE)
Câu 1. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của
tam giác SAB và SC ;
D E, F lần lượt là trung điểm của AB và CD. Khi đó: a) SJ 2 = SF 3 b) IJ / /(ABC ) D .
b) BC song song với mặt phẳng (SA ) D ,(SEF)
d) BC cắt mặt phẳng (AIJ)
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi G là trọng tâm tam giác SAD
và E là điểm trên cạnh DC sao cho DC = 3DE, I là trung điểm AD . Khi đó:
a) OI song song với mặt phẳng (SAB)
b) OI song song với mặt phẳng (SC ) D
c) IE song song với AC d) GE / /(SBC)
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H, I, K lần lượt là trung điểm của S , A S ,
B SC . Gọi M là giao điểm của AI và K ,
D N là giao điểm của DH và CI . Khi đó:
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) HI / /(ABC ) D
b) (HIK) / /(ABC ) D
c) SM và HI chéo nhau
d) (SMN) cắt (HIK)
Câu 2. Cho hình bình hành ABCD và ABEF nằm ở hai mặt phẳng khác nhau. Gọi M là trọng tâm ABE . Gọi ( )
P là mặt phẳng đi qua M và song song với mặt (ADF). Lấy N là giao điểm của ( )
P và AC . Khi đó:
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) EFDC là hình thang
b) FD / /EC
c) (ADF) / /(BCE)
d) AN = 3 NC
Câu 3. Cho hình hộp ABCD ABCD
có các cạnh AA, BB,CC, DD song song với nhau. Khi đó:
Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) (BDA)/ /(BDC)
b) Đường chéo AC đi qua trọng tâm G ,G của tam giác BDA và BDC . 1 2
c) AG = 2G G 1 1 2
d) Mặt phẳng (ABG cắt hình hộp ABCD ABCD
tạo thành một tứ giác 2 ) là hình bình hành IV.
TRẢ LỜI NGẮN, TỰ LUẬN 2 x − x − 2 neáu x 2
Câu 1. Tìm m để hàm số sau liên tục tại điểm được chỉ ra: f (x) = x − 2 ; x = 2 0 m+1 neáu x = 2
Câu 2. Cho tứ diện ABCD, M là trọng tâm của tam giác ABC . Gọi N là hình chiếu song song của
điểm M theo phương CD lên mặt phẳng (ABD) . Khi đó EN bằng bao nhiêu? E là trung ED
điểm của BD (làm tròn đên hàng phần trăm)
Câu 3. ( 1,0 điểm): Tính giới hạn sau 2 n − 7n +12 a. lim
b. lim ( 2n +3 − 4n) 2 x→+ n − 3n x→+
Câu 4. Tính giới hạn sau 2 x − 7x +12 a. lim b. lim ( 2 4x + 3 − 2x) 2 x 3 → x − 3x x→+
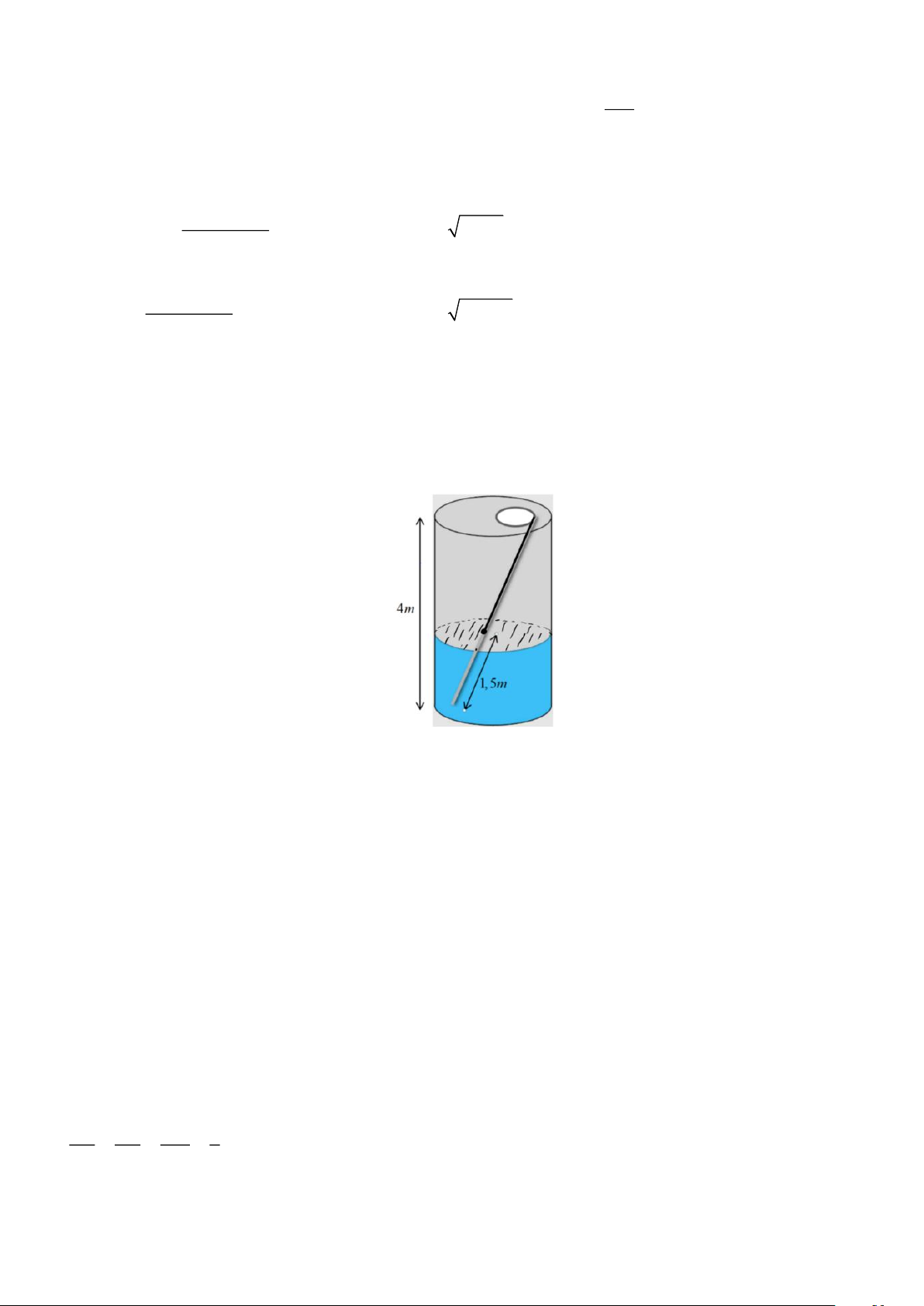
Câu 5. Một bồn chứa nước hình trụ bằng bê tông cao 4, chỉ chừa 1 nắp nhỏ bên ngoài để bơm nước
vào thùng, trong thùng có sẵn 1 lượng nước. Để đo chiều cao mực nước trong thùng bác An có cách
như sau: lấy 1 cây sào tre dài 5m nhúng vào thùng nước sao cho một đầu chạm đáy và một đầu
chạm với mặt trên của bồn nước. Sau khi rút sào tre ra thì đo được phần sào tre bị ướt là 1,5m. Hỏi
mực nước trong hồ cao bao nhiêu mét?
Câu 6. Cho hình chóp S.ABCD có đáy ABCD hình bình hành tâm O, Gọi M trên cạnh SA sao cho
MA= 2. MS và N trên cạnh BC sao cho NB= 2. NC.
a. Tìm giao tuyến của mp(SAD) và mp(MNB) b. CMR: MN // (SCD)
c. Tìm giao điểm P của mp(MNO) với SB
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB ,
I là trung điểm của AB và M là điểm trên cạnh AD . Biết rằng đường thẳng MG song song với mặt
phẳng SCD . Tỉ số giữa hai đoạn thẳng AM và AD là bao nhiêu?(Làm tròn đến hàng phần trăm).
Câu 8. Cho hình bình hành ABCD nằm trong mặt phẳng ( ) và S là điểm nằm ngoài mặt phẳng
( ). Gọi M, N lần lượt là trọng tâm của các tam giác SAB và SAD.
a).Tìm giao tuyến của hai mặt phẳng (SMN )và ( ).
b).Gọi là giao tuyến của hai mặt phẳng ( AMN )và ( ). Chứng minh / /MN.
Câu 9. Cho tứ diện đều ABCD cạnh a. Gọi I, J, K thứ tự thuộc các cạnh AB, BC và CD sao cho
AI = CJ = DK = 1 . AB CB DC 3
a) Chứng minh AC// (IJK).
b) Xác định giao điểm H của mp(IJK) với đường thẳng AD
Câu 10. Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song với
BC. Các điểm M, N lần lượt là trung điểm của các cạnh AB, CD; G là trọng tâm tam giác SAD.
a. Chứng minh rằng đường thẳng BC song song với mặt phẳng (SMN).
b. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (GMN). Thiết diện là hình gì?
Câu 11. hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của SA.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm I của đường thẳng CM và mặt phẳng (SBD). Gọi H, K lần lượt là trọng tâm
của tam giác SBC và BCD. Chứng minh HK //(SAD).
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy M trên cạnh SA sao
cho MA = 2MS và N trên cạnh BC sao cho NB = 2NC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (MBN).
b) Chứng minh: MN // (SCD).
c) Tìm giao điểm P của mặt phẳng (MNO) với SB.
Câu 13 Cho hình chóp S.ABC ,
D ABCD là hình bình hành tâm O. Gọi M , N lần lượt là trung điểm các đoạn thẳng S ,
A SB và P là điểm thuộc cạnh SC sao cho SP =3PC. (MNP) (SCD)
a) Chứng minh MN // (SCD). Tìm giao tuyến của hai mặt phẳng và . (SBD)
b) Tìm giao điểm I của đường thẳng MP với mặt phẳng . SI
c) Tính tỉ số SO . Câu 14
a. Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh A ,
B BC ; trên cạnh AD lấy P
sao cho PA = 2P .
D Gọi K là giao điểm của đường thẳng BD với mặt phẳng (MNP).
b. Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).



