






















































Preview text:
lOMoARcPSD| 38841209 BỘ MÔN VẬT LÝ
TRƯỜNG ĐẠI HỌC XÂY DỰNG Chương 1 ĐỘNG HỌC
TÓM TẮT LÝ THUYẾT
1. Phương trình chuyển động của chất điểm
r OM
r t hoặc x x t ; y y t ; z z t 2. Vận tốc
- Vector vận tốc của chất điểm trong toạ độ Descartes: dr dx dy dz v i j k dt dt dt dt
- Vận tốc trong toạ độ cong:
vs với v lim s ds s t 0 t dt lOMoARcPSD| 38841209 3. Gia tốc
- Vector gia tốc trong toạ độ Descartes: dv d r2
d x2 d y2 d z2 a 2 2 i 2 j 2 k dt dt dt dt dt
- Vector gia tốc trong toạ độ cong: dv a at an dt v trong đó a dv t v là gia tốc tiếp tuyến, an 2 là gia tốc pháp R tuyến, R là bán dt
kính cong của quỹ đạo.
4. Chuyển động tròn - Vận tốc góc: d ; v R dt
- Gia tốc góc: d d2 ; at R 2 dt dt
5. Tổng hợp vận tốc và gia tốc trong chuyển động tịnh tiến
- Tổng hợp vận tốc: v13 v12 v23 - Tổng hợp gia tốc: a13 a12 a23 BÀI TẬP VÍ DỤ
Ví dụ 1. Một chất điểm chuyển động được mô tả bởi các phương trình sau: x 2t (1) 2 y 4t
4 (2) x, y tính bằng mét, t tính bằng giây.
a. Tìm quỹ đạo chuyển động của chất điểm.
b. Tìm vận tốc của chất điểm khi t 2s. Lời giải: x a. Từ (1) rút ra t 2 , t hay vào (2) có: y 2 x 4
- Quỹ đạo của chất điểm là một nhánh parabol ( x 0). lOMoARcPSD| 38841209 b. Vận tốc tại t 2 s - Thay t '
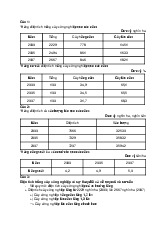
Ví dụ 2. Từ điểm O vx xt 2 2 2 2 ' v v v 4 64t v y 8t x y
trên mặt đất một chất điểm y t
được ném lên với vận tốc 2 s ta được: 2 v 4 64.2 16 ,12m/s .
ban đầu v0 hợp với phương ngang một góc α.
a. Tìm phương trình chuyển động, phương trình quỹ đạo.
b. Tìm bán kính cong của quỹ đạo tại O và tại điểm cao nhất của quỹ đạo. Lời giải
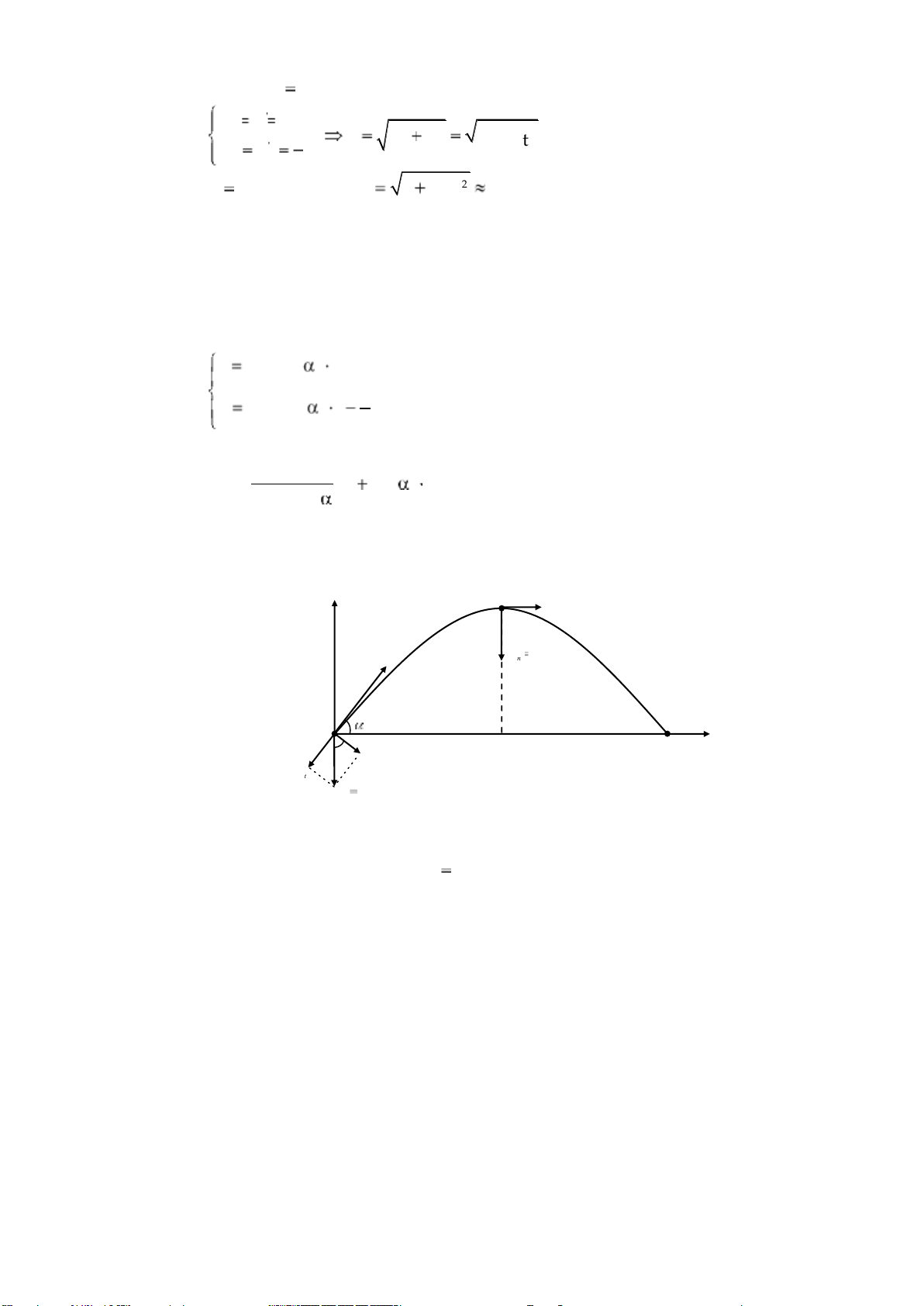
a. Phương trình chuyển động: x v cos0 t (1) 1 2 y v sin0 t gt (2) 2
- Rút t từ (1) thay vào (2) ta được phương trình quỹ đạo: g 2 y 2 2 x tg x (3) 2v cos0
b. Bán kính cong của quỹ đạo: A y v x n 0 v ag N O H x na
ta ag
- Tại mọi điểm gia tốc toàn phần a g. lOMoARcPSD| 38841209 0 )
- Mặt khác ta có công thức: 2 2 v v an R R an n a.cos g.cos 2 2 v v 0 R an g.cos
- Tại điểm cao nhất A: an g ; v vx v0 cos (do vy 2 2 2 2 v v vcos A 0 R an an g - Tại O: a
BÀI TẬP ÁP DỤNG
1.1 Tại cùng một thời điểm hai tàu thuỷ A và B trên một kinh tuyến. A ở phía Bắc so
với B và cách B một đoạn d0. A chạy về phía Đông với vận tốc không đổi vA ; B chạy
về phía Bắc với vận tốc không đổi vB . Độ cong của mặt đất không đáng kể. a. Xác định
khoảng cách cực tiểu giữa A và B.
b. B phải chạy theo hướng nào, sau thời gian bao lâu thì sẽ gặp A.
1.2 Cho phương trình chuyển động của một chất điểm: 2 x x0 at 2 y y0 2
z z0 ct bt (với a, b, c là các hằng số)
a. Tìm phương trình quỹ đạo và dạng quỹ đạo của chất điểm.
b. Tính quãng đường chất điểm đi được kể từ thời điểm ban đầu đến thời điểm t.
c. Xác định vận tốc và gia tốc của chất điểm ở thời điểm t.
1.3 Một ôtô đang chạy trên đường thẳng với vận tốc v 1 H A B
v1 50km/ h . Một người đứng ở A cách đường ấy một khoảng
AH h 100m thì nhìn thấy ôtô vừa đến B cách mình một khoảng
AB 500m thì người ấy bắt đầu chạy ra đường để đón ôtô. lOMoARcPSD| 38841209
a. Người ấy phải chạy theo hướng nào để có thể gặp được ôtô, nếu người đó chạy với vận tốc v2 20/ 3 km/ h.
b. Muốn gặp được ôtô người ấy phải chạy ra đường với vận tốc nhỏ nhất bằng bao nhiêu? Theo hướng nào?
1.4 Một người chèo thuyền qua sông từ điểm A. Vận tốc 10 D B C
của nước đối với bờ là v2, vận tốc của thuyền đối với nước là v1.
Nếu hướng mũi thuyền tới B thì sau thời gian t1
phút thuyền tới C về phía hạ lưu cách B một đoạn A BC
s 120 m. Nếu hướng mũi thuyền về phía thượng lưu
lệch một góc α so với AB thì sau thời gian t2 12,5 phút thuyền tới B. a.
Tính vận tốc v1, v2 và chiều rộng của con sông. b. Xác định góc lệch .
1.5 Một người đứng ở điểm A trên ruộng cách đường H B (d)
(d) một khoảng AH a 1km cần đi tới điểm B trên đường, cách
H một khoảng BH b 3km . Vận tốc đi trên ruộng là v1 3km/ h, trên đường cái là A
v26km/ h. Hỏi phải đi theo quỹ đạo nào thì thời gian tới B là ngắn nhất, tính thời gian ấy.
1.6 Một máy bay bay từ vị trí A tới vị trí B, AB nằm theo hướng Tây Đông và cách
nhau một khoảng s 300km. Xác định thời gian bay nếu: a. Không có gió.
b. Có gió thổi theo hướng Nam Bắc.
c. Có gió thổi theo hướng Tây Đông.
Cho biết vận tốc của gió v1 20m/s và vận tốc của máy bay đối với không khí là v2 600km/ h. 1.7
Một vật chuyển động nhanh dần đều trên hai đoạn đường liên tiếp bằng nhau
và bằng 100m lần lượt trong 5s và 3,5s. Tính gia tốc của vật. 1.8
Một người đứng ở sân ga nhìn thấy một đoàn tầu đang bắt đầu chuyển bánh,
biết toa thứ nhất chạy ngang qua trước mặt người đó trong 6 giây. Coi chuyển động
của đoàn tầu là nhanh dần đều. Hỏi toa thứ n qua trước mặt người quan sát trong bao lâu? Áp dụng với n 7 . 1.9
Một đoàn tàu chuyển động thẳng chậm dần đều tiến vào sân ga. Một người
quan sát đứng cạnh đường tàu thấy toa thứ nhất chạy ngang qua trước mặt mình trong
4 giây, toa thứ hai qua trong 5 giây. Khi tàu dừng lại, đầu toa thứ nhất cách người ấy
75m. Hãy xác định gia tốc của đoàn tàu. lOMoARcPSD| 38841209 1.10
Một chất điểm chuyển động thẳng không vận tốc ban đầu. Lúc đầu chất điểm
chuyển động nhanh dần đều với a 0,5m / s2 , sau đó chuyển động đều rồi cuối cùng
chuyển động chậm dần đều với gia tốc có độ lớn như lúc đầu và dừng lại. Thời gian
tổng cộng của chuyển động là 25s, vận tốc trung bình trong khoảng thời gian đó là
2m/s. Tính khoảng thời gian chất điểm chuyển động đều. 1.11
Từ độ cao h 80m phải ném một vật theo phương thẳng đứng với vận tốc ban
đầu v0 bằng bao nhiêu để nó rơi tới mặt đất.
a. Trước 1 giây so với trường hợp rơi tự do.
b. Sau 1 giây so với trường hợp rơi tự do. Lấy g 10m / s2 .
1.12 Vật A được thả rơi tự do từ độ cao (H h) so với mặt đất. Cùng lúc đó vật B được
ném thẳng đứng từ mặt đất với vận tốc v0 hướng tới A. a. Tính v0 để hai vật gặp nhau ở độ cao h.
b. Xác định khoảng cách x giữa hai vật trước lúc gặp nhau theo thời gian.
c. Nếu không có vật thứ nhất thì vật thứ hai lên tới độ cao lớn nhất là bao nhiêu? Áp
dụng: H 20m; h 10m; g 10m / s2 .
1.13 Một tàu hoả chuyển động chậm dần đều trên quãng đường s 800m có dạng cung
tròn bán kính R 800m . Vận tốc ở đầu quãng đường là v0 54km/ h và ở cuối quãng
đường là v 18km / h . Tính:
a. Gia tốc của tàu tại điểm đầu và điểm cuối quãng đường.
b. Thời gian cần thiết để tàu đi hết quãng đường đó. 1.14
Từ ba điểm A, B, C trên một vòng tròn người ta thả đồng B A
thời ba vật. Vật thứ nhất rơi theo phương thẳng đứng AM. Vật
thứ hai chuyển động trên mặt phẳng nghiêng BM, vật thứ ba theo
mặt nghiêng CM. Hỏi vật nào sẽ rơi tới điểm M trước nhất. Bỏ C M
qua ma sát và sức cản không khí. 1.15
Từ máy bay đang bay ngang với vận tốc 720km/h người ta
thả một vật. Tìm bán kính cong của quỹ đạo sau khi vật chuyển động được 5s. Bỏ qua
sức cản của không khí. 1.16
Từ một đỉnh tháp cao H 25m người ta ném một hòn đá theo phương ngang với
vận tốc ban đầu v0 15m/ s. Tìm: a. Quỹ đạo của hòn đá.
b. Thời gian chuyển động của hòn đá.
c. Khoảng cách từ chân tháp đến điểm hòn đá chạm đất.
d. Vận tốc, gia tốc tiếp tuyến, gia tốc pháp tuyến của hòn đá khi chạm đất.
e. Bán kính cong của quỹ đạo tại điểm bắt đầu ném và điểm chạm đất. Bỏ qua sức
cản không khí lấy g 10m / s2 .
1.17 Một viên đạn được bắn lên từ mặt đất với vận tốc ban đầu v0 200m/ s hợp với 0
phương ngang một góc 30 . Tìm:
a. Độ cao cực đại và tầm xa mà viên đạn đạt được. lOMoARcPSD| 38841209
b. Gia tốc tiếp tuyến và gia tốc pháp tuyến của viên đạn sau lúc bắn 1 giây.
c. Với góc bắn bằng bao nhiêu để: tầm xa của đạn là cực đại; độ cao cực đại và tầm xa của đạn bằng nhau.
1.18 Hai viên đạn được bắn lên lần lượt bởi một súng đại bác với vận tốc v0 250m/ s. 1
Viên đạn thứ nhất bắn dưới góc 600 , viên thứ hai bắn dưới góc 0
2 45 (trong cùng một mặt phẳng thẳng đứng). Bỏ qua sức cản không khí, lấy g 10m /
s2 . Hãy xác định khoảng thời gian giữa hai lần bắn để cho hai viên đạn gặp nhau.
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ
1.1 Bài toán hai tàu thuỷ chạy trên cùng kinh tuyến 2 vA d0 2 2
a. Khoảng cách cực tiểu: dmin vA vB
b. Tàu B phải chạy theo hướng chếch về phía Đông một góc so với đường kinh v tuyến với: A sin vB d0 t 2 2
- Tàu B đuổi kịp tàu A sau thời gian: vB vA
1.2 Chất điểm chuyển động trong hệ toạ độ Descartes a. Khử t trong phương x x0 y y0 z z0 trình chuyển động a b c t2 x x y y z z
- Thu được phương trình quỹ đạo : 0 0 0 a b c
- Quỹ đạo là đường thẳng qua điểm M0 x ,y ,z0 0 0 và có vector chỉ phương 2 2 2 2 2 2 2 s x x0 y y0 z z0 a b c.t u a,b,c .
c. Vận tốc của chất điểm tại thời điểm t 2 2 2 b. Tại t0 0, v0 0. Quãng dx dy dz 2 2 2 2 a b c.t
đường chất điểm đã đi dt dt dt được đến t:
- Gia tốc của chất điểm tại thời điểm t v 2 2 2 2 2 2 dx dy dz 2 2 2 2 a b c 2 2 2 dt dt dt a lOMoARcPSD| 38841209
- Ta thấy gia tốc của chất điểm là một hằng số, vậy chuyển động của chất điểm là một
chuyển động thẳng nhanh dần đều.
1.3 Người đi bộ đón ôtô
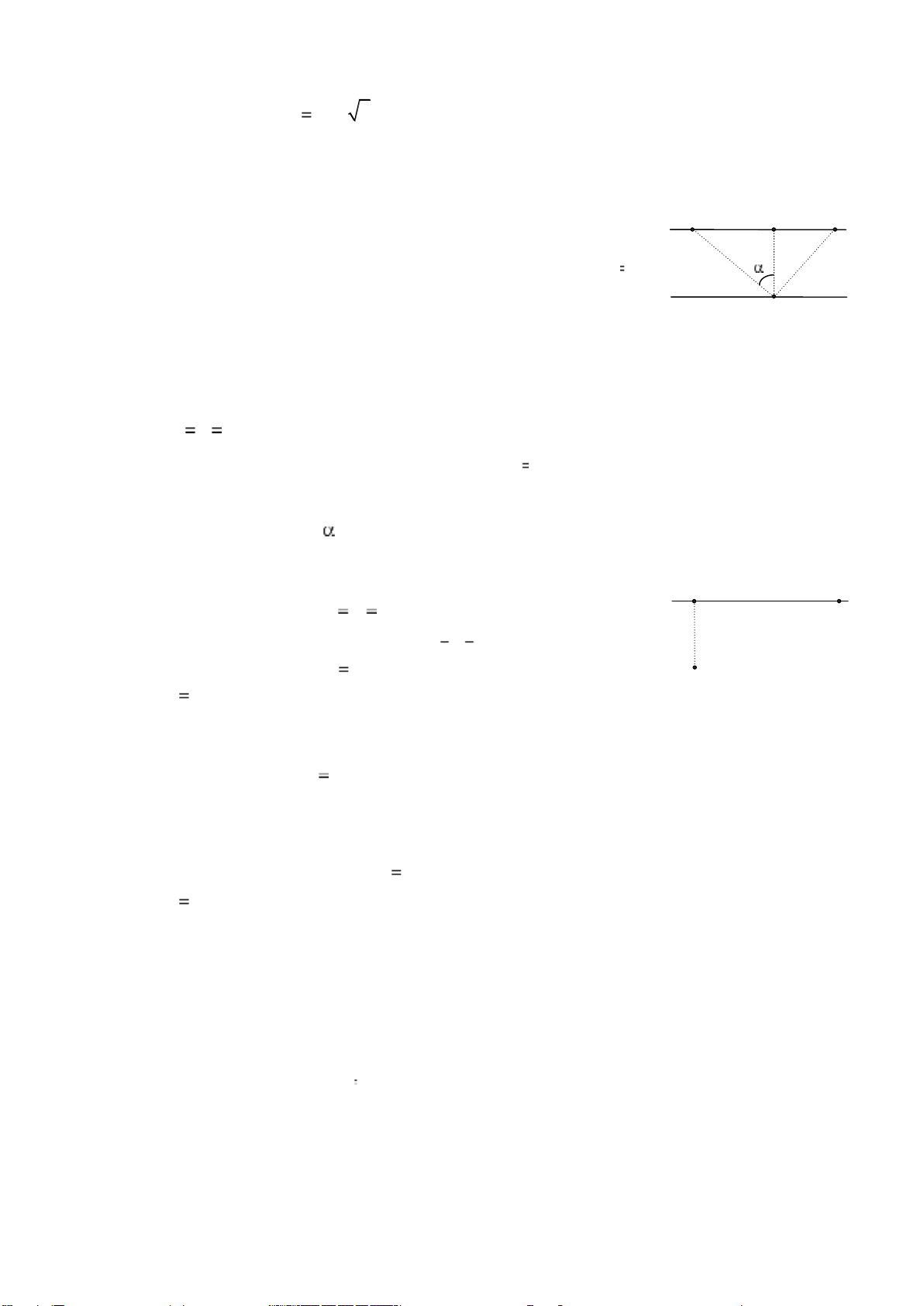
a. Xe (1), người (2), đất (3) v23 v 21 v B 13 H C - Ta có: v23 v21 v13 - Th eo hình vẽ: A v13 v13 v23 sin sin v AH h 13 sin = sin ; với : sin = v AB 23 v h 3 1 0 sin 60 hoặc 0 120 v2 2
b. Xác định hướng chạy với vận tốc cực tiểu -
Từ hệ thức ở phần trên ta có:
v h1 ; Vì v , ,h 1 const v2 sin - Để v2 min sin max 1
900 . Người đó phải chạy theo hướng có: 0 90 h với vận tốc: v2min v1 10 km / h
1.4 Người chèo thuyền qua sông B C a. Tính v , v ,1 2 M N
- Lần 1: Hướng mũi thuyền từ A tới B 1 v v
- Vận tốc của thuyền so với bờ v13 v12 v23 v v1 v2 A v2
- Do ABC AMN nên ta có BC AB AC t1 (1) v2 v1 v BC 120 lOMoARcPSD| 38841209 v2 0,2 m / s B D t1 600 v 2 P Q v ' v - Từ (1) AB v t 1 1 (2) A 1
- Lần 2: Hướng mũi thuyền từ A tới D - Vận tốc của thuyền so với bờ: v' v1 v2 - Do ADB APQ nên ta có: AB AD BD t2 v v1 v2 2 2 AB v.t 2 v1 v2 .t 2 (3) 1 - Từ (2) và (3) có : 2 2 1 vt v1 2 vt 2 v1 m/s 1 ,2 km/h 3 - Ta có AB 11 vt 200 m b. Xác định góc v2 0 sin 0 , 6 arcsin0,6 3652 ' v 1
1.5 Xác định quỹ đạo có thời gian đi ngắn nhất H C B
- Quỹ đạo có thời gian tới B ngắn nhất gồm 2 đoạn đường (d) x AC và CB với x
HC. Muốn tìm tmin thì phải chọn x thích hợp. A - Thời gian đi: t 2 2 2 a x b x 21 x x 3 v1 v2 6
- Lấy đạo hàm của t theo x và cho đạo hàm này triệt tiêu 2 dt 12 x 1 x 1 0 x0 0 ,58 km HC 2 dx 6 1 x 3
- Thời gian đi t0 0 , 79 giờ ( ứng với x0 0 ,58 km )
- Vậy thời gian ngắn nhất là 0,79 giờ và phải đi theo quỹ đạo ACB có HC 0,58km.
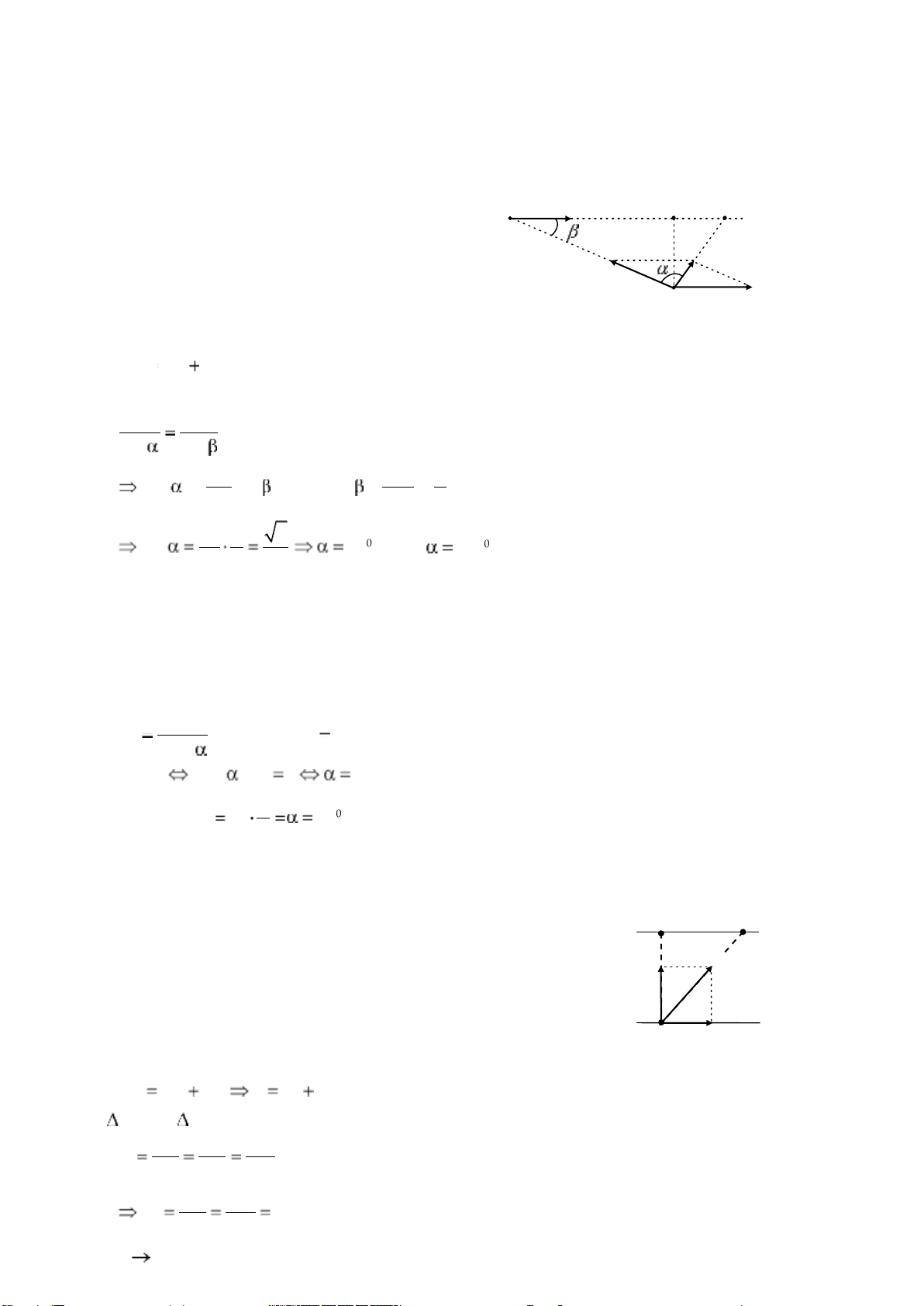
1.6 Máy bay bay từ A tới B lOMoARcPSD| 38841209 B v1 v ' T Đ
Nam một góc so với phương AB với: v 3 v2 1 sin v2 25 N - Khi đó 2 2 v v2 v1 165,46 m/s - Thời gian bay: AB t 1813,127 s 30, 2 phút v
c. Gió thổi theo hướng Tây Đông 560 v1 v2 m/s 3 AB - Thời gian bay t 1607,143 s 28,78 phút v a. Không có gió: t s 0,5 h 30 phút v2
b. Gió thổi theo hướng Nam Bắc máy bay phải chếch về phía v
1.7 Chất điểm chuyển động nhanh dần đều - Áp dụng s v t0
at2 ; (v0 là vận tốc ban đầu) -
Đi hết quãng đường đầu hết: t1 5 s s1 5v0 12,5a 100 m (1) -
Đi hết toàn bộ 2 quãng đường hết t2 5 3,5 8,5 s s2 8,5v0 a 200 m (2) -
Từ (1) và (2) ta được a 2 m/ s2 .
1.8 Đoàn tàu rời ga chuyển động nhanh dần đều lOMoARcPSD| 38841209 -
Gọi là chiều dài mỗi toa, tn là thời gian để n toa tầu đầu tiên đi qua trước mặt người quan sát. - Khi toa đầu tiên đi qua: 1at2 (với v 2 0 0 ) 2 t1 2 a 1 toa đầu đi qua : - Khi n 1 2 n 1 n 1 2 2 atn1 tn1 2 a
- Khi n toa đầu tiên đi qua: 1.9 - Chọn t lOMoARcPSD| 38841209
1.10 Chất điểm chuyển động thẳng -
Gọi quãng đường, thời gian đi hết chặng, vận tốc cuối của mỗi chặng lần lượt
là: s , t , v ; s , t , v ; s , t , v1 1 1 2 2 2 3 3 3 - Ta có: t s t1 t2 t3 25 s s1 s2 s3 tb vt 50 m
1.11 Ném một vật theo phương thẳng đứng -
Chọn chiều (+) hướng xuống, t
0 là lúc vật được thả rơi tự do. 1 2 gt t 4 s -
Trường hợp rơi tự do: h 2
a. Phải ném vật xuống dưới 1 2 35 h v0 t 1 g t 1 v0 11,67 m / s 2 3 b. Phải ném vật lên trên 2 h v0 t 1g t 1 v0 9 m / s
1.12 Hai vật A, B chuyển động thẳng đứng -
Chọn trục toạ độ thẳng đứng, chiều (+) hướng lên, gốc toạ độ tại mặt đất, gốc
thời gian là lúc thả vật. -
Quãng đường chuyển động của vật rơi tự do và của vật được ném lên từ mặt đất có dạng: 1 1 s gt2 ; s' v t0 gt2 2 2
a. Hai vật gặp nhau ở độ cao h khi s H và s h lOMoARcPSD| 38841209 - Ta có: 1 2 1 H gt ; 2 h 0 vt gt 2 2 g h H gH 2 v0 h H 2 H 2 H
b. Khoảng cách x giữa hai vật trước lúc gặp nhau x H h s s h H gH 2 H h H h 2 H 2 gH 2H 2 H
c. Vật 2 ném lên sẽ chuyển động chậm dần đến khi vt
0 thì vật đạt độ cao cực đại: v 2 t v0 gt 0 2 v h H 2 0 gt ; hm ax h 2 g 4 H m ax 0 vt 2
- Áp dụng v0 15 m/s ; x 30 15 t ta được: hm ax 11 ,25 m
1.13 Tàu hoả chuyển động trên cung tròn -
Chọn chiều (+) là chiều chuyển động. A v s atB A B a B anA v B a tA nB a A a O 2 2 v v 0 2 atA atB 0 ,125m/s 2s a. Tại A ta có: 2 v 2 2 a 0 2 A atA anA với anA 0 ,28m/s R 2 2 2 A (0,125) 0, 28 0,31m /s a - Tại B ta có: 2 v 2 2 a 2 B atB anB với anB 0 ,03m/s R 2 2 2 B (0,125) 0 , 03 0 ,13m/s a
b. T hời gian tàu đi hết quãng đường: v v 5 15 0 t 80 s 2 a 0,125
1.14 Chuyển động của ba vật tới điểm M
- Gọi R là bán kính vòng tròn - Vật 1: s1 AM
2R; a1 g. Vậy thời gian chuyển động từ A đến M là: lOMoARcPSD| 38841209 2S1 4R t1 g g
- Vật 2: chuyển động tự do trên mặt phẳng nghiêng BM. s2 BM AM.cosAMB2R.cosAMB a2 g.cosAMB 2s2 4R t2 a2 g
- Vật 3: chuyển động tự do trên mặt phẳng nghiêng CM. s3 CM AM.cosAMC2R.cosAMC a3 g.cosAMC 2s3 4R t3 a3 g M vx a n v a y v0 720 k m/h 200 m/s g 2 2 2 2 2 vt vx vy v0 gt 2 v - Áp dụng công thức: an (1) R v v - Trong đó: x 0 an g.cos g g (2) vt vt 32 2 3 2 2 v v0 gt t - Từ (1) và (2) R gv0 gv0 - Với v0 200 m/s ; 2 g 9,8m /s ; t 5 s có: R 4500 m . - Dễ thấy t1 t2
t3 nghĩa là 3 vật sẽ tới M cùng một lúc. O v 0 x
1.15 Vật chuyển động ném ngang -
Chọn hệ trục toạ độ xOy.
- Chuyển động của vật có dạng chuyển động của vật được ném ngang, với: lOMoARcPSD| 38841209 a
1.16 Vật được ném ngang từ đỉnh tháp
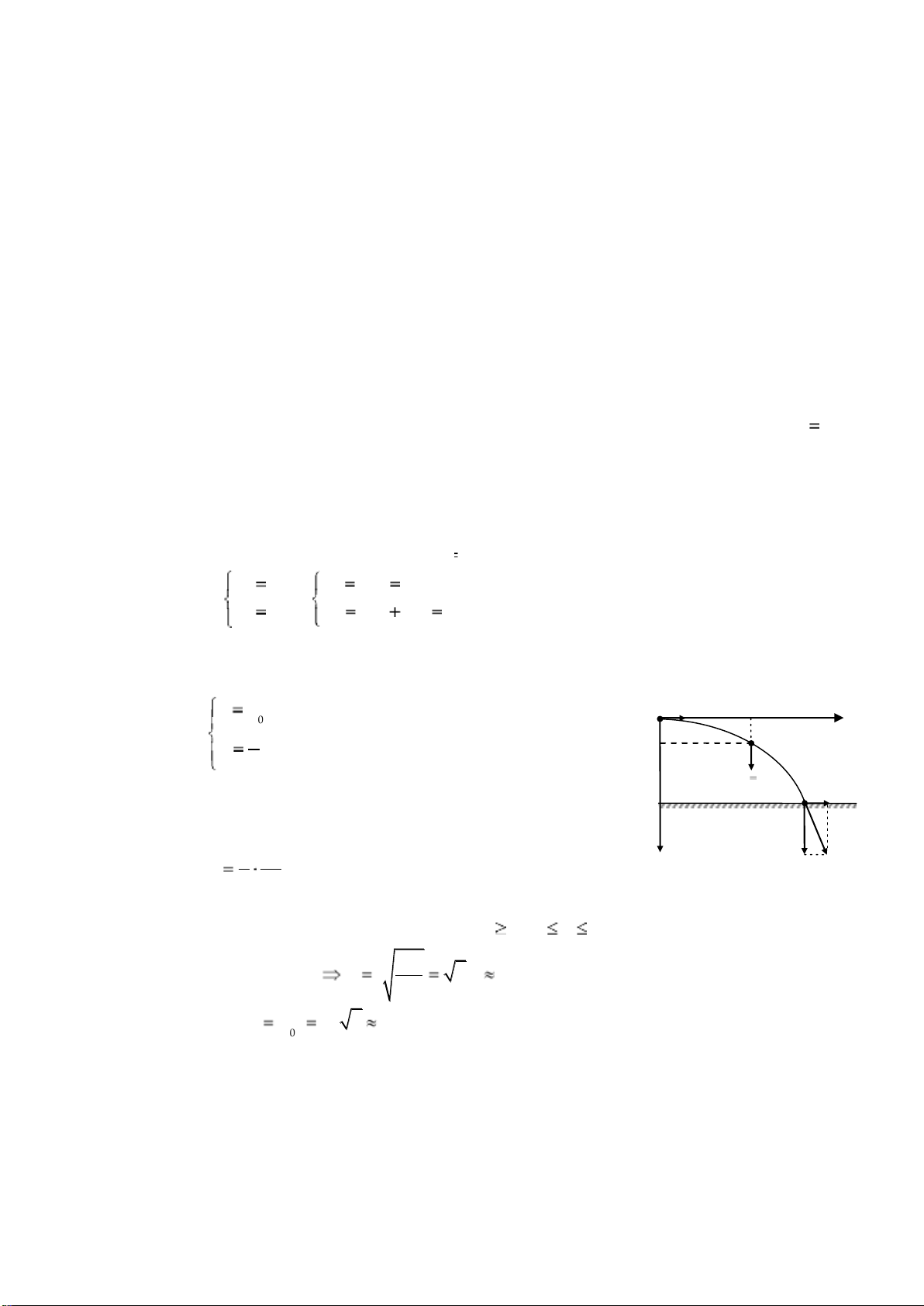
- Chọn mặt phẳng hình vẽ là mặt phẳng thẳng đứng chứa v0 , hệ trục xOy, t 0 là lúc ném vật.
a. Tại t, chất điểm ở M(x, y) và có a g ax 0 vx v0x v0 a ; v ay g vy v0y a ty gt
- Phương trình chuyển động theo Ox và Oy: O x 0 vt v0 x x 1 M 2 y gt y 2 ag vx N -
Khử t trong phương trình trên ta được phương trình quỹ đạo: v y v 1 g 2 y y 2 x 2 v0 -
Quỹ đạo có dạng 1 phần parabol ON (x 0; 0 y H) b. Hòn đá chạm đất khi : 2 H H 25 m t 5 s 2 ,24s y g 0 vt 155 33 ,54s c. Tầm xa: s d. Vận tốc: lOMoARcPSD| 38841209 2 2 2 dx dy 2 vN v0 gt 26 ,93m/s dt dt - Tại N: vy gt 0 vM ,v x sin 0 , 83 56 vN vN e. Bán - Gia tốc toàn phần : 2 a g 10 m/s kính cong 2 at asin gsin 8 ,3m/s 2 an acos gcos 5 ,6m/s của quỹ đạo v2 R 22,5 m
an - Tại điểm bắt đầu ném: v v ; a v 0 n g R0 02 22,5 m g
- Tại điểm hòn đá chạm đất: 2
2 vn 129,5 m v v ; an n acos 5,6 m/s R an
1.17 Viên đạn chuyển động ném xiên
a. Phương trình chuyển động, phương trình quỹ đạo lOMoARcPSD| 38841209 - Đặt - Tầm xa: x 2g g
1.18 Hai viên đạn được
bắn lên lần lượt bởi một súng đại bác - Hoàn toàn tương tự như bài 1.18, ta có phương trình chuyển
động của hai viên đạn là: 2 v sin 0 1 2 t t2 t1 10 ,7 s g cos 1 cos 2 Chương 2 lOMoARcPSD| 38841209
ĐỘNG LỰC HỌC CHẤT ĐIỂM
TÓM TẮT LÝ THUYẾT
1. Định luật II Newton F a hay F ma m
với F là tổng hợp các ngoại lực tác dụng lên chất điểm; m khối lượng của chất điểm;
a là vector gia tốc của chất điểm.
2. Lực hướng tâm v2 Fn m
(R là bán kính cong của quỹ đạo) R
3. Định lí về động lượng dp - Định lí 1: F; (p
mv là vector động lượng của chất điểm) dt t2 - Định lí 2: p p2 p1 Fdt t1
4. Biểu thức lực ma sát trượt (khô) Fms
kN; (k là hệ số ma sát, N là phản lực pháp tuyến)
5. Định lí về mô men động lượng
đối với điểm O và đối với trục dL/O dL/ M/O hoặc M/ dt dt
- Trong đó L OM mv r
p là mô men động lượng của chất điểm đối với điểm O
cố định. M/O OM F r F là mô men của lực tác dụng lên chất điểm đối với gốc O cố định.
6. Định luật Newton áp dụng cho chất điểm trong hệ qui chiếu phi quán tính
- Trong hệ quy chiếu O' chuyển động tịnh tiến so với hệ qui chiếu quán tính O với
gia tốc A ma' F Fqt lOMoARcPSD| 38841209
Với a' là gia tốc chất điểm trong hệ O’; F ngoại lực tác dụng lên chất điểm; Fqt mA
là lực quán tính đặt lên chất điểm. BÀI TẬP VÍ DỤ
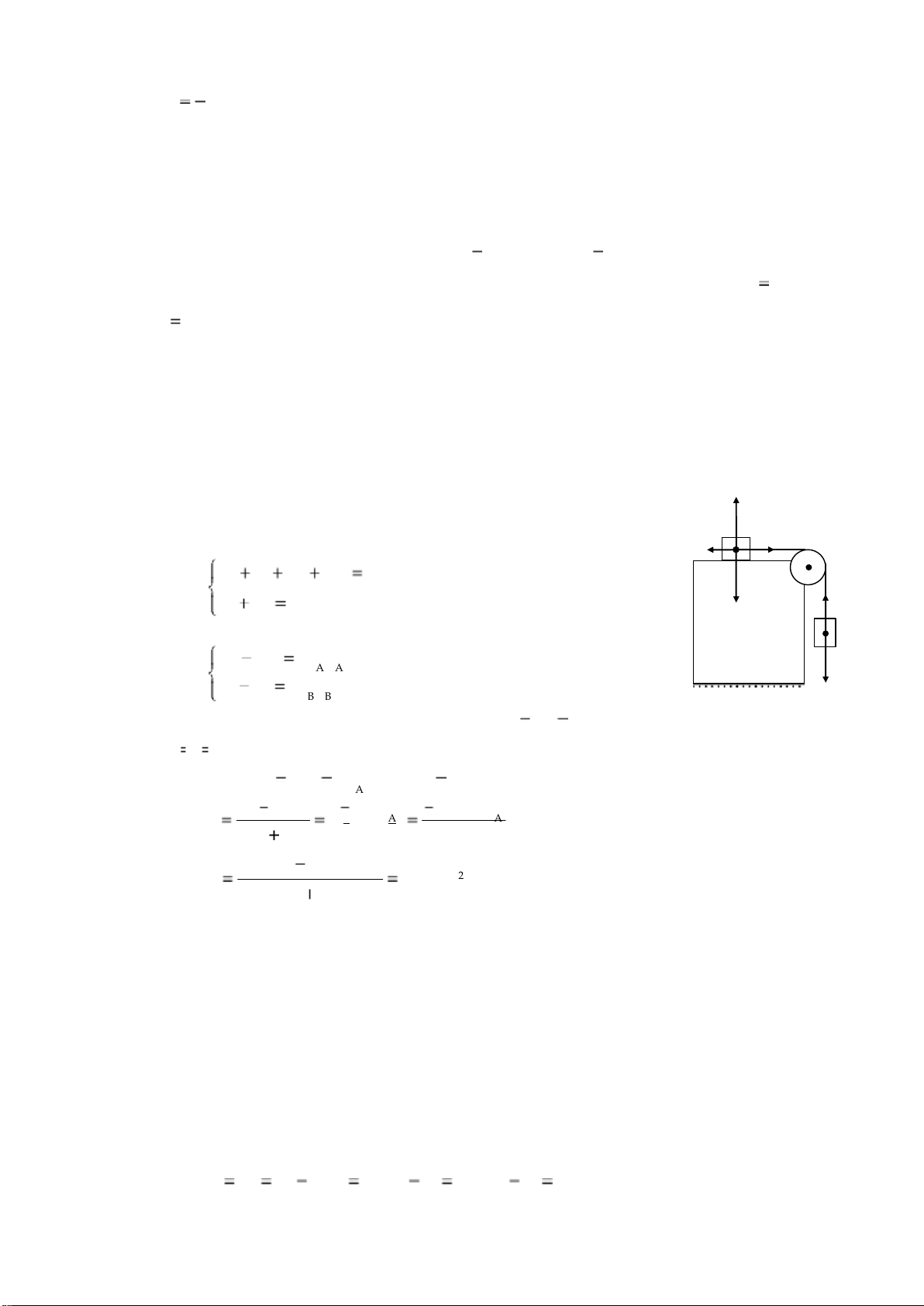
Ví dụ 1. Người ta gắn vào mép bàn một ròng rọc có khối lượng không đáng kể. Hai
vật A và B có khối lượng lần lượt mA 200g và mB 300g được nối với nhau bằng một sợi
dây vắt qua ròng rọc. Ma sát giữa vật A và mặt bàn có k 0,25. Lấy g 10m / s2 .
a. Xác định gia tốc chuyển động của hệ vật.
b. Tính lực căng của dây và lực nén lên trục của ròng rọc. Bỏ qua khối lượng dây và ma sát ở ròng rọc.
c. Nếu thay đổi vị trí vật A và B cho nhau thì lực căng của dây sẽ bằng bao nhiêu.
Xem hệ số ma sát giữa vật và bàn vẫn như cũ. Lời giải
a. Xác định gia tốc của hệ N
- Theo định luật II Newton ta có: A A T ms F PA N TA Fms m aA A (1) P A P BTB m aBB (2) A T ms F A ma A (3) - Chiếu P T ma (4) (1) và (2) B B B B
tương ứng lên phương chuyển
- Ở đây ta chú ý, vì dây không giãn nên aA aB
động của A và T B B T T .
B, chọn chiều dương là chiều - M ặt khác ms F kN A kP (do A P
chuyển động, ta được: B B P Fms B P A kP mB kmA a g mA mB mA mB mA mB PB 100,3 0 ,25.0, 2 2 5 m/s 0 , 2 0 , 3
a , ròng rọc không khối lượng nên TA
N). Kết hợp với (3) và (4) ta có gia tốc của hệ:
b. Tính lực căng của dây, lực nén lên trục ròng rọc -
Để xác định lực căng T, thay a vào (4) ta có: T TB PB m aB m (gB a) 0,3(10 5) 1,5 N lOMoARcPSD| 38841209
- Ròng rọc chịu hai lực căng T và phản lực của trục ròng rọc, như vậy ta thấy lực nén
lên trục ròng rọc chính là hợp lực của hai lực căng T, do đó ta có lực nén lên trục ròng rọc: Q 2T 1,5 2 N
c. Thay đổi vị trí vật A và B, ta cũng tính tương tự như trên và sẽ tìm được những biểu
thức về gia tốc của hệ và lực căng T của dây tương tự như phần trên, chỉ khác là
thay mA bằng mB và thay mB bằng mA, dễ dàng thấy rằng lực căng T của dây vẫn không thay đổi.
Ví dụ 2. Một vật đặt trên đỉnh dốc dài 165m, góc nghiêng của dốc 2
y là , hệ số ma sát giữa vật và mặt 9 ,8m/s . dốc k 0,2 . Lấy g N m F sn
a. Với giá trị nào của vật sẽ nằm yên mà không O trượt. x 0 P
b. Cho 30 . Hãy tìm thời gian vật trượt xuống hết
đoạn dốc và vận tốc của vật ở chân dốc. Lời giải
a. Xác định giá trị của để vật nằm cân bằng -
Chọn hệ trục xOy như hình vẽ. Khi vật nằm cân bằng ta có: P N Fmsn 0 (1)
- Chiếu (1) lên các trục Ox, Oy: Psin m F sn 0 (2) N Pcos 0 (3) -
Từ (2) ta có Fmsn Psin . Để vật nằm yên không bị trượt trên dốc thì lực ma sát
nghỉ lực ma sát trượt, nên: Fmsn kN kPcos Psin kPcos tg k 0,2 110 -
Vậy để vật nằm yên trên mặt dốc thì 110 .
b. Tính thời gian trượt và vận tốc ở chân dốc khi 300 - Với
300 , vật sẽ trượt trên mặt dốc, ta có: P N Fms ma (4) - Chiếu (4) lên Ox, Oy Psin Fms ma (5) N Pcos 0 (6)
- Từ (5) và (6) ta tìm được: a g(sin kcos ) 0 0 2 9,8 sin30 0,2.cos30 3,2 m / s lOMoARcPSD| 38841209
- Thời gian để vật trượt hết đoạn dốc s 165m (chú ý rằng vận tốc ban đầu bằng 0): s 1at2 t 2s 10,16 s 2 a
- Vận tốc của vật ở chân dốc: v at 3,2.10,16 32,5 m / s
Ví dụ 3. Một chất điểm có khối lượng m được ném lên từ một điểm O trên mặt đất,
với vận tốc ban đầu v0 theo hướng nghiêng một góc
với mặt phẳng ngang. Xác
định mô men động lượng của chất điểm đối với điểm O, tại thời điểm chất điểm đạt
độ cao cực đại. (Áp dụng với: m 100g; 300 ; v0 25m / s). Lời giải
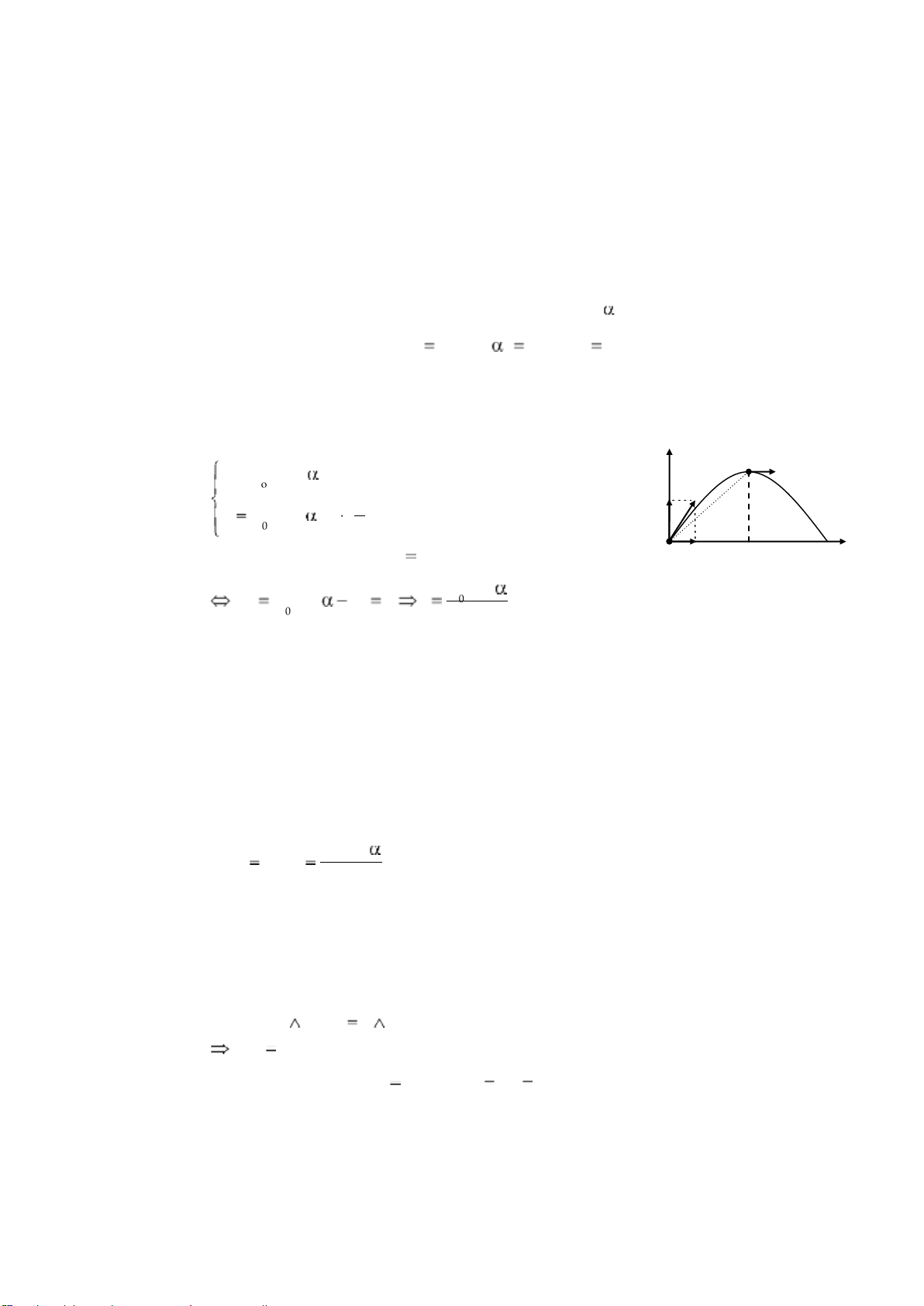
- Chọn hệ trục toạ độ xOy như hình vẽ, gốc thời gian là lúc ném. A x v v A o cos .t 1 v 2 oy r y v m h ax 0 sin .t gt 2 O
- Tại độ cao cực đại A ta có v x ox v y 0 vsin 0 vy v0 sin gt 0 t t1
- Phương trình chuyển động: y g
- Thay vào phương trình chuyển động ta được: v sin02 hmax y(t )1 2g
- Mômen động lượng của chất điểm tại A đối với O: L/O OA mvA r mvA L/O mv r.sin(r,v )A A -
Mặt khác ta có: r.sin r,vA hmax ; vA vx vox nên: L/O lOMoARcPSD| 38841209 2 2 3 2 - Thay số ta được: v0 sin mv0 sin .cos L hm ax mvx mv0 cos 2 g 2 g 2 Ví dụ 4. /O 28 ,18kgm/s . m
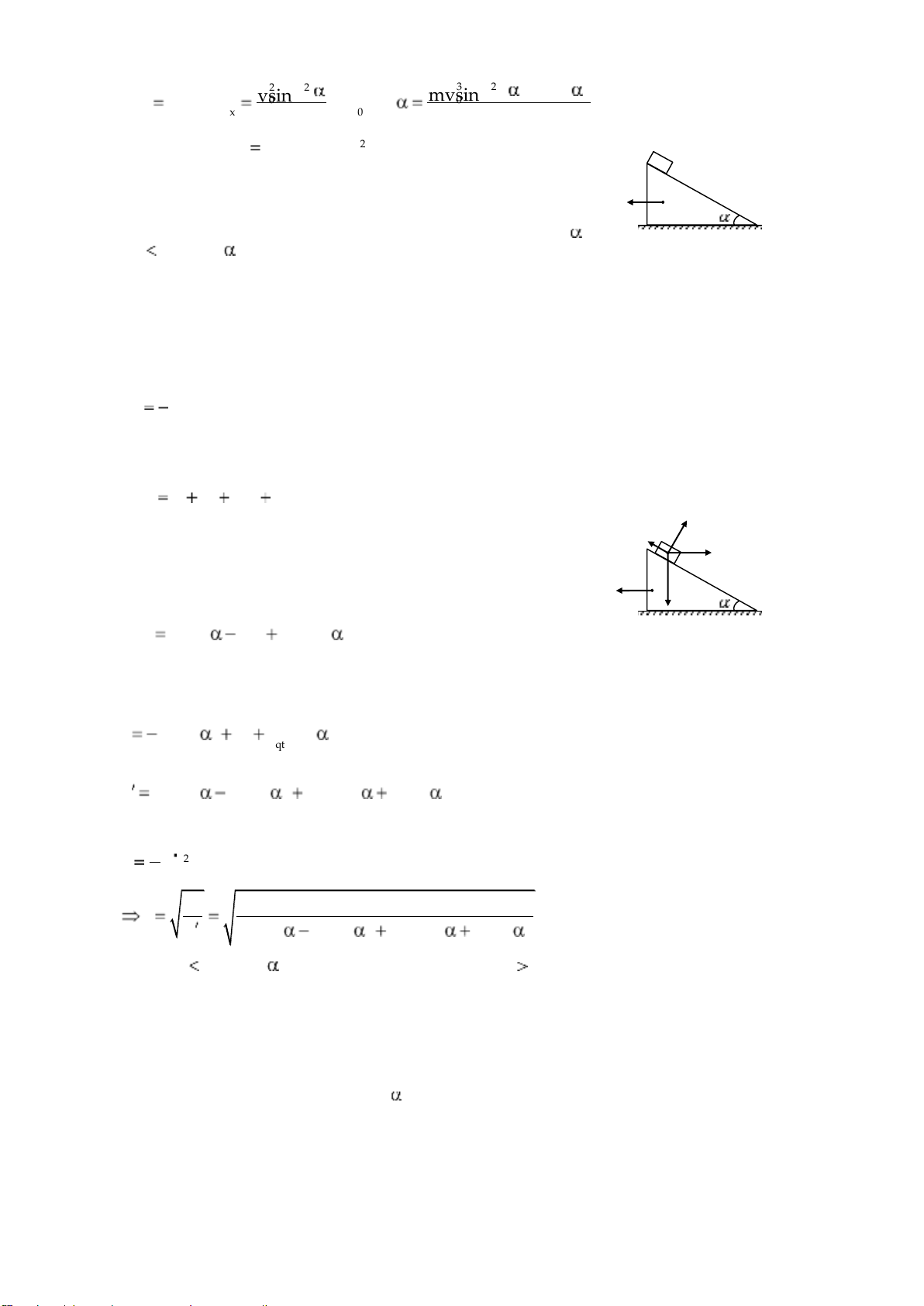
Một vật khối lượng m đứng yên ở đỉnh một cái nêm nhờ
ma sát. Tìm thời gian vật trượt hết nêm khi cho nêm 0 a
chuyển động nhanh dần đều sang trái với gia tốc là a0 . Hệ và
số ma sát giữa mặt nêm và vật m là k, chiều dài mặt nêm là
, góc nghiêng là gia tốc a0 g.cotg . Lời giải -
Xét trong hệ quy chiếu gắn với nêm là hệ quy chiếu chuyển động tịnh tiến với
gia tốc a0 , vật m sẽ chịu thêm lực quán tính: Fqt ma0 -
Áp dụng định luật Newton cho vật m trong hệ quy chiếu chuyển động có gia
tốc gắn với nêm, ta có phương trình chuyển động: ma'PN N F F ms ms Fqt (1) qt F a
với a' là gia tốc của vật m trong hệ quy chiếu gắn với nêm. 0 P -
Chiếu (1) lên hướng chuyển động của vật: ma' Psin Fms F cosqt (2) -
Chiếu (1) lên hướng vuông góc với hướng chuyển động của vật và chọn chiều dương hướng lên: 0 Pcos N qt F sin (3)
- Từ (2) và (3) suy ra gia tốc: a gsin kcos a0 cos ksin
- Để tìm thời gian vật trượt hết nêm, áp dụng phương trình: 1 2 at 2 2 2 t a gsin kcos a0 cos ksin - Chú ý: với a0 g.cotg
để phản lực pháp tuyến N 0 . BÀI TẬP ÁP DỤNG
2.1 Một người di chuyển một chiếc xe với vận tốc không đổi. Lúc đầu người ấy kéo xe
về phía trước, sau đó người ấy đẩy xe về phía sau. Trong cả hai trường hợp, càng xe
hợp với mặt phẳng ngang một góc . Hỏi trong trường hợp nào, người đó phải đặt lên
xe một lực lớn hơn. Biết trọng lượng của xe là P, hệ số ma sát giữa bánh xe và mặt đường là k. lOMoARcPSD| 38841209
2.2 Một dây xích có chiều dài 1m được đặt trên mặt bàn sao cho một phần của nó
buông thõng xuống đất có chiều dài là '. Cho biết hệ số ma sát giữa xích và bàn là k
1/ 3. Tìm chiều dài ' để dây xích bắt đầu trượt trên mặt bàn.
2.3 Một xe vận tải chạy trên đường nằm ngang với vận tốc không đổi. Sau đó xe lên 0
dốc, nghiêng với mặt nằm ngang một góc 15 . Muốn xe vẫn chuyển động đều với vận
tốc như cũ thì lực kéo của động cơ phải lớn gấp bao nhiêu lần
so với khi chạy trên đường nằm ngang. Ma sát trong hai trường 0 , 05 . hợp đều có k
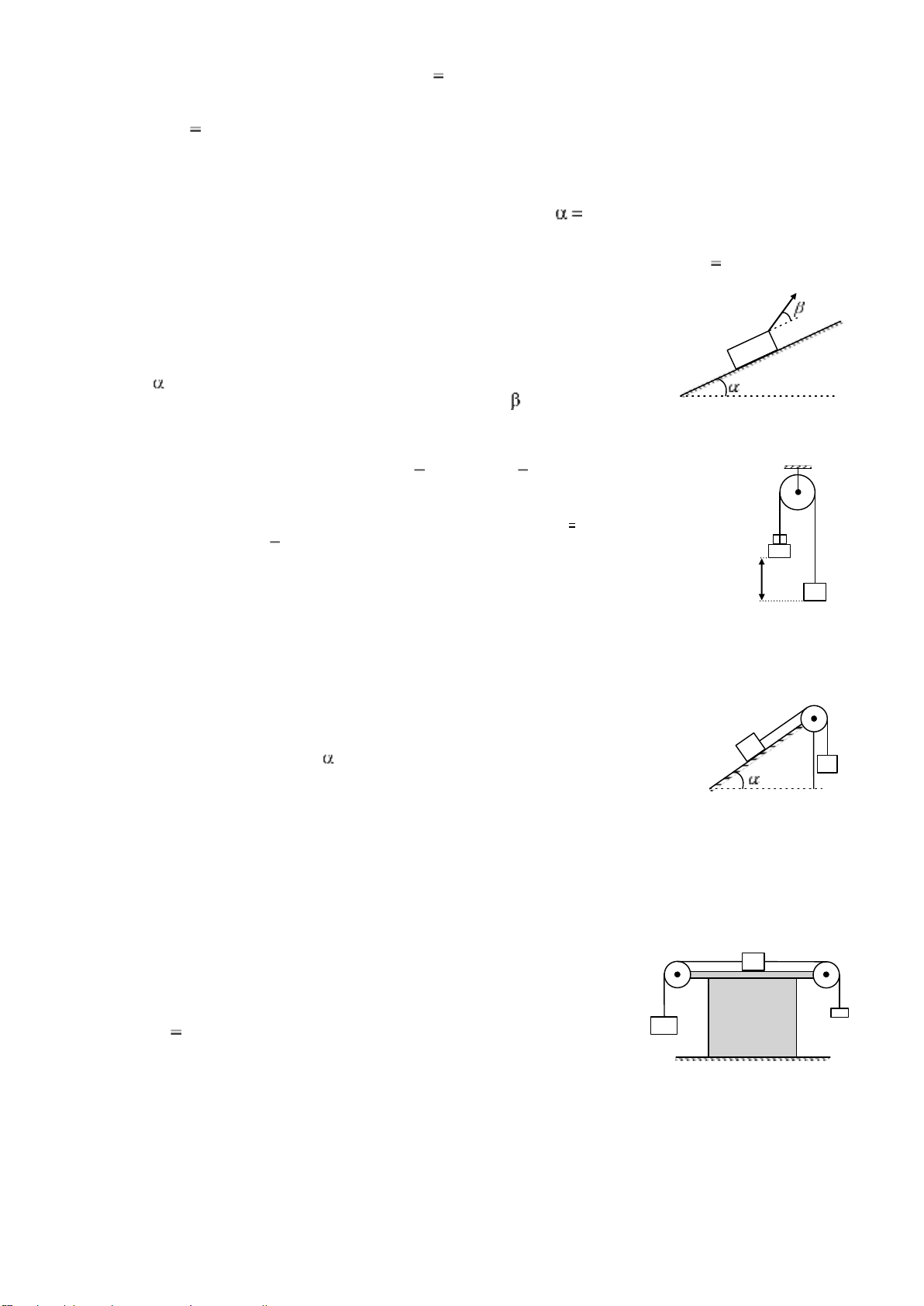
2.4 Một vật khối lượng m được kéo đi với vận tốc không đổi m
bởi một sợi dây trên một mặt phẳng nghiêng có góc nghiêng
với mặt phẳng ngang. Hệ số ma sát giữa vật và mặt phẳng
nghiêng bằng k. Xác định góc giữa sợi dây và mặt phẳng nghiêng để cho sức căng
nhỏ nhất. Tính giá trị sức căng đó.
2.5 Hai vật có khối lượng m1 300 g; m2 480 g được buộc vào hai đầu một
sợi dây vắt qua một ròng rọc có khối lượng không đáng kể. Lúc đầu, giữ
vật m1 ở dưới vật m2 một khoảng h 2m và trên vật m2 có đặt vật m3 200 m 3
g , sau thả cho hệ vật chuyển động. Xác định: m 2 h
a. Gia tốc của các vật và sức căng của dây. m1
b. Sau bao lâu vật m1 và m2 ở độ cao như nhau.
c. Lực tác dụng của vật m3 lên vật m2 khi hệ chuyển động. Bỏ qua khối lượng dây và ma sát ở ròng rọc.
2.6 Có hai vật khối lượng m1, m2 liên kết với nhau bằng một m
sợi dây vắt qua ròng rọc ở đỉnh của mặt phẳn nghiêng hợp với 1 m2
mặt ngang một góc . Vật m1 nằm trên phẳng nghiêng. Hệ số ma sát giữa m
1 và mặt nghiêng là k. Giả thiết lúc đầu hai vật đứng yên.
a. Với điều kiện nào của tỉ số các khối lượng ( m / m2 1 ) để cho vật m2: đi xuống; đi lên; đứng yên.
b. Xác định gia tốc của hệ vật trong hai trường hợp đầu. Bỏ qua khối lượng ròng rọc
và dây, ma sát ở ròng rọc không có.
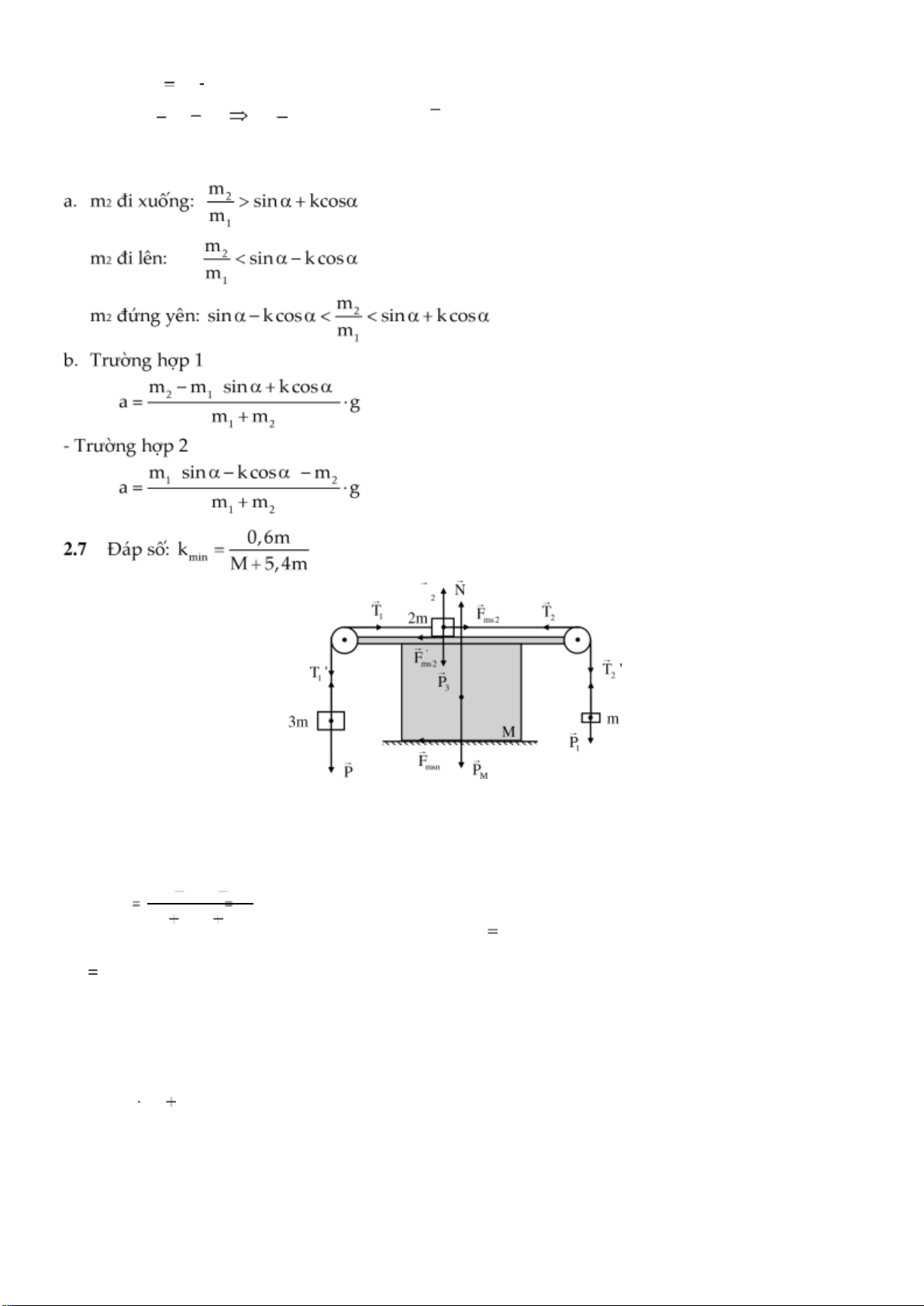
2.7 Trên một cái bàn có khối lượng M, đặt một hệ gồm 2m
ba vật có khối lượng: m, 2m, 3m được liên kết với nhau
bằng các sợi dây. Hệ số ma sát giữa vật 2m và bàn là k 0,1. M m
Hỏi hệ số ma sát giữa bàn và mặt sàn phải có giá trị nhỏ 3 m
nhất bằng bao nhiêu để bàn đứng yên khi hệ vật chuyển động. Bỏ qua khối lượng
dây và ròng rọc, ma sát ở các ròng rọc là không đáng kể. lOMoARcPSD| 38841209
2.8 Trên mặt nghiêng hợp với mặt ngang 0 30 có m 2
một góc đặt hai vật tiếp giáp nhau khối 1 kg , m 1
lượng lần lượt là m1 m2 2kg . Hệ số
ma sát giữa các vật và mặt nghiêng lần lượt là k1 0,25 và k2 0,1.
a. Xác định lực tương tác giữa hai vật khi chuyển động.
b. Góc nghiêng phải có giá trị nhỏ nhất bằng bao nhiêu để cho các vật có thể trượt xuống.
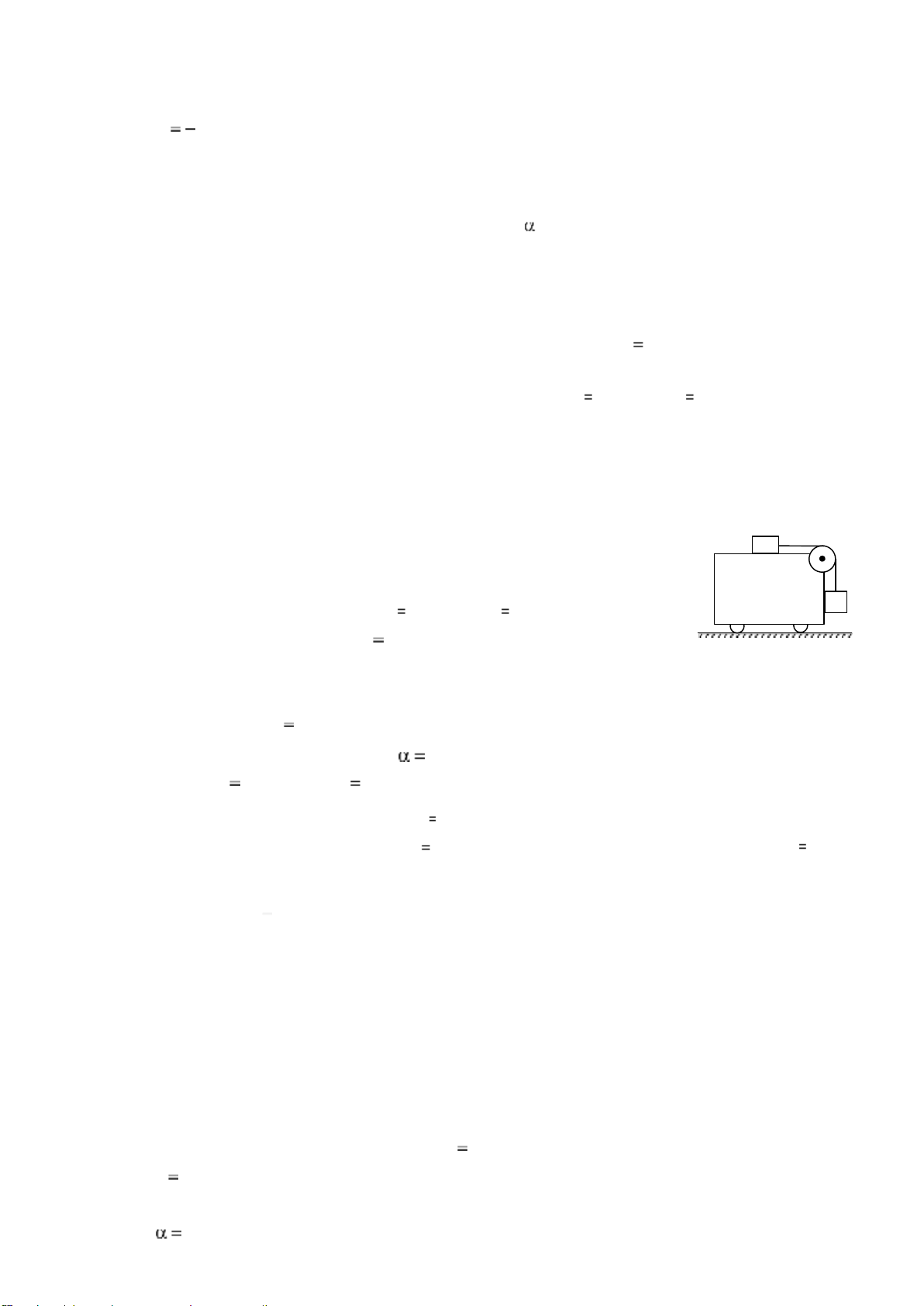
2.9 Một chiếc xe có khối lượng M 20kg có thể chuyển động không m
ma sát trên mặt phẳng ngang. Trên xe đặt một hòn đá khối lượng M F
m 5kg. Hệ số ma sát giữa đá và xe là k 0,2 . Người ta
đặt lên xe một lực F có phương nằm ngang và hướng dọc theo xe. Hỏi:
a. Muốn hòn đá không trượt trên xe khi xe chuyển động thì lực F chỉ có thể có giá trị
lớn nhất bằng bao nhiêu?
b. Nếu lực F 60N hòn đá và xe sẽ chuyển động thế nào? Xác định gia tốc của hòn đá
và xe đối với mặt đất. 2.10
Một viên đạn khối lượng 10g chuyển động với vận tốc v0 200m/ s xuyên thẳng
vào một tấm gỗ và chui sâu vào một đoạn . Biết thời gian chuyển động của đạn trong
tấm gỗ là t 4.10 4 s. Xác định lực cản trung bình của gỗ và độ xuyên của viên đạn. 2.11
Một phân tử khí có khối lượng m 4,65.10 23 g chuyển động với vận tốc v 160m/s 0
tới va chạm đàn hồi vào thành bình với góc nghiêng 60 so với
pháp tuyến của thành bình. Tính xung lượng của lực va chạm của phân tử khí lên thành bình. 2.12
Một vật có khối lượng m 1kg chuyển động thẳng trên mặt sàn ngang theo
phương x, với vận tốc ban đầu v0 10m/s và chịu lực cản Fc rv, với r 1kg /s là hệ số cản
và v là vận tốc chuyển động của vật.
a. Chứng minh rằng vận tốc của vật giảm dần theo hàm số bậc nhất của quãng đường đi.
b. Tính quãng đường đi được tới lúc dừng.
2.13 Một viên đạn có khối lượng m 10g bay theo phương ngang trong không khí với
vận tốc ban đầu v0 500m/ s. Cho biết lực cản của không khí tỉ lệ và ngược
3 chiều với vận tốc v của viên đạn: Fc rv với r 3,5.10 kg /
s là hệ số cản của không khí. Bỏ qua ảnh hưởng của trọng lực. Hãy xác định:
a. Khoảng thời gian để vận tốc viên đạn bằng một nửa vận tốc ban đầu v0.
b. Quãng đường viên đạn bay được theo phương ngang trong khoảng thời gian trên. lOMoARcPSD| 38841209
2.14 Một vật khối lượng m chuyển động từ dưới lên theo phương thẳng đứng Ox với
vận tốc ban đầu v0. Biết lực cản của không khí tỉ lệ với bình phương vận tốc: F
rv2 (r là hệ số tỉ lệ). Tính độ cao cực đại vật lên được và thời gian vật lên đến độ cao cực đại.
2.15 Một chất điểm khối lượng m được ném lên từ một điểm O trên mặt đất với vận
tốc ban đầu v0 theo hướng nghiêng một góc với mặt phẳng ngang. Bỏ qua sức cản
không khí. Hãy xác định tại một thời điểm t và đối với điểm O. a. Mô men ngoại lực
tác dụng lên chất điểm.
b. Mô men động lượng của chất điểm.
2.16 Trên trần một thang máy đang đi lên với gia tốc a0 1,2 m / s2 có gắn một lực kế.
Đầu dưới lực kế có treo một ròng rọc, người ta vắt qua ròng rọc một sợi dây và hai
đầu dây treo hai vật khối lượng lần lượt là m1 200g , m2 300g. Bỏ qua khối lượng và ma
sát ở ròng rọc, dây không giãn và có khối lượng không đáng kể đáng kể. Xác định:
a. Gia tốc của vật m1 so với đất và với thang máy.
b. Số chỉ trên lực kế. 2.17
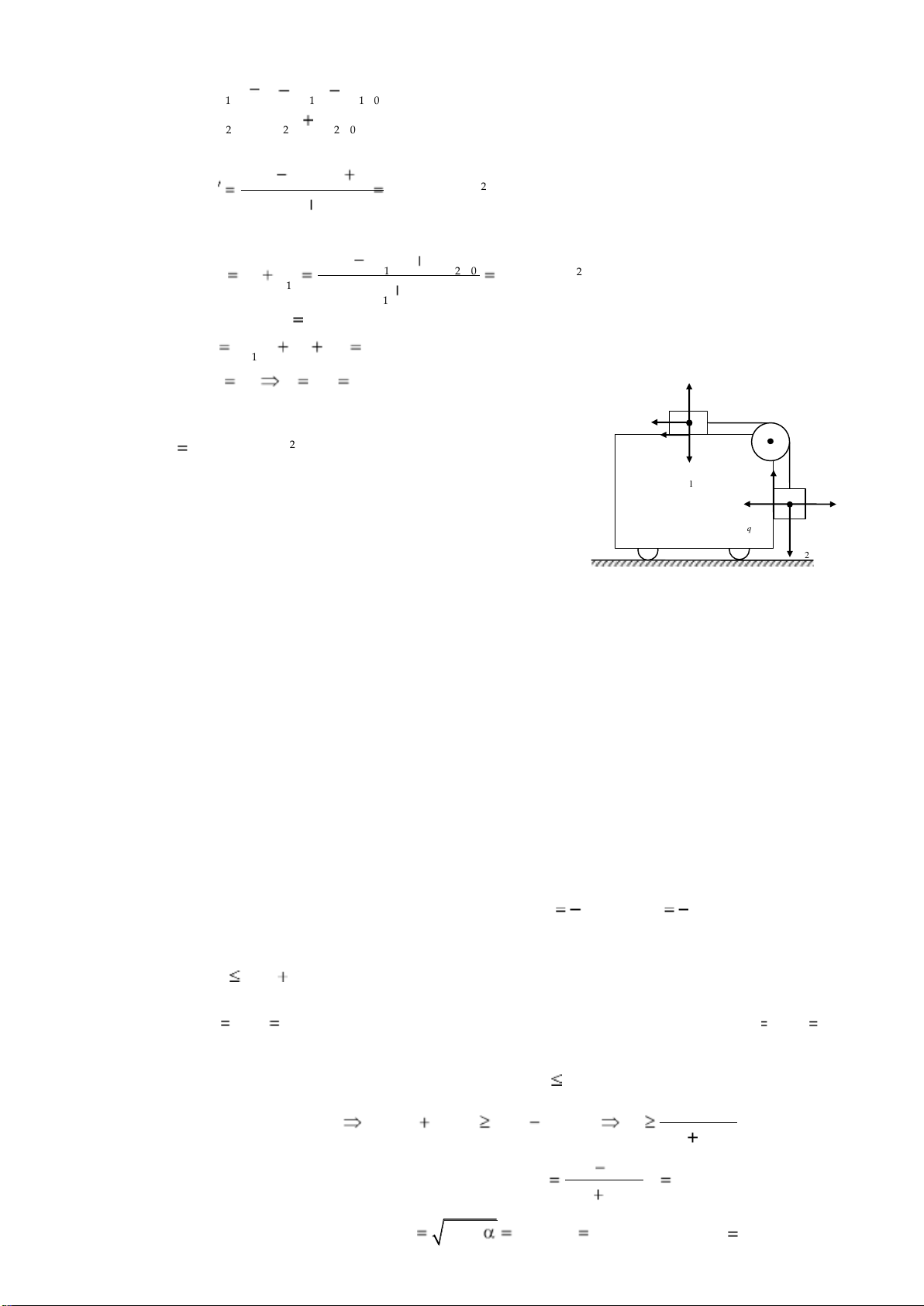
Cho hệ vật như hình vẽ bên. Cần phải dịch chuyển một m 1
chiếc xe theo phương ngang với gia tốc nhỏ nhất bằng bao nhiêu
để cho các vật m1 và m2 không chuyển động đối với xe. Cho khối
lượng các vật m1 300g , m2 500g; hệ số ma sát giữa vật m1, m2 và m 2
xe là k 0,2 . Bỏ qua khối lượng ròng rọc và dây nối, ma sát ở ròng rọc không đáng kể. 2.18
Hỏi tàu hoả phải có vận tốc bằng bao nhiêu khi chạy qua một đoạn đường vòng
có bán kính R 98m để sợi dây treo quả cầu buộc vào trần toa tàu lệch so với phương
thẳng đứng một góc 450 . Xác định sức căng của dây, biết khối lượng quả cầu là m 500g. Lấy g 9,8m / s2 . 2.19
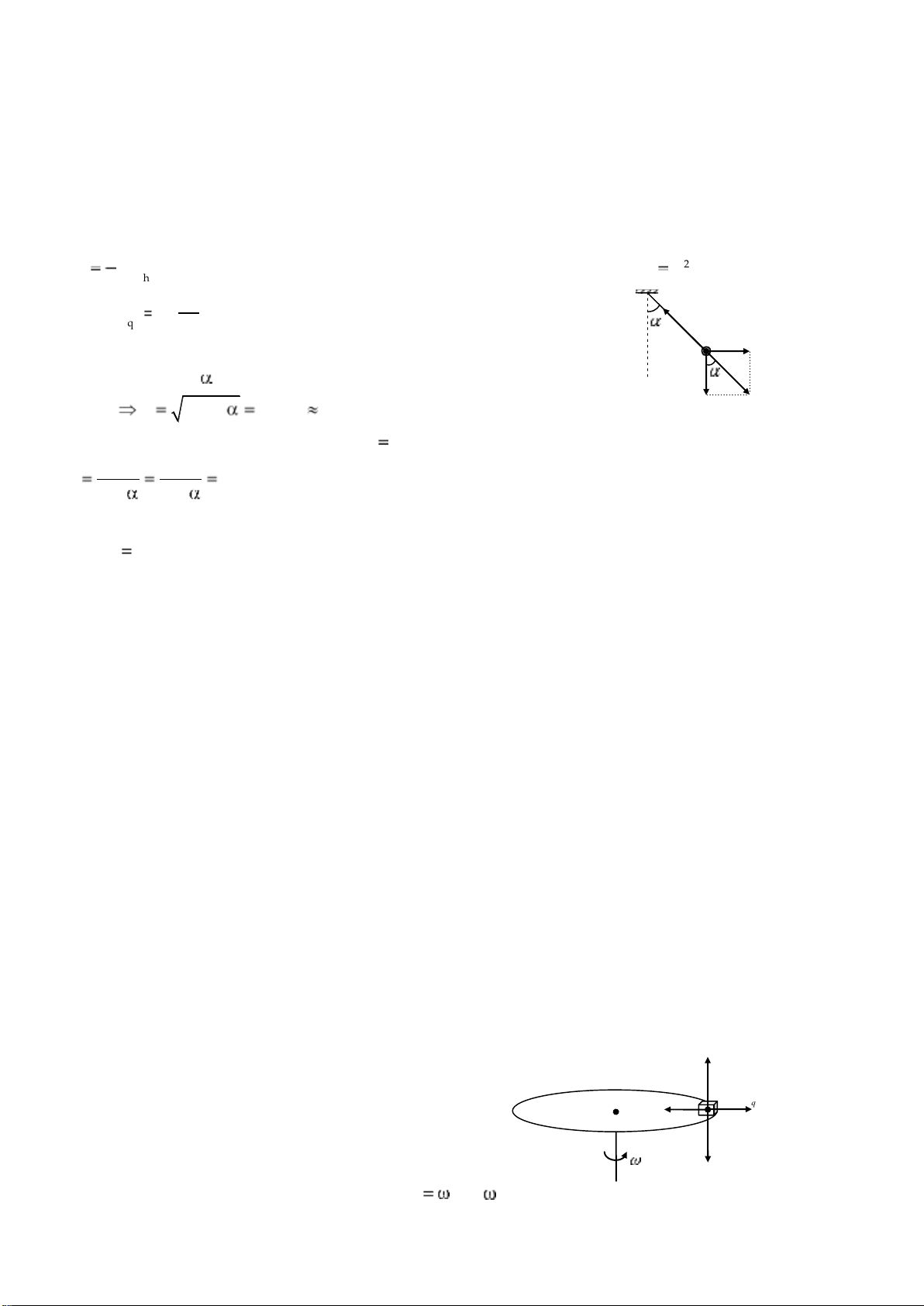
Một vật nhỏ khối lượng m 1kg được đặt trên một đĩa phẳng ngang và cách trục
quay của đĩa một khoảng r 0,5m . Hệ số ma sát giữa vật và đĩa bằng k 0,25. Hỏi:
a. Lực ma sát phải có độ lớn bằng bao nhiêu để vật giữ trên đĩa, nếu đĩa quay với vận tốc n 12 vòng/phút.
b. Với vận tốc góc nào của đĩa thì vật bắt đầu trượt khỏi đĩa.
2.20 Một máy bay thực hiện một vòng nhào lộn có bán kính 400m trong mặt phẳng
thẳng đứng với vận tốc 540km/h.
a. Xác định lực nén của phi công lên ghế máy bay ở điểm cao nhất và thấp nhất của
vòng nhào lộn, nếu khối lượngcủa phi công bằng 60kg.
b. Muốn cho người lái ở trạng thái không trọng lượng tại điểm cao nhất của vòng
nhào lộn thì vận tốc của máy bay phải bằng bao nhiêu ?
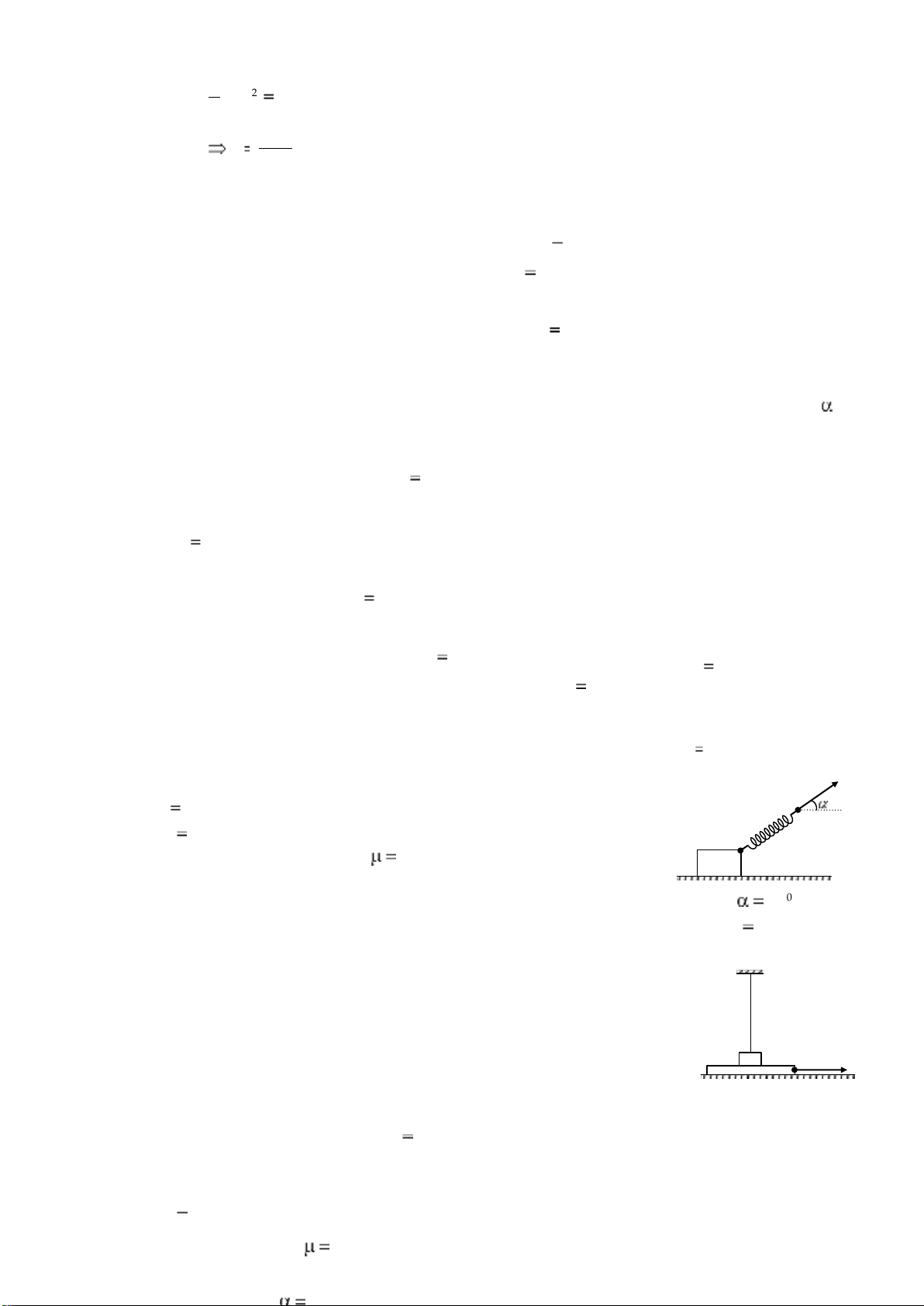
2.21 Một quả cầu khối lượng m 500g được treo vào đầu một sợi dây dài 50cm. Quả
cầu quay trong mặt phẳng nằm ngang với vận tốc không đổi sao cho sợi dây vạch một lOMoARcPSD| 38841209
mặt nón. Cho biết góc tạo bởi sợi dây và phương thẳng đứng là 300 . Xác định lực căng
dây, vận tốc dài và vận tốc góc của quả cầu.
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ
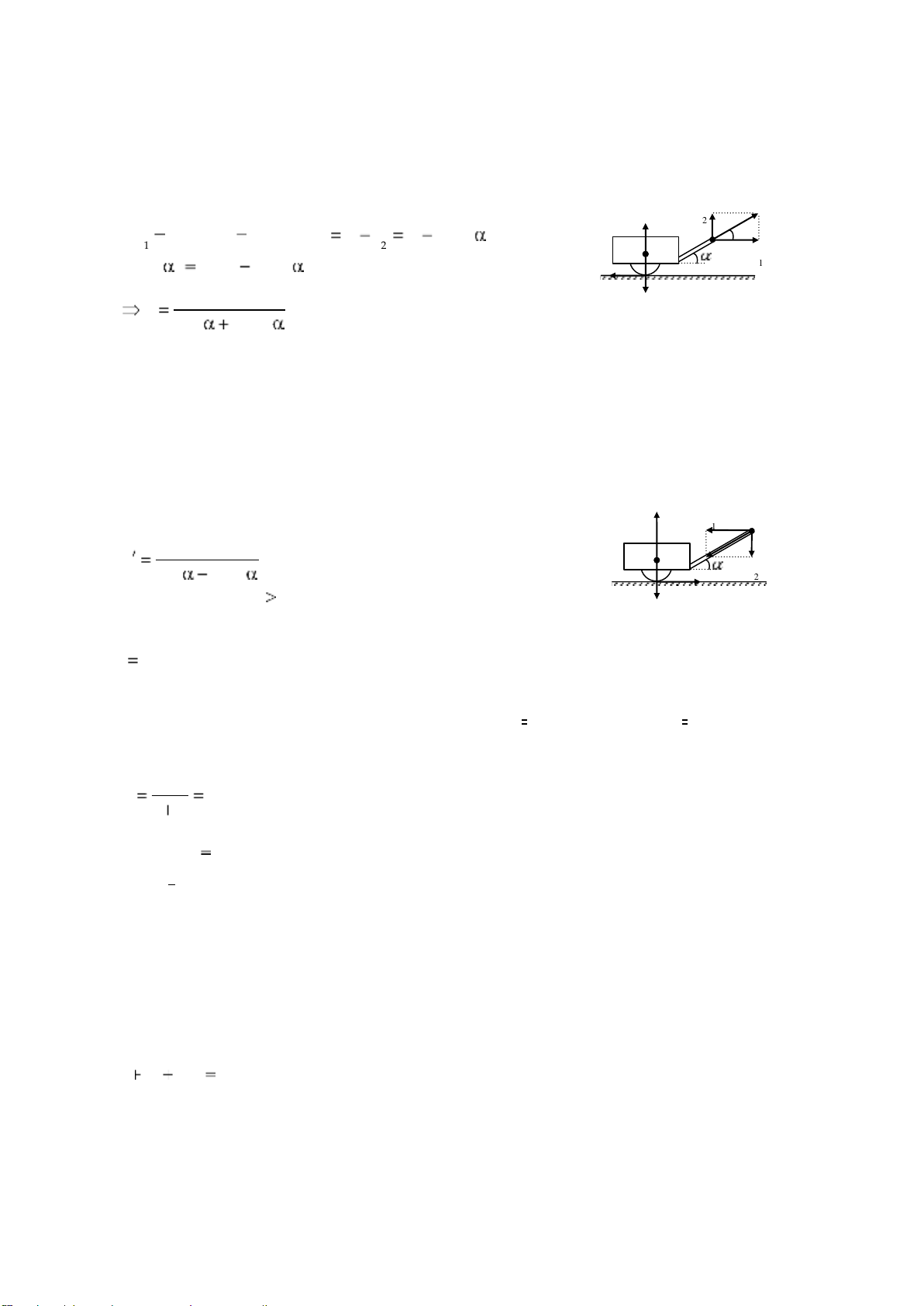
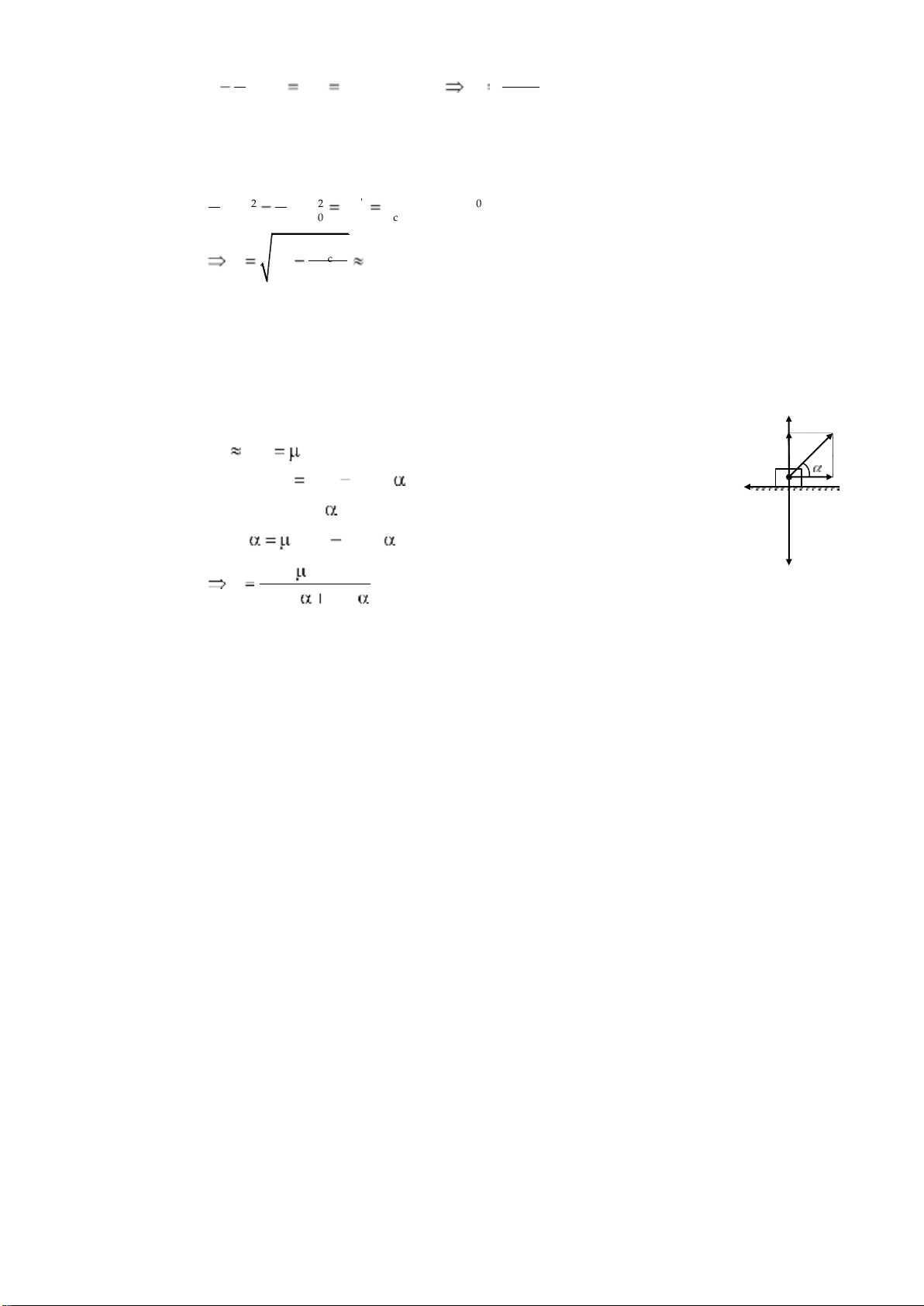
2.1 Trường hợp đẩy xe về phía sau phải dùng lực lớn hơn. N 2 F phải có: 1 F ms F , ms F kN và N P 2 F P Fsin . 1F - Hay: Fcos kP Fsin kP ms F P F cos ksin
- Trường hợp kéo xe về phía trước, muốn xe chuyển động đều F -
Trường hợp đẩy xe về phía sau, xe chịu trọng lực P, lực đẩy F, phản lực pháp
tuyến N' và lực ma sát Fms' bằng cách phân tích tính tương tự: kP , N 1 F F , F cos ksin , 2 F -
So sánh F và F' thấy F' F, suy ra trường hợp đẩy xe về phía , P m F s
sau phải dùng lực lớn hơn. 2.2 ' 0,25 m -
Gọi P1 là trọng lượng của phần buông thõng; P2 là trọng lượng của phần dây
xích nằm trên mặt bàn. Muốn dây bắt đầu trượt phải có P1 Fms ; trong đó Fms kP2 (chú ý:
trọng lượng của các phần dây xích tỉ lệ với chiều dài), từ đó suy ra: ' k0,25 m 1 k
2.3 Đáp số F2 6,1 lần. F1 -
Gọi F1, F2 là lực kéo của động cơ trên đường ngang và đường dốc, muốn xe
chuyển động đều thì tổng hợp lực tác dụng lên ôtô gồm: lực kéo của động cơ, trọng lực
P, phản lực pháp tuyến N của mặt đường và lực ma sát của mặt đường
Fms phải bằng không. F P N Fms 0 -
Chiếu phương trình lên hướng chuyển động được biểu thức: F1, F2 và suy ra tỉ số F / F2 1 lOMoARcPSD| 38841209 mgsin kcos k; Tm in 2.4 Đáp số: tg 2 1 k -
Lực tổng hợp tác dụng lên vật: F T P N Fms 0 (1) -
Chiếu (1) lên hướng chuyển động và lên phương vuông góc với hướng chuyển động, ta có: Tcos Psin ms F 0 (2) Tsin N Pcos 0 (3) NPcos Tsin ms F kN kPcos Tsin mgsin kcos - Th ay vào (2) rút ra: T cos ksin
- Theo bất đẳng thức Bunhiacốpxki - Côsi: 2 2 2 2 cos ksin 1 k cos sin const 2 1 cos ksin lớn nhất khi: tg k - Vậy: cos k sin 2 ksin 1 k suy ra: - Và cos max mgsin kcos m T in 2 1 k a. a 3,8 m/s2 ; T 2.5 Đáp số: 4,08 N b. t 0,73 s c. F32 1,2 N Hướng dẫn:
a. Viết phương trình của đinh luật II Niutơn cho từng vật: T 1 ma 1 2 m3 a2 23 P T'
- Chiếu lên phương trình chuyển động của hệ: 1 1 P T (1) 2 m3 a 2 P 3 P T (2)
- Chú ý: T T và a là gia tốc của hệ. Từ (1) và (2) giải ra: a và T. h 1 b. Ta có: 2 h 2 s at t 0 ,73s 2 2 a 3, 8
c. Tính F 23 . Xét riêng vật m 3 , ta có phương trình: P1 m m a m lOMoARcPSD| 38841209
m a32 P3 F23 ; (F23 là lực do m2 tác dụng lên m3) hay: m a3 P3 F23 F23 m3 g a và F32 F23 2.6 Đáp số: N 3 -
Khi bàn đứng yên, hệ vật chuyển động, ta tìm được gia tốc chuyển động của hệ 3 vật: P3 kP2 P1
0,3g (với g là gia tốc trọng trường) a m 2m 3m -
Lực căng dây nối giữa vật 3m và 2m là: T1
2,1mg; giữa vật 2m và m là: T2 1,3mg . -
Xét riêng bàn, để bàn đứng yên thì: ' T1 T ' F1 ms2 P2 PM T2 T ' N2 Fmsn 0 (1)
- Trong đó: Fms2' là lực ma sát do vật 2m tác dụng lên bàn khi nó trượt trên mặt bàn, lOMoARcPSD| 38841209
có: Fms2' 2kmg 0,2mg . N là phản lực của mặt sàn tác dụng lên bàn; Fmsn là tổng các lực
ma sát nghỉ tác dụng lên các chân bàn.
- Chiếu (1) lên phương thẳng đứng, chọn chiều dương hướng lên trên; và chiếu (1) lên
phương ngang với chiều dương hướng sang phải, ta được: 2.8 a. F12 b. tg
a. Xác định lực tương tác giữa hai vật
- Vì hệ số ma sát k1 k , n 2
ên hai vật sẽ cùng trượt xuống trên mặt nghiêng; áp dụng định
luật II Newton cho hệ 2 vật tìm được gia tốc a của hệ. Sau xét riêng từng vật m1 (hoặc m2), sẽ tính
được lực tương tác F21(hoặc F12). b. Xác định góc min
- Muốn hệ hai vật trượt xuống, các thành phần lực Pt1 , Pt2 của trọng lực P1 , P2 theo
hướng song song mặt nghiêng thoả mãn điều kiện: Pt1 Pt2 Fms1 Fms2 (1). Fms1 , Fms2 là lực ma
sát tác dụng lên m1, m2 của mặt phẳng nghiêng. Pt1m gsin1 ; Pt2 m gsin2 Fms1k m gcos ; F1 1 ms2 k m gcos2 2 lOMoARcPSD| 38841209 - Th ay vào (1): km km 1 1 2 2 tg suy ra tg và m min min 1 m2 2.9 Đáp số: a. m F ax 49 N b. 2 2 a , 1 96 m/s ; a 2 , 51 m/s 1 da 2 xe Hướng dẫn:
a. Xác định lực cực đại Fmax -
Vì hòn đá không trượt trên xe, nên hệ (đá + xe) cùng chuyển động với gia tốc a (1). Và
lực do xe tác dụng lên đá khi chuyển đông (xét riêng hòn đá): F lOMoARcPSD| 38841209 chạm t). -
Chiếu phương trình (1) lên phương pháp tuyến của thành bình, chiều (+) hướng ra, ta được: mvcos mvcos F. t 2mvcos F. t -
Lực do phân tử khí tác dụng lên thành bình F' F suy ra xung lượng của lực do
phân tử khí va chạm lên thành bình: F t 2mvcos 7,44.10 24 Ns 2.12 Đáp số: r v0 x m m v0 10 m a. v b. s r Hướng dẫn:
a. Theo định luật II Newton dv ma Fc m rv dt mdv
rvdt; dx vdt (phương trình chuyển động của vật là phương x) r mdv rdx dv dx (1) m
- Lấy tích phân 2 vế của (1): v x r r dv dx v v0 x ( 2) v 0 m m
b. Cho v 0 suy ra quãng đường đi đến lúc dừng, từ (2) có: r 0 v0 x m m s x v0 10 m r 0 2.13 Đáp số: lOMoARcPSD| 38841209 a. m ln2 1 ,98 s r r t mv b. 0 m x 1 e 714 m r Hướng dẫn:
a. Theo định luật II Newton ta có: dv dv r m rv dt (1) dt v m
- Tích phân hai vế phương trình (1) ta được: v t r t dv r v r m dt ln t v 0 ve (2) v v m v m 0 0 0 v m - Th ay 0 v vào (2) tìm được ln2 1 ,98 s 2 r
b. Gọi x là quãng đường đi được theo phương ngang -
Từ (2) ta có: v dx v e mr t dx v e0 mr tdt (3) 0 dt -
Tích phân hai vế phương trình (3) ta được: lOMoARcPSD| 38841209 - Đặt - Thay Hướng dẫn: - Xem bài mẫu (Ví dụ 2); chọn hệ toạ
độ xOy; điểm O là gốc; trục Ox nằm ngang, Oy thẳng đứng; gốc thời gian là lúc bắt đầu
ném. Ta có phương trình chuyển động: x v0 cos t (1) 1 2 y v0 sin t gt 2 (2) - Ngoài ra ta có: vx v cos0 (3) vy v sin0 gt (4)
a. Mô men của trọng lực P
mg đối với điểm gốc O:
M/O OM mv r p (r OM là bán kính vector xác định vị trí chất điểm đối với điểm gốc O).
- Từ đó suy ra: M/O Px mg v cos0 t
b. Mômen động lượng của chất điểm m với điểm gốc O: L/O r mv
- Từ đó suy ra độ lớn của mômen động lượng: 1 2 lOMoARcPSD| 38841209 L/O m xvyyvx
- Thay (1), (2), (3), (4) vào ta tính được: L/O mg v cos0 t2 2.16 Đáp số: a. a13,4 m/s2 ; a' 2,3 m/s2 F a b. F 5, 28 N 0 Hướng dẫn: T ' T '
- Chọn hệ quy chiếu O gắn với đất (hệ quy chiếu quán tính), hệ quy T T
chiếu O' gắn với thang máy (hệ quy chiếu phi quán tính); ' 2 a
trong hệ O’các vật chịu thêm lực quán tính: ' a 1 F qt F 1 qt 2 Fqt1m a ; F1 0 qt2 m a2 0 P -
Gọi a '1 ; a '2 là gia tốc các vật m1, m2 trong hệ O’. Ta có: P2 1 a '1 a '2 a . -
Phương trình động lực học của các vật m1, m2 trong hệ O’ (chiếu theo hướng
chuyển động của mỗi vật): lOMoARcPSD| 38841209 m1 a' T 1 mg 1 ma 0 (1) m2 a' 2 mg 2 ma 0 T (2) - Từ (1) và (2) giải ra: m2 m1 g a0 2 a 2 ,2m/s m1 m2
- Suy ra gia tốc của vật m 1 với mặt đất: m2 m1 g 2 2 ma 0 2 a1 a0 1 a' 3 ,4m/s m1 m2
- Số chỉ lực kế: F 2 T' , từ (1): T 1 m(g a0 a') 2 ,64 N T' T F 2T 5 ,28N m 1 qt F 1
2.17 Đáp số: Dịch xe sang phải với gia tốc 2 10 ,78 m/s F 1 ms Hướng dẫn: 1 P F m ms2 2
- Có thể xem bài mẫu (ví dụ 4). Khi xe đứng yên, F N qt2 2
hệ 2 vật có xu hướng vật m 2 đi xuống, muốn hệ 2 P
vật không chuyển động đối với xe, phải dịc h xe 2 . N1 a0
sang phải với gia tốc a0 . Xét trong hệ quy chiếu gắn với xe là hệ quy chiếu không
quán tính (hệ O’), còn hệ quy chiếu gắn với mặt đất là hệ tuyệt đối (hệ O). Trong hệ
O’, các vật m1, m2 chịu thêm lực quán tính: Fqt1 m a ; F1 0 qt2 m a2 0 . Muốn hai vật m1, m2
đứng yên trên xe phải có điều kiện liên hệ giữa các lực: P2 Fms1 Fms2 Fqt1 (1) Và F kF km a ms2 qt2
2 0 (lực ma sát giữa m2 và xe); Fms1 kN1 hay Fms2 km g1 (lực ma sát trượt giữa m1 và xe ).
- Vậy (1) có thể viết thành: m g2 km g1 km a2 0 m a1 0 m2 km1 g a0 m1 km2 m2 km1 g a0 m1 km2 lOMoARcPSD| 38841209 m2 km1 g 10,87 m / s2
- Suy ra gia tốc nhỏ nhất: a0 min m1 km2 2.18 Đáp số: v Rgtg 31m / s 111,6 km/h ; T 6,93 N Hướng dẫn: maht ; aht 2 ht v/R 2 v T qt F m R qt F - Từ đó rút ra: 2 v Rg.tg P f v Rg.tg 30 , 99 31 m /s
- Lực căng của dây theo hình vẽ: T P mg 6 ,93 N cos cos 2.19 Đáp số: ms 0 ,79 N
- Xét trong hệ quy chiếu gắn với toa tàu, quả cầu chịu thêm lực quán tính li tâm: Fqt là
gia tốc hướng tâm khi tàu đi qua đường vòng, có: a
f , khi vật ở trạng thái cân bằng tương đối: T a. F b. 2,2 rad/s Hướng dẫn: a. Xác định lực ma sát -
Hệ quy chiếu O' gắn với đĩa quay là hệ quy N
chiếu phi quán tính, hệ quy chiếu O gắn với mặt đất m qt F là hệ quán tính. ms F P 2 r ( lOMoARcPSD| 38841209 -
Trong hệ O’, vật m chịu các lực: P, phản lực pháp tuyến N , lực ma sát Fms và lực quán tính li tâm
Fqt maht ; aht là gia tốc hướng tâm: aht vận tốc góc quay của đĩa; 2 r). Phương trình
động lực học của vật m trong hệ O': ma' P N Fms Fqt (1)
- Chiếu (1) xuống phương ngang và phương đứng: Fms maht ma (2) P N 0 (3)
- Vì m đứng yên trong hệ O’ nên a 0, Fms maht 0. Fms maht m 2r m 2 n 2 r
- Thay số vào ta được: Fms 0,79 N
b. Vật muốn trượt trên đĩa, phải có điều kiện: qt F F mstruot 2 kg m r kmg ( ms F kN kP ) r kg
- Vật sẽ bắt đầu rời khỏi đĩa khi 2 ,2 rad/s . r 2.20 Đáp số: a. 2,787 N ; 3,963 N b. v 62,61 m / s Hướng dẫn: a. Tại điểm 1 N - Lực hướng tâm F
P N , chiếu lên chiều của lực F ht ht 1 2 cao P v P N1 m (1) nhất R 2 phi N 2 v 1 N1 m mg 2 ,787 N công R 2 chịu v
- Tại điểm thấp nhất: ht F P N2 m P; R P 3 phản v - Lực nén: N2 N2 m mg 3 ,963 N lực ghếN1 . R lOMoARcPSD| 38841209 Fht - Lực nén: N
b. Tại điểm cao nhất, phi công ở trạng thái không trọng lượng thì N1 0. - Từ (1) suy ra: v Rg 62,61 m / s 2.21 Đáp số: T 5,66 N ; v 1,19 m/s ; 4,76 rad/s Hướng dẫn: T -
Quả cầu chịu tác dụng của trọng lực P T
P mg và lực căng T, vì quay tròn O R 2 trong mặt v
phẳng nằm ngang với vận tốc ht F ht m R không
đổi nên: Fht - Lực hướng tâm: F P
( R sin bán kính quỹ đạo tròn). P mg 2 F mv - Lực căng: T 5,66 N ; ht tg v Rg.tg 1 ,19 m/s cos cos P mgR v - Vận tốc góc: 4 ,76 rad/s R Chương 3
CÔNG SUẤT VÀ NĂNG LƯỢNG TRONG HỆ QUI CHIẾU GALILEO
TÓM TẮT LÝ THUYẾT
1. Công của lực F trong chuyển dời CD bất kỳ A FdOM Fds Fdss CD CD CD -
Trong đó dOM ds là vector chuyển dời nguyên tố, FS là hình chiếu của F trên phương ds. -
Trường hợp lực F không đổi, CD là đoạn thẳng A F.s.cos
là góc hợp bởi lực F và phương chuyển dời CD. lOMoARcPSD| 38841209
2. Công suất của lực (hay của máy) dA P Fv dt
v là vector vận tốc của điểm đặt lực.
3. Động năng của chất điểm 2 mv EK 2
- Định lý động năng: EK EK2 EK1 A
4. Thế năng của chất điểm trong trọng trường đều EP mgh
h là độ cao của chất điểm (so với mặt đất) - Định lý thế năng: EP EP2 EP1 EP1 EP2 A
A là công của lực trọng trường
5. Định luật bảo toàn cơ năng trong trọng trường mv2 EM mgh =const. 2 BÀI TẬP VÍ DỤ
Ví dụ 1. Một xe ô tô có khối lượng m
103 kg bắt đầu chạy trên đường nằm ngang.
Động cơ sinh ra lực lớn nhất bằng 103N. Tính thời gian tối thiểu để xe đạt được vận
tốc u 3m / s trong trường hợp:
a. Công suất cực đại của động cơ ô tô bằng P 4kW .
b. Công suất cực đại ấy là P 1kW. Bỏ qua mọi ma sát. Lời giải v(m/s)
a. Theo giả thiết Fmax 103 N, suy ra gia tốc cực đại: 3 1 Fmax 1m / s2 at ; Khi v u 3 m/s thì O 1 a 3 5 max m F.u 3.10 W 3 kW ,
- Công suất động cơ:P Fv mà vt(s) t 3s. Lúc ấy công suất động cơ P
chưa vượt công suất cực đại là điều kiện khả dĩ.
b. Trường hợp sau, vì công suất cực đại của động cơ P103 W nên vận tốc chỉ P v1
1s. bằng: v1 1 m/s sau thời gian t1 lOMoARcPSD| 38841209 F a -
Sau giai đoạn chuyển động nhanh dần đều này, để vận tốc tiếp tục tăng thì F P v
phải giảm, chuyển động là nhanh dần không đều, vận tốc tăng chậm hơn giai đoạn
trước. Công A của động cơ chuyển thành độ tăng động năng của xe trong thời gian t2
để đưa vận tốc từ v1 1 m/s lên v2 u 3 m/s. A P t2 m 1 v 22 v12 (1) 2 t2 4 s -
Vậy thời gian tổng cộng để xe ô tô đạt vận tốc u là: t t1 t2 5 s -
Chú ý: Từ (1) tìm thấy sự phụ thuộc của vận tốc vào thời gian (ở giai đoạn 2) v2t v22 2P t v t 12 hay v t m - Ta có đồ thị v(t) trong 1 kW . trường hợp P
Ví dụ 2. Một bị đựng cát trượt không vận tốc ban đầu từ độ cao h 2 m theo mặt phẳng 0
nghiêng góc 45 so với phương nằm ngang, va chạm với sàn rồi trượt trên mặt sàn nằm
ngang. Nó dừng lại ở điểm cách chân mặt nghiêng bao nhiêu?. Biết hệ số ma sát giữa
bị cát với mặt nghiêng hoặc với sàn là k 0,5, lấy g 10 m/s2 . Lời giải -
Xét giai đoạn trượt trên mặt nghiêng chiều dài: h s h 2 2 2 m . sin -
Gọi v là vận tốc ở chân mặt nghiêng thì định luật bảo toàn năng lượng cho ta: mgh mv2 kmgs.cos mà s.cos h 1 2 - Suy ra v 2gh 1 k 4,5 m/s (1) -
Trong va chạm ở chân mặt nghiêng, thành phần thẳng đứng của động lượng Py
bị triệt tiêu bởi phản lực Q của sàn, sinh ra xung lực Q. t trong thời gian va chạm t: Q. t Py mvsin (2) -
Thành phần nằm ngang: Px mvcos của động lượng không bị triệt tiêu nhưng
cũng giảm trong thời gian va chạm, vì bị cát sinh áp lực bằng Q lên sàn nên có lực ma
sát Fms kQ xuất hiện; xung lực Fms t trong thời gian t làm giảm Px. Fms t
mvcos mu (u là vận tốc của bị cát sau va chạm). kQ t mvcos mu (3) -
Từ (1) và (3) ta có u v cos ksin 1,6 m / s -
Xét giai đoạn chuyển động trên sàn, động năng mu2 chuyển thành công của
lực ma sát trên đoạn đường x. lOMoARcPSD| 38841209 1 2 mu kmgx 2 2 u x 0 ,25 m 2kg BÀI TẬP ÁP DỤNG
3.1. Tính công cần thiết để một lò xo giãn ra x0 20cm, biết rằng lực kéo tỉ lệ với độ giãn
của lò xo và hệ số đàn hồi của lò xo là k 3000N/ m.
3.2. Động năng của một hạt chuyển động trên đường tròn bán kính R phụ thuộc vào
quãng đường đi được s theo quy luật: EK as2 , a là một hằng số. Tính lực tác dụng lên
hạt, coi lực là hàm số của s.
3.3. Một vật khối lượng m được ném lên dọc theo một mặt phẳng nghiêng góc so
với mặt phẳng ngang. Vận tốc ban đầu là v0; hệ số ma sát bằng k. Tính quãng đường
đi được của vật đến khi dừng lại và công của lực ma sát trên quãng đường ấy.
3.4. Một vật có khối lượng m
3 kg trượt từ đỉnh một mặt phẳng nghiêng ở độ cao
0,5m, chiều dài mặt phẳng nghiêng là 1m. Khi tới chân mặt nghiêng, vận tốc của vật là v 2,45 m/s .
a. Tính công của lực ma sát khi vật trượt trên mặt nghiêng. Biết vận tốc ban đầu của
vật bằng không, lấy g 10 m/s 2 .
b. Xác định hệ số ma sát giữa vật và mặt nghiêng.
3.5. Một viên đạn khối lượng m 10 g đang bay với vận tốc v0 100 m/s thì gặp một bản
gỗ dày và cắm sâu vào bản gỗ một đoạn s 4 cm. Hãy tìm: a. Lực cản trung bình của gỗ lên viên đạn
b. Vận tốc viên đạn sau khi ra khỏi bản gỗ, nếu bản gỗ chỉ dày s' 2 cm.
3.6. Một lò khối lượng không đáng kể có độ cứng k 300 N/m , F
một đầu lò xo buộc vào vật, khối lượng m 12 kg nằm trên mặt
phẳng nằm ngang. Hệ số ma sát
giữa vật và mặt phẳng là 0,4. m Lúc 0 30 so với đầu lò 0 ,4 m . Hãy xo chưa O bị biến
dạng. Sau đó đặt vào đầu tự do của lò xo một lực F nghiêng m F
góc phương nằm ngang thì vật dịch chuyển rất chậm một đoạn
đường s tính công của lực F trong dịch chuyển trên.
3.7. Một vật khối lượng m 1 kg được đặt trên một tấm gỗ phẳng,
cả hai lại được đặt trên mặt sàn nằm ngang. Vật được nối với 0 lOMoARcPSD| 38841209
điểm O bằng một sợi dây nhẹ, đàn hồi, có chiều dài tự nhiên 0 40
cm và dây có phương thẳng đứng. Hệ số ma sát giữa vật và tấm
gỗ là 0,2. Từ từ kéo tấm gỗ theo phương nằm ngang cho đến khi
vật bắt đầu trượt trên tấm gỗ, khi ấy dây lệch khỏi phương thẳng
đứng một góc 30 . Tính công của lực ma sát tác dụng lên vật kể
từ lúc kéo tấm gỗ đến lúc vật bắt đầu trượt trên tấm gỗ, cho g 10 m/s2 .
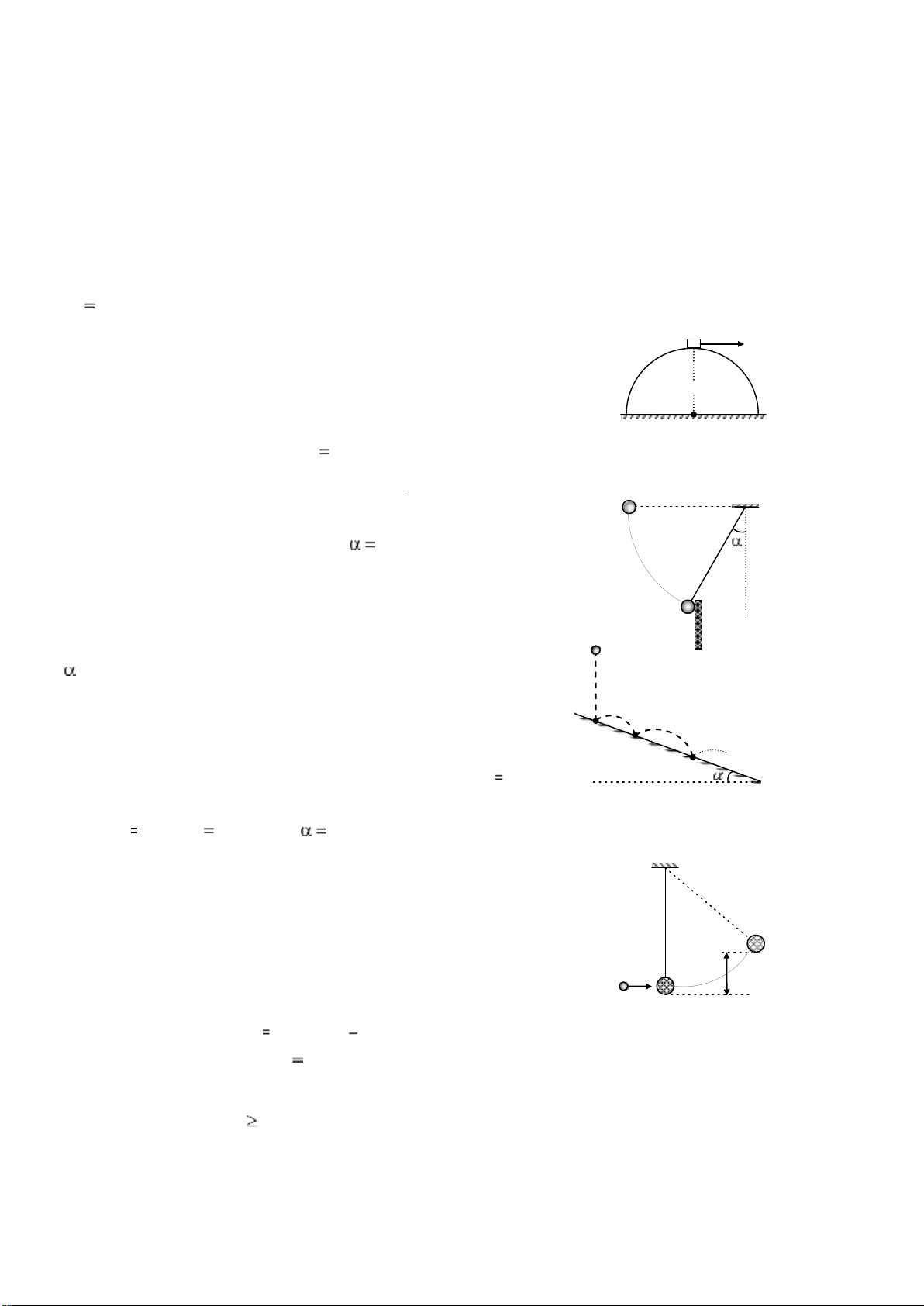
3.8. Một vật nhỏ trượt không ma sát trên mặt ngoài của một bán cầu có bán kính
R1,5 m. Biết vật trượt từ đỉnh xuống. Hỏi
a. Vật sẽ rời khỏi mặt bán cầu ở độ cao nào? (so với đáy bán cầu). 0v
Nếu vận tốc ban đầu v0 của vật bằng không. R
b. Cần phải truyền cho vật vận tốc ban đầu v0 theo phương ngang
nhỏ nhất bằng bao nhiêu để vật có thể rời khỏi mặt bán cầu mà
không trượt. Cho g 10 m / s2 . 3.9.
Một viên bi sắt treo vào dây dài 1 m được kéo cho dây nằm
ngang rồi thả cho rơi xuống không vạn tốc ban đầu. Khi góc giữa 0
dây và đường thẳng đứng là 30 thì viên bi va chạm đàn hồi vào một
tấm sắt được đặt thẳng đứng. Hỏi viên bi nảy tới độ cao h bằng bao
nhiêu sau va chạm? (so với vị trí cân bằng).
3.10. Một viên bi rơi từ độ cao h xuống một mặt phẳng nghiêng góc M
so với mặt phẳng nằm ngang. h
a. Tính tỉ số khoảng cách giữa các điểm va chạm của viên
bi với mặt phẳng nghiêng. Coi va chạm là đàn hồi tuyệt A 0 đối. A 1 A
b. Tính khoảng thời gian kết từ lúc viên bi bắt đầu 5 r cm ơi t 2 ; ừ
điểm M đến lúc nó bắt đầu chạm đất. Biết h A B0 2m ; g 10 m / s2 ; 300 .
3.11. Một con lắc thử đạn khối lượng M, viên đạn khối lượng m
bay theo phương nằm ngang, xuyên vào bao cát (con lắc) và bị
mắc lại trong bao cát đồng thời bao cát được nâng lên độ cao h.
a. Hãy lập biểu thức tính vận tốc viên đạn ngay trước va chạm m với bao cát. M h
b. Tính tỉ số phần trăm động năng của viên đạn biến thành nhiệt khi va chạm. Cho m 20 g; M 1,2 kg.
c. Khối lượng viên đạn m 20g . Hỏi khối lượng bao cát tối đa là bao nhiêu để bao cát
chuyển động được. Biết bao cát (có cả viên đạn bên trong) chuyển động được khi
động năng bao cát 1% động năng viên đạn trước va chạm. lOMoARcPSD| 38841209
3.12. Một quả cầu đặc đồng chất có bán kính R và khối lượng m 1 kg , lăn không
trượt với vận tốc v1 36km/ h đến va chạm vào thành tường rồi bật
ra với vận tốc v2 28,8km/ h . Tính nhiệt lượng toả ra trong va chạm O đó.
3.13. Một thanh đồng chất có chiều dài và khối lượng M, có thể
quay xung quanh một trục nằm ngang đi qua đầu trên của thanh.
Một viên đạn có khối lượng m bay theo phương ngang tới xuyên
vào m đầu dưới của thanh và bị mắc lại trong thanh. Biết sau va chạm thanh bị lệch
đi góc so với phương thẳng đứng, coi m
M. Tìm vận tốc viên đạn trước lúc va chạm.
3.14. Một đầu máy xe lửa khối lượng m mở máy chạy từ nhà ga sao cho vận tốc của
nó cho bởi quy luật v a s , với a là hằng số, s là quãng đường đi được. Tính công tổng
cộng của tất cả các lực tác dụng lên đầu máy thực hiện trong t giây đầu kể từ lúc mở máy.
3.15. Một khẩu pháo khối lượng M 450 kg nhả đạn theo phương nằm ngang. Đạn
pháo có khối lượng m 5 kg , vận tốc đầu nòng v 450 m / s . Khi bắn bệ pháo giật về
phía sau một đoạn S 45 cm. Tìm lực hãm trung bình tác dụng lên pháo.
3.16. Một quả cầu khối lượng m 0,1 kg được gắn ở đầu một thanh nhẹ, O
khối lượng không đáng kể, dài 1,27 m . Hệ quay trong mặt phẳng thẳng
đứng xung quanh đầu kia của thanh. Tại điểm cao nhất quả cầu có vận tốc v0 4,13 m/s. A v
a. Tìm sự phụ thuộc của thế năng và động năng của quả cầu theo góc A
hợp bởi thanh và phương thẳng đứng. Gốc tính thế năng tại vị trí thấp nhất.
b. Xác định lực tác dụng F của quả cầu lên thanh theo góc . Tính F tại các điểm thấp nhất và cao nhất?
3.17. Một vật chuyển động khối lượng m1 tới va chạm vào một vật thứ hai đang đứng
yên, khối lượng m2. Coi va chạm là đàn hồi xuyên tâm. Hãy xác định số phần trăm
động năng ban đầu của vật thứ nhất đã truyền cho vật thứ hai sau va chạm? Áp dụng
cho các trường hợp: m1 m2 ; m1 9m2 .
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ
3.1. Tính công của lực kéo -
Theo định nghĩa ta có biểu thức tính công: lOMoARcPSD| 38841209
3.3. Tính quãng đường và công của lực ma sát -
Động năng ban đầu của vật bằng tổng của công sinh ra để thắng ma sát Ams'
và thế năng của vật Wt khi dừng lại: mv02 mgh Ams' mgssin k mgcos s (1) -
Quãng đường vật đi được cho đến khi dừng lại: 2 v0 s 2 gsin kcos - Công của lực ma sát: 2 ' kmv0 A A ms ms 2 k tg
3.4. Vật trượt từ đỉnh mặt phẳng nghiêng a. Công của lực ma sát
- Theo định luật bảo toàn và chuyển hoá năng lượng 1 2 1 mgh mv A 2 ms A mgh v 6 J 2 ms 2
b. Hệ số ma sát giữa vật và mặt nghiêng 2 2 s h - Ta có Ams ms Fs kmgscos , mặt khác cos s 2 2 Ams Ams kmgs h k 0 , 23 2 2 mgs h
3.5. Viên đạn xuyên vào tấm gỗ a.
Xác định lực cản trung bình của tấm gỗ lên viên đạn - Theo định lý động năng ta có: lOMoARcPSD| 38841209 0 1 mv2 Ac F s.cos180 0 F mv02 1250 N 0 c c 2 2S b.
Vận tốc của viên đạn khi xuyên qua tấm gỗ 1 2 1 2 ' 0 mv mv0 Ac c F s'.cos180 2 2 2 2 c F s' v v0 70 m/s m
3.6. Tính công của lực kéo F -
Công của lực F gồm 2 phần: Công A1 làm giãn lò xo, tạo thế năng cho lò xo và
công và công A2 làm dịch chuyển vật. N
- Vì vật dịch chuyển rất chậm nên: F F n K F ms F N - Ta có áp lực: N mg Fsin F K - Mặt khác ms F K F Fcos - Vậy Fcos mg Fsin P mg F 45 N ksin cos lOMoARcPSD| 38841209 F
- Độ giãn của lò xo: 0,15m k 1 O A k 2 1 3 ,4J A2 K Fs Fcos s 15 ,6J 2 - Vậy công của lực T F : A A 1 A2 19 J Q 3.7. F
Tính công c ủa lực ma sát ms m
- Công của lực ma sát làm vật dịch chuyển so với sàn nhà cũng bằng
độ tăng thế năng đàn hồi của dây liên kết giữa vật với điểm treo O. 0 P -
Lúc vật bắt đầu trượt 30 , vật chịu các lực sau: Trọng lực P, phản lực Q , lực
căng T, lực ma sát nghỉ cực đại Fms . - Vật đè lên tấm gỗ áp lực: N Q P Tcos Fms N P Tcos (1) -
Đối với vật, lực ma sát Fms đóng vai trò lực kéo, còn thành phần Tsin đóng vai
trò lực cản. Lúc vật bắt P
đầu trượt trên tấm gỗ thì T 2 , 97 3 N (3) cos sin
Fms Tsin (2) - Từ (1) và (2) - Độ giãn của dây là: ta được: 1 1 0,062 0 0 cos
- Công của lực ma sát bằng độ tăng thế năng của dây: 2 1 T A
k ; với k là hệ số đàn hồi của dây: k m 2 1 A T 0 ,09J 2
3.8. Vật nhỏ trượt trên mặt bán cầu
a. Xét vật đang trượt trên mặt bán cầu ở vị trí (A) các B v 0
lực tác dụng lên vật: trọng lực P, phản lực N . N - A Hợp lực P giữa N và 2 h 2 v một phần ht F 2 P N m mgcos N P R trọng lực P2 2 v N mgcos m 0 tạo thành R
lực hướng tâm: P1
- Ta thấy N giảm dần khi vật trượt từ đỉnh bán cầu xuống. Khi N 0 là lúc vật rời khỏi mặt bán cầu: 2 2 lOMoARcPSD| 38841209 v h v (1) cos h R Rg g
- Mặt khác theo định luật bảo toàn cơ năng: 1 2 v2 mgR mgh mv 2 R h (2) 2 g 2R - Từ (1) và (2): h 1 m 3
b. Xét vật ở vị trí (B) có vận tốc ban đầu v0 0 2 2 v0 N mg mv0 Fht P N m R R -
Điều kiện để vật rời khỏi mặt cầu mà không trượt xuống: N 0 v0min Rg 3,87 m/s
3.9. Từ định luật bảo toàn cơ năng suy ra vận tốc viên bi ngay trước lúc va chạm: 1 mg mg 2 1 cos mv0 2 v 2 g 0 cos (1) -
Ta có v0 hợp với pháp tuyến của tấm sắt góc , do va chạm đàn hồi nên vận tốc
viên bi ngay sau va chạm có độ lớn bằng v0: v v0 2g cos (2) - O
Vector cũng tạo với pháp tuyến của tấm sắt góc (góc phản xạ bằng góc tới). n v -
Sau va chạm viên bi chuyển động theo quỹ đạo tròn đi lên, với 0 v v vận tốc v n vuông góc dây: t v vn vcos2 2g cos .cos2 -
Còn thành phần vt vsin2 dọc theo sợi dây có tác dụng kéo giãn dây và phần
động năng tương ứng: mv / 22t của viên bi biến thành nội năng làm dây nóng lên. -
Áp dụng định luật bảo toàn cơ năng: 1 2 mvn mgh 2 2 v 3 n h 2 cos.cos2 21 ,7 cm 2 g 8 -
Nhận xét: Do va chạm đàn hồi nên không có sự mất mát động năng của viên bi
khi không va chạm với tấm sắt, nhưng ngay sau va chạm viên bi lại bị mất một phần
động năng do dây bị giãn đột ngột. lOMoARcPSD| 38841209
3.10. Thời gian rơi đoạn MA0 h là: 2h t0 0,1 s g y -
Vận tốc bi ngay trước lúc va chạm tại A0: v0 M 2gh 1 m/s (1) h v -
Chọn hệ quy chiếu xOy (O A0 ); t 0 là thời điểm O A 0 A 1
ngay sau va chạm ở A0 và vận tốc ban đầu v (v v , v A 2 0 hướng x
lên lệch so với y góc ). Ta có phương trình chuyển động: lOMoARcPSD| 38841209 sin 2 xt vsin t g t 2 0 2 gcos 2 yt vcos t 0 t 3 2 vx v0 sin gsin t vy v0 cos gcos t
- Sau thời gian t 1 viên bi lại va chạm với mặt phẳng nghiêng ở A 1 . Tại A 1 : y 0 , từ (3) 2v 0 t1 0 ,2s g (5) -
Lập luận tương tự, ta thấy viên bi lại va chạmvới mặt nghiêng ở A3: 2v0 t1 0,2 s A A23 24hsin t3 g A A12 2; A A2 3 3; ... lOMoARcPSD| 38841209 - Vậy A A01 A A01 - Hay A A :A A :A A :...0 1 1 2 2 3 1:2:3... - Thay số A A0 1 20cm , A A1 2 40cm , A A2 3 60cm, A A3 4 80cm, ... - Theo giả thiết: AB 2 m - Mà A A0 1 A A1 2 A A2 3 A A3 4 2 m -
Như vậy sau 5 lần va chạm viên bi chạm vào điểm B tức là bắt đầu chạm đất.
- Tổng thời gian kể từ lúc bắt đầu rơi ở M đến lúc chạm đất ở B là T t0 t1 ...t4 0,9 s
3.11. Con lắc thử đạn
a. Gọi v và V lần lượt là vận tốc viên đạn và vận tốc bao cát ngay sau khi đạn xuyên vào. -
Theo định luật bảo toàn động lượng - Thay số H
3.12. Nhiệt lượng toả ra trong va chạm đúng bằng độ giảm động năng của quả cầu.
Mà động năng quả cầu: lOMoARcPSD| 38841209 1 1 7 2 2 2 EK mv I0 mv 2 2 10 2 v - Với: 2 I0 mR; 5 R 7 - Vậy: 2 2 Q mv 1 v2 25 ,2J 10
3.13. Xét hệ đạn và thanh; theo định luật bảo toàn mô men động lượng trước va chạm và ngay sau va chạm: 2 M 2 M 2 3 mv m mv 12 4 3 m M -
Áp dụng định luật bảo toàn cơ năng :
cho hệ từ thời điểm ngay sau va m 2 1 M 2 M 2 2 2
chạm đến lúc đạt góc mgh Mgh 2 2 12 4 - Vì mM
Lực tác dụng lên đầu máy -
Phương trình chuyển động S t 1 t2 1a t2 2 dS 1a tdt2 (2) 2 4 2 - Công lOMoARcPSD| 38841209 t 1 4 1 4 2 A FdS FdS ma tdt ma t (3) 0 4 8
3.15. Từ định luật bảo toàn động lượng suy ra vận tốc giật lùi của pháo 2 2 m V v (1) 1 M - Độ 2
ng năng giật lùi của pháo bằng đúng công của lực hãm tác dụng lên pháo EK MV2 A F.s (2) - Từ (1) và (2): m v22 F 12500 N 2MS
3.16. Quả cầu gắn vào thanh cứng
a. Thế năng và động năng quả cầu được tính theo công thức:
EP mg1 cos (1) EK mv02 mg1 cos (2)
b. Lực tác dụng F của quả cầu lên thanh 2 mv F 1 P ht F mgcos (3) - Từ (2) 2 2 mv mv mg 0 2 1 cos - Th ay vào (3) ta có: 2 v 0 F m2g 3 gcos + (4)
- Tại điểm cao nhất F 0 ,36 N
, tại điểm thấp nhất F 6 ,2 N , ,
3.17. Định luật bảo toàn động lượng m v1 1 m v11 m v22 lOMoARcPSD| 38841209 - Hay: lOMoARcPSD| 38841209 Chương 4
HỆ CHẤT ĐIỂM. VẬT RẮN
TÓM TẮT LÝ THUYẾT
1. Khối tâm của hệ chất điểm
- Khối tâm G của hệ chất điểm n mi M i G 0 i1
- Toạ độ khối tâm G đối với gốc O cố định n 1 n OG G r ii mr ; với m mi và i r i OM m i1 i1 - Vận tốc khối tâm n n dr 1 dr 1 G i vG mi i mv i dt m i1 dt m i1
- Phương trình chuyển động của khối tâm n 2 dr G i F maG với aG 2 i1 dt 2. Động lượng
- Động lượng của một hệ chất điểm n n pi i mv i i1 i1 p
- Định luật bảo toàn động lượng: Tổng động lượng của một hệ cô lập được bảo toàn: p const
- Bảo toàn động lượng theo phương: Fx 0 px const - Công
thức Xiôncôpxki cho vận tốc tên lửa lOMoARcPSD| 38841209 4. Mômen quán tính -
Mômen quán tính của một số vật đồng chất đối với trục đối xứng chính đi qua khối tâm của chúng G 1 2 - Thanh dài: I m 12 -
Đĩa tròn (hoặc trụ đặc): IG mR2 -
Vành tròn (hoặc trụ rỗng): IG mR2 - Quả cầu đặc: IG mR2 -
Định lý Huygen - Stener: I IG md2
5. Mômen động lượng
- Mômen động lượng của một hệ chất điểm với điểm O cố định n n L/O Li/O ri mvi i 1 i 1
- Mômen động lượng của vật rắn quay quanh trục cố định L/ I
- Định lý về mômen động lượng
đối với điểm O và đối với trục quay dL/O dL/ M/O và M/ dt dt
- Định luật bảo toàn mômen động lượng dL
M 0 0 L const dt
6. Động năng của vật rắn quay
- Động năng của vật rắn quay quanh trục cố định EK I 1 2 2
- Động năng toàn phần của vật rắn EK 1 mvG2 1 I 2 2 2 lOMoARcPSD| 38841209 BÀI TẬP VÍ DỤ
Ví dụ 1. Một hình trụ đặc khối lượng m13kg có thể quay xung quanh
một trục nằm ngang trùng với trục của nó. Trên hình trụ được cuốn một m 2 m1 sợi
dây mảnh, mềm, không giãn, khối lượng không đáng kể. Đầu tự do của sợi dây có treo
một vật có khối lượng m2 500g. Thả cho vật m2 rơi thẳng đứng. Hãy tìm gia tốc của m2
và sức căng của dây. Bỏ qua sức cản không khí, bỏ qua ma sát ở trục quay của hình trụ, lấy g 10m/s2. Lời giải -
Chuyển động của hệ bao gồm chuyển động tịnh tiến của m2 và
chuyển động quay của m1. Ta có: O P2 T2 m a2 (1) m 2 m1 T1 M/O(T1) I0 (2) T2 -
Chiếu phương trình (1), (2) lên các chiều chuyển động tương ứng, ta được: P2 T2 m a2 (3) P2 M/O(T1) I0 (4) - Ở đây ta có: a 1 2 M/O TR1 ; ; T1 T2 T ; I0 m R1 (5) R 2 -
Kết hợp (5) với phương trình (3), (4) ta được gia tốc chuyển động của m2 và sức căng của dây: 2 m 2.0,5 a 2 2 g 10 2 ,5m/s m1 2 m2 3 2.0,5 1 3.2,5 T 1 ma 3 ,75N 2 2
Ví dụ 2. Một người đứng thẳng đứng ở giữa ghế Giucôpxki sao cho giá của trọng lực
tác dụng lên người trùng với trục quay của ghế. Hai tay của người đó đang dang ra
và cầm hai quả tạ giống nhau, mỗi quả có khối lượng m 2kg , hai quả tạ cách đề thân
người và khoảng cách giữa hai quả tạ là 1 160cm. Cho hệ người và ghế quay đều với vận tốc góc 1 3,14rad/s. lOMoARcPSD| 38841209
Khi hệ đang quay thì người này hạ đều hai tay xuống sao cho khoảng cách giữa hai
quả tạ chỉ còn là 2 60cm. Hãy xác định vận tốc góc quay 2 của hệ.
Cho biết mômen quán tính của người và ghế (không kể các quả tạ) đối với trục quay
là I0 2,5kgm2 . Bỏ qua sức cản không khí, coi kích thước của các quả tạ là rất nhỏ. Lời giải -
Mômen ngoại lực tác dụng lên người và ghế Giucôpxki trong trường hợp này
triệt tiêu, do đó mômen động lượng của hệ được bào toàn. Ta có: I L2 I1 1 I2 2 1 2 1 L1 I2 -
Khi người dang tay và khi người hạ tay xuống, mômen quán tính của hệ đối với
trục quay được xác định: 2 2 1 I 2 1 I0 2m ; I2 I0 2 m 2 2 - Vậy ta có: 2 2 1 1 ,6 I0 2 m 2 , 5 2.2. 2 2 2 3, 14 5 ,5rad/s 2 1 2 2 0 , 6 I 2m 2 ,5 2.2. 0 2 2 BÀI TẬP ÁP DỤNG
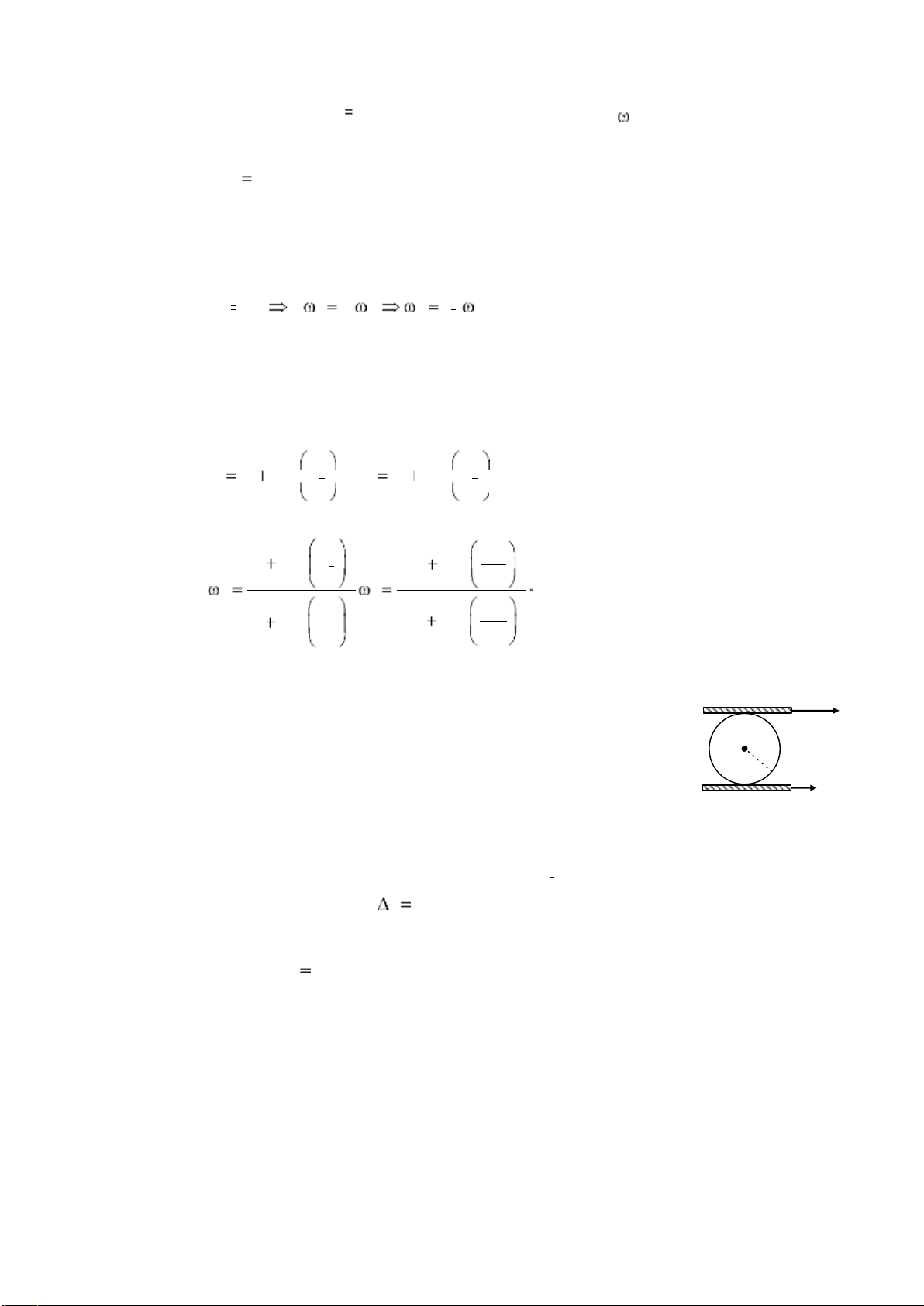
4.1. Một con lăn hình trụ bán kính R được đặt giữa hai đường
băng song song. Các đường băng chuyển động về cùng một phía O v1 R v 2
với vận tốc lần lượt là v1 và v2 . Biết con lăn lăn không trượt.
Xác định vận tốc góc quay quanh trục và vận tốc chuyển động tịnh tiến của con lăn.
4.2. Một ôtô đang chuyển động với vận tốc v0 72 km/h thì hãm phanh và dừng lại sau
một khoảng thời gian 5s, coit chuyển động của ôtô kể từ khi hãm phanh là chậm dần đều.
a. Hỏi bánh ôtô quay thêm được bao nhiêu vòng kể từ lúc hãm phanh. Biết bánh ôtô có bán kính R 35cm.
b. Tính gia tốc góc của bánh xe. 4.3.
Trên một đĩa tròn mỏng, phẳng, đồng chất bán kính R có khoét một lỗ tròn nhỏ
bán kính r, tâm O’ của lỗ khoét cách tâm O của đĩa tròn một khoảng R / 2 . Xác định vị trí khối tâm của đĩa. lOMoARcPSD| 38841209 4.4.
Một hình trụ rỗng có khối lượng m 50kg, bán kính R 50cm đang quay
quanh trục của nó với vận tốc góc 600vòng/phút thì bị một lực hãm tiếp tuyến
với mặt trụ và vuông góc với trục quay. Sau 1 phút thì trụ dừng lại. m
a. Tính công của lực hãm.
b. Xác định mômen lực hãm và độ lớn của lực hãm tiếp tuyến. 4.5.
Trên một hình trụ rỗng khối lượng m 1kg người ta cuốn một sợi dây mềm,
nhẹ, khối lượng không đáng kể. Đầu tự do của sợi dây được gắn vào một giá cố định.
Thả cho hình trụ rơi thẳng dưới tác dụng của trọng lực. Tìm gia tốc rơi của hình trụ
và lực căng của sợi dây. Bỏ qua sức cản không khí, lấy g 10m/s2. 4.6.
Hai vật có khối lượng m1 300g và m2 100g được nối với nhau bằng
một sợi dây mềm, mảnh, không giãn, khối lượng không đáng kể và được m
vắt qua một ròng rọc cố định. Ròng rọc là một hình trụ đặc có khối lượng
m 200g . Thả nhẹ cho hệ chuyển động. Bỏ m1
qua mọi ma sát, dây không trượt trên ròng rọc. Lấy g 10m/s2. Hãy m2 xác định gia tốc
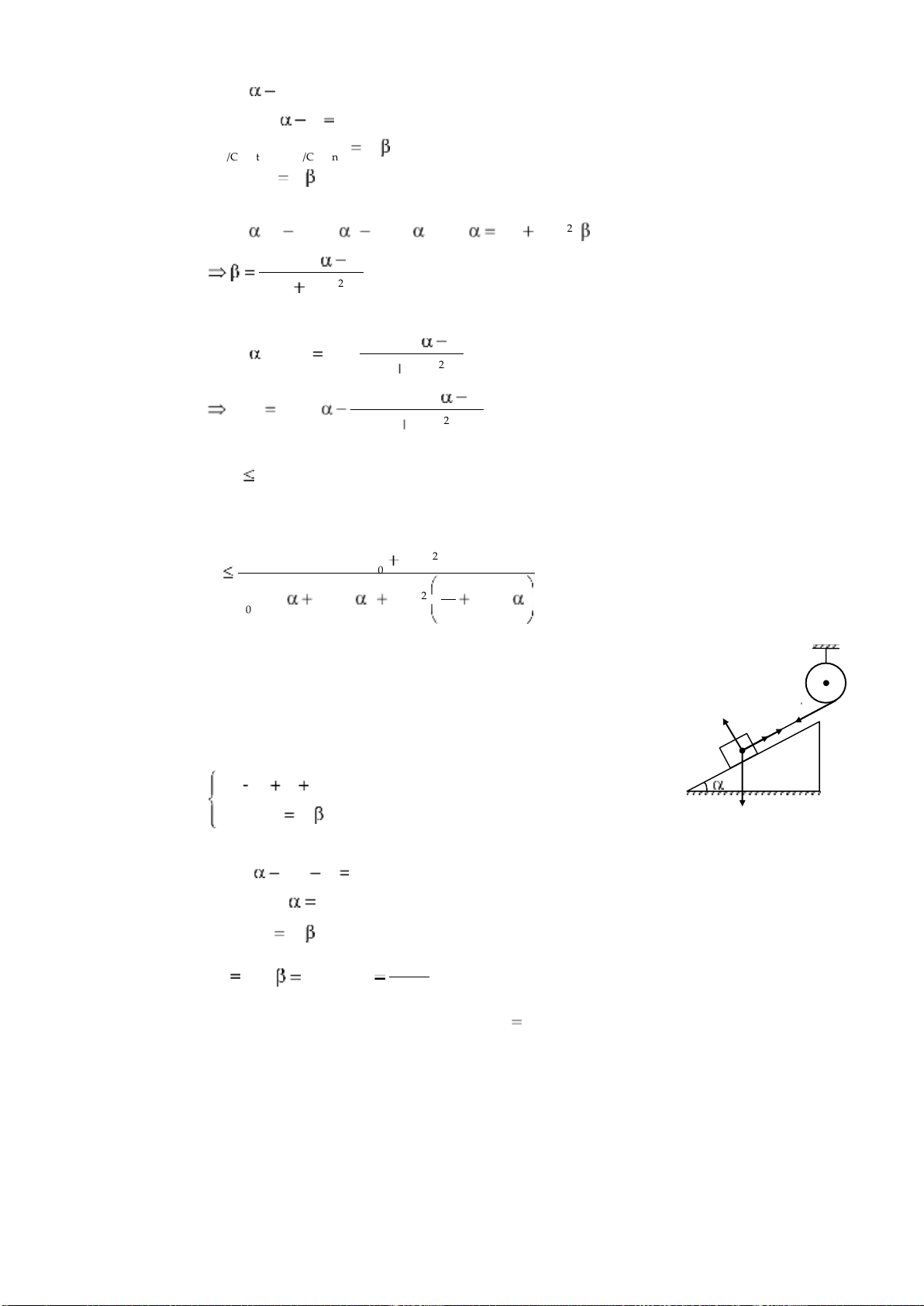
chuyển động của hệ và lực căng của dây treo ở hai nhánh. 4.7.
Cho hai vật khối lượng m1 m2 1kg được nối với m 1
nhau bằng một sợi dây mềm, không giãn, khối m lượng
không đáng kế và vắt qua một ròng rọc. Ròng rọc là một
hình trụ đặc có khối lượng m 1kg. Ma sát giữa m 2 mặt
bàn nằm ngang và m1 có hệ số k 0,2 . Tính gia tốc chuyển
động của hệ và lực căng của dây ở hai nhánh. Bỏ qua sức cản không khí, bỏ qua ma
sát ròng rọc, lấy g 10m/s2. 4.8.
Một cuộn chỉ có khối lượng m được đặt trên mặt bàn nằm
ngang. Vành ngoài cuộn chỉ có bán kính R, phần cuốn chỉ có bán F
kính r. Mômen quán tính của cuộn chỉ đối với trục của nó là I r 0. R
Người ta cầm đầu buông của sợi chỉ để kéo cuộn chỉ một lực F hợp
với phương ngang một góc .
a. Tìm điều kiện về góc để cuộn chỉ chuyển động về phía trước (phía kéo cuộn chỉ).
b. Cho hệ số ma sát giữa cuộn chỉ và mặt bàn là k. Hãy xác định điều kiện về
độ lớn của lực F để cuộn chỉ không trượt. lOMoARcPSD| 38841209
4.9. Cho một ròng rọc cố định là một hình trụ đặc có khối lượng m1
200g, trên hình trụ có cuốn một sợi dây mềm, không giãn, khối m 1
lượng không đáng kể. Đầu tự do của sợi dây được nối với một vật m có khối lượng m 2
2 500g , vật được đặt trên một mặt phẳng nghiêng
góc 450 . Ma sát giữa m2 và mặt phẳng nghiêng có hệ số k 0,1. Thả
nhẹ m2 cho hệ chuyển động, lấy g 10m/s2.
a. Tính gia tốc chuyển động của vật m2.
b. Tìm quãng đường m2 đi được sau 2 giây kể từ khi bắt đầu chuyển động.
4.10. Cho hai hình trụ đặc, đồng chất giống hệt nhau, khối lượng mỗi hình
1 trụ là m 2kg . Trên hai hình trụ người ta cuốn cuốn một cách đối xứng hai
sợi dây nhẹ. Hình trụ phía trên có trục quay cố định. Khi thả cho hệ chuyển
động, hình trụ phía dưới luôn nằm ngang. Hãy tính gia tốc chuyển động 2
của hệ và lực căng của mỗi dây treo. Lấy g 10m/s2.
4.11. Tính mômen động lượng của Trái Đất đối với trục quay của nó.
Coi Trái Đất là một hình cầu đặc đồng chất có bán kính R 6400km và 24 6.10 kg,
khối lượng M chu kì quay quanh trục của Trái Đất là T 24h.
4.12. Một đĩa tròn đồng chất có khối lượng m và bán kính R có thể R
quay xung quanh một trục nằm ngang vuông góc với đĩa và cách tâm O
đĩa một khoảng R / 2 . Ban đầu giữ đĩa ở vị trí sao cho tâm đĩa cao nhất,
sau đó thả nhẹ cho đĩa quay không vận tốc đầu. Hãy xác định vận tốc
góc và mômen động lượng của đĩa đối với trục quay khi đĩa đi qua vị
trí mà tâm đĩa thấp nhất.
4.13. Hãy tính động năng toàn phần của các vật sau:
a. Một đĩa đặc đồng chất khối lượng m 2kg lăn không trượt trên mặt phẳng nằm
ngang với vận tốc v 4m/s.
b. Một quả cầu đặc đồng chất khối lượng m 250g, bán kính R 6cm lăn không trượt
trên mặt bàn nằm ngang với vận tốc góc 20rad/s, trong quá trình chuyển động trục
quay của nó có phương không đổi (song phẳng)
4.14. Một thanh cứng có chiều dài 50cm và khối lượng m1 200g có thể quay tự do
xung quanh một trục nằm ngang đi qua đầu trên của thanh và vuông góc với thanh.
Khi thanh đang nằm đứng yên ở vị trí cân bằng bền, một viên đạn có khối lượng m2
50g bay theo phương ngang vuông góc với trục quay của thanh với vận tốc v 100m/s
xuyên và mắc vào đầu dưới của thanh. Hãy tìm vận tốc góc của thanh ngay sau va chạm.
4.15. Một hệ chất điểm có tổng động lượng là p và mômen động lượng L/O đối với một
chất điểm O. Hãy xác định mômen động lượng của hệ đối với điểm O’. Khi nào thì
mômen động lượng của hệ chất điểm không phụ thuộc vào điểm O. lOMoARcPSD| 38841209
4.16. Chứng minh rằng mômen động lượng L/O của một hệ chất điểm đối với điểm O
gắn với hệ quy chiếu K có thể cho bởi: L/O L/G rG p
trong đó L/G là mômen động lượng của hệ chất điểm đối với khối tâm của nó,
rGOG là bán kính vector của khối tâm đối với điểm O trong hệ K, p là tổng động lượng của hệ.
4.17. Một chiếc bút chì có chiều dài 20cm được giữ thẳng đứng, sau đó buông nhẹ
để nó đổ xuống mặt bàn nằm ngang, coi rằng trong quá trình đổ đầu bút chì không bị
trượt trên bàn. Hãy xác định vận tốc góc của bút chì tại thời điểm bút chì hợp với
phương thẳng đứng một góc . Áp dụng tại thời điểm bút chì nằm ngang. Lấy g 10m/s2.
4.18. Từ đỉnh của một mặt phẳng nghiêng có độ cao h 50cm có các vật khác nhau được
thả lăn không trượt không vận tốc đầu. Lấy g 10m/s2. Tính vận tốc dài của các vật tại
chân mặt phẳng nghiêng, nếu: a. Vật được thả là một trụ đặc.
b. Vật được thả là một trụ rỗng.
4.19. Một đĩa tròn đồng chất có khối lượng m1 100kg và bán kính R 1,5 m đang quay
đều với vận tốc góc / 3rad/s quanh trục của nó được đặt thẳng đứng, trên đĩa có một
người khối lượng m2 50kg đứng tại mép đĩa.
a. Xác định vận tốc góc của đĩa khi người này đi vào và đứng tại tâm đĩa (coi người
này như một chất điểm)
b. Tính công thực hiện bởi người này khi di chuyển từ mép đĩa vào tâm đĩa.
4.20. Một quả cầu đặc, đồng chất bán kính r bắt đầu lăn không m,r
trượt từ đỉnh một bán cầu bán kính R. Xác định vị trí quả cầu rời
mặt bán cầu và vận tốc góc của quả cầu ở đó. R
4.21. Một khẩu pháo có khối lượng m1 104 kg có thể chuyển
động không ma sát trên đường nằm ngang, khi chuyển động khẩu pháo mang một
quả đạn có khối lượng m2 100kg , viên đạn có thể được bắn ra khỏi nòng với vận tốc u
500m/s so với nòng pháo. Hãy xác định vận tốc của khẩu pháo ngay sau khi bắn trong các trường hợp sau:
a. Khi bắn khẩu pháo đứng yên, quả đạn được bắn theo phương ngang.
b. Khi bắn khẩu pháo đứng yên, quả đạn được bắn hướng lên trên hợp với phương ngang một góc 600 .
c. Khi bắn khẩu pháo chuyển động với vận tốc v0
18 km/h, quả đạn được bắn
theo phương ngang về phía trước. lOMoARcPSD| 38841209
4.22. Cho một chiếc nêm có dạng một tam giác vuông cân, khối lượng m 2
m1 5kg đang nằm yên trên mặt sàn nằm ngang. Thả rơi vào mặt nêm một vật nhỏ khối lượng m h
2 0,5kg từ độ cao h 1m (so với điểm chạm mặt nêm).
Sau va chạm, vật m2 bị bật ra theo phương nằm ngang. Hãy xác định
vận tốc chuyển động của nêm ngay sau va chạm. m 1
Bỏ qua mọi ma sát, lấy g10m/s2, coi va chạm là đàn hồi.
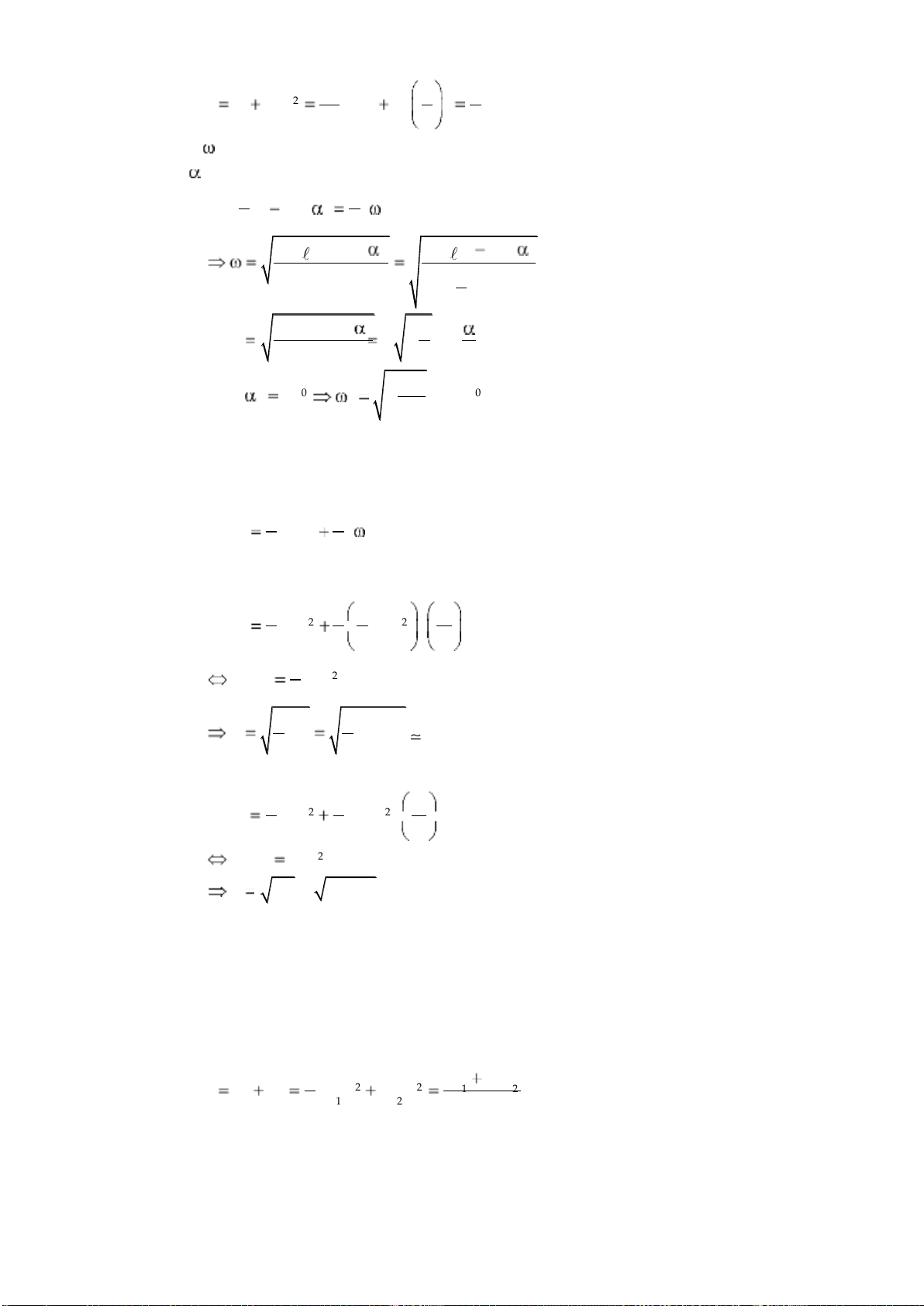
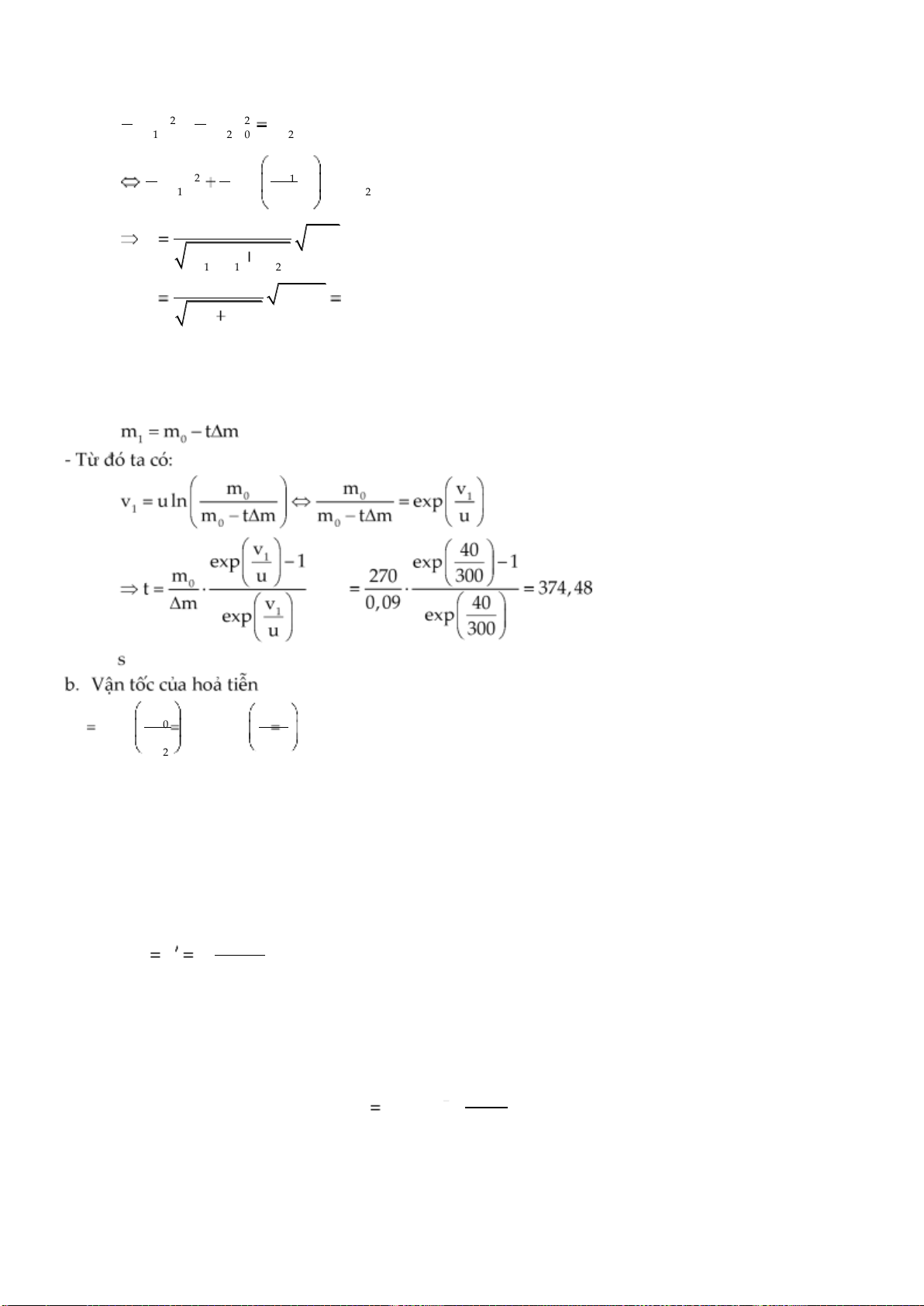
4.23. Một hoả tiễn lúc đầu đứng yên có khối lượng tổng cộng là m0 270kg, sau đó
phụt khí đều đặn ra phía sau với vận tốc không đổi u 300m/s so với hoả tiễn, lượng
khí phụt ra trong mỗi giây là m 90g.
a. Sau bao lâu hoả tiễn đạt vận tốc v1 40 m/s.
b. Khi khối lượng tổng cộng của hoả tiễn còn lại là m2 90kg thì vận tốc của hoả tiễn là bao nhiêu?
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ
4.1. Con lăn và băng chuyền -
Gọi v và lần lượt là vận tốc chuyển động tịnh tiến của con lăn và vận tốc quay
của con lăn quanh trục của nó. -
Vận tốc dài của một điểm nằm ở mép con lăn đối với trục quay (hệ toạ gắn với
con lăn) là R và chính bằng vận tốc của điểm tiếp xúc giữa con lăn và băng chuyền. -
Do con lăn không trượt, nên trong hệ toạ độ gắn với mặt đất ta có sự tổng hợp vận tốc: v1 v vt1 v1 v vt1 v R (1) v2 v vt2 v2 v vt2 v R (2)
- Từ (1) và (2) ta tính được: 1 v v1 v2 2 1 v1 v2 2 R
4.2. Xe ôtô hãm phanh chuyển động chậm dần đều và dừng lại -
Gọi a là gia tốc chuyển động của ôtô khi hãm phanh, có: vt v0 0 20 4 m/s2 a t 5 -
Quãng đường xe đi thêm được cho đến khi dừng lại: s v0 t 1a t2 20.5 1 4.52 50m 2 2
a. Số vòng mà bánh ôtô quay thêm được s 50 22,74 vòng n 2 R 2 .0,35 lOMoARcPSD| 38841209
b. Gia tốc góc của bánh xe at a 4 11,43rad/s2. R R 0,35
4.3. Khối tâm của đĩa phẳng bị khoét -
Khi chưa bị khoét, khối tâm của đĩa tại tâm O là điểm đặt của trọng lực P
được coi là hợp lực của P1 (đặt tại O1) là trọng lực tác dụng vào phần được khoét bỏ
đi và P2 là trọng lực tác dụng vào phần đĩa đã bị khoét. -
Trọng lực P2 có điểm đặt tại khối tâm G, do tính đối xứng nên G nằm trên đường
OO1, khác phía với O1 so với O. -
Theo quy tắc hợp lực song song ta có: OGP2 m2 OO1P1 m1 -
Do đĩa phẳng đồng chất nên khối lượng tỷ lệ với diện tích: 2 2 m S r r 2 2 2 2 2 2 m1 S1 R r R r - Vậy nên ta có: 2 2 r Rr OG OO 2 2 1 2 2 R r 2( R r)
4.4. Hình trụ rỗng chịu lực hãm tiếp tuyến -
Chuyển động của trụ là chuyển động quay chậm dần đều. Ta có vận tốc góc ban đầu 0 600 vòng/phút 20 rad/s -
Mômen quán tính của hình trụ đối với trục quay: I0 mR2 50.0,52 12,5kgm2. -
Gia tốc góc của chuyển động t 0 0 20 rad/s2. t 60 3 a. Công của lực hãm
- Công của lực hãm bằng độ biến thiên động năng của vật 1 2 EK EKt EK0 0 I0 0 A 2 12,5.(20 )2 24,67.103 J
b. Mômen lực hãm và độ lớn lực hãm -
Theo phương trình cơ bản của vật rắn quay quanh trục cố định: lOMoARcPSD| 38841209 M/G I0 12,5.( ) 13 , 09 Nm 3
- Độ lớn lực hãm tiếp tuyến M 13 , 09 /G M/G t RF t F 26 , 18 N R 0 , 5
(Trong các đáp số trên, dấu “-“ thể hiện tính cản).
4.5. Trụ rỗng có cuốn dây được thả rơi -
Chuyển động của trụ gồm chuyển động quay quanh trục và chuyển động tịnh
tiến của khối tâm. Trục quay tức thời là tiếp điểm C của sợi dây và hình trụ. - Ta có: P T ma (1) M/C (P ) M/C (T ) IC m T
- Chiếu (1) lên chiều chuyển động tương ứng, có R C P T ma (2) M/C (P ) IC (3) P a a - Mặt khác ta có 2 2 IC I0 mR 2 mR ; t ; M/C (P) PR mgR . Kết hợp với R R (2), (3) ta được: g 10 5 m/s 2 . 2 2 P ma m(g a) 1(10 5) a T 5N 4.6.
Chuyển động của hệ gồm 3 chuyển động: chuyển động tịnh tiến của m1, m2 và
chuyển động quay của ròng rọc. lOMoARcPSD| 38841209 M/O(T2 ) 4m/s2 4.7.
Chuyển động của hệ gồm 3 chuyển động: chuyển lOMoARcPSD| 38841209 N F P1 N1 T1 Fms1 m a11 được: T1 P2 M/O(T2' ) a lOMoARcPSD| 38841209 -
Khi cuộn chỉ lăn không trượt trên bàn, nó có trục quay tức thời là được thẳng
song song với trục của nó và đi qua tiếp điểm C của Fn F cuộn chỉ O với mặt bàn. r F -
Mômen quán tính của cuộn chỉ đối với trục quay: t R IC I0 mR2
a. Tìm điều kiện về góc kéo C
- Phân tích lực F thành hai lực: F Ft
Fn , tương ứng gây ra các mômen quay M/C (F) t , M/C (F) n
- Để cuộn chỉ chuyển động về phía trước: M/C (F) t M/C (F) n Fcos(R rcos ) Fsin.rsin 2 2 FRcos Fr(cos sin ) 0 r cos R
- Vậy để cuộn chỉ chuyển động về phía trước thì r cos. R
b. Cuộn chỉ chịu tác dụng của các lực P, N, Fmsn , F . Ta có phương trình chuyển động
của cuộn chỉ (vừa chuyển động tịnh tiến, vừa chuyển động quay): (1) PN F Fmsn ma M/C F IC -
Chiếu (1) lên phương ngang và phương thẳng đứng, lên chiều chuyển động tương ứng, ta được: lOMoARcPSD| 38841209 Fcos m F sn ma (2) N Fsin P 0 (3) M/C (F) t M/C (F) n IC (4) - Ở đây ta có a R (5) - Từ (4) ta có: 2 Fcos(R r.cos ) Fsin.r.sin ( I0 mR) F(Rcos r) (6) 2 I0 mR
- Thay (6) vào (2), kết hợp với (5) ta được: F(Rcos r) Fcos m F sn mR 2 I0 mR mRF(Rcos r) m F sn Fcos (7) 2 I0 mR -
Để cuộn chỉ không bị trượt, ta phải có điều kiện: Fmsn kN (8) -
Kết hợp (3), (7), (8) ta được: 2 kmg(I0 mR) 2 r 0 I(cos ksin ) mR ksin F R
4.9. Hoàn toàn tương tự, chuyển động của hệ gồm chuyển động
tịnh tiến của m2 và chuyển động quay của m1, ta có: m 1 O ' T N T P N T F m a m 2 ms F 2 ' ms 2 (1) M/O(T ) IO P -
Chiếu (1) lên chiều chuyển động tương ứng, ta có: P sin2 Fms T m a2 (2) N P cos2 0 (3) 2 M/O(T' ) IO (4) mR2 ' - Ta có T T', a/R , I0 , M/O(T ) RT' (5). 2 lOMoARcPSD| 38841209
a. Gia tốc chuyển động của m 2
- Kết hợp (2), (3), (4), (5) ta được: m2 (sin kcos ) a g 0 ,5m m - Ta có s 1 2 0 0 500( sin 45 0 ,1cos 45) 2
10 5 ,3m/s 4.10. Do hai sợi dây đối xứng và 0,5.200 500
giống hệt nhau cho nên ta giả sử chỉ
b. Quãng đường m 2 đi được sau 2 giây
có 1 sợi dây. - Hình trụ (1) chỉ có 1 2 1 2 at 5,3.2 10, 6 m
chuyển động quay, hình trụ (2) vừa 2 2
chuyển động tịnh tiến, vừa chuyển
động quay. Do chuyển động có tính tương đối nên có thể coi trục quay tức thời của
hình trụ (2) là trục của nó. - Ta c ó: P T ma 2 2 2 1 M (T ) I (1) O1 /O1 1 0 1 T M 1 /O2 ( 2 T ) I0 2 T 2
- Chiếu (1) lên chiều chuyển động tương ứng: O2 2 2 P 2 T ma2 (2) M/O1 ( 1 T ) I0 1 (3) P2 M/O2 ( 2 T ) I0 2 (4) 2 mR - Ở đây ta có I0 , 1 T 2 T 2T ; a2 ( 1 2 )R (5) 2
- Từ (3) và (4) viết cụ thể ta có 1 2 (6).
- Từ (2), (3), (4), (5), (6) ta có: 4 4 g 10 a 5 5 8m/s2. 1 1 1 T T1 mg 2.10 2N 2 10 10
4.11. Mômen động lượng của Trái Đất -
Trái Đất là một vật rắn quay quanh trục, do đó mômen động lượng đối với trục quay được xác định: L0 I0
- Độ lớn của mômen động lượng: 2 2 2 L0 I0 MR 5 T 2 2 24 6 2 33 6.10(6,4.10) 7,15.10 kgm 2 /s 5 24.60.60
4.12. Mômen động lượng của đĩa phẳng -
Mômen quán tính của đĩa đối với trục quay: R 2 1 2 1 2 3 2 I I0 m mR mR mR lOMoARcPSD| 38841209 2 2 4 4 -
Gọi là vận tốc góc tức thời tại vị trí thấp nhất, theo bảo toàn cơ năng ta có (khối
tâm hạ thấp một đoạn bằng R): 1 2 2 mgR 2 mgR 8 g I 3 2 2 I 3 R mR mgR 4
- Mômen động lượng tại vị trí thấp nhất được xác định: L/ I 3 8 g 3 2 L/ I mR mR gR 4 3 R 2
4.13. Tính động năng toàn phần của các vật -
Động năng toàn phần của một vật được xác định: EK EKtt EKq 1 mv2 1 I 2 2 2
a. Đĩa đặc đồng chất lăn không trượt 1 2 1 2 1 2 1 1 2 v 2 3 2 EK mv I0 mv . mR mv 24J 2 2 2 2 2 R 4
b. Quả cầu đặc đồng chất lăn không trượt EK 1 mv21 I0 2 1 mR2 2 1 2. mR2 2 7 mR2 2 0,252J 2 2 2 2 5 10
4.14. Viên đạn xuyên vào thanh treo thẳng đứng -
Mômen quán tính của thanh đối với trục quay: 2 1 2 1 I md m m m 2 01 1 1 1 1 12 2 3 2 I1 -
Ngay trước và sau va chạm mômen ngoại lực tác dụng lên hệ đối với trục quay
bằng 0, do đó mômen động lượng của hệ bảo toàn: - Ngay trước va chạm: L L1 L2 m v2 -
Ngay sau va chạm, gọi là vận tốc góc quay của thanh: ' 1 L I ( I I) m 2 m 2 1 2 1 2 3
- Mômen động lượng bảo toàn: ' L L 1 3 mv mv m 2 m 2 2 2 1 2 3 ( m 3 m ) 1 2 3.0,05.100 120 rad/s (0 , 2 0,05)0 , 5 lOMoARcPSD| 38841209
4.15. Xét một điểm O’ (cố định so với O). -
Mômen động lượng của hệ chất điểm đối với O’: ' dr ' ' ' i L Li i r mi dt '
- Mà ta có ir O'O ir ir 0r với 0r OO' - Nên ta có: ' d d L ( ir 0 r) mi ( ir 0 r) ( ir 0 r) mi i r dt dt d d i r mi i r 0 r mi i r L 0r i mv i dt dt ' L L 0 r p -
Để mômen động lượng của hệ chất điểm không phụ thuộc vào điểm O, tức là L L' với mọi r0 thì ta phải có p 0.
4.16. Hoàn toàn tương tự như bài 3.19, ta có: -
Mômen động lượng đối với điểm O được xác định: ' L L r0 p ' - Chọn điểm O'
G trùng với khối tâm. Khi đó L LG L0 là mômen động lượng
của hệ đối với khối tâm của nó; r0 OO' OG làn bán kính vector của khối tâm kẻ từ
gốc O. Vậy rõ ràng ta có:' L L r0 p
4.17. Chiếc bút chì đổ trên mặt bàn nằm ngang -
Trong quá trình đổ, chuyển động của bút chì là chuyển động quay quanh trục
cố định, trục quay nằm ngang, đi qua điểm tiếp xúc của bút chì với mặt bàn và vuông
góc với mặt phẳng quỹ đạo của bút chì. -
Mômen quán tính của bút đối với trục quay: lOMoARcPSD| 38841209 2 1 2 2 1 I I md m m m 2 0 12 2 3
- Gọi là vận tốc góc của bút chì ở thời điểm bút hợp với phương thẳng đứng mộ t
góc . Theo bảo toàn cơ năng, có: 1 2 mg (1 cos ) I 2 2 mg (1 cos ) mg (1 cos ) I 1 m 2 3 3 g (1 cos ) g 6 sin 2 10 - Áp dụng 0 1 90 0 rad/s 1 6 sin45 12 , 23 0 ,2
4.18. Vật trượt trên mặt phẳng nghiêng -
Áp dụng định luật bảo toàn cơ năng, ta có: 1 2 1 2 mgh mv I 2 2
a. Vật là một trụ đặc 2 1 2 1 1 2 v mgh mv mR 2 2 2 R 3 2 mgh mv 4 4 4 v gh 10.0,5 2 , 56 m/s 3 3
b. Vật là một trụ rỗng 2 1 2 1 2 v mgh mv mR 2 2 R 2 mgh mv v gh 10.0,5 2 , 24 m/s
4.19. Người di chuyển trên đĩa quay nằm ngang, mômen động lượng của hệ được bảo toàn.
a. Xác định vận tốc góc quay -
Khi người ở ngoài mép đĩa, mômen quán tính của hệ đối với trục quay được xác định: 1 2 2 m1 2 m2 2 I ID IN 1 mR 2 mR R 2 2 lOMoARcPSD| 38841209
- Khi người đi vào tâm đĩa, 1 2
mômen quán tính của hệ: I1 ID IN 1 mR 2
b. Công thực hiện khi người di
- Theo bảo toàn mômen động lượng, ta có: L1 L chuyển I1 1 I
- Công thực hiện bằng độ biến 1 2 m1 2 m2 2
thiên động năng của hệ: 1 mR 1 R 2 2 m 2 m 100 2.50 2 1 2 1 rad/s m1 100 3 3 1 1 2 A EK1 EK I1 1 I 2 2 m m 2 m 1 2 2 1 2 2 2 A R 1 R 4 4 -
Thay số ta được A 123,37 J
4.20. Quả cầu đặc lăn trên mặt bán cầu -
Chọn gốc tính thế năng tại mặt bàn nằm ngang. Xét tại vị trí M của quả cầu trên
mặt bán cầu có AOM. -
Theo định luật bảo toàn cơ năng: mg R r 1 cos 1 mv2 1 I0 2 2 2 -
Ta có động năng chuyển động của quả cầu: 1 2 1 2 1 2 1 2 2 v 2 7 2
mv I0 mv . mr mv 2 2 2 2 5 r 10 - Vì vậy ta được: mg(R r)(1 cos ) mv2 (1) -
Xét lực tác dụng lên quả cầu theo phương hướng tâm, có: v2 Pcos N m A (2) N M R r - Rút mv
2 từ (1) thay vào (2) ta được: O P 1 N mg 17cos 10 (3) 7 -
Quả cầu còn lăn trên mặt cầu thì N
0, vậy thời điểm quả cầu bắt đầu rời
khỏi mặt cầu thì ta có N 0. 1 10 N mg 17cos 10 0 cos (4) 7 17 -
Thay (4) vào (1) ta xác định được vận tốc dài của quả cầu: 10g(R r) v (5) lOMoARcPSD| 38841209 17 -
Vậy vận tốc góc của quả cầu tại thời điểm quả cầu bắt đầu rời khỏi mặt cầu: v 10g(R r) 2 r 17r
4.21. Khẩu pháo trên đường nằm ngang -
Hệ kín theo phương ngang, do đó động lượng của hệ được bảo toàn theo
phương ngang. Chọn chiều dương là phương ngang hướng theo chiều bắn. a. Quả
đạn bắn theo phương ngang khi pháo đứng yên -
Gọi v là vận tốc của khẩu pháo ngay sau 0 1 mv 2 mu khi bắn m2 v u 500 m 100 5 m/s 1 10000 b.
Quả đạn được bắn xiên 0 1 mv m2 ucos lên khi pháo đứng yên m2 0 v ucos 500 cos 60 m 100 2,5m/s 1 10000
c. Quả đạn được bắn ngang khi pháo chuyển động
- Vận tốc của quả đạn so với đất khi bắn ra là v' u v0 v' u v0 500 5 505 m/s - Tương tự ta có: ( m m)v mv' ( m 1 2 0 1 2 m)v 0 1 mv m2 v' 2 v m1 (10000 100)5 100.505 0 m/s 10000 -
Trong các đáp số trên, dấu “-“ thể hiện khẩu pháo bị giật lùi ngược với hướng bắn.
4.22. Động lượng của hệ được bảo toàn theo phương ngang. -
Gọi v0 là vận tốc của m2 ngay sau khi bật ra khỏi mặt nêm, v là vận tốc chuyển
động của nêm sau va chạm. -
Theo bảo toàn động lượng, ta có: m v1m v2 0 0 v0 m1 v (1) m2 lOMoARcPSD| 38841209 -
Mặt khác, do va chạm đàn hồi nên năng lượng của hệ được bảo toàn: 1 1 2 2 1 mv 2 mv 0 2 mgh 2 2 2 1 1 m 2 1 1 mv m2 v m2 gh 2 2 m2 m 2 v 2 gh 1 m(m 1 2 m) 0 , 5 2.10.1 0,426 m/s 5(5 0 , 5)
4.23. Áp dụng công thức Xiôncôpxki.
a. Gọi t là thời gian kể từ lúc bắt đầu chuyển động đến khi đạt vận tốc v1.
- Khối lượng tại thời điểm đó: m0 270 uln 300 ln 329,58 m/s v m 90 2 2 Chương 5
TRƯỜNG HẤP DẪN
TÓM TẮT LÝ THUYẾT
1. Định luật hấp dẫn Vũ trụ m m1 2 F F G 2 r 2
- Với G là hằng số hấp dẫn Vũ trụ G 6,67.10 11 Nm2 kg lOMoARcPSD| 38841209
2. Gia tốc trọng trường trên mặt đất M g0 G 2 R
- Với M, R là khối lượng và bán kính Trái Đất.
3. Gia tốc trọng trường ở độ cao h GM R 2 g 2 g0 R h R h - Nếu h R : g g0 1 2h R
4. Vận tốc Vũ trụ cấp I và II vI g R0 7,9 km / s vII 2g R0 11,2 km / s BÀI TẬP VÍ DỤ
Ví dụ 1. Bán kính của Mặt Trời lớn gấp 110 lần bán kính Trái Đất, khối lượng riêng D1
của Mặt Trời bằng 1:4 khối lượng riêng D2 của Trái Đất. Hỏi gia tốc rơi tự do ở trên bề
mặt Mặt Trời bằng bao nhiêu? Cho gia tốc rơi tự do ở trên mặt Trái Đất g2 9,8 m / s2 . Lời giải GM4 3 - Áp dụng công thức g 2 với M D.V và V R R3 4 g G.D 3 R -
Do đó, tại bề mặt Mặt Trời: g1 G.D1 R1 -
Tại bề mặt Trái Đất: 4 D R11 g2 G.D2 R2 g1 g2 3 D R22 -
Với D ,D1 2 là khối lượng riêng của Mặt Trời và Trái Đất, R ,R1 2 là bán kính của
Mặt Trời và Trái Đất. - Thay vào ta có g1 269,5 m/s2 .
Ví dụ 2. Biết khoảng cách trung bình của một vệ tinh nhân tạo chuyển động tròn xung
quanh Trái Đất tới mặt đất là h 1700km. Tìm vận tốc dài và chu kỳ quay của nó?. Cho
bán kính Trái Đất là R 6370km. Lời giải: lOMoARcPSD| 38841209 -
Vệ tinh chuyển động tròn xung quanh Trái Đất. Lực hấp dẫn đóng vai trò lực hướng tâm 2 GMm mv F 2 r r - T
trong đó r là khoảng cách từ vệ tinh tới tâm Trái Đất, r R h 2 gR - Lại có: GM 2 v r r T 2 2 gR g v R R h R h - Do đó suy 2 3 3 9 ,8m/s ;R 6370.10 m; h 1700.10 m ra: v 2 2 2 2 2 GM R R - Thay số: g T R 4 3156.10 s v2 1 T 27,322.24.3600 s 7019,6 m/s 7 ,02km/s - Ta có:T 2 R h 3 T 7,22.10 s v v BÀI TẬP ÁP DỤNG 5.1.
Tìm một điểm trên đường thẳng nối tâm Trái Đất và tâm Mặt Trăng mà tại đó
lực hút của Trái Đất và lực hút của Mặt Trăng tác dụng vào cùng một vật sẽ cân bằng
nhau. Cho biết khoảng cách giữa Trái Đất và Mặt Trăng bằng 60 lần bán kính Trái Đất,
còn khối lượng Mặt Trăng nhỏ hơn khối lượng Trái Đất 81 lần. Bán kính Trái Đất R 6378km. 5.2.
Tìm trọng lượng của một vật có khối lượng 100kg ở độ cao 200km trên mặt đất? 5.3.
Vệ tinh nhân tạo của Trái Đất chuyển động trong mặt phẳng xích đạo từ Tây
sang Đông với vận tốc góc bằng vận tốc góc của Trái Đất quay xung quanh trục của
nó (vệ tinh địa tĩnh). Tính độ cao của vệ tinh? Cho bán kính Trái Đất R 6,37.10 m6 . 5.4.
Vệ tinh nhân tạo của Trái Đất chuyển động tròn gần mặt đất có chu kỳ quay 1 2 3
bằng T. Chứng tỏ rằng ta có: T G
. Trong đó: là mật độ khối lượng trung
bình của Trái Đất và G là hằng số hấp dẫn vũ trụ. 5.5.
Khối lượng của Trái Đất bằng 81,3 lần khối lượng của Mặt Trăng. Cho biết bán
kính của Trái Đất R 6378km, bán kính Mặt Trăng Rt 1738km, gia tốc rơi tự do ở mặt
đất g 9,8m / s2 . Xác định gia tốc rơi tự do ở bề mặt Mặt Trăng. lOMoARcPSD| 38841209 5.6.
Bán kính của Mặt Trời R 6,95.10 m8 , bán kính quỹ đạo của Trái Đất r 1,49.1011
m , chu kỳ quay của Trái Đất xung quanh Mặt Trời là 1 năm ( 365,255
ngày đêm 3156.104 s). Tính gia tốc rơi tự do g của vật ở bề mặt Mặt Trời ? 5.7.
Vệ tinh nhân tạo của Trái Đất chuyển động theo quỹ đạo tròn có bán kính r
6600km . Xác định số vòng quay của vệ tinh trong một ngày đêm. Cho bán kính Trái
Đất R 6,4.10 m6 và gia tốc rơi tự do ở gần mặt đất g 9,8m / s2 . 5.8.
Tìm vận tốc vũ trụ cấp I và cấp II đối với Mặt Trăng, cho khối lượng của Mặt
Trăng là 7,35.1025g, bán kính Mặt Trăng bằng 3:11 bán kính Trái Đất (bán kính Trái Đất là 6370km).
HƯỚNG DẪN - LỜI GIẢI - ĐÁP SỐ 5.1. x 6R -
Gọi x là khoảng cách từ điểm đó đến Mặt Trăng. Viết biểu thức lực hút của Mặt
Trăng và của Trái Đất vào vật m và cân bằng 2 lực này. Ta có: mM mM T D G G 2 2 x 60 R x - Từ đó rút ra: x 6R 390 N 5.2. P
- Trọng lượng của một vật ở một nơi có gia tốc tự do là g sẽ bằng: mg P GM - Ở độ cao h: D gh
(M D : khối lượng Trái Đất, R D : bán kính Trái Đất ). 2 RD h GMD g0 2 - Ở RD mặt 2 h RD đất: g 2 0 RD h 2 g RD 2 h 2 g0 g 1 9,3m /s 2 0 RD 2 h RD 1 RD
- Từ đó ta tính được P 390 N .
5.3. Vệ tinh chuyển động tròn. - Vậy g - Hay g lOMoARcPSD| 38841209 -
Lực hấp dẫn đóng vai trò lực hướng tâm: 2 GMm v F m 2 r r - Trong đó 2 GM gR 2 v r r; r R h ; h là độ cao. T 2 2 2 2 2 gR v R h T R h 1 2 3 2 T R h gR 2 2 g 9 ,8 m/s; T 24 h 86400 s 6 R 6,37.10m 7 R h 4,22.10m 7 6 7 h 4,22.10 6,37.10 3 ,583.10m h 35830 km
(Loại vệ tinh để sóng phát vô tuyến truyền hình). 2 GMm v
5.4. Ở gần mặt đất: F m 2 R R 2 GM 2 2 2 2 2 v R R T R 4 3 M V R 3 1 2 2 4 GM 4 3 G T 2 3 T R 3 G -
Suy ra: Phóng vệ tinh nhân tạo gần mặt hành tinh biết chu kỳ quay T tìm được của hành tinh.
5.5. Gọi M, Mt là khối lượng của Trái Đất và của Mặt Trăng. -
Gọi g và gt là gia tốc rơi tự do ở Mặt Đất và bề mặt của Mặt Trăng. GMm - Ở mặt đất: 2 mg R - Ở bề mặt Mặt Trăng: GMm t mg 2 t Rt 2 M R t gt g M Rt M R 6378 81 ,3 ; 3, 64 Mt Rt 1738 2 3 ,64 2 gt 9 ,8 1 ,59m/s 81 ,3 lOMoARcPSD| 38841209
5.6. Gọi M, MD là khối lượng của Mặt Trời và Trái Đất. 2 GMMD D Mv 2 GM rv 2 r r 2 2 2 2 r 4 3 GM rv r r 2 T T -
Gia tốc rơi tự do g ở gần bề mặt của Mặt Trời: GMm GM mg g 2 2 R R 2 3 GM 4 r g 2 2 2 R R T 11 r ,49.10 m 1 8 R 6,95 .10 m T 1 năm 4 3156.10 s - Ta có: 2 g 271 m/s m/s 2 . 5.7. 1 ngày đêm 24 giờ 86400 s -
Gọi T là chu kỳ quay của vệ tinh tính theo giây thì số vòng quay 1 ngày đêm sẽ là: 86400 n T 2 v GM T ; ; v r r 3 r 2 3 gR GM T 2 5 ,3.10 s 2 gR n 16 vòng. 5.8. I V 1 ,67km/s ; II V 2 ,37km/s