Đề cương môn công nghệ web- Trường Đại học bách khoa - Đại học đà nẵng.

Chương 3 HÌNH HỌC FRACTAL
Trong thực tế có nhiều loại đường cong có một tính chất đặc trưng là đồng dạng, được biểu
diễn bởi sự giống nhau giữa một phần rất nhỏ của đường cong được phóng lớn với một phần khác
lớn hơn của cùng một đường cong đó. Chương này trình bày về ứng dụng của hình học phân hình
nhằm xây dựng các loại đường cong có tính tự đồng dạng.
7.1. TÍNH TỰ ĐỒNG DẠNG CỦA HÌNH ẢNH
Một số hình ảnh có những phần của nó giống nó nhưng nhỏ hơn. Trong thiên nhiên có nhiều
hình ảnh như thế. Khi nhìn toàn bộ một đám mây cũng giống như nhìn một mảnh của nó nhưng
gần hơn. Các hình ảnh khác trong thiên nhiên như: cây cối, rặng đồi, hình ảnh ven bờ biển, cấu
trúc tế bào của một chiếc lá, …
Các hình ảnh như vậy được gọi là tự đồng dạng.
Hình 7.1. Các hình ảnh tự đồng dạng
Fractal xuất hiện từ hình học phân hình (Fractional Dimensional Geometry: Hình học phân
nhỏ số chiều) do Benoit Mandelbrot ở Trung tâm nghiên cứu IBM là người tiên phong đề xuất.
Năm 1983 ông viết sách Hình học phân hình và ông gọi hình ảnh này là fractal.
Trong hình học Euclid cổ điển thì một đường có số chiều là 1, một mặt có số chiều là 2 và
một khối có số chiều là 3. Nhưng một đường dài vô hạn vẫn nằm gọn trong một mặt giới hạn phải
có số chiều giữa 1 và 2. Số chiều của các fractal thường được đo bằng số chiều Hausdorff –
Besicovitch. Ngoài ra còn có các số chiều khác là số chiều Compa và số chiều Box-counting. Số
chiều để biểu hiện độ lan toả của các fractal.
Hai trong số những thuộc tính quan trọng nhất của các Fractal là tự đồng dạng và số chiều
không nguyên. Thông thường người ta sử dụng kỹ thuật đệ qui để sinh các fractal. Các đường cong
đệ quy cơ bản như đường cong Koch, đường cong C,...
7.2. SỐ CHIỀU FRACTAL
Trong toán học, số chiều Hausdorff (còn gọi là số chiều Hausdorff – Besicovitch) là một số
thực không âm mở rộng (có thể có giá trị  ) ứng với một không gian metric nào đó. Số chiều
Hausdorff tổng quát hoá khái niệm chiều của một không gian vector thực. Đó là, số chiều
Hausdorff của một không gian tích trong n-chiều bằng n. Ví dụ như số chiều Hausdorff của một
điểm là 0, số chiều Hausdorff của một đường thẳng là 1, và số chiều Hausdorff của mặt phẳng là
2. Tuy nhiên, có rất nhiều tập kì dị có số chiều Hausdorff không phải là số nguyên. Cho S1, S2, …, SN:
n  n là các phép đồng dạng với hệ số co tương ứng 0 < Ti < 1. Một
tập bất biến với N các phép đồng dạng trên được gọi là tập tự đồng dạng (self-similar-set) nếu tồn
tại một tập mở bị chặn, không trống V sao cho: n
 S (V ) V . i i1
Với các Si(V) rời nhau đôi một thì họ {Si} được gọi là thoả điều kiện tập mở. N
Số chiều d của V được tính theo phương trình: T d  1. i i1
Thông thường các tỷ lệ đồng dạng bằng nhau và bằng T. Nên ta có: 1
NTd =1 hay T d  d  . T 1 log( ) Do đó: d  N . log(T )
d không phụ thuộc vào cơ số logarit. log(N )
Vì 0 < T < 1 và hệ số co T thường là số hữu tỷ, ta có: d  . 1 log( ) T
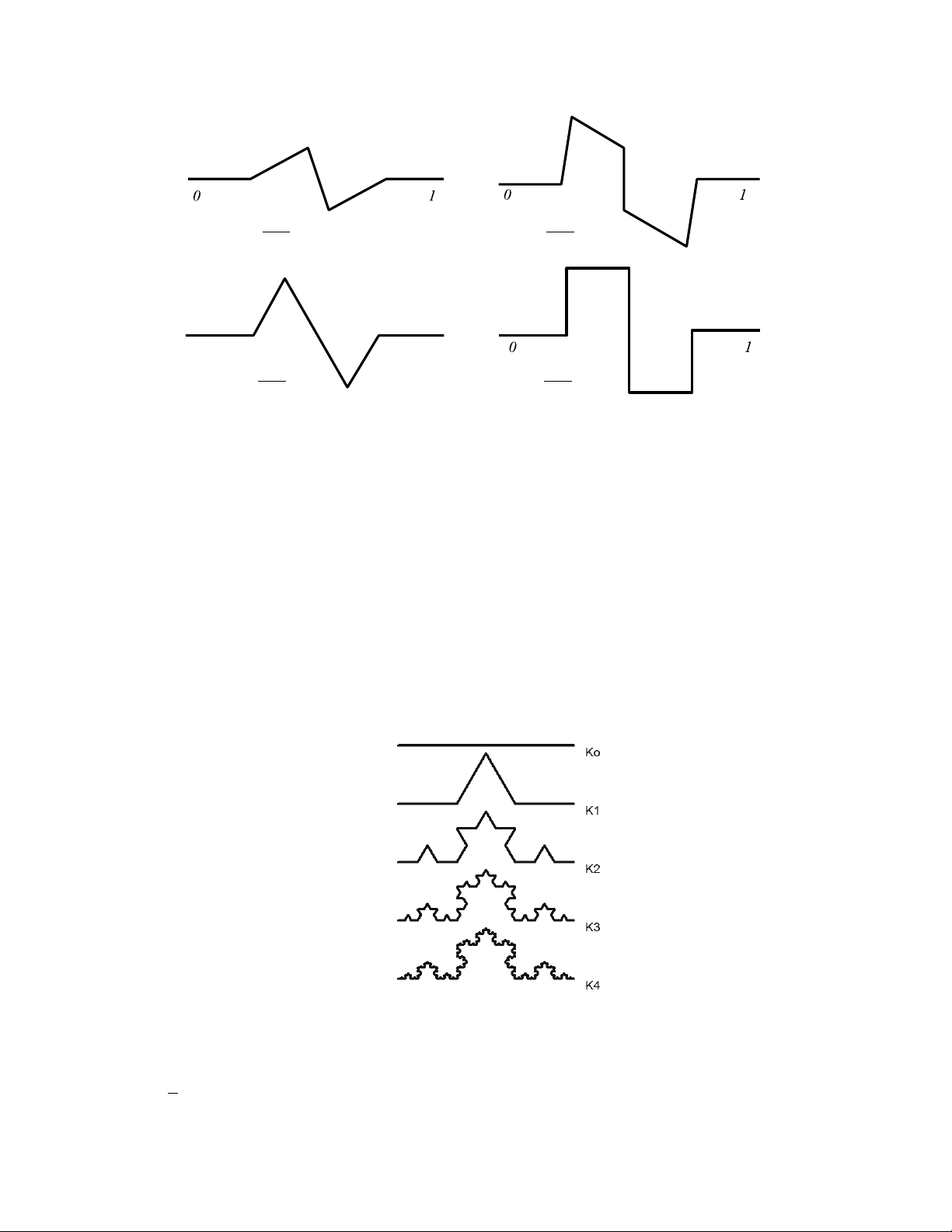
Giả sử ta có một đoạn thẳng đơn vị, cấp n có được từ cấp n − 1 bằng cách chia mỗi đoạn thẳng 1
thành 4 đoạn bằng nhau (hệ số co T  ) và thay hai đoạn giữa bởi 3, 4, 5, 6 đoạn, nghĩa là 4
N = 5, 6, 7, 8 tương ứng như hình vẽ thì số chiều của các fractal này được tính như sau: log 5 d   1.16 log 7 d   1.40 log 4 log 4 0 1 log 6 d   1.29 log 8 d   1.5 log 4 log 4
Hình 7.2. Biểu diễn số chiều Hausdorff
7.3. CÁC ĐƯỜNG CONG ĐỆ QUY CƠ BẢN 7.3.1. Đường cong Koch
Đường cong Koch được phát hiện bởi nhà toán học Thụy Sĩ Helge Von Koch vào năm 1904.
Mỗi đường cong đệ quy có một cấp. Gọi Kn là đường cong Koch cấp n và Kn được xác định như sau: 
K0 là đoạn thẳng đơn vị; 
Kn có được từ Kn-1 bằng cách chia mỗi đoạn thẳng thành ba đoạn bằng nhau và thay
đoạn giữa bởi một chóp tam giác đều.
Hình 7.3. Đường cong Koch
Một đường cong Koch cấp n có được từ cấp n − 1 bằng cách dùng N = 4 phép co với hệ số 1
co T  . Số chiều của đường cong Koch được xác định: 3 log 4 d   1.26. log 3 4 Gọi L 
n là độ dài của Kn. Ta có hệ thức truy hồi: L
L với L0 = 1.  n 3 n1  4 n 
Giải ra ta được L   . Vậy L  . n    3 
Các bước vẽ Kn độ dài len hướng dir:
1. Vẽ Kn-1 độ dài len/3; 2. Quay trái 600;
3. Vẽ Kn-1 độ dài len/3; 4. Quay phải 1200;
5. Vẽ Kn-1 độ dài len/3; 6. Quay trái 600;
7. Vẽ Kn-1 độ dài len/3.
Hàm vẽ Kn độ dài len hướng dir được cài đặt như sau: #define RADS M_PI/180
void Koch(int n, float len, float dir,) { if (n> 0) { Koch (n-1, len/3, dir); dir += 60.0; Koch (n-1, len/3, dir); dir -= 120.0; Koch (n-1, len/3, dir); dir += 60.0; Koch(n-1, len/3, dir); }
else linerel(int(len *cos(dir *RADS)),int(len *sin(dir *RADS))); }
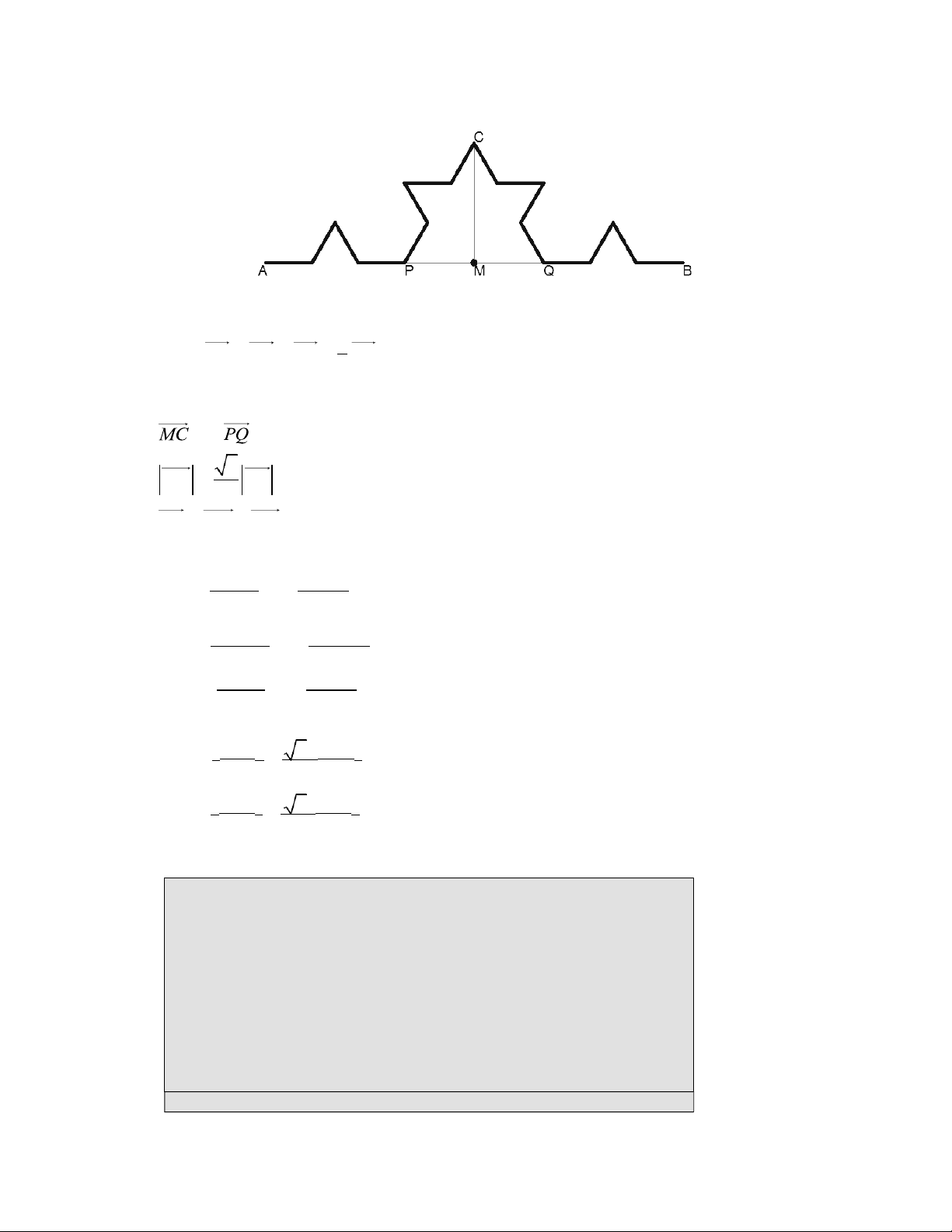
Cách khác để vẽ đường cong Kn từ điểm A(a, b) đến điểm B(c, d) bẳng cách vẽ 4 đường cong Kn-1 như sau:
1) Vẽ đường cong Kn-1 từ điểm A đến điểm P
2) Vẽ đường cong Kn-1 từ điểm P đến điểm C
3) Vẽ đường cong Kn-1 từ điểm C đến điểm Q
4) Vẽ đường cong Kn-1 từ điểm Q đến điểm B
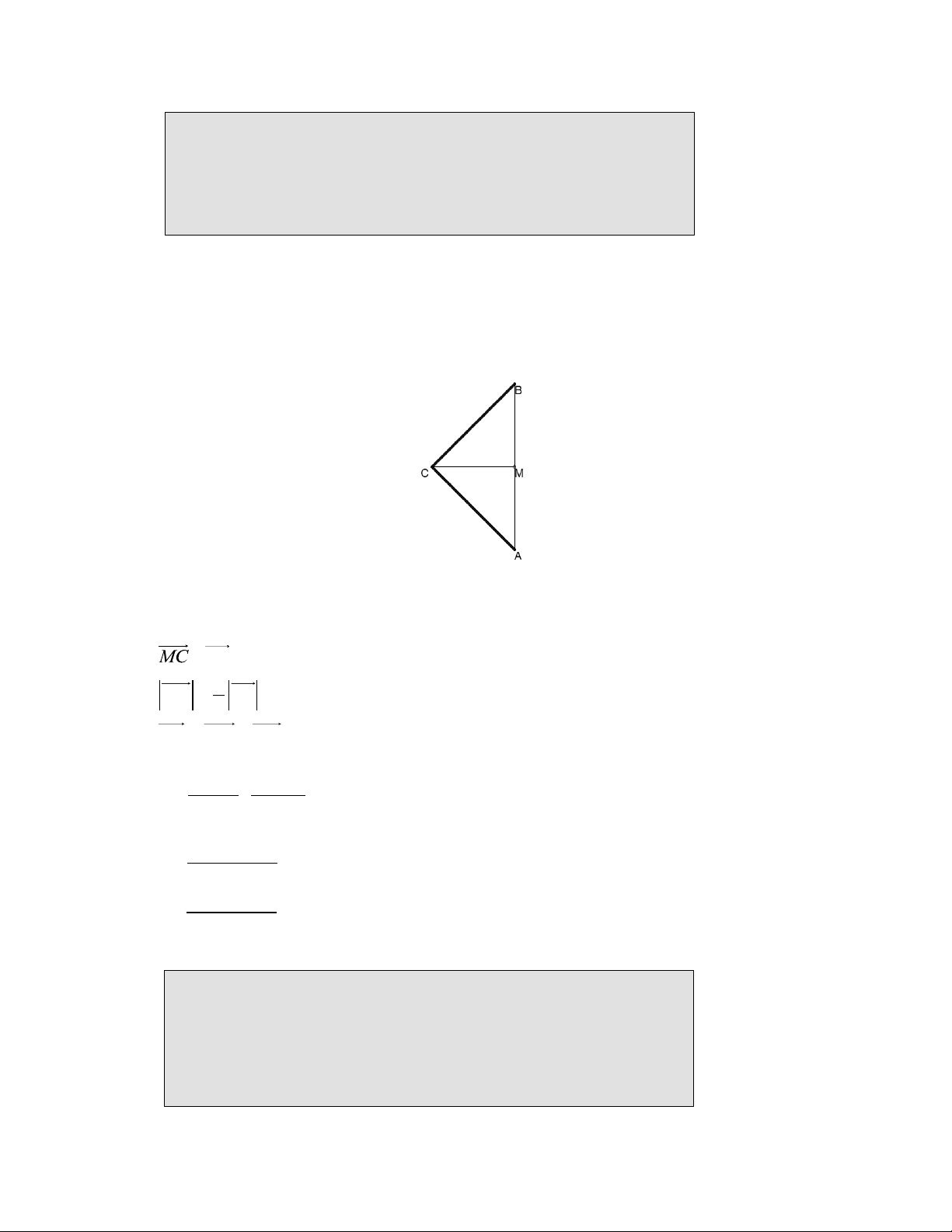
Hình 7.4. Vẽ đường K2 bằng cách vẽ 4 đường K1 1
Ta có AP  PQ  QB  AB. 3
Với M là trung điểm của AB:  3 MC  PQ 2
PC  PM  MC
thì toạ độ các điểm P, Q và C(u, v) được tính như sau:  (c  a) (d  b)  P  a  , b   3 3   
2(c  a)
2(d  b)  Q  a  , b   3 3    c  a
d  b  M  a  , b  2 2   
c  a 3 d  b u  a   2 2 3
d  b 3 a  c v  b   . 2 2 3
Hàm vẽ Kn từ điểm A đến điểm B được cài đặt như sau:
void K(int n, int a, int b, int c, int d) { int u,v; if (n>0){
u=int(a+(c-a)/2+FACT*(d-b)/3);
v=int(b+(d-b)/2+FACT*(a-c)/3);
K(n-1, a, b, a+(c-a)/3, b+(d-b)/3);
K(n-1, a+(c-a)/3, b+(d-b)/3, u, v);
K(n-1, u, v, a+2*(c-a)/3, b+2*(d-b)/3);
K(n-1, a+2*(c-a)/3, b+2*(d-b)/3, c, d); } else line(a, b, c, d); }
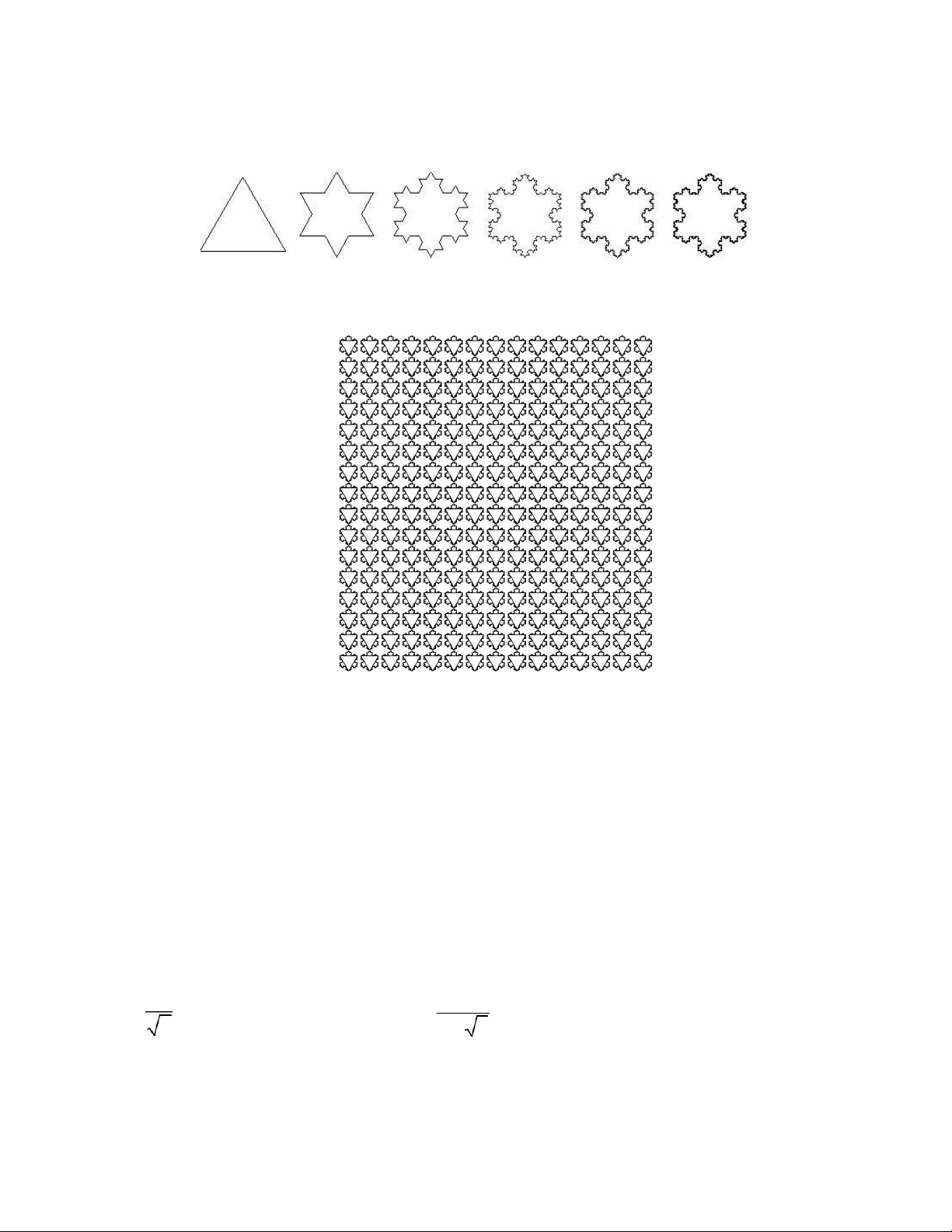
Nếu thay đoạn thẳng khởi đầu K0 bởi tam giác đều cạnh K0 thì ta sẽ nhận được kết quả là hình bông tuyết.
Hình 7.5. Hình bông tuyết
Có thể dùng các hình bông tuyết để tạo hoa văn như sau:
Hình 7.6. Đường cong Koch tạo hoa văn 7.3.2. Đường cong C
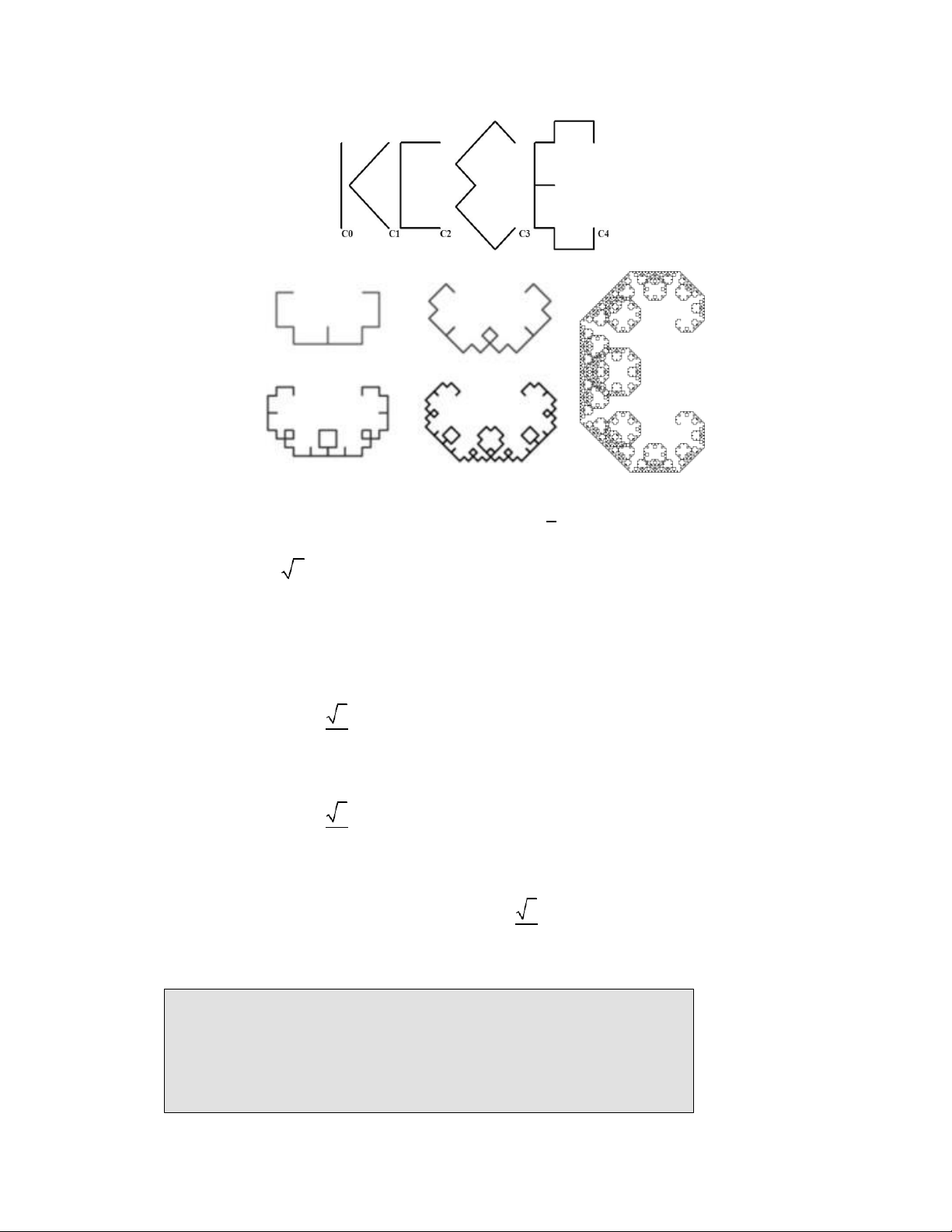
Đường cong C có tên gọi do hình dáng của đường cong này giống ký tự C. Các đường cong
C chuẩn được xây dựng bằng 450 hình tam giác vuông cân. Biến thể của đường cong C có thể được
xây dựng bằng cách sử dụng hình tam giác cân với các góc khác góc nhỏ hơn 600. Nhưng với góc
nhỏ hơn 450 sẽ cho ra một fractal không có độ cong tốt. Quá trình vẽ đường cong liên tiếp sẽ hướng
đến một đường cong giới hạn.
C0 là đoạn thẳng đơn vị.
Cn có được từ Cn-1 bằng cách thay mỗi đoạn thẳng bởi một chóp tam giác vuông cân.
Một đường cong C cấp n có được từ cấp n – 1 bằng cách dùng N = 2 phép co với hệ số co 1 T 
. Số chiều của đường cong C là d  log 2  2. 2 log 2
Hình 7.7. Đường cong C
Gọi Ln là độ dài của Cn. Ta có hệ thức truy hồi: Ln = √2 Ln−1 với L0 = 1.
Giải được L   2 n . n Vậy L   .
Các bước vẽ Cn độ dài len hướng dir: 1. Quay trái 450 ; 2
2. Vẽ Cn-1 độ dài len; 2 3. Quay phải 900 ; 2
4. Vẽ Cn-1 độ dài len; 2
5. Quay trái 450 để trả hướng. 2
Giả sử có khai báo số radian của 10 và nhân tử
, hàm vẽ đường cong C cấp n có độ dài 2
len hướng dir được cài đặt như sau: #define FACT sqrt(2)/2 #define RADS M_PI/180
void C(int n, float len, float dir) { if (n > 0) { dir += 45.0; C(n-1, len* FACT, dir); dir -= 90.0; C(n-1, len* FACT, dir);
} else linerel(int(len *cos(dir *RADS)), int(len *sin(dir *RADS))); }
Cách khác để vẽ đường cong Cn từ điểm A(a, b) đến điểm B(c, d) bằng cách vẽ 2 đường cong Cn−1 như sau:
1) Vẽ đường cong Cn−1 từ điểm A đến điểm C
2) Vẽ đường cong Cn−1 từ điểm C đến điểm B
Hình 7.8. Vẽ đường cong C1 bằng cách vẽ 2 đường cong C0
Với M là trung điểm của AB:  AB 1 MC  AB 2
AC  AM  MC
thì toạ độ các điểm M và C(u, v) được tính như sau:
 a  c b  d   M ,   2 2  
a  c  b  d u  2
b  d  c  a v  . 2
Hàm vẽ Cn từ điểm A đến điểm B được cài đặt như sau:
void C(int n, int a, int b, int c, int d) { if (n>0){
C(n-1, a, b, (a+c+b-d)/2, (b+d+c-a)/2);
C(n-1, (a+c+b-d)/2, (b+d+c-a)/2, c, d); } else line(a, b, c, d); } 7.3.3. Đường cong Rồng
Đường cong Rồng (Dragon curve) tương tự đường cong C nhưng hướng vẽ thay đổi theo từng đoạn.
Hàm vẽ đường cong Rồng Dn cần thêm tham số s = ±1 để đánh dấu đổi hướng.
Đoạn chương trình vẽ đường cong Rồng cấp n có độ dài len hướng dir được cài đặt như sau: #define FACT sqrt(2)/2
void Dragon(int n , float len, float dir, int s) { if (n > 0) { dir += 45.0*s;
Dragon (n-1, len* FACT, dir, 1); dir -= 90.0*s;
Dragon (n-1, len* FACT, dir,-1); }
Else linerel(int(len * cos(dir * RADS)), int(len * sin(dir * RADS))); }
Hình 7.9. Đường cong Rồng
Cách khác để vẽ đường cong Rồng Dn từ điểm A(a, b) đến điểm B(c, d) bẳng cách vẽ 2 đường cong Dn-1 như sau:
1) Vẽ đường cong Dn-1 từ điểm A đến điểm C
2) Vẽ đường cong Dn-1 từ điểm B đến điểm C
Với cách này thì bút vẽ không liên tục.
Hàm vẽ đường cong Rồng Dn từ điểm A đến điểm B theo cách này được cài đặt như sau:
void D(int n, int a, int b, int c, int d) { if (n>0){
D(n-1, a, b, (a+c+b-d)/2, (b+d+c-a)/2);
D(n-1, c, d, (a+c+b-d)/2, (b+d+c-a)/2); } else line(a, b, c, d); }
Ta nhận thấy với cách vẽ thứ hai cho các fractal thì không dùng các hàm toán học và các
tham số đều nguyên nên thao tác vẽ được nhanh hơn và có thể vẽ được cấp cao hơn. 7.4. KẾT CHƯƠNG
Hình học phân hình được xây dựng dựa trên hai cơ sở quan sát: tính hỗn độn của các quá
trình phát triển có quy luật trong tự nhiên và sự mở rộng khái niệm số chiều và độ đo trong lý
thuyết hình học Euclide cổ điển. Fractal là những vật thể có tính đối xứng sắp xếp trong một phạm
vi nhất định, khi ta chia một vật thể fractal, với hình dáng gồ ghề, gãy góc ra thành những vật nhỏ,
thì mỗi phần nhỏ đó vẫn giữ những đặc tính đối xứng trong một cấu trúc tưởng như là hỗn loạn.
Hiện nay có 3 hướng ứng dụng lớn của lý thuyết hình học phân hình, bao gồm: ứng dụng trong
vấn đề tạo ảnh trên máy tính, ứng dụng trong công nghệ nén ảnh và ứng dụng trong nghiên cứu khoa học cơ bản. BÀI TẬP
7.1. Viết chương trình nhập n để vẽ đường cong Kock bậc n.
7.2. Viết chương trình nhập n và vẽ đường cong C cấp n.
7.3. Viết chương trình nhập n và vẽ đường cong Rồng cấp n.
7.4. Viết chương trình sinh tập Mandelbrot.
7.5. Viết chương trình sinh đường Pythagoras.
7.6. Viết chương trình sinh tập Julia.
7.7. Viết chương trình vẽ các đường cong tô vùng: Phoenix, Hilbert, Sierpinxki.