Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.

I. BỘ LỌC KALMAN LINEAR (LKF) A. Mô Hình Cơ Bản
Hệ Thống Tuyến Tính: LKF giả định rằng hệ thống và các biến đầu vào, đầu ra đều là tuyến tính.
Ma Trận Chuyển Động và Ma Trận Đo Đạc: Sử dụng ma trận tuyến tính để mô tả chuyển
động của hệ thống và quá trình đo đạc.
Mô hình của đối tượng tuyến tính rời rạc được biểu diễn thông qua hệ phương trình trạng thái sau: x = Ax + Bu +w k k−1 k−1 k−1 z =Hx + v k k k Trong đó: - x: biến trạng thái. - u: biến đầu vào.
- z: trạng thái đầu ra (đo lường được).
- w, v: nhiễu quá trình và nhiễu đo lường tương ứng.
B. Các Bước Triển Khai Thuật Toán : Chú ý rằng x^ Thuật
k là giá trị dự đoán được cập nhật từ giá trị ước lượng x ^ k−1 toán này
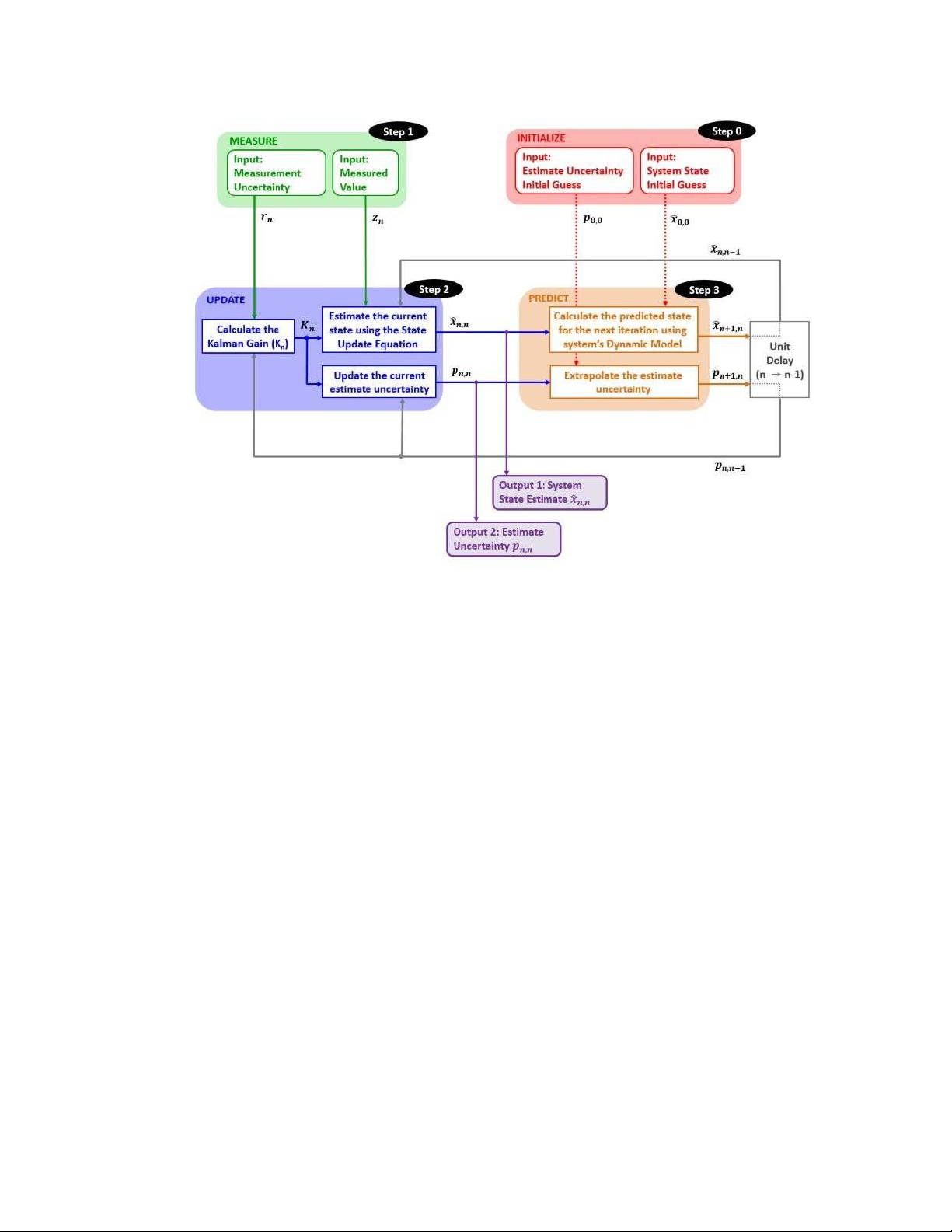
được trình bày trên sơ đôi khối như sau
Mô hình bộ lọc Kalman cho hệ tuyến tính Bước 0: Khởi tạo
Như đã đề cập ở trên, việc khởi tạo chỉ được thực hiện một lần và nó cung cấp hai tham số:
Trạng thái hệ thống ban đầu ( x^ ,0 0 )
Phương sai trạng thái ban đầu (P0 , 0)
Việc khởi tạo được theo sau bởi dự đoán. Bước 1: Đo lường
Quá trình đo cung cấp hai tham số:
Trạng thái hệ thống được đo (zN )
Phương sai đo lường (r N)
Bước 2: Cập nhật trạng thái
Quá trình cập nhật trạng thái chịu trách nhiệm ước tính trạng thái hiện tại của hệ thống.
Đầu vào của quá trình cập nhật trạng thái là: Gia trị đo (zN )
Phương sai đo lường (r N)
Ước tính trạng thái hệ thống được dự đoán trước đó ( x^ n ,n−1)
Phương sai ước tính trạng thái hệ thống được dự đoán trước đó ( P^ n , n−1)
Dựa trên đầu vào, quy trình cập nhật trạng thái tính toán Kalman Gain và cung cấp hai đầu ra:
Ước tính trạng thái hệ thống hiện tại ( x^ n ,n)
Phương sai ước tính trạng thái hiện tại ( P^ n , n)
Các tham số này là đầu ra của Bộ lọc Kalman. Bước 3: Dự đoán
Quá trình dự đoán ngoại suy ước tính trạng thái hệ thống hiện tại và phương sai của nó
với trạng thái hệ thống tiếp theo dựa trên mô hình động của hệ thống.
Ở lần lặp lại bộ lọc đầu tiên, việc khởi tạo được coi là Ước tính và phương sai trạng thái trước đó.
Các kết quả đầu ra dự đoán được sử dụng làm Ước tính và phương sai trạng thái trước
(dự đoán) trên các lần lặp bộ lọc sau.
II. BỘ LỌC KALMAN NON-LINEAR (EKF)
A. Mô Hình Cơ Bản
Mô hình của đối tượng phi tuyến được biểu diễn thông qua hệ phương trình trạng thái sau: x = Ax + Bu +w k k−1 k−1 k−1 z =Hx + v k k k
Ở đây w k và v k là các nhiễu quá trình và quan sát, cả hai đều được coi là nhiễu Gaussian
đa biến trung bình bằng 0 với hiệp phương sai tương ứng là Q k và R k . u k là vectơ điều khiển.
Hàm f có thể được sử dụng để tính toán trạng thái dự đoán từ ước tính trước đó và tương
tự, hàm h có thể được sử dụng để tính toán số đo dự đoán từ trạng thái dự đoán. Tuy
nhiên, f và h không thể áp dụng trực tiếp cho hiệp phương sai. Thay vào đó, một ma trận
đạo hàm riêng ( Jacobian ) được tính toán.
Tại mỗi bước thời gian, Jacobian được đánh giá với các trạng thái dự đoán hiện
tại. Những ma trận này có thể được sử dụng trong các phương trình lọc Kalman. Quá
trình này về cơ bản tuyến tính hóa hàm phi tuyến tính xung quanh ước tính hiện tại.
B. Phương trình dự đoán và cập nhật: 1. Dự đoán:
Ước tính trạng thái dự đoán
Ước tính hiệp phương sai dự đoán
2. Cập nhật
Sự đổi mới hoặc số dư đo lường
Hiệp phương sai đổi mới (hoặc phần dư)
Mức tăng Kalman gần tối ưu
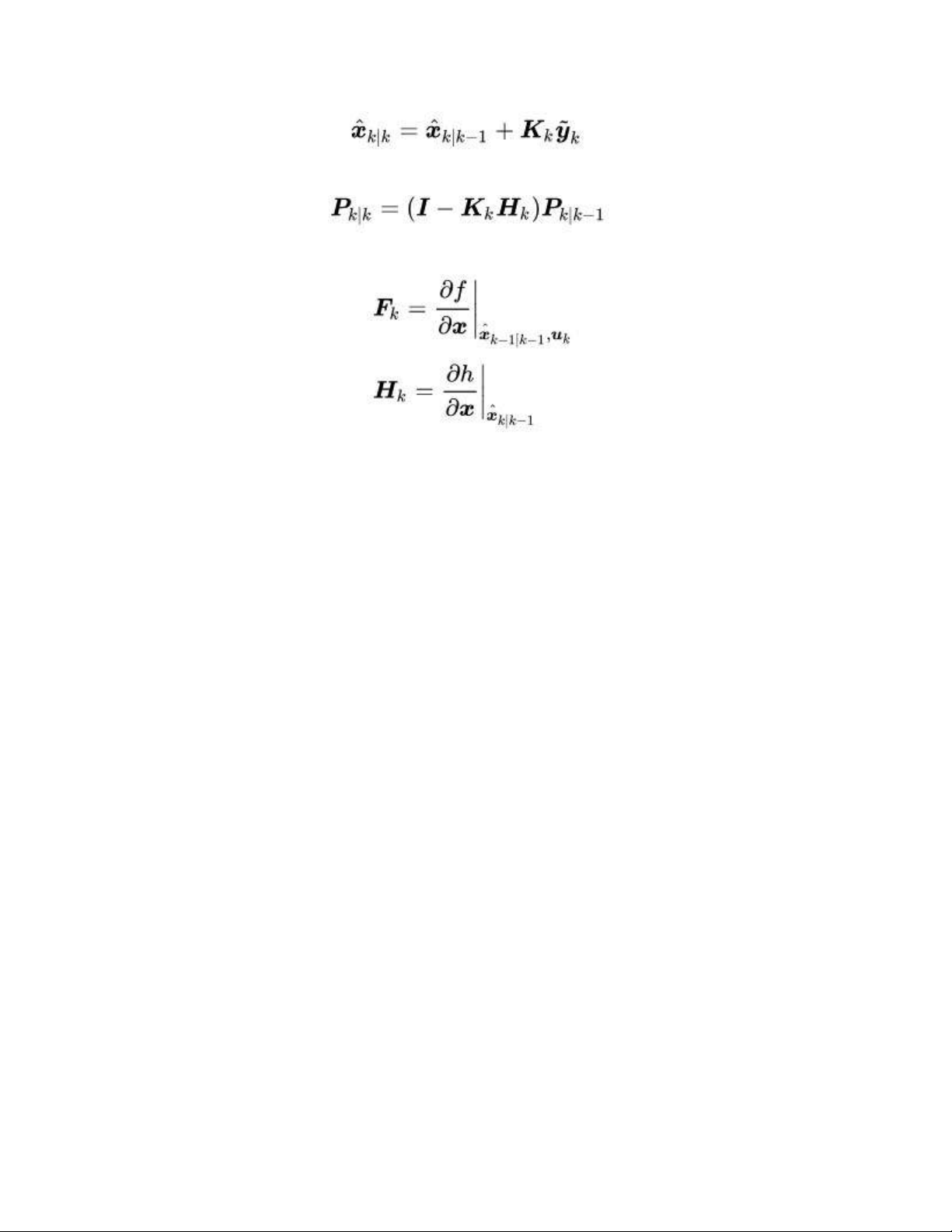
Ước tính trạng thái được cập nhật
Ước tính hiệp phương sai được cập nhật
trong đó ma trận chuyển trạng thái và ma trận quan sát được xác định là Jacobians sau