Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
.
Bàitoánthườngmôtảmứcđộsinhtrưởngcủamộtquầnthểđộngvật,thựcvậtnàođó qua 1 chu kì
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
Tài liệu gồm 42 trang , giúp bạn tham khảo, ôn tập và đạt kết quả cao.
Môn: Đại số tuyến tính (ĐSTT1) 57 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 1.7 K tài liệu
Tác giả:
Preview text:
HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
TRƯỜNG ĐẠI HỌC QUỐC GIA HỒ CHÍ MINH
TRƯỜNG BÁCH KHOA HỒ CHÍNH MINH
HCMUT-CNCP &TỔNG HỢP CÔNG THỨC
ĐẠI SỐ TUYẾN TÍNH HK231
(Bản lưu hành nội bộ trong lớp )
Biên soạn: Nguyễn Quốc Vương
Chủ sở hữu:……………
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 1 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG Mục Lục
I. Phần Lý Thuyết .......................................................................................................................................... 3
1. Chương Ma trận ..................................................................................................................................... 3 1.1
Định nghĩa .................................................................................................................................. 3 1.2
Các loại ma trận ......................................................................................................................... 3 1.3
Các phép biến đổi sơ cấp đưa về ma trận bậc thang .................................................................. 4 1.4
Hạng ma trận ............................................................................................................................. 4 1.5
Các phép toán trên ma trận ........................................................................................................ 5 1.6
Ma trận nghịch đảo .................................................................................................................... 5
2. Chương định thức ma trận ..................................................................................................................... 6 2.1
Định thức ................................................................................................................................... 6 2.2
Một số tính chất của định thức .................................................................................................. 6 2.3
Môi quan hệ giữa ma trận nghịch đảo và định thức ................................................................... 7
3. Các dạng toán ứng dụng ........................................................................................................................ 7 3.1
Mô hình Leslie........................................................................................................................... 7 3.2
Mô hình Markov ........................................................................................................................ 8 3.3
Mô hình Input-Output .............................................................................................................. 9 3.4
Mô hình lưu lượng giao thông ................................................................................................. 10 3.5
Bài toán mạch điện 1 chiều ...................................................................................................... 10
4. Chương hệ phương trình ...................................................................................................................... 11 4.1
Hệ phương trình tuyến tính tổng quát ...................................................................................... 11 4.2
Hệ Cramer ............................................................................................................................... 11 4.3
Hệ phương trình tuyến tính thuần nhất .................................................................................... 12
5. Chương không gian Vecto ................................................................................................................... 12 5.1
Không gian vecto ..................................................................................................................... 12 5.2
Tọa độ vecto và không gian con .............................................................................................. 13
6. Không gian Euclide ............................................................................................................................. 14 6.1
Định nghĩa tích vô hướng ........................................................................................................ 14 6.2
Các định nghĩa sử dụng tích vô hướng .................................................................................... 15 6.2.1
Tính độ dài vecto .................................................................................................................... 15 6.2.2
Tính khoảng cách giữa 2 vecto ............................................................................................... 15 6.2.3
Tính góc giữa 2 vecto ............................................................................................................ 15 6.2.4
Sự vuông góc ......................................................................................................................... 15
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 2 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG 6.3
Bù vuông góc của không gian con ........................................................................................... 15 6.4
Hình chiếu vuông góc .................................................................................................................. 16 6.5
Trực giao ..................................................................................................................................... 17
7. Chương ánh xạ tuyến tính .................................................................................................................... 17 7.1
Định nghĩa ............................................................................................................................... 17 7.2
Nhân và ảnh của ánh xạ tuyến tính .......................................................................................... 18 7.3
Ma trận ánh xạ tuyến tính ........................................................................................................ 19 7.4
Các phép đổi tuyến tính ........................................................................................................... 20 7.5
Tổng và hợp 2 ánh xạ tuyến tính ............................................................................................. 21
8. Chương trị riêng và vecto trị riêng ...................................................................................................... 22 8.1
Trị riêng và vecto trị riêng ....................................................................................................... 22 8.2
Chéo hóa ma trận ..................................................................................................................... 23
II Cấu trúc đề thi HK231 ............................................................................................................................. 24
Đối với các bạn học dự thính ................................................................................................................... 24
Đối với các bạn đại trà, clc ...................................................................................................................... 24
Đối với các bạn Việt Pháp = Đại Trà + Dự Thính ................................................................................... 25
III Bài tập mẫu format đề thi (muốn trên 7 phải làm được hết) ................................................................... 25 I. Phần Lý Thuyết 1. Chương Ma trận 1.1 Định nghĩa
Ma trận mxn là tập hợp bảng số (thực hoặc phức) có m hàng và n cột 𝑎11 𝑎12 … 𝑎1𝑛 … 𝑎2𝑛 𝐴 = ( 𝑎 2…1 𝑎… 22 … … ) 𝑎 … 𝑎 𝑚1 … 𝑚𝑛 1.2 Các loại ma trận
Nếu m = n gọi là ma trận vuông
Ma trận không là các ma trận các phần tử trong ma trận đó đều bằng 0
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 3 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG 0 0 0 𝐴 = (0 0 0) 0 0 0
Phần tử cơ sở của một hàng là phần tử khác không đầu tiên tính từ trái sang phải Ma trận bậc thang khi
• Hàng toàn số không thì nằm dưới cùng (nếu có)
• Phần từ cơ sở hàng dưới nằm bên phải phần tử cơ sở hàng trên.
Ma trận chuyển vị là ma trận 𝐴𝑇 = (aji)n×m thu được từ A bằng cách chuyển hàng thành cột.
Đường chéo chính của ma trận vuông A là đường đi qua các phần tử 𝑎11, 𝑎22, …, 𝑎𝑛𝑛
Vết=trace(A)= 𝑎11+ 𝑎22 + …+𝑎𝑛𝑛 Ma trận tam giác
• Ma trận tam giác trên nếu các phần tử dưới đường chéo chính bằng 0
• Ma trận tam giác dưới nếu các phần tử trên đường chéo chính bằng 0
Lưu ý, ma trận tam giác phải là ma trận vuông
Ma trận chéo là ma trận vuông mà tất cả phần tử không thuộc đường chéo chính bằng 0
1.3 Các phép biến đổi sơ cấp đưa về ma trận bậc thang
Nguyên tắc 1: Nhân 1 hàng với một số khác 0; ℎ𝑖 → 𝛼ℎ𝑖
Nguyên tắc 2: Cộng vào một hàng một hàng khác đã được nhân với 1 số tùy ý;
ℎ𝑖 → ℎ𝑖 + 𝛽ℎ𝑗
Kết hợp nguyên tắc 1 và 2
ℎ𝑖 → 𝛼ℎ𝑖 + 𝛽ℎ𝑗
Nguyên tắc 3: Đổi chỗ 2 hàng; ℎ𝑖 ↔ ℎ𝑗 1.4 Hạng ma trận
Hạng của ma trận A là số hàng khác 0 khi đưa A về ma trận bậc thang
Tính chất hạng ma trận cần nhớ
• 𝐴 = 0 => 𝑟(𝐴) = 0
• 𝐴𝑚𝑥𝑛 𝑡ℎì 𝑟(𝐴) ≤ min(𝑚, 𝑛)
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 4 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
1.5 Các phép toán trên ma trận
Hai ma trận bằng nhau nếu chúng có cùng kích thước
Với A, B là 2 ma trận bằng nhau
• Phép tổng A + B ta được 1 ma trận với các phần tử là tổng các phần tử tương ứng
• Phép tổng A - B ta được 1 ma trận với các phần tử là trừ các phần tử tương ứng
• Pháp a.A với a là hằng số ta được ma trân mới với các phần tử bằng ma trận cũ nhân với a Tính chất cần nhớ • A + B = B + A • (A + B) + C = A + (B + C) • A + 0 = A
Phép nhân 2 ma trận 𝐴𝑚𝑥𝑛.𝐵𝑛𝑥𝑝 = 𝐶𝑚𝑥𝑝. Quy tắc nhân lấy từng hàng của ma trận A nhân
với từng cột của ma trận B Tính chất cần nhớ • ABC = A.(BC) • A.(B+C) = AB+AC • (B+C).A = BA+CA
• I.A = A.I = A (I là ma trận đơn vị) • AB # BA Quy tắc nâng lũy thừa • 𝐴0 = 𝐼
• 𝐴𝑛 = 𝐴. 𝐴. 𝐴. . 𝐴 1.6 Ma trận nghịch đảo
Ma trận vuông A gọi là khả nghịch nếu tồn tại ma trận B sao cho A.B = I = B.A
Khi đó, B gọi là nghịch đảo của A, ký hiệu là 𝐴−1
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 5 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Điền kiện để ma trận A khả nghịch (có ma trận nghịch đảo) • Ma trận vuông cấp n • Det(A) # 0
Để Det(A) # 0 thì r(A) = n hay còn gọi là ma trận không suy biến
Một số tính chất cần nhớ • (𝐴−1)−1 = 𝐴
• (𝐴𝐵)−1 = 𝐵−1. 𝐴−1
• (𝐴𝑇)−1 = (𝐴−1)𝑇
2. Chương định thức ma trận 2.1 Định thức
Định thức của ma trận vuông A là một số, được kí hiệu bởi: Det(A) hay |A| Cách tính thủ công:
Bước 1: Đưa ma trận A về ma trận bậc thang
Lưu ý, chỉ sử dụng phép biến đổi ℎ𝑖 → ℎ𝑖 + 𝛼ℎ𝑗
Bước 2: Det(A) = |A|= Tích các phần tử trên đường chéo chính
Quy tắc tính nhanh định thức: - Ma trận 2x2 𝑎 𝐴 = ( 11
𝑎12) => det(𝐴) = 𝑎 𝑎 − 𝑎 𝑎 𝑎21 𝑎22 11 22 12 21
- Ma trận 3x3, det bằng tống các tích đường dấu huyền trừ tổng dấu sắc (xem live để rõ)
Ngoài ra cần phải biết cách tính bằng • Dùng skill casio m=1000
• Dùng phần bù đại số
Xem tại đây: https://www.youtube.com/watch?v=n_CutTR69nE
2.2 Một số tính chất của định thức Tính chất 1:
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 6 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Tính chất 2: Cho ma trận vuông A cấp n • det(𝐴𝑇) = det(𝐴)
• |𝛼𝐴| = 𝛼𝑛|𝐴|
• |𝐴. 𝐵| = |𝐴|. |𝐵|
• 𝑁ế𝑢 1 ℎà𝑛𝑔 ℎ𝑜ặ𝑐 1 𝑐ộ𝑡 𝑐ủ𝑎 𝐴 𝑏ằ𝑛𝑔 0 𝑡ℎì det(𝐴) = 0 𝑛ó𝑖 𝑐á𝑐ℎ 𝑘ℎá𝑐 𝑟(𝐴) < 𝑛 => det(𝐴) = 0 • |𝐴𝑚| = |𝐴|𝑚
• det(A + B) ≠ det(𝐴) + det(𝐵)
Điều kiện để ma trận A khả nghịch • Ma trận vuông cấp n • Det(A) # 0
2.3 Môi quan hệ giữa ma trận nghịch đảo và định thức
𝐶ℎ𝑜 𝑚𝑎 𝑡𝑟ậ𝑛 𝑣𝑢ô𝑛𝑔 𝐴 𝑘ℎả 𝑛𝑔ℎị𝑐ℎ ∶ 1 𝐴−1 = . 𝑃
𝑣ớ𝑖 𝑃 𝑔ọ𝑖 𝑙à 𝑚𝑎 𝑡𝑟ậ𝑛 𝑝ℎù ℎợ𝑝 𝑐ủ𝑎 𝐴 |𝐴| 𝐴 . 𝐴 Tính chất • |𝐴−1| = 1 |𝐴|
• |𝑃𝐴 | = 𝐴𝑛−1
𝑛 , 𝑛ế𝑢 𝑟(𝐴) = 𝑛
• 𝑟(𝑃𝐴) = {1, 𝑛ế𝑢 𝑟(𝐴) = 𝑛 − 1
0, 𝑛ế𝑢 𝑟(𝐴) < 𝑛 − 1
3. Các dạng toán ứng dụng 3.1 Mô hình Leslie
Bài toán thường mô tả mức độ sinh trưởng của một quần thể động vật, thực vật nào đó qua 1 chu kì PHƯƠNG PHÁP:
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 7 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Lớp(Nhóm) 1 Lớp(Nhóm) 1 Lớp(Nhóm) 1 Lớp(Nhóm) 1 𝑥11 𝑥12 𝑥13 Lớp(Nhóm) 2 𝑥21 0 0 Lớp(Nhóm) 3 0 𝑥32 𝑥33 Ý nghĩa: Hàng 1 là tỉ lệ sinh
• 𝑥11 Tỉ lệ sinh Lớp(N) 1 sinh ra Lớp(N) 1
• 𝑥12 Tỉ lệ sinh Lớp(N) 2 sinh ra Lớp(N) 1
• 𝑥13 Tỉ lệ sinh Lớp(N) 3 sinh ra Lớp(N) 1
Các phần tử còn lại là tỉ lệ sống sót qua 1 chu kì
• 𝑥21 Tỉ lệ sống sót lớp 1 qua lớp 2 sau 1 chu kì
• 𝑥21 Tỉ lệ sống sót lớp 3 qua lớp 3 sau 1 chu kì
• 𝑥21 Tỉ lệ sống sót lớp 3 sau 1 chu kì
Vậy ta có ma trận Leslie như sau 𝑥11 𝑥12 𝑥13 𝐴 = (𝑥21 0 0 ) 0 𝑥32 𝑥33 Các câu hỏi hay gặp
• Sau n năm thì số lượng đối tượng thay đổi như nào biết số lượng bao đầu là b? 𝑨𝒏. 𝒃 3.2 Mô hình Markov
Mô hình áp dụng cho các bài toán thể hiện sự dịch chuyển qua lại giữa các nhóm đối tượng Phương pháp Lập bảng như sau
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 8 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG A B C 𝑥11 𝑥12 𝑥13 A 𝑥21 𝑥22 𝑥23 B 𝑥31 𝑥32 𝑥33 C Nguyên tắc:
- Tổng các cột là băng 1
- 𝑥𝑖𝑗 Tỉ lệ đối tượng cột i chuyển qua hàng j
Vậy ta có ma trận Markov như sau 𝑥11 𝑥12 𝑥13 𝑀 = (𝑥21 𝑥22 𝑥23) 𝑥21 𝑥32 𝑥33 Các câu hỏi hay gặp
• Sau n năm thì số lượng đối tượng thay đổi như nào biết số lượng bao đầu là b? 𝑀𝑛. 𝑏
• Xác định số lượng các đối tượng khi đạt trạng thái cân bằng 3.3 Mô hình Input-Output
Biết rằng muốn sản xuất ra một lượng hàng có giá trị 1 đô của nghành công nghiệp
cần có lượng hàng có giá trị 0.15 đô của ngành công nghiệp, 0.1 đô của ngành nông
nghiệp và 0.05 đô của ngành dịch vụ. Để sản xuất ra 1 đô của ngành nông nghiệp cần
0.25 đô ngành công nghiệp, 0.15 đô ngành nông nghiệp, 0.1 đô ngành dịch vụ. Để sản
xuất ra 1 đô của ngành dịch vụ cần 0.1 đô ngành công nghiệp, 0.15 đô ngành nông
nghiệp, 0.2 đô ngành dịch vụ. Tìm đầu ra cho mỗi ngành, biết nhu cầu cuối cùng của
các ngành lần lượt là 300, 200, 150 . Ta có bảng Bảng CNCP Công nghiệp Nông nghiệp Dịch vụ Công nghiệp 0.15 0.25 0.1 Nông nghiệp 0.1 0.15 0.15 Dịch vụ 0.05 0.1 0.2
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 9 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Ma trận đầu vào (gọi cách khác là hệ số chi phí trực tiếp, ma trận kỹ thuật) 0.15 0.25 0.1 𝐴 = ( 0.1 0.15 0.15) 0.05 0.1 0.2 300
Nhu cầu cuối cùng của mỗi ngành 𝑏 = (200) (cầu cuối, ý nghĩa là giá trị hàng hoá 150
của ngành i cần cho lao động, tiêu dùng và xuất khẩu, nhu cầu thị trường ,)
Đầu ra cho mỗi ngành (thể hiện lượng hàng hóa thực tế phải sản xuất): 1 0 0 0.15 0.25 0.1 300 483
𝑋 = (𝐼 − 𝐴)−1. 𝑏 = [(0 1 0) − ( 0.1 0.15 0.15)]−1. (200) = (338) 0 0 1 0.05 0.1 0.2 150 260
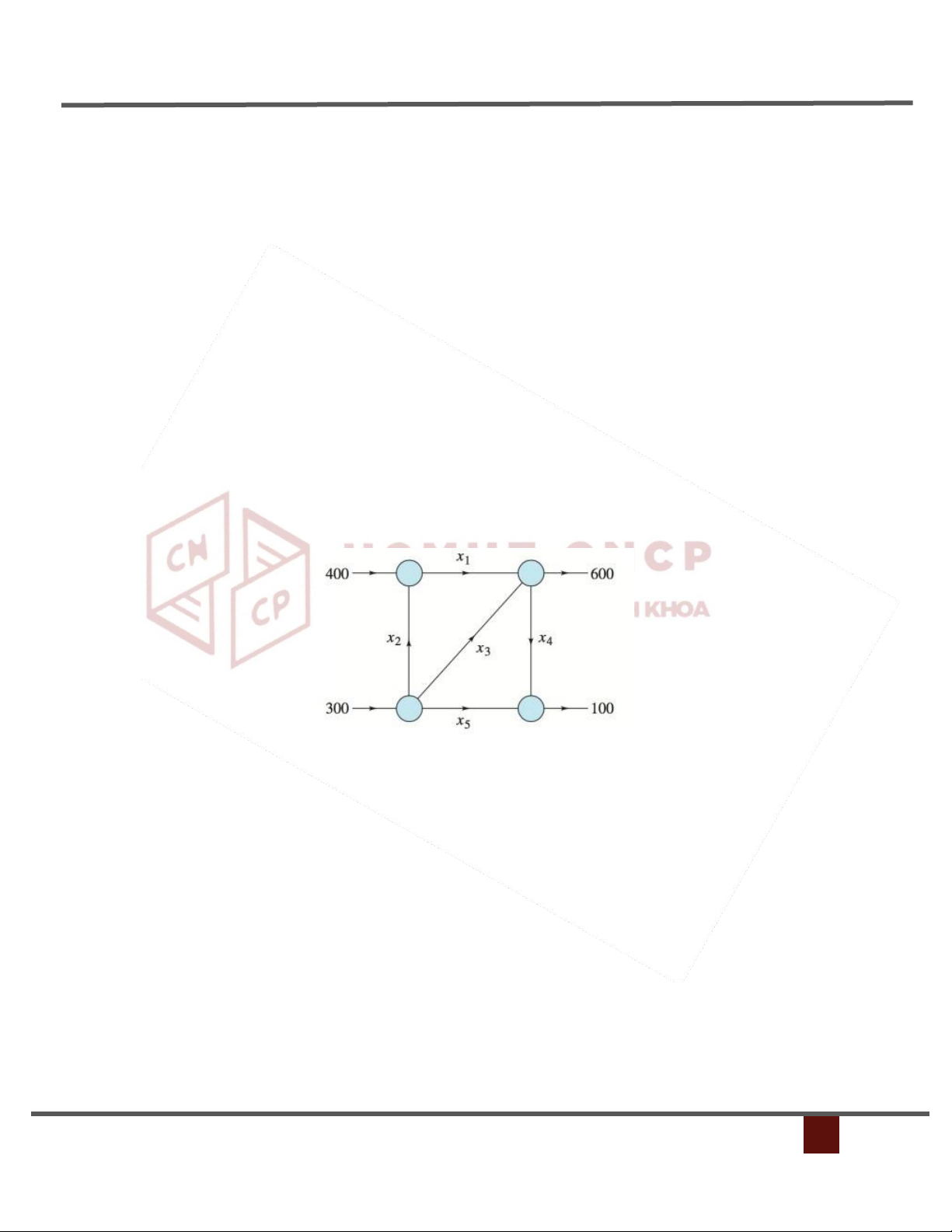
3.4 Mô hình lưu lượng giao thông
Lượng xe đi vào bằng lượng xe đi ra
Số lượng xe đi qua các con đường trong 1 giờ được cho bởi đồ thị sau. Hãy tìm xi .
3.5 Bài toán mạch điện 1 chiều
• Cường độ dòng điện: ký hiệu là I, đơn vị là A(ambe).
• Điện trở: Ký hiệu là R, đơn vị là Ω(om).
• Hiệu điện thế: ký hiệu là U, đơn vị là V(vôn).
• Dòng điện chạy từ điện thế cao đến điện thế thấp. C
• ông thức liên hệ: U = I · R. Định lí Kirchoff
Tại mỗi nút: tổng dòng điện vào và ra bằng nhau. Tại mỗi vòng kín: tổng điện thế bằng 0.
Lưu ý, nếu có n nút ta chỉ viết được n-1 phương trình và nếu có m vòng kín thì ta chỉ
viết được m-1 phương trình Áp dụng
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 10 HCMUT CNCP
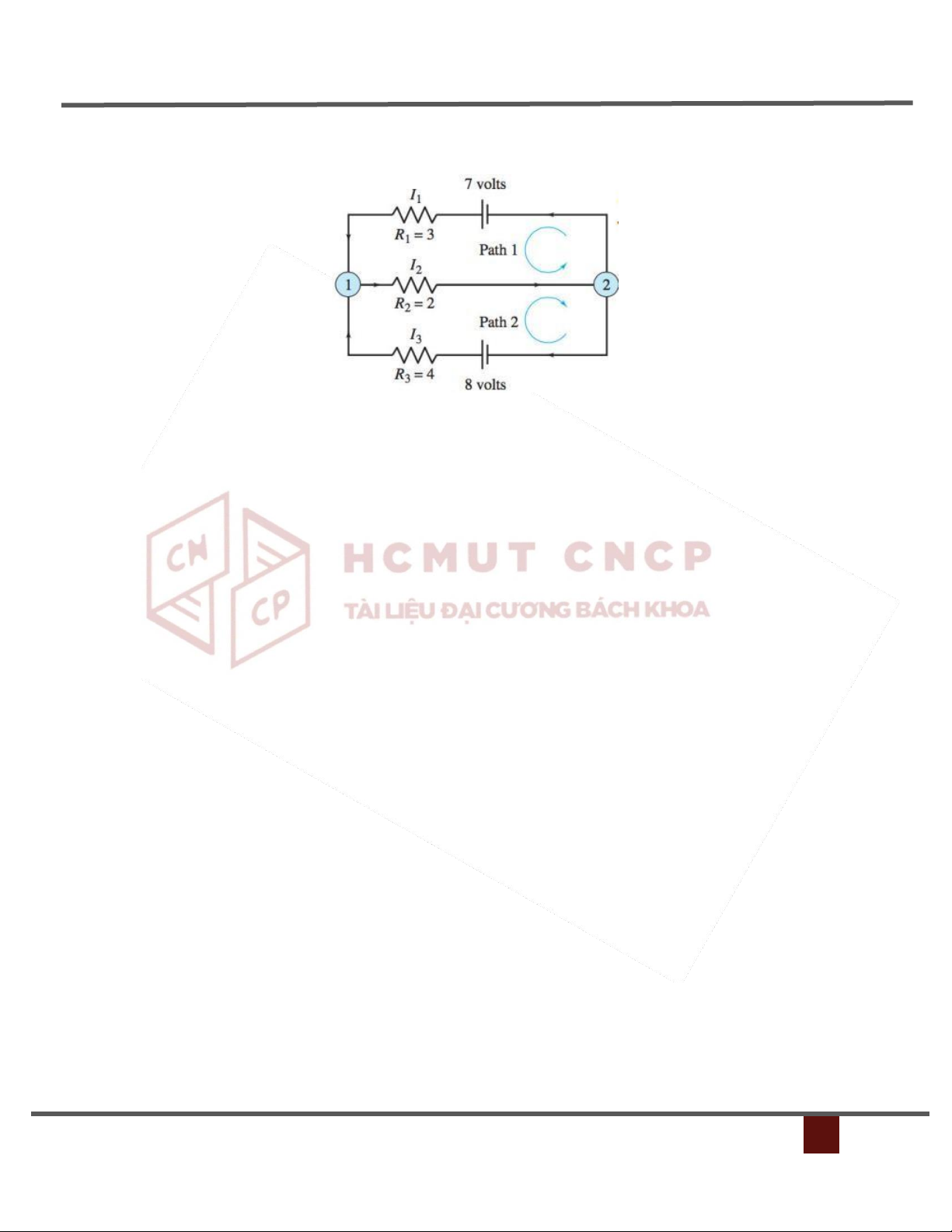
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Ví dụ 1: Cho mạch điện 1 chiều như hình vẽ. Hãy tìm cường độ dòng điện qua mỗi tụ điện
4. Chương hệ phương trình
4.1 Hệ phương trình tuyến tính tổng quát
𝑎11𝑥1 + 𝑎12𝑥2 + ⋯ + 𝑎1𝑛𝑥𝑛 = 𝑏1
𝑎 𝑥 + 𝑎 𝑥 + ⋯ + 𝑎 𝑥 = 𝑏 { 21 1 22 2 2𝑛 𝑛 2
… … … … … … … … … … … … … … … . .
𝑎𝑚1𝑥1 + 𝑎𝑚2𝑥2 + ⋯ + 𝑎𝑚𝑛𝑥𝑛 = 𝑏𝑚 Ta ký hiệu: 𝑎11 𝑎12 … 𝑎1𝑚 𝑥1 𝑏1 … 𝑎 𝐴 = ( 𝑎 2 2𝑚 …1 𝑎22 ) , 𝑋 = (𝑥2 ) , 𝑏 = (𝑏2 ) … … … … …
𝑎𝑛1 … … 𝑎𝑛𝑚 𝑥𝑛 𝑏𝑛
Vậy hệ phương trình trên có thể được ghi lại là A.X = b hoặc (A|b) Định lý Kronecker Capelli
Nếu r(A|b) # r(A) thì hệ AX = b vô nghiệm.
Nếu r(A|b) = r(A) thì hệ AX = b có nghiệm.
• Nếu r(A|b) = r(A) =số ẩn thì hệ AX = b có nghiệm duy nhất.
• Nếu r(A|b) = r(A) Lưu ý, nếu số ẩn nhiều hơn số phương trình thì không thể có nghiệm duy nhất 4.2 Hệ Cramer
Hệ AX = b gọi là hệ Cramer nếu A có số ẩn bằng số phương trình và det(A) # 0
Hệ Cramer có nghiệm duy nhất là:
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 11 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG |𝐴𝑖| 𝑥 𝑖 = |𝐴|
𝑉ớ𝑖 𝐴𝑖 𝑙à 𝑚𝑎 𝑡𝑟ậ𝑛 𝑡ℎ𝑢 đượ𝑐 𝑡ừ 𝐴 𝑏ằ𝑛𝑔 𝑐á𝑐ℎ 𝑡ℎ𝑎𝑦 𝑐ộ𝑡 𝑡ℎứ 𝑖 𝑡ℎà𝑛ℎ 𝑐ộ𝑡 𝑏
Lưu ý, với hệ phương trình có số ẩn bằng số phương trình:
• Nếu det(A) # 0 thì đó là hệ Cramer và có nghiệm duy nhất.
• Nếu det(A)=0 thì hệ vô nghiệm hoặc vô số nghiệm
4.3 Hệ phương trình tuyến tính thuần nhất
Hệ AX = b gọi là thuần nhất nếu tất cả các hệ số tự do b1 = b2 = · · · = bm = 0 Tính chất:
• Hệ thuần nhất luôn có nghiệm tầm thường. x1 = x2 = · · · = xn = 0
• Hệ thuần nhất có nghiệm duy nhất khi và chỉ khi r(A) = n =số ẩn.
• Cho A là ma trận vuông. Hệ thuần nhất AX = 0 có nghiệm không tầm
thường(nghiệm khác 0 ) khi và chỉ khi 5. Chương không gian Vecto 5.1 Không gian vecto
a/Định nghĩa không gian Vecto
Không gian vecto là một vùng không gian chứa các vecto có gốc tại O có thể biểu
diễn bằng các vecto kết hợp với phép toán cộng nhân
Kí hiệu: 𝑉 = {𝑥1, 𝑥2, 𝑥3, … } với 𝑥1, 𝑥2, 𝑥3, … là các vecto
Ví dụ 1: Nhờ vào 2 vecto 𝑥1(1,0), 𝑥2(0,1) kết hợp với phép toán cộng nhân ta sẽ xác
được 1 miền không gian đó là mặt phẳng Oxy hay còn gọi là miền không gian 2 chiều kí hiệu 𝑅2
Tương tự ta có không gian vecto 1 chiều (𝑅1), 3 chiều (𝑅3), 4 chiều (𝑅4),…..
Một số miền không gian đặc biệt
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 12 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
• 𝑉2 = {𝑎𝑥2 + 𝑏𝑥 + 𝑐| 𝑎, 𝑏, 𝑐 ∈ 𝑅} là miền không gian chứa các trường hợp
của các hệ số tự do a, b,c => nó là không gian vecto 3 chiều. Kí hiệu 𝑃2[𝑥] • 𝑎 𝑏 𝑉3 = {(
)| 𝑎, 𝑏, 𝑐, 𝑑 ∈ 𝑅} là miền không gian chứa các trường hợp của 𝑐 𝑑
phần tử ma trận 2X2 => nó là không gian vecto 4 chiều. Kí hiện 𝑀2[𝑅]
• 𝑉4 = {2𝑥1 − 𝑥2 + 𝑥3 = 0| 𝑎, 𝑏, 𝑐 ∈ 𝑅} là một không gian 2 chiều b/Tổ hợp tuyến tính
Cho không gian vecto 𝑀 = {𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑚}:
• X là tổ hợp tuyến của M khi tồn tại 𝛼1, 𝛼2, 𝛼3, … , 𝛼𝑚 sao cho
𝛼1𝑥1 + 𝛼2𝑥2 + ⋯ + 𝛼𝑚𝑥𝑚 = 𝑋
M là phụ thuộc tuyến tính khi trong M chứa 1 vecto là THTT của các vecto còn lại
• Giải phương trình 𝛼1𝑥1 + 𝛼2𝑥2 + ⋯ + 𝛼𝑚𝑥𝑚 = 0
+ Nếu phương trình có nghiệm tầm thường => M độc lập tuyến tính
+ Nếu phương trình có nghiệm không tầm thường => M phụ thuộc tuyến tính
Nhiều vecto biểu diễn qua ít vecto thì M PTTT c/Hạng của họ vecto
Hạng của họ vecto M là số vecto ĐLTT trong M. Cách tìm là đưa M về dạng ma trận
và tìm rank như đã học.
Số hạng của họ vecto M thể hiện số chiều của không gian vecto d/Cở sở và số chiều
𝑀 = {𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑚} gọi M là tập sinh của V nếu mọi vecto x (mọi điểm) của V
đều là tổng hợp tuyến tính của M. Kí hiệu
𝑉 =< 𝑀 >=< 𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑚 >
M là cơ sở của không gian vecto V khi M sinh ra V và M độc lập tuyến tính
M1 = {2x + y + z, x + 2y + z, x + y + z}. b) M2 = {2x, 3y, z, x + y + z}.
Số chiều của không gian vecto V = hạng không gian vecto V = số vecto trong tập cơ sở của V Kí hiệu dim(V)
5.2 Tọa độ vecto và không gian con
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 13 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG a/ Tọa độ vecto
Ta có vecto x , E là tập cơ sở cở không gian V, [𝑥]𝐸 là tọa độ của vecto x trong không gian V
[𝑥]𝐸 = 𝐸−1. 𝑥𝑇 <=> 𝑥𝑇 = 𝐸. [𝑥]𝐸
Lưu ý: Ma trận E, [𝑥]𝐸, 𝑥𝑇 viết theo dạng cột
b/ Ma trận chuyển cơ sở
Cho 2 cơ sở của KGVT V là E và E’:
• Ma trận chuyển cơ sở từ E sang E’ (viết dưới dạng cột) là 𝑃 = 𝐸−1. 𝐸′
• Ma trận chuyển cơ sở từ E’ sang E (viết dưới dạng cột) là 𝑃′ = 𝐸′−1. 𝐸 Tính chất
[𝑥]𝐸 = 𝑃. [𝑥]𝐸′ c/ Không gian con
Ví dụ 4: Cho 𝐹 = {𝑝(𝑥) ∈ 𝑝2[𝑥]|𝑝(1) = 0 ∩ 𝑝(2) = 0}.Tìm cơ sở và số chiều của F
Ví dụ 5: Tìm cơ sở và số chiều của không gian con 𝐹 = {(𝑥1, 𝑥2, 𝑥3) ∈ 𝑅3|𝑥1 + 𝑥2 +
𝑥3 = 0 ∩ 𝑥1 − 𝑥2 + 3𝑥4 = 0}. 6. Không gian Euclide
6.1 Định nghĩa tích vô hướng
Tích vô hướng của hai véctơ u và v trong một không gian vecto là một số thực, được ký
hiệu bởi (u,v), thỏa mãn 4 tiên đề sau: - Tính xác định dương
(u V ) (u,u) 0;(u,u) = 0 u = 0 - Tính giao hoán
u,v V ) (v,u) = (u,v) - Tính tuyến tính
( R,u,v V ) (u,v) = (u,v)
(u,v, wV ) (u + v, w) = (u, w) + (v, w)
Không gian hữu hạn chiều cùng với tính vô hướng trên gọi là không gian euclide.
Tích vô hướng chính tắc trong không gian 𝑅𝑛
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 14 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
( x, y) = (( x ) )) + +
1, x2 ,..., xn ,( y1, y2 ,..., yn
= x1y1 x2 y2 ... + xn yn
6.2 Các định nghĩa sử dụng tích vô hướng
Giúp mình tính toán độ dài của vecto, khoảng cách, góc giữa 2 vecto và hình chiếu vuông
góc của một vecto bằng tích vô hướng của vecto 6.2 .1 Tính độ dài vecto
Độ dài véctơ u là số thực không âm ký hiệu bởi ||u|| và được định nghĩa như sau
|| u ||= (u,u)
Véc tơ có độ dài bằng 1 gọi là véc tơ đơn vị.
6.2.2 Tính khoảng cách giữa 2 vecto
Cho hai véctơ u và v của không gian Euclide V, khoảng cách giữa hai véctơ u và v, ký hiệu
bởi d(u,v), là độ dài của véctơ u – v sau:
d(u,v) = ||u – v|| = √(𝑢 − 𝑣, 𝑢 − 𝑣)
6.2.3 Tính góc giữa 2 vecto
Góc α giữa 2 véc tơ u và v được xác định bởi cos = (u, v)
|| u || . || v ||
Ma trận tích vô hướng M là ma trận vuông có các phần tử là hệ số 𝑎𝑖𝑗 của 𝑥𝑖𝑦𝑖 trong
công thức nhân vô hướng
Ta sẽ có công thức thứ 2 để tính tích vô hướng của 2 vecto 𝑢, 𝑣 là
(𝑢, 𝑣) = 𝑥𝑀𝑦𝑇 Ma trận M có tính chất
• M là ma trận đối xứng
• M phải là ma trận xác định dương (xem live để hiểu) 6.2.4 Sự vuông góc
Hai véc tơ u,v vuông góc với nhau khi (u,v) = 0, kí hiệu 𝑢 ⊥ 𝑣 2 2 2
Định lý Pytagore: ||𝑢|| + ||𝑣|| = ||𝑢 + 𝑣|| nếu 𝑢 ⊥ 𝑣
Vecto x vuông góc với tập hợp M, nếu x vuông góc với mọi vecto trong M kí hiệu
(y M ) x ⊥ y
Mệnh đề 1: Véctơ x vuông góc với không gian con F khi và chỉ khi x vuông góc với tập
sinh hoặc tập cơ sở của F=<𝑓1, 𝑓2, . . , 𝑓𝑛>
6.3 Bù vuông góc của không gian con
Cho không con F của không gian Euclide V. Tập hợp
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 15 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
F ⊥ ={x V | x ⊥ F}
được gọi là bù vuông góc của không gian con F
Không gian bù vuông góc còn gọi là không gian bù trực giao.
Cách tìm số chiều và cơ sở của không gian con 𝐹⊥ của 𝐹 trong không gian 𝑅𝑛
Bước 1: Tìm tập sinh hoặc tập cơ sở của F (nên tìm tập cơ sở nhé)
F=<𝑓1, 𝑓2, . . , 𝑓𝑛>
Bước 2: Tìm không gian con bù vuông góc ⊥
x F x ⊥ F nên ta có x ⊥ f 1 (x, f1) = 0 x ⊥ f (x, f 2 2 ) = 0 ... ... x ⊥ f n (x, fn ) = 0
Giải hệ phương trình tuyến tính thuần nhất ở trên ta sẽ thu được cơ sở của 𝐹⊥
Lưu ý: 𝑥 là vecto có dạng tông quát 𝑥 = (𝑥1, 𝑥2, … 𝑥𝑛) (n là số chiều của không gian V)
Một số tính chất quan trọng
Cho F là KG con của KG Euclide V . Khi đó:
• 𝐹⊥ cũng là không gian con của V
• F F ⊥ = 0 •
F + F ⊥ = V
• F F ⊥ = V •
dim( F ) + dim(F ⊥ ) = dim(V ) 6.4 Hình chiếu vuông góc
Trong KG Euclide V , cho không gian con F và véc tơ v.
Véc tơ v được biểu diễn duy nhất dưới dạng 𝑣 = 𝑓 + 𝑔 trong đó ⊥
f F, g F
Véc tơ 𝑓 được gọi là hình chiếu vuông góc của v xuống F, ký hiệu: prF v = f
Độ dài của véctơ g là khoảng cách từ v đến không gian con F và được ký hiệu bởi
d (v, F ) = g = v − prFv
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 16 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
Dạng toán: Cho không gian con F và một vectơ v.
a/ Tìm hình chiếu vuông góc của v xuống F
b/ Tìm khoảng cách từ v đến F Phương pháp làm:
a/ Tìm hình chiếu vuông góc của v xuống F
Tìm tập sinh hoặc tập cơ sở của F (nên tìm tập cơ sở nhé)
F=<𝑓1, 𝑓2, . . , 𝑓𝑛> Mà: + + + +
v = f g = x1 f1 x2 f2 ... + xn fn g Suy ra:
x1( f1, f1) + x2 ( f1, f2 ) + ... + xn ( f1, fn ) + (g, f1) = (v, f1)
x1( f2 , f1) + x2 ( f2 , f2 ) + ... + xn ( f2 , fn ) + (g, f2 ) = (v, f2 ) ... ... ... x =
1( fn , f1) + x2 ( fn , f2 ) + ... + xn ( fn , fn ) + (g, fn ) (v, fn )
Giải hệ phương trình để tìm 𝑥1, 𝑥2, 𝑥3, . . 𝑥𝑛
Kết luận: Hình chiếu của v xuống 𝐹 là pr + +
Fv = f = x1 f1 x2 f2 ...xm fm
b/ Tìm khoảng cách từ v đến F
d (v, F ) =|| g ||=|| v − prFv || 6.5 Trực giao
❖ Hai vecto 𝑥, 𝑦 ∈ 𝐸 được gọi là trực giao khi 𝑥 ⊥ 𝑦
❖ Vecto x được gọi là trực giao với tập hợp M nếu vecto x vuông góc với mọi vecto của tập M
Để chứng minh x là trực giao với tập hợp M (vuông góc với không gian M) thì cỉ cần
chứng mình x vuông góc vói tập sinh hoặc cơ sở của M
❖ Hệ véctơ {x1, x2, . . . , xn} được gọi là trực giao ⇔ chúng trực giao với nhau từng đôi một.
7. Chương ánh xạ tuyến tính 7.1 Định nghĩa
Cho V và W là hai không gian véctơ trên cùng tập số K.
Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊 giữa 2 không gian vecto V, W là một ánh xạ thỏa mãn
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 17 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
❖ ∀𝑣1, 𝑣2 ∈ 𝑉; 𝑓(𝑣1 + 𝑣2) = 𝑓(𝑣1) + 𝑓(𝑣2)
❖ ∀𝑣 ∈ 𝑉 𝑣à ℎằ𝑛𝑔 𝑠ố 𝛽; 𝑓(𝛼𝑣) = 𝛼𝑓(𝑣)
Mẹo giải nhanh: Kiểm tra 𝑓(𝑥) = 0 có phải là hệ phương trình tuyến tính thuần nhất hay
không? Nếu đúng thì là AXTT
Một số phép AXTT cần nhớ: Phép đối xứng qua một đường thẳng (qua O) hoặc mặt
phẳng (qua O), qua gốc tọa độ, phép chiếu vuông góc hoặc song song xuống một đường
thẳng(qua O) hoặc mặt phẳng(qua O), các phép quay và phép vị tự...
Cho 𝑓: 𝑉 → 𝑊 là ánh xạ tuyến tính . Cho 𝐸 = {𝑒1, 𝑒2, 𝑒3, … . 𝑒𝑛} là tập sinh của V. Giả sử
biết ảnh của tập sinh là 𝑓(𝑒1), 𝑓(𝑒2), 𝑓(𝑒3), … 𝑓(𝑒𝑛) thì ta có thể tìm được ảnh của mọi vecto tròn V Chứng minh:
Vì ∀𝑥 ∈ 𝑉 nên x là tổ hợp tuyến tính của tập sinh của V
𝑥 = 𝛼1𝑒1 + 𝛼1𝑒1 + 𝛼2𝑒2+. . +𝛼𝑛𝑒𝑛
Tổng quát: Ta đang cần tìm ảnh của 𝑥 là 𝑓(𝑥)
𝑓(𝑥) = 𝑓(𝛼1𝑒1 + 𝛼1𝑒1 + 𝛼2𝑒2+. . +𝛼𝑛𝑒𝑛)
Sử dụng 2 tính chất của AXTT ở phần định nghĩa, ta được:
𝑓(𝑥) = 𝑓(𝛼1𝑒1 + 𝛼1𝑒1 + 𝛼2𝑒2+. . +𝛼𝑛𝑒𝑛)
↔ 𝑓(𝑥) = 𝑓(𝛼1𝑒1) + 𝑓(𝛼2𝑒2) + ⋯ + 𝑓(𝛼𝑛𝑒𝑛)
↔ 𝑓(𝑥) = 𝛼1𝑓(𝑒1) + 𝛼2𝑓(𝑒2) + ⋯ + 𝛼𝑛𝑓(𝑒𝑛)
Giờ ta chỉ cần giải phương trình và tìm 𝛼1, 𝛼2, 𝛼3, .. là tìm được 𝑓(𝑥) Công thử tổng quát:
𝑓(𝑥) = 𝑓(𝑒). 𝐸−1. 𝑥 = 𝑀. 𝑥 với 𝑓(𝑒), 𝐸−1, 𝑥 là các ma trận với dưới dạng cột. M gọi là
ma trận hệ số của 𝑓(𝑥) gọi tắt ma trận 𝑓(𝑥)
7.2 Nhân và ảnh của ánh xạ tuyến tính Định nghĩa
Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊
❖ Nhân của ánh xạ tuyến tính f là tập hợp tất cả các vectơ x của không gian véctơ V,
sao cho f(x) = 0. (hoặc hiểu là nhân là vùng không gian chứa các vecto sao cho ảnh của nó bằng 0)
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 18 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
𝐾𝑒𝑟𝑓 = {𝑥 ∈ 𝑉|𝑓(𝑥) = 0}
❖ Ảnh của ánh xạ tuyến tính f là tập hợp tất cả các phần tử y của không gian véctơ
W sao cho tồn tại để y = f(x). (hoặc hiểu là vùng không gian chứ các ảnh vecto của V)
𝐼𝑚𝑓 = {𝑦 ∈ 𝑊|∃𝑥 ∈ 𝑉: 𝑦 = 𝑓(𝑥)}
Định lý:Cho Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊
❖ ker 𝑓 là không gian con của 𝑉
❖ 𝐼𝑚 𝑓 Cho Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊 là không gian con của 𝑊
❖ dim(ker 𝑓) + dim(𝐼𝑚 𝑓) = dim(𝑉)
❖ Ảnh của ánh xạ tuyến tính là không gian con được sinh ra bởi ảnh của một tập sinh của V.
𝑉 =< 𝑒1, 𝑒2, … >→ 𝐼𝑚𝑓 =< 𝑓(𝑒1), 𝑓(𝑒2), … . >
Bài toán thường gặp: Cho Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊
➢ Cách xác định dim và cơ sở của nhân ảnh ker 𝑓 : • B1:Tìm AXTT 𝑓(𝑥)
• B2:Giải phưng trình 𝑓(𝑥)} = 0
➢ Cách xác định dim và cơ sở của ảnh ánh xạ tuyến tính:
• B1: Tìm tập sinh của V là 𝐸 =< 𝑒1, 𝑒2, … >
• B2: Tìm ảnh của tập sinh 𝑓(𝑒1), 𝑓(𝑒2), ….
• B3: Tập sinh của 𝐼𝑚 𝑓 là 𝐼𝑚𝑓 =< 𝑓(𝑒1), 𝑓(𝑒2), … . >
7.3 Ma trận ánh xạ tuyến tính
Định nghĩa ma trận của ánh xạ tuyến tính
Cho Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑊
❖ 𝐸 = {𝑒1, 𝑒2, 𝑒3, … } là một cơ sở của 𝑉
❖ 𝐹 = {𝑓1, 𝑓2, 𝑓3, … } là một cơ sở của 𝑊
Ma trận A cở mxn với cột thứ j là tọa độ của véctơ 𝑓(𝑒𝑖) trong cơ sở F được gọi là ma
trận của f trong cặp cơ sở E và F A = E,F [ f (e )] [ f (e )] 1 F [ f (e )] 2 F n F
Cách khác 𝐴𝐸,𝐹 = 𝐹−1. 𝑀. 𝐸 (F, E là ma trận cở viết viết theo cột, M là ma trận hệ số của
ánh xạ tuyến tính 𝑓(𝑥) trong cơ sở chính tắc)
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 19 HCMUT CNCP
LỚP ĐẠI SỐ TUYẾN TÍNH NGUYỄN QUỐC VƯƠNG
[ f (x)] = A [x] F E,F E Tóm lại
• Ma trận Axtt 𝑓(𝑥) trong tập cơ sở E, F là 𝐴𝐸,𝐹 = 𝐹−1. 𝑀. 𝐸
• Ánh xạ tuyến tính 𝑓(𝑥) trong sở trong tập cơ sở E, F là [𝑓(𝑥)] = 𝐴𝐸,𝐹. [𝑥]𝐸
Trường hợp đặc biệt: Cho Ánh xạ tuyến tính 𝑓: 𝑉 → 𝑉, với 𝐸 = {𝑒1, 𝑒2, 𝑒3, … } là một cơ sở của 𝑉
Ma trận A cở mxn với cột thứ j là tọa độ của véctơ 𝑓(𝑒𝑖) trong cơ sở E được gọi là ma
trận của f trong cặp cơ sở E A = E,E
[ f (e1)]E [ f (e [ f (e 2 )]E n )]E [ f (x)] = F
AE,F [x]E
Cách khác 𝐴𝐸,𝐸 = 𝐸−1. 𝑀. 𝐸 (F, E là ma trận cở viết viết theo cột, M là ma trận hệ số của
ánh xạ tuyến tính 𝑓(𝑥) trong cơ sở chính tắc) Tóm lại
• Ma trận Axtt 𝑓(𝑥) trong tập cơ sở E là 𝐴𝐸,𝐸 = 𝐸−1. 𝑀. 𝐸
• Ánh xạ tuyến tính 𝑓(𝑥) trong sở trong tập cơ sở E là [𝑓(𝑥)] = 𝐴𝐸,𝐸. [𝑥]𝐸
7.4 Các phép đổi tuyến tính
Các phép biến đổi tuyến tính Ma trận AXTT 1 0
f1 là phép đối xứng qua Ox 𝐴1 = ) ( 0 −1
f2 là phép đối xứng qua Oy. −1 0 𝐴2 = ( ) 0 1
f3 là phép đối xứng qua đường thẳng ∆y = x 0 1 𝐴3 = ( ) 1 0 𝑘1 0
f4 phép giãn (hoặc co) hệ số k1 > 1(0 < k1 < 1) theo 𝐴4 = ) (nếu k1 = k2 = k là
phương x và k2 theo phương y. ( 0 𝑘2 phép vị tự.)
FACEBOOK:HCMUT-CNCP TÀI LIỆU BÁCH KHOA
KHÓA HỌC ĐẠI SỐ TUYẾN TÍNH 20
Tài liệu liên quan:
-
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
54 27 -
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
149 75 -
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
34 17 -
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
43 22 -
Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.
41 21