Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.

CHƯƠNG 1: ÁNH XẠ PHẦN 1: LÝ THUYẾT
notes: (X Y, A con X, B con Y)
* ảnh của A là tập hợp f(A)= y thuộc Y sao cho với mọi x thuộc A thì f(x)=y.
*Nghịch ảnh của tập hợp B tồn tại khi với mọi phần tử x thuộc A có f(x)=y.
y=[f(f-1(B))]. ( bên x là nghịch ảnh của bên y )
-Tương tự: nghịch ảnh của phần tử y thuộc Y là mọi x thuộc X sao cho f(x)=y. *Đơn ánh:
- đơn ánh là với mọi a, b thuộc X thì f(a) khác f(b), f(a) = f(b) => a=b.
(a thuộc X sẽ là phần tử duy nhất tương ứng với một phần tử bên Y, b thuộc X cũng tương tự là phần tử duy nhất
tương ứng với một phần tử khác thuộc Y) *Toàn ánh:
- f(X) = Y xảy ra khi các phần tử của X đủ để tác động f(x) vào phủ sạch tập Y.
Hay nói cách khác với mọi y thuộc Y đều có một x thuộc X tương ứng. *Song ánh:
- song ánh xuất hiện khi việc các phần tử thuộc X đủ nhiều để tạo ra các đơn ánh phủ sạch Y.
<=>Điều đó có nghĩa rằng trong song ánh và toàn ánh, mọi phần tử y thuộc Y sẽ luôn có một
phần tử x Thuộc X tương ứng.
=> từ song ánh sẽ sinh ra ánh xạ ngược: có một hàm số mà tác động y thuộc Y sẽ có x thuộc X tương ứng.
*Hợp thành ánh xạ: -nếu ta có: X Y
Z, khi đó ta nói phần tử x thuộc X tương ứng với z f(x) h(f(x))
thuộc Z là: g=h(f(x)) là hợp thành ánh xạ.
+) lưu ý: chúng ta có thể hợp ánh xạ của một chuỗi dài hơn là chỉ ba tập hợp: X Y Z K … K.H: u=h o f.
*Ánh xạ ngược: là hàm f-1 (y) = ( rút x theo y ) Ví dụ ở bài 3. *Ánh xạ đồng nhất:
-K/n: idx : X X, tức ta gọi là ánh xạ đồng nhất là khi một phần tử x thuộc X tương ứng với phần
tử x (khác) cũng thuộc chính X.
-K.H: idx (x) = x, với mọi x thuộc X.
*Các tính chất của ánh xạ: Kết luận: -
Đối với phép toán hợp của hai tập hợp: CHỈ KHÔNG BẢO TOÀN VỚI PHÉP GIAO
(GIAO CỦA NGỊCH ẢNH BẢO TOÀN MÀ LÀ TẬP CON .) PHẦN 2
Miền giá trị của f(x) là tất cả các giá trị y có thể ra. X2 luôn dương xt(0;p inf)
• Nghịch ảnh của ytY là các ptu xtX mà có f(x)=y => PHẦN 3: LỜI GIẢI Bài 3: Còn bài 5.
CHƯƠNG 3: MA TRẬN- ĐỊNH THỨC VỀ MA TRẬN
I. PHÉP TOÁN MA TRẬN
*tóm tắt lý thuyết:
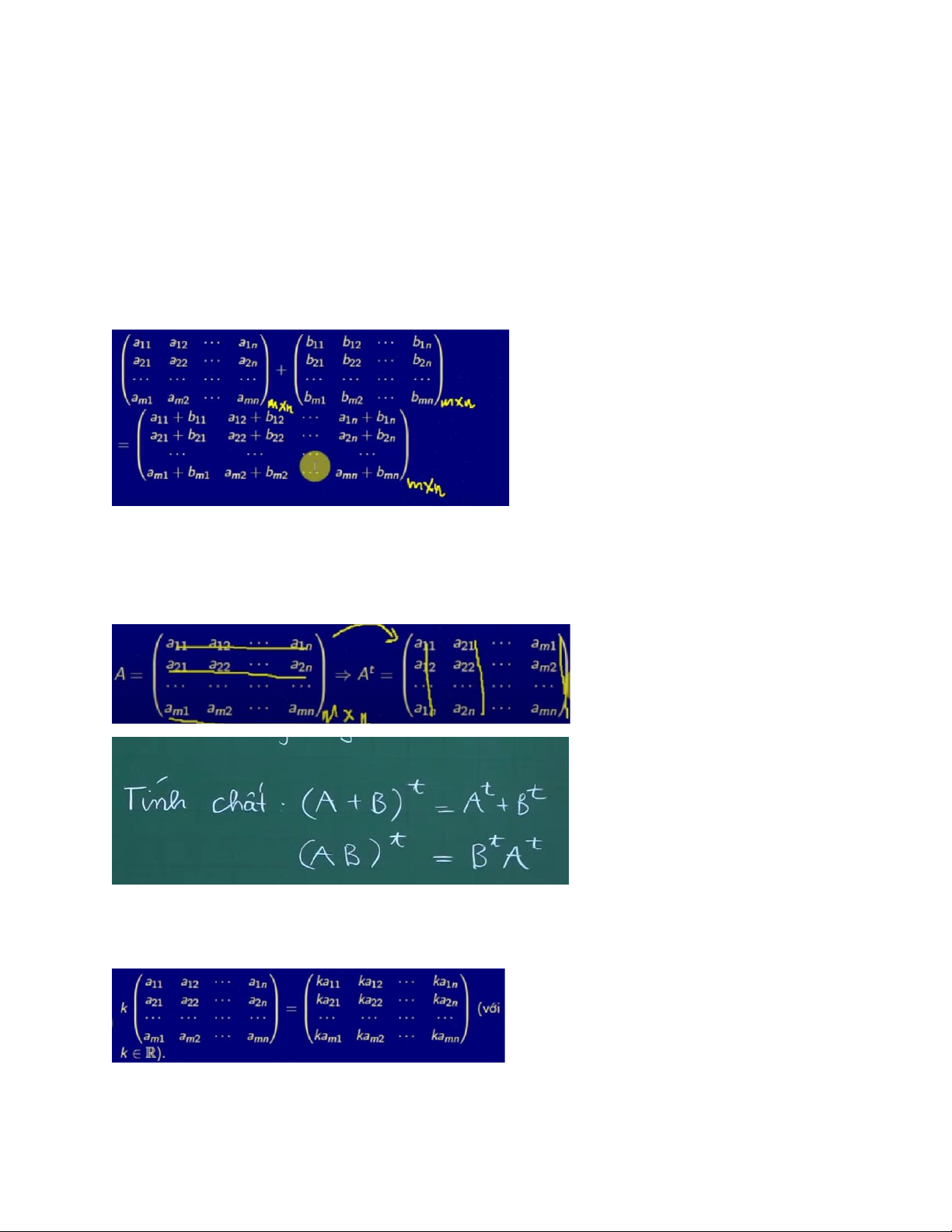
1. cộng hai ma trận
Notes: chỉ cộng hai ma trận đồng cấp ra một ma trận kết quả cũng đồng cấp.
2. chuyển vị ma trận
Từ ma trận A ban đầu chuyển vị dòng tương ứng thành cột tương ứng:
3. nhân ma trận với một số thực: 4. Nhân ma trận:
- Cho A là ma trận cấp m x n và B là ma trận cấp n x p, khi đó A.B = C với ma trận C có cấp m x p được xđ:
➔ tích vô hướng của phần tử dòng thứ i của ma trận A và cột thứ j của ma trận B.
LƯU Ý: A x B chưa chắc bằng B x A (không giao hoán), giao hoán khi nhân hai ma trận vuông cùng cấp. *Lũy thừa:
-hướng giải: ta dự đoán bằng cách thử lũy thừa bậc 2 (bình phương) rồi bậc ba (lập phương) => sau
đó rút ra được dự đoán : Ma trận sẽ là
Bước chứng minh: giả sử ta coi dự đoán trên đúng với n=k, để chắc chắn nó phải đúng với k+1 Ta có: = = = (dpcm)
II. CÁC LOẠI MA TRẬN VÀ TÍNH CHẤT
1. Ma trận vuông (ma trận đường chéo)
Là ma trận cấp n x n, khác với ma trận hình chữ nhật thì ma trận vuông trên đường chéo chính chứa các phần tử.
2. Ma trận đơn vị
- là ma trận đường chéo, các phần tử trên đường chéo chính = 1. k.h là “I”
3 . Ma trận tam giác trên:
Là ma trận vuông và mọi phần tử dưới đường chéo chính bằng không
4. Ma trận tam giác dưới:
-(ngược lại với ma trận tam giác trên)
5. Ma trận bậc thang: -tính chất:
+ nếu có hàng bằng 0 phải nằm dưới cùng
+ phần tử khác 0 đầu tiên của hàng dưới lệch sang bên phải so với phần tử khác 0 đầu tiên của hàng trên. *định nghĩa 3.4:
-Ma trận A được gọi là ma trận đối xứng khi A=At
+)Tính chất: ma trận vuông và đối xứng qua đường chéo thứ nhất.
-Ma trận A được gọi là ma trận phản đối xứng khi A=-At
+)tính chất: ma trận vuông có đối dấu qua đường chéo thứ nhất
+) các phần tử đường chéo thứ nhất bằng 0 III. ĐỊNH THỨC 1. HOÁN VỊ.
-Hoán vị của n phần tử là một cách sắp xếp n phần tử theo thứ tự khác nhau. Số hoán vị: n!
*Phương pháp tim được công thức tổng quát của ma trận lũy thừa:
[ĐSTT] Ba cách tim lũy thừa của một ma trận - YouTube