Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

TRÊN LớP) Chử Văn Tiệp
Giải tích II- 2023-2024, ĐHBKĐN
CÂU 12. Dùng tích phân hai lớp tính diện tích các miền sau:
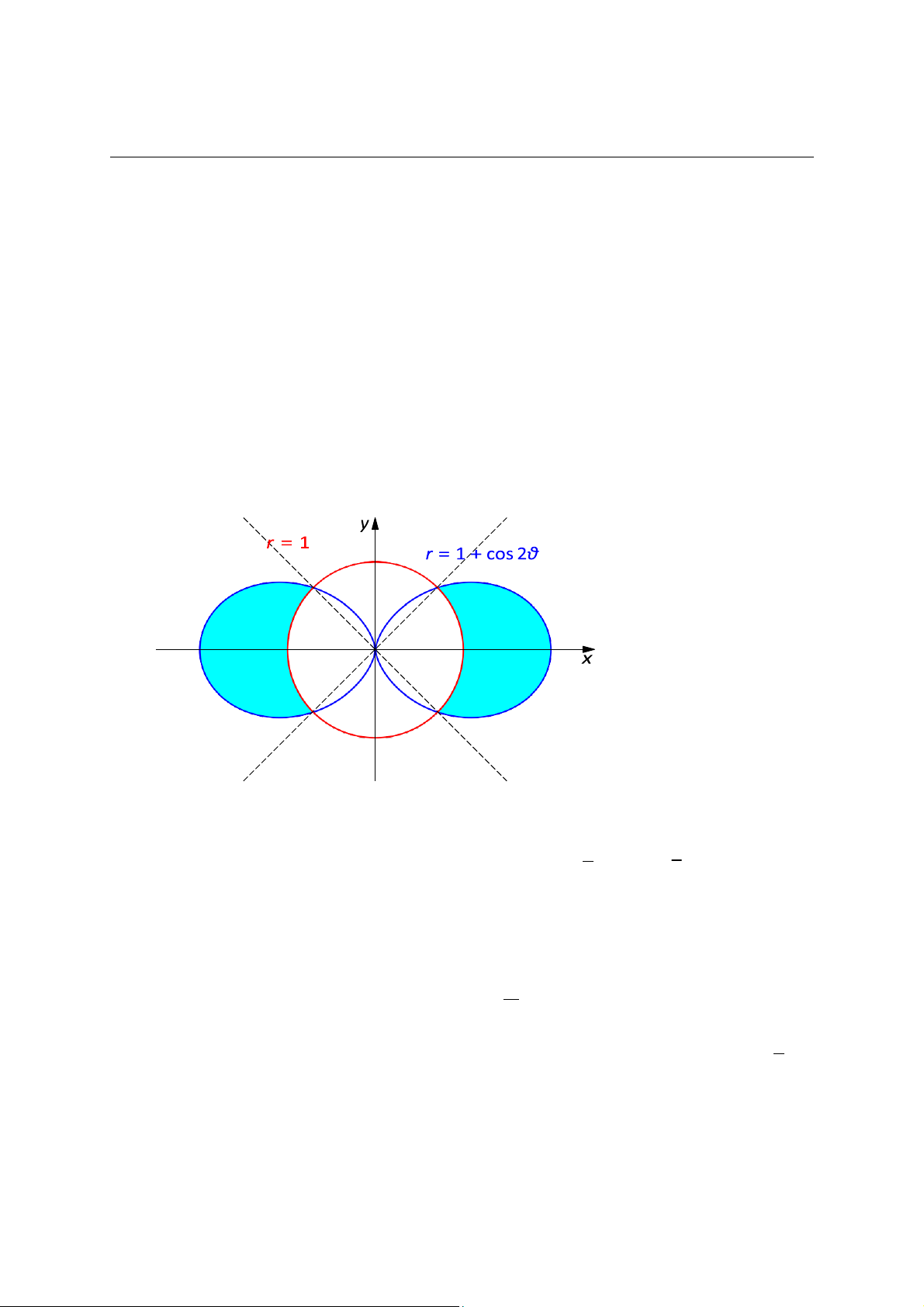
1. Tính diện tích của miền nằm bên trong đường cardioid r = 1 + cos 2θ và bên ngoài đường tròn r = 1
2. Tính diện tích của một nhánh cách hoa hồng cho bởi r = 12 cos 3θ
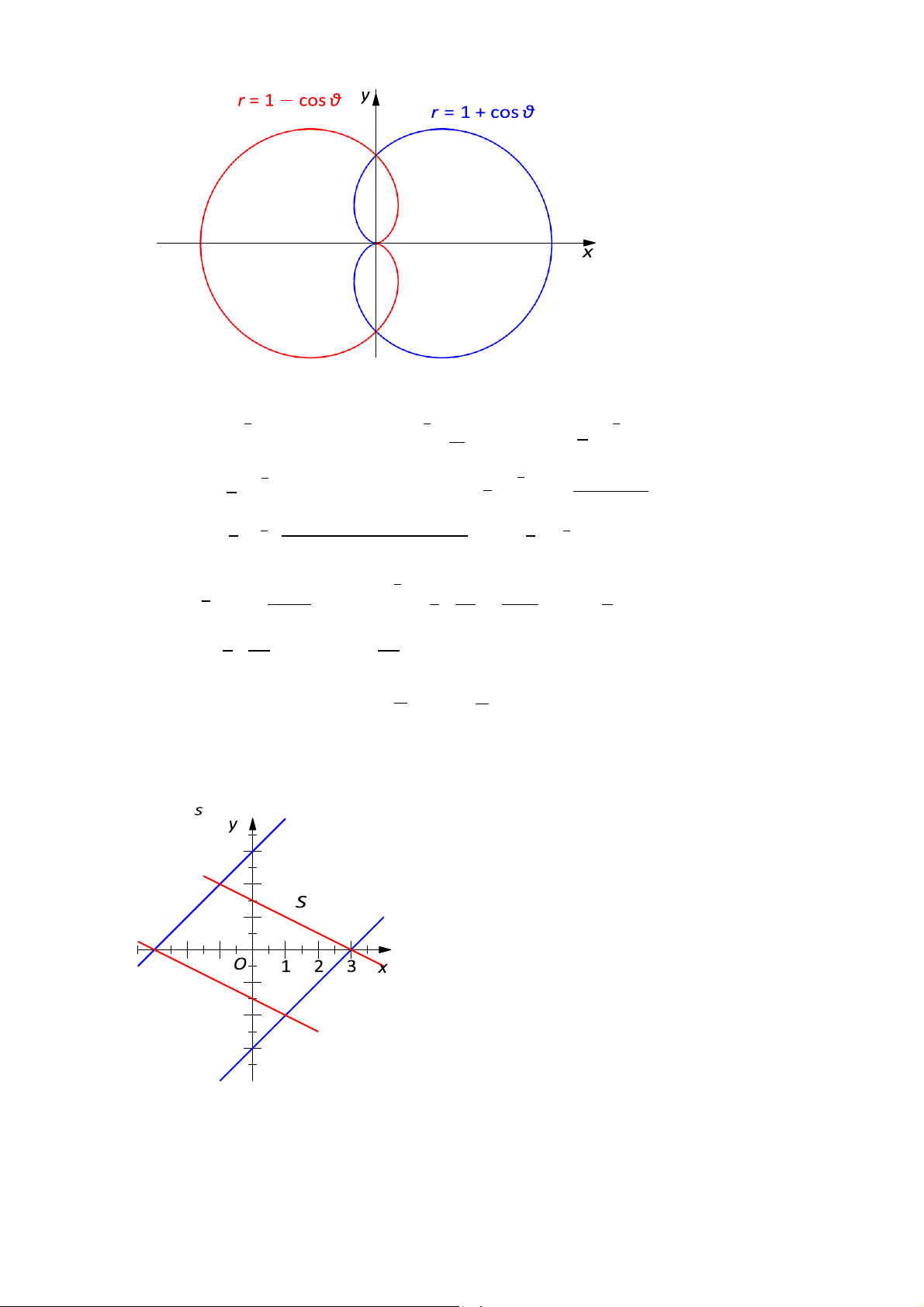
3. Tính diện tích của miền nằm trong 2 đường cardioid r = 1 + cos θ và r = 1 − cos θ
Lời giải. 1. Tính diện tích của miền nằm bên trong đường r = 1 + cos 2θ và bên ngoài đường tròn r = 1. Giải hệ phương trình: π π
1 + cos 2θ = 1 ⇔ cos 2θ = 0 ⇔ 2θ = ± ⇔ θ = ± . 2 4
Do tính đối xứng diện tích cần tính bằng 4 lần diện tích miền màu xanh nằm trong
góc phần tư thứ nhất. Sử dụng tọa độ cực ta có ∫ ∫ ∫ π/4 1+cos 2θ
π/4 r2 1+cos 2θ S(D) = 4 dθ rdr = 4 dθ 2 0 1 ∫ 0 1 ∫ π/4 π/4 π = 2
(1 + cos 2θ)2 − 1dθ = 2
cos2 2θ + 2 cos 2θdθ = ... = 2 + . 0 0 4
Qua ví dụ trên ta có thể đặt ra thêm các câu hỏi sau:
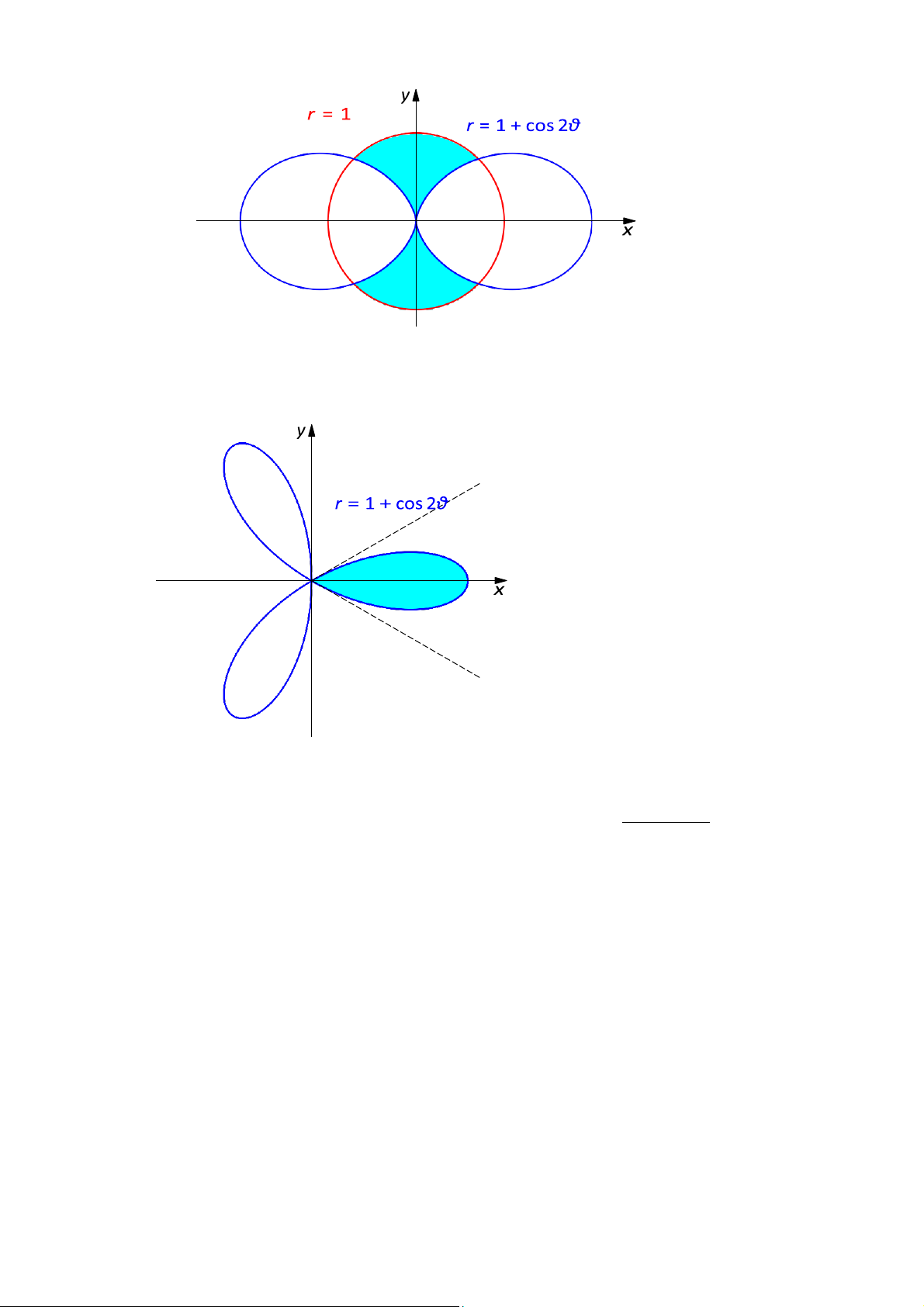
(a) Hãy tính diện tích miền xanh sau: 1 / 5
(b) Tính diện tích hình nằm trong đường cong r = 1 + cos 2θ.
2. Tính diện tích của một nhánh cách hoa hồng cho bởi r = 12 cos 3θ. Gợi ý: ∫ ∫ ∫ ∫ π/6 S(D) = π/6 12 cos 3θ (12 cos 3θ)2 dxdy =
r dr dθ = dθ D −π/6 0 −π/6 2 ∫ π/6 = 72 cos2 3θdθ −π/6 ∫ π/6 =
36(1 + cos 6θ)dθ −π/6 = 12π.
3. Tính diện tích của miền nằm trong 2 đường cardioid r = 1 + cos θ và r = 1 − cos θ. 2 / 5
Diện tích phần cần tính bằng 4 lần diện tích A trong góc phần tư thứ nhất ∫ π ∫ ∫ (1−cos θ) π (1−cos θ) ∫ π 2 2 r2 2 dθ =
(1 − cos θ)2 − 0 dθ 1 A = rdrdθ = 0 0 0 2 0 2 0 ∫ π π ∫ 1 2 2 =
1 + cos2 θ − 2 cos θ dθ = 1
1 + 1 + cos 2θ — 2 cos θ dθ 2 0 2 0 2 ∫ π ∫ π 1
2 + 1 + cos 2θ − 4 cos θ] 1 2 2 dθ =
[3 + cos 2θ − 4 cos θ]dθ = = 2 2 0 4 0 π 1 sin 2θ 2 1 3π sin π π 3θ + — 4 sin θ = + − 4 sin 4 2 0 4 2 2 2 — [0 + 0 − 0] 1 3π 3π = + 0 − 4 = − 1 . 4 2 8
Vậy diện tích cần tính là: 4 · 3π − 1 = 3π − 4 8 2 □ ∫∫ CÂU 21. xydxdy,
S : |x + 2y| ≤ 3, |x − y| ≤ 3. 3 2 1
Đặt u = x + 2y, v = x − y. Khi đó (u, v) ∈ [−3, 3] × [−3, 3]. 3 / 5 u + 2v u − v
Viết lại ta được x = , y = . Jacobian: 3 3 1 2 x′ x′ 3 3 1 J = u v = ′ ′ = − . y y yv 1 1 3 − 3 3 Suy ra ∫∫ ∫ ∫ 3 ∫ ∫ 3
u + 2v u − v 1 3 3 xydxdy = du · 1 dv = du
(u + 2v)(u − v)dv −3 3 3 3 3 27 −3 3 S ∫ ∫ 1 3 3 = du
u2 + uv − 2v2dv = ... = −4. 27 −3 3
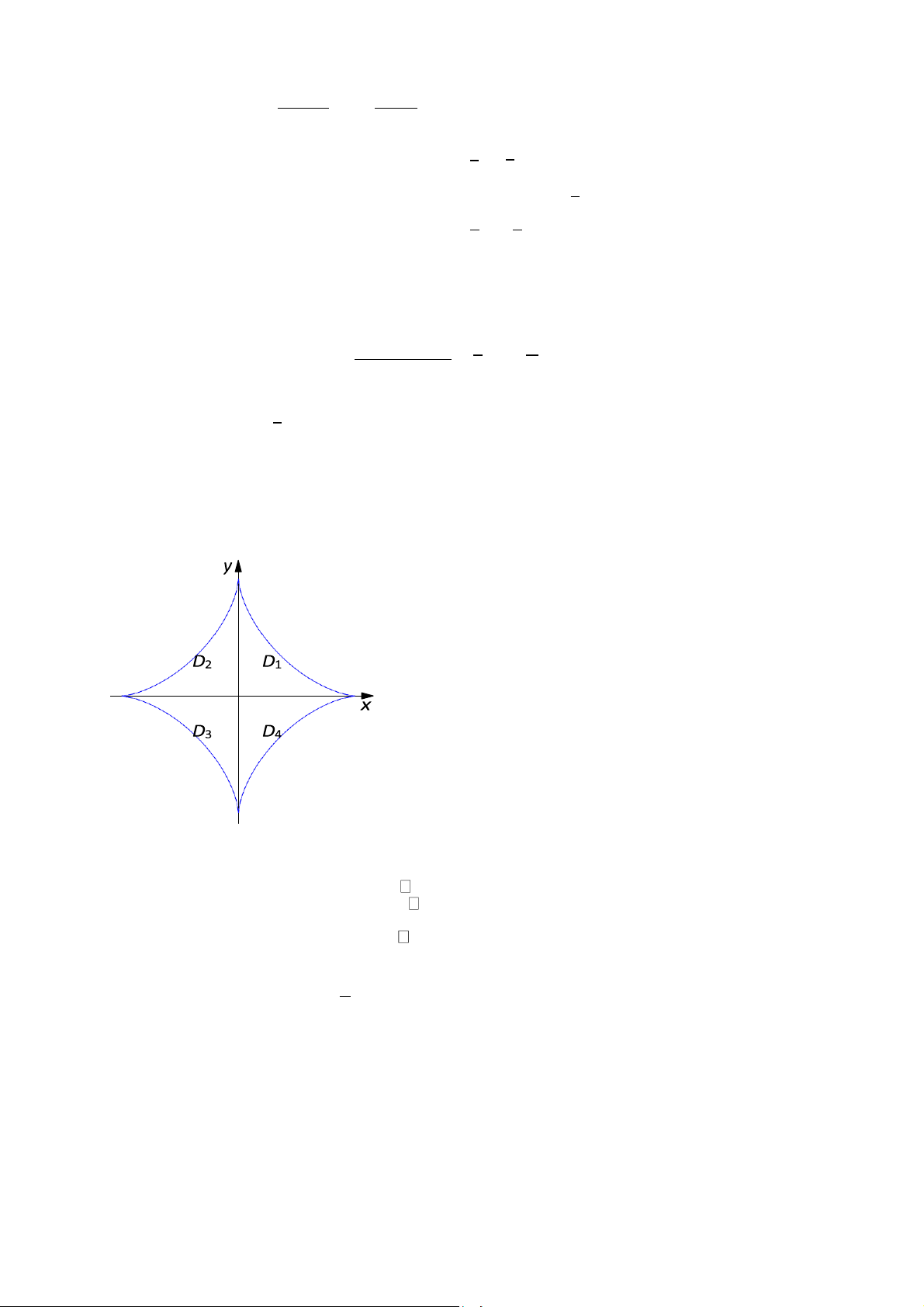
CÂU 38. Tính diện tích hình phẳng bị chặn bởi đường cong phương trình
x2/3 + y2/3 = 1.
Lời giải. Diện tích cần tính bằng 4 lần diện tích D1. Đổi biến
x = r3 cos3 ϕ
 y = r3 sin3 ϕ
Từ hình vẽ ta thấy 0 ≤ ϕ ≤ π . Từ phương trình đường cong ta suy ra 2
x2/3 + y2/3 = r2 cos2 ϕ + r2 sin2 ϕ = r2 = 1.
Suy ra 0 ≤ r ≤ 1. Tính Jacobian của phép đổi biến:
x′ x′ 3r2 cos3 ϕ −3r3 cos2 ϕ sin ϕ J = r ϕ = ′ ′ 2 3 3 2 y 3r sin ϕ
3r sin ϕ cos ϕ r yϕ
= 9r5 cos4 ϕ sin2 ϕ + 9r5 sin4 ϕ cos2 ϕ = 9r5 cos2 ϕ sin2 ϕ 4 / 5
Do đó từ công thức đổi ta có ∫∫ ∫ π/2 ∫ 1 S(D1) = dxdy = dϕ
9r5 cos2 ϕ sin2 ϕdr D1 0 0 ∫ ∫ 9 π/2 =
sin2 2ϕdϕ × 1 r5dr 4 0 0   ∫ π/2 9 π/2 r6 1 3 sin cos 4ϕ 3π =
1 − cos 4ϕdϕ ×   = ϕ − = . 8 0 6 16 4 32 0 0 3π
Vậy S(D) = 4S(D ) =
. Chú ý: Ta cũng có thể đổi biến như sau: 1 8
x = r cos3 ϕ
 y = r sin3 ϕ
Từ hình vẽ ta thấy 0 ≤ ϕ ≤ π . Từ phương trình đường cong ta suy ra 2
x2/3 + y2/3 = r2/3 cos2 ϕ + r2/3 sin2 ϕ = r2/3 = 1.
Suy ra 0 ≤ r ≤ 1. Tính Jacobian của phép đổi biến:
x′ x′ cos3 ϕ −3r cos2 ϕ sin ϕ J = r ϕ = ′ ′ 3 2 y
sin ϕ 3r sin ϕ cos ϕ r yϕ
= 3r cos4 ϕ sin2 ϕ + 3r sin4 ϕ cos2 ϕ = 3r cos2 ϕ sin2 ϕ. Khi đó ∫∫ ∫ ∫ π/2 1 S(D1) = dxdy = dϕ
3r cos2 ϕ sin2 ϕdr D1 0 0 ∫ ∫ 3 π/2 =
sin2 2ϕdϕ × 1 rdr 4 0 0   ∫ π/2 3 π/2 r2 1 3 sin cos 4ϕ 3π =
1 − cos 4ϕdϕ ×   = ϕ − = . 8 0 2 16 4 32 0 0 3π
Vậy S(D) = 4S(D ) = . □ 1 8 Câu hỏi bổ sung:
1. Hãy tính diện tích trên bằng một cách nữa.
2. Tìm chiều dài của đường cong cho bởi phương trình
x2/3 + y2/3 = 1.
3. Tìm trọng tâm của mảnh kim loại phẳng đồng chất có diện tích D1.
4. Tính diện tích của mặt tròn xoay khi quay đường cong trên quanh trục Ox. 5 / 5