Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Phân tích: Ta hãy hình dung có một mặt S hai phía được nhúng chìm trong một môi trường của vật chất lỏng đang chạy ở chế độ dừng tức là tại mỗi điểm M(x,y,z) thì vậntốccủaphầntửchấtlỏngtạiđólàmộtvectơv⃗(x,y,z)khôngphụthuộcvàothờigian
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Tài liệu gồm 16 trang , giúp bạn tham khảo, ôn tập và đạt kết quả cao
Môn: Giải tích 2(GT2101) 46 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 1.7 K tài liệu
Tác giả:
Preview text:
BÀI TậP TíCH PHÂN MặT Chử Văn Tiệp Giải tích II- ĐHBKĐN 1 Tóm tắt lý thuyết 1.1 Mặt cong
Phương trình mặt cong trong không gian thường được cho bởi các dạng sau:
i) Dạng tổng quát (dạng ẩn): F(x, y, z) = 0. ii) Dạng tham số x = x(u, v) y = y(u, v) (u, v) ∈ D ⊂ R2 z = z(u, v), hay dạng vector
r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k, (u, v) ∈ D ⊂ R2
trong đó i, j, k lần lượt là ba vector đơn vị trên các trục Ox, Oy, Oz.
iii) Dạng hiển z = f(x, y) hoặc y = g(x, z) hoặc x = h(y, z).
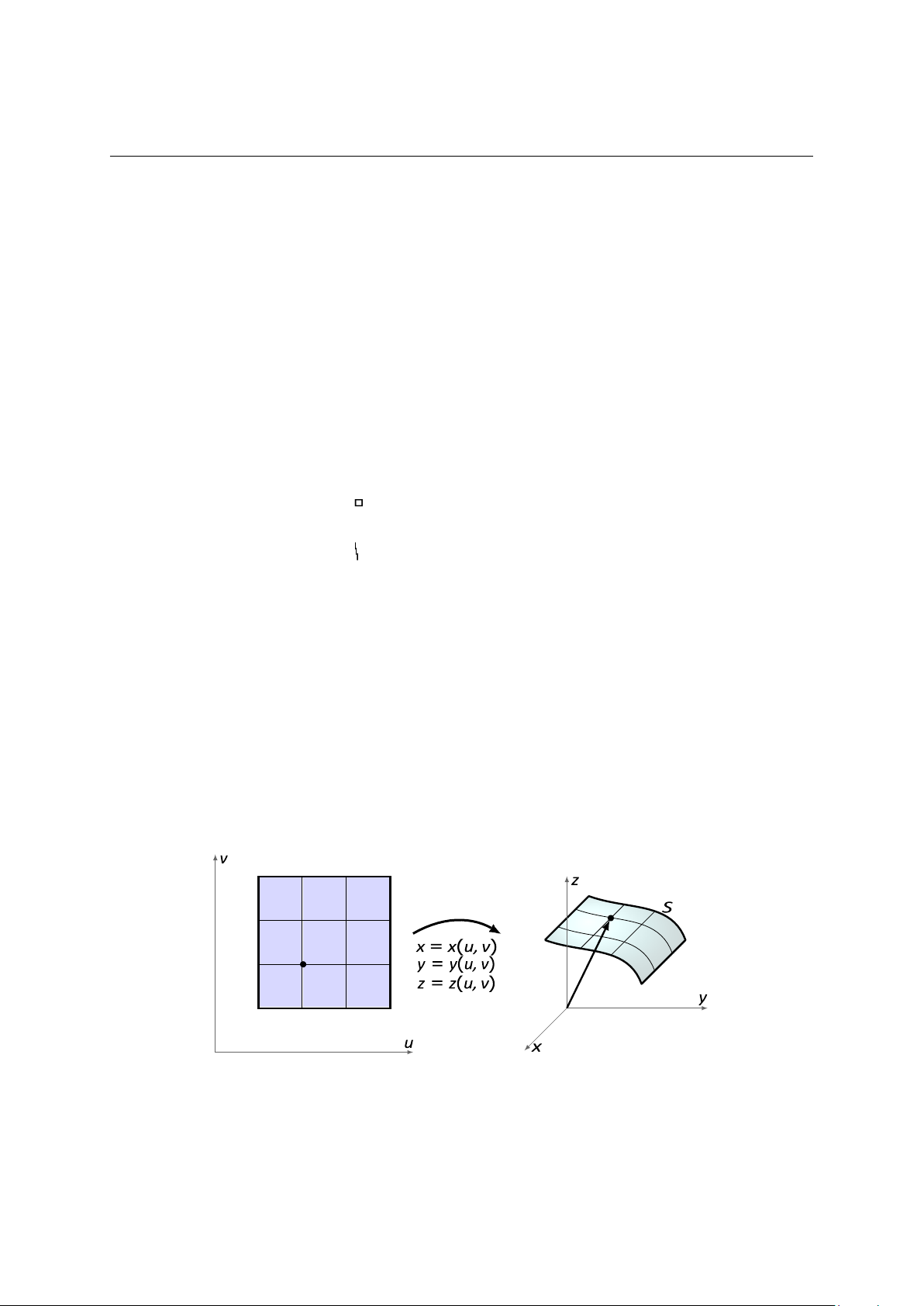
1.1.1 Phương trình tham số mặt cong R2 D (u, v) r(u, v) 0
Hình 1: Tham số hóa mặt cong S trong R3
Ví dụ 1. Viết phương trình tham số của mặt cầu tâm (0, 0, 0) bán kính a.
Ví dụ 2. Viết phương trình tham số của các mặt sau 1 / 16
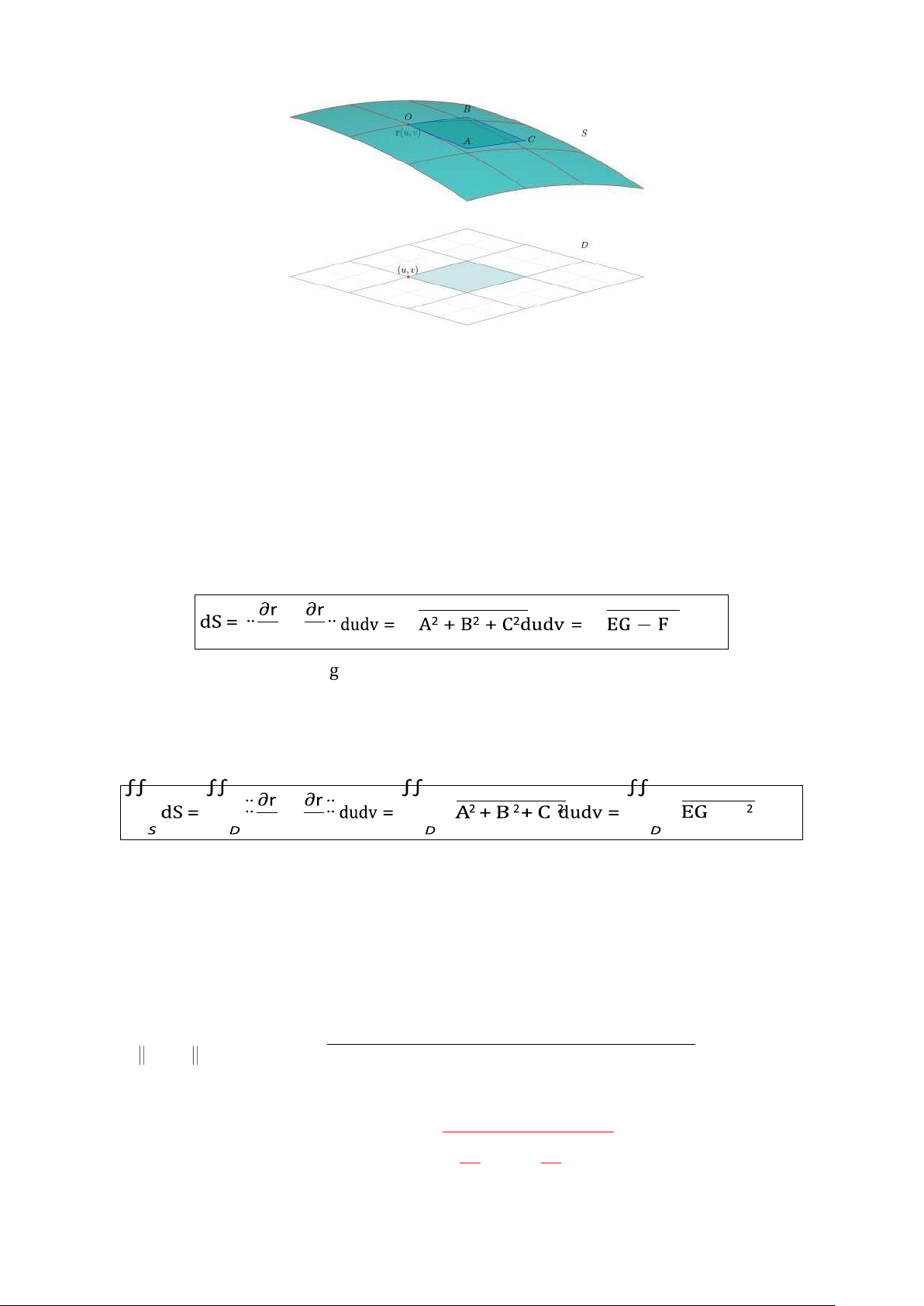
Hình 2: Vi phân diện tích mặt (a) 3x − 2y + z = 2 (b) z = x2 + y2
1.2 Công thfíc diện tích mặt cong
1.2.1 Vi phân diện tích mặt cong √ √ ∂u × ∂v 2dudv. Diện tích của m ột mặt cong trơn
r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k, (u, v) ∈ D ⊂ R2 là √ √ ∂u × ∂v — F dudv.
Ở đây ta sử dụng ký hiệu tích có hướng của hai vec tor: i j k a a a 2 a3 1 a3 1 a2 a × b = a i − j + k (1) 1 a2 a3 = b 3 2 b b 3 2 1 1 b b b b 1 b 2 b 3
= (a2b3 − a3b2)i − (a1b3 − a3b1)j + (a1b2 − a2b1)k, (2) √
a × b := |a × b| = (a2b3 − a3b2)2 + (a1b3 − a3b1)2 + (a1b2 − a2b1)2
• Công thức diện tích mặt của mặt cong dạng z = z(x, y), (x, y) ∈ Dxy là s ∫∫ ∫∫ 2 ∂z ∂z 2 dS = + + 1 dxdy. ∂x ∂y S D 2 / 16
• Công thức diện tích mặt của mặt cong dạng x = x(y, z), (y, z) ∈ Dyz là ∫∫ ∫∫ s ∂x 2 ∂x 2 dS = + + 1 dydz. ∂y ∂z S D
• Công thức diện tích mặt của mặt cong dạng y = y(x, z), (x, z) ∈ Dxz là ∫∫ ∫∫ s ∂y 2 ∂y 2 dS = + + 1 dxdz. ∂x ∂z S D
1.3 Tích phân mặt loại I
Bài toán đưa đến việc xây dựng tích phân mặt loại I: Tính khối lượng mặt cong có hàm
mật độ khối lượng f(x, y, z).
ĐịnH LÝ 1. Cho S là một mặt cong trong R3 được tham số bởi r(u, v) = x(u, v)i +
y(u, v)j + z(u, v)k, và f(x, y, z) là hàm xác định trên tập con của R3 ∫∫ chứa S. Khi đó ∫∫ f(x, y, z) dS = f ∂r (x(u, v), y(u, v), z(u, v)) ∂r du dv × ∂u ∂v S D ∫∫ √ =
f(x(u, v), y(u, v), z(u, v)) A2 + B2 + C2 du dv D ∫∫ √ =
f(x(u, v), y(u, v), z(u, v)) EG − F 2 du dv . D D D D trong đó A (y, z) (z, x) (x, y) = , B = , A = , D(u, v) D(u, v) D(u, v) E = ∂r 2
2, F = ∂r · ∂r ∂u , G = ∂r ∂v ∂u ∂v
• Nếu mặt S cho bởi z = z (x, y) , (x, y) ∈ D thì công thức tính tích phân mặt loại I có dạng ∫∫ ∫∫ s ∂z 2 ∂z 2 f (x, y, z) dS = f (x, y, z (x, y)) + + 1 dxdy ∂x ∂y S D
• Nếu mặt S cho bởi y = y (x, z) , (x, z) ∈ D thì công thức tính tích phân mặt loại I có dạng ∫∫ ∫∫ s 2 ∂y ∂y 2 f (x, y, z) dS = f (x, y(x, z), z) + + 1 dxdz. ∂x ∂z S D 3 / 16
• Nếu mặt S cho bởi x = x (y, z) , (y, z) ∈ D thì công thức tính tích phân mặt loại I có dạng ∫∫ ∫∫ s 2 ∂x ∂x 2 f (x, y, z) dS = f (x (y, z) , y, z) + 1 dydz ∂y + ∂z S D
1.4 Tích phân mặt loại II
Mặt không định hướng được: Dải Mobius, chai Klein, . . . (sẽ không xét tích phân mặt
loại II trên các mặt này)
Hình 3: Dải Mobius và Chai Klein
Mặt định hướng được: mặt cầu, mặt trụ, mặt paraboloid,...
Bài toán đưa đến việc xây dựng tích phân mặt loại II: Tính từ thông qua một mặt S,
tính lưu lượng nước chảy qua một mặt S (thông lượng, lưu lượng).
Hình 4: Lưu lượng chất lỏng chảy qua mặt cong S
Phân tích: Ta hãy hình dung có một mặt S hai phía được nhúng chìm trong một môi
trường của vật chất lỏng đang chạy ở chế độ dừng tức là tại mỗi điểm M(x, y, z) thì vận
tốc của phần tử chất lỏng tại đó là một vectơ v⃗(x, y, z) không phụ thuộc vào thời gian 4 / 16
t. Hãy tính lưu lượng F của chất lỏng chảy qua mặt S tức là lượng chất lỏng chảy qua
S trong một đơn vị thời gian theo một phía nào đó xác định bởi chiều của vectơ pháp tuyến n⃗.
Xét một diện tích vi phân dS tại điểm M(x, y, z). Trong một đơn vị thời gian lượng
chất lỏng chảy qua mảnh dS lấp đầy một hình trụ nghiêng có đáy dS và đường sinh song
song với vectơ vận tốc v⃗(x, y, z) và bằng độ dài vectơ đó .
Thể tích của hình trụ bằng lượng chất lỏng chạy qua F trong một đơn vị thời gian và bằng
dF = đáy × chiều cao = v⃗ · n⃗dS
(Nếu góc (v⃗, n⃗) < π/2, lượng chất lỏng chảy qua dS theo phía n⃗ có dấu dương. Còn
nếu góc (v⃗, n⃗) > π/2, lượng chất lỏng chảy qua dS theo phía n⃗ có dấu âm)
Giả sử vận tốc v⃗ và n⃗ lần lượt có các thành phần P (x, y, z) cos(O⃗x, n⃗) cos α v⃗ =
Q(x, y, z) , n⃗ = cos(O⃗y, n⃗) = cos β . R(x, y, z) cos(O⃗z, n⃗) cos γ Khi đó
dF = (P(x, y, z) cos α + Q(x, y, z) cos β + R(x, y, z) cos γ)dS
Vì vậy lưu lượng F của chất lỏng chảy qua mặt S bằng ∫∫ ∫∫ F = dF = v⃗ · n⃗dS ∫∫ S S =
(P(x, y, z) cos α + Q(x, y, z) cos β + R(x, y, z) cos γ) dS ∫∫ S =
P(x, y, z)dydz + Q(x, y, z)dzdx + R(x, y, z)dxdy. Sn⃗
1.4.1 Cosin chỉ phương của pháp tuyến của mặt S ∂ Ta biết N⃗ r =
× ∂r = (A, B, C) trong đó ∂u ∂v D (y, z) y′ y′ D(z, x) z′ z′ D(x, y) x′ x′ A = = u v v ′ ′ , B = = u ′ ′ , C = = v u . ′ ′ D(u, v) z z D(u, v) x x D(u, v) y y u v u v u v
N⃗ là vector pháp tuyến của của mặt cong S. Từ đó dễ thấy, cosin chỉ phương của vector pháp tuyến bằng A , cos(O⃗x, N⃗) = √ A2 + B2 + C2 B cos(O⃗y, N⃗) = √ , A2 + B2 + C2 C cos(O⃗z, N⃗) = √ . A2 + B2 + C2 5 / 16
• Nếu mặt cong S có phương trình
z = z(x, y), (x, y) ∈ DxOy.
Khi đó ta có thể quan niệm S là mặt tham số như sau (u = x, v = y) x = x y = y (x, y) ∈ D ⊂ R2 z = z(x, y), hay dạng vector
r(x, x) = xi + yj + z(x, y)k, (x, y) ∈ D ⊂ R2 Khi đó
N⃗ = (−z′ , −z′ , 1) x y
Cosin chỉ phương của vector pháp tuyến bằng ⃗ ⃗ ′ −zx cos(Ox, N) = q , 1 + (z′ )2 x + (z′ y )2 ′ cos(O⃗y, N⃗) = q −zy ,
1 + (z′ x )2 + (z′ y )2 1 cos(O⃗z, N⃗ ) = q . 1 + (z′ )2 + (z′ )2 x y π Do ⃗ ⃗ 1
nên góc (O⃗z, N⃗) < . cos(Oz, N) = q > 0 1 + (z′ 2 ′ 2 2 x) + (zy)
Nếu phương trình mặt cong có dạng z = z(x, y) thì N⃗ = (−z′ , −z′ , 1) là pháp tuyến x y
hướng lên phía trên của S.
1.4.2 Định nghĩa tích phân mặt loại II
Cho một trường vector F (x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)) và một mặt cong S hai phía
r (u, v) = x (u, v) · i + y (u, v) · j + z (u, v) · k., (u, v) ∈ D
Giả sử x (u, v) , y (u, v) , z (u, v) khả vi liên tục và ma trận " # ∂x ∂y ∂z ∂u ∂u ∂u ∂x ∂y ∂z ∂v ∂v ∂v 6 / 16
có hạng bằng 2. Giả sử S được định hướng dương theo vector pháp tuyến đơn vị n⃗ =
n (x, y, z) là pháp tuyến đơn vị đối với mặt cong S tại điểm (x, y, z).
Nếu vector N⃗ cùng hướng với n⃗ thì ∫∫ ∫∫ ∫∫ Pdydz + Qdzdx + Rdxdy = F · dS = (F · n) dS S S S ` ˛¸ x ` ˛¸ x ` ˛¸ x
∫∫ ký hiệu tp mặt loại II ký h iệu tp mặt lo ại I ký hiệu tp mặt loại I :=
(P cos α + Q cos β + R cos γ) dS S ` ˛ ¸ x ∫ ∫ tp mặ t loại I A B C = P √ + Q√ + R√ dS A2 A2 A2 ` + B2 + C2 + B2 + C2 + B2 + C2 S ˛ ¸ x ∫ ∫ tp mặ t loại I A √ = P √ + Q√ B + R√ C A2 + B2 + C2dudv A2 + B2 + C2 A2 + B2 + C2 A2 + B2 + C2 D ` ˛ ¸ x ∫ ∫ tích p h â n kép = (PA + QB + RC) dudv D ` ˛ ¸ x tích p h â n kép
Nếu vector N⃗ ngược hướng với n⃗ thì ∫∫ ∫∫ Pdydz + Qdzdx + Rdxdy = − (PA + QB + RC) dudv. S D
Các trường hợp đặc biệt
1. z = z(x, y), (x, y) ∈ DxOy ⊂ R2. Khi đó chọn u = x, v = y ta có phương trình tham số của S
r(u, v) = r(x, y) = (x, y, z(x, y)), (x, y) ∈ DxOy. Ta có
ru(u, v) = rx(x, y) = (1, 0, zx(x, y))
rv(u, v) = ry(x, y) = (0, 1, zy(x, y)) Khi đó vector pháp tuyến i j k N⃗
= rx(x, y) × ry(x, y) = 1 0 z
= −zxi − zyj + k. x(x, y) 0 1 zy(x, y)
Tích vô hướng N⃗ · k = 1 > 0 nên góc (N⃗, Oz) là góc nhọn nên N⃗ là vector pháp hướng lên trên. 7 / 16
• Nếu S được định hướng lên trên thì ∫∫ Pdydz + Qdzdx + Rdxdy S ∫∫ = −
[ P(x, y, z(x, y))zx(x, y) − Q(x, y, z(x, y))zy(x, y) + R(x, y, z(x, y)] dxdy. DxOy ∫∫ ∫∫
Đặc biệt nếu P = Q = 0 thì R(x, y, z)dxdy = R(x, y, z(x, y))dxdy. DxOy S
• Nếu S được định hướng xuống dưới thì ∫∫ Pdydz + Qdzdx + Rdxdy S ∫∫ = −
[−P(x, y, z(x, y))zx(x, y) − Q(x, y, z(x, y))zy(x, y) + R(x, y, z(x, y)] dxdy. DxOy ∫∫ ∫∫
Đặc biệt nếu P = Q = 0 thì R(x, y, z)dxdy = − R(x, y, z(x, y))dxdy. DxOy S
2. y = y(x, z), (x, z) ∈ DxOz ⊂ R2 và x = x(y, z), (y, z) ∈ DyOz ⊂ R2. Ta cũng có kết luận tương tự.
Mọi thứ trên đều trở nên vô nghĩa nếu ta không áp dụng vào các ví dụ cụ thể.
1.5 Công thfíc Gauss-Ostrogradsky
ĐịnH LÝ 2. Nếu các hàm P(x, y, z), Q(x, y, z), R(x, y, z) liên tục và tất cả các đạo hàm
riêng cấp 1 của chúng cũng liên tục trong miền V thì ∫∫ ∫∫∫ ∂P ∂Q ∂R Pdydz + Qdxdz + Rdxdy = + + dxdydz ∂x ∂y ∂z S V
trong đó mặt S được định hướng theo pháp tuyến ngoài.
Dạng vector của công thức Ostrograksky ∫∫ ∫∫∫ F · dS = (∇ · F) dV , S V
với F (x, y, z) = P (x, y, z) ,Q (x, y, z) ,R (x, y, z) . Ta có các công thức tính thể tích sau: ∫∫ ∫∫ ∫∫ ∫∫∫ V = xdydz = ydxdz = zdxdy = dxdydz S S S V 1.6 Công thfíc Stokes
ĐịnH LÝ 3. Cho S là mặt trơn với biên là đường cong đóng C và
F (x, y, z) = P (x, y, z) , Q (x, y, z) , R (x, y, z) 8 / 16 Khi đó I ∫∫ ∫∫ F · dr = (∇ × F) · dS = (∇ × F) · ndS, C S S trong đó i j k ∂R ∂Q ∂P ∂R ∂Q ∂P ∇ × ∂ ∂ ∂ − F= = − − ∂x ∂y ∂z i + ∂y ∂z ∂z ∂x j + ∂x ∂y k P Q R
là curl của trường vector F. Hướng của đường cong và hướng của mặt được xác định theo quy tắc bàn tay phải.
Dạng viết khác của công thức Stokes I ∫∫ ∂R ∂P ∂Q Pdx + Qdy + Rdz = − ∂Q dydz+ − ∂R dzdx+ − ∂P dxdy. ∂y ∂z ∂z ∂x ∂x ∂y C S
Hình 5: Định lý Stokes và quy tắc bàn tay phải 2 Bài tập áp dụng ∫∫ CÂU 1. Tính
x2dS trong đó S là mặt cầu đơn vị x2 + y2 + z2 = 1. S ĐS: 4π . 3 ∫∫ CÂU 2. Tính
ydS trong đó S là mặt cầu đơn vị z = x + y2, 0 ≤ x ≤ 1, 0 ≤ y ≤ 2. S
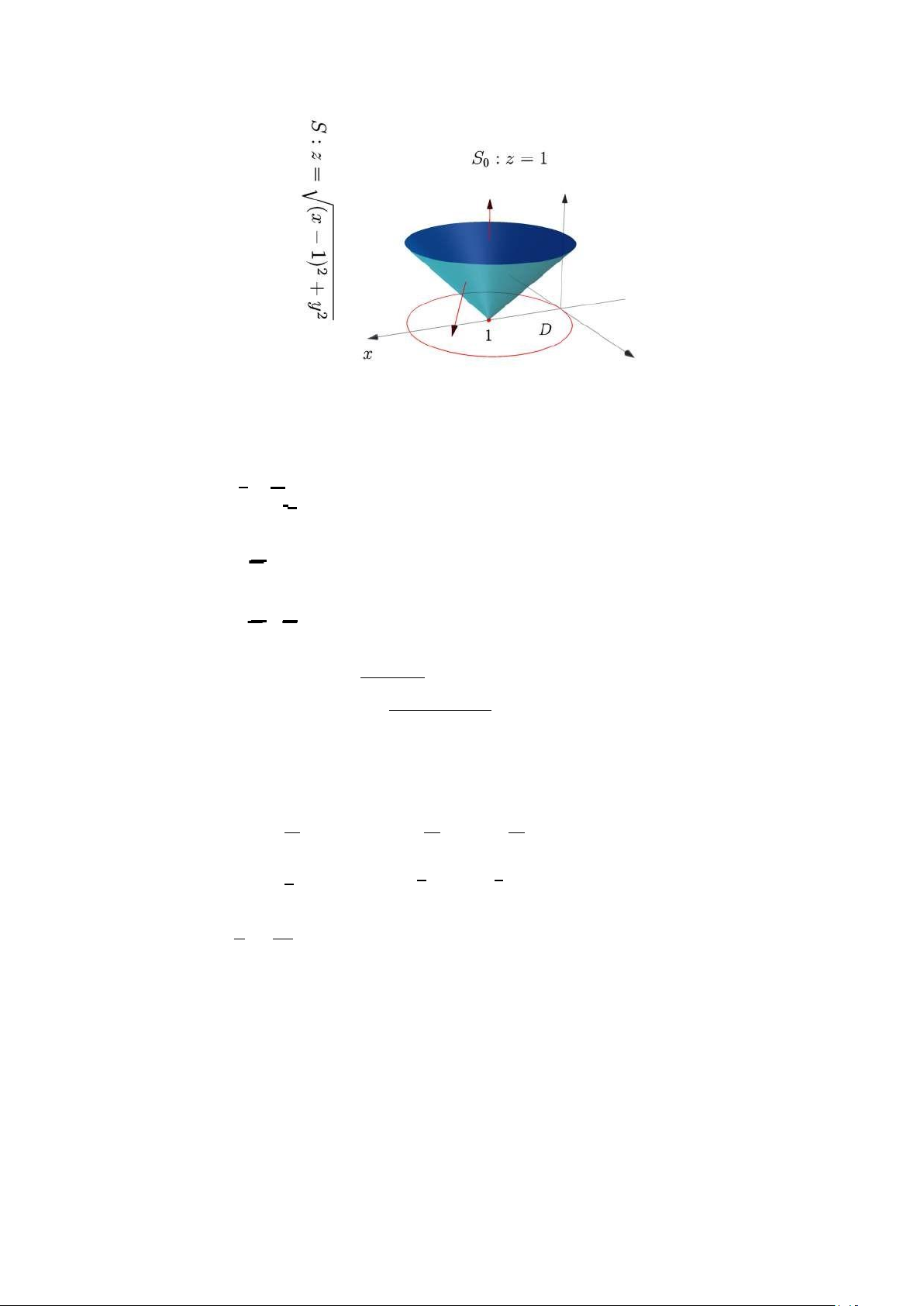
CÂU 3. Tính tích phân mặt loại hai sau ∫∫ I = zdxdy + (x − 1)2dydz S √ trong đó S là mặt z =
(x − 1)2 + y2 nằm trong mặt trụ (x − 1)2 + y2 = 1 lấy phía trên (theo hướng Oz). 9 / 16
Lời giải. Hình chiếu D của S lên mặt phẳng xOy có dạng
D = {(x, y) ∈ R2 : (x − 1)2 + y2 ≤ 1}. √
Phương trình mặt S có công thức z = (x − 1)2 + y2 và vector pháp tuyến !
N = (−z′ , −z′ , 1) = −√ (x − 1) y x y , −√ , 1 (x − 1)2 + y2 (x − 1)2 + y2
có hướng đi lên theo trục Oz (vì tích vô hướng N · k = 1 > 0 nên góc tạo bởi pháp tuyến
N và Oz là góc nhọn) nên ta có ∫∫ ∫∫ I zdxdy + (x − 1)2dydz = =
(x − 1)2dydz + `˛0¸xdzdx + `˛z¸xdxdy S S ` ˛ ¸ x Q R ∫∫ P √ ∫∫ 3 2 2 (x − 1)3 −(x − 1) + (x − 1) + y 2 2 = −√ + 0 + √ (x − 1) + y dxdy = dxdy. D (x − 1)2 + y2 D (x − 1)2 + y2
Đổi biến tọa độ cực (suy rộng) x = r cos φ + 1, y = r sin φ, khi đó φ ∈ [0, 2π), r ∈ [0, 1] và Jacobian J = r. Ta có ∫ ∫ ∫ 2π ∫ 2π 1 1 I −r3 cos3 φ + r2 rdr dφ − 3 r 3 2 = dφ = cos φ + r dr r 0 0 0 0 ∫ 1 2π −r4 cos3 φ r3 ∫ 2π − = + dφ = cos3 φ + 1dφ 0 4 3 0 0 4 3 ∫ ∫ ∫ ∫ 2π − cos3 φ 2π dφ 2π 2π + 1 dφ = (sin2 φ − 1) d sin φ + 1 dφ = 0 4 0 3 0 4 0 3 2π sin3 φ sin φ 2π φ 2π = − + = . 12 4 0 3 0 3
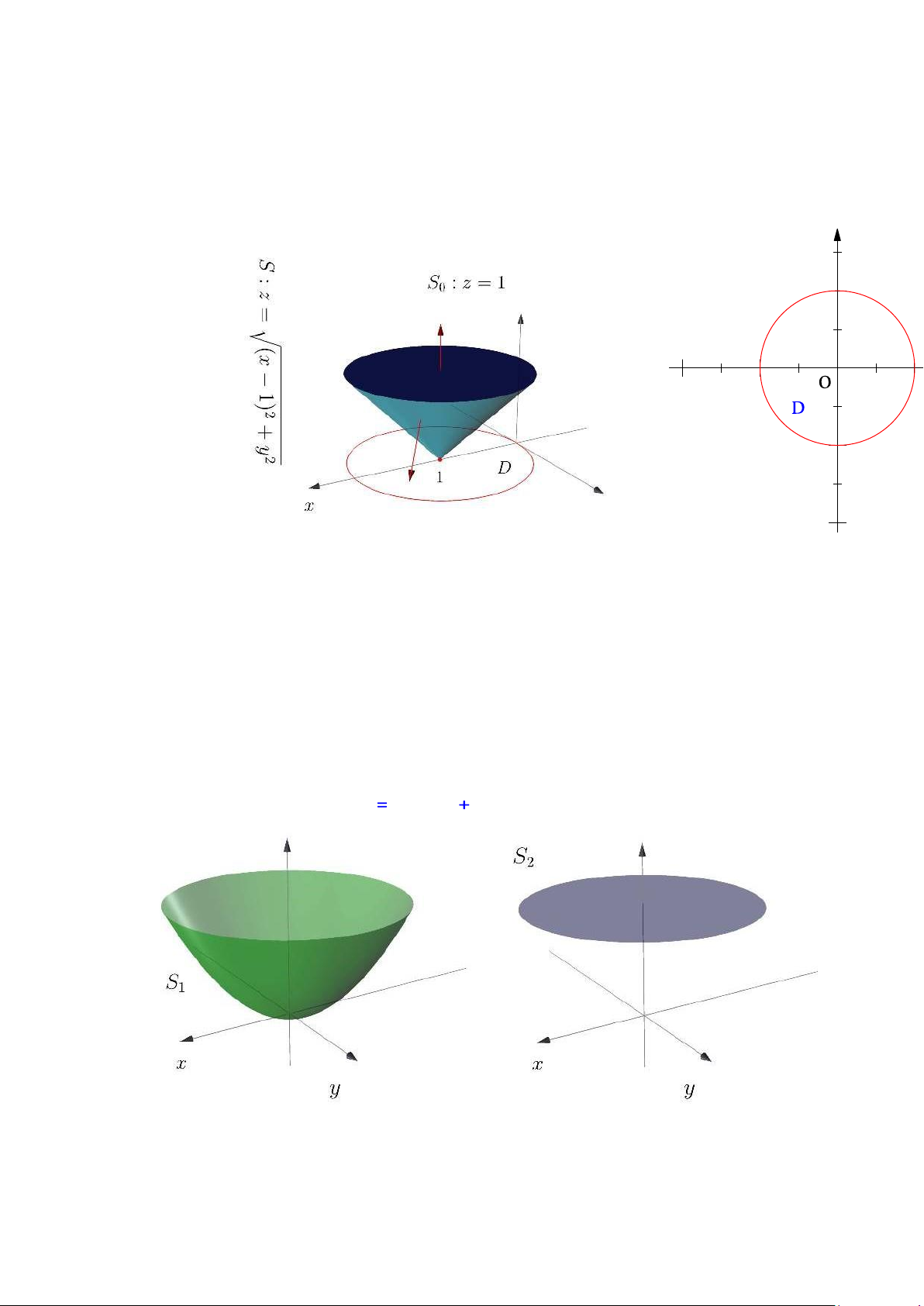
Cách hai dùng công thức Gauss-Ostrogradsky, ta dùng một đĩa tròn đơn vị trong mặt
phẳng z = 1 đạy kín mặt nón, ký hiệu là S0. 10 / 16 Khi đó ta có ∫∫ I =
(x − 1)2dydz + `˛0¸xdzdx + `˛z¸xdxdy ¸ S ` ˛ x Q R P ∫∫ ∫∫∫ = (x − 1)2dydz + divFdxdydz `˛0¸xdzdx + `˛z¸xdxdy − S+ ` ˛¸ x 0 E P Q R ∫∫ ∫∫∫ =
(x − 1)2dydz + `˛0¸xdzdx + `˛z¸xdxdy − 2(x − 1) + 1dxdydz S+ ` ˛¸ x 0 Q R E ∫∫ P ∫∫ ∫ 1 = dxdy − √ 2x − 1dzdxdy (x−1)2+y2 D D ∫∫ √ = π −
(2x − 1)(1 − (x − 1)2 + y2dxdy ∫ D ∫ 2π 1 = π − dφ (2r cos φ + 1)(1 − r)rdr 0 0 ∫ 2π r3 r4 r2 1 = π − (2 cos φ − 1) − cos φ + dφ 0 3 4 2 0 ∫ 2π 1 1 1 = π — (2 cos φ − 1) − cos φ + dφ 0 3 4 2 π 2π = π − = . 3 3 ■ ∫∫ CÂU 4. Tính
x3dydz + y3dxdz + z3dxdy, trong đó S là mặt cầu x2 + y2 + z2 = a2. S
được định hướng theo pháp tuyến ngoài. 11 / 16 n −n 0 Lời giải.
Áp dụng định lý Ostrogradsky ta có ∫∫ ∫∫∫ I = x3dydz + y3dxdz + z3dxdy = 3x2 + 3y2 + 3z2 dxdydz S ∫∫∫ V = 3 x2 + y2 + z2 dxdydz V
Đổi biến tọa độ cầu ta có: ∫∫∫ ∫∫∫ I = 3 x2 + y2 + z2 dxdydz = 3 r2 · r2 sin θdrdψdθ V V ∫ 2π ∫ π ∫ a = 3 dψ sin θdθ r4dr 0 0 0 π r5 a 12πa5
= 3 · 2π · [ (− cos θ)|0 ] · = . 5 0 5 ■ ∫∫ CÂU 5. Tính
2xdydz+ (3y + x) dxdz+ (2y + 4z) dxdy, trong đó S là mặt ngoài của S hình tứ diện x y z ≤ a + b + c 1, x ≥ 0, y ≥ 0, z ≥ 0.
Lời giải. Sử dụng định lý Ostrogradsky ∫∫ ∫∫∫
2xdydz + (3y + x) dxdz+ (2y + 4z) dxdy = (2 + 3 + 4) dxdydz S V ∫∫∫ = 9 dxdydz. V 12 / 16 Ta có a b(1− x ) c(1− x − y ) a b(1− x ) ∫∫∫ ∫ ∫ a ∫a b ∫ ∫ a x y dxdydz = dx dy dz = dx c 1 − − dy a b V 0 0 0 0 0 ∫a # h x x x 2 1 − = bc 1 − 1 − a dx — a a 2 0 ∫ bc a bc ∫a = (a − x)2dx = a2 − 2ax + x2 dx 2a2 2a2 0 0 bc x3 a = a2x − ax2 + 2a2 3 0 bc a3 abc 3 3 = a − a = . 2a2 + 3 6 ■
CÂU 6 (ĐỀ THI CÁC NĂM). Tính tích phân ∫∫ I = z2dxdy, S
trong đó S là mặt nón z2 = x2 + y2 nằm trong miền x ≤ 0, y ≥ 0, 0 ≤ z ≤ 1, lấy phía trên theo hướng 0z. ĐS: π/8. CÂU 7. Tính tích phân ∫∫ zdxdy, I = S
trong đó S là mặt paraboloid z = 1 − x2 − y2 nằm trong miền x ≤ 0, y ≥ 0, z ≥ 0, lấy phía trên theo hướng Oz. ĐS: π/8. 13 / 16
CÂU 8 (ĐỀ THI CÁC NĂM). Tính tích phân ∫∫ I = x3dydz + (x + y3)dzdx, S
trong đó S biên phía ngoài của vật thể ∆ được giới hạn bởi các mặt z = x2 + y2, z = 1 . y −2 −1 −1 Lời giải. −2 Cách 1. Tính trực tiếp I = I1 + I2 trong đó ∫∫ I1 = x3dydz + (x + y3)dzdx S1
trong đó S1 là phần mặt z = x2 + y2 nằm dưới mặt phẳng z = 1 như hình vẽ lấy dưới và ∫∫ I2 = x3dydz + (x + y3)dzdx S2
trong đó S2 là phần mặt phẳng z 1 với x2 y2 ≤ 1 như hình vẽ lấy hướng phía trên.
Mặt S1 có vector pháp tuyến hướng xuống dưới dạng
n = (z′ , z′ , −1) = (2x, 2y, −1). x y 14 / 16 Khi đó ∫∫ I1 = x3dydz + (x + y3)dzdx + 0dydx ∫∫ S1 =
x3 × 2x + (x + y3)2y + 0 × (−1)dxdy D
trong đó D là hình chiếu của S1 lên mặt phẳng xOy:
D = {(x, y) ∈ R2 : x2 + y2 ≤ 1}. ■ Từ đó ∫∫ ∫∫ ∫∫ I x4 1 = 2x4 + 2xy + 2y4dxdy = 2 + xy + y4dxdy = 2 (x2 + y2)2 − 2x2y2 + xydxdy ∫ D ∫ D D 2π 1 = 2 dφ
r4 − 2r4 cos2 φ sin2 φ + r2 cos φ sin φ rdr ∫ 0 0 ∫ 2π 1 = 2 dφ
r5 − 2r5 cos2 φ sin2 φ + r3 cos φ sin φ dr 0 0 ∫ 1 2π 6 r r6 r4 = 2 — 2 cos2 φ sin2 φ + cos φ sin φ dφ 0 6 6 4 ∫ 0 2π 1 2 1 cos2 φ sin2 φ + cos φ sin φ dφ = — 3 3 2 ∫ 0 2π 1 sin 2φ = − 1 − cos 4x + dφ 12 4 0 3 ∫ 2π π 1 cos 4x = + + sin 2φ dφ = . 0 4 12 4 2
Mặt S2 có vector pháp tuyến hướng lên trên dạng
n = (−z′ , −z′ , 1) = (0, 0, 1). x y Khi đó ∫∫ I x3dydz 2 = + (x + y3)dzdx + 0dydx ∫∫ S1 =
x3 × 0 + (x + y3) × 0 + 0 × 1dxdy = 0 D
trong đó D là hình chiếu của S2 lên mặt phẳng xOy có phương trình như ở trên. Vậy π π I = I1 + I2 = + 0 = . 2 2
Cách 2 đây là miền kín nên có thể dụng công thức Gauss-Ostrogradsky: ∫∫ ∫∫∫ ∂P ∂Q ∂R Pdydz + Qdxdz + Rdxdy = + + dxdydz. ∂x ∂y ∂z S V 15 / 16 Ta có ∫∫ I = x3dydz + (x + y3)dzdx + 0dydx S ∫∫∫ ∫∫∫ = 3x2 + 3y2 + 0dxdydz = 3(x2 + y2)dxdydz ∆ ∆
trong đó ∆ được cho bởi
∆ = {(x, y, z) ∈ R3 : (x, y) ∈ D, x2 + y2 ≤ z ≤ 1}
với D như ở phần trên. Ta có ∫∫∫ ∫∫ ∫ 1 I = 3(x2 + y2)dxdydz = dxdy 3(x2 + y2)dz ∆ D x2+y2 ∫∫ =
3(x2 + y2)(1 − x2 − y2)dxdy (tọa độ cực) ∫ D ∫ ∫ ∫ 2π 1 2π 1 = dφ 3r2(1— r2)rdr = dφ × 3r3 − 3r5dr 0 0 0 0 3r4 3r6 1 3 3 π = 2π × − = 2π − = . 4 6 4 6 2 0 16 / 16
Tài liệu liên quan:
-
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng
35 18 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
41 21 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
39 20 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
36 18 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
43 22