Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Vídụ1.1.Tính∬𝑧(𝑥2+𝑦2)d𝑥d𝑦trongđó𝑆lànửamặtcầu
𝑦2+𝑧2=3,𝑧≥0,hướngcủa𝑆làphíangoàimặtcầu.Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Tài liệu gồm 20 trang , giúp bạn tham khảo, ôn tập và đạt kết quả cao
Môn: Giải tích 2(GT2101) 46 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 1.7 K tài liệu
Tác giả:
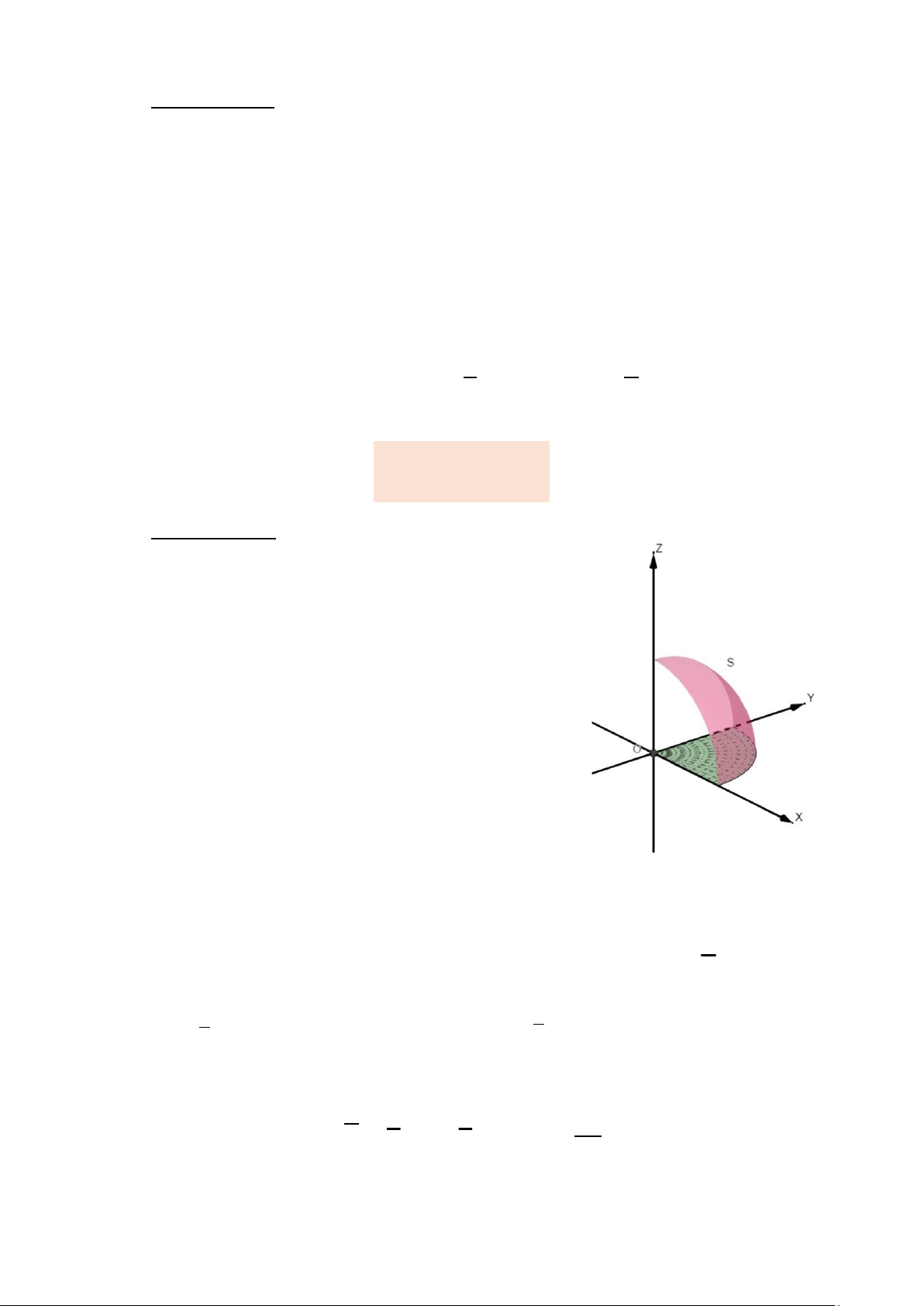
Preview text:
EUREKA! UNI – YOUTUBE GIẢI TÍCH 2
CHƯƠNG 3. TÍCH PHÂN MẶT
Đạo diễn: Hoàng Bá Mạnh
Tài liệu tham khảo
1. Bùi Xuân Diệu (2017). Bài giảng Giải tích II. Cập nhật 2017. Viện Toán ứng dụng và Tin học. ĐH BKHN.
2. Nguyễn Đình Trí, Tạ Văn Dĩnh, Nguyễn Hồ Quỳnh (2006). Giáo trình Toán học cao cấp tập
III. Tái bản lần 10. NXB Giáo Dục. Free Video Playlists 1. ĐẠI SỐ: https://tinyurl.com/DaiSoFull 2. GIẢI TÍCH 1:
https://tinyurl.com/GiaiTich1Full 3. GIẢI TÍCH:
https://tinyurl.com/GiaiTichFull 4. GIẢI TÍCH 2:
https://tinyurl.com/GiaiTich2Full 5. TOÁN CAO CẤP NEU:
https://tinyurl.com/ToanCaoCapNEU
6. XÁC SUẤT & THỐNG KÊ:
https://eureka-uni.tiny.us/XSTKFull 7. KINH TẾ LƯỢNG:
https://eureka-uni.tiny.us/KinhTeLuongFull
8. KINH TẾ LƯỢNG NÂNG CAO: https://tinyurl.com/KinhTeLuongNangCao DONATE cho Eureka! Uni
* Vietinbank: 107006662834 - Hoang Ba Manh * Ví Momo: 0986.960.312 1
3.4. TÍCH PHÂN MẶT LOẠI II
3.4.1 Tóm tắt công thức
Mặt định hướng (mặt 2 phía)
Mặt không định hướng Kí hiệu
𝐼 = �𝑃(𝑥, 𝑦, 𝑧)d𝑦d𝑧 + 𝑄𝑄(𝑥, 𝑦, 𝑧)d𝑧d𝑥 + 𝑅(𝑥, 𝑦, 𝑧)d𝑥d𝑦 𝑆 Cách tính
1) Đưa về tích phân bội 2 S: 𝐹(𝑥, 𝑦, 𝑧) = 0
𝐼 = �𝑃(𝑥, 𝑦, 𝑧)d𝑦d𝑧 + �𝑄𝑄(𝑥, 𝑦, 𝑧)d𝑧d𝑥 + �𝑅(𝑥, 𝑦, 𝑧)d𝑥d𝑦 𝑆 𝑆 𝑆 = 𝐼1 + 𝐼2 + 𝐼3 Tính
𝐼3 = �𝑅(𝑥, 𝑦, 𝑧)d𝑥d𝑦 𝑆 𝑆: 𝑧 = 𝑧(𝑥, 𝑦)
𝐷𝐷 là hình chiếu của 𝑆 lên mặt 𝑧 = 0. 2
Hướng đã chọn tạo với tia Oz một góc nhọn/tù:
𝐼3 = ± � 𝑅(𝑥, 𝑦, 𝑧(𝑥, 𝑦))d𝑥d𝑦 𝐷
Tương tự với 𝐼1, 𝐼2.
2) Công thức Ostrogradsky – đưa về tích phân bội 3
𝑃, 𝑄𝑄, 𝑅 là các hàm khả vi, liên tục trên miền 𝑉 ⊂ ℝ3 giới hạn bởi mặt cong kín 𝑆.
�𝑃(𝑥, 𝑦, 𝑧)d𝑦d𝑧 + 𝑄𝑄(𝑥, 𝑦, 𝑧)d𝑧d𝑥 + 𝑅(𝑥, 𝑦, 𝑧)d𝑥d𝑦 𝑆
= �(𝑃′ + 𝑄𝑄′ + 𝑅′ )d𝑥d𝑦d𝑧 𝑥 𝑦 𝑧 𝑉
Tích phân bội 3 lấy theo hướng pháp tuyến ngoài. 3
3.4.2. Bài tập vận dụng
3.4.2.1. Tính theo tích phân bội 2
Ví dụ 1.1. Tính ∬ 𝑧(𝑥2 + 𝑦2)d𝑥d𝑦 trong đó 𝑆 là nửa mặt cầu 𝑥2 + 𝑆
𝑦2 + 𝑧2 = 3, 𝑧 ≥ 0, hướng của 𝑆 là phía ngoài mặt cầu.
Ví dụ 1.2. Tính ∬ 𝑦d𝑥d𝑧 + 𝑧2d𝑥d𝑦 trong đó 𝑆 là phía ngoài mặt 𝑥2 + 𝑆 𝑦2 𝑧2 +
= 1, 𝑧 ≥ 0, 𝑦 ≥ 0, 𝑥 ≥ 0. 4 9
Ví dụ 1.3. Tính ∬ 𝑥2𝑦2𝑧d𝑥d𝑦 trong đó 𝑆 là mặt trên của nửa mặt cầu 𝑆
𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑧 ≤ 0.
Ví dụ 1.4. Tính ∬ 𝑥𝑦𝑧d𝑥d𝑦 trong đó 𝑆 là mặt ngoài của phần hình cầu 𝑆
xác định bởi 𝑥2 + 𝑦2 + 𝑧2 = 2, 𝑥 ≥ 0, 𝑦 ≥ 0.
Ví dụ 1.5. Tính ∬ 𝑥d𝑦d𝑧 + d𝑧d𝑥 + 𝑥𝑧2d𝑥d𝑦 trong đó 𝑆 là mặt ngoài 𝑆
của phần hình cầu xác định bởi 𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0.
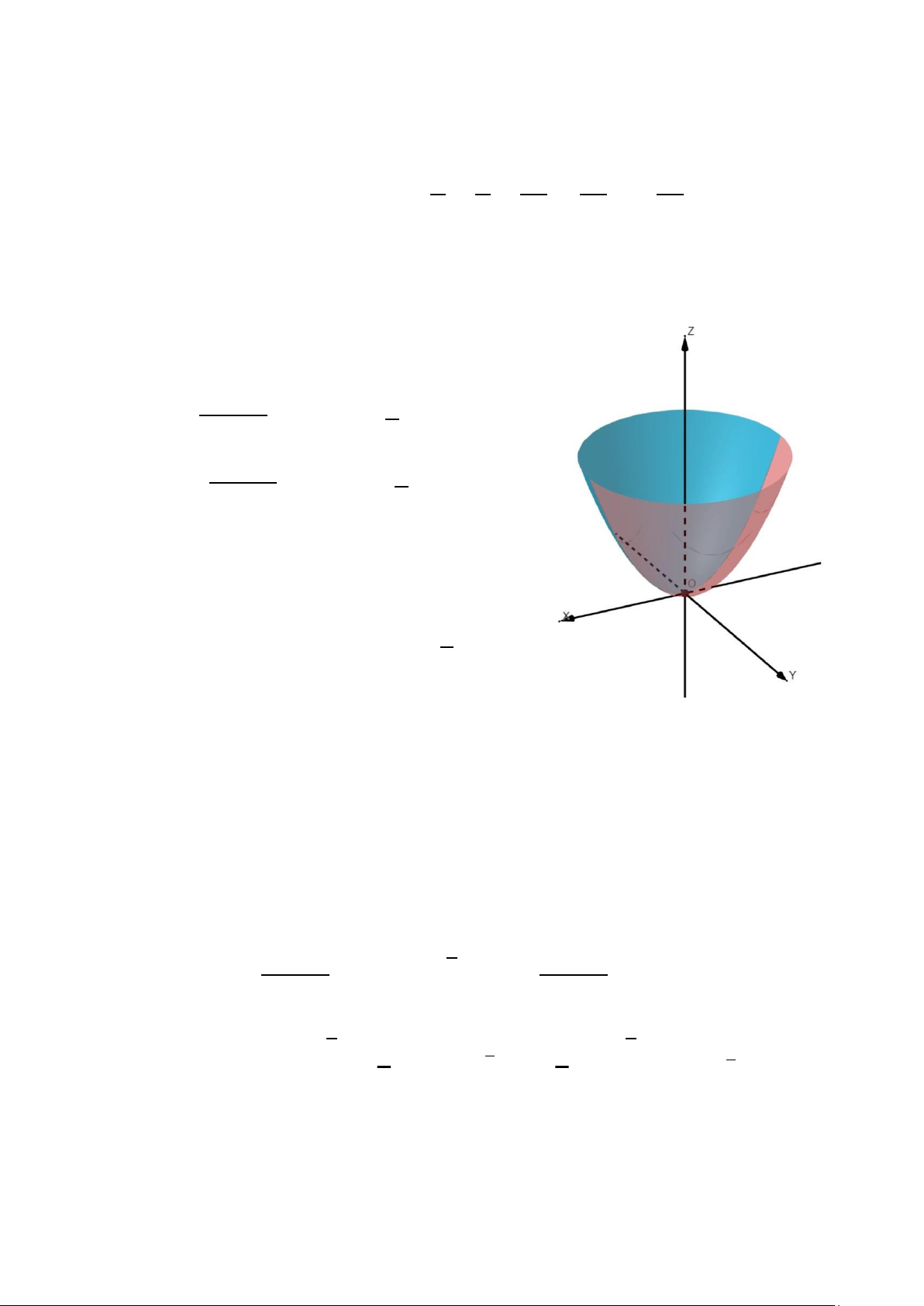
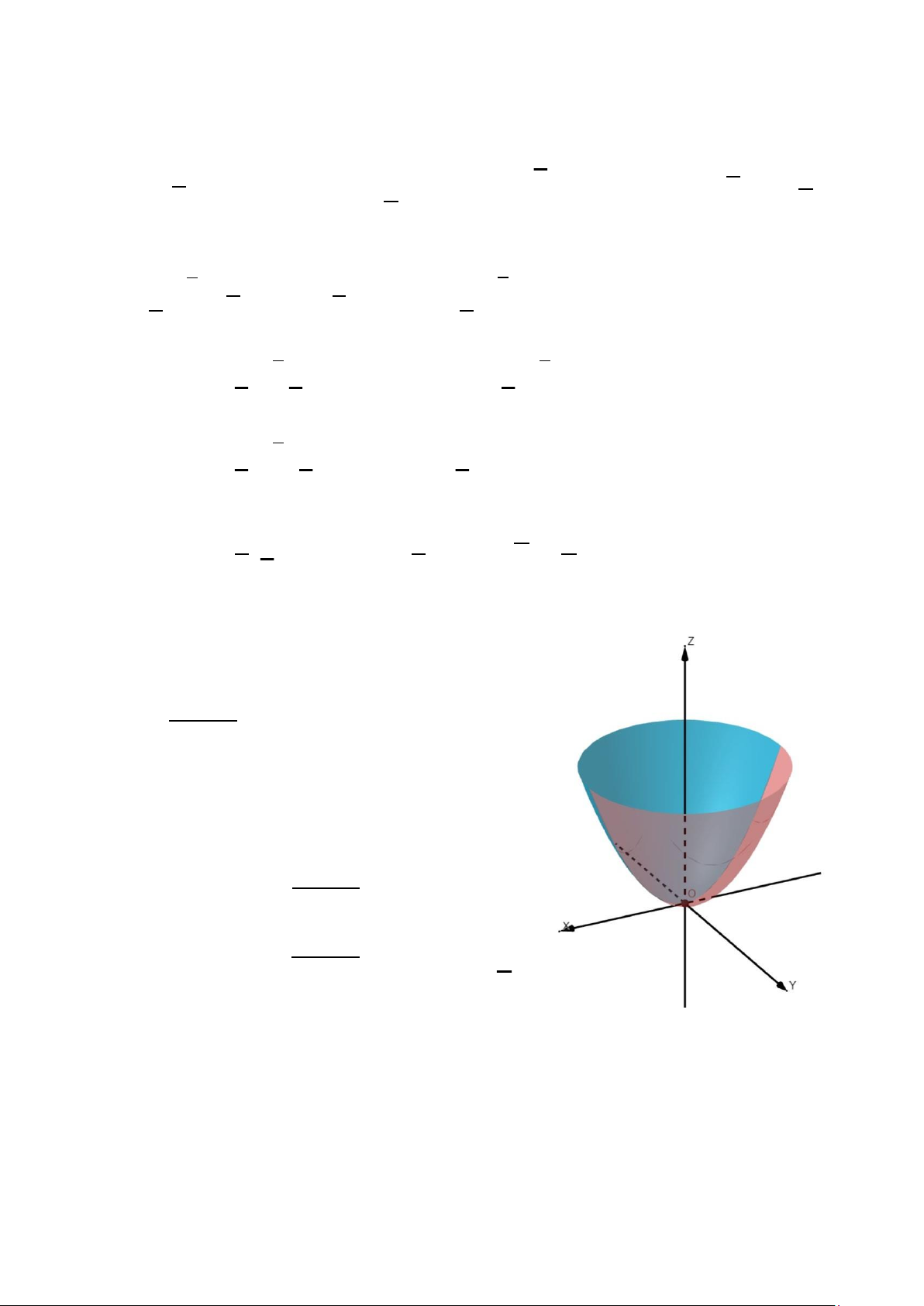
Ví dụ 1.6. Tính tích phân mặt ∬ 𝑦d𝑧d𝑥, trong đó 𝑆 là phía ngoài của 𝑆
mặt Paraboloid 𝑧 = 𝑥2 + 𝑦2 (0 ≤ 𝑧 ≤ 2).
Toán cao cấp - Eureka! Uni | Facebook
Xác suất Thống kê - Eureka! Uni | Facebook 4
Ví dụ 1.1. Tính ∬ 𝑧(𝑥2 + 𝑦2)d𝑥d𝑦 trong đó 𝑆 là nửa mặt cầu 𝑥2 + 𝑦2 +
𝑧2 = 3, 𝑧 ≥ 0, hướng của 𝑆 là phía ngoài mặt cầu. Giải
𝑧 ≥ 0 ⇒ 𝑧 = √3 − 𝑥2 − 𝑦2
Hình chiếu của 𝑆 lên mặt 𝑧 = 0 là D ròn tâm O bán kính √3. 𝑥2 + 𝑦2 ≤ 3
Hướng đã chọn tạo với tia Oz một góc nhọn, vì vậy:
𝐼 = �𝑧(𝑥2 + 𝑦2)d𝑥d𝑦 = � (𝑥2 + 𝑦2)√3 − (𝑥2 + 𝑦2)d𝑥d𝑦 𝑆 𝐷
Chuyển sang tọa độ cực 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ √3, 0 ≤ 𝜑 ≤ 2𝜋, 𝐽 = 𝑟 √3 2𝜋 √3 2𝜋 𝐼 = �
d𝑟 � 𝑟2√3 − 𝑟2𝑟d𝜑 = �
𝑟2√3 − 𝑟2𝑟d𝑟 � d𝜑 0 0 0 0 √3 = 2𝜋 � 𝑟2√3 − 𝑟2𝑟d𝑟 0 Đặt 0
𝑡 = √3 − 𝑟2 ⇒ 𝑟2 = 3 − 𝑡2, 𝑟d𝑟 = −𝑡d𝑡, 𝑟 �√3 ⇒ 𝑡 � 0 √3 5 0 √3
⇒ 𝐼 = 2𝜋 � (3 − 𝑡2)𝑡(−𝑡d𝑡) = 2𝜋 � (3𝑡2 − 𝑡4)d𝑡 √3 0 1 3 5 √3 1 12√3 = 2𝜋 (𝑡 − 𝑡 ) � = 2𝜋 (3√3 − 9√3) = 𝜋 5 0 5 5
Ví dụ 1.2. Tính ∬ 𝑦d𝑥d𝑧 + 𝑧2d𝑥d𝑦 trong đó 𝑆 là phía ngoài mặt 𝑥2 + 𝑦2 𝑧2 +
= 1, 𝑧 ≥ 0, 𝑦 ≥ 0, 𝑥 ≥ 0. 9 Giải
𝐼 = �𝑦d𝑥d𝑧 + 𝑧2d𝑥d𝑦 𝑆
= �𝑦d𝑥d𝑧 + �𝑧2d𝑥d𝑦 = 𝐼1 + 𝐼2 𝑆 𝑆 𝐼1 = �𝑦d𝑥d𝑧 𝑆 1
𝑦 ≥ 0 ⇒ 𝑦 = 2�1 − 𝑥2 − 𝑧2 9
Hình chiếu của 𝑆 lên mặt 𝑦 = 0 là miền 𝐷𝐷𝑦 có phương trình: 1 𝑥2 + 𝑧2 ≤ 1, 𝑥 ≥ 0, 𝑧 ≥ 0 9
Hướng đã chọn tạo với Oy góc nhọn nên: 1
𝐼1 = � 2�1 − 𝑥2 − 𝑧2 d𝑧d𝑥 9 𝐷𝑦
Toán cao cấp - Eureka! Uni | Facebook
Xác suất Thống kê - Eureka! Uni | Facebook 6 Đổi biến 𝜋 𝑥 = 𝑟 cos 𝜑 , 𝑧 = 3𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ 2 𝑥′ 𝑟 𝑥′ 𝜑 𝐽 = � � = 3𝑟 𝑧′ 𝑧′ 𝑟 𝜑 𝜋 1 1 1 2
𝐼1 = � d𝜑 � 2 √1 − 𝑟 23𝑟d𝑟 = −2𝜋 × 3 � (1 − 𝑟 2)2d(1 − 𝑟2) 0 0 0 2 3 2 1
= −6𝜋 × (1 − 𝑟 )2 � = 4𝜋 3 0
𝑑(1 − 𝑟2) = (1 − 𝑟2)′𝑑𝑟 = −2𝑟𝑑𝑟 𝐼2 = �𝑧2d𝑥d𝑦 𝑆 1
𝑧 ≥ 0 ⇒ 𝑧 = 3�1 − 𝑥2 − 𝑦2 4
Hình chiếu của 𝑆 lên mặt 𝑧 = 0 là miền 𝐷𝐷𝑧 có phương trình: 1 𝑥2 + 𝑦2 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0 4
Hướng đã chọn tạo với Oz góc nhọn nên: 1 2 2 𝐼 − 𝑦 2 = � 9 (1 − 𝑥 ) d𝑧d𝑥 𝐷 4 𝑧 Đổi biến
Xác suất Thống kê - Eurek a! 7 𝜋 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 2𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ , 𝐽 = 2𝑟 2 𝜋 1 1 2 ( 2) 3
𝐼2 = � d𝜑 � 9 1 − 𝑟
2𝑟d𝑟 = 2𝜋 × 18 � (𝑟 − 𝑟 )d𝑟 0 0 0 1 1 1
= 36𝜋 ( 𝑟2 − 𝑟4) � = 9𝜋 2 4 0
Vậy 𝐼 = 𝐼1 + 𝐼2 = 4𝜋 + 9𝜋 = 13𝜋
Ví dụ 1.3. Tính ∬ 𝑥2𝑦2𝑧d𝑥d𝑦 trong đó 𝑆 là mặt trên của nửa mặt cầu
𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑧 ≤ 0. Giải
Hình chiếu của 𝑆 lên mặt 𝑧 = 0 là
Hướng đã chọn tạo với 𝑂𝑂𝑧 góc nhọn nên
𝐼 = �𝑥2𝑦2𝑧d𝑥d𝑦 = � 𝑥2𝑦2 (−√1 − 𝑥2 − 𝑦2) d𝑥d𝑦 𝑆 𝐷
= − � 𝑥2𝑦2√1 − 𝑥2 − 𝑦2d𝑥d𝑦 𝐷 Đổi sang tọa độ cực 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ 2𝜋, 𝐽 = 𝑟 8 2𝜋 1
𝐼 = − � d𝜑 � 𝑟4 sin2 𝜑 cos2 𝜑 √1 − 𝑟2𝑟d𝑟 0 0 2𝜋 1
= − � sin2 𝜑 cos2 𝜑 d𝜑 � 𝑟4√1 − 𝑟2𝑟d𝑟 0 0 2𝜋 1 2𝜋 1 2𝜋
𝐼1 = � sin2 𝜑 cos2 𝜑 d𝜑 = � sin2 2𝜑 d𝜑 = � (1 − cos 4𝜑)d𝜑 0 4 0 8 0 1 1 2𝜋 𝜋 = (𝜑 − sin 4𝜑) � = 8 4 0 4 1
sin 2𝑎 = 2 sin 𝑎 cos 𝑎 , sin2 𝑎 = (1 − cos 2𝑎) 2 1
𝐼2 = � 𝑟4√1 − 𝑟2𝑟d𝑟 0 1 0
Đặt √1 − 𝑟2 = 𝑡 ⇒ 𝑟2 = 1 − 𝑡2, 𝑟d𝑟 = −𝑡d𝑡, 𝑟 � ⇒ 𝑡 � 0 1 0 1
𝐼2 = � (1 − 𝑡2)2𝑡(−𝑡d𝑡) = � (𝑡2 − 2𝑡4 + 𝑡6)d𝑡 1 0 1 2 = 3 5 1 7 1 8
( 𝑡 − 𝑡 + 𝑡 ) � = 3 5 7 0 105 𝜋 8 2𝜋
⇒ 𝐼 = −𝐼1𝐼2 = − × = − 4 105 105
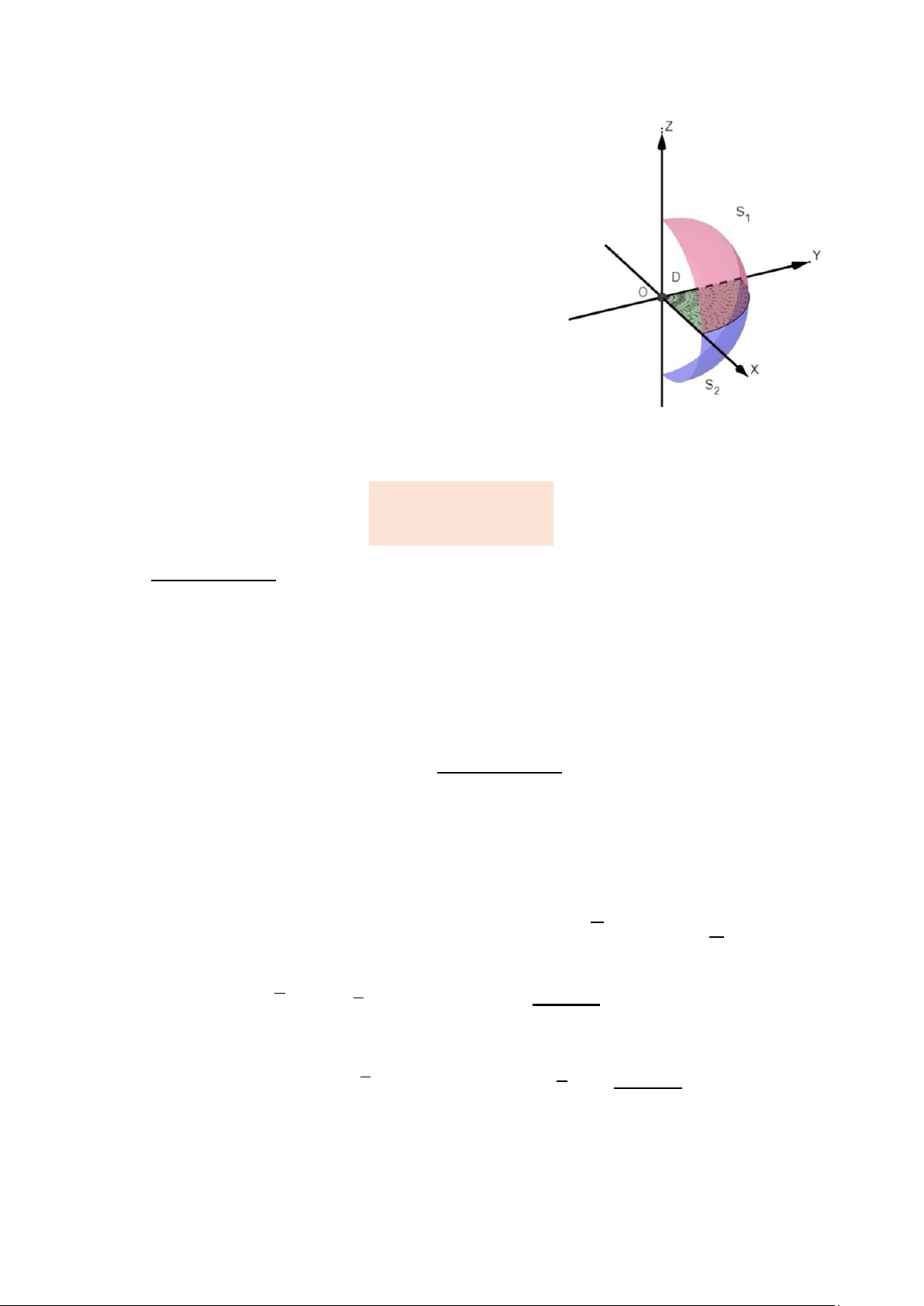
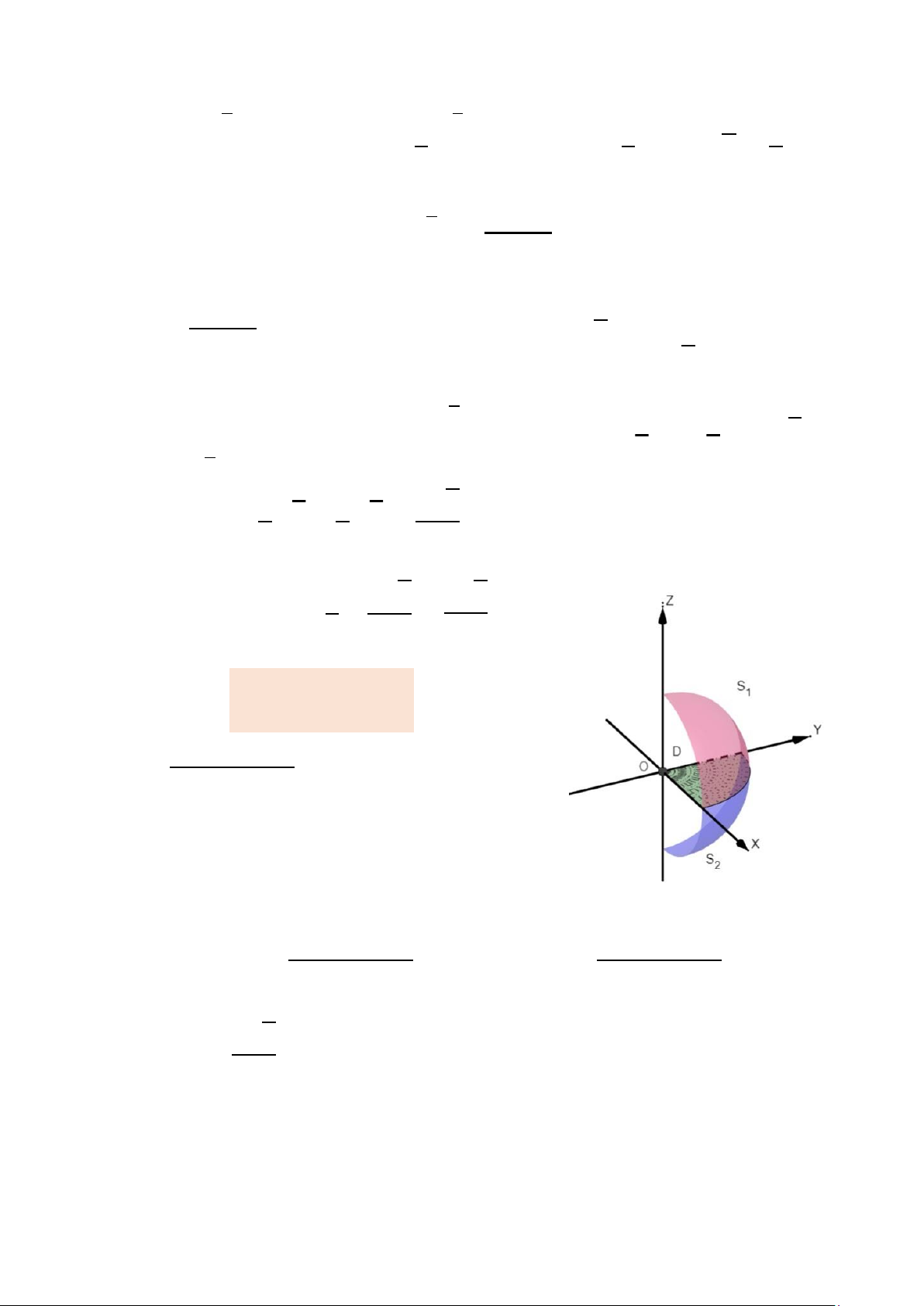
Ví dụ 1.4. Tính ∬ 𝑥𝑦𝑧d𝑥d𝑦 trong đó 𝑆 là mặt ngoài của phần hình cầu 𝑆
xác định bởi 𝑥2 + 𝑦2 + 𝑧2 = 2, 𝑥 ≥ 0, 𝑦 ≥ 0. 9
Mặt phẳng 𝑧 = 0 cắt 𝑆 thành 2 nửa:
𝑆1 (𝑥2 + 𝑦2 + 𝑧2 = 2, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0)
𝑆2 (𝑥2 + 𝑦2 + 𝑧2 = 2, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≤ 0)
𝐼 = �𝑥𝑦𝑧d𝑥d𝑦 𝑆
= � 𝑥𝑦𝑧d𝑥d𝑦 + � 𝑥𝑦𝑧d𝑥d𝑦 𝑆1 𝑆2 = 𝐼1 + 𝐼2
𝐼1 = � 𝑥𝑦𝑧d𝑥d𝑦 𝑆1
𝑧 = √2 − 𝑥2 − 𝑦2
Hình chiếu của 𝑆1 lên mặt 𝑧 = 0 là 𝐷𝐷: 𝑥2 + 𝑦2 ≤ 2, 𝑥 ≥ 0, 𝑦 ≥ 0.
Phương đã chọn tạo với 𝑂𝑂𝑧 góc nhọn.
𝐼1 = � 𝑥𝑦√2 − 𝑥2 − 𝑦2d𝑥d𝑦 𝐷 Đổi sang tọa độ cực 𝜋 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ √2, 0 ≤ 𝜑 ≤ , 𝐽 = 𝑟 2 𝜋 √2 2 𝐼1 = � d𝜑 �
𝑟2 cos 𝜑 sin 𝜑 √2 − 𝑟 2𝑟d𝑟 0 0 𝜋 √2 2
= � cos 𝜑 sin 𝜑 d𝜑 �
𝑟 2√2 − 𝑟 2𝑟d𝑟 0 0 10 𝜋 𝜋 𝜋 2 1 2 1 1
𝐼11 = � cos 𝜑 sin 𝜑 d𝜑 = � sin 2𝜑 d𝜑 = − cos 2𝜑 � 2 4 2 = 2 0 0 0 √2
𝐼12 = � 𝑟2√2 − 𝑟2𝑟d𝑟 0 Đặt 0
𝑡 = √2 − 𝑟2 → 𝑟2 = 2 − 𝑡2, 𝑟d𝑟 = 𝑡d𝑡, 𝑟 �√2 ⇒ 𝑡 � 0 √2 0 √2 2 1 √2
𝐼12 = � (2 − 𝑡2)𝑡(−𝑡d𝑡) = �
(2𝑡2 − 𝑡4)d𝑡 = ( 𝑡3 − 𝑡5) � 3 5 √2 0 0 4 4 8√2 = √2 − √2 = 3 5 15 1 8√2 4√2 ⇒ 𝐼 = 1 = 𝐼11𝐼12 = × 2 15 15
𝐼2 = � 𝑥𝑦𝑧d𝑥d𝑦 𝑆2
𝑧 = −√2 − 𝑥2 − 𝑦2
Hình chiếu của 𝑆2 lên mặt 𝑧 = 0 cũng là 𝐷𝐷
Hướng đã chọn tạo với tia 𝑂𝑂𝑧 góc tù.
𝐼2 = − � 𝑥𝑦 (−√2 − 𝑥2 − 𝑦2) d𝑥d𝑦 = � 𝑥𝑦√2 − 𝑥2 − 𝑦2d𝑥d𝑦 = 𝐼1 𝐷 𝐷 4√2 = 15 Vậy 11 8√2 𝐼 = 𝐼1 + 𝐼2 = 15
Ví dụ 1.5. Tính ∬ 𝑥d𝑦d𝑧 + d𝑧d𝑥 + 𝑥𝑧2d𝑥d𝑦 trong đó 𝑆 là mặt ngoài của 𝑆
phần hình cầu xác định bởi 𝑥2 + 𝑦2 + 𝑧2 = 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0. 𝐼1 = �𝑥d𝑦d𝑧 𝑆
𝑥 = √1 − 𝑦2 − 𝑧2
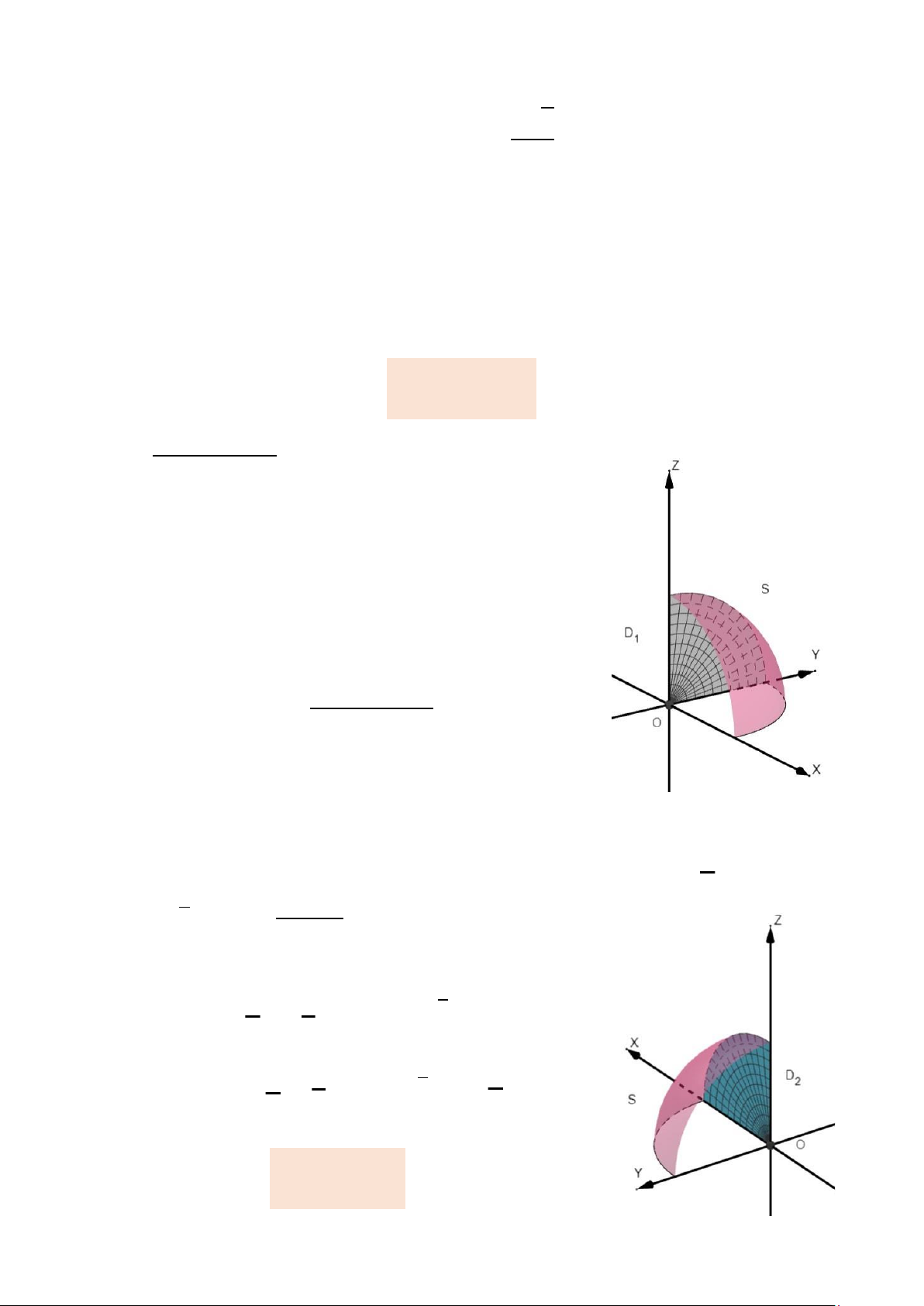
Hình chiếu của 𝑆 xuống mặt 𝑥 = 0 là 𝐷𝐷1 𝑦2 + 𝑧2 ≤ 1, 𝑦 ≥ 0, 𝑧 ≥ 0
Hướng dương đã chọn tạo với tia 𝑂𝑂𝑥 góc nhọn.
𝐼1 = � √1 − 𝑦2 − 𝑧2d𝑦d𝑧 𝐷1 Đặt 𝜋 𝑦 = 𝑟 cos 𝜑 , 𝑧 = 𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ , 𝐽 = 𝑟 2 𝜋 1 2
𝐼1 = � 𝑑𝜑 � √1 − 𝑟 2𝑟d𝑟 0 0 𝜋 1 1 1
= (− � (1 − 𝑟2)2𝑑(1 − 𝑟2)) 2 2 0 𝜋 2 3 2 1 𝜋 = − × (1 − 𝑟 )2 � = 4 3 0 6 𝐼2 = �d𝑧d𝑥 𝑆 12
𝑦 = √1 − 𝑥2 − 𝑧2
Hình chiếu của 𝑆 xuống mặt 𝑦 = 0 là 𝐷𝐷2 𝑥2 + 𝑧2 ≤ 1, 𝑥 ≥ 0, 𝑧 ≥ 0
Hướng dương đã chọn tạo với tia 𝑂𝑂𝑦 góc nhọn. 1 𝜋
𝐼 = � d𝑧d𝑥 = (𝜋 × (1)2) = 2 𝐷 4 4 2
𝐼3 = �𝑥𝑧2d𝑥d𝑦 𝑆
𝑧 = √1 − 𝑥2 − 𝑦2
Hình chiếu của 𝑆 xuống mặt 𝑧 = 0 là 𝐷𝐷3 𝑥2 + 𝑦2 ≤ 1, 𝑦 ≥ 0, 𝑥 ≥ 0
Hướng dương đã chọn tạo với tia 𝑂𝑂𝑧 góc nhọn.
𝐼3 = � 𝑥(1 − 𝑥2 − 𝑦2)d𝑥d𝑦 𝐷3 Đặt 𝜋 𝑥 = 𝑟 cos 𝜑 , 𝑦 = 𝑟 sin 𝜑 ,
0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ , 𝐽 = 𝑟 2 𝜋 𝜋 1 2 2 ( 2) 1 ( 2 4)
𝐼3 = � d𝜑 � 𝑟 cos 𝜑 1 − 𝑟
𝑟d𝑟 = � cos 𝜑 d𝜑 � 𝑟 − 𝑟 d𝑟 0 0 0 0 𝜋 1 1 1 2
= (sin 𝜑 �2) ( 𝑟3 − 𝑟5) � = 0 3 5 0 15 13 Vậy 𝜋 𝜋 2 5 2
𝐼 = 𝐼1 + 𝐼2 + 𝐼3 = + + = 𝜋 + 6 4 15 12 15
Ví dụ 1.6. Tính tích phân mặt ∬ 𝑦d𝑧d𝑥, trong đó 𝑆 là phía ngoài của 𝑆
mặt Paraboloid 𝑧 = 𝑥2 + 𝑦2 (0 ≤ 𝑧 ≤ 2).
Mặt phẳng 𝑦 = 0 chia 𝑆 thành 2 nửa:
𝑆1: 𝑦 = √𝑧 − 𝑥2, 0 ≤ 𝑥 ≤ √2, 0 ≤ 𝑧 ≤ 2
𝑆2: 𝑦 = −√𝑧 − 𝑥2, 0 ≤ 𝑥 ≤ √2, 0 ≤ 𝑧 ≤ 2
Hình chiếu của 𝑆1 và 𝑆2 lên mặt 𝑦 = 0 đều
là miền 𝐷𝐷 giới hạn bởi: 𝑥2 ≤ 𝑧 ≤ 2, 0 ≤ 𝑥 ≤ √2
𝐼 = �𝑦d𝑧d𝑥 = � 𝑦d𝑧d𝑥 + � 𝑦d𝑧d𝑥 = 𝐼1 + 𝐼2 𝑆 𝑆1 𝑆2 𝐼1 = � 𝑦d𝑧d𝑥 𝑆1
Hướng được chọn hợp với tia 𝑂𝑂𝑦 thành góc nhọn. √2 2
𝐼1 = � √𝑧 − 𝑥2d𝑧d𝑥 = �
𝑑𝑥 � √𝑧 − 𝑥2𝑑𝑧 𝐷 0 𝑥2 √2 2 3 2 2 √2 3
= � 𝑑𝑥 � (𝑧 − 𝑥2)2 � 2� = � (2 − 𝑥2)2d𝑥 0 3 𝑥 3 0 14 Đặt 𝜋 𝜋 √2 𝑥 = √2 sin 𝑡 , 0 ≤ 𝑡 ≤ , d𝑥 = √2 cos 𝑡 d𝑡, 𝑥 � ⇒ 𝑡 �2 2 0 0 𝜋 𝜋 2 2 3 8 2 4
𝐼1 = � (√2 cos 𝑡) √2 cos 𝑡 d𝑡 = � cos 𝑡 d𝑡 3 3 0 0 𝜋 𝜋 8 2 1 2 2 = �
( 1 + cos 2𝑡)2 d𝑡 = � (1 + 2 cos 2𝑡 + cos2 2𝑡 )d𝑡 3 0 4 3 0 𝜋 2 2 3 1
= � ( + 2 cos 2𝑡 + cos 4𝑡) d𝑡 3 0 2 2 𝜋 2 3 1 𝜋
= ( 𝑡 + sin 2𝑡 + sin 4𝑡) � 3 2 8 2 = 0 2 𝐼2 = � 𝑦d𝑧d𝑥 𝑆2 𝑦 = −√𝑧 − 𝑥2
Hướng được chọn hợp với tia 𝑂𝑂𝑦 thành góc tù.
⇒ 𝐼2 = − � (−√𝑧 − 𝑥2) d𝑧d𝑥 𝐷 𝜋
= � √𝑧 − 𝑥2d𝑧d𝑥 = 𝐼1 = 𝐷 2
Vậy 𝐼 = 𝐼1 + 𝐼2 = 2𝐼1 = 𝜋 15
3.4.2.2. Công thức Ostrogradsky
Ví dụ 2.1. Tính ∬ 𝑥3d𝑦d𝑧 + 𝑦3d𝑧d𝑥 + 𝑧3d𝑥d𝑦 trong đó 𝑆 là phía 𝑆
ngoài của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4.
Ví dụ 2.2. Tính ∬ 𝑥2d𝑦d𝑧 + 𝑦2d𝑧d𝑥 + 𝑧2d𝑥d𝑦 trong đó 𝑆 là phía 𝑆
ngoài của biên của hình lập phương: 0 ≤ 𝑥 ≤ 2, 0 ≤ 𝑦 ≤ 2, 0 ≤ 𝑧 ≤ 2.
Ví dụ 2.3. Tính ∬ 𝑥𝑧d𝑦d𝑧 + 𝑦𝑥d𝑧d𝑥 + 𝑧𝑦d𝑥d𝑦 trong đó 𝑆 là phía 𝑆
ngoài của biên của hình chóp 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0, 𝑥 + 𝑦 + 𝑧 ≤ 1.
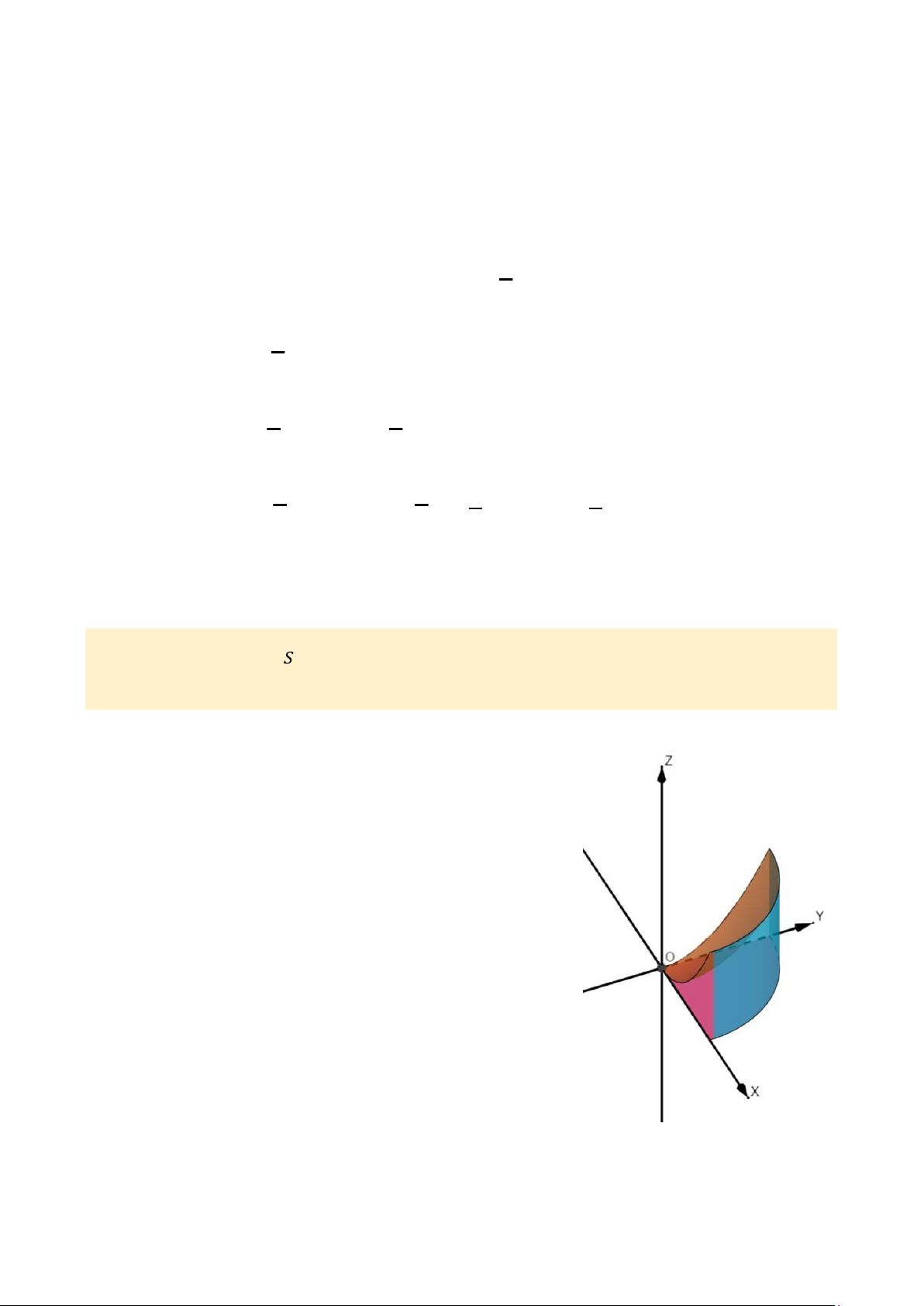
Ví dụ 2.4. Tính ∬ 𝑦2𝑧d𝑥d𝑦 + 𝑥𝑧d𝑦d𝑧 + 𝑥2𝑦d𝑥d𝑧, trong đó 𝑆 là phía 𝑆
ngoài của miền 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑥2 + 𝑦2 ≤ 1, 0 ≤ 𝑧 ≤ 𝑥2 + 𝑦2.
𝑃, 𝑄𝑄, 𝑅 là các hàm khả vi, liên tục trên miền 𝑉 ⊂ ℝ3 giới hạn bởi mặt cong kín 𝑆.
�𝑃(𝑥, 𝑦, 𝑧)d𝑦d𝑧 + 𝑄𝑄(𝑥, 𝑦, 𝑧)d𝑧d𝑥 + 𝑅(𝑥, 𝑦, 𝑧)d𝑥d𝑦 )d𝑥d𝑦d𝑧
Tích phân bội 3 lấy theo hướng pháp tuyến ngoài.
Ví dụ 2.1. Tính ∬ 𝑥3d𝑦d𝑧 + 𝑦3d𝑧d𝑥 + 𝑧3d𝑥d𝑦 trong đó 𝑆 là phía ngoài
của mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4.
Gọi 𝑉 là vật thể giới hạn bởi mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4.
𝑃(𝑥, 𝑦, 𝑧) = 𝑥3, 𝑄𝑄(𝑥, 𝑦, 𝑧) = 𝑦3, 𝑅(𝑥, 𝑦, 𝑧) = 𝑧3 và các đạo hàm riêng
cấp một của chúng liên tục trong miền 𝑉. 16
Áp dụng công thức Ostrogradsky
𝐼 = �𝑃d𝑦d𝑧 + 𝑄𝑄d𝑧d𝑥 + 𝑅d𝑥d𝑦 = �(𝑃′ + 𝑄𝑄′ + 𝑅′ )d𝑥d𝑦d𝑧 𝑥 𝑦 𝑧 𝑆 𝑉
= 3 �(𝑥2 + 𝑦2 + 𝑧2 )d𝑥d𝑦d𝑧 𝑉
Chuyển sang tọa độ cầu:
𝑥 = 𝑟 sin 𝜃𝜃 cos 𝜑 0 ≤ 𝑟 ≤ 2, 0 ≤ 𝜃𝜃 ≤ 𝜋,
Δ → 𝑉: �𝑦 = 𝑟 sin 𝜃𝜃 sin 𝜑 , ( ) 0 ≤ 𝜑 ≤ 2𝜋, 𝐽 = −𝑟2 sin 𝜃𝜃 𝑧 = 𝑟 cos 𝜃𝜃 2𝜋 𝜋 2
𝐼 = 3 �𝑟4 sin 𝜃𝜃 d𝑟d𝜃𝜃d𝜑 = 3 �
d𝜑 � sin 𝜃𝜃 d𝜃𝜃 � 𝑟4d𝑟 Δ 0 0 0 𝜋 1 2 12
= 3(2𝜋) (− cos 𝜃𝜃 � 𝑟5 � ) = 25𝜋 ) ( 0 5 0 5
Ví dụ 2.2. Tính ∬ 𝑥2d𝑦d𝑧 + 𝑦2d𝑧d𝑥 + 𝑧2d𝑥d𝑦 trong đó 𝑆 là phía ngoài
của biên của hình lập phương: 0 ≤ 𝑥 ≤ 2, 0 ≤ 𝑦 ≤ 2, 0 ≤ 𝑧 ≤ 2.
Gọi 𝑉 là vật thể giới hạn bởi hình lập phương có biên 𝑆.
𝑃(𝑥, 𝑦, 𝑧) = 𝑥2, 𝑄𝑄(𝑥, 𝑦, 𝑧) = 𝑦2, 𝑅(𝑥, 𝑦, 𝑧) = 𝑧2 và các đạo hàm riêng
cấp một của chúng liên tục trong miền 𝑉.
Áp dụng công thức Ostrogradsky 17
𝐼 = �𝑥2d𝑦d𝑧 + 𝑦2d𝑧d𝑥 + 𝑧2d𝑥d𝑦 = 2 �(𝑥 + 𝑦 + 𝑧)d𝑥d𝑦d𝑧 𝑆 𝑉 2 2 2
= 2 � d𝑥 � d𝑦 � (𝑥 + 𝑦 + 𝑧)d𝑧 0 0 0 2 2 1
= 2 � d𝑥 � �(𝑥𝑦 + 𝑦𝑧 + 𝑧2) � 2� d𝑦 2 0 0 0 2 2 2 1 2
= 4 � d𝑥 � ( 1 + 𝑥 + 𝑦)d𝑦 = 4 � �(𝑦 + 𝑥𝑦 + 𝑦2) � � d𝑥 2 0 0 0 0 2 2
= 4 � (4 + 2𝑥)d𝑥 = 4(4𝑥 + 𝑥2) � = 48 0 0
Ví dụ 2.3. Tính ∬ 𝑥𝑧d𝑦d𝑧 + 𝑦𝑥d𝑧d𝑥 + 𝑧𝑦d𝑥d𝑦 trong đó 𝑆 là phía ngoài 𝑆
của biên của hình chóp 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0, 𝑥 + 𝑦 + 𝑧 ≤ 1.
Đặt 𝑉 = {(𝑥, 𝑦, 𝑧): 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑥 + 𝑦 + 𝑧 ≤ 1}
𝑃(𝑥, 𝑦, 𝑧) = 𝑥𝑧, 𝑄𝑄(𝑥, 𝑦, 𝑧) = 𝑦𝑥, 𝑅(𝑥, 𝑦, 𝑧) = 𝑧𝑦 liên tục cùng với các
đạo hàm riêng cấp một của chúng trong miền 𝑉.
Áp dụng công thức Ostrogradsky 18
𝐼 = �𝑥𝑧d𝑦d𝑧 + 𝑦𝑥d𝑧d𝑥 + 𝑧𝑦d𝑥d𝑦 = �(𝑥 + 𝑦 + 𝑧)d𝑥d𝑦d𝑧 𝑆 𝑉 1 1−𝑥 1−𝑥−𝑦 = � d𝑥 � d𝑦 � (𝑥 + 𝑦 + 𝑧)d𝑧 0 0 0 1 1−𝑥 1 1 − 𝑥 − 𝑦 = � d𝑥 �
�(𝑥 + 𝑦 + 𝑧) 𝑧 � 2 � d𝑦 0 0 0 1 1 1−𝑥 = � d𝑥 � [1 − (𝑥 + 𝑦)2]d𝑦 2 0 0 1 1 1 1 − 𝑥 = � ��𝑦 − (𝑥 + 𝑦)3� � � d𝑥 2 0 3 0 1 1 1 1 1 = � (1 − 𝑥 − + 𝑥3) d𝑥 = 2 0 3 3 8
Ví dụ 2.4. Tính ∬ 𝑦2𝑧d𝑥d𝑦 + 𝑥𝑧d𝑦d𝑧 + 𝑥2𝑦d𝑥d𝑧, trong đó 𝑆 là phía
ngoài của miền 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑥2 + 𝑦2 ≤ 1, 0 ≤ 𝑧 ≤ 𝑥2 + 𝑦2.
Gọi 𝑉 là vật thể giới hạn bởi mặt ngoài của 𝑆.
𝑃(𝑥, 𝑦, 𝑧) = 𝑦2𝑧, 𝑄𝑄(𝑥, 𝑦, 𝑧) = 𝑥𝑧, 𝑅(𝑥, 𝑦, 𝑧) =
𝑥2𝑦 và các đạo hàm cấp 1 của chúng liên tục trong 𝑉.
Áp dụng công thức Ostrogradsky
𝐼 = �𝑦2𝑧d𝑥d𝑦 + 𝑥𝑧d𝑦d𝑧 + 𝑥2𝑦d𝑥d𝑧 𝑆
= �(𝑦2 + 𝑧 + 𝑥2)d𝑥d𝑦d𝑧 𝑉 Tọa độ trụ ! 19 𝑥 = 𝑟 cos 𝜑 𝜋 �𝑦 = 𝑟 sin 𝜑 ,
(0 ≤ 𝑟 ≤ 1, 0 ≤ 𝜑 ≤ , 0 ≤ 𝑧 ≤ 𝑟2, 𝐽 = 𝑟) 𝑧 = 𝑧 2 𝜋 𝜋 1 𝑟2 1 𝑟2 2 2
⇒ 𝐼 = � d𝑟 � d𝜑 �
(𝑧 + 𝑟2)𝑟d𝑧 = � d𝑟 � d𝜑 � (𝑧 + 𝑟2)𝑟d𝑧 0 0 0 0 0 0 𝜋 1 1 𝑟2 𝜋 1 1
= � d𝑟 ( 𝑟𝑧2 + 𝑟3𝑧) � = � ( 𝑟3 + 𝑟5) d𝑟 2 0 2 0 2 0 2 𝜋 1 1 = 4 6 1 7𝜋 ( 𝑟 + 𝑟 ) � = 2 8 6 0 48
Tài liệu liên quan:
-
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng
35 18 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
41 21 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
39 20 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
36 18 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
43 22