






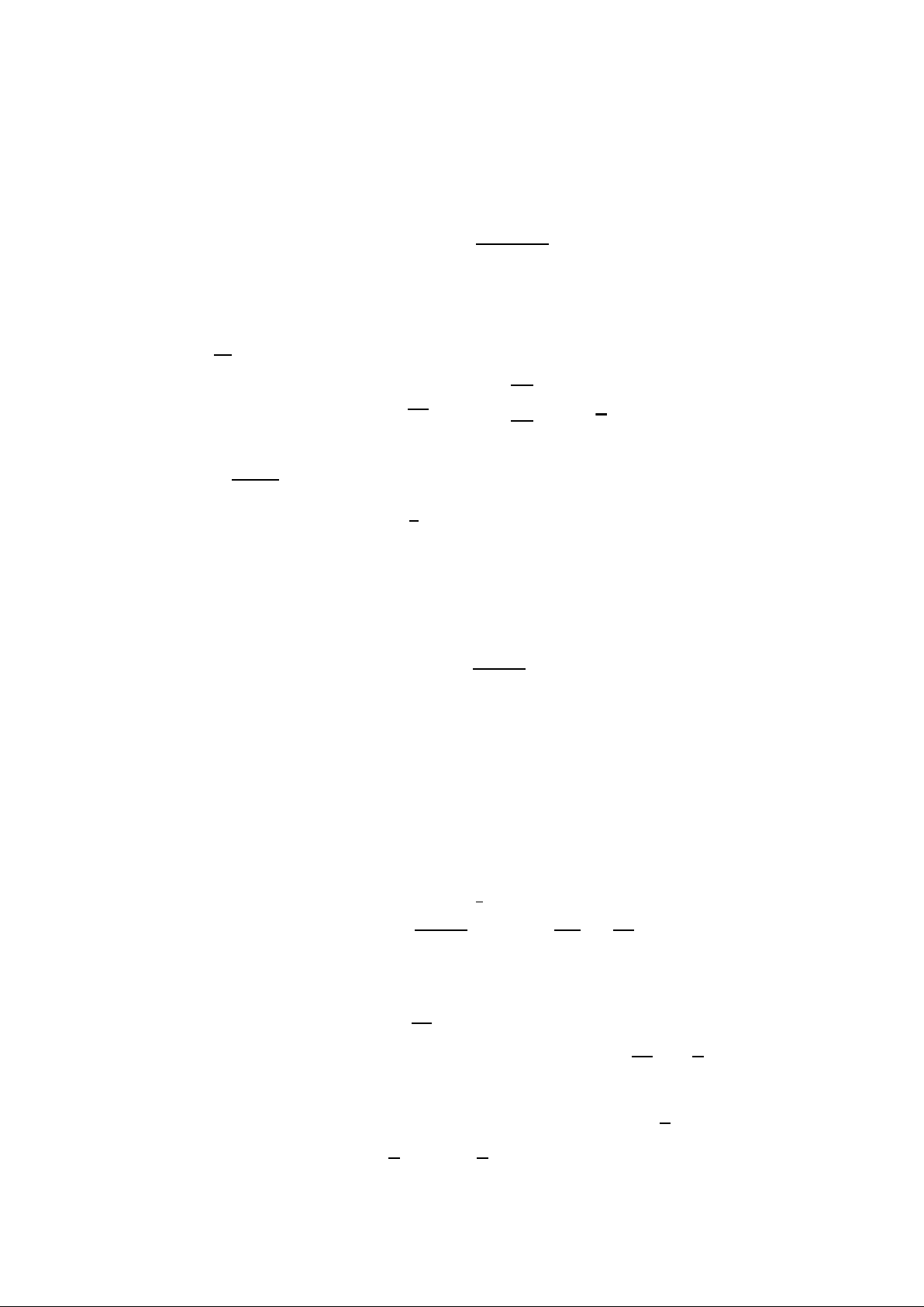




Preview text:
MỤC LỤCPHẦN DỊCH:
Chuỗi lũy thừa là một chuỗi có dạng [1]
trong đó 𝑥 là một biến và cn’s là hằng số được gọi là hệ số của chuỗi. Với mỗi 𝑥 cố định,
chuỗi [1] là một chuỗi các hằng số mà chúng ta có thể kiểm tra sự hội tụ hoặc phân kỳ.
Một chuỗi lũy thừa có thể hội tụ đối với một số giá trị của 𝑥 và phân kỳ đối với các giá
trị khác của 𝑥. Các tổng của chuỗi là một hàm
miền của nó là tập hợp tất cả 𝑥 mà chuỗi hội tụ. Chú ý rằng 𝑓 giống với một đa thức. Sự
khác biệt duy nhất là có vô số điều kiện.
Ví dụ, nếu chúng ta lấy cn = 1 với mọi n, chuỗi lũy thừa sẽ trở thành chuỗi hình học [2]
được gọi là chuỗi lũy thừa trong (𝒙 − 𝒂) hoặc chuỗi lũy thừa có tâm tại a hoặc chuỗi
lũy thừa về a. Lưu ý rằng khi viết ra số hạng tương ứng với 𝑛 = 0 trong Phương trình
1 và 2, chúng ta đã chấp nhận quy ước rằng (𝑥 − 𝑎)0 = 1 ngay cả khi 𝑥 = 𝑎. Cũng chú
ý rằng khi 𝑥 = 𝑎 tất cả các số hạng đều bằng 0 với 𝑛 ≥ 1 và do đó chuỗi lũy thừa [2]
luôn hội tụ khi 𝑥 = 𝑎.
VÍ DỤ 1 Với những giá trị nào của chuỗi ∑∞
𝑛=0 𝑛! 𝑥𝑛 hội tụ?
BÀI GIẢI Chúng tôi sử dụng Kiểm tra Tỷ lệ. Nếu chúng ta đặt 𝑎𝑛, như thường lệ, biểu
thị số hạng thứ 𝑛 của chuỗi, thì 𝑎𝑛 =
𝑛! 𝑥𝑛. Nếu 𝑥 ≠ 0, chúng ta có
Bằng Kiểm tra Tỷ lệ, chuỗi phân kỳ khi 𝑥 ≠ 0 . Do đó, chuỗi đã cho chỉ hội tụ khi nào 𝑥 = 0. (𝑛−3)𝑛
VÍ DỤ 2 Với những giá trị nào của 𝑥 thì chuỗi ∑∞ hội tụ? 𝑛=1 𝑛 (𝑥−3)𝑛
BÀI GIẢI Đặt 𝑎 = . Sau đó 𝑛 𝑛
Bằng kiểm tra tỷ lệ, chuỗi đã cho là hoàn toàn hội tụ, và hội tụ khi |𝑥 − 3| < 1 và phân
kỳ khi |𝑥 − 3| > 1. Bây giờ ta có 4
vì vậy chuỗi hội tụ khi 2 < 𝑥 < 4 và phân kỳ khi 𝑥 < 2 hoặc 𝑥 > 4.
Kiểm tra Tỷ lệ không có thông tin khi |𝑥 − 3| = 1 vì vậy chúng ta phải xem xét 𝑥 = 2
và 𝑥 = 4 riêng biệt. Nếu chúng ta đặt 𝑥 = 4 trong chuỗi, nó sẽ trở thành∑ 1, chuỗi điều 𝑛
hòa, phân kỳ. Nếu 𝑥 = 2, chuỗi sẽ là∑ (−1)𝑛, chuỗi này hội tụ bằng Kiểm tra Chuỗi xen 𝑛
kẽ. Do đó, chuỗi lũy thừa đã cho hội tụ tại 2 ≤ 𝑥 < 4.
Chúng ta sẽ thấy rằng công dụng chính của chuỗi lũy thừa là nó cung cấp một cách
để biểu diễn một số hàm quan trọng nhất phát sinh trong toán học, vật lý và hóa
học. Cụ thể, tổng của chuỗi lũy thừa trong ví dụ tiếp theo được gọi là hàm Bessel,
theo tên nhà thiên văn học người Đức Friedrich Bessel (1784–1846), và hàm cho
trong Bài tập 33 là một ví dụ khác của hàm Bessel. Trên thực tế, những chức năng
này xuất hiện lần đầu tiên khi Bessel giải được phương trình Kepler để mô tả
chuyển động của hành tinh. Kể từ thời điểm đó, các chức năng này đã được ứng
dụng trong nhiều trường hợp vật lý khác nhau, bao gồm sự phân bố nhiệt độ
trong một đĩa tròn và hình dạng của một trống rung (xem các bức ảnh ở trang 700).
VÍ DỤ 3 Tìm miền của hàm Bessel bậc 0 được xác định bởi (−1)𝑛𝑥2𝑛 BÀI GIẢI Đặt 𝑎 = . Khi đó 𝑛 [22𝑛(𝑛!)2
Do đó, bằng Kiểm tra tỷ lệ, chuỗi đã cho hội tụ với tất cả các giá trị của 𝑥. Nói cách
khác, miền 𝐽0 của hàm Bessel là (−∞, ∞) = ℝ.
Nhớ lại rằng tổng của một chuỗi bằng giới hạn của chuỗi các tổng riêng phần. Vì
vậy, khi chúng ta xác định hàm Bessel trong Ví dụ 3 là tổng của một chuỗi, chúng
ta có nghĩa rằng, với mọi số thực 𝑥, 5
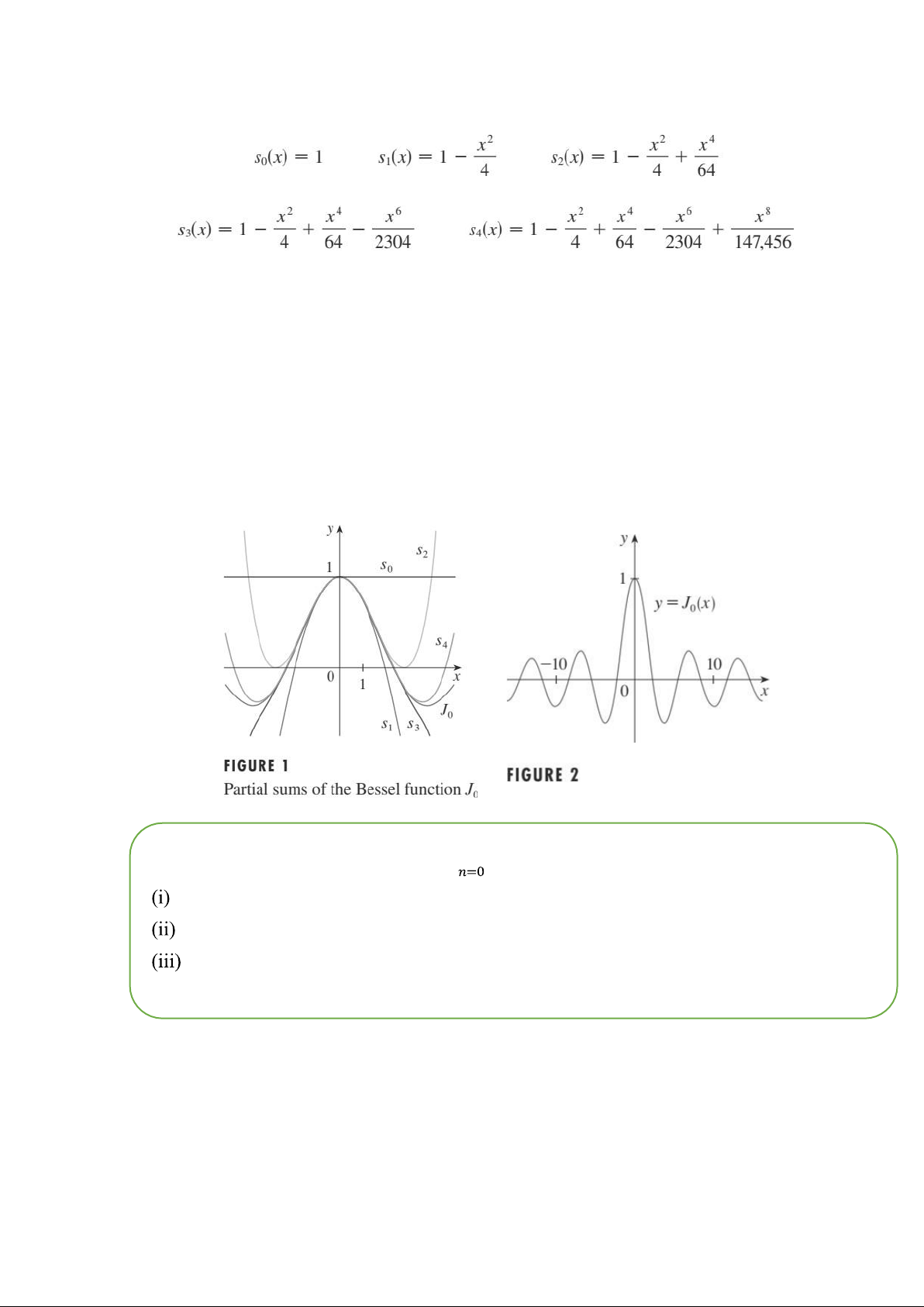
Một vài tổng đầu tiên là
Hình 1 cho thấy đồ thị của các tổng từng phần này, là các đa thức. Tất cả chúng đều là
giá trị gần đúng cho hàm, nhưng lưu ý rằng giá trị gần đúng sẽ trở nên tốt hơn khi có
nhiều số hạng hơn. Hình 2 cho thấy một đồ thị đầy đủ hơn của hàm Bessel.
Đối với chuỗi lũy thừa mà chúng ta đã xem xét cho đến nay, tập các giá trị 𝑥 mà chuỗi
hội tụ luôn biến thành một khoảng [một khoảng hữu hạn đối với chuỗi hình học và chuỗi
trong Ví dụ 2, khoảng vô hạn (−∞, ∞) trong Ví dụ 3 và một khoảng thu gọn [0,0] =
{0} trong Ví dụ 1]. Định lý sau đây, được chứng minh trong Phụ lục F, nói rằng điều này nói chung là đúng.
Định lý Đối với một chuỗi lũy thừa ∑∞
𝑐𝑛(𝑥 − 𝑎)𝑛 đã cho, chỉ có ba khả năng:
Chuỗi chỉ hội tụ khi 𝑥 = 𝑎.
Chuỗi hội tụ với mọi 𝑥.
Có một số dương sao cho chuỗi hội tụ nếu |𝑥 − 𝑎| < 𝑅 và phân kỳ nếu |𝑥 − 𝑎| > 𝑅. 6
Con số trong trường hợp (iii) được gọi là bán kính hội tụ của chuỗi lũy thừa. Theo
quy ước, bán kính hội tụ là 𝑅 = 0 trong trường hợp (i) và 𝑅 = ∞ trong trường
hợp (ii). Khoảng thời gian hội tụ của một chuỗi lũy thừa là khoảng bao gồm tất cả các giá trị 𝑥 mà chuỗi
đó hội tụ. Trong trường hợp (i) khoảng thời gian chỉ bao gồm một điểm 𝑎 duy
nhất. Trong trường hợp (ii) khoảng là (−∞, ∞). Trong trường hợp (iii) lưu ý rằng
bất đẳng thức |𝑥 = 𝑎| < 𝑅 có thể được viết lại thành 𝑎 − 𝑅 < 𝑥 < 𝑎 + 𝑅. Khi 𝑥 là
điểm cuối của khoảng, nghĩa là, 𝑥 = 𝑎 ± 𝑅, bất kỳ điều gì có thể xảy ra, chuỗi có
thể hội tụ tại một hoặc cả hai điểm cuối hoặc nó có thể phân kỳ ở cả hai điểm cuối.
Do đó, trong trường hợp (iii) có bốn khả năng xảy ra đối với khoảng hội tụ:
Tình huống này được minh họa ở Hình 3.
Dưới đây là bảng tóm tắt bán kính và khoảng thời gian hội tụ cho mỗi ví dụ đã
được xem xét trong phần này.
Nói chung, Kiểm tra tỷ lệ (hoặc đôi khi Kiểm tra gốc) nên được sử dụng để xác
định bán kính hội tụ R. Kiểm tra Tỷ lệ và Gốc thường gặp lỗi khi 𝑥 là điểm cuối của
khoảng hội tụ, vì vậy các điểm cuối phải được kiểm tra bằng một số kiểm tra khác.
VÍ DỤ 4 Tìm bán kính hội tụ và khoảng hội tụ của chuỗi 7 (−3)𝑛𝑥𝑛 BÀI GIẢI Đặt 𝑎 = . Ta có 𝑛 √𝑛+1
Bằng Kiểm tra Tỷ lệ, chuỗi đã cho hội tụ nếu 3|𝑥| < 1 và phân kỳ nếu 3|𝑥| > 1.
Do đó, nó hội tụ nếu |𝑥| < 1 và phân kỳ nếu |𝑥| > 1. Điều này có nghĩa là bán kính 3 3
của hội tụ là 𝑅 = 1. 3
Chúng tôi biết chuỗi hội tụ trong khoảng (− 1 , 1 ) , nhưng bây giờ chúng tôi phải 3 3
kiểm tra hội tụ tại các điểm cuối của khoảng này. Nếu 𝑥 = − 1, chuỗi trở thành 3
mà nó phân kỳ. (Sử dụng Kiểm tra Tích phân hoặc chỉ cần quan sát rằng nó là một
chuỗi với 𝑝 = 1 < 1 . Nếu 𝑥 = 1 thì chuỗi là 2 3
mà hội tụ bởi Kiểm tra Chuỗi xen kẽ. Do đó, chuỗi lũy thừa đã cho hội tụ khi − 1 < 3 1 1 1
𝑥 ≤ , nên khoảng hội tụ là (− , ]. 3 3 3
VÍ DỤ 5 Tìm bán kính hội tụ và khoảng hội tụ của chuỗi
BÀI GIẢI Nếu 𝑎𝑛 = 𝑛(𝑥+2)𝑛 thì 3𝑛+1
Sử dụng Kiểm tra tỷ lệ, chúng ta thấy rằng chuỗi hội tụ nếu |𝑥+2| < 1 và nó phân kỳ 3
nếu |𝑥+2| > 1. Vì vậy, nó hội tụ nếu |𝑥 + 2| < 3 và phân kỳ nếu |𝑥 + 2| > 3 . Do 3
đó, bán kính hội tụ sẽ là 𝑅 = 3. 8
Bất đẳng thức |𝑥 + 2| < 3 có thể được viết dưới dạng −5 < 𝑥 < 1, vì vậy chúng
tôi kiểm tra chuỗi tại điểm cuối là -5 và 1. Khi 𝑥 = −5, chuỗi sẽ là
phân kỳ bởi Kiểm tra phân kỳ [(−1)𝑛𝑛 không hội tụ về 0]. Khi 𝑥 = 1 , chuỗi là
mà cũng phân kỳ bởi Kiểm tra sự phân kỳ. Do đó, chuỗi chỉ hội tụ khi −5 < 𝑥 < 1,
nên khoảng đồng biến là (−5, 1). 9 II. CÁC VÍ DỤ:
Ví dụ 1: Xác định bán kính hội tụ và khoảng hội tụ của chuỗi lũy thừa sau : ∞ (−1)𝑛𝑛 ∑ (𝑥 + 3)𝑛 (*) 𝑛=1 4𝑛 Bài giải Đặt 𝑎𝑛 = (−1)𝑛 4𝑛
Sử dụng tiêu chuẩn d’Alembert để giải quyết bài toán : (
𝜌 = lim |𝑎𝑛+1| = lim | −1)𝑛+1(𝑛+1) 4𝑛 |= lim |−(𝑛+1)| = lim 𝑛+1 = 1 𝑛→∞ 𝑎𝑛 𝑛→∞ 4𝑛+1 (−1)𝑛𝑛 𝑛→∞ 4𝑛 𝑛→∞ 4𝑛 4
Bán kính hội tụ : R= 1 = 4 . 𝜌 Xét ( x +3) = -4 → x=-7
∑∞ (−1)𝑛𝑛 (−4)𝑛 ↔ ∑∞ (−1)𝑛(−1)𝑛 𝑛 ↔ ∑∞ (−1)𝑛𝑛 (𝑥 + 3)𝑛 ↔ ∑∞ 𝑛 𝑛=1 4𝑛 𝑛=1 𝑛=1 4𝑛 𝑛=1
Suy ra chuỗi này phân kì vì lim 𝑛 = ∞ 𝑛→∞ Xét (x +3)=4 → x=1
∑∞ (−1)𝑛𝑛 4𝑛 = ∑∞ (−1)𝑛 𝑛 𝑛=1 4𝑛 𝑛=1
Suy ra chuỗi này phân kì vì lim (−1)𝑛𝑛 không tồn tại 𝑛→∞
Vì vậy, chuỗi lũy thừa không hội tụ tại 2 điểm cuối, miền hội tụ là (-7,1).
Ví dụ 2: Xác định bán kính hội tụ và miền hội tụ của chuỗi lũy thừa sau: ∞ 2𝑛 ∑ (4𝑥 − 8)𝑛 𝑛 𝑛=1 Bài giải:
Trong bài toán này, ta sử dụng tiêu chuẩn D’Alembert để giải quyết. Ta có: 2𝑛 𝑎𝑛 = và 𝑋 = 4𝑥 − 8 𝑛 Suy ra: 2𝑛+1 𝑎𝑛+1 = 𝑛+1 𝑎𝑛+1 2𝑛+1 𝑛 2𝑛 𝜌 = lim | | = lim | . | = lim | | = 2 𝑛→∞ 𝑎 2 𝑛 𝑛 𝑛→∞ 𝑛 + 1 𝑛→∞ 𝑛 + 1 Bán kính hội tụ: 1 1 𝑅 = = 𝜌 2 10 1 1 Khoảng hội tụ của chuỗi lũy thừa ∑∞ , ) 𝑛=1 𝑎𝑛 . 𝑋𝑛 là (− 2 2 Xét 1 𝑋 = 𝑅 = 2 2𝑛 1 ∞ ∑ . ( )𝑛 = 1 ∑∞
; ta nhận thấy ∑∞ 1 không âm và lim 1 = lim 1 với 𝑛=1 𝑛 2 𝑛=1 𝑛 𝑛=1 𝑛 𝑛→∞ 𝑛 𝑛→∞ 𝑛1
𝛼 = 1 nên chuỗi phân kì theo điều kiện cần. Xét 1 𝑋 = −𝑅 = − 2 ∑∞ 2𝑛 −1 𝑛
∑∞ (−1)𝑛 ; ta nhận thấy chuỗi đan dấu ∑∞ (−1)𝑛 có: 𝑛=1 . ( ) = 𝑛 2 𝑛=1 𝑛 𝑛=1 𝑛 1. 1 lim 𝑎 = lim = 0 𝑛 𝑛→∞ 𝑛→∞ 𝑛 2. Dãy 1 {𝑎 }+∞ +∞ là dãy giảm. 𝑛 𝑛=1 = { } 𝑛 𝑛=1
Khi đó chuỗi hội tụ. Miền hội tụ theo X là 1 −1 ≤ 𝑋 < 2 2 Ta có: 1 17
−1 ≤ 𝑋 = 4𝑥 − 8 < ↔ 15 ≤ 𝑥 < 2 2 8 8
Vậy miền hội tụ của chuỗi lũy thừa trên là [15 ; 17 . ) 8 8
Ví dụ 3:Xác định bán kính hội tụ và khoảng hội tụ của chuỗi lũy thừa sau. ∞ ∑ 𝑛! (2𝑥 + 1)𝑛 𝑛=𝑜 Bài giải F(x) = 2x +1 𝑎𝑛 = n! Bán kính hội tụ R= (𝑛+1)! 1 p = lim | | = lim (𝑛 + 1) = ∞ 𝑝 𝑛→∞ 𝑛! 𝑛→∞
R = 1 ≈ 0 ⇒ Bán kính hội tụ R = 0 ∞ Khoảng hội tụ F(x) = 2x +1 =0 ⇒ x = - 1 2
Vậy khoảng hôi tụ tai một điểm x = - 1 2 11
Ví dụ 4:Xác định bán kính hội tụ và miền hội tụ của chuỗi lũy thừa sau: ∞ (𝑥 − 6)𝑛 ∑ 𝑛=1 𝑛𝑛 Bài giải:
Trong bài toán này, để thuận tiện, chúng ta sẽ khảo sát chuỗi theo tiêu chuẩn Cauchy.
Đặt 𝑎𝑛 = 1 𝑣à 𝑋 = 𝑥 − 6 𝑛𝑛 𝑛 𝑛 1 1
ρ = lim √𝑎𝑛 = lim √ = lim = 0 𝑛 𝑛→∞ 𝑛→∞ 𝑛 𝑛→∞ 𝑛 (𝑥−6)𝑛 Chuỗi ∑∞
hội tụ theo tiêu chuẩn Cauchy. 𝑛=1 𝑛𝑛
Bán kính hội tụ của chuỗi là: 𝑅 = 1 = +∞ 𝜌
Vậy miền hội tụ của chuỗi là (−∞; +∞).
Ví dụ 5: Xác định bán kính hội tụ và khoảng hội tụ của chuỗi lũy thừa sau. ∞ 𝑥2𝑛 ∑ (−3)𝑛 𝑛=1 Bài giải:
ta sử dùng tiêu chuẩn Cauchy để giải bài toán này:
Chúng ta sẽ sử dụng phép toán sau để kiểm tra phép thử lặp lại. 1 𝑥2𝑛 𝑛 𝑥2 𝑥2 𝐿 = lim | | = lim | | = 𝑛→∞ (−3) 𝑛 𝑛→∞ −3 3
Vậy nó sẽ hội tụ nếu 𝑥2 < 1 → 𝑥2 < 3 3
Tuy nhiên, bán kính hội tụ KHÔNG phải là 3. Do đó √𝑥2 < √3 |𝑥| < 3
Trong trường hợp này, có vẻ như bán kính hội tụ là 𝑅 = √3.
Xét khoảng hội tụ: −√3 < 𝑥 < √3 12
Kiểm tra các điểm cuối 𝑥 = −√3 Chuỗi lũy thừa ∞ 2𝑛 ∞ (−√3) ((−3)2)𝑛 ∑ = ∑ (−3)𝑛 ( −3)𝑛 𝑛=1 𝑛=1 =∑∞ 3𝑛 = ∑∞ (−1)𝑛 𝑛=1 (−1)𝑛(3)𝑛 𝑛=1
Chuỗi này phân kỳ do lim (−1)𝑛 không tồn tại. 𝑛→∞
Với 𝑥 = √3, ta có chuỗi: ∞ ∞ (√3)2𝑛 ∑ = ∑(−1)𝑛 (−3)𝑛 𝑛=1 𝑛=1 Mà chuỗi này phân kỳ.
Vậy khoảng hội tụ: −√3 < 𝑥 < √3 13 III.
ỨNG DỤNG THỰC TẾ CỦA CHUỖI
Đề tài: ỨNG DỤNG CỦA CHUỖI SỐ ĐỂ GIẢI PHƯƠNG TRÌNH VI PHÂN 1) MỞ ĐẦU
Một số phương trình vi phân rất khó (nếu không muốn nói là không thể) tìm nghiệm
ở dạng tổ hợp của các hàm số sơ cấp xác định. Điều này cũng xảy ra ngay cả khi các
phương trình vi phân có dạng rất đơn giản. Ví dụ như phương trình sau:
𝑦′′ − 2𝑥𝑦′ + 𝑦 = 0 (1)
Đây là phương trình vi phân cấp hai, hệ số hàm nhưng ta không thể tìm được 1
nghiệm riêng dưới dạng hàm số sơ cấp. Tuy nhiên, việc giải các phương trình như
dạng phương trình (1) là rất quan trọng vì nó nảy sinh từ các vấn đề, các bài toán của
vật lý, cụ thể, nó liên quan đến phương trình Schrödinger trong cơ học lượng tử. Vì
vậy, ta cần thiết phải xây dựng các phương pháp nhằm tìm nghiệm cho các phương trình dạng này.
Một trong các phương pháp thông dụng là ứng dụng lý thuyết chuỗi để tìm
nghiệm của phương trình dưới dạng chuỗi lũy thừa: ∞
𝑦 = ∑ 𝑐𝑛. 𝑥𝑛 = 𝑐0 + 𝑐1𝑥 + 𝑐2𝑥2 + ⋯ + 𝑐𝑛𝑥𝑛 (2) 𝑛=0
2) CƠ SỞ LÍ THUYẾT CỦA PHƯƠNG PHÁP:
Cơ sở Toán học của phương pháp này là ta thay thế biểu thức (2) vào phương
trình vi phân và từ đó xác định giá trị của các hằng số sao cho nó
nghiệm đúng phương trình vi phân
3) ĐIỀU KIỆN ĐỂ ÁP DỤNG PHƯƠNG PHÁP:
Chuỗi lũy thừa ứng với các hệ số tìm được phải là chuỗi hội tụ. 4) VÍ DỤ MINH HỌA Xét phương trình : 𝑦′′ + 𝑦 = 0 (3)
Theo phương pháp sơ cấp, ta đã biết nghiệm của phương trình (3) có dạng:
𝑦 = 𝐶1 cos(𝑥) + 𝐶2 sin(𝑥)
Sử dụng phương pháp chuỗi số. Ta giả sử nghiệm của phương trình (3) có dạng: ∞
𝑦 = ∑ 𝑐𝑛. 𝑥𝑛 = 𝑐0 + 𝑐1𝑥 + 𝑐2𝑥2 + ⋯ + 𝑐𝑛𝑥𝑛 𝑛=1 Khi đó, ta có: 14
𝑦′′ = 2𝑐2 + 2.3𝑐3𝑥 + 3.4𝑐4𝑥2 + ⋯ + 𝑛. (𝑛 − 1)𝑐𝑛𝑥𝑛−2 ∞ ∞
= ∑ 𝑛. (𝑛 − 1)𝑐𝑛𝑥𝑛−2 = ∑(𝑛 + 1). (𝑛 + 2)𝑐𝑛+2𝑥𝑛 (4) 𝑛=2 𝑛=0
Khi đó, từ (2),(3) và (4), ta sẽ có: ∞ ∞
∑(𝑛 + 1). (𝑛 + 2)𝑐𝑛+2𝑥𝑛 + ∑ 𝑐𝑛. 𝑥𝑛 = 0 𝑛=0 𝑛=1 Hay
∑∞ [(𝑛 + 1). (𝑛 + 2)𝑐𝑛+2𝑥𝑛 + 𝑐𝑛. 𝑥𝑛] = 0 (5) 𝑛=0
Theo phương pháp hệ số bất định, hai chuỗi số muốn bằng nhau thì từng hệ số tương
ứng phải bằng nhau. Vì vậy,hệ số 𝑥𝑛 ở biểu thức (5) phải bằng 0 Ta có:
(𝑛 + 1). (𝑛 + 2)𝑐𝑛+2 + 𝑐𝑛 = 0 𝑐𝑛
⇔ 𝑐𝑛+2 = − (𝑛 + 1). (𝑛 + 2)
Ta có công thức truy hồi, theo đó, sẽ có: 𝑛 = 0: 𝑐2 = − 𝑐0 1.2 𝑛 = 1: 𝑐3 = − 𝑐1 2.3
𝑛 = 2: 𝑐 = − 𝑐2 = 𝑐0 = 𝑐0 4 3.4 1.2.3.4 4!
𝑛 = 3: 𝑐 = − 𝑐3 = 𝑐0 = 𝑐0 5 4.5 1.2.3.4.5 5!
𝑛 = 4: 𝑐 = − 𝑐4 = − 𝑐0 = − 𝑐0 6 5.6 4!.5.6 6!
𝑛 = 5: 𝑐 = − 𝑐5 = − 𝑐0 7 6.7 7!
Theo quy luật trên, ta có:
Với các hệ số chẵn: 𝑐2𝑛 = (−1)𝑛 𝑐0 (2𝑛)! 𝑐 Với các hệ số lẻ: 0
𝑐2𝑛+1 = (−1)𝑛 (2𝑛+1)!
Từ đó, thế vào chuỗi (2), ta có:
𝑦 = 𝑐0 + 𝑐1𝑥 + 𝑐2𝑥2 + ⋯ + 𝑐𝑛𝑥𝑛 𝑥2 𝑥4 𝑥2𝑛 = 𝑐 + − ⋯ + (−1)𝑛 + ⋯ ) + 0 (1 − 2! 4! (2𝑛)!
𝑐 (𝑥 − 𝑥3 + 𝑥5 − ⋯ + (−1)𝑛 𝑥2𝑛+1 + ⋯ ) 1 3! 5! (2𝑛+1)! Hay ∞ ∞ 𝑥2𝑛 𝑥2𝑛+1 𝑦 = 𝑐0 ∑(−1)𝑛 + 𝑐1 ∑(−1)𝑛 (2𝑛)! (2𝑛 + 1)! 𝑛=0 𝑛=0
Như vây ta có phương trình phụ thuộc vào 2 chuỗi số với 𝑐0, 𝑐1là 2 hằng số tùy ý. 15 16




