Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

TíCH PHÂN KÉP (TíCH PHÂN 2 LîP) Chả Văn Ti»p
Giải tích II- 2021-2022, ĐHBKĐN
1 Tóm tắt lj thuyết 1. Đ°t bài toán:
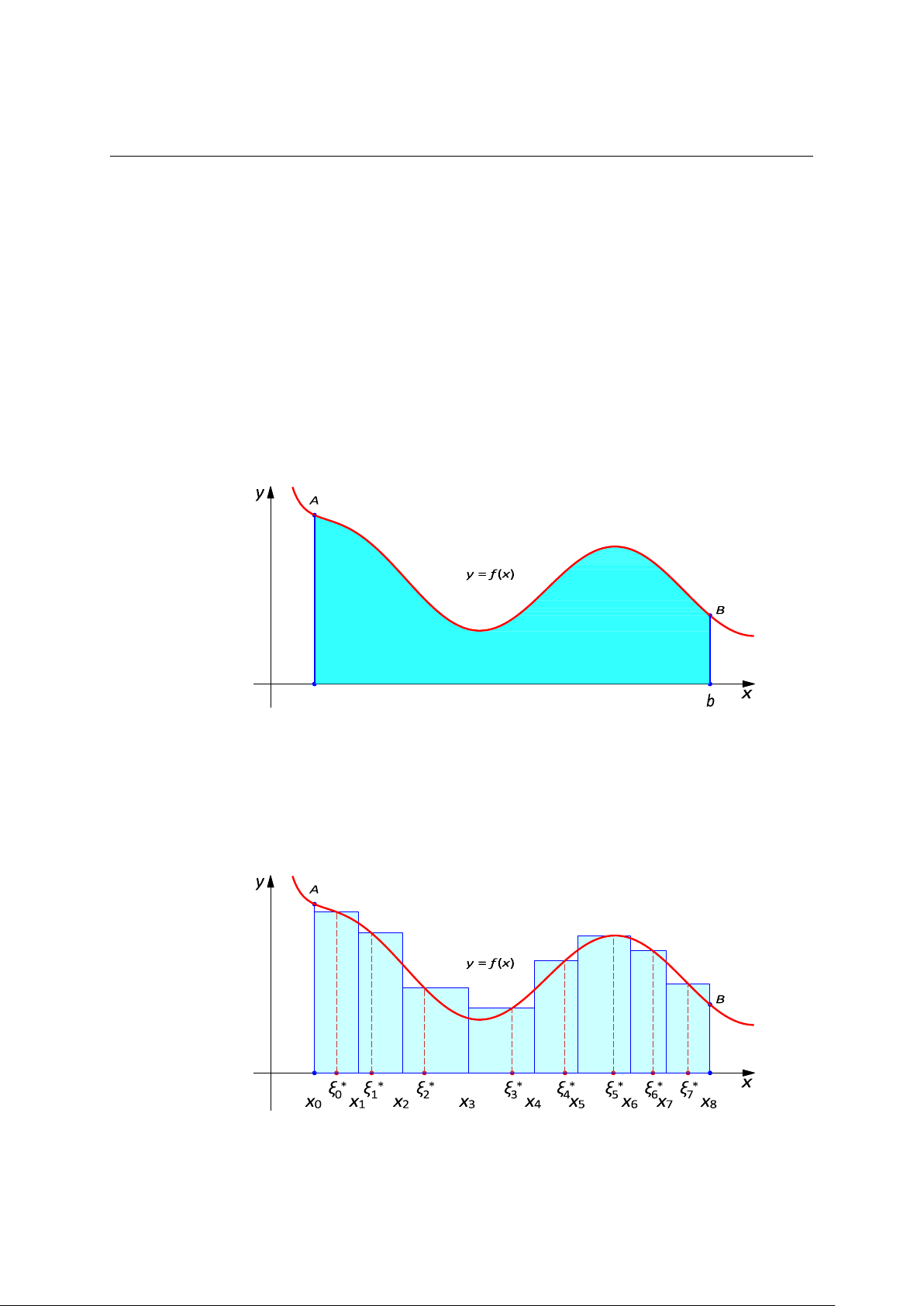
• Tích phân xác định (Tích phân m®t lớp) xuất phát tà bài toán tính DINN TÍCH hình thang cong.
Bài toán: Hãy tính di»n tích hình phẫng nằm bên dưới đồ thị của hàm số
y = f (x) trên đoạn [a, b] như hình vě bên dưới. a
Chia đoạn [a, b] thành các đoạn nhỏ bởi n + 1 điễm chia x0 = a < x1 < · · · < x ∗
n−1 < xn = b, trên mối đoạn nhỏ đó lấy m®t điễm ξi tùy ý và lªp tỗng Σ n S ≈ f (ξ ∗ i )∆xi i=1 ∫ b Σ n S =
f (x)dx = lim f (ξ ∗ i )∆xi. a |∆xi|→0 i=1 Chả Văn Ti»p (BKĐN) 1 / 12
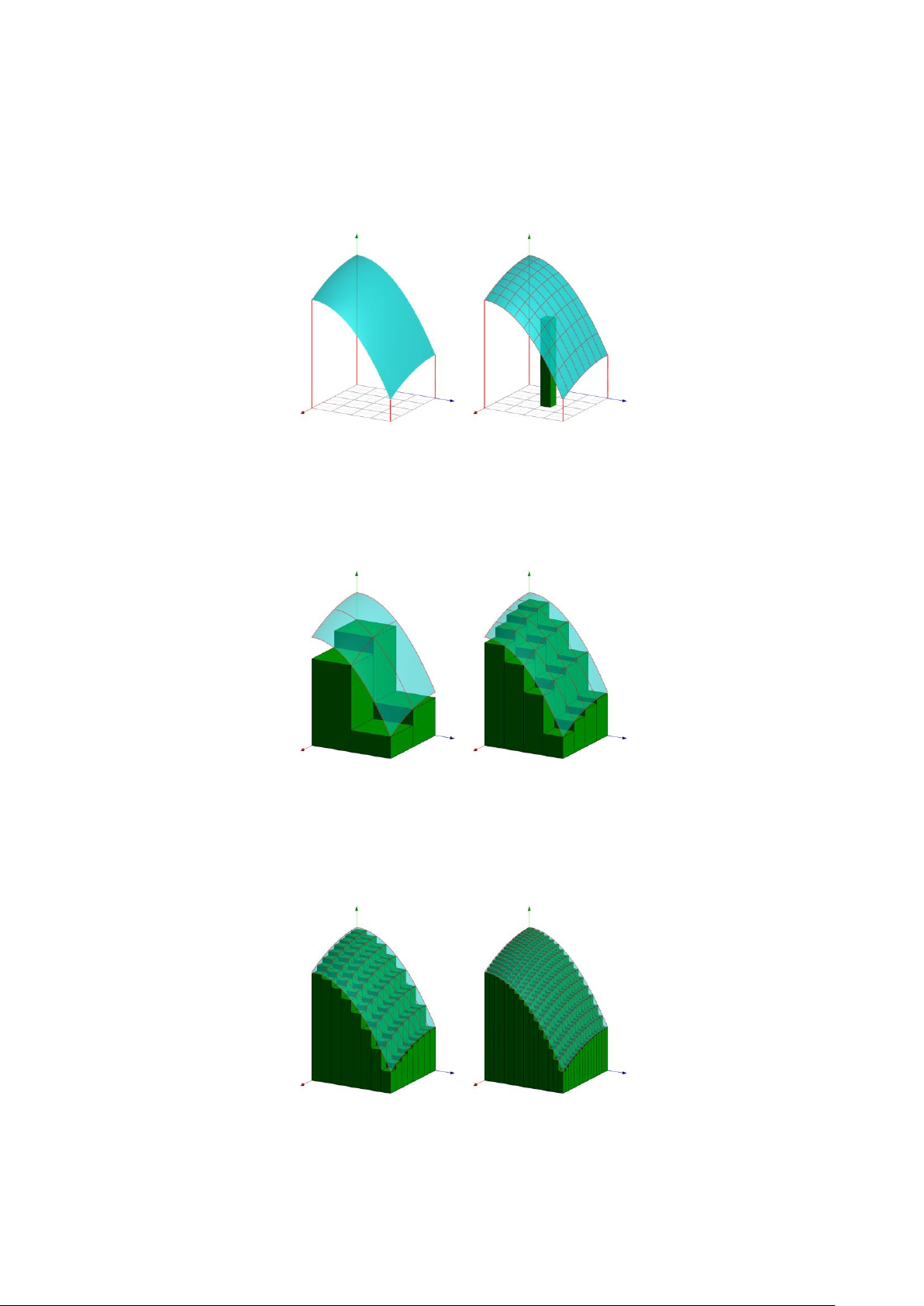
• Tích phân kép (Tích phân hai lớp) xuất phát tà bài toán tính THỄ TÍCH hình trụ cong.
Bài toán: Hãy ước lượng thễ tích m®t nhà kho có mái vòm là m°t cong z =
f (x, y) như hình vě bên dưới. Hình 1: Thễ tích ?
Ước lượng thô cªn dưới
Hình 2: (m, n) = (2, 2) và (m, n) = (4, 4)
Đễ tăng đ® chính xác, ta giảm kích thước hình chǎ nhªt đáy. m n Σ Σ Hình 3: V = lim f (x ∗ ∗
i , yj )∆xi∆yj
m,n→∞ i=1 j=1 Chả Văn Ti»p (BKĐN) 2 / 12
2. Định nghĩa: Tích phân kép của hàm f trên hình chǎ nhªt D là ∫∫ ∫∫ Σ n
f (x, y)dxdy =
f (x, y)dA = lim f (x ∗ ∗ i , yi )∆Ai D D |∆Ai|→0 i=1
nếu giới hạn trên tồn tại.
Nếu D là m®t miền bị ch°n bất kỳ trong m°t phẫng R2. Khi đó tồn tại m®t hình
chǎ nhªt R sao cho D ⊂ R. Đ°t hàm mới  
f (x, y),
nếu (x, y) ∈ D F (x, y) = 0
nếu (x, y) ∈ R \ D Khi đó ta định nghĩa ∫∫ ∫∫
f (x, y)dxdy =
F (x, y)dxdy. D R
3. Công thác tính tích phân kép trong tọa đ® Decartes
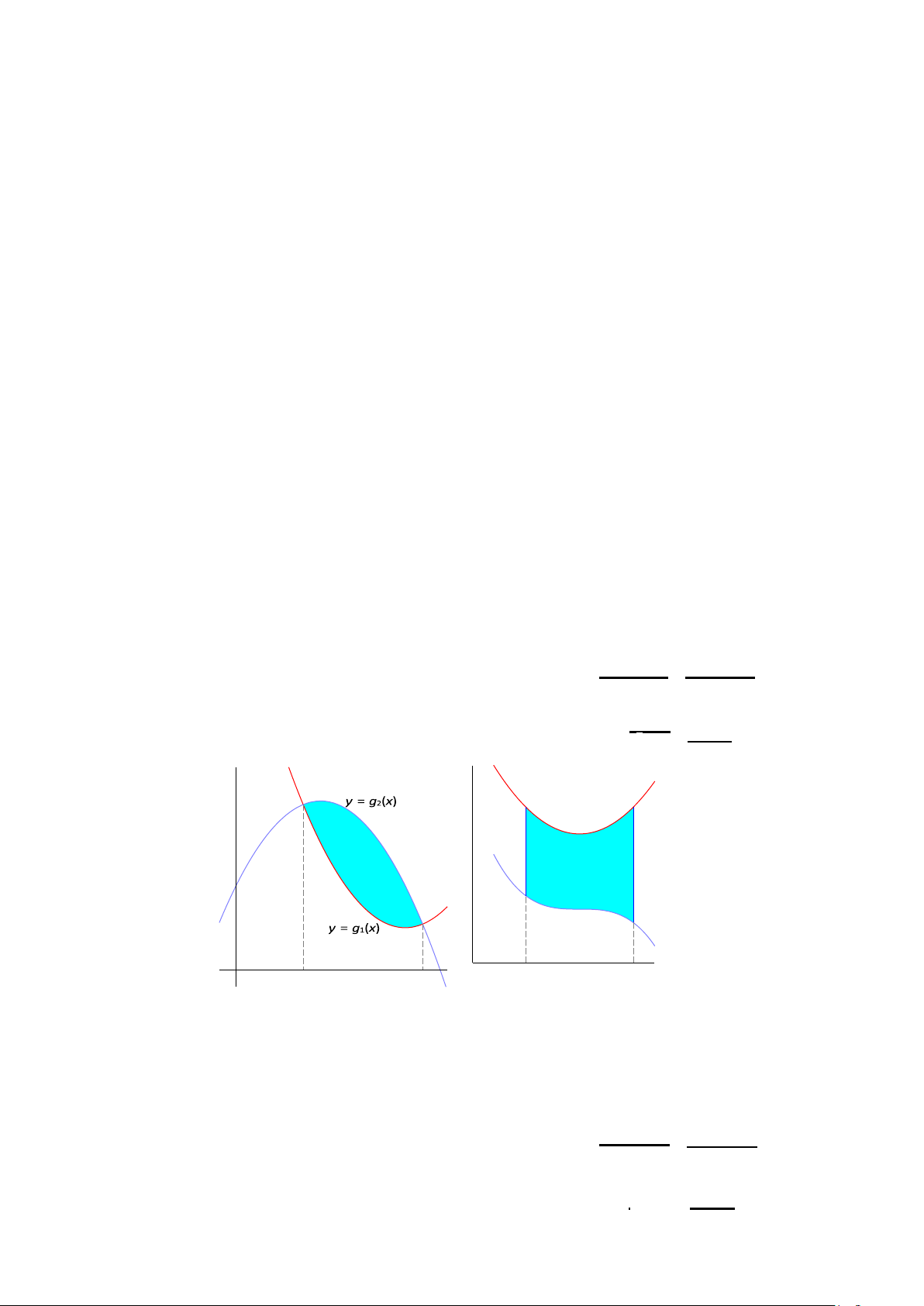
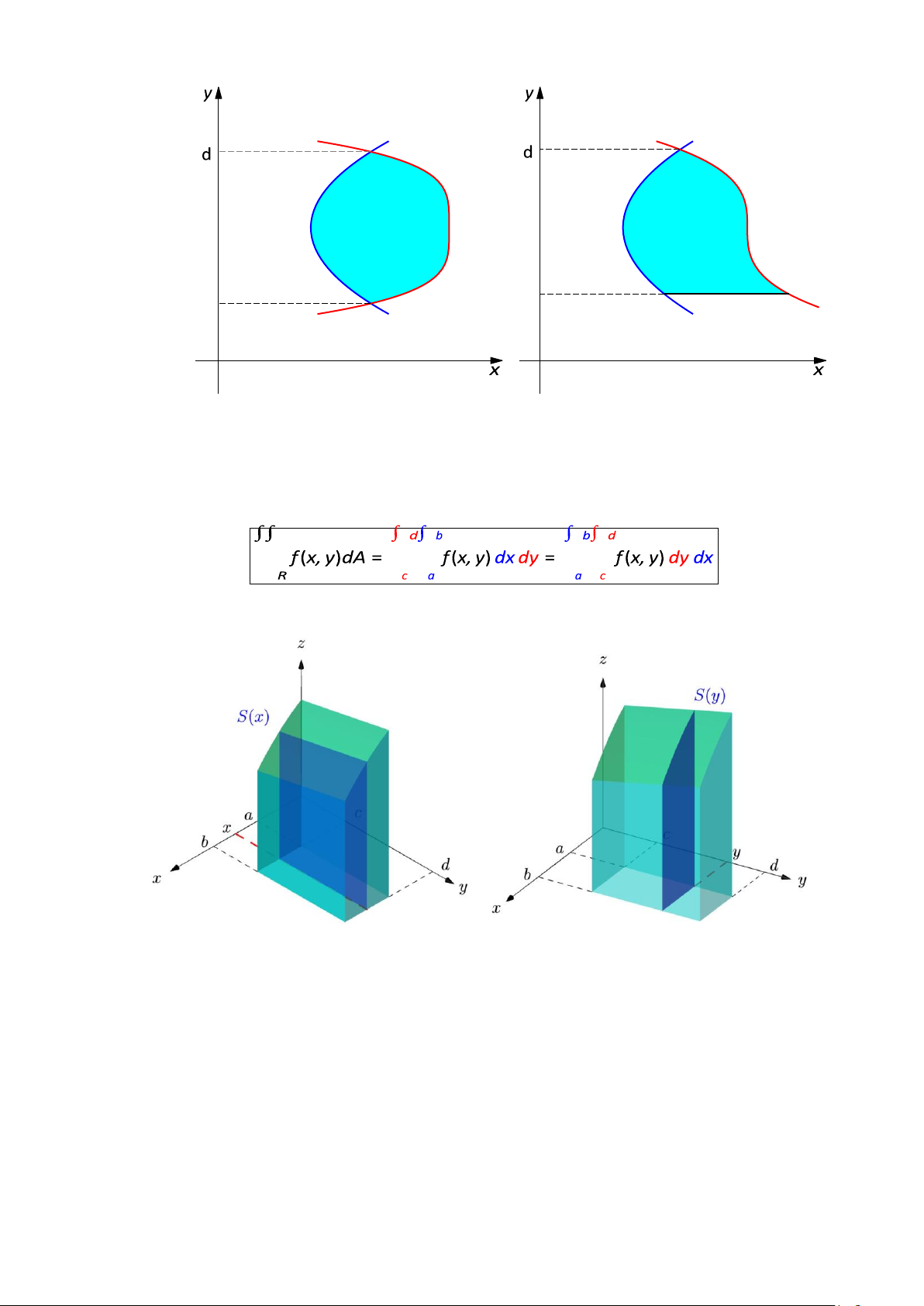
(a) Nếu f : D → R liên tục trên miền D có dạng
D = {(x, y) ∈ R2 : a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)} thì ∫∫ ∫ ∫ ¸ b g 2(x) b ∫ x` ˛ g2(x)
f (x, y)dxdy = dx
f (x, y)dy =
f (x, y)dy dx . D a g1(x)
a ` g1(x) ˛¸ x
y = g2(x)
y = g1(x) a b
(b) Nếu f : D → R liên tục trên miền D có dạng
D = {(x, y) ∈ R2 : c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)} thì ¸ ∫∫ ∫ ∫ d h 2(y) ∫ d ∫ x` ˛ h2(y)
f (x, y)dxdy = dy
f (x, y)dx =
f (x, y)dx dy . D c h1(y)
c ` h1(y) ˛¸ x Chả Văn Ti»p (BKĐN) 3 / 12 x x x x = = = = h h h h 1 2 1 2 ( ( ( ( y y y y ) ) ) ) c c
ĐịnH LÝ 1 (ĐịnH LÝ FuBINI). Nếu hàm f liên tục trên hình chǎ nhªt
R = {(x, y) : a ≤ x ≤ b, c ≤ y ≤ d}, thì
Hình 4: Minh họa công thác Fubini
4. Tích phân kép trong tọa đ® cực.
Nếu miền D trong h» tọa đ® cực có dạng
{(r, θ) : α ≤ θ ≤ β, r1(θ) ≤ r ≤ r2(θ)} thì ∫∫ ∫ ∫ β r 2(θ)
f (x, y)dxdy = dθ
f (r cos θ, r sin θ)rdr. D α r1(θ) Chả Văn Ti»p (BKĐN) 4 / 12 5. Công thác đỗi biến ∫∫ ∫∫
f (x, y)dxdy =
f (x(u, v), y(u, v))|J|dudv D Duv
trong đó Jacobian J được tính như sau: ∂(x, y) xr xr u v J = =
= xr yr − xr yr . ∂(x, y) y r r u v v u u yv
6. Úng dụng (Xem trong Giáo trình)
• Tính di»n tích hình phẫng
• Tính thễ tích khối trụ cong • Di»n tích m°t cong
• Khối lượng bản phẫng không thuần nhất • Tọa đ® trọng tâm • Moment 2 Matlab ∫∫
Ví dö 1 (TínH TíCH PHÂN DÙNG MATLAB). Tính
(|x| + |y|)dxdy |x|+|y|≤1 Matlab code
syms x y; f(x,y)=abs(x)+abs(y);
I=int(int(f,y,-(1-abs(x)),1-abs(x)),x,-1,1) 3 Ví dṇ mẫu ∫∫ Ví dö 2 (M 1
INH HọA địnH LÝ FuBINI). Tính tích phân kép sau dxdy
D (1 + x + y)2
trong đó D là miền giới hạn bởi các đường
x = 2y, y = 2x, x + y = 6.
Ví dö 3. Tính các tích phân sau bằng cách đỗi thá tự lấy tích phân ∫ 1 ∫ 3 2 x 1. e dxdy 0 3y ∫ 4 ∫ 2 1 2. √ dydx 0 x y3 + 1 Chả Văn Ti»p (BKĐN) 5 / 12 ∫ 1 ∫ π 2 √ 3. I =
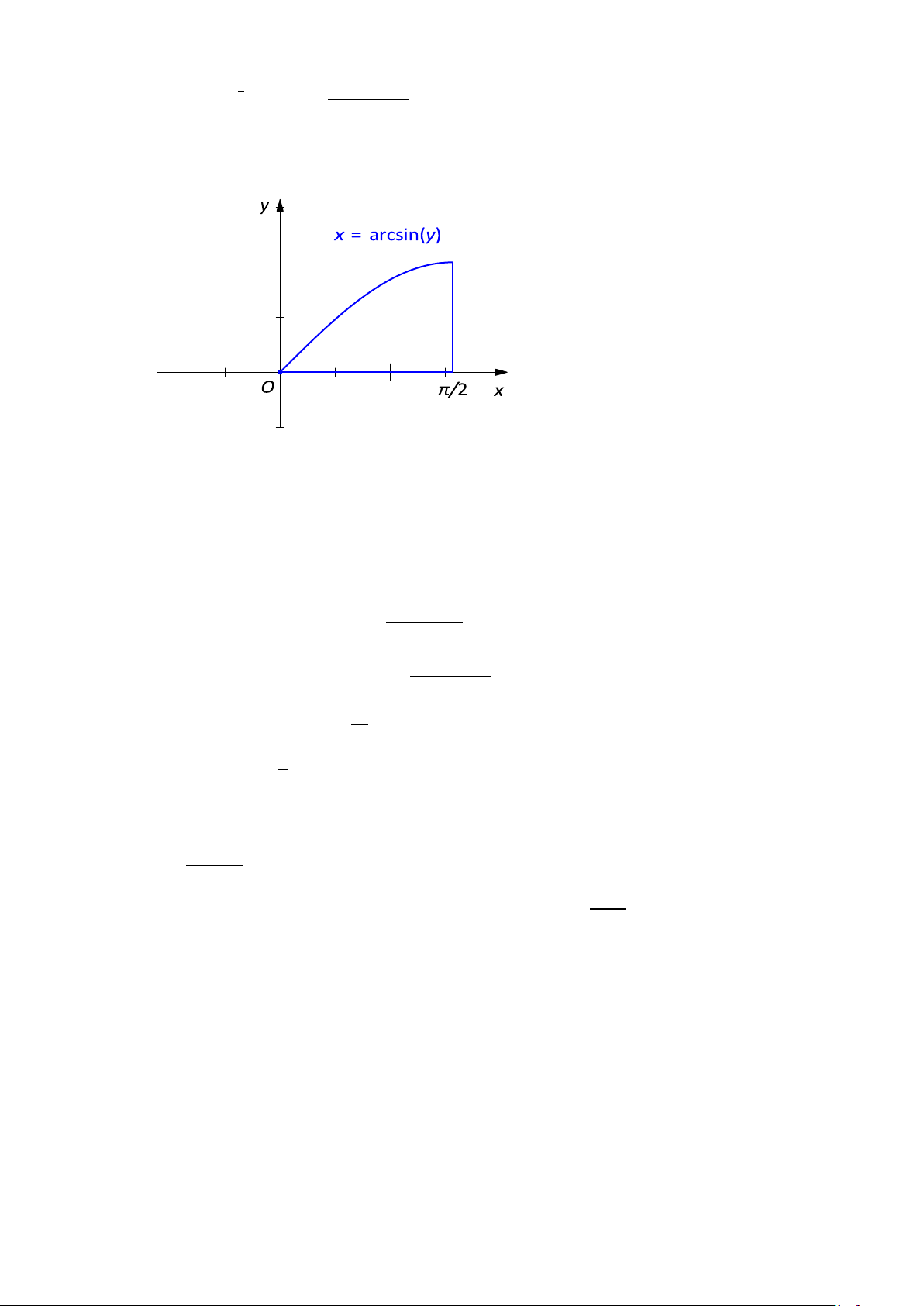
cos x 1 + cos2 xdxdy 0 arcsin y
D = {(x, y) ∈ R2 : 0 ≤ y ≤ 1, arcsin y ≤ x ≤ π/2} 1 −1 1
D = {(x, y) ∈ R2 : 0 ≤ x ≤ π/2, 0 ≤ y ≤ sin x} ∫ ∫ π/2 sin x √ I =
cos x 1 + cos2 xdydx 0 0 ∫ π/2 sin x √ =
y cos x 1 + cos2 x dx 0 ∫ 0 π/2 √ =
sin x cos x 1 + cos2 xdx (Đỗi biến t = 1 + cos2 x) 0∫ 1 dt = — t1/2 √ 2 2 1 8 − 1 ∫ . 2 =
t1/2dt = t3/2 2 = 2 1 3 1 3
Ví dö 4 (ĐỗI BIẾN TọA TọA đỘ CỰC). Tính thễ tích miền V bị ch°n bởi x2 +y2 +z2 ≤ 4 √
và z ≥ x2 + y2. ∫∫ dxdy
Ví dö 5 (ĐỗI BIẾN TỖNG QUÁT). Tính tích phân sau ,
S : 3y = x, y = x2y2 S
3x, y = 4 − 5x, y = 4 − x; 7 ∫∫
Ví dö 6 (Ví dö TỖNG HñP). Tính tích phân kép sau
xdxdy trong đó D là miền D
4x ≤ x2 + y2 ≤ 25.
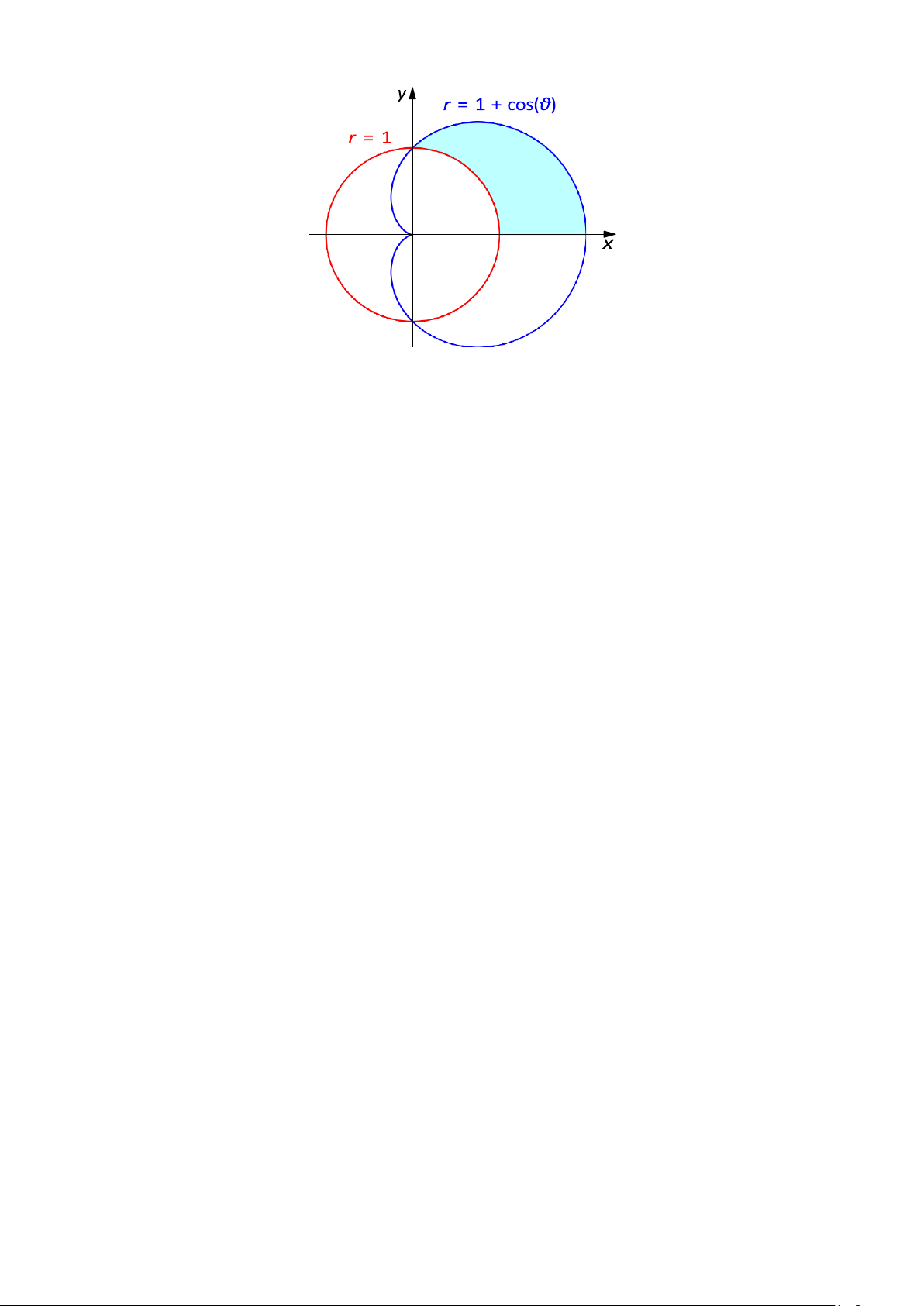
Ví dö 7 (Ứng döng TínH DIỆn TíCH). Tính di»n tích miền tô màu dưới đây
Ví dö 8 (CÁCH TínH TíCH ∫
PH ÂN LIÊN QUAN đẾN PHÂN PHỐI CHUẪN TẮC TRONG XÁC ∞
suẤT THỐNG KÊ). Tính I =
e−x2 dx 0 Chả Văn Ti»p (BKĐN) 6 / 12
Ví dö 9 (Ứng döng TínH THỄ TíCH). Tính thễ tích của miền nằm bên dưới paraboloid
z = 4 − (x − 2)2 − y2 bị ch°n bởi m°t phẫng xoy và bị giới hạn bởi (x − 1)2 + y2 = 1 và
(x − 2)2 + y2 = 4.
Ví dö 10 (Ứng döng TRONG VªT LÝ). 4 Luy»n tªp ∫∫ CÂU 1. Tính tích phân
y sin(xy)dA trong đó R = [1, 2] × [0, π] bằng 2 cách. R
CÂU 2. Tìm thễ tích của vªt rắn S bị ch°n bởi elliptic paraboloit x2 + 2y2 + z = 16, các
m°t phẫng x = 2, y = 2 và ba m°t phẫng tọa đ®. ∫∫ CÂU 3. Tính
x + 2ydA, trong đó D là bị ch°n bởi hai parabol y = 2x2 và y = 1 + x2. D
CÂU 4. Tính thễ tích vªt rắn nằm phía dưới paraboloid z = x2 + y2 và phía trên miền
D trong m°t phẫng xy bị ch°n bởi đường thẫng y = 2x và parabol y = x2.
CÂU 5. Tính thễ tích của tá di»n sau tạo bởi bốn m°t phẫng sau:x + 2y + z = 2, x =
2y, x = 0, z = 0. ∫ ∫
CÂU 6. Tính tích phân sau: 1 1 sin(y2)dydx. 0 x
CÂU 7. Tính các tích phân sau: ∫∫ (a)
y2dA, D = {(x, y)| − 1 ≤ y ≤ 1, −y − 2 ≤ x ≤ y} D ∫∫ (b)
xdA, D = {(x, y)|0 ≤ x ≤ π, 0 ≤ y ≤ sin x} D ∫∫ (c)
y2exydA, D = {(x, y)|0 ≤ y ≤ 4, 0 ≤ x ≤ y} D ∫∫ (d)
x cos ydA, D bị ch°n bởi y = 0, y = x , x = 1. D 2 ∫∫ (e)
(2x − y)dA, D bị ch°n bởi hình tròn tâm tại gốc tọa đ® và bán kính D bằng 2 Chả Văn Ti»p (BKĐN) 7 / 12
CÂU 8. Tính thễ tích của vªt rắn sau:
(a) Bên dưới m°t phẫng x + 2y − z = 0 và bên trên miền bị ch°n bởi y = x và y = x4
(b) Nằm dưới m°t z = xy và trên tam giác có ba đỉnh (1, 1), (4, 1) và (1,2)
(c) Bị ch°n bởi các m°t phẫng tọa đ® và m°t phẫng 3x + 2y + z = 6
(d) Bị ch°n bởi z = x2, y = x2 và các m°t phẫng z = 0, y = 4
(e) Bị ch°n bởi y = 1 − x2, y = x2 − 1 và các m°t phẫng x + y + z = 2, 2x +
2y − z + 10 = 0
CÂU 9. Vě miền lấy tích phân và đỗi thá tự lấy tích phân sau: ∫ 4 ∫ √x (a)
f (x, y)dydx 0 0 √ ∫ 3 ∫ 9−y2 (b) √
f (x, y)dxdy 0 − 9−y2 ∫ ∫ 2 ln x (c)
f (x, y)dydx 1 0
CÂU 10. Tính các tích phân sau bằng cách đỗi thá tự lấy tích phân ∫ 1 ∫ 3 2 x (a) e dxdy 0 3y ∫ 4 ∫ 2 1 (b) √ dydx 0 x y3 + 1 ∫ 1 ∫ π 2 √ (c)
cos x 1 + cos2 xdxdy 0 arcsin y
CÂU 11. Tính tích phân sau bằng cách chuyễn sang tọa đ® cực. ∫∫ (a)
(3x + 4y2)dA,
D là miền thu®c nảa m°t phẫng trên bị ch°n bởi hai D
đường tròn x2 + y2 = 1 và x2 + y2 = 4 √ ∫ 1 ∫ 1−y2 (b) √
(x2 + y2)dydx −1 − 1−y2 √ (c) ∫ ∫ a a−x2 √ dydx
−a − a2−x2 ∫ ∫ 0 0 2 (d) √ dydx √ − 1 + x2 + y2 1 — 1−x2 ∫ ∫ √ 1 0 4 x2 + y2 (e) dydx √ ___ −1 −
1−y2 1 + x2 + y2 √ ∫ ∫ 2
1−(x−1)2 x + y (f) dxdy 0 0 x2 + y2 Chả Văn Ti»p (BKĐN) 8 / 12
CÂU 12. Dùng tích phân hai lớp tính di»n tích các miền sau:
(a) Tính di»n tích của miền nằm bên trong đường cardioid r = 1 + cos 2θ và
bên ngoài đường tròn r = 1
(b) Tính di»n tích của m®t nhánh cách hoa hồng cho bởi r = 12 cos 3θ
(c) Tính di»n tích của miền nằm trong 2 đường cardioid r = 1 + θ và r = 1 − θ
CÂU 13. Sả dụng tọa độ cực tính thễ tích của các vật sau:
(a) Tính thễ tích của vªt thễ bị ch°n bởi m°t phẫng z = 0 và paraboloid
z = 1 − x2 − y2.
(b) Tính thễ tích của vªt thễ nằm bên dưới paraboloid z = x2 + y2, bên trên
m°t phẫng xy và bên trong của hình trụ x2 + y2 = 2x.
CÂU 14. Tính các tích phân kép sau (a) ∫∫ √
(12x2y2 + 16x3y3)dxdy, S : x = 1, y = x2, y = − x; S (b) ∫∫ √
(9x2y2 + 48x3y3)dxdy, S : x = 1, y = x, y = −x2; S (c) ∫∫ √
(36x2y2 − 96x3y3)dxdy, S : x = 1, y = 3 x, y = −x3; S (d) ∫∫ √
(18x2y2 + 32x3y3)dxdy, S : x = 1, y = x3, y = − 3 x; S (e) ∫∫ √
(27x2y2 + 48x3y3)dxdy, S : x = 1, y = x2, y = − 3 x; S (f) ∫∫ √
(18x2y2 + 32x3y3)dxdy, S : x = 1, y = 3 x, y = −x2; S (g) ∫∫ √
(18x2y2 + 32x3y3)dxdy, S : x = 1, y = x3, y = − x; S (h) ∫∫ √
(27x2y2 + 48x3y3)dxdy, S : x = 1, y = x, y = −x3; S (i) ∫∫ √
(4xy + 3x2y2)dxdy,
S : x = 1, y = x2, y = − x; S (j) ∫∫ √
(12xy + 9x2y2)dxdy,
S : x = 1, y = x, y = −x2. S ∫∫ CÂU 15. y2dxdy,
S : 1 ≤ xy ≤ 3, 0 < x ≤ y ≤ 2x; S Chả Văn Ti»p (BKĐN) 9 / 12 ∫∫ x4 CÂU 16. e 2 y2 dxdy,
S : y = x, y = 2x, y = x ; S ∫∫ CÂU 17. xdxdy,
S : y = x2, 8y = x2, x = y2, 8x = y2; y S ∫∫ CÂU 18.
(x + y)dxdy,
S : xy = 1, xy = 3, y = x, y = x − 2; S ∫∫ dxdy CÂU 19. ,
S : 2y = x, y = 2x, y = 1 − x, y = 1 − 3x; x2y2 S ∫∫ CÂU 20. x2dxdy,
S : xy = 2, xy = 4, y = x, y = 3x(x > 0, y > 0); S ∫∫ CÂU 21.
(2x + y)dxdy,
S : xy = 1, xy = 2, x + y = 3; S ∫∫ x CÂU 22. dxdy,
S : xy = 1, xy = 2, x + y = 3; y S ∫∫ CÂU 23. xydxdy,
S : |x + 2y| ≤ 3, |x − y| ≤ 3. S ∫∫
CÂU 24. Tính tích phân kép sau
x2 + y2dxdy trong đó D
D = {(x, y) ∈ R2 : 0 ≤ x ≤ 2, x2 ≤ y ≤ 2x}. ∫∫
CÂU 25. Tính tích phân kép
(x − 2y)dxdy trong đó D là miền giới hạn bởi các đường D 1
x = 0, y = 7 − x, y = x + 1. 2 ∫∫
CÂU 26. Tính tích phân kép sau
xdxdy trong đó D là miền giới hạn bởi D
2x ≤ x2 + y2 ≤ 6x, y ≤ x. ∫∫ √
CÂU 27. Tính tích phân kép sau
1 + x2 + y2dxdy trong đó D là miền giới hạn bởi D
2x ≤ x2 + y2 ≤ 16, x ≥ 0, y ≥ 0.
CÂU 28. Tính tích phân kép sau √ √ 0 ∫
∫ 1−x2 ln(1 + x2 + y2) dx √ dy. −1 0 x2 + y2 Chả Văn Ti»p (BKĐN) 10 / 12 ∫∫ 1 CÂU 29. Tính tích phân
cos πx2dxdy trong đó D là miền giới hạn bởi các đường D 2 sau
y = 0, x = 1, y = x. √
CÂU 30. Tính thễ tích của vªt thễ bị ch°n trên bởi nón z = 2 − x2 + y2 và bị ch°n
dưới bởi hình tròn (x − 1)2 + y2 ≤ 1. ∫∫ 1
CÂU 31. Tính tích phân kép sau
dxdy trong đó D là tam giác OAB
D (1 + x + y)3/2
với đỉnh O = (0, 0), A = (1, 0) và B = (1, 1).
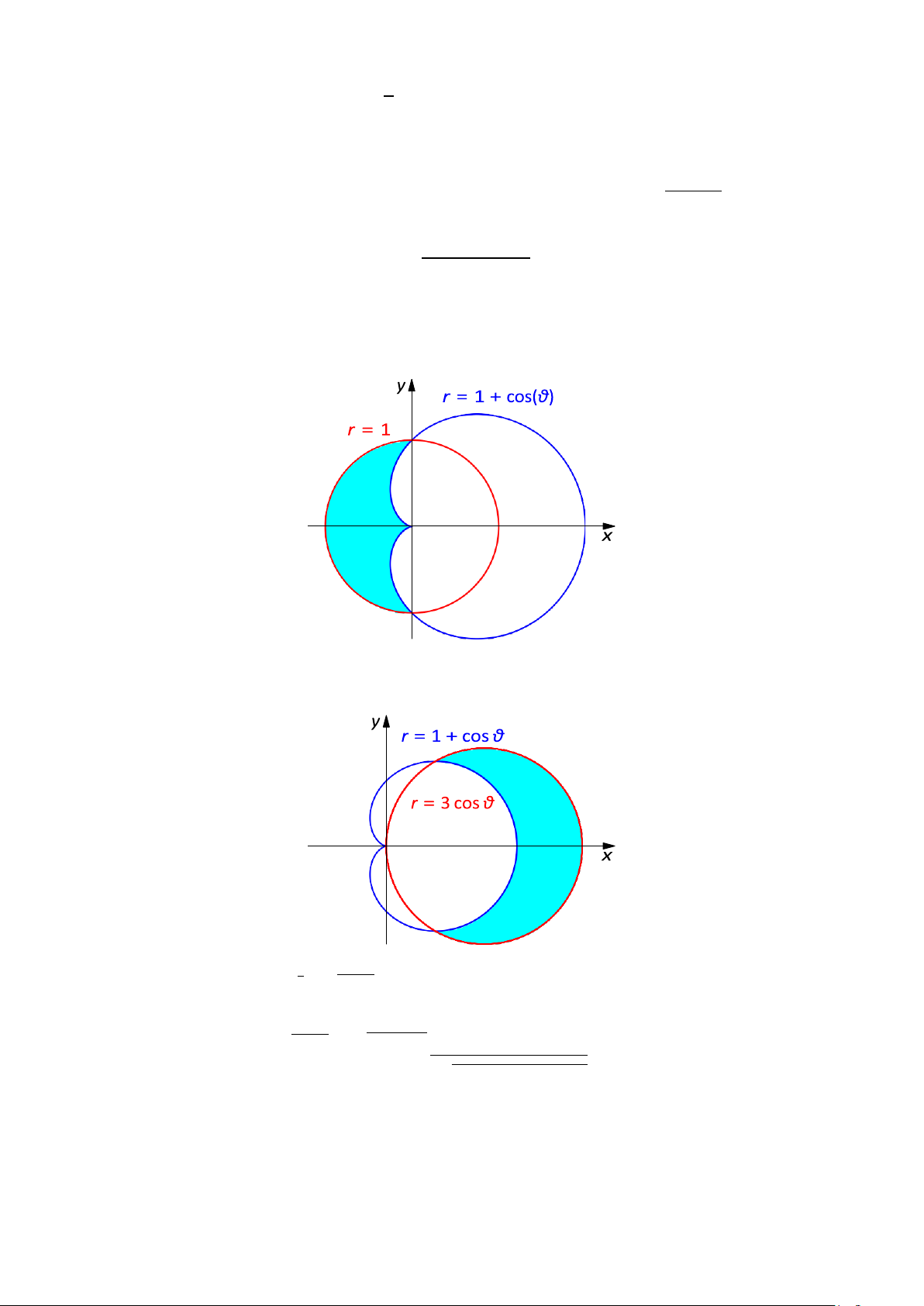
CÂU 32. Tính diện tích miền tô màu dưới đây
CÂU 33. Tính di»n tích miền tô màu dưới đây ∫ ∫ √ ∫ √ 4 2 z 4z−x2 CÂU 34. Tính dydxdz. 0 0 0 √ ∫ √ a ∫ a2−x2 ∫
a2−x2−y2 dzdydx CÂU 35. Tính √ . 0 0 0
a2 − x2 − y2 − z2
CÂU 36. Tính thễ tích của miền bị ch°n bởi m°t cầu x2 + y2 + z2 = a2 nằm trong m°t
trụ x2 + y2 = ay.
CÂU 37. Tính tích phân ∫∫ xdxdy D Chả Văn Ti»p (BKĐN) 11 / 12
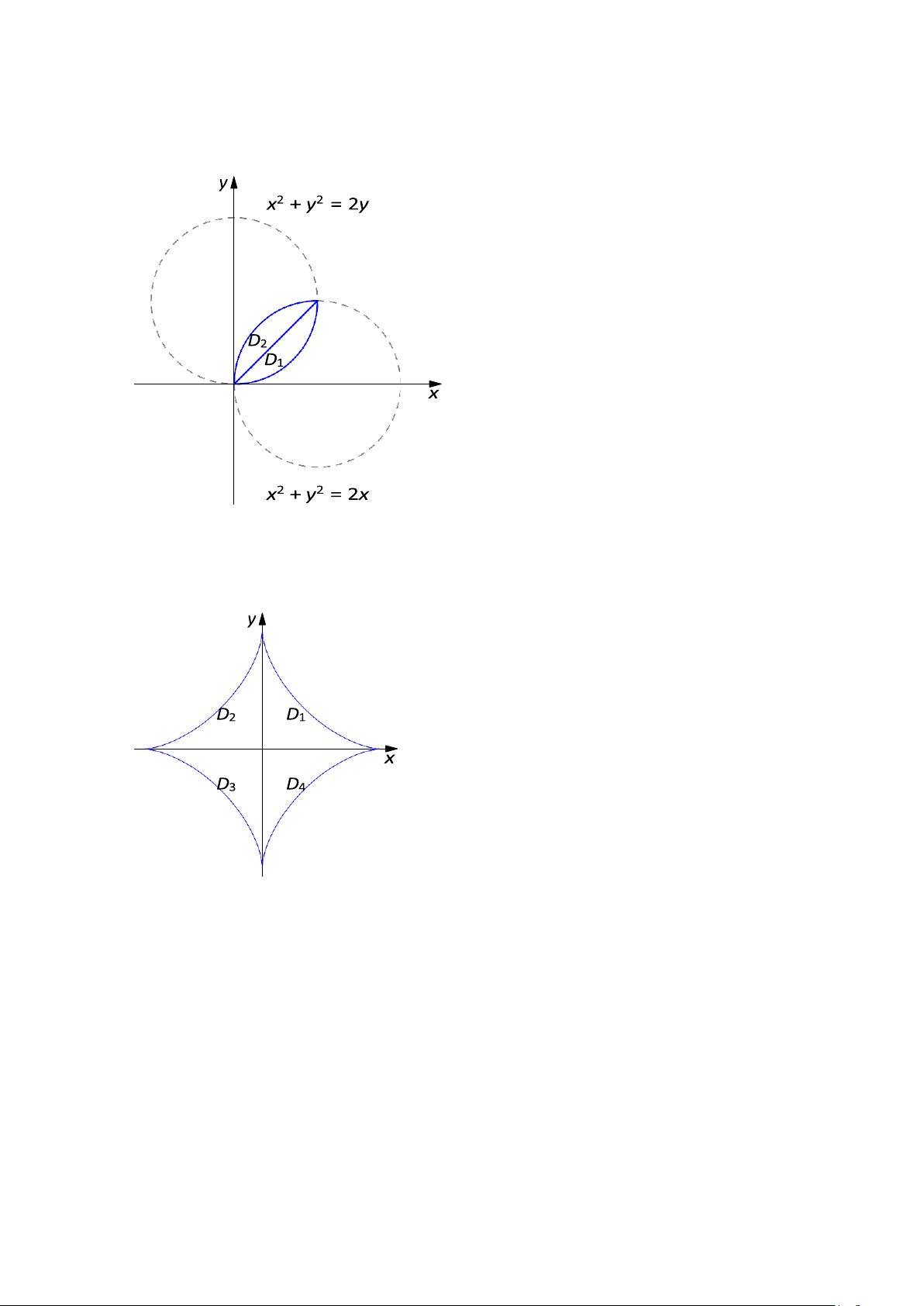
trong đó D là miền bị ch°n bởi hai đường tròn
x2 + y2 = 2x, x2 + y2 = 2y
CÂU 38. Tính di»n tích hình phẫng bị ch°n bởi đường cong phương trình
x2/3 + y2/3 = 1.
Bản phác thảo (còn lối sai) Lưu hành n®i b®. Làm hoàn thi»n m®t ý nhỏ được tính m®t điễm. Chả Văn Ti»p (BKĐN) 12 / 12