Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

Khóa học: "Giải tích 2 HCMUT" ĐẶNG TIẾN QUANG
Tóm tắt nội dung thi cuối kỳ Giải tích 2 (Chỉ áp dụng cho HK232)
1 Tích phân đường (5 câu)
1.1 Tham số hóa đường cong ( x = t
a/ PTTS đường cong y = y(x), a ≤ x ≤ b:
, a ≤ t ≤ b y = y(t) ( x = x
b/ PTTS đoạn thẳng AB:
A + (xB − xA)t , 0 ≤ t ≤ 1
y = yA + (yB − yA)t
( x = R cos t
c/ PTTS đường tròn x2 + y2 = R2:
, 0 ≤ t ≤ 2π
y = R sin t y
y = mx ⇒ t = arctan
+ kπ = arctan(m) + kπ x (
x = a + R cos t
d/ PTTS đường tròn (x − a)2 + (y − b)2 = R2:
, 0 ≤ t ≤ 2π
y = b + R sin t y − b
y = mx + n đi qua (a, b) ⇒ t = arctan
+ kπ = arctan(m) + kπ x − a ( x2 y2
x = a cos t e/ PTTS đường ellipse + = 1 :
, 0 ≤ t ≤ 2π a2 b2
y = b sin t y a a
y = mx ⇒ t = arctan .
+ kπ = arctan m. + kπ x b b
f/ Tham số hóa trong tọa độ cực (đường tròn + ellipse):
Thay x = r cos ϕ, y = r sin ϕ vào phương trình đường cong C để xác định r = r(ϕ). (
Khi đó C: x = r(ϕ). cos ϕ
y = r(ϕ). sin ϕ y Đường tròn: y
tan ϕ = x ⇒ ϕ = arctan + kπ x y a y a
Ellipse: tan ϕ = . ⇒ ϕ = arctan . + kπ x b x b Lưu ý:
Khi đề cho C là đường tròn hoặc ellipse, thì trong đầu luôn nhớ là có 2 cách tham số.
Hãy nhìn vào các đáp án để suy luận ra cách tham số.
Nếu đáp án có dạng x = f (t) cos(t), y = f (t) sin(t) thì tham số theo tọa độ cực.
g/ Tham số hóa đường cong trong không gian: ( F (x, y) = 0
Bước 1: Biến đổi, đưa đường cong về dạng:
z = f (x, y) ( x = x(t)
Bước 2: Tham số hóa phẳng cho đường cong F (x, y) = 0:
, a ≤ t ≤ b y = y(t)
1.2 Tích phân đường loại 1 ∫ ∫
Tích phân đường loại 1 có dạng:
f (x, y) ds hoặc
f (x, y, z) ds C C ∫∫
Cần phân biệt ký hiệu tích phân đường loại 1 với tích phân mặt loại 1
f (x, y, z) dS S
Phương pháp giải: Đưa về tích phân xác định (tích phân 1 biến) ( ∫ ∫ t2 x = x(t) √ a/ TH1: C :
, t1 ≤ t ≤ t2 ⇒
f (x, y) ds =
f x(t), y(t)
x′(t)2 + y′(t)2 dt (thi nhiều) y = y(t) C t1 ∫ ∫ b √
b/ TH2: C : y = y(x), a ≤ x ≤ b ⇒
f (x, y) ds = f x, y(x)
1 + y′(x)2 dx C a ∫ ∫ d √
c/ TH3: C : x = x(y), c ≤ y ≤ d ⇒
f (x, y) ds =
f x(y), y
1 + x′(y)2 dy C c ∫ ∫ β √
d/ TH4: C : r = r(ϕ), α ≤ ϕ ≤ β ⇒
f (x, y) ds =
f r(ϕ) cos ϕ, r(ϕ) sin ϕ
r(ϕ)2 + r′(ϕ)2 dϕ C α
Được phép thay phương trình đường cong C vào hàm f (x, y) dưới dấu tích phân.
Ứng dụng của tích phân đường loại 1:
a/ Tính độ dài của đường C: ∫ L = 1 ds C
b/ Tính khối lượng sợi dây kim loại mỏng có hàm mật độ ρ(x, y): ∫ m =
ρ(x, y) ds C
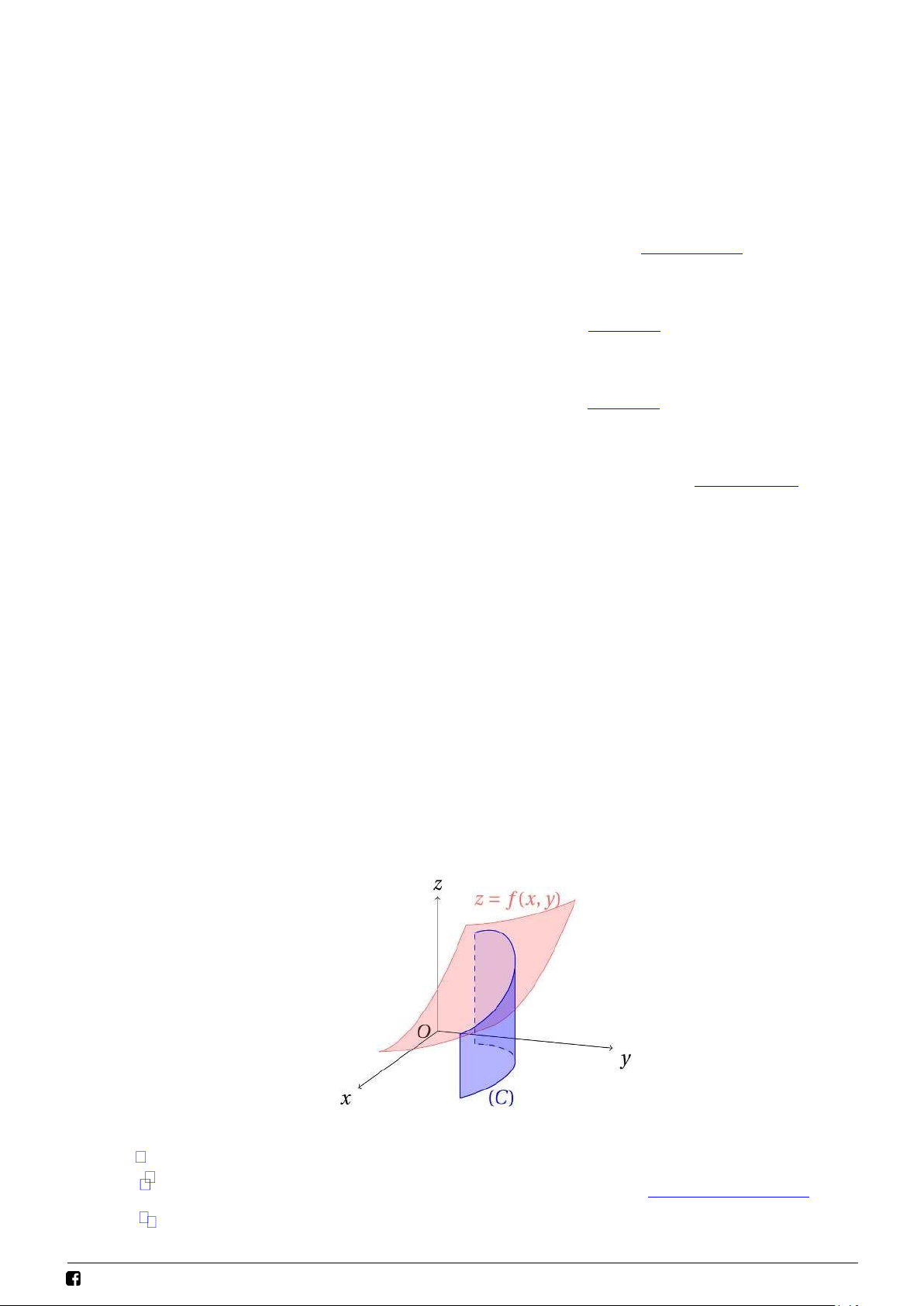
c/ Tính diện tích mặt trụ song song với trục Oz có biên dưới là đường cong C nằm trong mp Oxy và
biên trên nằm trong mặt cong z = f (x, y): ∫ S =
f (x, y) ds C
Tích phân đường loại 1 trong không gian: 
 x = x(t) ∫ ∫ t2 C : y = y(t) √ , t
f (x, y, z) ds =
f x(t), y(t), z(t)
x′(t)2 + y′(t)2 + z′(t)2 dt  1 ≤ t ≤ t2 ⇒
z = z(t) C t1 Trang 2
1.3 Tích phân đường loại 2 ∫ ∫
Tích phân đường loại 2 là tích phân có dạng F · dr = Pdx + Qdy C C
với F = ⟨P, Q⟩ = P i + Q j là một trường véctơ ∫
HK232 KHÔNG THI tích phân đường loại 2 trong không gian
Pdx + Qdy + Rdz C
Phương pháp giải: Đưa về tích phân xác định (tích phân 1 biến) ( ∫ ∫ ∫ t2 x = x(t)
, t : t → t ⇒ a/ TH1: C : 1 2 F · dr = Pdx + Qdy =
P.x′(t) + Q.y′(t) dt y = y(t) C C t1
với dx = x′(t)dt, dy = y′(t)dt ∫ ∫ ∫
b/ TH2: C : y = y(x), x : a → b ⇒ F · dr = Pdx + Qdy =
P + Q.y′(x) dx C C C với
dy = y′(x)dx ∫ ∫ ∫d
c/ TH3: C : x = x(y), y : c → d ⇒ F · dr = Pdx + Qdy =
P.x′(y) + Q dy C C c
với dx = x′(y)dy (
x = r(ϕ) cos ϕ
d/ TH4: C : r = r(ϕ), ϕ : α → β ⇒ C :
, ϕ : α → β ⇒ làm tương tự TH1
y = r(ϕ) sin ϕ
Được phép thay phương trình đường cong C vào hàm P và Q.
Ứng dụng của tích phân đường loại 2:
a/ Công của trường lực F = ⟨P, Q⟩ = P i + Q j tác dụng lên vật làm vật di chuyển theo đường cong C: ∫ W = Pdx + Qdy C
b/ Diện tích miền D được bao quanh bởi đường cong C I I I — 1 S(D) = xdy = ydx = xdy − ydx C+ C+ 2 C+
Xem chi tiết hơn ở phần ứng dụng của định lý Green
1.4 Định lý Green và fíng dụng Định lý Green:
Nếu C là biên định hướng dương của miền D thì ∫ ∫∫
Pdx + Qdy G r=ee n +
(Qx − Py)dxdy + C D
Đề thi hay cho miền D đối xứng qua trục tọa độ, nên trước khi tính tích phân kép, em hãy bỏ đi các hàm
lẻ (nếu có) tương ứng với tính đối xứng.
Khi đã chuyển về tích phân kép thì không được phép thế phương trình C vào hàm dưới dấu tích phân.
Ứng dụng của định lý Green:
Diện tích miền D với C là biên định hướng dương của D ∫ ∫ ∫ 1 S(D) = xdy = — ydx = xdy − ydx C+ C+ 2 C+ ∫ ∫ b — ′
Nếu x(t) tính đạo hàm đơn giản hơn y(t) thì dùng công thức S(D) = ydx =
−y(t).x (t) dt C a ∫ ∫ b
Nếu y(t) tính đạo hàm đơn giản hơn x(t) thì dùng công thức S(D) = xdy =
x(t).y ′( t) dt C a
Do thi trắc nghiệm nên em không cần quan tâm đến chiều định hướng dương của C là t : a → b hay t : b → a ∫ ∫ b a Vì
x(t).y′(t) dt và
x(t).y′(t) dt đều có độ lớn bằng nhau, và ta chỉ cần quan tâm đến độ lớn của 1 a b trong 2 tích phân này. ∫ b
Như vậy, điều cần thiết là em phải tính đúng y ′( t) để ráp vào công thức S(D) =
x(t).y ′( t) dt ∫ a b
hoặc tính đúng x′(t) để ráp vào công thức S(D) =
—y (t).x′(t) dt. a Tóm lại, ∫ ∫ b b S(D) =
x(t).y′(t) dt =
y(t).x′(t) dt a a
1.5 Tích phân không phụ thuộc đường đi ∫ Tích phân
Pdx + Qdy không phụ thuộc vào đường đi (hay F = P i + Q j là một trường bảo toàn) khi và C chỉ khi Qx = Py
Khi đó, nếu C là đường cong đi từ điểm A(xA, yA) đến điểm B(xB, yB) thì ta đổi đường đi thành 2 đoạn
thẳng song song với 2 trục tọa độ: C ∫
∫ 1: x = xA, y : y∫ A → yB và C2: y = yB, x : xA → xB Pdx + Qdy = Pdx + Qdy +
Pdx + Qdy = I1 + I2 C C1 C2 ∫ ∫ yB
C1: x = xA = const ⇒ dx = 0 ⇒ I1 = Qdy =
Q(xA, y) dy yA C1 ∫ ∫ xB
C2: y = yB = const ⇒ dy = 0 ⇒ I2 = Pdx
P (x, yB) dx xA C2 Trang 4 1.6 Ví dụ mẫu ∫ ∫ 3 √ ∫ 3 5 √ 2 2 I = 1 + (6x)2 dx = (4x − 4xy ) 2 ds =
4x − 4x(3x ) 4x − 36x
1 + 36x2 dx = −67390.0692 C 1 1 ∫ ∫ 4 h i√ I =
(3x − 6y) ds =
3(6 − 4t) − 6(3t − 1) (−4)2 + 32 dt = −720 C 0
3/ Một sợi dây mỏng có hình dạng là phần đường tròn tâm O bán kính 3.8 trong góc phần tư thứ nhất.
Biết hàm mật độ là ρ(x, y) = x + 1.6y, tính khối lượng của sợi dây. ( C:
x = 3.8 cos t
, 0 ≤ t ≤ π/2
y = 3.8 sin t ∫ ∫ π/2 h i√ m =
(x + 1.6y) ds =
3.8 cos t + 1.6 × 3.8 sin t
(−3.8 sin t)2 + (3.8 cos t)2 dt = 37.544 C 0
4/ Một bờ tường mỏng có dạng trụ đứng với đáy là đường tròn bán kính 6 m nằm trong mặt phẳng Oxy
và được xác định bởi phương trình:
x = 6 + 6 cos t, y = 6 sin t, với t ∈ [0, 2π]
Chiều cao của tường ở vị trí (x, y) là h(x, y) = x2 + y2 (m). Biết rằng mỗi lít sơn tô được 100 m2. Hỏi sẽ
mất bao nhiêu lít sơn để tô cả hai mặt của bức tường? ( C: x = 6 + 6 cos t
, 0 ≤ t ≤ 2π y = 6 sin t Diện tích bờ tường: ∫ ∫ 2π √ S =
(x2 + y2 ) ds =
(6 + 6 cos t)2 + (6 sin t) 2
(−6 sin t)2 + (6 cos t)2 dt = 864π C 0 864π × 2
Lượng sơn để tô hai mặt tường là = 54.2867 (lít) 100 ∫ ∫ 2 h 2i I =
3xy2 dx − 4xdy =
3 × t 3 × (t 3 — 1) 2 × 3t 2 — 4t 3 × 3t dt = 2017.75 C 1 ∫ ∫ 9 h i I =
4ydx − 2xydy =
4y × 2(y − 5) − 2 × (y − 5) 2 × y dy = 72 C 3 √
C: y = 0.2 x, x : 4.4 → 5.6 ∫ ∫ 5.6 √ √ 0.2 W =
4.7ydx − 5.3xydy = 4.7 × 0.2 x × √ C
x − 5.3x × 0.2 dx = 1.8848 4.4 2 x
Nếu đề không nói cụ thể hướng của C thì mặc định lấy định hướng dương. I ∫∫ ∫∫ 2 I =
5x2y dx − 4xy dy Gr=een
(−4y − 5x2)dxdy =
−5x dxdy (miền đối xứng, bỏ hàm lẻ) + C+ D D ∫ ∫ √ √ ∫ ∫ 2π 6 2π 6 I = dϕ
−5r 2 cos2 ϕ .rdr = cos2 ϕ dϕ −5r 3dr
= −45π = −141.3717 0 0 0 0
9/ Tính công thực hiện bởi trường lực F = 10x4y i + 6y3 j tác dụng lên chất điểm làm di chuyển một lượt
đường tròn x2 + y2 = 8 theo hướng ngược chiều kim đồng hồ (counterclockwise).
C+: x2 + y2 = 8 ⇒ D: x2 + y2 ≤ 8 ∫ ∫∫ ∫∫ 4 W =
10x4ydx + 6y3dy Gr=een
(0 − 10x4)dxdy = −10x dxdy + C+ D D ∫ ∫ √ √ ∫ ∫ 2π 8 2π 8 I = dϕ
−10r 4 cos4 ϕ .rdr = cos4 ϕ dϕ −10r 5dr
= −640π = −2010.6193 0 0 0 0 Trang 6
Khóa học: "Giải tích 2 HCMUT" ĐẶNG TIẾN QUANG ∫ ∫∫ I =
2.6x2ydx − 1.6xy2dy Gr=een +
− 1.6y2 − 2.6x2 dxdy C+ ABC 2
Phương trình AC: y = x + 6 3 2
Phương trình BC: y = — x + 6 3 ∫ ∫ ∫∫ 9 −2x/3+6 2 2 I =
— 1.6y — 2.6x 2 dxdy = 2 dx
— 1.6y — 2.6x 2 dy ABC 0 0 ∫ 9 h 1 i 3 2 I = 2
— 1.6. .(−2x/3 + 6) — 2.6x .(−2x/3 + 6) dx = −2413.8 0 3
Thi trắc nghiệm, không cần quan tâm chiều dương của t, chỉ cần quan tâm độ lớn tích phân ∫ ∫ 0 S(D) = −ydx = 2
− 13 cos(t) − 5 cos(2t) − 2 cos(3t) − cos(4t) × (−16).3 sin t. cos t dt = 180π C −2π 4
F = P i + Q j với P = αy2, Q = −4.4xy ∫
F · dr không phụ thuộc đường đi ⇔ Qx = Py ⇔ −4.4y = 2αy ⇒ α = −2.2 C ∫ W =
F · dr không phụ thuộc đường đi ⇒ ta chỉ quan tâm điểm đầu và điểm cuối. C 3 — 10 — 10
Khóa học: "Giải tích 2 HCMUT" ĐẶNG TIẾN QUANG
P = x3y4, Q = x4y3, Qx = 4x3y3, Py = 4x3y3
Ta có Qx = Py ⇒ I là tích phân không phụ thuộc đường đi ( ( ∫ ∫ − 6,6)
t = 0 ⇒ x = 0, y = −2 ⇒ I =
x3y4 dx + x4y3 dy =
x3y4 dx + x4y3 dy
t = 1 ⇒ x = −6, y = 6 C (0,−2)
Gọi C∫ 1: x = 0, y : −2 → 6 và C
∫ 2: y = 6, x : 0 → −6 I1 =
x3y4 dx + x4y3 dy =
x4y3 dy = 0 C1 C1 ∫ ∫ ∫ −6 3 I1 =
x3y4 dx + x4y3 dy =
x3y4 dx = x × 4 6 dy = 419904 0 C2 C2
I = I1 + I2 = 419904
14/ Xem Câu 11 trong đề 222 Final Test,
Xem Câu 11 trong đề 222 Sample Test 1,
Xem Câu 11 trong đề 222 Sample Test 2. Trang 8