Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

Mục lục 1 Giới thiệu 3
2 Các phương pháp tìm giá trị cực đại và cực tiểu của hàm hai biến 3
2.1 Phân loại điểm tới hạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2 Khoảng đóng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 Nhân tử Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3 So sánh ưu điểm và nhược điểm của 3 phương pháp 8 4 Bài tập 8
4.1 Sec 14.8 exc. 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.2 Sec 14.8 exc. 36 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 5 Kết Luận 10 2 1 Giới thiệu
Dự án này tập trung vào việc tìm giá trị cực đại và cực tiểu của hàm hai biến. Chúng ta sẽ giới
thiệu lại các phương pháp để giải quyết vấn đề này và áp dụng chúng vào ba ví dụ cụ thể. Chúng
ta cũng sẽ sử dụng một phần mềm miễn phí để giải quyết vấn đề Sec 14.8 exc.2,36 và vấn đề tùy chọn khác.
2 Các phương pháp tìm giá trị cực đại và cực tiểu của hàm hai biến
2.1 Phân loại điểm tới hạn
Tiêu chuẩn đạo hàm cấp hai Giả sử các đạo hàm riêng cấp hai của f liên tục trên một đĩa tròn
tâm (a,b), và giả sử fx(a, b) = 0 và fy(a, b) = 0 [tức là, (a,b) là điểm tới hạn của f]. Cho
D = D(a, b) = fxx(a, b)fyy(a, b) − [fxy(a, b)]2
(a) Nếu D > 0 và fxx(a, b) > 0 thì f (a, b) là cực tiểu địa phương.
(b) Nếu D > 0 và fxx(a, b) < 0 thì f (a, b) là cực đại địa phương.
(c) Nếu D < 0 thì f (a, b) không phải là cực đại hoặc cực tiểu địa phương.
Lưu ý 1: Trong trường hợp (c), điểm (a, b) được gọi là điểm yên ngựa của f và đồ thị của
f cắt mặt phẳng tiếp xúc tại (a, b).
Lưu ý 2: Nếu D = 0, phép kiểm tra không có thông tin: f có thể cực đại địa phương hoặc
cực tiểu địa phương tại (a, b) hoặc (a, b) có thể là điểm yên ngựa của f .
Lưu ý 3: Để nhớ công thức tính D, cần viết nó như một định thức: (Ma trận Hessian) f D = xx fxy 2 = fxx f f yy — (fxy) yx fyy
Ví dụ 1 Tìm cực trị của hàm số dưới đây:
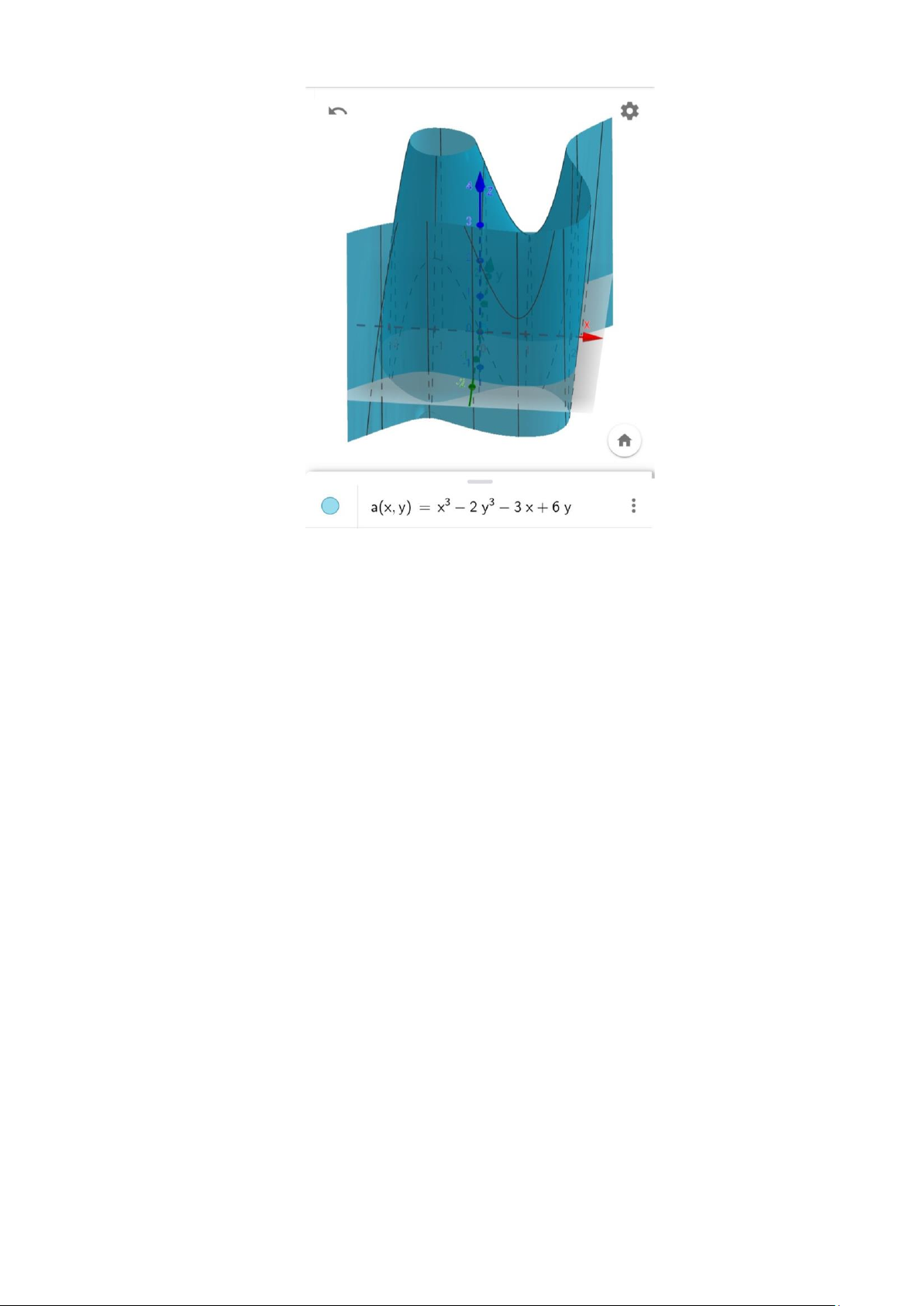
f (x, y) = x3 − 2y3− 3x + 6y
Trước hết ta đi tìm đạo hàm riêng: fx = 3x2 − 3 fy = −6y2 + 6
Vì các đạo hàm riêng này tồn tại mọi noi nên các điểm tới hạn xảy ra khi cả 2 đạo hàm riêng bằng 0
fx = 3x2 − 3 = 0
fy = −6y2 + 6 = 0 3
Hình 1: Đồ thị minh họa Ví dụ 1
Giải hệ trên ta thu được 4 điểm dừng: M (1, 1), N (1− , 1), P (− 1, 1), Q( −
1, − 1). Tiếp đến,
ta tìm đạo hàm riêng cấp hai: fxx = 6x fyy = −12y fxy = 0 2
⇒ D(x, y) = fxxfyy − (fxy) = 6x(−12y) − 0
Tại M (1, 1): fxx(1, 1) = 6 > 0, D(1, 1) = −72 < 0 Vậy hàm không đạt cực trị tại M (1, 1).
Tại N (1, −1): fxx = 6 > 0, D(1, −1) = 72 > 0 Vậy hàm đạt cực tiểu địa phương tại
N (1, −1). Giá trị cực tiểu địa phương f (1, −1) = −6.
Tại P (−1, 1): fxx = −6 < 0, D(−1, 1) = 72 > 0 Vậy hàm đạt cực đại địa phương tại
P (−1, 1). Giá trị cực đại địa phương f (−1, 1) = 6.
Tại Q(−1, −1): fxx = −6 < 0, D(−1, −1) = −72 < 0 Vậy hàm không đạt cực trị tại Q(−1, −1). 2.2 Khoảng đóng
Tập hợp đóng trong R2 là một tập hợp chứa tất cả các điểm biên. Một điểm biên D là điểm
(a, b) sao cho mọi đĩa tròn tâm (a, b) chức các điểm trong D và cả các điểm không ở trong D.
Tập hợp bị chặn trong R2 là tập hợp mà được chứa bên trong một đĩa tròn nào đó. Nói cách 4
khác, nó là giới hạn trong một phạm vi. Khi đó, theo tập hợp đóng và bị chặn, ta có thể phát
biểu Định lý giá trị cực biên của hàm hai biến.
Định lý giá trị cực biên của hàm hai biến Nếu f liên tục trên tập hợp D đóng và bị chặn
trong R2, thì f có giá trị cực đại tuyệt đối f (x1, y1) và giá trị cuẹ tiểu tuyệt đối f (x2, y2) tại các
điểm (x1, y1) và (x2, y2) náo đó trong D.
Để tìm các cực trị được khẳng định bởi Định lý trên, chúng ta lưu ý rằng, nếu f có cực trị tại
(x1, y1) là điểm tới hạn của f hoặc điểm biên của D. Do đó chúng ta có Phương pháp Khoảng
đóng mở rộng như sau.
Để tìm giá trị cực đại tuyệt đối và giá trị cực tiểu tuyệt đối của hàm liên tục f trên tập hợp
đóng và bị chặn D:
1. Tìm các giá trị của f tại các điểm tới hạn của f trong D.
2. Tìm các cực trị của f trên biên của D.
3. Giá trị lớn nhất trong số các giá trị từ bước 1 và bước 2 là giá trị cực đại tuyệt đối; giá trị
nhỏ nhất trong số các giá trị này là giá trị cực tiểu tuyệt đối.
Ví dụ 2 Bài 33 Section 14.7
Đạo hàm riêng của f (x, y) = 0 dẫn đến (2x + 2xy, 2y + x2) = (0, 0), từ đó suy ra:
2x(1 + y) = 0 và 2y + x2 = 0
⇒ x = 0 hoặc y = −1 và 2y + x2 = 0
Khi x = 0 ⇒ 2y + 02 = 0 ⇒ y = 0 √
Khi y = −1 ⇒ 2(−1) + x2 = 0 ⇒ x = ± 2.
Vì vậy (0, 0) là số tới hạn duy nhất trong D vì — 1 ≤ x ≤ 1 và f (0, 0) = 4.
Tiếp theo, ta tìm các điểm tối ưu trên L1, L2, L3, L4.
Xét L1 : y = −1 2 2 2
⇒ f (x, −1) = x + (−1) + x (−1) + 4
= x2 + 1 − x2 + 4 = 5
⇒ f (x, −1) = 5 với − 1 ≤ x ≤ 1. Xét L2, x = 1. 2 2 2
⇒ f (1, y) = 1 + y + 1 (y) + 4 = y2 + y + 5 ∂f 1 ⇒
(1, y) = 2y + 1 = 0 ⇒ y = −
là một số tới hạn. ∂y 2
f (1, −1) = 5, 1 19 f (1, − ) = , 2 4
f (1, 1) = 7.
Tương tự, ta có thể xét L3 và L4, và cuối cùng ta kết luận rằng f (±
1, 1) = 7 là giá trị lớn
nhất tuyệt đối và f (0, 0) = 4 là giá trị nhỏ nhất tuyệt đối. 5
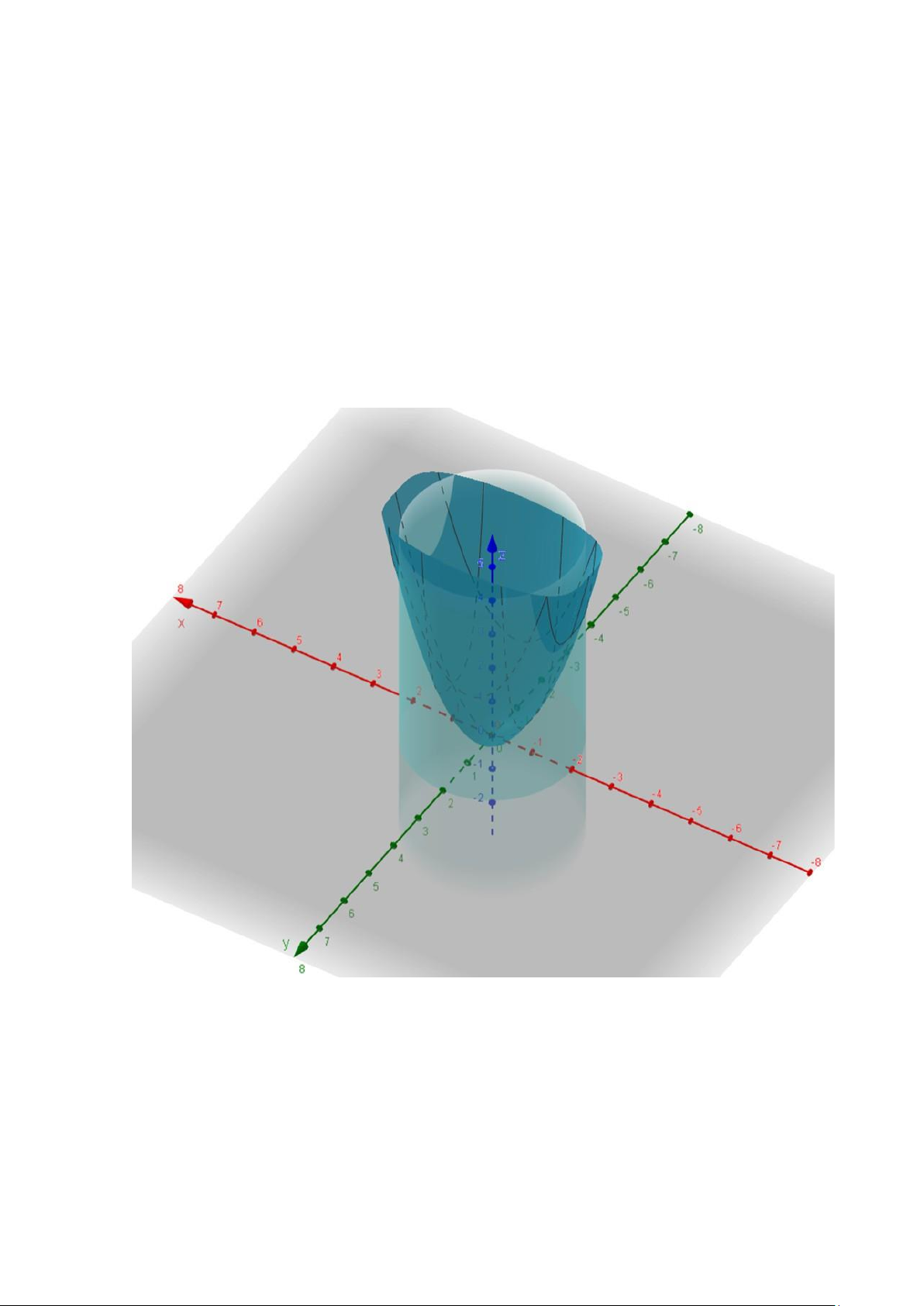
Hình 2: Đồ thị minh họa ví dụ 2
2.3 Nhân tử Lagrange
Phương Pháp Nhân Tử Lagrange Để tìm giá trị lớn nhất và nhỏ nhất của f (x, y, z) phụ thuộc
vào điều kiện ràng buộc g(x, y, z) = k [giả sử các cực trị này tồn tại v ∇
à g(x) ̸ = 0 trên mặt
g(x, y, z) = k ]:
(a) Tìm tất cả các giá trị của x, y, z và λ sao cho
∇f (x, y, z) = λ∇g(x, y, z)
và g(x, y, z) = k
(b) Tính f tại mọi điểm (x, y, z) tìm được từ bước (a). Giá trị lớn nhất trong số các giá trị
này là giá trị lớn nhất của f ; giá trị nhỏ nhất trong số các giá trị này là giá trị nhỏ nhất của f .
Với các hàm số hai biến, phương pháp nhân tử Lagranges tương tự với phương pháp vừa được
mô tả. Để tìm các giá trị cực biên của f (x, y) tùy thuộc vào điều kiện ràng buộc g(x, y) = k, ta
tìm các giá trị của x, y và Λ sao cho
∇f (x, y) = λ∇g(x, y)
và g(x, y) = k
Ví dụ 3: Tìm các giá trị cực trị của hàm số f (x, y) = x2 + 2y4 trên đường tròn x2 + y2 = 4. GIẢI
Tìm giá trị cực trị của hàm f tuân theo ràng buộc g(x, y) = x2 + y2 = 4.
Sử dụng hệ số nhân Lagrange, ta giải phương trình ∇f = λ∇g và g(x, y) = 4. Được viết là (2) 2x = 2λx, (3) 8y3 = 2λy,
(4) x2 + y2 = 4. 6
Từ (2) ta có 2x(1 — λ) = 0
λx = 0 hoặc λ = 1.
Vậy (4) cho rằng y = ± 2.
Nếu λ = 1 thì từ (3) ta có y = 0.
Vậy (4) cho rằng x ± = 2.
Do đó, có thể có giá trị cực trị từ các điểm (0, 2), (0, − 2), (2, 0), ( −
2, 0). Đánh giá 4 điểm này ta thấy rằng:
f (0, 2) = 32,
f (0, −2) = 32, f (2, 0) = 4,
f (−2, 0) = 4.
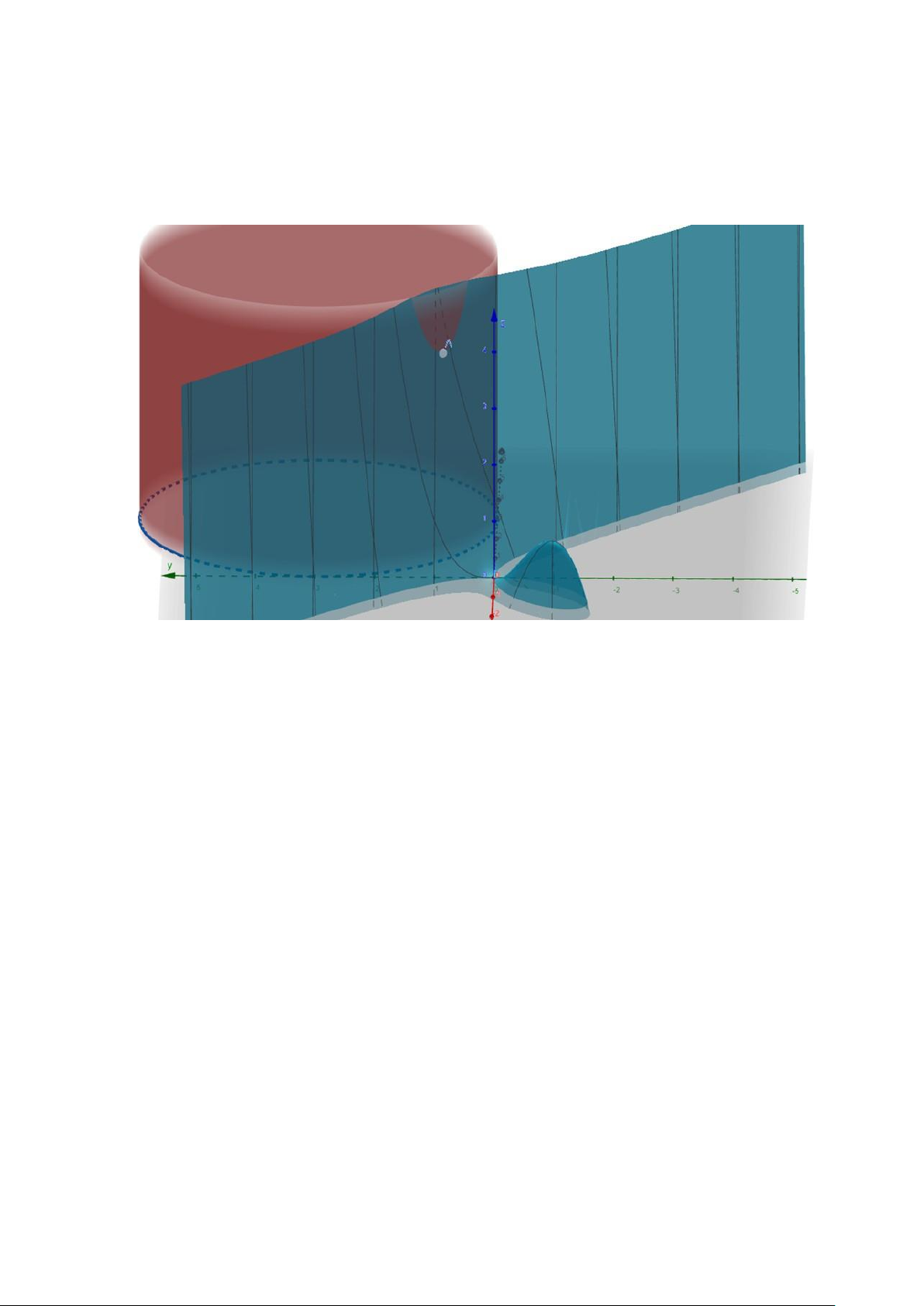
Hình 3: Đồ thị minh họa Ví dụ 3
Vì vậy, giá trị lớn nhất của f trên đường tròn x2 + y2 = 4 là f (0, 2) và f (0, −2).
Giá trị nhỏ nhất của f trên đường tròn x2 + y2 = 4 là f (2, 0) và f (−2, 0). 7
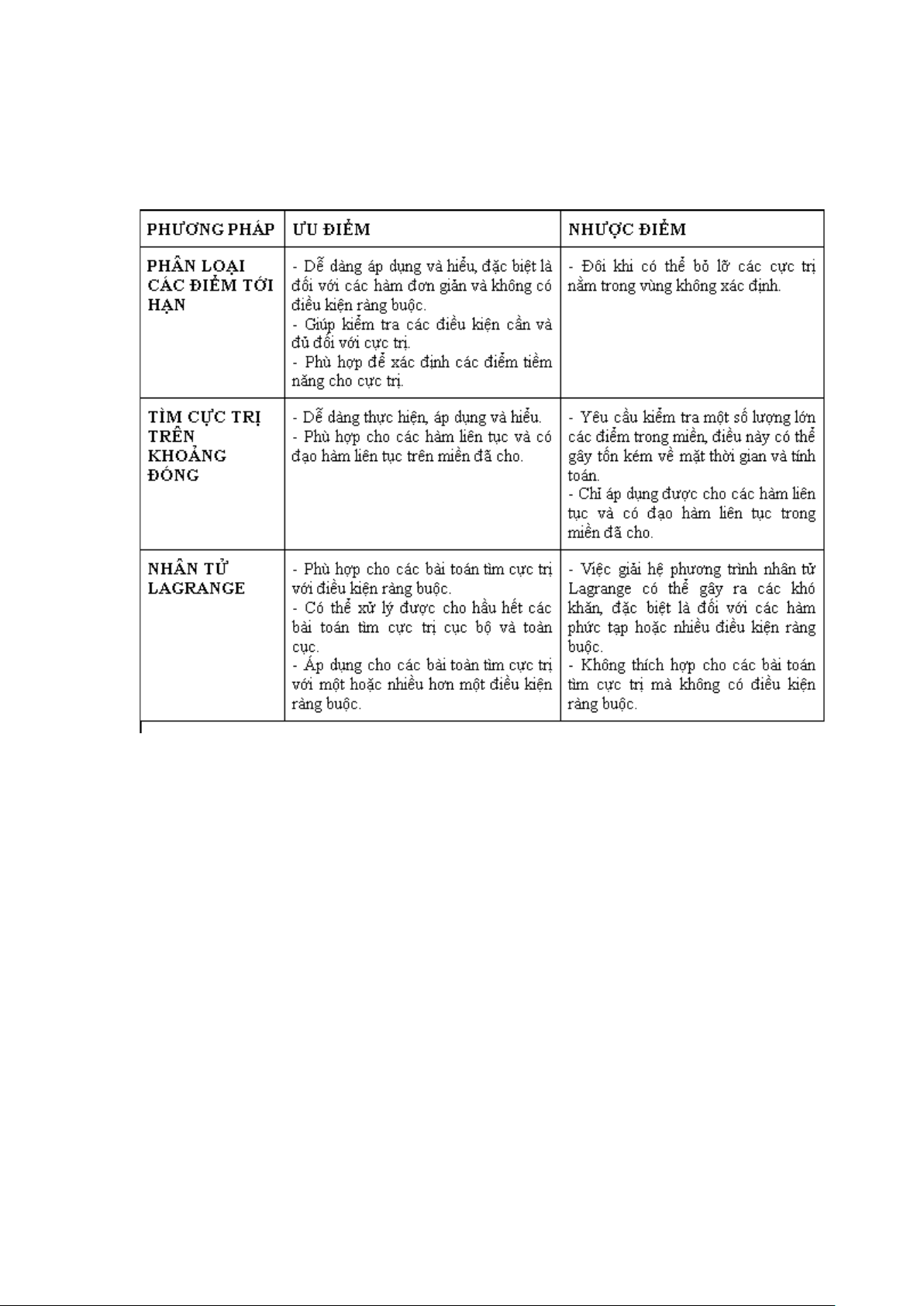
3 So sánh ưu điểm và nhược điểm của 3 phương pháp
Hình 4: Bảng so sánh 3 phương pháp. 4 Bài tập 4.1 Sec 14.8 exc. 2
f (x, y, λ) = x2 + y − λ(x2 + y2 − 1)
fx(x, y, λ) = 2x − 2λx
fy(x, y, λ) = 1 − 2λy
fλ(x, y, λ) = x2 + y2 = 1
2x(1 − λ) = 0 (1) 2λy = 1 (2) x2 + y2 = 1 (3) 8 Với 1
x = 0 ⇒ y = ±1 ⇒ λ = ±2 Với √ 1 3 λ = 1 ⇒ y = ⇒ x = ± 2 √ √ 2 3 1 3 1
(0, 1), (0, −1), ( , ), (− , ) 2 2 2 2 là các điểm cực biên. Giá trị cực biên tại (0, 1) = 1 (0, −1) = −1 √3 1 5 ( , ) = 2 2 4 √3 1 5 — ( , ) = 2 2 4 Hình 5: Sec14.8 exc.2 4.2 Sec 14.8 exc. 36
[a] Cực tiểu thỏa mãn A(0.88, 0.88, 3.68)
[b] Minimize f (x, y) = x3 + y3 + 3xy subject to f (x, y) = (x − 3)2 + (y − 3)2 − 9 = 0 Đặt hàm Lagrange:
L(x, y, λ) = f (x, y) — λg(x, y) Ta có:
(x, y, λ) = x3 + y3 + 3xy − λ((x − 3)2 + (y − 3)2 − 9)
∂x∂L = 3x2 + 3y − 2λ(x − 3) = 0
∂y∂L = 3y2 + 3x − 2λ(y − 3) = 0
∂λ∂L = (x − 3)2 + (y − 3)2 − 9 1. ∂x∂L = 0
3x2 + 3y − 2λ(x − 3) = 0
3x2 + 3y − 2 + 6λ = 0 2. ∂y∂L = 0
3y2 + 3x − 2λ(y − 3) = 0 9
3y2 + 3x − 2λy + 6λ = 0 }
⇒ min x3 + y3 + 3xy | (x − 3)2 + (y − 3)2 = 9 ≈ 3.67305 at (x, y) ≈
(0.87868, 0.87868) Hình 6: Sec14.8 exc.36 5 Kết Luận
Qua quá trình thực hiện bài tập nhóm, các thành viên trong nhóm đã cùng nhau xem lại, ôn tập
lại những kiến thức, nội dung đã được học; qua đó không chỉ nắm bắt được kiến thức mà còn
rèn luyện kỹ năng làm việc nhóm, giao tiếp và giải quyết vấn đề. Dựa trên kết quả thu được,
nhóm 3 đã đạt được mục tiêu đề ra ban đầu, bao gồm liệt kê các phương pháp tìm giá trị cực
đại và cực tiểu của hàm hai biến, đưa ra 3 ví dụ nhằm thể hiện phương pháp, và sử dụng phần
mềm để làm bài tập Sec14.8 exc.2 và exc.36. Tuy nhiên, trong quá trình thực hiện, nhóm cũng
gặp phải một số thách thức như sử dùng phần mềm để vẽ đồ thị. Từ đó, nhóm đã học được cách
thích nghi, tìm kiếm giải pháp hiệu quả hơn.
Tài liệu tham khảo
[1] Calculus: Early Transcendentals 9th Edition by Daniel K. Clegg, James Stewart, Saleem Watson
[2] Geogebra: https://www.geogebra.org/calculator 10