Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Vớichuỗikhôngâm,dãytổngriêng Sn làdãykhônggiảm.
Vậychuỗikhôngâmhộitụkhivàchỉkhibịchặntrên.
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
Tài liệu gồm 30 trang , giúp bạn tham khảo, ôn tập và đạt kết quả cao.
Môn: Giải tích 2(GT2101) 46 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 1.7 K tài liệu
Tác giả:
Preview text:
TRƯỜNG ĐH BÁCH KHOA ĐÀ NẴNG
------------------------------------------------------------------------------------- Giải tích 2
Chương 5. Chuỗi số, chuỗi hàm.
• Giảng viên Ts. Phạm Quý Mười 1 Nội dung
---------------------------------------------------------------------------------------------------------------------------
I – Khái niệm chuỗi số.
II – Chuỗi không âm.
III- Chuỗi có dấu tuỳ ý. Hội tụ tuyệt đối.
IV- Chuỗi đan dấu. Tiêu chuẩn Leibnitz.
V- Chuỗi luỹ thừa. Bán kính và miền hội tụ. 2 1 II. Chuỗi không âm
Định nghĩa chuỗi không âm +∞ n=1 Nhận xét
Với chuỗi không âm, dãy tổng riêng S là dãy không giảm. n
Vậy chuỗi không âm hội tụ khi và chỉ khi bị chặn trên. 3 Tiêu chuẩn so sánh 1 +∞ +∞
Hai chuỗi Σa , Σb thoả điều kiện n n
0 ≤ a ≤ b ,6n ≥ n n n 0 n=1 n=1 +∞ +∞ hội tụ. n=1 n=1 +∞ +∞
2) Nếu chuỗi Σa phân kỳ, thì chuỗi Σb phân kỳ. n n n=1 n=1 + ∞ CM
hội tụ nên dãy tổng riêng S bị chặn trên n n = 1 n n ' ≤ S dãy n n n n=1 k =0 k =0
bị chặn trên, vậy chuỗi hội 4 2 Tiêu chuẩn so sánh 2 +∞ +∞ thoả
0 ≤ a ,b ,6n ≥ n n n 0 n=1 n=1 a K = lim n n→+∞ bn
1) K = 0 : Nếu chuỗi (2) hội tụ, thì chuỗi (1) hội tụ.
2) K hữu hạn, 0 : Chuỗi (1) và (2) cùng HT hoặc cùng PK
3) K = +∞ : Nếu chuỗi (1) HT, thì chuỗi (2) HT. 5 cos2 n
Ví dụ Khảo sát sự hội tụ của chuỗi n=1 1 1 a ≤ n n(n +1)
n(n +1) n2 1 Chọn chuỗi số = b n n=1 n 2 n=1 a lim n = 1 Suy ra hai chuỗi n=1 n=1 b = 1 n
hội tụ, nên chuỗi đã cho hội tụ. n=1 n=1 n 2 6 3 ∞ n ∞ 5 + 3(–1) = 2n+3 n=1 n=1 Chuỗi dương 5 + 3(–1)n 8 1 0 < ≤ = 2n+3 2n+3 2n ∞ 1 1
, |q | = < 1 hội tụ, nên chuỗi đã cho hội tụ. n=1 2 n 2 ∞ ∞ en + n3
Ví dụ Khảo sát sự hội tụ của chuỗi = n 3 n=1 2 + ln n n=1 Chuỗi dương en + n3 en
2n + ln3 n 2n chuỗi Σ e
> 1 FK, nên chuỗi đã cho FK. 2 , |q |= 2 7 ln(1 + sin(1/ n) = a n n=1 n + ln2 n n=1
Chuỗi dương ln(1+ sin(1/ n) 1/ n 1 = n + ln2 n n n2 1
hội tụ, nên chuỗi đã cho hội tụ. 2 n=1 n ( π n cosh n n=1 n n=1 ( π 2 ( 2 1/ 2 a = n cosh –1 n n n 1+ 2n 2 2n 3 / 2 2 chuỗi HT, nên chuỗi đã cho HT. n=1 2n 3/ 2 8 4 ∞ ∞ n=1 n=1 1 n 2n3 / 2 ∞ 1
hội tụ, nên chuỗi đã cho hội tụ. n=1 2n 3 / 2
∞ arctan(n 2 + 2n) ∞ = n=1 3n + n2 n=1 arctan(n2 + 2n) π / 2 π 1 a = = n 3n + n2 3n 2 3n ∞ 1 chuỗi HT, nên chuỗi đã cho HT. n=1 3 n 9 để chuỗi HT n=1 ( ( 1 1 1 1– n – n 3!n
Chuỗi đã cho hội tụ khi và chỉ khi α 1 > 2 ∞ ( 1 1 để chuỗi HT ( ( 1 1 1 ( ( 1 1 a n ln – ln 1– 3 n 6n n
Chuỗi đã cho hội tụ khi và chỉ khi α 1 > 2 10 5 ∞ ( 1 để chuỗi HT ( 1 ( 1 a n 3 2 2n ( 1 ( 1 a n 1–1/ 6n 2 2n ( 1 ( 1 1 1 a 1+ 6n 2 2n
Chuỗi đã cho hội tụ khi và chỉ khi α 1 > 2 11 ∞ e
– 1 + 1/ n n để chuỗi HT 2
n=1 (1– cos(1/ n)) ( 1 n = 2 n ln(1+1/ n) n(1/ n– 1/ 2n ) 1–1/ 2n 1 e = (
e – e.e–1/ 2n e – e 1– = 2n 1 = 4n4 ⇒ a n
2α –2 nα –4
2α +2 n4–α
Chuỗi đã cho hội tụ khi và chỉ khi α – 4 > 1 α > 5 12 6 Tiêu chuẩn d'Alembert +∞ a n+1 . Giả sử lim = D n=1 an
1) D < 1: chuỗi hội tụ.
2) D > 1: chuỗi phân kỳ.
3) D = 1: không kết luận được, chuỗi có thể HT, hoặc PK. 13 Tiêu chuẩn Cô si +∞
. Giả sử lim n a = C n n=1
1) C < 1: chuỗi hội tụ.
2) C > 1: chuỗi phân kỳ.
3) C = 1: không kết luận được, chuỗi có thể HT, hoặc PK. 14 7 ∞ n ∞
Ví dụ Khảo sát sự hội tụ của chuỗi = nn n=1 n=1 a = = = n+1 (n +1)n+1 (n + 1)n 3 3 =
n→∞→ > 1 Phân kỳ a (n +1)n (1+1/ n)n e ∞ ( 3n + 2 ∞
Ví Khảo sát sự hội tụ của chuỗi Σn5 n n=1 n=1 3 lim n a
= < 1 HT theo t/c Cô si. n n→∞ 4n + 3 4 15 n=1 n a n+1 n (5n +1) a 3n + 2 ⇒ lim n+1 = lim 3 = < 1 a n→∞ 5n +1 5 n
Chuỗi hội tụ theo tiêu chuẩn d'Alembert. 16 8 ∞ n=1 n a n+1 n 2(n + 2) a 3n + 5 3 ⇒ lim n+1 = lim = > 1 a n→∞ 2n + 4 2 n
Chuỗi phân kỳ theo tiêu chuẩn d'Alembert. 17 ,α > 0 n / 2 n=1 (ln(n +1)) 1 lim n a = lim n = lim = 0 < 1 n
(ln(n +1)) n / 2 ln(n +1)
Chuỗi hội tụ theo tiêu chuẩn Cô si với mọi 3 ∞ (
Ví dụ Khảo sát sự hội tụ của chuỗi 2 ( 3 2 ( 1 1
lim n a = lim n cos n 2 2n 1 = e–1/ 2 = < 1 Hội tụ theo Cô si. e 18 9 4
∞ ( n –1 n +3n+ 1
Ví dụ Khảo sát sự hội tụ của chuỗi –2 n4 +3n+1 3 · n ( n –1 lim n a = lim n 2 2 n 1 = < 1 n +1 e2
Chuỗi hội tụ theo tiêu chuẩn Cô si. ∞ ( n + 2 2
Ví Khảo sát sự hội tụ của chuỗi Σ3n+1 n=1 n ( 1 1 lim n a = lim 3 1 – 3 n = > 1 Phân kỳ n + 3 e 19
II. Chuỗi có dấu tuỳ ý. Hội tụ tuyệt đối.
Định nghĩa hội tụ tuyệt đối +∞ +∞ hội tụ n=1 n=1 Định lý +∞ +∞ hội tụ. n=1 n=1
Theo định lý: chuỗi hội tụ tuyệt đối thì hội tụ.
Mệnh đề ngược lại không đúng: có những chuỗi hội tụ,
tuy nhiên chuỗi của trị tuyệt đối không hội tụ. 20 10 ∞
Ví dụ Khảo sát sự hội tụ của chuỗi
(2n + 3) cos 3n 3 n=1 n7 + n +1 ∞
Chuỗi có dấu tuỳ ý. Xét chuỗi Σ| a | là chuỗi dương n n=1 Hội tụ (2n + 3) cos 3n 2n + 3 2n 2 | a |= ≤ = n 3 n 7 / 3 n 4 / 3 tuyệt đối n7 + n +1 n + n +1 ∞
Ví dụ Khảo sát sự hội tụ của chuỗi arctan(–n)n 4 n=1 n6 + 3n +1
| arctan(–n)n | π / 2 π | a |= ≤ = n 4 n6 + 3n +1 n 6 / 4 2n 3 / 2 21
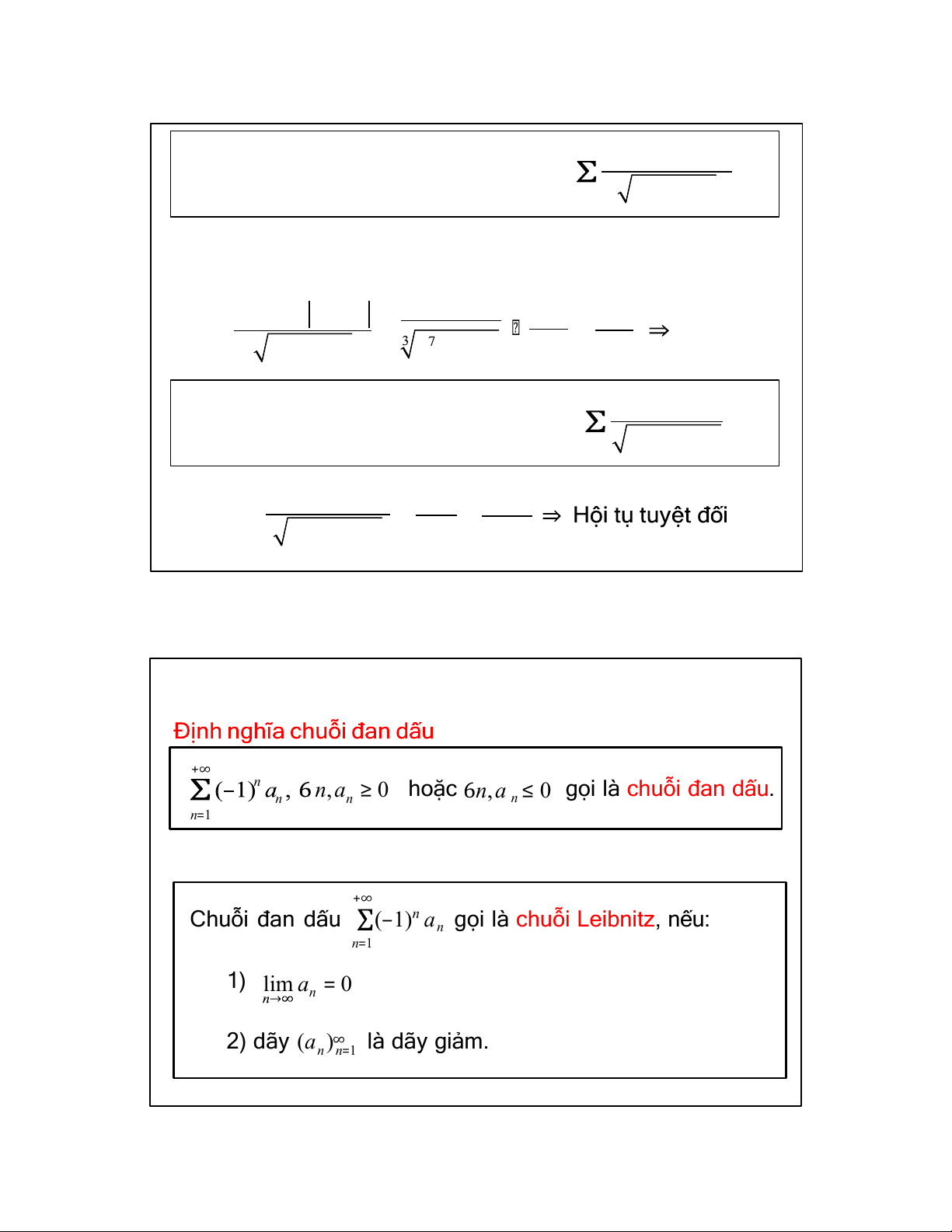
II. Chuỗi đan dấu. Tiêu chuẫn Leibnitz. +∞ n n
, a ≥ 0 hoặc 6n, a ≤ 0 gọi là chuỗi đan dấu. n n n n=1
Định nghĩa chuỗi Leibnitz +∞
Chuỗi đan dấu Σ(–1)n a gọi là chuỗi Leibnitz, nếu: n n=1 1) lim a = 0 n
2) dãy (a )∞ là dãy giảm. n n=1 22 11
II. Chuỗi đan dấu. Tiêu chuẫn Leibnitz. Định lý (Leibnitz)
Chuỗi Leibnitz hội tụ. Tổng của chuỗi này thoả 0 ≤| S |≤ a1 23 1) n a n n=1 n + 2 n=1 1
Chuỗi không hội tụ tuyệt đối. lim a = lim = 0 n + 2 ( 1
là dãy giảm. Đây là chuỗi Leibnitz và hội tụ. n + 2 n+1 (–1) ln n n = (–1) a n n=1 n n=1 ln n ( lnn lim a = lim = 0. n n
dãy giảm (có thể k/s đạo hàm) n
Chuỗi Leibnitz nên hội tụ (theo tiêu chuẩn Leibnitz) 24 12
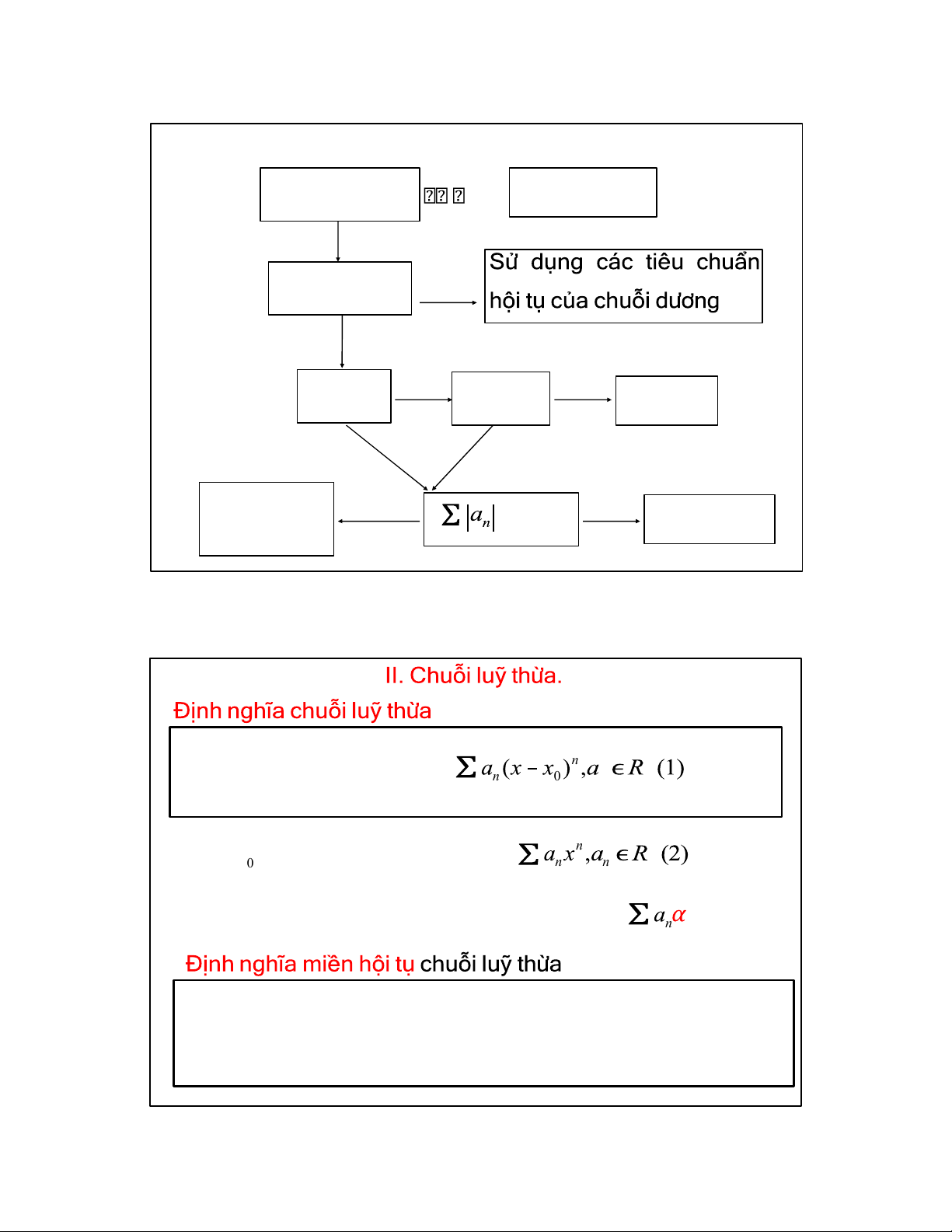
Sơ đồ khảo sát sự hội tụ của chuỗi số
Điều kiện cần khoâng→ Phân kỳ thô có Chuỗi dương có không có có đan dấu Leibnitz Hội tụ không không +∞ Đ/nghĩa, các hội tụ có HT tuyệt đối t/chuẩn khác không n=1 25 +∞ n
Chuỗi luỹ thừa là chuỗi n 0 n n=0 +∞ n
Khi x = 0 ta có chuỗi luỹ thừa 0 n n n=0 +∞ n
Cho x = một giá trị cụ thể ta có chuỗi số n n=0
Tập hợp các giá trị của x, khi thay vào chuỗi (1) hoặc (2)
được chuỗi số hội tụ, gọi là miền hội tụ của (1) hoặc (2) 26 13 Bổ đề Abel +∞ Nếu chuỗi a x n hội tụ tại
, thì nó hội tụ tuyệt đối n x 0 0 n=0
trong khoảng (– | x |,| x |). 0 0 27 Định lý +∞ Cho chuỗi
a x n . Khi đó tồn tại duy nhất 0 ≤ R ≤ +∞ thoả n n=0
1) Chuỗi hội tụ 6x, x < R
2) Chuỗi phân kỳ 6x, x > R 28 14 Định nghĩa +∞ n
Số R trong định lý gọi là bán kính hội tụ của chuỗi a x . n=0
Định lý (dấu hiệu d'Alembert để tìm bán kính hội tụ) +∞ n Cho chuỗi a x n n=0 a 1 lim n+1 = p R = a p n (Qui ước: 1 1 = ∞, = 0 ) 0 ∞ 29
Định lý (dấu hiệu Côsi- Hadamard tìm bán kính hội tụ) +∞ n Cho chuỗi a x . Giả sử lim n a = p n n=0 1
Khi đó, bán kính hội tụ R = p 1 1 (Qui = ∞, = 0 ) 0 30 15 ∞ (2n –1)!! x n n=1 n! a p = lim n+1 = (2n +1)!! lim n! a
(n +1)! (2n –1)!! p 2 n ∞ ( 1 1
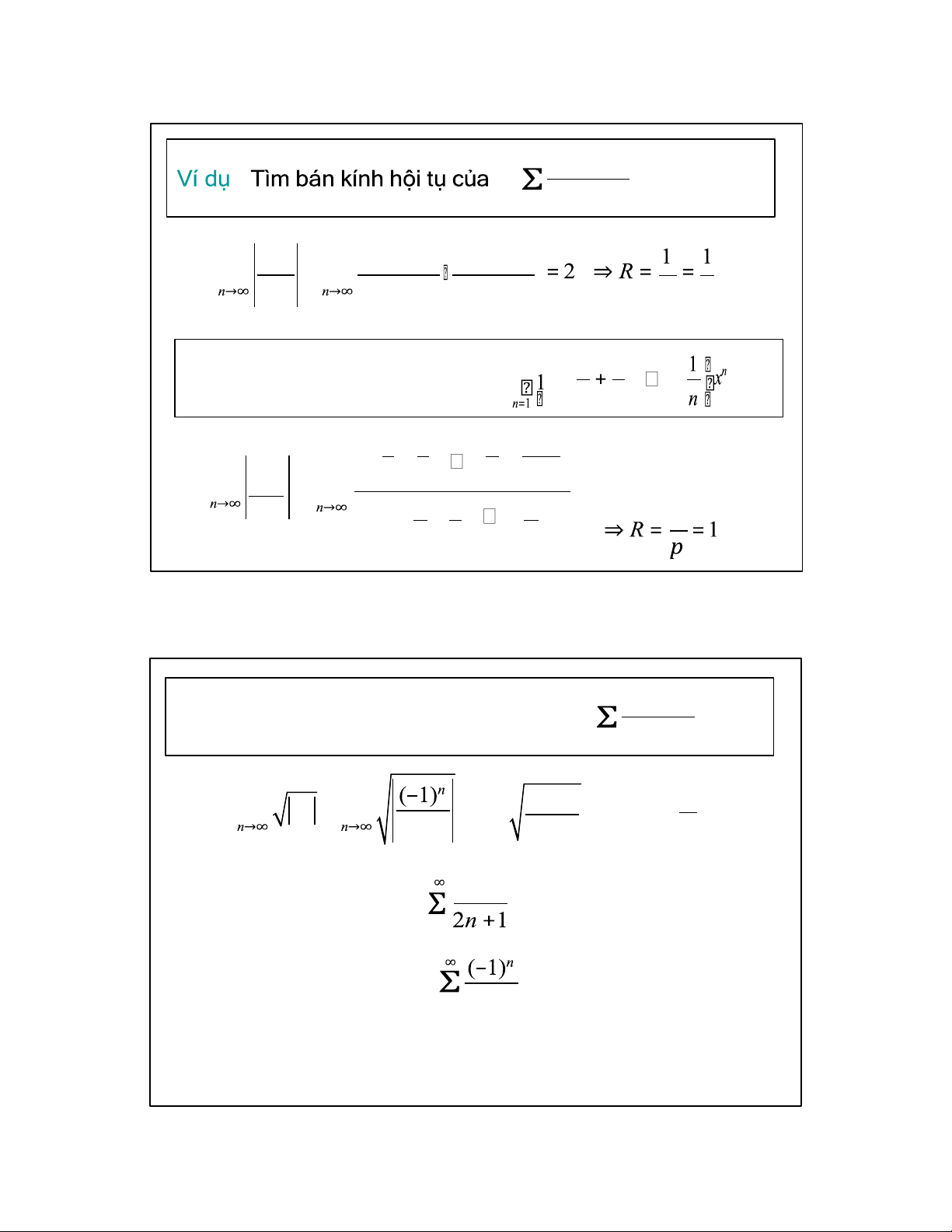
Ví dụ Tìm bán kính hội tụ của Σ + + 1 + + 2 3 1 1 1 1 1+ + + + + p a = lim n+1 = lim 2 3 n n +1 = 1 a 1 1 1 n 1+ + + + 1 2 3 n 31 ∞ (–1)n xn
Ví dụ Tìm bán kính và miền hội tụ của (1) n=1 2n + 1 1 1
p = lim n a = lim n n = lim n = 1⇒ R = = 1
2n +1 n→∞ 2n +1 p 1
Tại x = –1 có chuỗi số Phân kỳ theo so sánh n=1
Tại x = 1 có chuỗi số hội tụ theo Leibnitz n=1 2n + 1
Miền hội tụ của đã cho –1 < x ≤ 1 32 16
∞ 5n + (–2)n
Ví dụ Tìm bán kính và miền hội tụ của x n (1) n=1 n +1 5n + (–3)n 1 1
p = lim n a = lim = 5 = = n n n→∞ n→∞ n +1 p 5 ∞ Tại 1 X = có chuỗi số
5n + (–2)n Phân kỳ theo so sánh 5 n=1 n ∞ Tại X = – 1
n 5n + (–2)n hội tụ (tách ra tổng) 5 n=1 n 1 1
Miền hội tụ của đã cho – ≤ x < 5 5 33
2n (x +1)n
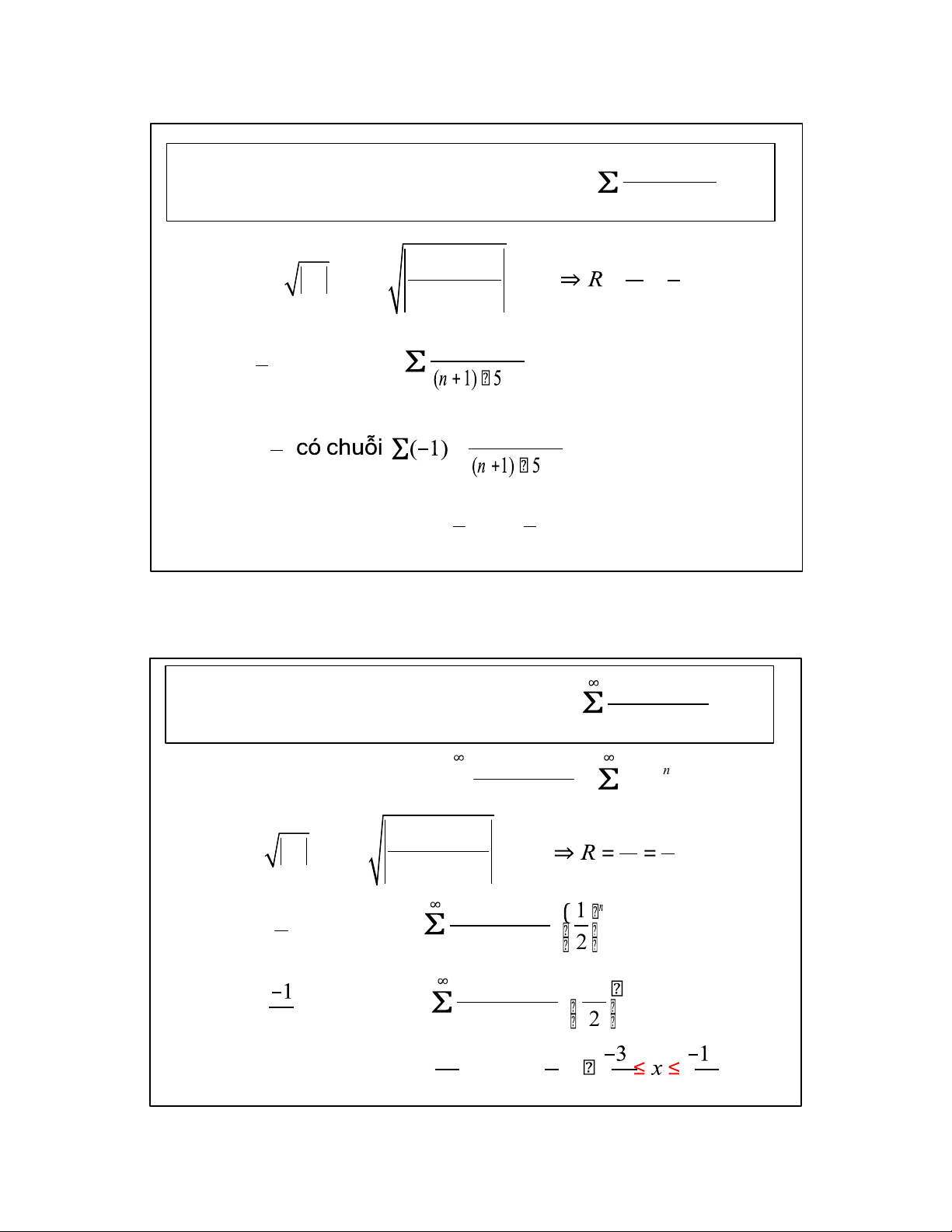
Ví dụ Tìm bán kính và miền hội tụ của (1) 2
n=1 n ln (n +1) 2n X n n
Đặt X = x +1 Xét chuỗi Σ = a X (2) n ln2 (n +1) n n=1 n=1 2n p 1 1 = lim n a = lim = 2 n n n→∞ n→∞ n ln 2 (n +1) p 2 2n 1
Tại X = có chuỗi số · 2 hội tụ. 2
n=1 n ln (n +1) 2 2n ( –1 Tại n hội tụ X = có chuỗi số · 2 2
n=1 n ln (n +1) 2 tuyệt đối – Miền hội tụ của (1) 1 1 ≤ x +1 ≤ 2 2 2 2 34 17 ∞ (x +1)n 3n - 2 ln (1) n=1 n +1 3n + 2 ∞ X n 3n - 2 ∞ Đặt X = x +1 Xét chuỗi Σ ln = a X (2) n +1 3n + 2 1 3n - 2 1
p = lim n a = lim n ln = 1 ⇒ R = = 1 n n→∞ n +1 3n + 2 p ∞ 1 3n - 2 ln hội tụ. n=1 n +1 3n + 2 ∞ (–1)n 3n - 2 hội tụ
Tại X = –1 có chuỗi số ln tuyệt đối n=1 n +1 3n + 2 Miền hội tụ của (1) –1 ≤ x +1 ≤ 1 35
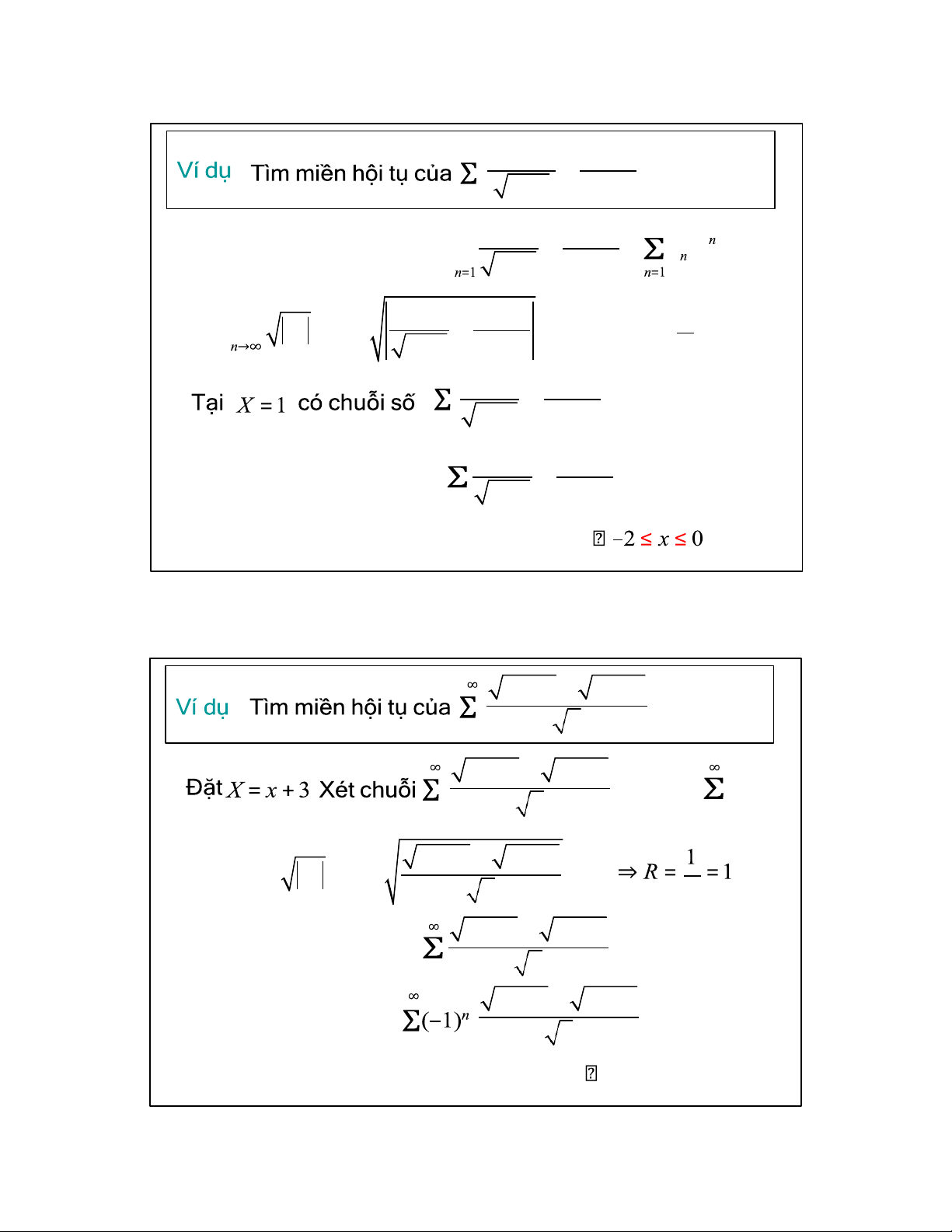
3 2n +1 – 3 2n –1 (x + 3) n (1) n=1 n
3 2n +1 – 3 2n –1 (x + 3) n = a X n n n=1 n n=1
3 2n +1 – 3 2n –1
p = lim n a = lim n = 1 n→∞ n n→∞ n p
3 2n +1 – 3 2n –1 Hội tụ.
Tại X = 1 có chuỗi số n=1 n
3 2n +1 – 3 2n –1
Tại X = –1 có chuỗi HT tuyệt đối n=1 n Miền hội tụ của (1)
–1 ≤ x + 3 ≤ 1 –4 ≤ x ≤ –2 36 18
Tổng của chuỗi luỹ thừa là một hàm liên tục trên miền hội tụ của nó.
Trong khoảng hội tụ: Đạo hàm của tổng bằng tổng ∞ ∞ các đạo hàm: ( ∞ n n a x a x ' = na x n = n n = = n 1 =
3) Trong khoảng hội tụ: Tích phân của tổng bằng tổng x ( ∞ ∞ x ∞ xn+1 a t dt a n n n n n=0 n=0 +1 0 37 n n=1 3 n 1 Ta có n 1,1) n=0
Đạo hàm hai vế (đạo hàm của tổng bằng tổng các đạo hàm) 1 = nx n=1 Cho x = 1 ta có: 3 4 3 Nhân hai vế cho 1/3: = n n 4 n=1 3 38 19 ∞ n+1 n=1 5 ∞ = nx n=1
Nhân hai vế cho x, đạo hàm hai vế: ∞ 1+ x = n x (x –1)3 n=1 2 ∞ Cho x = ta có: 875 = 5 81 n=1 70 = ∞ 2 n Nhân hai vế cho 2/25: 1 81 n=1 5 n+ 39
∞ 3n3 – 4n2 + 5 4n n=1 3 2 3 Ta có: 3n – 4n + 5 n = 3 – 4 n 2 + 5 n n 1 n 4n n=1 n=1 4 n=1 4 n=1 4 1+ x = n x (x –1)3 n=1 x 2 + 4x +1 – = n x (x –1)4 n=1 P (n) k an n=0 40 20
Tài liệu liên quan:
-
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng
17 9 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
14 7 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
16 8 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
16 8 -
Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.
21 11