Đề cương môn giải tích - Trường Đại học bách khoa - Đại học đà nẵng.

TíCH PHÂN KÉP (MộT SỐ BÀI TRAO đổI TRÊN LớP) Chử Văn Tiệp
Giải tích II- 2023-2024, ĐHBKĐN
CÂU 12. Dùng tích phân hai lớp tính diện tích các miền sau:
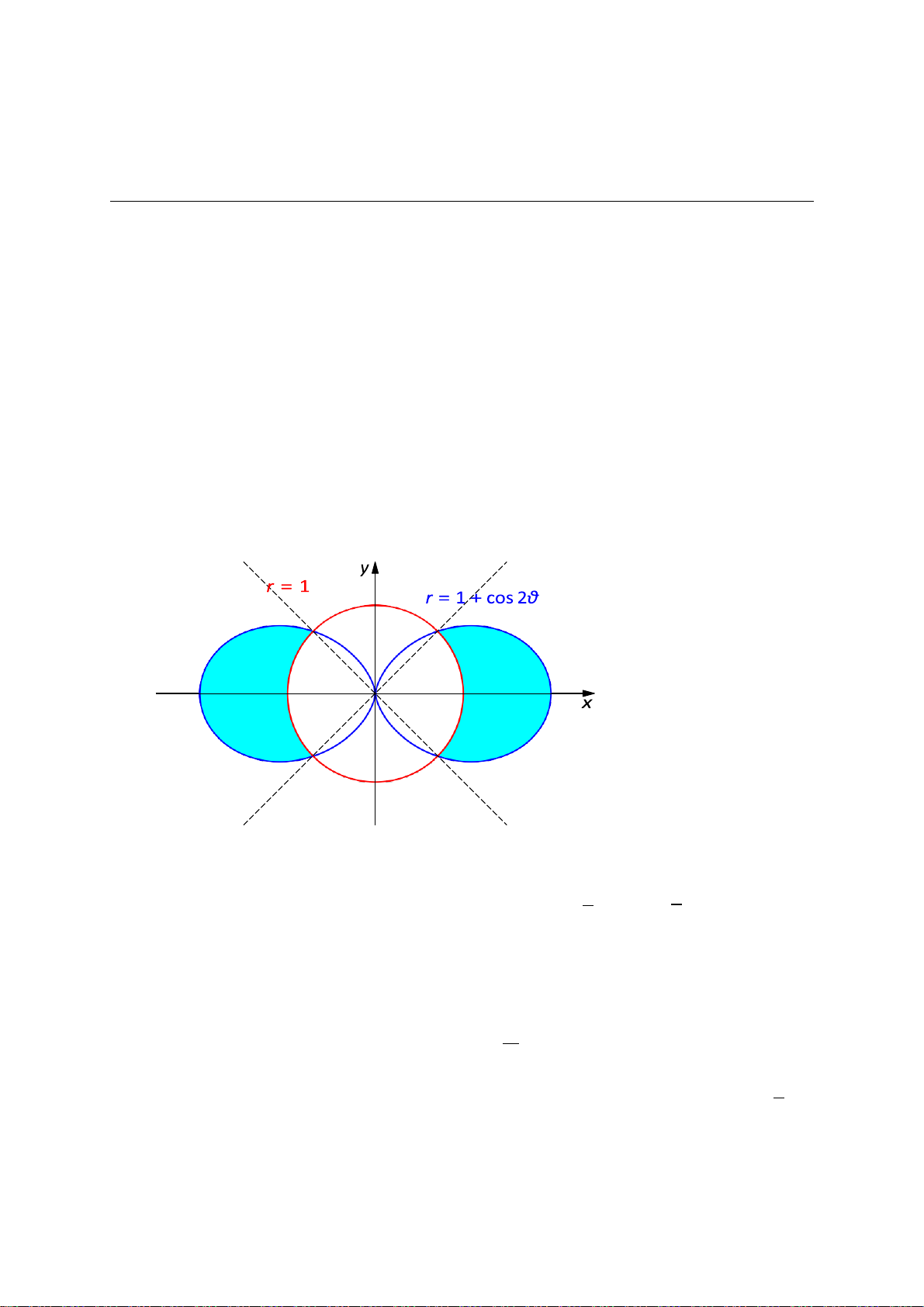
1. Tính diện tích của miền nằm bên trong đường cardioid r = 1 + cos 2θ và bên ngoài đường tròn r = 1
2. Tính diện tích của một nhánh cách hoa hồng cho bởi r = 12 cos 3θ
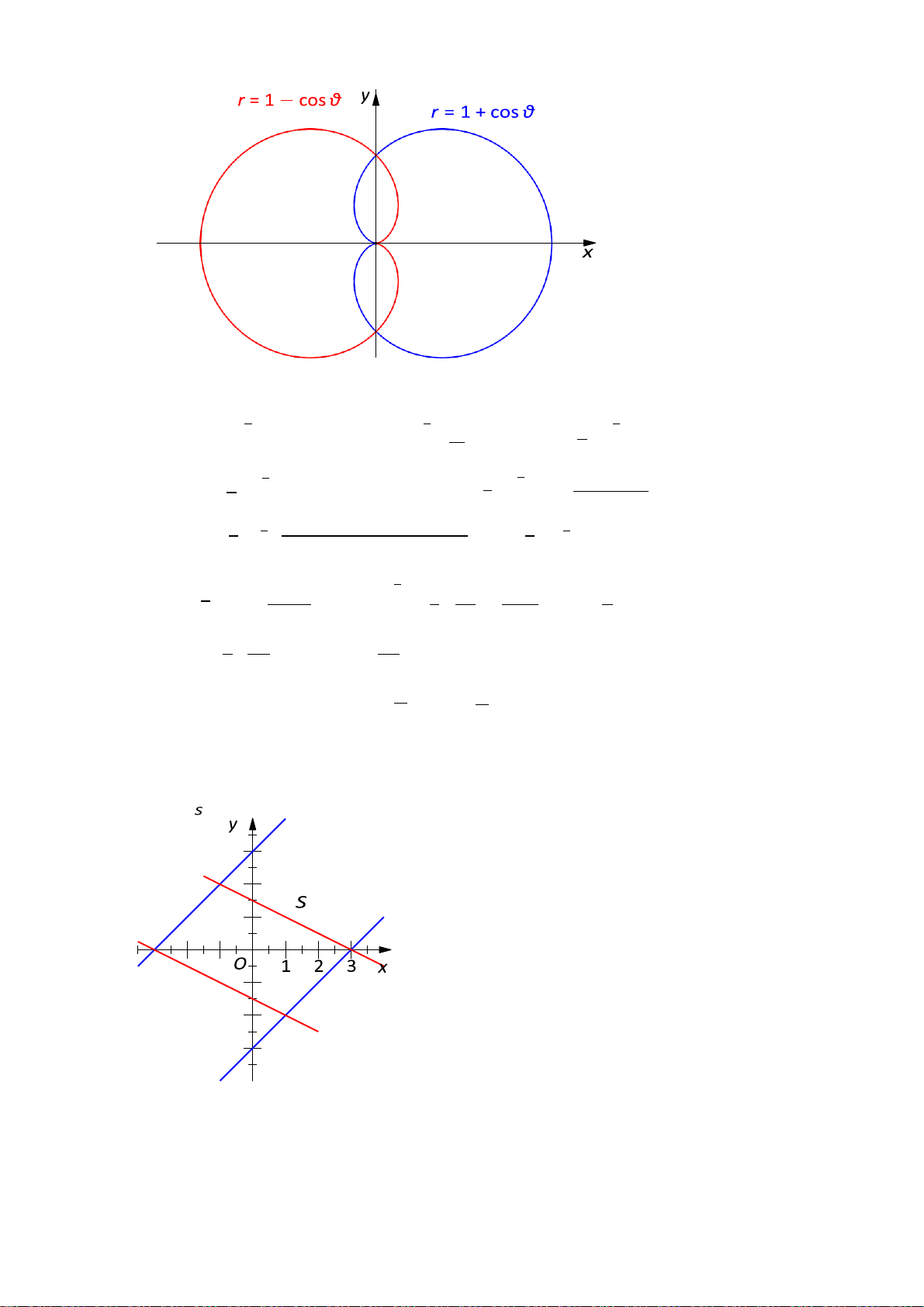
3. Tính diện tích của miền nằm trong 2 đường cardioid r = 1 + cos θ và r = 1 − cos θ
Lời giải. 1. Tính diện tích của miền nằm bên trong đường r = 1 + cos 2θ và bên ngoài đường tròn r = 1. Giải hệ phương trình: π π
1 + cos 2θ = 1 ⇔ cos 2θ = 0 ⇔ 2θ = ± ⇔ θ = ± . 2 4
Do tính đối xứng diện tích cần tính bằng 4 lần diện tích miền màu xanh nằm trong
góc phần tư thứ nhất. Sử dụng tọa độ cực ta có ∫ ∫ ∫ π/4 1+cos 2θ
π/4 r2 1+cos 2θ S(D) = 4 dθ rdr = 4 dθ 2 0 1 ∫ 0 1 ∫ π/4 π/4 π = 2
(1 + cos 2θ)2 − 1dθ = 2
cos2 2θ + 2 cos 2θdθ = ... = 2 + . 0 0 4
Qua ví dụ trên ta có thể đặt ra thêm các câu hỏi sau:
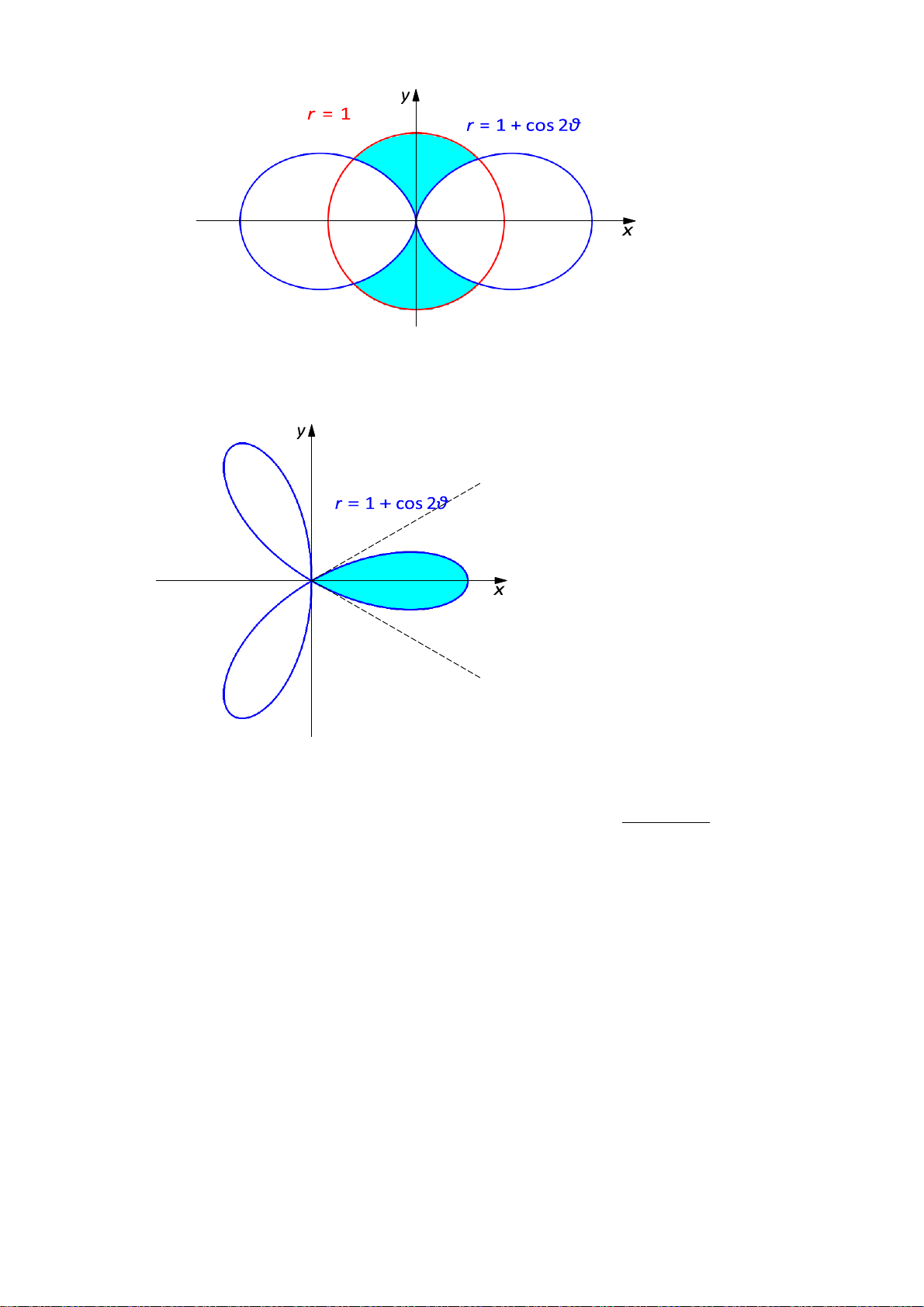
(a) Hãy tính diện tích miền xanh sau: Chử Văn Tiệp (BKĐN) 1 / 5
(b) Tính diện tích hình nằm trong đường cong r = 1 + cos 2θ.
2. Tính diện tích của một nhánh cách hoa hồng cho bởi r = 12 cos 3θ. Gợi ý: ∫ ∫ ∫ ∫ π/6 12 cos 3θ π/6 S(D) = (12 cos 3θ)2 dxdy =
r dr dθ = dθ 2 D −π/6 0 −π/6 ∫ π/6 = 72 cos2 3θdθ −π/6 ∫ π/6 =
36(1 + cos 6θ)dθ −π/6 = 12π.
3. Tính diện tích của miền nằm trong 2 đường cardioid r = 1 + cos θ và r = 1 − cos θ. Chử Văn Tiệp (BKĐN) 2 / 5
Diện tích phần cần tính bằng 4 lần diện tích A trong góc phần tư thứ nhất ∫ π ∫ ∫ (1−cos θ) π (1−cos θ) ∫ π 2 2 r2 2 dθ =
(1 − cos θ)2 − 0 dθ 1 A = rdrdθ = 0 0 0 2 0 2 0 ∫ π π ∫ 1 2 2 =
1 + cos2 θ − 2 cos θ dθ = 1
1 + 1 + cos 2θ — 2 cos θ dθ 2 0 2 0 2 ∫ π ∫ π 1
2 + 1 + cos 2θ − 4 cos θ] 1 2 2 dθ =
[3 + cos 2θ − 4 cos θ]dθ = = 2 2 0 4 0 π 1 sin 2θ 2 1 3π sin π π 3θ + — 4 sin θ = + − 4 sin 4 2 0 4 2 2 2 — [0 + 0 − 0] 1 3π 3π = + 0 − 4 = − 1 . 4 2 8
Vậy diện tích cần tính là: 4 · 3π − 1 = 3π − 4 8 2 □ ∫∫ CÂU 21. xydxdy,
S : |x + 2y| ≤ 3, |x − y| ≤ 3. 3 2 1
Đặt u = x + 2y, v = x − y. Khi đó (u, v) ∈ [−3, 3] × [−3, 3]. Chử Văn Tiệp (BKĐN) 3 / 5 u + 2v u − v
Viết lại ta được x = , y = . Jacobian: 3 3 1 2 x′ x′ 3 3 1 u v J = = ′ ′ = − . y 3 y yv 1 1 − 3 3 Suy ra ∫∫ ∫ ∫ ∫ ∫ 3
3 u + 2v u − v 1 3 3 xydxdy = du · 1 dv = du
(u + 2v)(u − v)dv −3 3 3 3 3 27 −3 3 S ∫ ∫ 1 3 3 = du
u2 + uv − 2v2dv = ... = −4. 27 −3 3
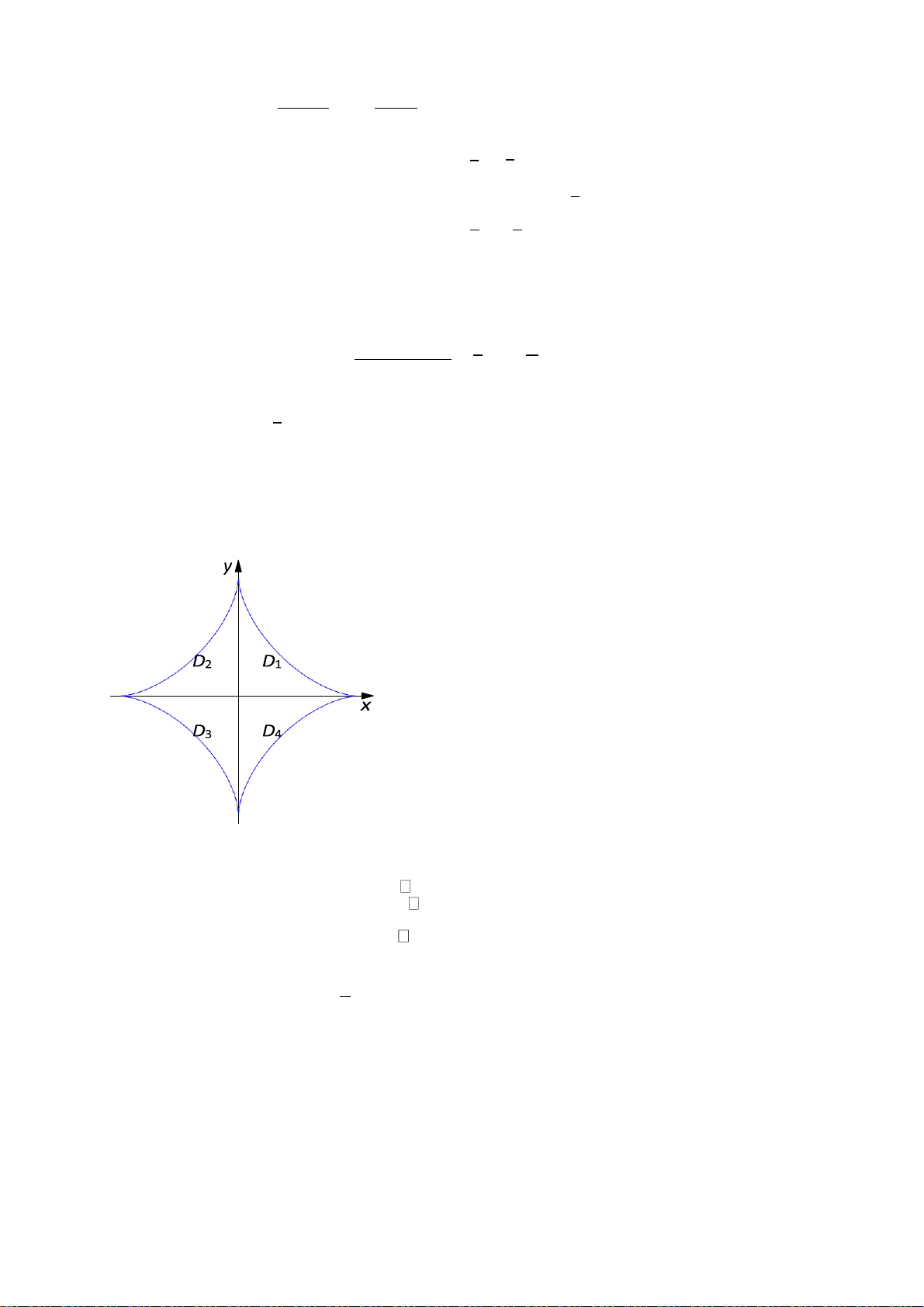
CÂU 38. Tính diện tích hình phẳng bị chặn bởi đường cong phương trình
x2/3 + y2/3 = 1.
Lời giải. Diện tích cần tính bằng 4 lần diện tích D1. Đổi biến
x = r3 cos3 ϕ
y = r3 sin3 ϕ
Từ hình vẽ ta thấy 0 ≤ ϕ ≤ π . Từ phương trình đường cong ta suy ra 2
x2/3 + y2/3 = r2 cos2 ϕ + r2 sin2 ϕ = r2 = 1.
Suy ra 0 ≤ r ≤ 1. Tính Jacobian của phép đổi biến: x′ x′ r ϕ
3r2 cos3 ϕ −3r3 cos2 ϕ sin ϕ J = = ′ ′ 2 3 3 2 y
3r sin ϕ 3r sin ϕ cos ϕ r yϕ
= 9r5 cos4 ϕ sin2 ϕ + 9r5 sin4 ϕ cos2 ϕ = 9r5 cos2 ϕ sin2 ϕ Chử Văn Tiệp (BKĐN) 4 / 5
Do đó từ công thức đổi ta có ∫∫ ∫ π/2 ∫ 1 S(D1) = dxdy = dϕ
9r5 cos2 ϕ sin2 ϕdr D1 0 0 ∫ ∫ 9 π/2 =
sin2 2ϕdϕ × 1 r5dr 4 0 0 ∫ 9 π/2 r6 1 3
sin cos 4ϕ π/2 3π = 1 − cos 4ϕdϕ × = ϕ − = . 8 0 6 16 4 32 0 0 3π
Vậy S(D) = 4S(D ) =
. Chú ý: Ta cũng có thể đổi biến như sau: 1 8
x = r cos3 ϕ
y = r sin3 ϕ
Từ hình vẽ ta thấy 0 ≤ ϕ ≤ π . Từ phương trình đường cong ta suy ra 2
x2/3 + y2/3 = r2/3 cos2 ϕ + r2/3 sin2 ϕ = r2/3 = 1.
Suy ra 0 ≤ r ≤ 1. Tính Jacobian của phép đổi biến: x′ x′ r ϕ
cos3 ϕ −3r cos2 ϕ sin ϕ J = = ′ ′ 3 2 y
sin ϕ 3r sin ϕ cos ϕ r yϕ
= 3r cos4 ϕ sin2 ϕ + 3r sin4 ϕ cos2 ϕ = 3r cos2 ϕ sin2 ϕ. Khi đó ∫∫ ∫ ∫ π/2 1 S(D1) = dxdy = dϕ
3r cos2 ϕ sin2 ϕdr D1 0 0 ∫ ∫ 3 π/2 =
sin2 2ϕdϕ × 1 rdr 4 0 0 ∫ 3 π/2 r2 1 3
sin cos 4ϕ π/2 3π = 1 − cos 4ϕdϕ × = ϕ − = . 8 0 2 16 4 32 0 0 3π
Vậy S(D) = 4S(D ) = . □ 1 8 Câu hỏi bổ sung:
1. Hãy tính diện tích trên bằng một cách nữa.
2. Tìm chiều dài của đường cong cho bởi phương trình
x2/3 + y2/3 = 1.
3. Tìm trọng tâm của mảnh kim loại phẳng đồng chất có diện tích D1.
4. Tính diện tích của mặt tròn xoay khi quay đường cong trên quanh trục Ox. Chử Văn Tiệp (BKĐN) 5 / 5