Đề cương môn giải tích - Trường Đại học bách khoa - Đại học đà nẵng.

TRƯỜNG ĐH BÁCH KHOA ĐÀ NẴNG
------------------------------------------------------------------------------------- Giải tích II
Chương 2: Tích phân bội ba
• Giảng viên PGS. TS. Phạm Quý Mười Nội dung
---------------------------------------------------------------------------------------------------------------------------
0.1 – Định nghĩa, cách tính tích phân bội ba
0.2 – Đổi biến số. Tọa độ trụ
0.3 – Tọa độ cầu
0.4 – Ứng dụng hình học
0.5 – Ứng dụng cơ học
I. Định nghĩa, cách tính tích phân bội ba
---------------------------------------------------------------------------------------------------------------------------
f = f (x, y, z) xác định trên vật thể đóng, bị chặn E
Chia E một cách tùy ý ra thành n khối nhỏ: E1, E2 ,..., En .
Thể tích tương ứng mỗi khối V (E ),V (E ),...,V (E ). 1 2 n
Trên mỗi khối E lấy
(x , y , z ). i
tuỳ ý một điểm Mi i i i n
Lập tổng Riemann: I = Σ f (M ) V (E ) n i i i=1
I = lim In , không phụ thuộc cách chia E, và cách lấy điểm Mi n I =
f (x, y, z)dxdydz E
được gọi là tích phân bội ba của f=f(x,y,z) trên khối E.
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Tính chất của tích phân bội ba
1) Hàm liên tục trên một khối đóng, bị chặn thì khả tích trên miền này. 2) V = E dxdydz E 3)
α f (x, y, z)dxdydz =α f (x, y, z)dxdydz E E
4) ( f + g)dxdydz = f dxdydz + gdxdydz E E E
5) Nếu E được chia làm hai khối E1 và E2 không dẫm lên nhau:
fdxdydz = fdxdydz + fdxdydz E E1 E2
6) 6(x, y, z) ϵ E, f (x, y, z) g(x, y, z) f g E E Định lý (Fubini)
I = f (x, y, z)dxdydz E
z = z (x, y) 2
Phân tích khối E: Chọn mặt chiếu là x0y.
Mặt phía dưới: z = z1(x, y)
Mặt phía trên: z = z2 (x, y) Hình chiếu: Pr E = D 0 xy
z = z1(x, y)
I = f (x, y, z)dxdydz E z = 2 ( x, y)
f (x, y, z)dz dxdy
D L z1( x, y) Hình chiếu: D Ví dụ
trong đó E là vật thể giới hạn bởi E
x2 + y2 = 1, z = 2 – x2 – y2, z = 0
Hình chiếu của E xuống 0xy:
D : x2 + y2 1
Mặt phía trên: z2 (x, y) = 2 – x2 – y2
Mặt phía dưới: z = 0 2–x2 – y2 I =
(x + z)dz dxdy x2 + y2 1 L 0 2–x2 – y2 I = xz + z2 dxdy x2 + y2 1 L 2 0 ( 2 2
(2 – x2 – y2 )2 I =
x(2 – x – y ) + dxdy 2 x2 + y2 1
Đổi sang tọa độ cực. ( 2π 1
2 – r 2 )(2r cosφ + 2 – r2 ) I = dφ · r dr 2 0 0 Ví dụ Tính tích phân bội ba
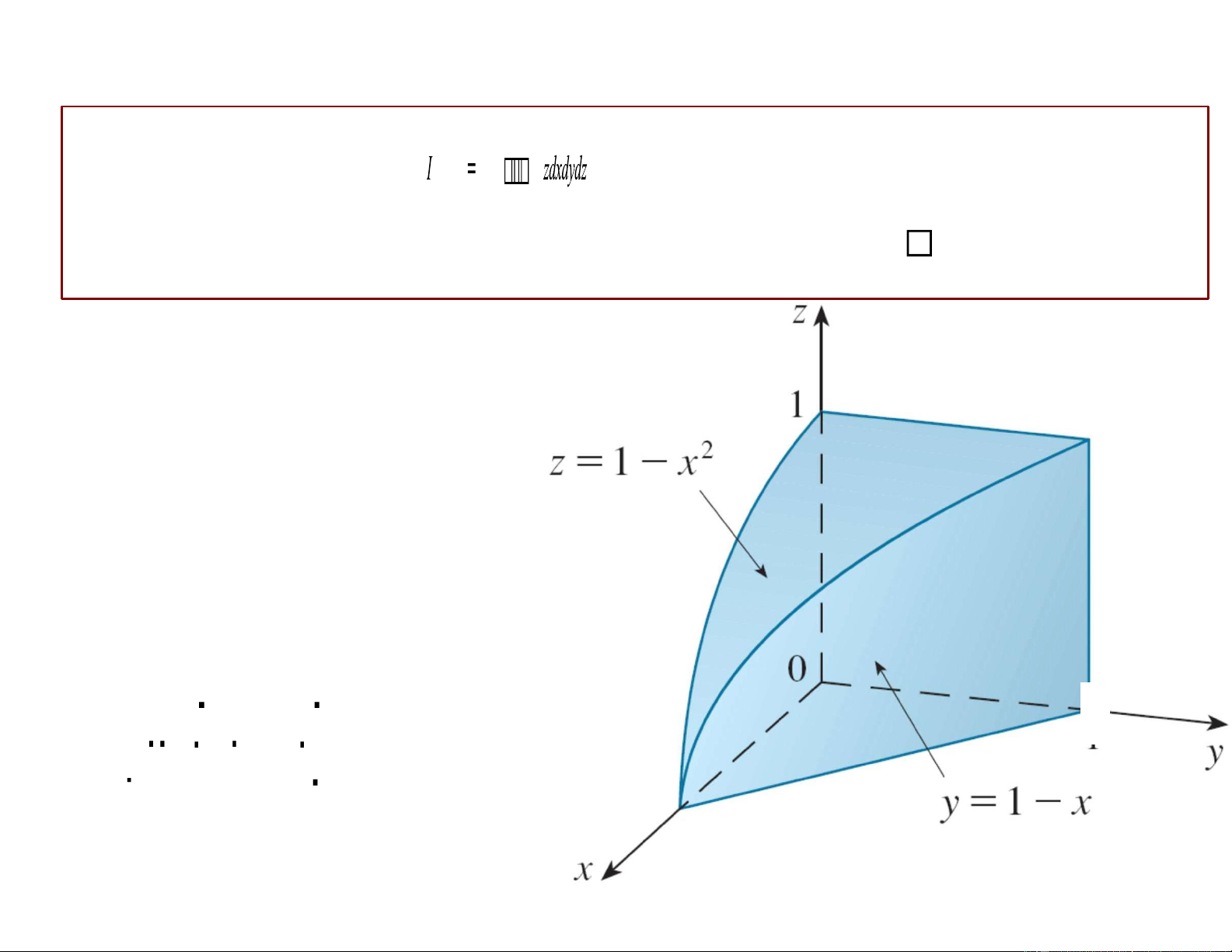
trong đó E là vật thể giới hạn bởi E
y = 1– x, z = 1– x2 và các mặt phẳng tọa độ (phần x, y, z 0 )
Hình chiếu của E xuống 0xy: Tam giác OAB
Mặt phía trên: z2 (x, y) = 1– x2
Mặt phía dưới: z = 0 1–x2 B I = zdz dxdy OAB L 0 A 1–x2 A I = zdz dxdy OAB L 0 1–x2 I = z2 dxdy B OAB 2 O 0 L (1 – x2 )2 I = dxdy OAB 2 – (1– x2 )2 1 1 x I 11 = dx dy = 0 0 2 60 Ví dụ Tính tích
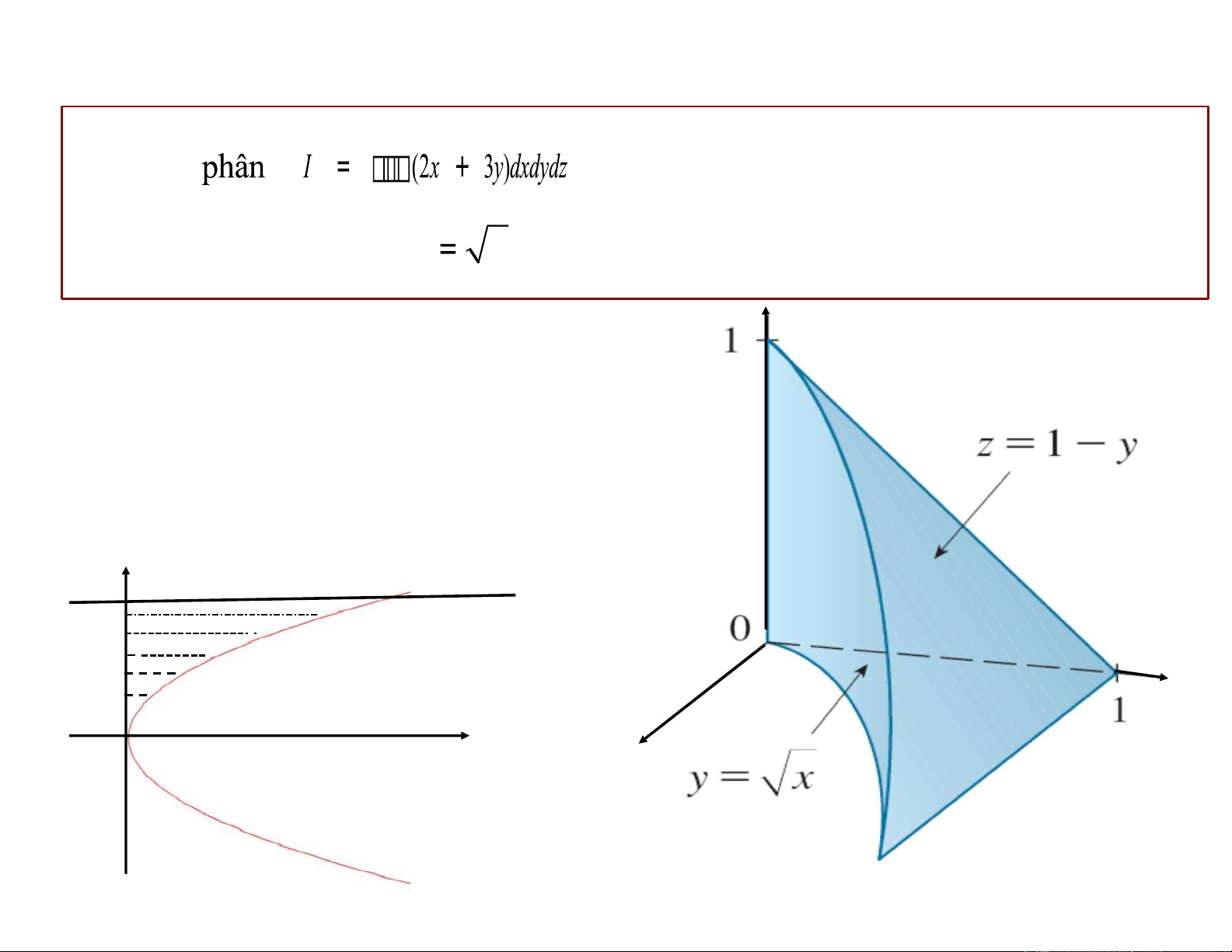
trong đó E là vật thể giới hạn bởi E
y x , z = 1 – y, x = 0, z = 0.
Mặt phía trên: z = 1– y
Mặt phía dưới: z = 0
Hình chiếu của E xuống 0xy: 1– y I = (2x + ) 3y dz dxdy D L 0
I = (2x + 3y)z 1–y dxdy L 0 D
I = ((2x + 3y )(1 – y))dxdy D 1 1
I = dx ((2x + 3y )(1 – y))dy 0 x I = 11 60 Ví dụ Tính tích phân
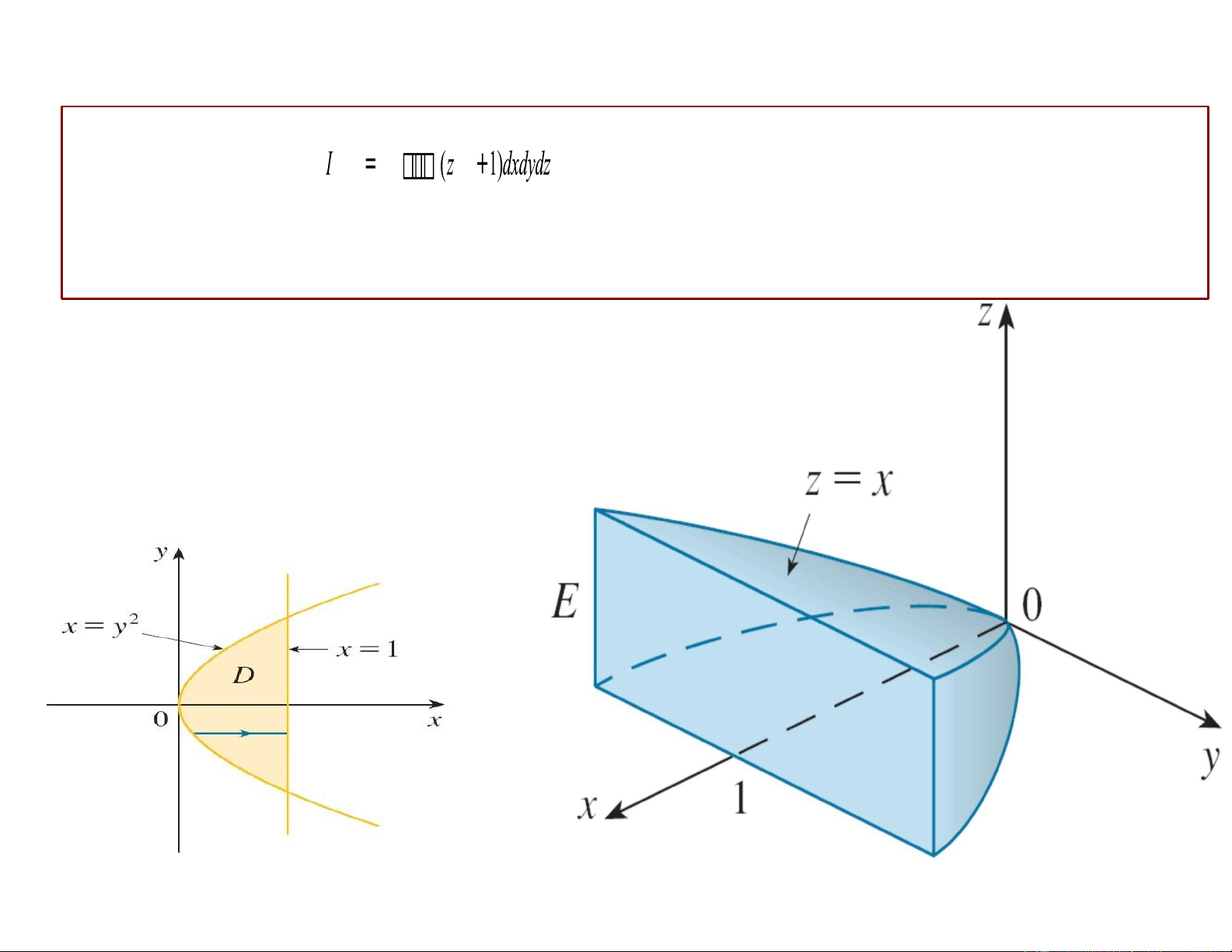
trong đó E là vật thể giới hạn bởi E
x = y2, z = x, z = 0, x = 1.
Mặt phía trên: z = x
Mặt phía dưới: z = 0
Hình chiếu của E xuống 0xy: x
I = (z + 1)dz dxdy D L0 ( x z2 I = + z dxdy D 2 0 L ( x2 I = + x dxdy 2 D 1 1 ( x2 I = dy + x dx –1 y2 2 I = 38 35 Đổi biến tích phân
• Xét I = f (x, y, z)dxdydz E • Phép đổi biến
1. x, y, z có các DHR liên tục x = 2. E là ánh của E’
x(u, v, w) 3. Jacobi
y = y(u, v, w) x ' y ' z ' z =
z(u, v, w) u u u J = x ' y '
z ' s 0, 6(u, v, w) ϵ E ' v v v x ' y ' z ' w w w Khi đó
f (x, y, z)dxdydz = f ( x(u, v, w), y(u, v, w), z(u, v, w)) J dudvdw E E ' II. Toạ độ trụ
---------------------------------------------------------------------------------------------------------------------------
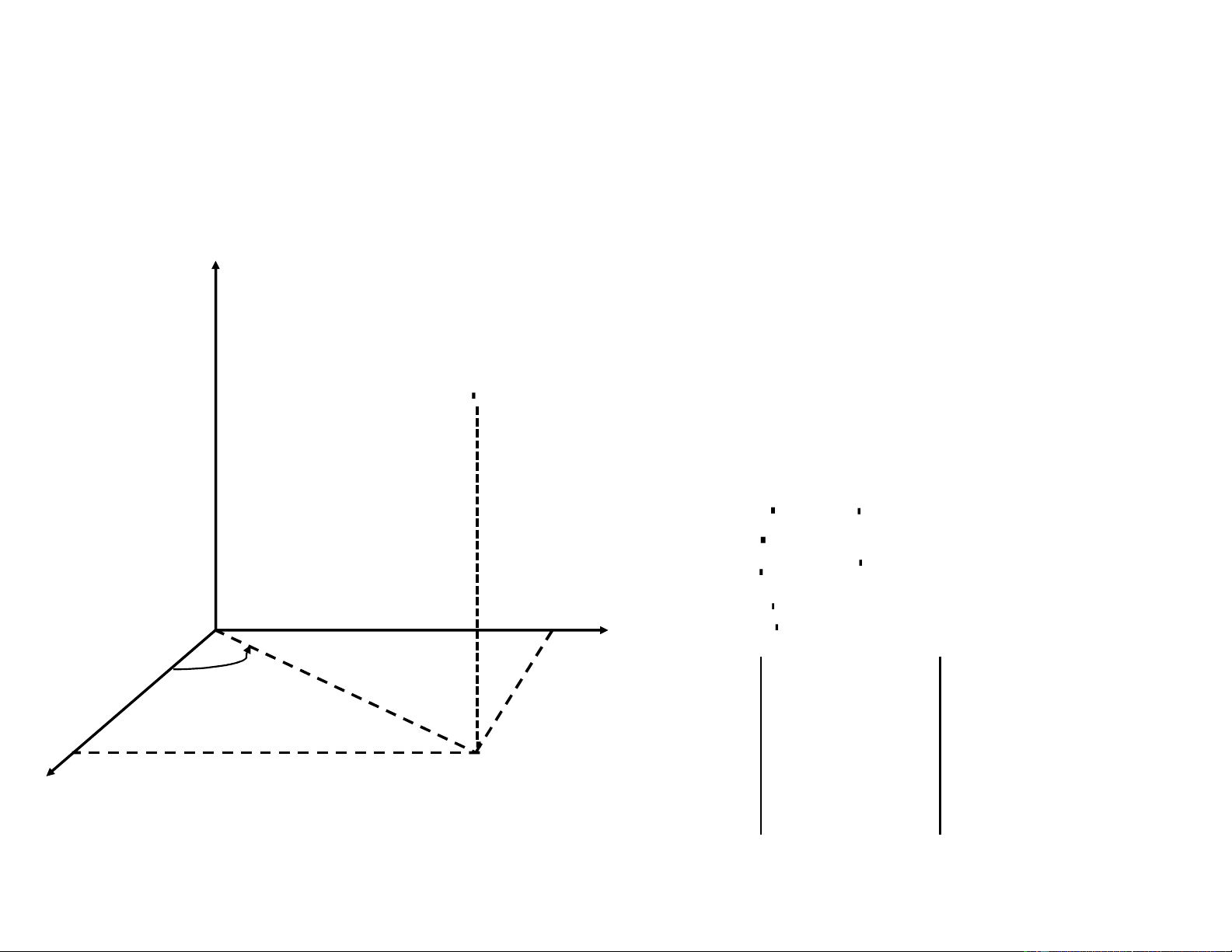
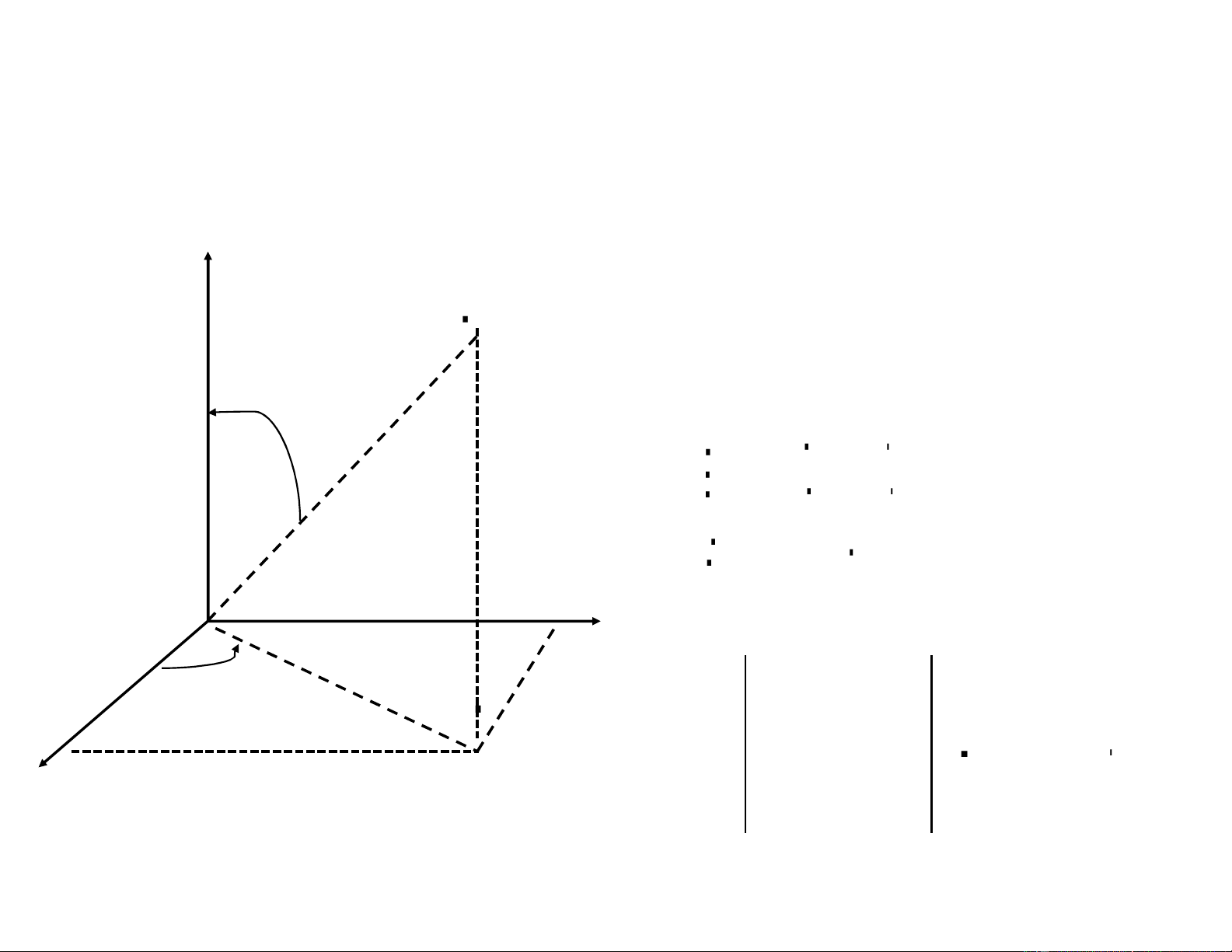
Điểm M(x,y,z) trong hệ trục tọa độ 0xyz. z
M được xác định duy nhất bởi bộ (r,φ, z)
(r,φ, z) được gọi là tọa độ trụ của điểm M.
M (x, y, z)
Công thức đổi biến từ tọa độ Decasters sang tọa độ trụ:
x = r cosφ z
y = r sinφ y z = z r ' x x ' ' x r φ z x ' '
M (x, y, 0) J = y y ' y 1 r φ z = r ' z z ' ' z r φ z
Đổi biến sang tọa độ trụ.
I = f (x, y, z)dxdydz E
x = r cosφ
y = r sinφ z = z
Mặt phía dưới: z = z1(r,φ) z = z z 2 (r,φ)
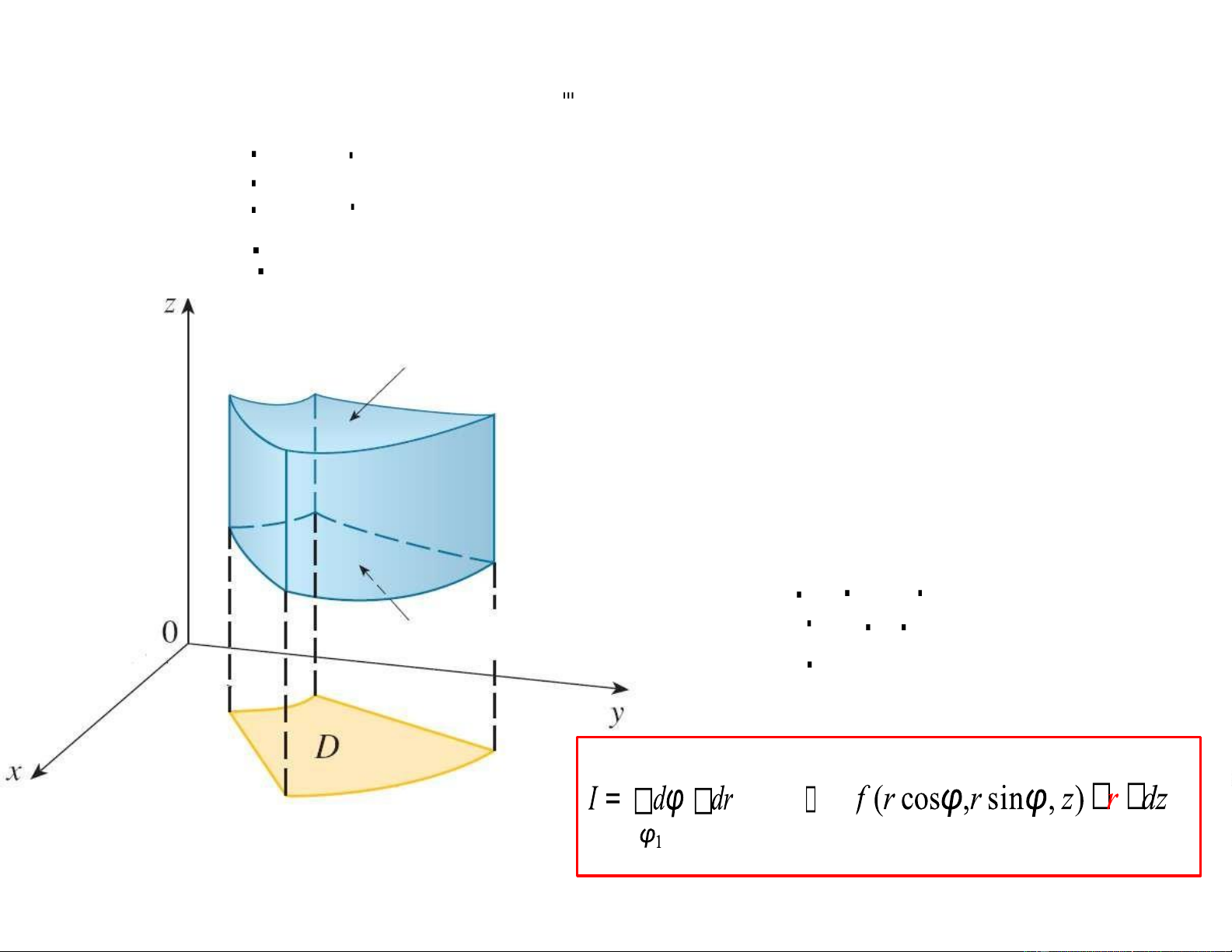
Mặt phía trên: z = 2 (r,φ) Hình chiếu: D Xác định cận r, của D:
z = z (r,φ)
φ1 φ φ2 D : 1 r r r 1 2 φ2 r z 2 2 (r,φ )
z1(r,φ ) r1 Ví dụ Tính tích phân
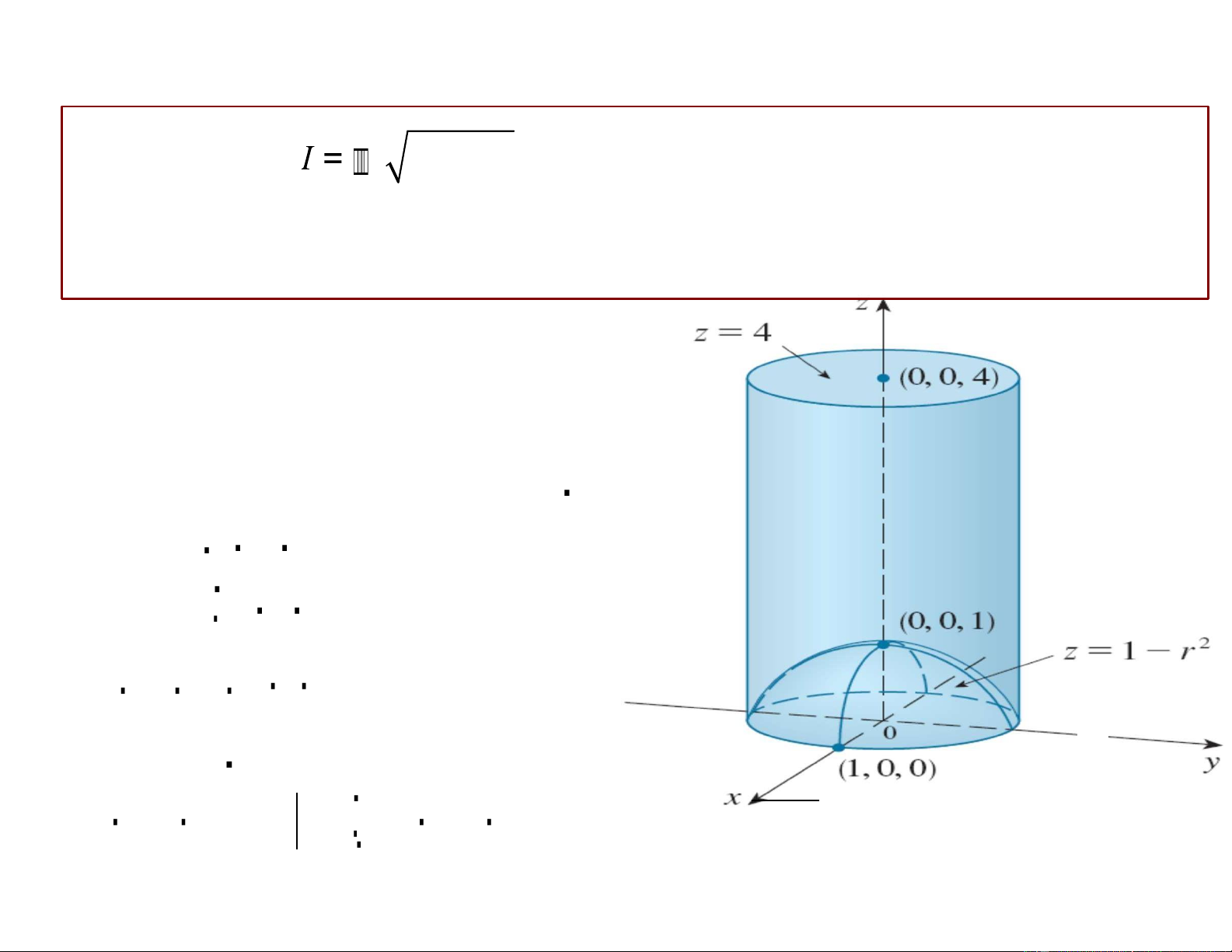
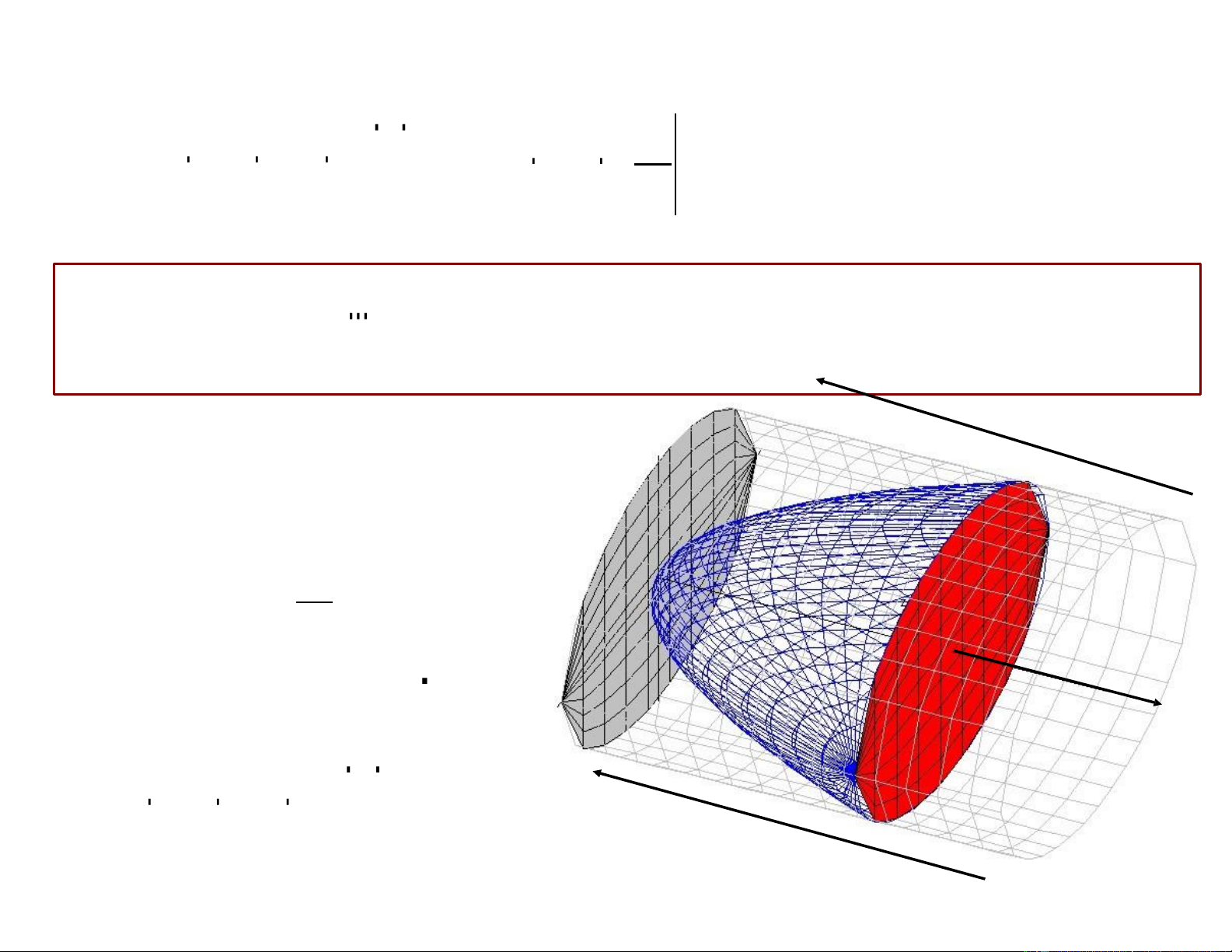
x2 + y2 dxdydz trong đó E là vật thể giới hạn bởi E
z = 4, z = 1 – x2 – y2, x2 + y2 = 1.
Mặt phía trên: z = 4
Mặt phía dưới: z = 1– r 2
Hình chiếu xuống 0xy: D : x2 + y2 1 0 φ 2π D : 0 r 1 2π 1 4
I = dφ dr r r dz 0 0 1–r2 2π 1 4 1
I = dφ dr r 2z (
2π dφ r 2 (3 + r2 ))dr = = 12π 1–r2 0 0 L 0 0 5 Ví dụ Tính tích phân
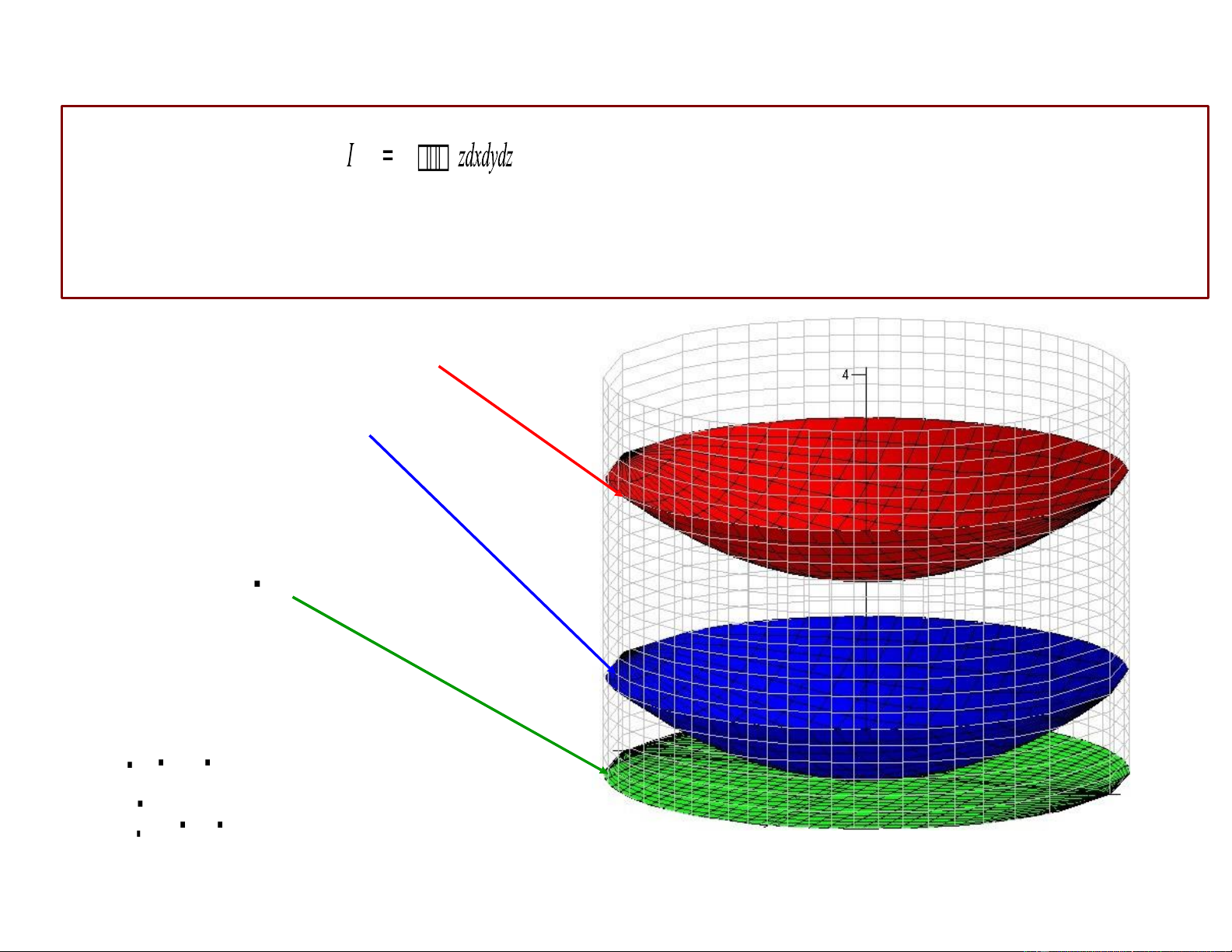
trong đó E là vật thể giới hạn bởi E
z = x2 + y2, z = 2 + x2 + y2, x2 + y2 = 1.
Mặt phía trên: z = 2 + r2
Mặt phía dưới: z = r 2
Hình chiếu của E xuống 0xy:
D : x2 + y2 1 Cận của D: 0 φ 2π D : 0 r 1 2+r2 2π 1 2+r2 I = dφ dr
z r dz =2 π 1 dφ r z2 dr = 3π 0 0 2 r2 0 0 r2 Ví dụ Tính tích phân
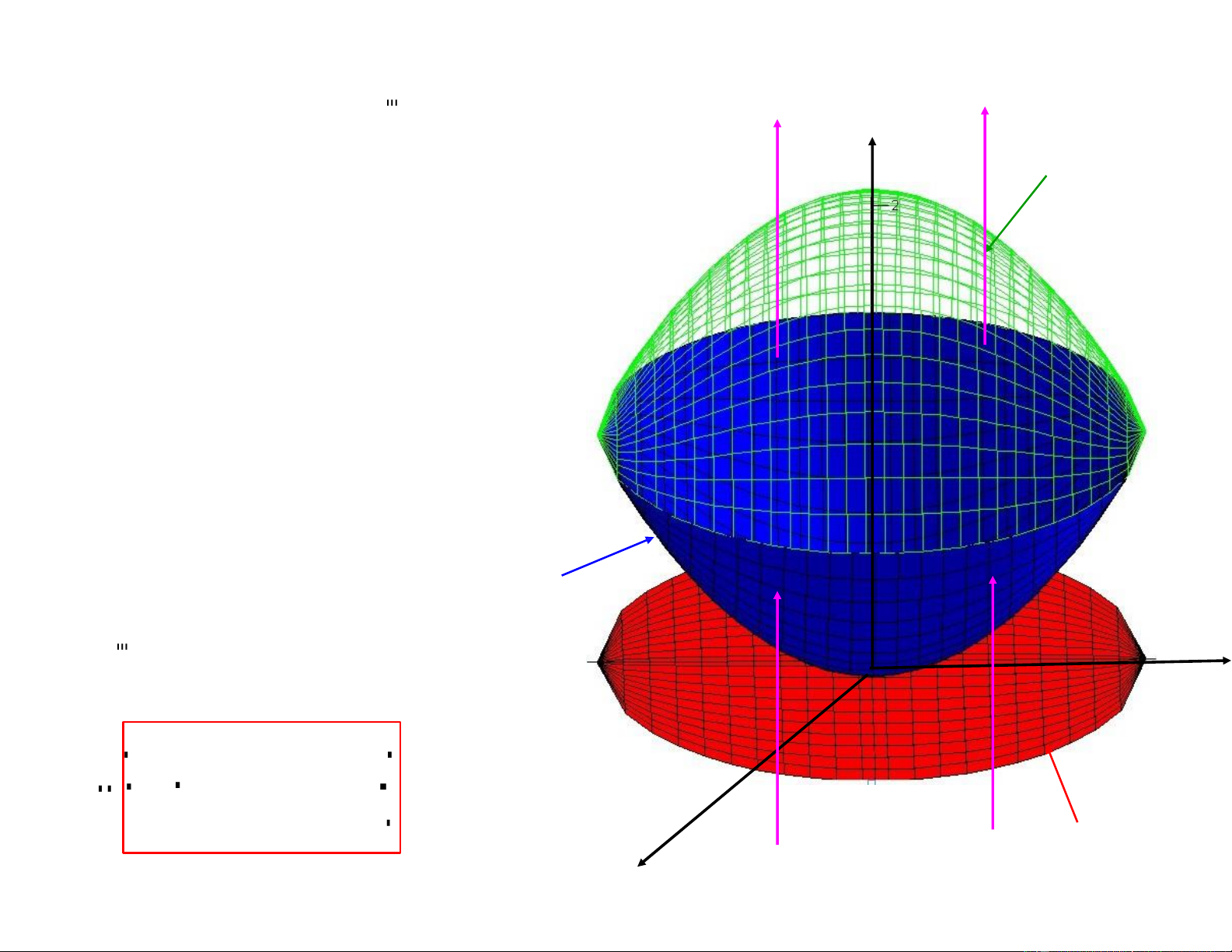
I = (x2 + z2 )dxdydz trong đó E: 2 y = x2 + z2, y = 2. E Chiếu xuống x0z Mặt trên: y = 2 r2 Mặt dưới: y = 2
Hình chiếu: D : x2 + z2 4 y 2π 2 2 I = dφ dr
r 2 r dy 0 0 r2 / 2 II. Toạ độ cầu
---------------------------------------------------------------------------------------------------------------------------
Điểm M(x,y,z) trong hệ trục tọa độ 0xyz. z
M được xác định duy nhất bởi bộ (θ ,φ, p )
M (x, y, z) (θ ,φ, p ) được gọi là tọa độ cầu của điểm M.
Công thức đổi biến sang tọa độ cầu: θ
x = p sinθ cosφ
= p sinθ sinφ y
z = p cosθ
z = p cosθ y
r = p sinθ x' x' x' p φ θ x
M (x, y,0) J = y' y' y' 2 1 p φ θ
| J |= p sinθ z' z' z' p φ θ