Đề cương môn thí nghiệm sức bền vật liệu- Trường Đại học bách khoa - Đại học đà nẵng.

Chương 5 THUYẾT BỀN
5.1 KHÁI NIỆM VỀ THUYẾT BỀN
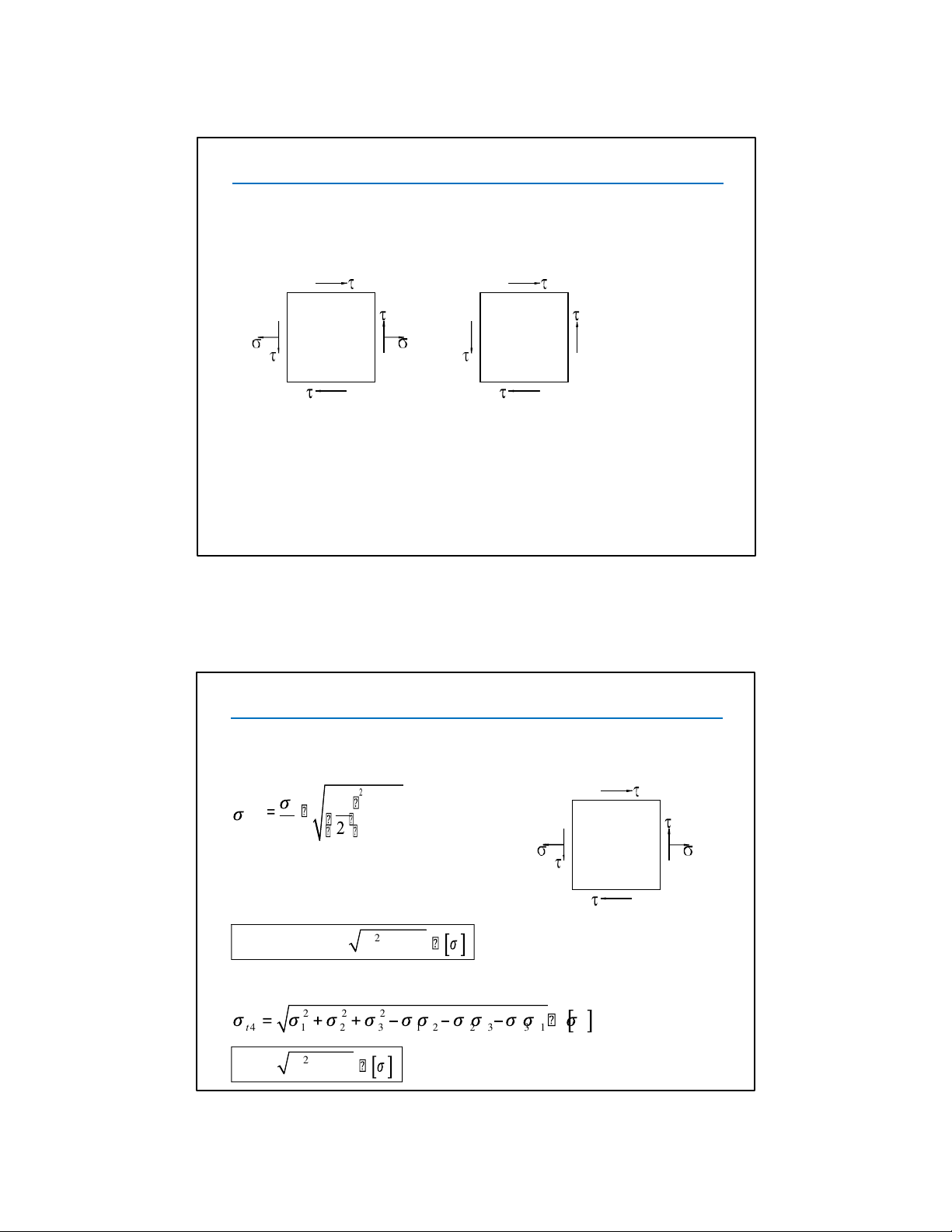
Trong trường hợp kéo nén đúng tâm như đã biết trong chương 3, điều kiện bền là: k σ = σ [σ ] min 3
[σ ] và [σ ] tìm được từ kết quả thí nghiệm kéo nén: k n n Trong đó:
[σ ] là ứng suất cho phép. n là hệ số an toàn.
σ là ứng suất nguy hiểm của vật liệu: o
+ Với vật liệu dẻo: σ = σ o ch
+ Với vật liệu dòn: σ = σ o b 1
5.1 KHÁI NIỆM VỀ THUYẾT BỀN
Để kiểm tra bền ở một điểm ở trạng thái ứng suất phức tạp, ta
cần làm thí nghiệm phá hoại mẫu trong điều kiện tương tự,
nhưng lại rất khó khăn phức tạp vì:
Ứng suất nguy hiểm không những phụ thuộc vào độ lớn
của các ứng suất chính mà còn phụ thuộc vào tỷ lệ giữa
những ứng suất này ==> số thí nghiệm phải rất nhiều.
Thí nghiệm kéo nén ba chiều đòi hỏi những thiết bị phức
tạp, trong khi đó thí nghiệm kéo nén một chiều rất phổ biến vì đơn giản.
Vì vậy, không thể căn cứ và thí nghiệm trực tiếp mà phải dựa
trên các phán đoán về nguyên nhân gây ra phá hỏng và giả thiết
về độ bền của vật liệu hay còn gọi là thuyết bền.
5.1 KHÁI NIỆM VỀ THUYẾT BỀN
Thuyết bền là những giả thuyết về nguyên nhân cơ bản của sự
phá hoại vật liệu, không phụ thuộc vào trạng thái ứng suất của
vật liệu, nhờ đó ta có thể đánh giá được độ bền của vật liệu ở
mọi trạng thái ứng suất khi ta chỉ biết độ bền của vật liệu ở
trạng thái ứng suất đơn.
Vậy, điều kiện bền có thể viết dưới dạng:
σ = f (σ ,σ ,σ ) [σ ] t 1 2 3
σ là ứng suất tính hay ứng suất tương đương. t
Vấn đề là xác định hàm f hay tìm thuyết bền tương ứng. 2
5.2 CÁC THUYẾT BỀN
5.2.1 Thuyết bền ứng suất pháp lớn nhất
(thuyết bền thứ nhất)
Theo thuyết bền này, nguyên nhân gây ra sự phá hoại vật liệu là
do ứng suất pháp lớn nhất của phân tố ở trạng thái ứng suất khối
đạt tới ứng suất nguy hiểm ở trạng thái ứng suất đơn. ok σ = σ = σ t1 1 k n σ σ = σ on = [σ ] t1 3 n n Trong đó:
σ là ứng suất tính hay ứng suất tương đương theo t1 thuyết bền thứ nhất.
σ là ứng suất kéo nguy hiểm. ok
σ là ứng suất nén nguy hiểm. on
5.2 CÁC THUYẾT BỀN
5.2.2 Thuyết bền biến dạng dài tương đối lớn nhất
(thuyết bền thứ hai)
Theo thuyết bền này, nguyên nhân gây ra sự phá hỏng của vật
liệu là do biến dạng dài lớn nhất của phân tố ở trạng thái ứng
suất khối đạt đến biến dạng dài ở trạng thái nguy hiểm của phân
tố ở trạng thái ứng suất đơn. ok
= σ –v σ + σ = t 2 1 2 3 σ k n 3
5.2 CÁC THUYẾT BỀN
5.2.3 Thuyết bền ứng suất tiếp cực đại (thuyết bền thứ 3)
Theo thuyết bền thứ 3, nguyên nhân gây ra sự phá hỏng của vật
liệu là do ứng suất tiếp lớn nhất của phân tố ở trạng thái ứng
suất khối đạt tới ứng suất tiếp nguy hiểm của phân tố ở trạng thái ứng suất đơn.
σ = σ – σ [σ ] t 3 1 3 k
5.2 CÁC THUYẾT BỀN
5.2.4 Thuyết bền thế năng biến đổi hình dáng cực đại (thuyết bền thứ 4)
= σ 2 + σ 2 + σ 2 – σ σ – σ σ – σ σ σ t 4 1 2 3 1 2 2 3 3 1 k 4
5.2 CÁC THUYẾT BỀN
5.2.5 Thuyết bền về trạng thái ứng suất giới hạn
(thuyết bền thứ 5 hay thuyết bền Mohr)
Khác với các thuyết bền trước, thuyết bền Mohr được xây dựng bằng thực nghiệm. Điều kiện bền: k k Với: α = n
5.3 VIỆC ÁP DỤNG CÁC THUYẾT BỀN
Đối với phân tố ở trạng thái ứng suất đơn: dùng thuyết bền 1.
Đối với phân tố ở trạng thái ứng suất khối: dùng thuyết
bền Mohr hay thuyết bền 2 cho vật liệu dòn; thuyết bền 3, 4 cho vật liệu dẻo. 5 5.4 BÀI TẬP 1
Viết điều kiện bền theo thuyết bền ứng suất tiếp và thuyết bền thế
năng biến đổi hình dáng cho trạng thái ứng suất phẳng đặt biệt và
trạng thái trượt thuần túy: 5.4 BÀI TẬP 1
a) Trạng thái ứng suất phẳng đặc biệt có các ứng suất chính như sau: ( σ + τ 2 1,3 2 σ = 0 2
Theo thuyết bền ứng suất tiếp: 2 2
σt3 = σ1 – σ 3 = σ + 4τ
Theo thuyết bền thế năng biến đổi hình dáng: 2 2 2 t 4 1 2 3 1 2 2 3 3 1 2 2
σt4 = σ + 3τ 6 5.4 BÀI TẬP 1
b) Đối với trạng thái trượt thuần túy, các ứng suất chính được xác định như sau:
σ = –σ = τ ;σ = 0 1 3 2
Theo thuyết bền ứng suất tiếp:
σt3 = σ1 – σ3 = 2 τ [σ ]
Theo thuyết bền thế năng biến đổi hình dáng: 2 2 2 t 4 1 2 3 1 2 2 3 3 1
σt4 = 3τ 2 5.5 BÀI TẬP 2
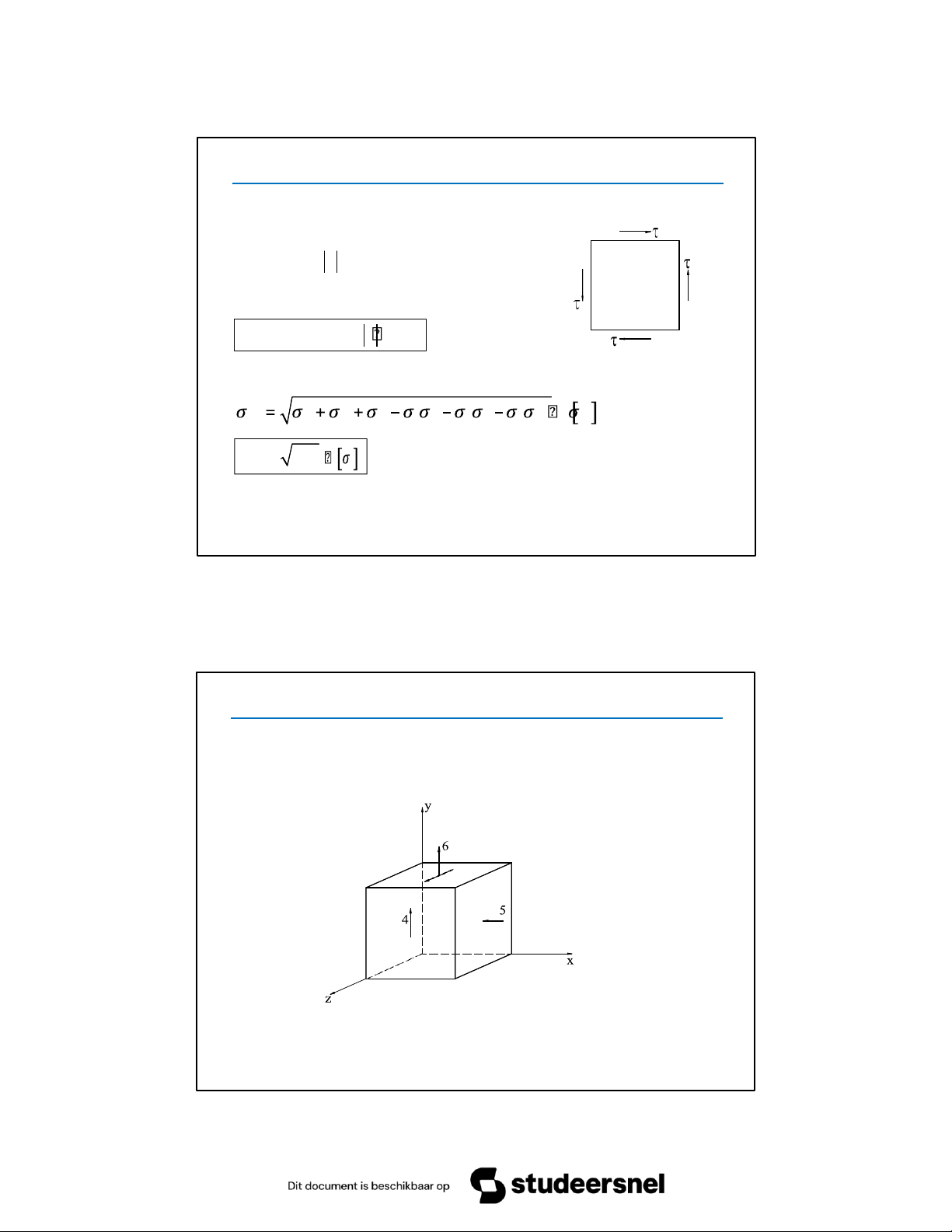
Kiểm tra bền cho phân tố ở trạng thái ứng suất khối cho trên
hình vẽ. Đơn vị của ứng suất là kN/cm2. [σ]=16 kN/cm2. 7 5.5 BÀI TẬP 2 Theo quy ước, ta có:
σ = –5kN / cm x
σ = 6kN / cm y σ = 0 z
τ = τ = 4kN / cm2 τ = τ = 0 xy yx τ = τ = 0 zx xz 5.5 BÀI TẬP 2
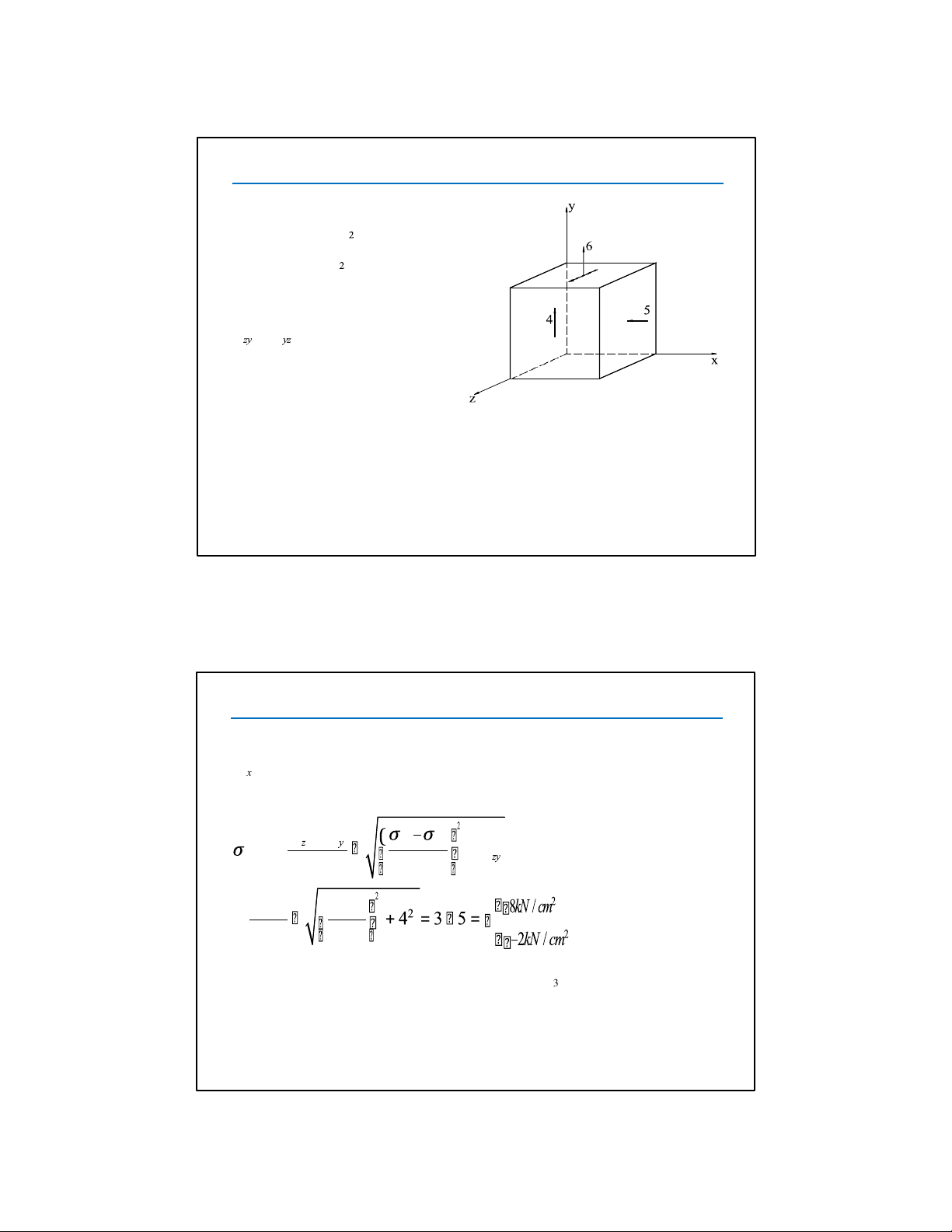
Mặt vuông góc với trục x là mặt chính với ứng suất chính là
σ = –5kN / cm 2. Hai ứng suất chính còn lại nằm trong mặt x
phẳng vuông góc với ứng suất chính đã cho và có giá trị bằng: σ + σ = z y 2 +τ max min 2 2 ( = 0 + 6 0 – 6 2 2
Do đó: σ = 8kN / cm 2 ;σ = –2kN / cm 2; σ = –5kN / cm 2 1 2 3 8 5.5 BÀI TẬP 2 2 2 2
Do đó: σ = 8kN / cm ;σ = –2kN / cm ;σ = – 5 kN / cm 1 2 3
Theo thuyết bền ứng suất tiếp: 2
Theo thuyết bền thế năng biến đổi hình dáng: t 4
σ = 8 + 2 + 5 – (–2)8 – 8(–5) – (–2)(–5) = 11, 79kN / cm t 4
Vậy, phân tố đảm bảo bền theo cả hai thuyết bền. 9