





Preview text:
BÀI TẬP LỚN SỨC BỀN VẬT LIỆU
Họ và tên sinh viên: Mr Khánh TEDI
Số điện thoại liên hệ (Zalo): 0983 376 556 Facebook: Mr Khánh TEDI Chuyên:
Ôn thi, Chạy cánh, Bài tập lớn, Đồ án, Phần mềm…UY TÍN!!!
Đề bài: Cho sơ đồ dầm có các số liệu như sau P M M q A B C D a b a a b M P q
SƠ ĐỒ cm cm daN.cm daN daN/cm 3 500 400 260000 2700 27
A. TÍNH DẦM VỀ ĐỘ BỀN Đổi đơn vị: a = 500cm = 5(m) ; b = 400cm = 4(m) ;
M = 260000daN.cm = 26(kN.m) ; P = 2700daN = 27(kN) ; q = 27daN/cm = 27(kN/m).
1. Vẽ biểu đồ lực cắt và mô men uốn do riêng tải trọng gây ra
Bước 1. Phân tích dầm thành các dầm cơ bản và dầm phụ thuộc (hay dầm đỡ - dầm gác)
Ta tưởng tượng bỏ các liên kết trung gian giữa các đoạn dầm với nhau (Khớp C)
Dầm cính là dầm cơ bản là những dầm không bị thay đổi hình dạng hình học,
Dầm phụ là những dầm bị thay đổi hình dạng hình học (biến hình). Như vậy ta có:
Dầm ABC là dầm cơ bản
Dầm CD là dầm phụ thuộc. P M q D C a VC VD M q VC A B C a b VA VB
Vẽ biểu đồ nội lực của dầm tĩnh định nhiều nhịp theo nguyên tắc: Lực tác dụng ở dầm cơ bản không
ảnh hưởng đến dầm phụ thuộc, ngược lại lực tác dụng lên dầm phụ thuộc truyền ảnh hưởng đến dầm
cơ bản thông qua các phản lực liên kết. Tính nội lực trên đoạn dầm phụ thuộc trước, sau đó truyền
phản lực lên các đoạn dầm cơ bản để tính nội lực ở các đoạn dầm cơ bản.
Bước 2. Tính và vẽ các biểu đồ nội lực trên các đoạn dầm
+ Đoạn dầm phụ thuộc CD Trang 1
- Xác định các phản lực liên kết
SMD=0 : VC*a - P*a - q*a*a/2 - M = 0
VC*5 - 27*5 - 27*5*5/2 - 26 = 0 SY=0 : VC + VD - P - q*a = 0 VC + VD - 27 - 27*5 = 0 Giải ra ta có VD = 62.3 kN VC = 99.7 kN P
- Viết biểu thức nội lực Qy và Mx M 1 Mx q
Dùng mặt cắt (1 - 1) , z thuộc [0,5]m
Xét cân bằng bên trái, ta có: C 1 Qy z
Qy = VC - P - q*z = 99.7 - 27 - 27*z VC Mx=VC*z - P*z - q*z2/2 - M = 99.7*z - 27*z - 27*z^2/2 - 26 Khi z= 0 (Tại điểm C): Qy= 72.7 kN ; Mx= -26 kN.m Khi z = 5m (Tại điểm D) Qy= -62.3 kN ; Mx= 0.0 kN.m
Xét cực trị: dMx/dz = VC - P - q*z = 0 => z = (VC - P)/q = (99.7 - 27)/27= 2.69m
Biểu đồ mô men đoạn này đạt cực trị tại z =2.69
Mô men lớn nhất M max = 71.88 kN.m P= 27 M= 26 1 q= 27 D C 1 z a= 5 VC VD 72.7 tt Q y 3. 2 6- 26 tt - Mx 71.88
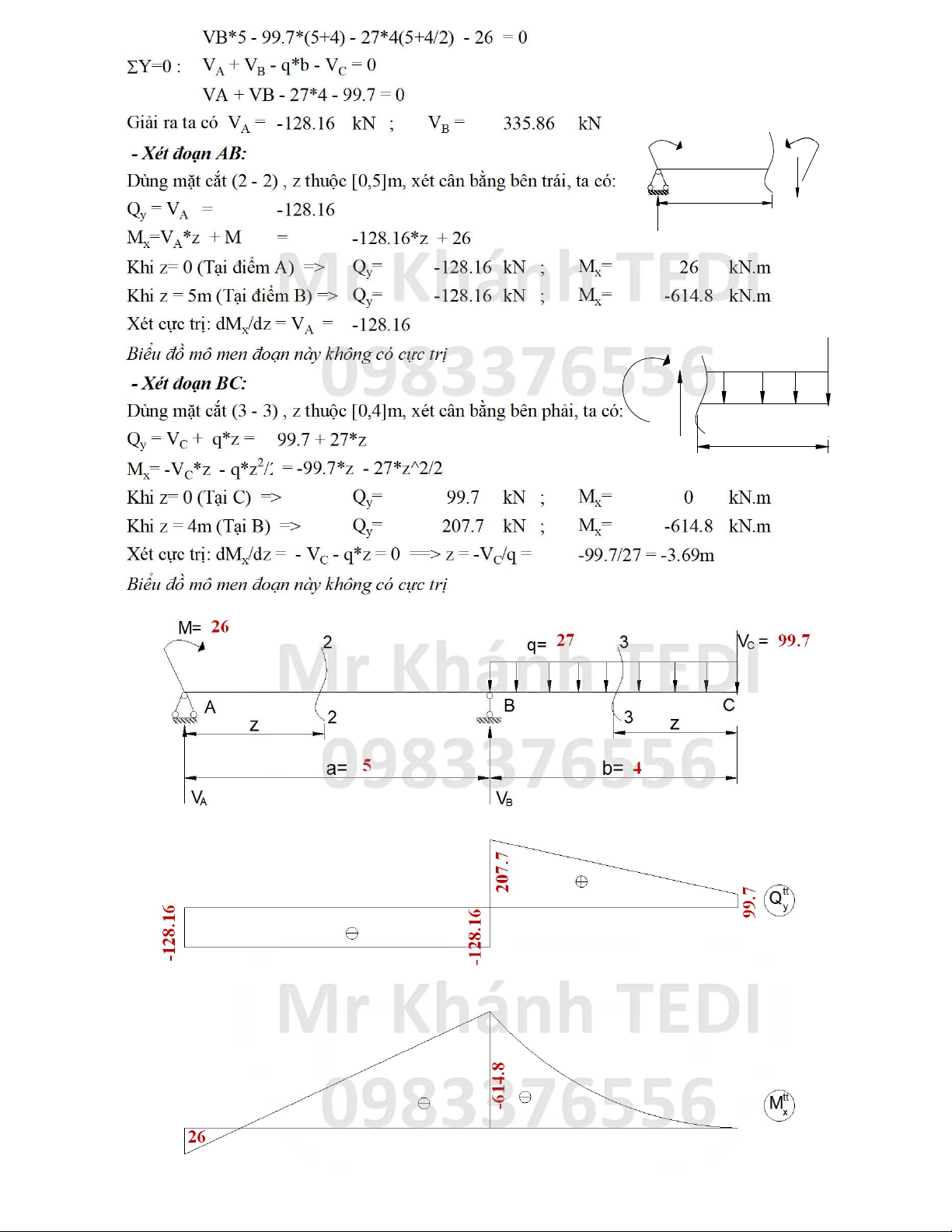
+ Đoạn dầm cơ bản ABC
- Xác định các phản lực liên kết
SMA=0 : VB*a - VC*(a+b) - q*b*(a+b/2) - M = 0 Trang 2
VB*5 - 99.7*(5+4) - 27*4(5+4/2) - 26 = 0
SY=0 : VA + VB - q*b - VC = 0 VA + VB - 27*4 - 99.7 = 0
Giải ra ta có VA = -128.16 kN ; VB = 335.86 kN M 2 Mx
- Xét đoạn AB:
Dùng mặt cắt (2 - 2) , z thuộc [0,5]m, xét cân bằng bên trái, ta có: A z 2 Qy Qy = VA = -128.16 VA Mx=VA*z + M = -128.16*z + 26
Khi z= 0 (Tại điểm A) => Qy= -128.16 kN ; Mx= 26 kN.m
Khi z = 5m (Tại điểm B) => Qy= -128.16 kN ; Mx= -614.8 kN.m
Xét cực trị: dMx/dz = VA = -128.16
Biểu đồ mô men đoạn này không có cực trị 3 q VC Mx
- Xét đoạn BC:
Dùng mặt cắt (3 - 3) , z thuộc [0,4]m, xét cân bằng bên phải, ta có: Qy C 3 Q z y = VC + q*z = 99.7 + 27*z
Mx= -VC*z - q*z2/ = -99.7*z - 27*z^2/2 Khi z= 0 (Tại C) => Qy= 99.7 kN ; Mx= 0 kN.m Khi z = 4m (Tại B) => Qy= 207.7 kN ; Mx= -614.8 kN.m
Xét cực trị: dMx/dz = - VC - q*z = 0 ==> z = -VC/q = -99.7/27 = -3.69m
Biểu đồ mô men đoạn này không có cực trị M= 26 2 q= 27 3 VC = 99.7 A B C z 2 3 z a= 5 b= 4 VA VB 07.7 tt 2 Q y 99.7 128.16 - 128.16- tt 614.8- Mx 26 Trang 3
Biểu đồ nội lực trên toàn dầm được ghép bởi biểu đồ nội lực của các đoạn dầm. Ta có kết quả: M= 26 P= 27 q= 27 M= 26 A B C D a= 5 b= 4 a= 5 P M q D C a VC VD M q VC A B C a b VA VB 7. 7 0 2 99.7 tt 3.Qy 2 6 128.16 72.7 - - 128.16 - tt 614.8 M x - 26 - 26 71.88
2. Chọn số hiệu mặt cắt và số lượng dầm
Chọn số hiệu mặt cắt và số lượng dầm theo điều kiện bền về ứng suất pháp, mặt cắt nguy hiểm là mặ
cắt có mô men uốn lớn nhất Mmax =
614.8 kN.m = 6148000daN.cm tại điểm B
Theo điều kiện bền ta có TT Mx = 6148000/1600 = 3842.5 cm3 W x R
Chọn 7 dầm I, số hiệu 36 tra bảng ta có thông số sau: h b d t F q Số hiệu 0 Jx Wx Sx cm cm cm cm cm2 daN/cm cm4 cm3 cm3 I36 36 14.5 0.75 1.23 61.9 0.486 13380 743 423
3. Vẽ biểu đồ nội lực do tải trọng và trọng lượng bản thân dầm
Từ kết quả chọn dầm ở bước 2, ta có trọng lượng bản thân dầm trên 1m dài là qt = 7*0.486
= 3.402kN/m. Để vẽ biểu đồ do tải trọng và trọng lượng bản thân dầm, có thể cộng tải trọng và trọng
lượng bản thân dầm và làm như bước 1, hoặc vẽ biểu đồ nội lực do riêng trọng lượng bản thân rồi cộ
hai biểu đồ lại với nhau. Ở đây dùng cách thứ hai. Để vẽ được biểu đồ nội lực do trọng lượng bản th â
gây ra ta làm tương tự như bước thứ 1 với tải trọng phân bố đều trên toàn dầm. Trang 4
Sơ đồ dầm chịu lực là trọng lượng bản thân dầm và các biểu đồ nội lực tương ứng 2 q = 3.402 tt 3 1 A B C D 2 3 1 a= 5 b= 4 a= 5
+ Đoạn dầm phụ thuộc CD
- Xác định các phản lực liên kết SMD=0 : VC*a - q*a*a/2 = 0 VC*5 - 3.402*5*5/2 = 0 SY=0 : VC + VD - q*a = 0 VC + VD - 3.402*5 = 0 Giải ra ta có VD = 8.5 kN 1 Mx qtt VC = 8.5 kN
- Viết biểu thức nội lực Qy và Mx
Dùng mặt cắt (1 - 1) , z thuộc [0,5]m C 1 Qy
Xét cân bằng bên trái, ta có: z Q V y = VC - q*z C Mx=VC*z - q*z2/2 Khi z= 0 (Tại C): Qy= 8.5 kN ; Mx= 0 kN.m Khi z = 5m (Tại D): Qy= -8.5 kN ; Mx= 0 kN.m
Xét cực trị: dMx/dz = VC - q*z = 0 => z = VC /q =8.51/3.402= 2.5 m
Biểu đồ mô men đoạn này đạt cực trị tại z =2.5 ;Mmax = 10.64 kN.m
+ Đoạn dầm cơ bản ABC
- Xác định các phản lực liên kết
SMA=0 : VB*a - VC*(a+b) - q(a+b)*(a+b)/2 = 0
VB*5 - 8.51*(5+4) - 3.402(5+4)(5+4)/2 = 0
SY=0 : VA + VB - q*(a+b) - VC = 0 2 Mx qtt
VA + VB - 3.402*(5+4) - 8.51 = 0 Giả i ra ta có VA = -3.75 kN ; VB = 42.87 kN
- Xét đoạn AB: A z 2 Qy
Dùng mặt cắt (2 - 2) , z thuộc [0,5]m, xét cân bằng bên trái, ta có: Qy = VA - q*z = -3.75 - 3.402*z VA Mx=VA*z - q*z2/2 = -3.75*z - 3.402*z^2/2 Khi z= 0 (Tại A) => Qy= -3.75 kN ; Mx= 0 kN.m Khi z = 5m (Tại B) => Qy= -20.8 kN ; Mx= -61.3 kN.m Xét cực trị: dMx/dz =
VA - q*z = 0 ==> z = VA/q = -3.75/3.402 = -1.1m
Biểu đồ mô men đoạn này không có cực trị
- Xét đoạn BC:
Dùng mặt cắt (3 - 3) , z thuộc [0,4]m, xét cân bằng bên phải, ta có: Trang 5 Qy = VC + q*z = 8.51 + 3.402*z
Mx= -VC*z - q*z2/ = -8.51*z - 3.402*z^2/2 Khi z= 0 (Tại C) => Qy= 8.51 kN ; Mx= 0 kN.m Khi z = 4m (Tại B)=> Qy= 22.1 kN ; Mx= -61.3 kN.m
Xét cực trị: dMx/dz = - VC - q*z = 0 ==> z = -VC/q = -8.51/3.402 = -2.5m Biểu 3 qtt V
đồ mô men đoạn này không có cực trị C Mx
Sơ đồ chịu lực và biểu đồ nội lực do trọng lượng bản thân dầm qtt Qy C 3 z 2 q = 3.402 tt 3 1 A B D 2 3 C 1 5 5 a= b= 4 a= 5 7 22.1 . 3 8.5 bt - Qy 8 8.5 . - 0 2- 3. 1 6 bt - Mx 10.64
Cộng tương ứng biểu đồ nội lực ta được kết quả sau: Đại lương A Btrái Bphải Ctrái Cphải D Đơn vị z 0 5 5 9 9 14 m tt Q y -128.16 -128.16 207.7 99.7 72.7 -62.3 kN bt Q y -3.75 -20.8 22.1 8.51 8.5 -8.5 kN tt bt Q y=Qy + Qy -131.91 -148.96 229.8 108.21 81.2 -70.8 kN tt M x 26 -614.8 -614.8 0 -26 0 kN.m bt M x 0 -61.3 -61.3 0 0 0 kN.m tt bt M x=Mx + Mx 26 -676.1 -676.1 0 -26 0 kN.m Trang 6
Biểu đồ mô men do tải trọng và trọng lượng bản thân dầm P= 27 M= 26
q+qtt= 30.402 M= 26 qtt= 3.402 A B C D a= 5 b= 4 a= 5 8 . 9 2. 2 2 8 0 1 131.91 8.96 1.2 0.8 Q - 8 7 y 14 - - 676.1 26- M - x 26 82.52
4. Kiểm tra độ bền của dầm dưới tác dụng của tải trọng và trọng lượng bản thân.
Dầm chịu uốn ngang phẳng do đó kiểm tra điều kiện bền của dầm theo các điều kiện sau:
+ Theo điều kiện bền của ứng suất pháp: Điểm có ứng suất pháp lớn nhất trong dầm là điểm nằm ở
mép dầm tại mặt cắt B có mô men lớn nhất M = 676.1 kN.m = 6761000 daN.cm x max M x max s = = max
6761000/(7*743) = 1299.94 daN/cm2 W x
0.75[s] = 1200 daN/cm2 < smax < 1.05[s] = 1.05*1600 = 1680 daN/cm2
+ Theo điều kiện bền của ứng suất tiếp: Điểm có ứng suất tiếp lớn nhất trong dầm là điểm trên
đường trung hòa tại mặt cắt bên phải B, có lực cắt lớn nhất. Q = y 22980 daN max t = Q .S = y x 22980*423 max 2 = 138.38 max daN/cm n.J .d 7*13380*0.75 x
tmax < 1.05[t] = 1.05*1000 = 1050 daN/cm2 Trang 7



