


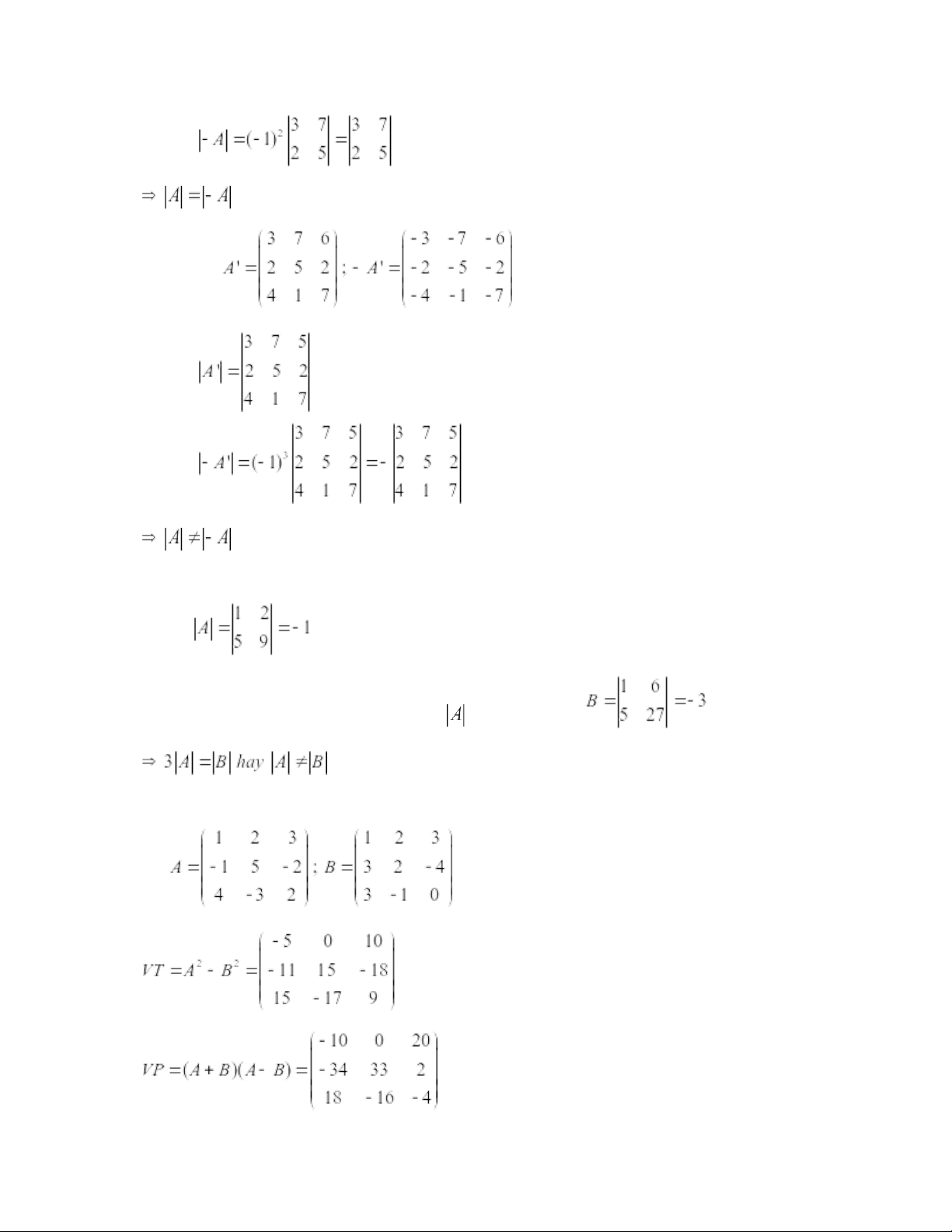





Preview text:
Trường ĐH Kinh tế TP.HCM GVHD: TS. Nguyễn Thanh Vân
Mã lớp học phần: 21C1MAT50800134
BÀI TẬP TỰ LUẬN CHƯƠNG 1
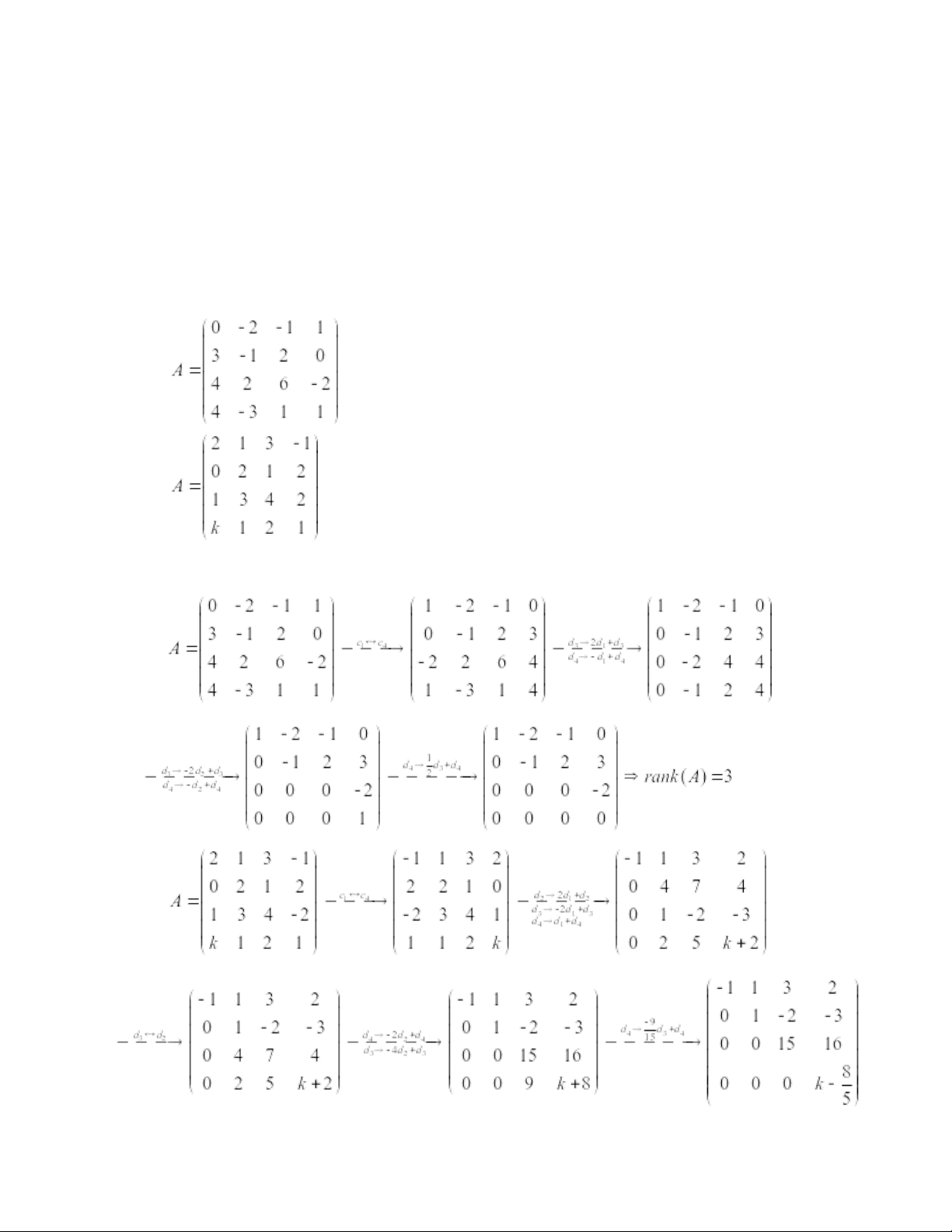
Bài 17 (SBT): Tìm hạng của các ma trận sau đây: a) . b) . Giải: a) b) • •
Bài 18 (SBT): Tìm m để ma trận không suy biến. Giải: Ycbt
Khai triển định thức theo dòng 3, ta có: Vậy thì A không suy biến.
Bài 19 (SBT): Cho ma trận và . Tìm ma trận . Giải:
Bài 20 (SBT): Cho A là ma trận vuông cấp 3 có và Khi đó hãy tính: a) . b) . Giải: a) ; b)
Bài 21 (SBT): Cho ma trận . Tính . Giải:
Khai triển theo cột 1, ta có:
Khai triển theo dòng 1, ta có:
Bài 23 (SBT): Cho ma trận vuông cấp 4 có . Tính . Giải:
Bài 24 (SBT): Cho A là ma trận vuông cấp n
. Mệnh đề nào sau đây là sai? Nếu sai, hãy cho một phản ví dụ. a)
không đổi khi ta đổi chỗ 2 dòng bất kỳ trong A. b)
không đổi khi ta biến đổi cột 1 thành cột 1 cộng với cột 2 trong . c) . d) . e)
không đổi khi ta nhân các phần tử của cột 2 trong với 3. f)
là các ma trận vuông cấp n. g) với . h)
vuông cấp n, khả nghịch. i) Giải: a) Sai. VD: Có
Sau khi đổi chỗ dòng 1 và dòng 2, ta được: b) Đúng. c) Sai. VD: Có mà Mặt khác: d) Sai. VD: TH1: Cho • • TH2: Cho • • e) Sai. VD: Ta có:
Sau khi nhân các phần tử của cột 2 trong với 3, ta được: f) Sai. VD: Có: g) Đúng. h) Đúng. i) Đúng.
Bài 30: Cho A là một ma trận vuông cấp 3 có và . Tính . Giải: Ta có: mà theo đề bài nên
A là một ma trận vuông cấp 3 Vậy Bài 31 (SBT): Cho
là các ma trận vuông cấp 4 có và thỏa mãn . a) Hãy tính . b) Hãy tính . c) Hãy tính . Giải: a) b) • • • c) • •
Bài 32 (SBT): Cho A là ma trận vuông cấp 3 thỏa mãn
a) Chứng minh: A khả nghịch. b) Tìm theo A và I. c) Nếu hãy tính theo k. Giải: a)
(tính chất ma trận nhân với ma trận đơn vị) Theo định nghĩa, ma trận thỏa mãn . Suy ra: A khả nghịch. b) Ta có:
Theo định nghĩa ma trận nghịch đảo, suy ra: Câu 1: Cho .
không khả đảo khi và chỉ khi nào? Giải: không khả đảo Vậy
không khả đảo khi và chỉ khi và .
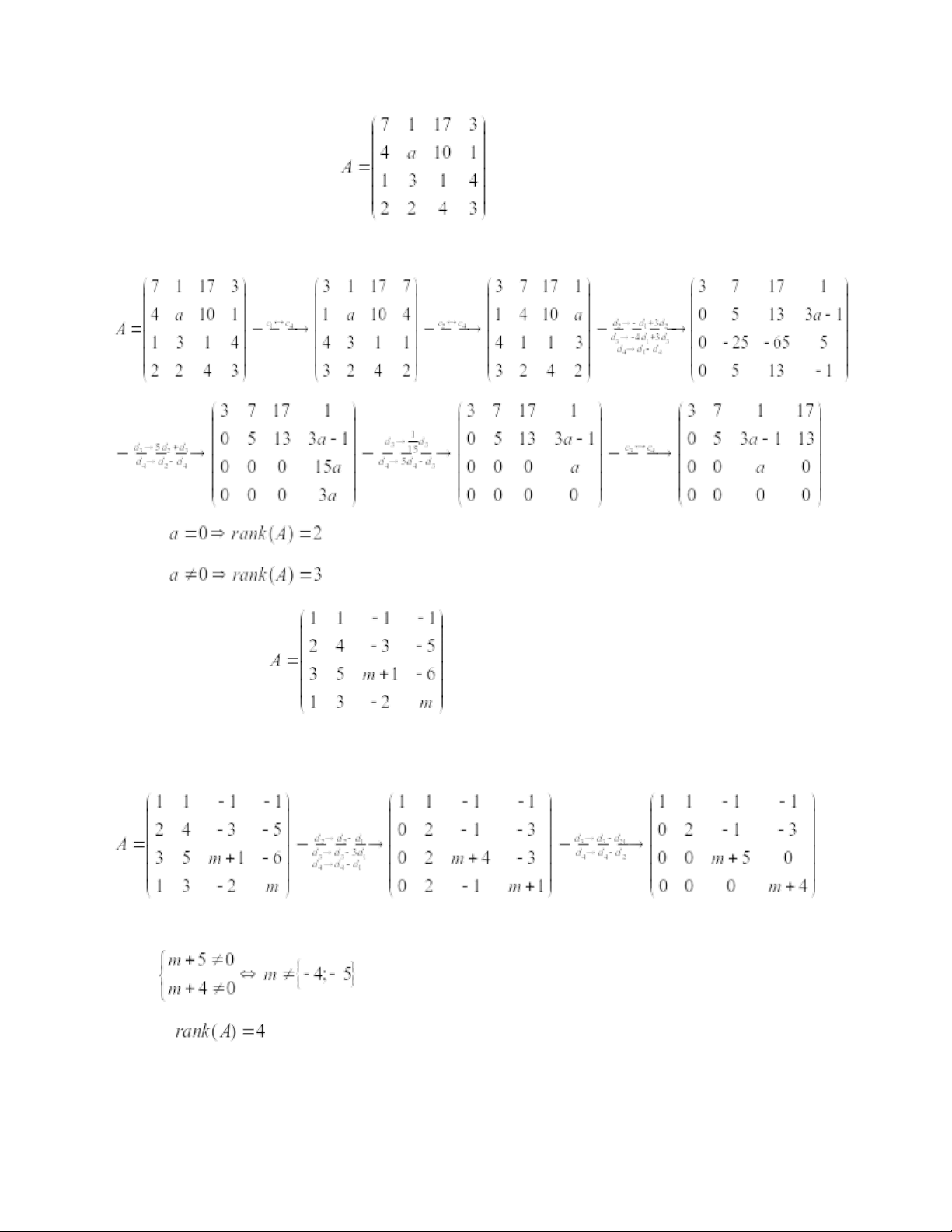
Câu 2: Tìm hạng của ma trận . Giải: • • Câu 3: Cho ma trận
. Biện luận hạng của ma trận A theo tham số thực m. Giải: Biện luận: TH1: Khi đó: TH2: Khi đó: Câu 4: Cho .
1) Tìm ma trận nghịch đảo của A.
2) Tìm ma trận X, Y sao cho Giải: 1) Ta có: Ta có: 2) • •
Câu 5: Cho A là một ma trận vuông cấp 4 có
. Gọi là ma trận phụ hợp của ma trận A. Tính . Giải:
Câu 6: Cho A là một ma trận vuông cấp 3 có và . Tính . Giải: Ta có: mà theo đề bài nên
A là một ma trận vuông cấp 3 Vậy
Câu 7: Cho A, B là các ma trận vuông cấp 4 có , và . Khi đó là: A. 36 B. 1296 C. 216 D. Tất cả đều sai. Giải: Có: (dựa vào công thức ) (dựa vào công thức )
Lấy định thức 2 vế, ta được: Mà nên Chọn C
Câu 8: Cho A, B là các ma trận vuông cấp n, biết . Khi đó: A) B) C)
D) Các câu trên đều sai. Giải: không thể tồn tại và Loại A và B.
Loại C vì ma trận không có tính giao hoán.




