


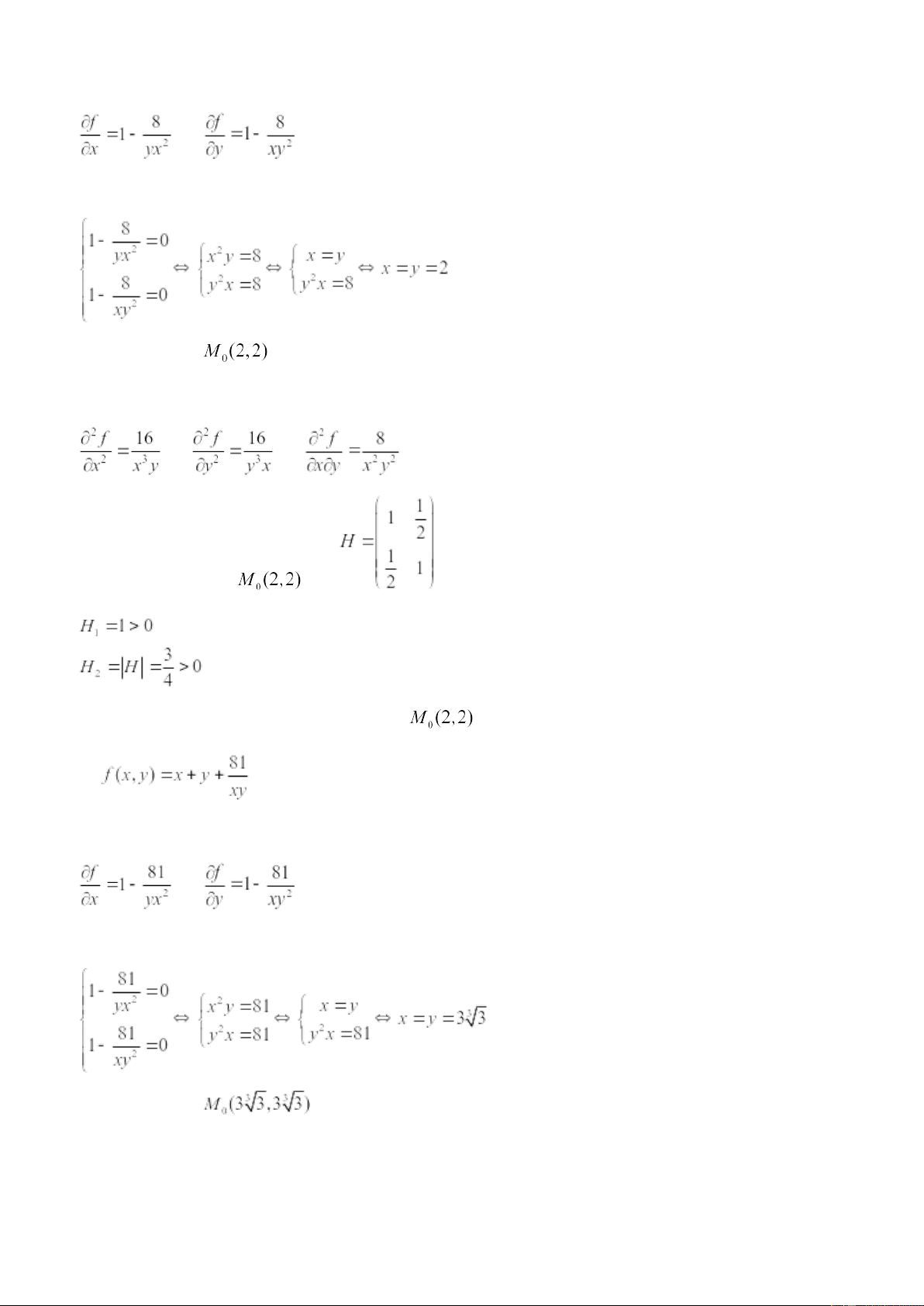

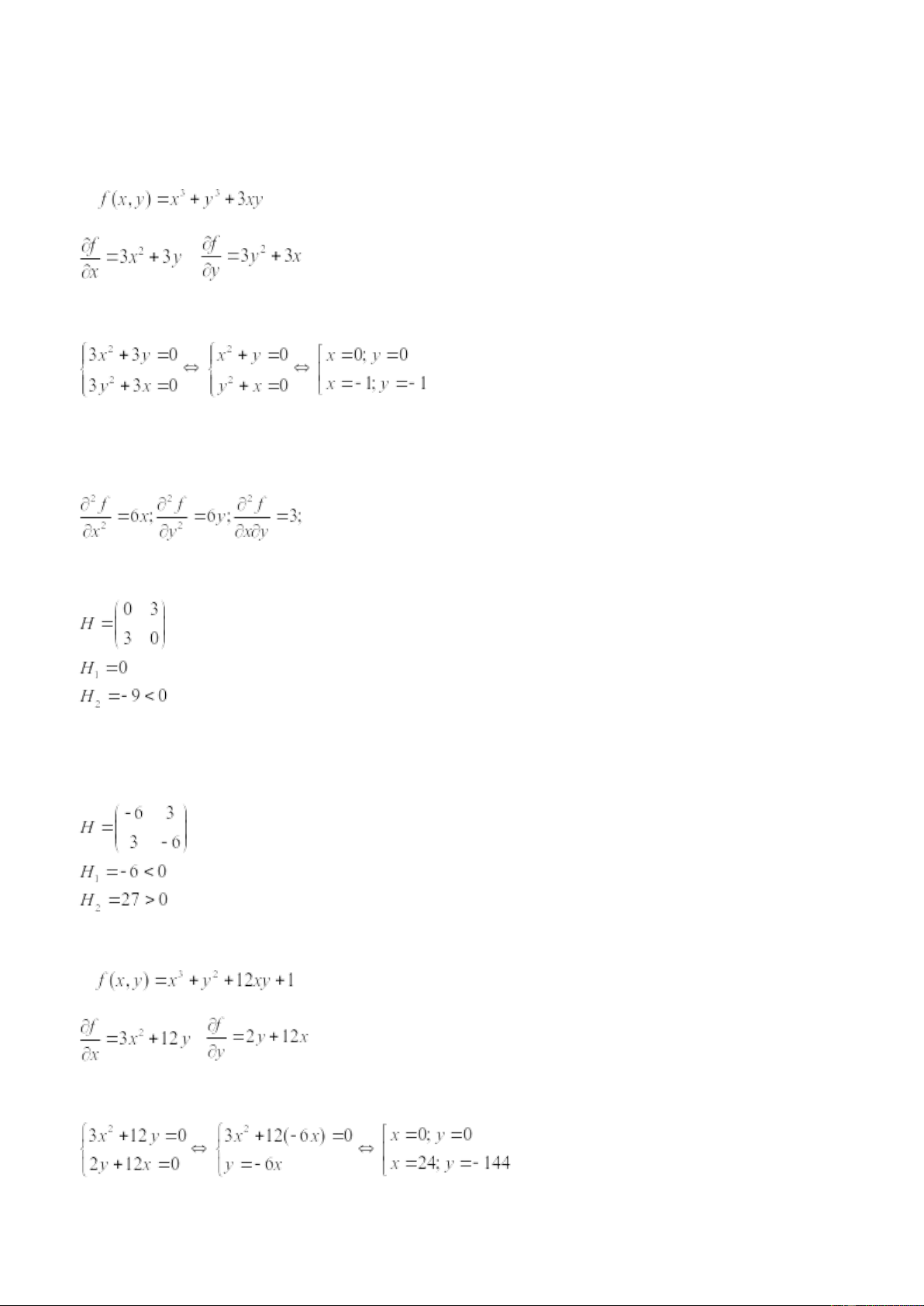







Preview text:
Bài 1: Tìm cực trị của hàm: 1/
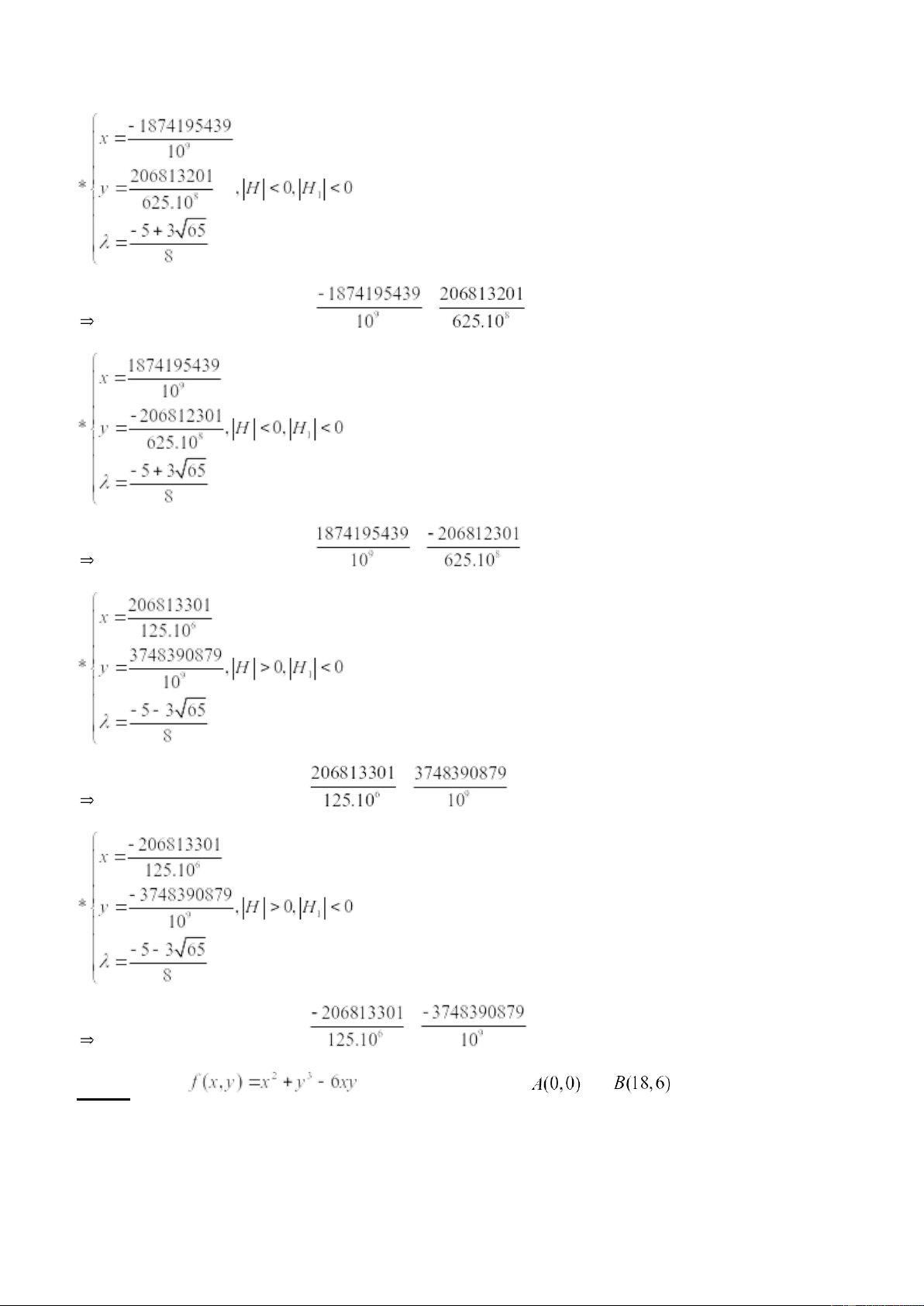
2/ f(x,y) =4x4+2y4-2x2-y2, với x>0, y>0 Giải: 1/ f(x, y) = x2 + y3 - 6xy ∂ u ∂u Ta có: =¿ 2x – 6y; =3 y 2 – 6x ∂ x ∂ y Giải hệ phương trình: 2 x−6 y=0 { 3 y2−6 x=0 { ⇔ x=3 y 3 y −6.3 y=0 {⇔ x=3 y y=0 , y=6 { ⇔ x=0 , y=0 2 x=18 , y=6
Vậy M1(0,0), M2(18,6) là 2 điểm dừng ∂2 u ∂2u ∂2 u = = ∂ x 2 ; 6 y ; 2 ∂ y2 ∂ x ∂ y=−6 ;
*Tại M1(0,0), ma trận Hesse H=( 2 −6) −6 0 H =2>0 Ta có: 1 { H 2=∣H∣=−36∈0
Vậy hàm số không đạt cực trị tại M1(0,0)
*Tại M2(18,6), ma trận Hesse H=( 2 −6) −6 36 H =2>0 Ta có: 1 { H 2=∣H∣=36>0
Vậy hàm số đạt cực tiểu tại M2(18,6) và giá trị cực tiểu tại f(18,6)= -108
2/ f(x,y) =4x4+2y4-2x2-y2, với x>0, y>0 Do Điểm dừng Ta có: ; ; Tại , xét ma trận Hesse: =>
đạt cực tiểu địa phương tại
Bài 2: Tìm cực trị của hàm: f(x,y)=x.y với điều kiện Giải: Ta có hàm Lagrange: Ta có hệ phương trình:
⇨ Hàm L có điểm dừng tại Xét: Ta có:
Vậy hàm f đạt cực đại địa phương tại .
Bài 5. Tìm cực trị của các hàm sau đây a) Ta có: Giải hệ phương trình: Điểm dừng là
Các đạo hàm riêng cấp 2 tại điểm là: Ma trận Hesse tại là:
Vậy suy ra hàm f(x,y) không đạt cực trị. b) Ta có: Giải hệ phương trình: Điểm dừng là
Các đạo hàm riêng cấp 2 là: Ma trận Hesse tại là:
Vậy suy ra hàm f(x,y) đạt cực tiểu tại
với giá trị cực tiểu f(2,2) = 6 c) Ta có: Giải hệ phương trình: Điểm dừng là
Các đạo hàm riêng cấp 2 là: Ma trận Hesse tại là:
Vậy suy ra hàm f(x,y) đạt cực tiểu tại
với giá trị cực tiểu f( ) = d) ; Giải hệ phương trình
Các đạo hàm riêng cấp 2
Xét tại M0(5;2) ta có ma trận Hesse tại M0(5;2)
Nên hàm f(x;y) đạt cực tiểu tại M0(5;2) và có giá trị cực tiểu là f(5;2)=30 e) ; Giải hệ phương trình
Vậy M1(0;0) và M2(-1;-1) là điểm dừng.
Các đạo hàm riêng cấp 2
Xét tại M1(0;0), có trận Hesse
⇨ Nên hàm f(x,y) không đạt cực trị tại M1(0,0)
Xét tại M2(-1;-1) có ma trận Hesse
⇨ Hàm f(x,y) đạt cực đại tại M2(-1;-1) và có giá trị cực đại là f(-1;-1)=1 f) ; Giải hệ phương trình
Vậy M1(0;0) và M2(24;-144) là điểm dừng.
Các đạo hàm riêng cấp 2
Xét tại M1(0;0), ta có ma trận Hesse
⇨ Nên hàm f(x,y) không đạt cực trị tại M1(0,0)
Xét tại M2(24;-144) có ma trận Hesse
⇨ Hàm f(x,y) đạt cực tiểu tại M2(24;-144) và có giá trị cực tiểu là f(24;-144)=-6911 Bài 6 a) với Ta có: Lập hàm: Ta có: Điểm dừng N ( , )
Ta có các đạo hàm cấp 2: ; ; =0 ; ; Ta có ma trận Hesse
Vậy hàm số đạt cực tiểu tại N ( , ) b)
nếu x và y thỏa mãn điều kiện Lập hàm: Ta có:
Điểm dừng N=(3, 4, -2) hay N=(0, 0, 0)
Ta có các đạo hàm cấp 2: , , , , Ta có ma trận Hesse • N (3, 4, -2) =50>0 =-14<0
Vậy hàm số f(x, y) đạt cực đại tại N (3, 4, -2) • N (0, 0, 0) =-50<0 =-9<0
Vậy hàm số f(x, y) đạt cực tiểu tại N (0, 0, 0) c) Giải hệ trên
Ta có các đạo hàm cấp 2: , , , , Ma trận Hesse:
Hàm số đạt cực tiểu tại ( , )
Hàm số đạt cực tiểu tại ( , )
Hàm số đạt cực đại tại ( , )
Hàm số đạt cực đại tại ( , ) Bài 9. Hàm
có 2 điểm dừng là và . Chọn kết luận đúng
a) Hàm f không đạt cực trị địa phương tại A, đạt cực đại địa phương tại B
b) Hàm f đạt cực tiểu địa phương tại A, đạt cực đại địa phương tại B
c) Hàm f không đạt cực trị địa phương tại A, đạt cực tiểu địa phương tại B
d) Hàm f đạt cực đại địa phương tại A, đạt cực tiểu địa phương tại B Ta có:
Các đạo hàm riêng cấp 2 là: • Ma trận Hesse tại là:
Vậy suy ra hàm f(x,y) không đạt cực trị địa phương tại • Ma trận Hesse tại là:
Vậy suy ra hàm f(x,y) đạt cực tiểu địa phương tại
Kết luận: câu c đúng. Bài 10: Cho hàm
. Chọn mệnh đề đúng trong các mệnh đề sau đây
A. Hàm z đạt cực tiểu tại M(0,1)
B. Hàm z đạt cực đại tại M(0,1)
C. Hàm z có điểm dừng nhưng không có cực trị
D. Hàm z không có điểm dừng Giải: Ta có hệ phương trình: ⇨ Hệ vô nghiệm vì
Vậy hàm z không có điểm dừng. CHỌN D. Bài 11: Cho hàm
. Chọn mệnh đề đúng trong các mệnh đề sau đây
A. Hàm f đạt cực tiểu tại M(0,0)
B. Hàm f đạt cực đại tại M(0,0)
C. Hàm f có điểm dừng nhưng không có cực trị
D. Hàm f không có điểm dừng Giải: Ta có hệ phương trình:
⇨ Hàm f có điểm dừng tại M(0,0) Xét: Ta có:
Vậy hàm f có điểm dừng nhưng không có cực trị. CHỌN C. Bài 12: Xét hàm
và điểm M(0;1). Chọn kết luận đúng
a) Hàm f đạt cực tiểu tại M
b) Hàm f đạt cực đại tại M
c) M là điểm dừng nhưng không phải cực trị của hàm f
d) M không phải là điểm dừng của hàm f Ta có hệ phương trình (1) Thay M(0,1) vào (1)
⇨ M(0;1) là điểm dừng của hàm f(x,y)
Các đạo hàm riêng cấp 2
Xét tại điểm M(0,1) có ma trận Hesse
⇨ Nên hàm f(x,y) không đạt cực trị tại M (0,1)
⇨ Câu c đúng: M là điểm dừng nhưng không phải cực trị của hàm f(x,y)
Bài 13. Vi phần toàn phần của hàm là kết quả nào? A. B. C. D.




