
















Preview text:
Phần I Logic
1 Biểu diễn Mệnh Đề Logic
Các bài tập sau được dịch thuật từ tài liệu: Discrete Mathematics and Its Applications Eighth
Edition, Kenneth H. Rosen.
Problem 1. 1. Smartphone A có 256 MB RAM và 32 GB ROM, và độ phân giải của camera
là 8 MP; Smartphone B có 288 MB RAM và 64 GB ROM, và độ phân giải của camera là 4
MP; và Smartphone C có 128 MB RAM và 32 GB ROM, và độ phân giải của camera là 5
MP. Xác định giá trị đúng của mỗi câu tuyên bố sau:
a) Smartphone B có nhiều RAM nhất trong ba điện thoại thông minh này.
b) Smartphone C có ROM nhiều hơn hoặc camera có độ phân giải cao hơn so với Smart- phone B.
c) Smartphone B có nhiều RAM, nhiều ROM, và camera có độ phân giải cao hơn so với Smartphone A.
d) Nếu Smartphone B có nhiều RAM và nhiều ROM hơn Smartphone C, thì nó cũng có
camera có độ phân giải cao hơn.
e) Smartphone A có nhiều RAM hơn Smartphone B nếu và chỉ nếu Smartphone B có nhiều RAM hơn Smartphone A. Problem 2.
1. Đặt p và q là các mệnh đề:
p : Tôi đã mua vé số tuần này.
q : Tôi đã trúng giải độc đắc một triệu đô.
Biểu diễn mỗi tuyên bố này thành một câu mệnh đề tiếng Việt: a) ¬p: e) p ↔ q: b) p ∨ q: f) ¬p → ¬q: c) p → q: g) ¬p ∧ ¬q: d) p ∧ q:
h) ¬p ∨ (p ∧ q): Problem 3.
1. Xác định xem các tuyên bố hai chiều sau là đúng hay sai:
a) 2 + 2 = 4 nếu và chỉ nếu 1 + 1 = 2.
b) 1 + 1 = 2 nếu và chỉ nếu 2 + 3 = 4.
c) 1 + 1 = 3 nếu và chỉ nếu khỉ có thể bay.
d) 0 > 1 nếu và chỉ nếu 2 > 1. 1
2. Xác định xem mỗi tuyên bố điều kiện sau là đúng hay sai:
a) Nếu 1 + 1 = 2, thì 2 + 2 = 5.
b) Nếu 1 + 1 = 3, thì 2 + 2 = 4.
c) Nếu 1 + 1 = 3, thì 2 + 2 = 5.
d) Nếu khỉ có thể bay, thì 1 + 1 = 3.
3. Xác định xem mỗi tuyên bố điều kiện sau là đúng hay sai:
a) Nếu 1 + 1 = 3, thì ngựa một sừng tồn tại.
b) Nếu 1 + 1 = 3, thì chó có thể bay.
c) Nếu 1 + 1 = 2, thì chó có thể bay.
d) Nếu 2 + 2 = 4, thì 1 + 2 = 3.
2 Xây dfing bảng chân trị tfi mệnh đề (Truth Table Construction) Problem 4.
1. Xây dựng một bảng chân trị
c) p ⊕ (p ∨ q)
cho mỗi tuyên bố phức sau:
d) (p ∧ q) → (p ∨ q) a) p ∧ ¬p
e) (q → ¬p) ↔ (p ↔ q) b) p ∨ ¬p
f) (p ↔ q) ⊕ (p ↔ ¬q)
c) (p ∨ ¬q) → q
3. Xây dựng một bảng chân trị cho mỗi tuyên
d) (p ∨ q) → (p ∧ q) bố phức sau:
e) (p → q) ↔ (¬q → ¬p)
a) (p ∨ q) → (p ⊕ q)
f) (p → q) → (q → p)
b) (p ⊕ q) → (p ∧ q)
2. Xây dựng một bảng chân trị cho mỗi tuyên
c) (p ∨ q) ⊕ (p ∧ q) bố phức sau:
d) (p ↔ q) ⊕ (¬p ↔ q) a) p → ¬p
e) (p ↔ q) ⊕ (¬p ↔ ¬r) b) p ↔ ¬p
f) (p ⊕ q) → (p ⊕ ¬q)
3 Các phép toán trên chuỗi nhị phân Problem 5.
1) Tìm phép OR bit, phép AND bit, và phép XOR bit của mỗi cặp chuỗi bit sau: a) 101 1110, 010 0001
b) 1111 0000, 1010 1010
c) 00 0111 0001, 10 0100 1000
d) 11 1111 1111, 00 0000 0000 2
2) Đánh giá mỗi biểu thức sau:
a) 1 1000 ∧ (0 1011 ∨ 1 1011)
b) (0 1111 ∧ 1 0101) ∨ 0 1000
c) (0 1010 ⊕ 1 1011) ⊕ 0 1000
d) (1 1011 ∨ 0 1010) ∧ (1 0001 ∨ 1 1011)
4 Ứng dụng của logic
Problem 6. Fuzzy logic được sử dụng trong trí tuệ nhân tạo. Trong Fuzzy logic:
• Một tuyên bố có một giá trị chân lý là một số từ 0 đến 1, bao gồm cả 0 và 1.
• Một tuyên bố có giá trị chân lý bằng 0 là sai và một tuyên bố có giá trị chân lý bằng 1 là đúng.
• Các giá trị chân lý nằm giữa 0 và 1 chỉ ra các mức độ chân lý khác nhau.
Ví dụ, giá trị chân lý 0.8 có thể được gán cho tuyên bố "Mận đang vui", vì Mận thường vui, và giá
trị chân lý 0.4 có thể được gán cho tuyên bố "Xoài đang vui", vì Xoài chỉ vui một phần nhỏ so với
một nửa thời gian. Sử dụng các giá trị chân lý này để giải các bài tập sau:
1. Giá trị chân lý của phủ định của một tuyên bố trong Fuzzy logic là 1 trừ đi giá trị chân lý
của tuyên bố. Những giá trị chân lý nào của các tuyên bố "Mận không vui"và "Xoài không vui"?
2. Giá trị chân lý của phép hợp của hai tuyên bố trong Fuzzy logic là giá trị nhỏ nhất của hai
tuyên bố. Những giá trị chân lý nào của các tuyên bố "Mận và Xoài đang vui"và "Hoặc Mận hoặc Xoài không vui"?
3. Giá trị chân lý của phép hoặc của hai tuyên bố trong Fuzzy logic là giá trị lớn nhất của hai
tuyên bố. Những giá trị chân lý nào của các tuyên bố "Mận vui, hoặc Xoài vui"và "Mận
không vui, hoặc Xoài không vui"?
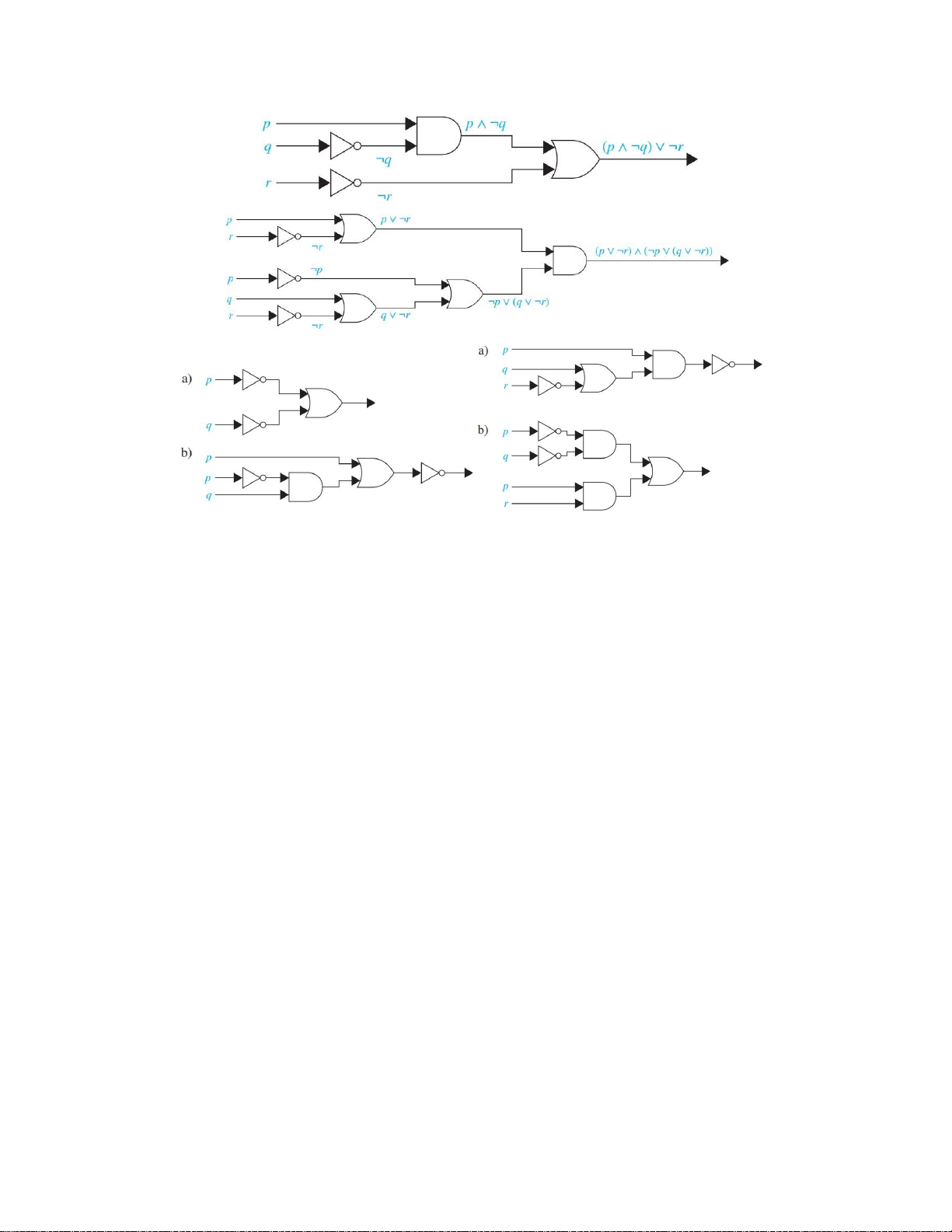
Problem 7. Lập bảng chân trị của các mạch logic trong Hinhf 7. 5 Bài Tập Nâng Cao
Problem 8. Bài toán "The Knight’s Tour"là một bài toán trong lý thuyết đồ thị và cũng là một
bài toán trò chơi. Trong bài toán này, một quân mã được đặt ở một ô bất kỳ trên bảng cờ hình
chữ nhật tiêu chuẩn và cố gắng di chuyển theo quy tắc của quân mã trên bảng cờ mà không được
di chuyển qua bất kỳ ô nào đã được đi qua trước đó. Mục tiêu là đi qua mỗi ô trên bảng cờ đúng một lần duy nhất.
1. Làm thế nào để tìm một hành trình của quân mã sao cho nó đi qua mỗi ô trên bảng cờ đúng
một lần và quay lại ô ban đầu?
2. Làm thế nào để tìm tất cả các hành trình của quân mã trên bảng cờ cho một kích thước bảng cụ thể? 3
3. Có bao nhiêu cách khác nhau để giải quyết bài toán "The Knight’s Tour"trên một bảng cờ
có kích thước cho trước?
Problem 9. Bài toán "The n-Queens"là một bài toán kinh điển trong lý thuyết đồ thị và cũng là
một bài toán quen thuộc trong lĩnh vực trò chơi và tối ưu. Trong bài toán này, mục tiêu là đặt n
quân hậu trên một bảng cờ hình chữ nhật kích thước n × n sao cho không có hai quân hậu nào có
thể "tấn công"nhau, nghĩa là không có hai quân hậu nào đặt trên cùng một hàng, cột hoặc đường chéo.
1. Làm thế nào để tìm một cách sắp xếp quân hậu sao cho không có hai quân hậu nào tấn công
nhau trên bảng cờ n × n?
2. Làm thế nào để tìm tất cả các giải pháp cho bài toán "The n-Queens"cho một kích thước bảng cụ thể?
3. Có những phương pháp nào để giải quyết bài toán "The n-Queens"một cách hiệu quả từ góc độ tính toán?
Problem 10. Bài toán Sudoku và Magic Square là hai bài toán rất phổ biến trong thế giới của
trò chơi logic và toán học. Bài toán Sudoku yêu cầu điền các chữ số từ 1 đến 9 vào một lưới 9x9
sao cho mỗi hàng, mỗi cột và mỗi phần lưới con 3x3 chứa tất cả các chữ số từ 1 đến 9 mà không
có chữ số nào lặp lại. Câu hỏi liên quan đến bài toán Sudoku:
1. Làm thế nào để tạo ra một trò chơi Sudoku có thể giải một cách duy nhất?
2. Làm thế nào để viết một chương trình máy tính để giải bài toán Sudoku?
3. Có bao nhiêu cách khác nhau để giải bài toán Sudoku cho một trò chơi cụ thể?
Magic Squaret là một lưới số hình vuông trong đó tổng của các số trên mỗi hàng, mỗi cột và đường
chéo chính đều bằng nhau. Thông thường, các magic square có kích thước là một số lẻ, ví dụ: 3x3, 5x5, 7x7, vv. 4
1. Làm thế nào để xây dựng một magic square với một số lẻ hàng và cột?
2. Làm thế nào để tìm tất cả các magic square có thể từ một bảng bắt đầu?
3. Có bí mật gì đằng sau tính chất của magic square? 5 Phần II Lj Thuyết Số 6 Phép chia lấy dư
Problem 11. Giải các bài toán siêu dễ sau:
1. Tìm thương và phần dư khi
2. Tìm thương và phần dư khi a) 19 chia cho 7? a) 44 chia cho 8? b) -111 chia cho 11? b) 777 chia cho 21? c) 789 chia cho 23? c) -123 chia cho 19? d) 1001 chia cho 13? d) -1 chia cho 23? e) 0 chia cho 19? e) -2002 chia cho 87? f) 3 chia cho 5? f) 0 chia cho 17? g) -1 chia cho 3? g) 1,234,567 chia cho 1001? h) 4 chia cho 1? h) -100 chia cho 101?
Problem 12. Cho a và b là số nguyên, a ≡ 4
Cho a và b là số nguyên, a ≡ 11 (mod 19),
(mod 13), và b ≡ 9 (mod 13). Tìm số nguyên c và b ≡ 3 (mod 19). Tìm số nguyên c sao cho
sao cho 0 ≤ c ≤ 12 và: 0 ≤ c ≤ 18 và:
1. c ≡ 9a (mod 13).
1. c ≡ 13a (mod 19).
2. c ≡ 11b (mod 13).
2. c ≡ 8b (mod 19).
3. c ≡ a + b (mod 13).
3. c ≡ a − b (mod 19).
4. c ≡ 2a + 3b (mod 13).
4. c ≡ 7a + 3b (mod 19).
5. c ≡ a2 + b2 (mod 13).
5. c ≡ 2a2 + 3b2 (mod 19).
6. c ≡ a3 − b3 (mod 13).
6. c ≡ a3 + 4b3 (mod 19).
Problem 13. Tìm số nguyên a sao cho
1. a ≡ 43 (mod 23) và −22 ≤ a ≤ 0.
2. a ≡ 17 (mod 29) và −14 ≤ a ≤ 14.
3. a ≡ −11 (mod 21) và 90 ≤ a ≤ 110.
4. a ≡ −15 (mod 27) và −26 ≤ a ≤ 0.
5. a ≡ 24 (mod 31) và −15 ≤ a ≤ 15.
7 Biểu diễn số dưới các hệ cơ số Problem 14. 6
1. Chuyển đổi phần mở rộng thập phân của (c) (1110111110)2
mỗi số nguyên này thành phần mở rộng nhị (d) (111110000011111) phân. 2
5. Chuyển đổi phần mở rộng bát phân của (a) 231:
mỗi số nguyên này thành phần mở rộng (b) 4532: nhị phân. (c) 97644: (a) (572)8
2. Chuyển đổi phần mở rộng thập phân của (b) (1604)
mỗi số nguyên này thành phần mở rộng nhị 8 phân. (c) (423)8 (d) (2417) (a) 8 321: (b) 1023:
6. Chuyển đổi phần mở rộng nhị phân của
mỗi số nguyên này thành phần mở rộng (c) 100632: bát phân.
3. Chuyển đổi phần mở rộng nhị phân của
mỗi số nguyên này thành phần mở rộng (a) (11110111)2 thập phân. (b) (101010101010)2 (c) (111011101110111) 2 (a) (11111)2 (d) (101010101010101)2 (b) (1000000001)2 (c) (101010101)2
7. Chuyển đổi phần mở rộng thập lục phân (d)
của mỗi số nguyên này thành phần mở rộng (110100100010000) 2 nhị phân.
4. Chuyển đổi phần mở rộng nhị phân của
mỗi số nguyên này thành phần mở rộng (a) (80E)16 thập phân. (b) (135AB)16 (a) (11011) (c) 2 (ABBA)16 (b) (1010110101)2 (d) (DEFACED)16
Problem 15 (*). Hàm x
π(x) tính số lượng số nguyên tố không vượt quá x, và f (x) = tiến gần ln x
đến 1 khi x tăng lên không giới hạn. (Ở đây, ln x là logarit tự nhiên của x.)
1. Viết pseudocode để tính f (x), với input là một số x nguyên tố.
2. Sử dụng python để lập trình pseudocode ở câu (1).
3. Nhập hai số lớn a và b, tính khoảng cách giữa hai số: |f (a) − f (b)|.
8 Hàm Băm (Hash Function)
Problem 16. Các vị trí bộ nhớ được gán bởi hàm băm h(k) = k mod 97 cho các hồ sơ của khách
hàng công ty bảo hiểm có các số Bảo hiểm Xã hội sau đây: 1. 034567981: 2. 183211232: 7 3. 220195744: 4. 987255335:
Problem 17. Các vị trí bộ nhớ được gán bởi hàm băm h(k) = k mod 101 cho các hồ sơ của
khách hàng công ty bảo hiểm có các số Bảo hiểm Xã hội sau đây: 1. 104578690: 2. 432222187: 3. 372201919: 4. 501338753:
Problem 18. ISBNs Tất cả các sách được nhận diện bằng Mã số Sách Tiêu chuẩn Quốc tế (ISBN-
10), một mã gồm 10 chữ số x1x2 . . . x10, được gán bởi nhà xuất bản. (Gần đây, một mã gồm 13
chữ số được biết đến là ISBN-13 đã được giới thiệu để xác định một số lượng lớn hơn các tác phẩm
được xuất bản; ISBN-10 bao gồm các khối nhận diện ngôn ngữ, nhà xuất bản, số được gán cho
cuốn sách bởi công ty xuất bản của nó, và cuối cùng, một chữ số kiểm tra có thể là một chữ số
hoặc chữ cái X (được sử dụng để đại diện cho số 10). Chữ số kiểm tra này được chọn sao cho: Σ 9 x10 ≡
i · xi (mod 11) i=1
hoặc tương đương, sao cho: Σ 10
i · xi ≡ 0 (mod 11) i=1
Trả lời các câu hỏi sau về ISBN-10:
1. Chín chữ số đầu tiên của ISBN-10 của ấn bản thứ sáu của cuốn sách này là 007288008. Chữ số kiểm tra là gì?
2. 084930149X có phải là ISBN-10 hợp lệ không? Gợi ý: 1. Chữ số kiểm tra: Σ • Ta có x 9 10 ≡
i=1 i · xi (mod 11).
• Thay vào các giá trị: x1 = 0, x2 = 0, x3 = 7, x4 = 2, x5 = 8, x6 = 8, x7 = 0, x8 = 0, x9 = 8.
• Tính toán: x10 = (1 · 0) +(2 · 0) +(3 · 7) +(4 · 2) +(5 · 8) +(6 · 8) +(7 · 0) +(8 · 0) +(9 · 8) =?.
• Vì ? ≡? (mod 11), nên chữ số kiểm tra là ?.
2. ISBN-10 084930149X là hợp lệ hay không: Σ
• Ta có 10 i·xi = (0·1)+(8·2)+(4·3)+(9·4)+(3·5)+(0·6)+(1·7)+(4·8)+(9·9)+(10·10) = i=1 220.
• Vì 220 ≡ 0 (mod 11), nên ISBN-10 084930149X là . 8
Hình 1: Caesar và Suy Nghĩ của anh ấy về môn Toán Rời Rạc
Problem 19. Số định danh vé máy bay: Các kỳ kỳ báo được xác định bằng cách sử dụng Mã
số Liên tục Tiêu chuẩn Quốc tế (ISSN). Một ISSN bao gồm hai khối bốn chữ số. Chữ số cuối cùng
trong khối thứ hai là chữ số kiểm tra. Chữ số kiểm tra này được xác định bằng phương trình đồng dư:
d8 ≡ 3d1 + 4d2 + 5d3 + 6d4 + 7d5 + 8d6 + 9d7 (mod 11)
Khi d8 ≡ 10 (mod 11), chúng ta sử dụng chữ cái X để đại diện cho d8 trong mã.
1. Đối với mỗi số đầu tiên của ISSN, xác định
2. Tất cả các mã có tám chữ số này có thể
chữ số kiểm tra (có thể là chữ cái X).
là ISSN không? Tức là, chúng có kết thúc
bằng chữ số kiểm tra chính xác không? • 1570-868 • 1059-1027 • 1553-734 • 0002-9890 • 1089-708 • 1530-8669 • 1383-811 • 1007-120X 9 Mật mã học 9.1 Mật mã Caesar
Problem 20. Tìm các chữ cái bị che lấp trong Hình 1. Số dịch chuyển giữa bộ mã hóa và bộ giải mã là bao nhiêu?
Problem 21. Sử dụng bộ mã hóa - giả mã trong Hình 1, mã hóa các câu sau: 1. Toi yeu Vietnam. 2. Tui iu Phenikaa. 9 3. Blackpink is in the area.
Problem 22. Giải mã đoạn code sau: Ebfrfnererq, Ivbyrgvfoyhr.Gbvgehbgzbaanlgbvxubpuhuh
dựa vào quy tắc: R '→ E, O '→ B, . . .
9.2 Định lj phần dư Trung Hoa và Mã RSA
Định lý phần dư Trung Quốc (CRT) là một trong những công cụ quan trọng trong lĩnh vực lý
thuyết số và có ứng dụng rộng rãi trong các hệ thống mật mã và công nghệ thông tin. CRT cung
cấp một phương pháp hiệu quả để giải quyết các hệ phương trình modul tương đối lớn một cách
hiệu quả. Trong định lý này, chúng ta có một hệ phương trình tuyến tính modulo với các modulo
khác nhau. CRT cho phép chúng ta kết hợp các giá trị của x được tìm thấy từ mỗi modulo thành
một giá trị duy nhất của x modulo bội số của tất cả các modulo. Điều này giúp chúng ta tìm ra
nghiệm của hệ phương trình một cách nhanh chóng và dễ dàng. Ngoài ra, CRT cũng có các ứng
dụng quan trọng trong mật mã học, như trong hệ thống mã hóa RSA. Bằng cách sử dụng CRT,
chúng ta có thể tăng hiệu suất của quá trình giải mã RSA bằng cách giảm độ phức tạp của các phép tính modul lớn.
Phát biểu của CRT như sau: Nếu m và n là hai số nguyên tố chỉ có ước chung duy nhất là 1;
i.e: gcd(a, b) = 1 thí hệ phương trình sau:
( x (mod m) = a (1)
x (mod n) = b
chỉ có duy nhất một nghiệm x trong khoảng từ 0 tới mn − 1
Problem 23. Giải phương trình theo CRT: Cho hệ phương trình: x ≡ 2 (mod 3) x ≡ 3 (mod 5) x ≡ 2 (mod 7)
Hãy tìm nghiệm của hệ phương trình này bằng CRT.
Problem 24. Tính chất của CRT: Chứng minh rằng nếu hai số nguyên dương m1 và m2 là hai số
nguyên tố cùng nhau thì hệ phương trình:
( x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
có nghiệm duy nhất modulo m1 · m2.
Problem 25. Ứng dụng CRT trong mã hóa RSA: Giả sử bạn muốn gửi một thông điệp bằng mã
hóa RSA với các tham số p = 17, q = 11, và e = 7. Hãy tính khóa bí mật và khóa công khai sử dụng CRT.
10 Bài Tập Nâng Cao
Problem 26 (*). Root-of-Unity: Đây là một bài toán về Root-of-Unity, một chủ đề thú vị trong
lý thuyết số: Root-of-Unity là một khái niệm quan trọng trong lý thuyết số và đại số trừu tượng. 10
Trong đó, một số phức ω được gọi là Root-of-Unity của bậc n nếu ωn = 1. Root-of-Unity đóng vai
trò quan trọng trong nhiều lĩnh vực như đa thức, biến đổi Fourier, và thậm chí trong một số thuật toán mã hóa.
Viết một bài luận nhỏ (2-3 trang) để giải các vấn đề sau: 1. Tìm số Root-of-Unity:
• Cho trước một số nguyên dương n, hãy tìm tất cả các Root-of-Unity của bậc n trong trường số phức.
• Tìm một công thức tổng quát để tính số lượng Root-of-Unity của bậc n.
2. Tính tích tổng các Root-of-Unity: Cho trước một số nguyên dương n, tính tổng của tất cả
các Root-of-Unity của bậc n trong trường số phức.
3. Root-of-Unity và Đa thức:
(a) Chứng minh rằng một đa thức có bậc n có thể có tối đa n Root-of-Unity trong trường số phức.
(b) Cho trước một đa thức f (x), hãy tìm số lượng Root-of-Unity của f (x) trong trường số phức.
4. Root-of-Unity và Biến đổi Fourier:
• Tìm hiểu về biến đổi Fourier và cách nó liên quan đến Root-of-Unity.
• Thực hiện biến đổi Fourier trên một tập dữ liệu số học và tìm hiểu cách Root-of-Unity
được sử dụng trong quá trình này.
5. Root-of-Unity trong thuật toán mã hóa: Nghiên cứu và trình bày cách Root-of-Unity được sử
dụng trong một thuật toán mã hóa cụ thể (ví dụ: RSA hoặc ElGamal) và giải thích tại sao
chúng lại quan trọng trong ngữ cảnh này.
Problem 27 (*). Máy Enigma là một thiết bị mã hóa được sử dụng trong Thế chiến thứ hai
bởi quân đội Đức. Được phát triển bởi Arthur Scherbius vào đầu những năm 1920, Enigma được
sử dụng để mã hóa và giải mã các tin nhắn quân sự bằng cách sử dụng một loạt các bánh xe xoay
và các vòng dây dẫn điện. Máy Enigma đã tạo ra một hệ thống mã hóa mạnh mẽ mà trong thời
kỳ đó được coi là không thể bị phá vỡ. Tuy nhiên, nhờ sự nỗ lực của các nhà mật mã học, máy
Enigma đã được phá vỡ bởi nhóm tình báo Ba Lan và Pháp dưới sự chỉ đạo của Marian Rejewski.
Việc phá mã Enigma đã đóng một vai trò quan trọng trong việc kết thúc Thế chiến thứ hai.
Viết một bài luận (2-3 trang) để xử lý các vấn đề sau:
1. Mô phỏng Máy Enigma: Hãy viết một chương trình Python để mô phỏng hoạt động của
máy Enigma. Sử dụng các tham số đầu vào như cấu hình của bánh xe xoay, vòng dây dẫn
điện và các kí tự đầu vào để mã hóa và giải mã các thông điệp.
2. Lịch sfi của Máy Enigma: Nghiên cứu về lịch sử và phát triển của máy Enigma. Trình bày
về cách mà máy này đã ảnh hưởng đến cuộc chiến tranh và lịch sử của mật mã học.
3. Phương pháp phá mã Enigma: Tìm hiểu về các phương pháp được sử dụng để phá mã
Enigma, bao gồm cả các kỹ thuật tấn công từ điển và các kỹ thuật phức tạp hơn như phân tích tần suất. 11
4. Ảnh hưởng của Máy Enigma: Viết một bài luận về cách mà máy Enigma đã thay đổi bối
cảnh của mật mã học và ảnh hưởng của nó đến công nghệ thông tin và an ninh mạng hiện đại.
5. So sánh với các hệ thống mã hóa hiện đại: So sánh máy Enigma với các hệ thống mã
hóa hiện đại như RSA, AES, và DES. Trình bày về sự tiến bộ trong công nghệ mã hóa và
những thách thức mà các hệ thống hiện đại phải đối mặt. 12 Phần III
Quy Tắc Đếm và Xác Suất Rời Rạc 11 Quy Tắc Đếm
Problem 28. Với các câu hỏi sau, viết đáp án chỉ bao gồm một số:
1. Một cửa hàng có 7 loại kẹo, 5 loại bánh và 9 loại nước giải khát. Nếu một khách hàng muốn
chọn một loại kẹo, một loại bánh hoặc một loại nước giải khát, thì số cách chọn của khách hàng là bao nhiêu?
2. Một người thợ làm vườn có 12 loại hoa hồng, 8 loại tulip và 5 loại cẩm chướng. Nếu người
thợ muốn chọn một loại hoa để trang trí, số cách chọn của anh ta là bao nhiêu?
3. Trong một cửa hàng đồ chơi, có 10 loại xe ô tô mô hình, 8 loại búp bê và 6 loại trò chơi xếp
hình. Một đứa trẻ muốn chọn một món đồ chơi, số lựa chọn có thể của đứa trẻ là bao nhiêu?
4. Trong một cuộc thi vẽ, có 15 màu sắc khác nhau của bút chì màu, 10 màu sắc của bút lông
và 5 màu sắc của bút chì sáp. Mỗi học sinh được chọn một loại bút để vẽ tranh. Hỏi có bao
nhiêu sự lựa chọn khác nhau mà một học sinh có thể làm?
5. Một nhà toán học có 6 quyển sách về Đại số, 4 quyển sách về Hình học và 3 quyển sách về
Phân tích. Nếu ông ta muốn chọn một quyển để đọc trong kỳ nghỉ, số cách chọn của ông ta là bao nhiêu?
6. Trên một kệ sách, có 9 cuốn sách giáo khoa, 7 cuốn tiểu thuyết và 4 cuốn sách nấu ăn. Nếu
một học sinh muốn chọn một cuốn sách để đọc, số lựa chọn của học sinh là bao nhiêu?
7. Một bộ sưu tập tem có 15 tem từ Việt Nam, 8 tem từ Thái Lan và 10 tem từ Malaysia. Một
nhà sưu tập muốn chọn ra một tem để trưng bày trong buổi triển lãm. Có bao nhiêu lựa chọn
khả dĩ cho nhà sưu tập?
8. Một nhà hàng phục vụ 5 loại pizza, 6 loại pasta và 3 loại salad. Nếu một thực khách muốn
chọn một món ăn chính, số lựa chọn có thể của thực khách là bao nhiêu?
9. Trong một buổi lễ tốt nghiệp, mỗi sinh viên có thể chọn một huy chương từ 3 loại huy chương
vàng, 2 loại huy chương bạc hoặc một huy chương đồng. Số lựa chọn huy chương mà một
sinh viên có là bao nhiêu?
10. Một cửa hàng bán hoa quả có 8 loại táo, 7 loại cam và 5 loại lê. Nếu một khách hàng chỉ
muốn mua một loại hoa quả, số lựa chọn mà khách hàng có là bao nhiêu?
Problem 29. Với các câu hỏi sau, viết đáp án chỉ bao gồm một số:
1. Có bao nhiêu số tự nhiên gồm 3 chữ số khác nhau được lập từ các chữ số từ 1 đến 5?
2. Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lập từ các chữ số từ 1 đến 7?
3. Từ các chữ số 1 đến 9, có bao nhiêu số tự nhiên gồm 2 chữ số khác nhau có thể được hình thành?
4. Nếu chúng ta có các chữ số từ 1 đến 6, có bao nhiêu cách để tạo ra một số tự nhiên gồm 5 chữ số khác nhau? 13
5. Một người muốn tạo một mã số gồm 3 chữ số khác nhau sử dụng các chữ số từ 1 đến 8, không
sử dụng lại chữ số nào. Có bao nhiêu mã số như vậy có thể được tạo ra?
6. Có bao nhiêu số tự nhiên gồm 4 chữ số khác nhau được lập từ các chữ số từ 1 đến 6?
7. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được lập từ các chữ số từ 1 đến 9?
8. Sử dụng các chữ số từ 1 đến 4, có bao nhiêu số có 2 chữ số khác nhau có thể được tạo ra?
9. Nếu chọn từ các chữ số 1 đến 8, có bao nhiêu cách tạo ra một số tự nhiên gồm 3 chữ số khác nhau?
10. Từ các chữ số 1 đến 5, có bao nhiêu số tự nhiên gồm 3 chữ số khác nhau có thể được hình thành?
Problem 30. Với các câu hỏi sau, viết đáp án chỉ bao gồm một số:
1. Cho a = 2, b = −1, và c = 3, hỏi có bao nhiêu số tự nhiên x thoả mãn phương trình sau?
2 × A2 − A2 + 3 = 0 x 2x
2. Nếu a = 1, b = 1, và c = −12, hỏi phương trình sau có bao nhiêu nghiệm tự nhiên x?
A2 + A2 − 12 = 0 x 2x
Problem 31. Với các câu hỏi sau, viết đáp án chỉ bao gồm một số:
1. Một câu lạc bộ bao gồm 8 nam và 12 nữ. Có bao nhiêu cách để thành lập một ủy ban gồm 5
thành viên sao cho ít nhất có một nam và một nữ?
2. Trong một lớp học, có 7 nam và 9 nữ. Giáo viên muốn chọn 4 học sinh đại diện lớp tham gia
một cuộc thi, đảm bảo lựa chọn bao gồm cả hai giới. Có bao nhiêu lựa chọn khác nhau có thể thực hiện được?
3. Trong một sự kiện cụ thể, cần chụp một bức ảnh của một nhóm 3 người từ một đội bóng
gồm 6 người đàn ông và 4 phụ nữ. Để thể hiện tính đa dạng, bức ảnh phải bao gồm ít nhất
một người đàn ông và một phụ nữ. Có bao nhiêu cách tổ chức tổng cộng cho bức ảnh này?
4. Một ủy ban gồm 6 người cần được thành lập từ một nhóm 17 nhân viên, trong đó có 11 người
quản lý và 6 nhân viên nhân viên. Nếu ủy ban phải có ít nhất một người quản lý và một
nhân viên nhân viên, có bao nhiêu ủy ban có thể thành lập được?
5. Đối với một dự án sắp tới, một người lãnh đạo phải thành lập một nhóm 4 người từ 5 kỹ sư
nam và 7 kỹ sư nữ. Nếu nhóm phải bao gồm ít nhất một kỹ sư nam và một kỹ sư nữ, người
lãnh đạo có thể thành lập bao nhiêu nhóm khác nhau?
6. Có bao nhiêu số tự nhiên có 3 chữ số chia hết cho 10 được tạo từ các chữ số 1, 2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12 mà không lặp lại bất kỳ chữ số nào?
7. Sử dụng các chữ số 1, 2, 3, 4, 5, 6, 7, có bao nhiêu số tự nhiên có 3 chữ số chia hết cho 5 được
tạo ra nếu mỗi chữ số phải khác nhau?
8. Có bao nhiêu số tự nhiên có 3 chữ số chia hết cho 6 được tạo từ các chữ số 1, 2, 3, 4, 5, mỗi chữ số đều khác nhau? 14
9. Có bao nhiêu số có 5 chữ số tận cùng là 3 và chia hết cho 7?
10. Trong hệ thập phân, có bao nhiêu số có 5 chữ số mà số đó tận cùng là 8 và chia hết cho 7?
11. Nếu chọn một số ngẫu nhiên có 5 chữ số kết thúc bằng 6 và số đó chia hết cho 7, số các lựa chọn có thể là:
12. Tính số lượng các số có 5 chữ số tận cùng là 0 và chia hết cho 7 là bao nhiêu?
13. Có bao nhiêu số tự nhiên 5 chữ số chia hết cho 7 mà chữ số cuối cùng là 1?
Problem 32. Với các câu hỏi sau, viết đáp án chỉ bao gồm một số:
1. Một ngũ giác lồi có bao nhiêu đường chéo?
2. Nếu một đa giác lồi có 10 đỉnh, hỏi đa giác đó có bao nhiêu đường chéo?
3. Trong một đa giác lồi có 15 đỉnh, có mấy đường chéo được tạo thành?
4. Một đa giác lồi có 20 đỉnh thì số đường chéo của nó là bao nhiêu?
5. Một đa giác lồi có 8 đỉnh. Hỏi số đường chéo của đa giác lồi đó là bao nhiêu?
Problem 33. Giải các bài tập sau:
1. Cho phương trình x + x+2 = 3 x+1 . Tính tích P của tất cả các giá trị x thoả mãn phương 3 3 3 trình.
2. Tính tích P của tất cả các giá trị x thoả mãn phương trình x + x+2 = 2 x+1 . 2 2 2
3. Xác định tích P của tất cả các giá trị x thoả mãn phương trình x + x+2 = 4 x+1 . 4 4 4
4. Trong trường hợp x + x+2 = 5 x+1 , tích P của tất cả các giá trị x là bao nhiêu? 5 5 5
5. Cho phương trình x + x+2 = 6 x+1 , tích P của tất cả các giá trị x thoả mãn phương 6 6 6 trình này là gì? Problem 34.
1. Giải hệ phương trình sau và
4. Nếu x = 7 và y = 3, giá trị của a và b trong tìm nghiệm (x, y):
hệ phương trình sau là bao nhiêu? ( 2 x Ay + 6 x Cy = 24 ( 3 x Ay + 9 x Cy = 36 aA3 + bC3 = 35 7 7 3A3 + 9C3 = 105
2. Trong tình huống sau, giá trị của x và y 7 7
thỏa mãn hệ phương trình nào? ( 4Ay + 12Cy = 48 x x 5 x Ay + 15 x Cy = 60
5. Tìm giá trị của x và y sao cho hệ phương
trình dưới đây có nghiệm hợp lệ:
3. Hệ phương trình nào dưới đây không có nghiệm hợp lệ? ( ( x x 7Ayx + 21 x Cy = 84 aAy + 4Cy = 16 bAyx + 8Cy x = 32 8Ay + 24Cy = 96 x x 15
12 Xác Suất Thống Kê Problem 35.
1. Từ một hộp chứa 16 quả bóng, bao gồm 7 quả màu đỏ và 9 quả màu xanh,
kéo đồng thời hai quả bóng. Xác suất kéo được hai quả bóng màu đỏ là gì?
2. Từ một hộp chứa 16 quả bóng, bao gồm 7 quả màu đỏ và 9 quả màu xanh, kéo đồng thời hai
quả bóng. Xác suất kéo ít nhất một quả bóng màu xanh là bao nhiêu?
3. Từ một hộp chứa 16 quả bóng, bao gồm 7 quả màu đỏ và 9 quả màu xanh, kéo đồng thời hai
quả bóng. Xác suất kéo được hai quả bóng màu xanh là bao nhiêu?
4. Từ một túi chứa 12 viên kẹo, gồm 4 viên màu vàng và 8 viên màu tím, lấy ngẫu nhiên đồng
thời hai viên. Xác suất để lấy được hai viên kẹo cùng màu là bao nhiêu?
5. Trong một hộp chứa 10 bút, gồm 6 bút màu xanh và 4 bút màu đen, lấy ngẫu nhiên đồng
thời hai bút. Xác suất để lấy được ít nhất một bút màu đen là bao nhiêu?
6. Từ một giỏ chứa 15 quả táo, gồm 9 quả màu xanh và 6 quả màu đỏ, lấy ngẫu nhiên đồng
thời hai quả. Xác suất để lấy được hai quả táo màu xanh là bao nhiêu?
7. Gieo một đồng xu cân đối, xác suất để mặt hiển thị là mặt "ngửa"là bao nhiêu?
8. Gieo một con súc sắc cân đối và đồng chất có 8 mặt, xác suất để mặt có số chấm lẻ xuất hiện là bao nhiêu?
9. Gieo hai con súc sắc cân đối và đồng chất, xác suất để tổng số chấm trên hai mặt xuất hiện là 7 là bao nhiêu?
10. Trong một túi có 12 viên bi được đánh số từ 1 đến 12. Lấy ngẫu nhiên 1 viên bi từ túi. Xác
suất để viên bi lấy được ghi số chẵn và chia hết cho 4 là bao nhiêu?
11. Một hộp chứa 15 thẻ được đánh số từ 1 đến 15. Lấy ngẫu nhiên 1 thẻ từ hộp. Xác suất thẻ
lấy được ghi số lẻ và chia hết cho 5 là bao nhiêu?
12. Trong một túi có 18 viên sỏi được đánh số từ 1 đến 18. Lấy ngẫu nhiên 1 viên sỏi từ túi. Xác
suất để viên sỏi lấy được ghi số chẵn và chia hết cho 3 là bao nhiêu?
13. Xếp ngẫu nhiên 6 nhân viên A, B, C, D, E, F ngồi vào một dãy 6 ghế thẳng hàng (mỗi người
ngồi một ghế). Xác suất để hai nhân viên A và C ngồi cạnh nhau là bao nhiêu?
14. Xếp ngẫu nhiên 4 bạn học M, N, O, P ngồi vào một dãy 4 ghế thẳng hàng (mỗi bạn ngồi một
ghế). Xác suất để hai bạn M và O không ngồi cạnh nhau là bao nhiêu?
15. Xếp ngẫu nhiên 7 giáo viên X, Y, Z, U, V, W, T ngồi vào một dãy 7 ghế thẳng hàng (mỗi
người ngồi một ghế). Xác suất để hai giáo viên X và Z ngồi cạnh nhau là bao nhiêu?
16. Cô Lan đặt lên bàn 15 viên bi đánh số từ 1 đến 15. Bạn Bình chọn ngẫu nhiên 5 viên bi. Xác
suất để trong 5 viên bi lấy ra có 3 viên mang số lẻ, 2 viên mang số chẵn trong đó chỉ có một
viên bi mang số chia hết cho 5 là bao nhiêu?
17. Anh Tuấn đặt lên bàn 20 hình tam giác đánh số từ 1 đến 20. Bạn Linh chọn ngẫu nhiên 6
hình. Xác suất để trong 6 hình lấy ra có 4 hình mang số chẵn, 2 hình mang số lẻ và không
có hình nào mang số chia hết cho 10 là bao nhiêu? 16
18. Chị Hà đặt lên bàn 10 viên ngọc đánh số từ 1 đến 10. Bạn Hùng chọn ngẫu nhiên 4 viên ngọc.
Xác suất để trong 4 viên ngọc lấy ra có 2 viên mang số lẻ, 2 viên mang số chẵn và không có
viên nào mang số chia hết cho 5 là bao nhiêu?
19. Ông Nam đặt lên bàn 18 hình vuông đánh số từ 1 đến 18. Bạn Mai chọn ngẫu nhiên 7 hình.
Xác suất để trong 7 hình lấy ra có 4 hình mang số chẵn, 3 hình mang số lẻ và có đúng một
hình mang số chia hết cho 9 là bao nhiêu?
20. Bà Tuyết đặt lên bàn 12 hình tròn đánh số từ 1 đến 12. Bạn Phong chọn ngẫu nhiên 5 hình.
Xác suất để trong 5 hình lấy ra có 3 hình mang số chẵn, 2 hình mang số lẻ và không có hình
nào mang số chia hết cho 6 là bao nhiêu?
21. Gọi U là tập hợp tất cả các số tự nhiên có 5 chữ số được lập từ tập hợp Z = 1;2;3;4;5;6;7.
Chọn ngẫu nhiên một số từ U. Xác suất để số chọn được chia hết cho 7 bằng bao nhiêu?
22. Trung vị của tập dữ liệu 5, 7, 12, 15, x, 20, 25 là 15. Giá trị của x là gì?
23. Một tập dữ liệu có mode là 5. Điều này chỉ ra điều gì?
24. Phạm vi của tập dữ liệu 3, 7, 10, 15, 18 là bao nhiêu?
25. Nếu trung bình của năm số là 10, tổng của chúng là bao nhiêu?
26. Trong các lựa chọn sau đây, lựa chọn nào là một đo lường về sự phân tán (dispersion)?
27. Skewness dương trong một phân phối dữ liệu chỉ ra điều gì?
28. Nếu một tập dữ liệu có phương sai (variance) cao, điều đó chỉ ra điều gì? Problem 36.
1. Trung vị của tập dữ liệu 5, 7, 12, 15, x, 20, 25 là 15. Giá trị của x là gì?
2. Trong các đo lường sau đây, đo lường nào chịu ảnh hưởng nhiều nhất bởi các điểm ngoại lai (outliers)?
3. Một tập dữ liệu có mode là 5. Điều này chỉ ra điều gì?
4. Phạm vi của tập dữ liệu 3, 7, 10, 15, 18 là bao nhiêu?
5. Nếu trung bình của năm số là 10, tổng của chúng là bao nhiêu?
6. Trong các lựa chọn sau đây, lựa chọn nào không phải là một đo lường về trung tâm?
7. Trong một phân phối chuẩn, khoảng bao nhiêu phần trăm dữ liệu nằm trong một độ lệch chuẩn của trung bình?
8. Nếu một tập dữ liệu có phương sai (variance) cao, điều đó chỉ ra điều gì?
Problem 37. Một cuộc khảo sát về thói quen xem truyền hình của một nhóm trong năm qua đã
cho thấy các thông tin sau:
• (i) 28% xem thể dục dụng cụ • (ii) 29% xem bóng chày • (iii) 19% xem bóng đá 17
• (iv) 14% xem cả thể dục dụng cụ và bóng chày
• (v) 12% xem bóng chày và bóng đá
• (vi) 10% xem thể dục dụng cụ và bóng đá
• (vii) 8% xem cả ba môn thể thao.
Tính phần trăm của nhóm không xem bất kỳ môn thể thao nào trong năm qua.
Problem 38. Xác suất một lần thăm bác sĩ chuyên khoa (PCP) không dẫn đến làm xét nghiệm
hoặc được chuyển đến chuyên gia chưa được là 35%. Trong số những người đến thăm bác sĩ PCP,
có 30% được chuyển đến chuyên gia và 40% cần phải làm xét nghiệm. Hãy tính xác suất một lần
thăm bác sĩ PCP dẫn đến cả việc làm xét nghiệm lẫn được chuyển đến chuyên gia.
Problem 39. Một hũ chứa 10 quả bóng: 4 quả màu đỏ và 6 quả màu xanh. Hũ thứ hai chứa 16
quả bóng màu đỏ và một số quả bóng màu xanh không biết. Khi lấy một quả bóng từ mỗi hũ, xác
suất để cả hai quả bóng cùng màu là 0,44. Tính số quả bóng màu xanh trong hũ thứ hai.
Problem 40. Một công ty bảo hiểm ô tô có 10.000 người tham gia bảo hiểm. Mỗi người tham gia
bảo hiểm được phân loại như sau: (i) Trẻ hoặc già;, (ii) Nam hoặc nữ; và, (iii) Đã kết hôn hoặc độc
thân. Trong số các người tham gia bảo hiểm này, có 3000 người trẻ, 4600 người là nam, và 7000
người đã kết hôn. Các người tham gia bảo hiểm cũng có thể được phân loại là 1320 nam trẻ, 3010
nam đã kết hôn và 1400 người trẻ đã kết hôn. Cuối cùng, có 600 người tham gia bảo hiểm là nam
trẻ đã kết hôn. Tính số người tham gia bảo hiểm của công ty là trẻ, nữ và độc thân.
Problem 41. Xem xét một tập dữ liệu có phân phối chuẩn.
I Trung vị bằng với trung bình chế độ (mode) trong một phân phối chuẩn.
II Khoảng cách xấp xỉ 68% dữ liệu nằm trong một độ lệch chuẩn so với trung bình.
III Phạm vi giữa tứ phân vị (IQR) bằng với phạm vi (range) trong một phân phối chuẩn. Câu nào sau đây là đúng? 1. Duy nhất I 2. Duy nhất I và II 3. Duy nhất II và III 4. Duy nhất I và III 5. Cả I, II và III 18
Document Outline
- Logic
- 1 Biểu diễn Mệnh Đề Logic
- 2 Xây dfing bảng chân trị tfi mệnh đề (Truth Table Construction)
- 3 Các phép toán trên chuỗi nhị phân
- 4 Ứng dụng của logic
- 5 Bài Tập Nâng Cao
- Lj Thuyết Số
- 6 Phép chia lấy dư
- 7 Biểu diễn số dưới các hệ cơ số
- 8 Hàm Băm (Hash Function)
- 9 Mật mã học
- 9.1 Mật mã Caesar
- 9.2 Định lj phần dư Trung Hoa và Mã RSA
- 10 Bài Tập Nâng Cao
- Quy Tắc Đếm và Xác Suất Rời Rạc
- 11 Quy Tắc Đếm
- 12 Xác Suất Thống Kê




