Đề cương môn Toán rời rạc - Trường Đại học lao động -  xã hội.

ĐỀ KIỂM TRA CUỐI KỲ
MÔN : TOÁN RỜI RẠC NĂM HỌC 202 - 202 LỚP : HỆ :
Thời gian làm bài : 90 phút
SV được sử dụng tài liệu. ĐÁP ÁN Câu Ý Nội dung Điểm
Cho quan hệ đồng dư theo modulo 3 trên tập số nguyên Z . Chứng minh rằng quan 1
hệ đồng dư modulo 3 là quan hệ tương đương. Hãy tìm tất cả các lớp tương đương 1
của quan hệ đồng dư theo modulo 3 trên Z .
Gọi R là quan hệ đồng dư theo modulo 3 trên tập số nguyên Z , ta có 6
a,b ϵ Z, a Ξ b mod 3 e (a – b) 3 e Ek ϵ Z a – b = k.3 Ta coù
6a ϵ Z, a – a = 0 = 0.3 aRa R phaûn xaï (I ). 1
6a,b ϵ Z, aRb e a – b = k.3 b – a = –k.3 bRa R ñoái xöùng (II ). 0,5
6a,b,c ϵ Z,
aRb e a – b = k.3 (1) (1) + (2) e a – c e (k + l).3 aRc R baéc caàu (III ).
bRc e b – c = l.3 (2) J ( ) ) ) I
,(I I ,(I II → R laø quan heä töông ñöông.
Quan hệ đồng dư theo modulo 3 phân hoạch Z thành 3 lớp tương đương như sau: Z = { 3 L0 , L1 , L2 } vôùi
L0 = {3k, k ϵ Z} = {...,–3, 0,3,6,9,...}, 2 0,5
L1 = {3k + 1, k ϵ Z} = {...,–2,1,4, 7,10,...} vaø
L2 = {3k + 2, k ϵ Z} = {...,–1,2,5,8,11,. .}. 2
Sử dụng các quy tắc suy diễn, hãy kiểm tra suy luận sau 1 (
p v q ) → r
r → (s v t ) s u u → t m p 1 0,5 2 0,5
Vậy suy luận trên là đúng.
Tìm số nghiệm nguyên của phương trình 3
x + x + x + x = 22 (1) 1 2 3 4 2 Sao cho x , x 2; x , x 4 1 2 3 4
Đặt y = x – 2, i = 1,2 vaø y = x – 4, j = 3,4 , ta có i i j j = – = + y x 2 x y 2 1 1 1 1 1
y = x – 2 x = y + 2 0,5 2 2 2 2
y = x – 4 x = y + 4 3 3 3 3
y = x – 4 x = y + 4 4 4 4 4 Suy ra (1) e x
1 + x2 + x3 + x4 = 22 2 0,5
e y + 2 + y + 2 + y + 4 + y + 4 = 22 1 2 3 4
e y + y + y + y = 10 1 2 3 4 3 Bài toán trở thành: 0,5 2
Tìm số bộ nghiệm nguyên của phương trình
y1 + y2 + y3 + y4 =10, yi 0, i = 1, 2,3, 4 (2)
Số bộ nghiệm nguyên của phương trình (2) là số tổ hợp lặp chập 10 của 4 bộ phần
tử, và được tính bằng 10 10 10 4 C = = = 0,5 4 C C 286 10+4–1 13
Vậy số bộ nghiệm của phương trình (2) cũng là số bộ nghiệm của phương trình (1) là 286. Giải hệ thức truy hồi 4 2 a = –a
+ 6a , n 2, a = 16, a = –3 n n–1 n–2 0 1
Ta có phương trình đặc trưng của (1): r2 + r – 6 = 0
nghiệm đặc trưng: r = 2,r = –3 1 2 1 1
nghiệm tổng quát của hệ thức: a = α rn + α rn = α 2n + α (–3)n (2) ,n ϵ n 1 1 2 2 1 2 α + α = 16 α = 9
Thay điều kiện đầu a = 16, a = –3 vào (2) ta được 1 2 e 1 0 1
2α – 3α = –3 α = 7 1 2 2
2 Vậy nghiệm của hệ thức truy hồi (1) là: 1
a = 9 2n + 7 (–3)n , n 0 n
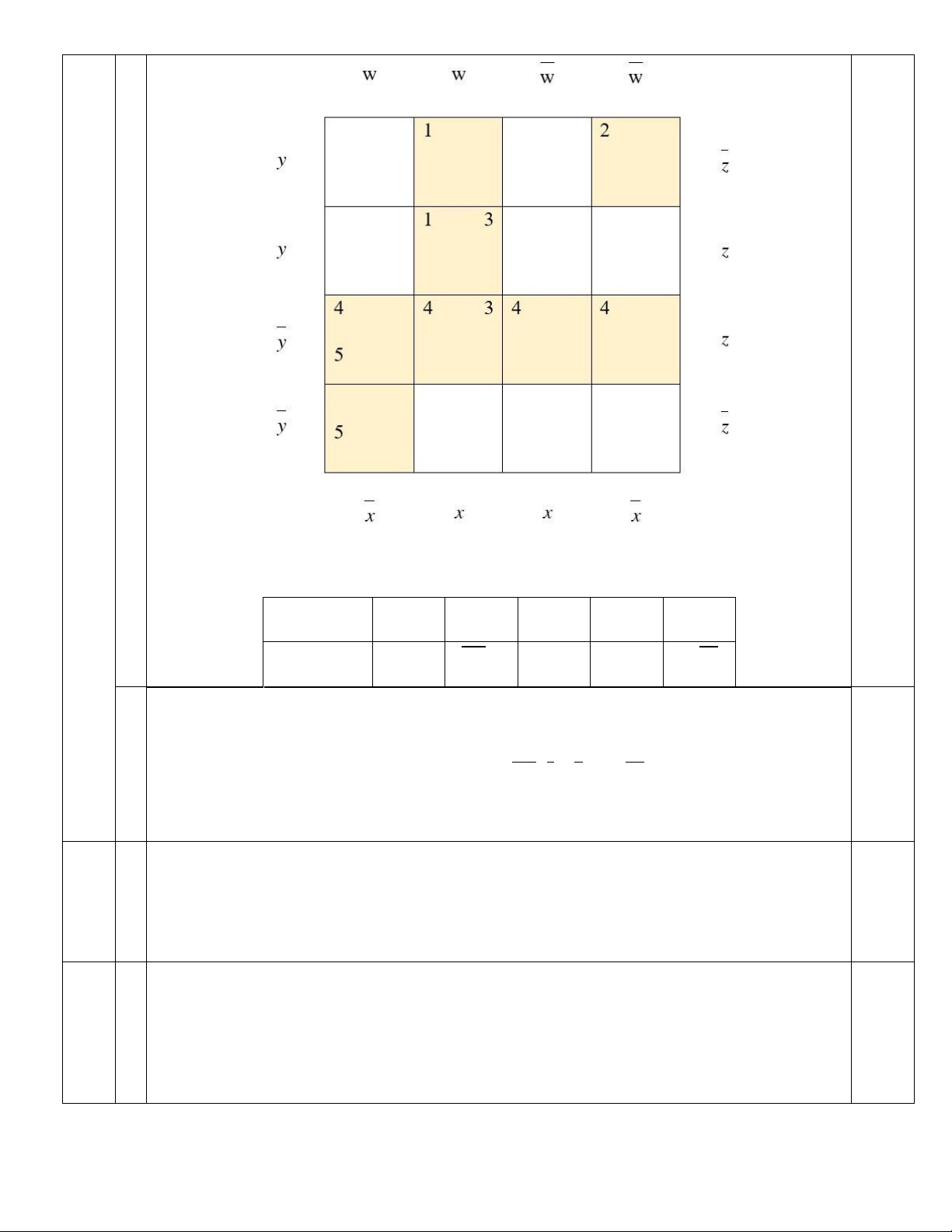
Dùng biểu đồ Karnaugh tìm công thức đa thức tối tiểu của hàm Boole 5 2
f (w, x, y, z) = wxyz + wxyz + wxyz + wxyz + wxyz + wxyz + wxyz + wxyz
1 Ta có biểu đồ Karnaugh của hàm Boole 1 3 Các tế bào lớn: Tế bào lớn 1 2 3 4 5 Công thức wxy wxyz wxz yz w xy
Suy ra một phép phủ tối tiểu gồm các tế bào: 1, 2, 4, 5
Với công thức đa thức tối tiểu: 2 1
f (w, x, y, z)=wxy + wxyz + yz + wxy
Khoa CNTT có 6 tổ bộ môn và mỗi tổ sẽ họp 1 lần/tháng. Cần tổ chức tối thiểu bao
nhiêu buổi họp mỗi tháng để không có Giảng viên nào có 2 buổi họp bị trùng, biết 6
rằng danh sách các tổ như sau 2
C = {A, B, Z},C = {B, L},C = {A, R, Z},C = {L, R, Z},C = {A, B},C = {B, R, Z} 1 2 3 4 5 6
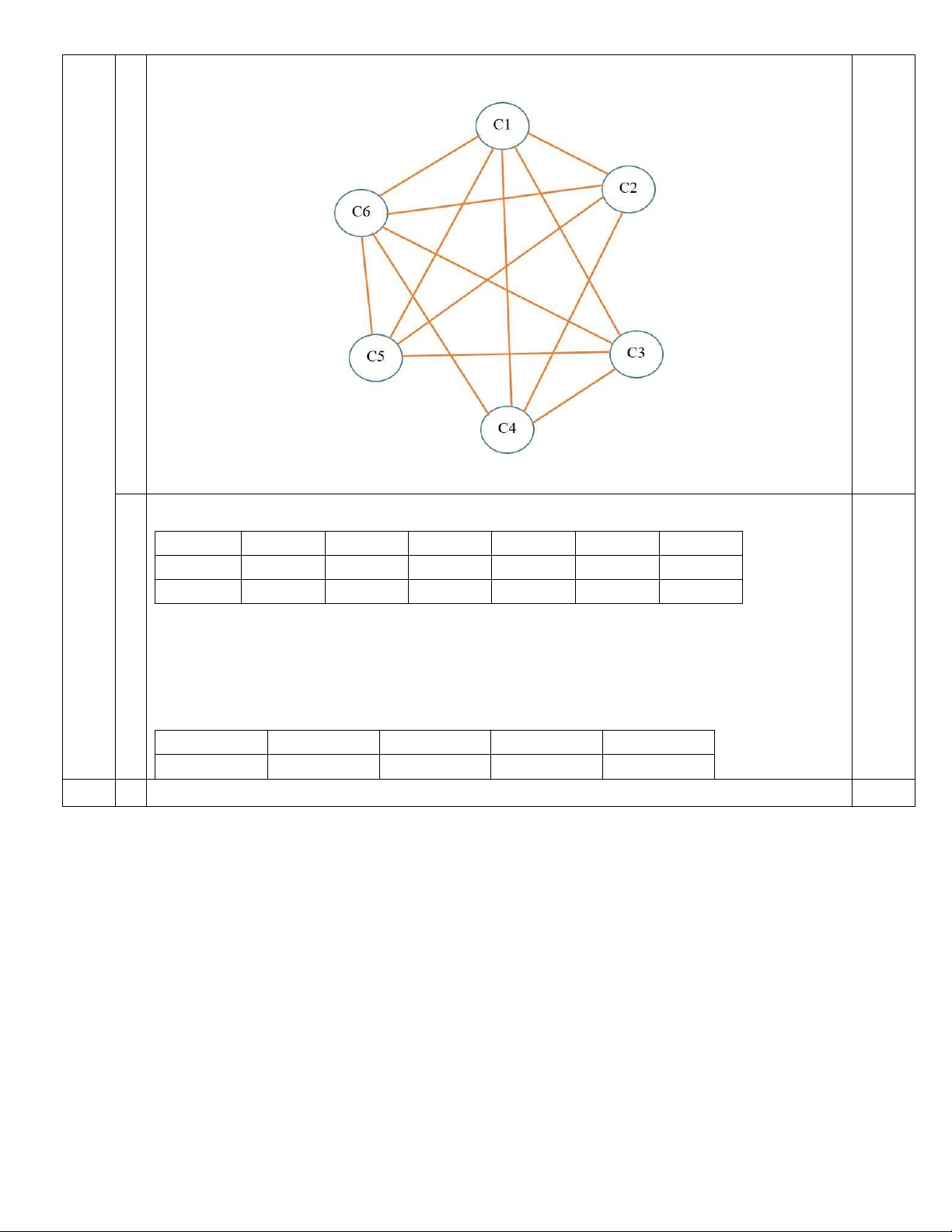
Gọi G là đồ thị được xây dựng bởi:
- Mỗi đỉnh của G là một tổ bộ môn. 1 1
- Mỗi 2 đỉnh của G có cạnh nối tương ứng với 2 tổ bộ môn có chung giảng viên. 4
Ta có đồ thị G từ dữ liệu bài toán
Sử dụng thuật toán tô màu Welsh-Powell, ta được Đỉnh C1 C6 C2 C3 C4 C5 Bậc 5 5 4 4 4 4 Màu tô I II III III IV IV
2 Ứng với mỗi màu tô ta phải tổ chức một ca họp, như vậy phải có tối thiểu 4 ca họp để 1
các Giảng viên không bị trùng lịch họp.
Một cách sắp xếp lịch họp thỏa yêu cầu trên là Ca họp I II III IV Tổ họp C1 C6 C2, C3 C4, C5 Ngày tháng năm 2023 Giảng Viên 5
Document Outline

• ĐỀ KIỂM TRA CUỐI KỲ
• ĐÁP ÁN