Đề cương môn Toán rời rạc - Trường Đại học lao động -  xã hội.

Tóm
thuyết Toán rời rạc tắt lý
Vũ Minh Hiếu 20225841
1. Các đồ thị đặc biệt
- Đồ thị đầy đủ (K) : Mỗi cạnh nối với n -1 cạnh còn lại
- Đồ thị vòng (C) :
- Đồ thị bánh xe (W)
2. Bậc của đồ thị vô hướng
- Tổng bậc của đồ thị là số chẵn và có công thức là : deg = 2 * e
Trong đó deg là tổng bậc và e là tổng số cạnh
- Số đỉnh lẻ của một đồ thị phải là số chẵn
3. Chu trình và đường đi
- Hành trình trong đồ thị G là một dãy đỉnh v1,v2,v3,v4 sao cho vi và vi+1 kề nhau
- Hành trình mà trong đó mọi đỉnh khác nhau được gọi là đường đi
- Hành trình v1,v2,v3 .......... v1 được gọi là chu trình nếu trong đó mọi đỉnh
khác nhau trừ đỉnh đầu và đỉnh cuối
+ Độ dài của chu trình là tổng số đỉnh hoặc tổng số cạnh mà chu trình đi qua
- Chu trình chứa mọi đỉnh trong đồ thị gọi là chu trình Hamilton
- Chu trình dùng mỗi cạnh đúng một lần được gọi là chu trình Euler
+ Một đồ thị vô hướng liên thông được gọi là đồ thị Euler khi nó có chu trình
Euler,khi đó mọi đỉnh của nó đều có bậc chẵn
- Độ dài của chu trình ngắn nhất trong đồ thị được gọi là chu vi nhỏ nhất của đồ thị đó
+ Định lý : Trong đồ thị liên thông G = (V,E) bất kì có chu vi nhỏ nhất g thỏa
mãn 3 <= g < vô cùng ta luôn có : e <= g * (v - 2) / (g - 2) 4. Đồ thị phẳng
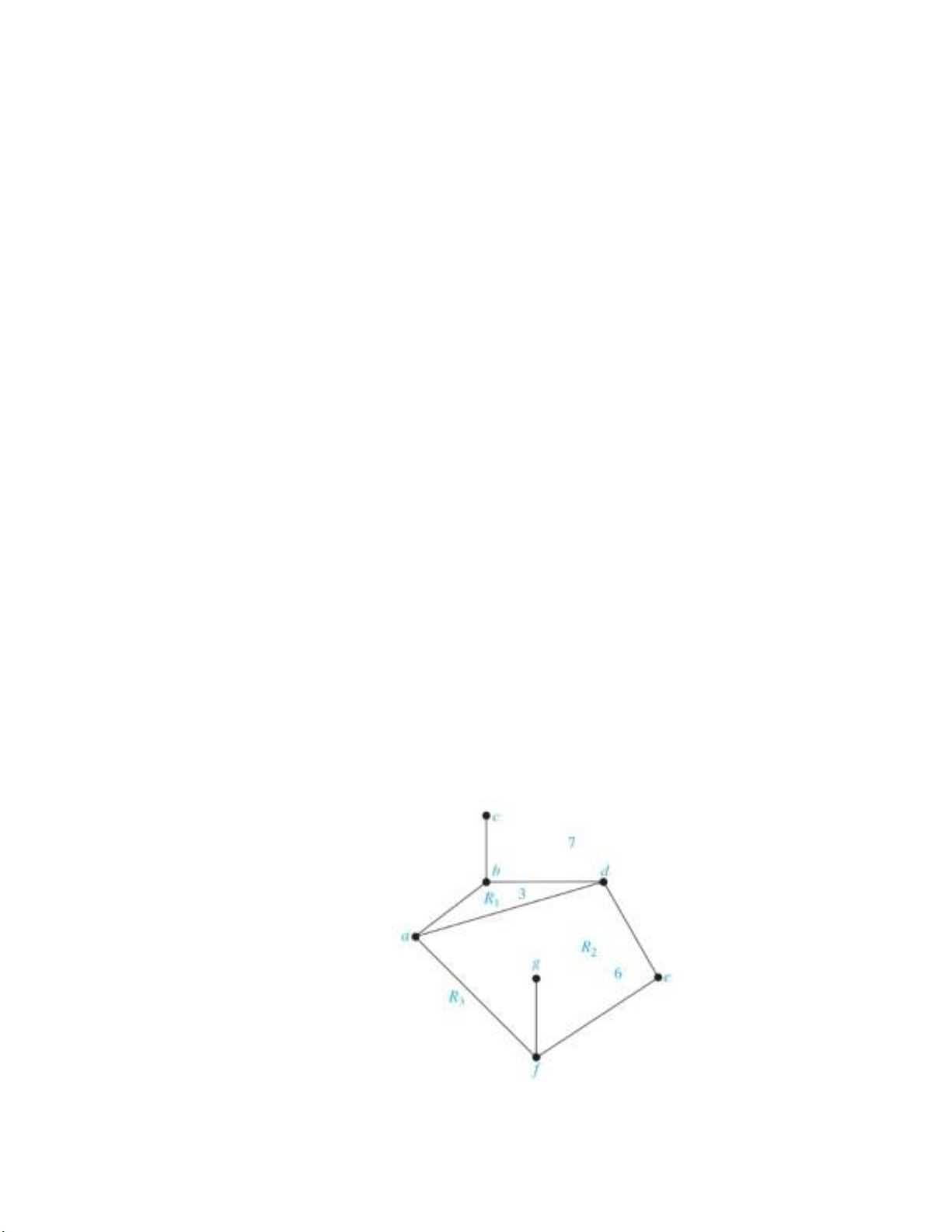
- Một đồ thị được gọi là phẳng nếu ta có thể vẽ nó trên mặt phẳng mà không
có cạnh nào cắt nhau. Hình vẽ đó được gọi là biểu diễn phẳng của đồ thị - Miền
trong đồ thị là vùng hoặc tập hợp các đỉnh hoặc cạnh trong đồ thị
+ Bậc của một miền là số cạnh trên biên của miền đó
+ Bậc của mỗi miền ít nhất phải bằng 3
+ Công thứDocwlniêlonadhedệbgy ihữuayensốthum(hiềuynenv2à2@srốepclyạlonohp.c:orm)<= 2 * e / 3
- Công thức Euler : r = e – v + 2
Trong đó r là số miền trong biểu diễn phẳng của đồ thị, e là tổng số cạnh, v là tổng bậc
- Một vài hệ quả của định lý Euler :
+ Nếu G là một đồ thị phẳng liên thông với e cạnh và v đỉnh thoải mãn v >= 3
thì ta có công thức sau e <= 3v – 6
+ Nếu G là một đồ thị phẳng liên thông thì G có một đỉnh bậc không quá 5
+ Nếu một đồ thị phẳng liên thông có e cạnh, v đỉnh trong đó v >= 3 và không
có chu trình độ dài 3 thì e <= 2v – 4
- Đồ thị là không phẳng nếu và chỉ nếu nó chứa một đồ thị con đồng phôi với
K3,3 hoặc K5 (K3,3 và K5 đều là đồ thị không phẳng)
5. Đồ thị Hamilton
- Đồ thị nửa Hamilton
+ Đường đi được gọi là đường đi Hamilton nếu nó chứa tất cả các đỉnh của G
+ Đồ thị được gọi là đồ thị nửa Hamilton nếu nó có đường đi Hamilton - Đồ thị Hamilton
+ Chu trình được gọi là chu trình Hamilton nếu nó chứa tất cả các đỉnh củaG
+ Đồ thị được gọi là đồ thị Hamilton nếu nó có chu trình Hamilton - Định lý :
+ Đồ thị đầy đủ (Kn) có chu trình Hamilton với mọi n >= 3
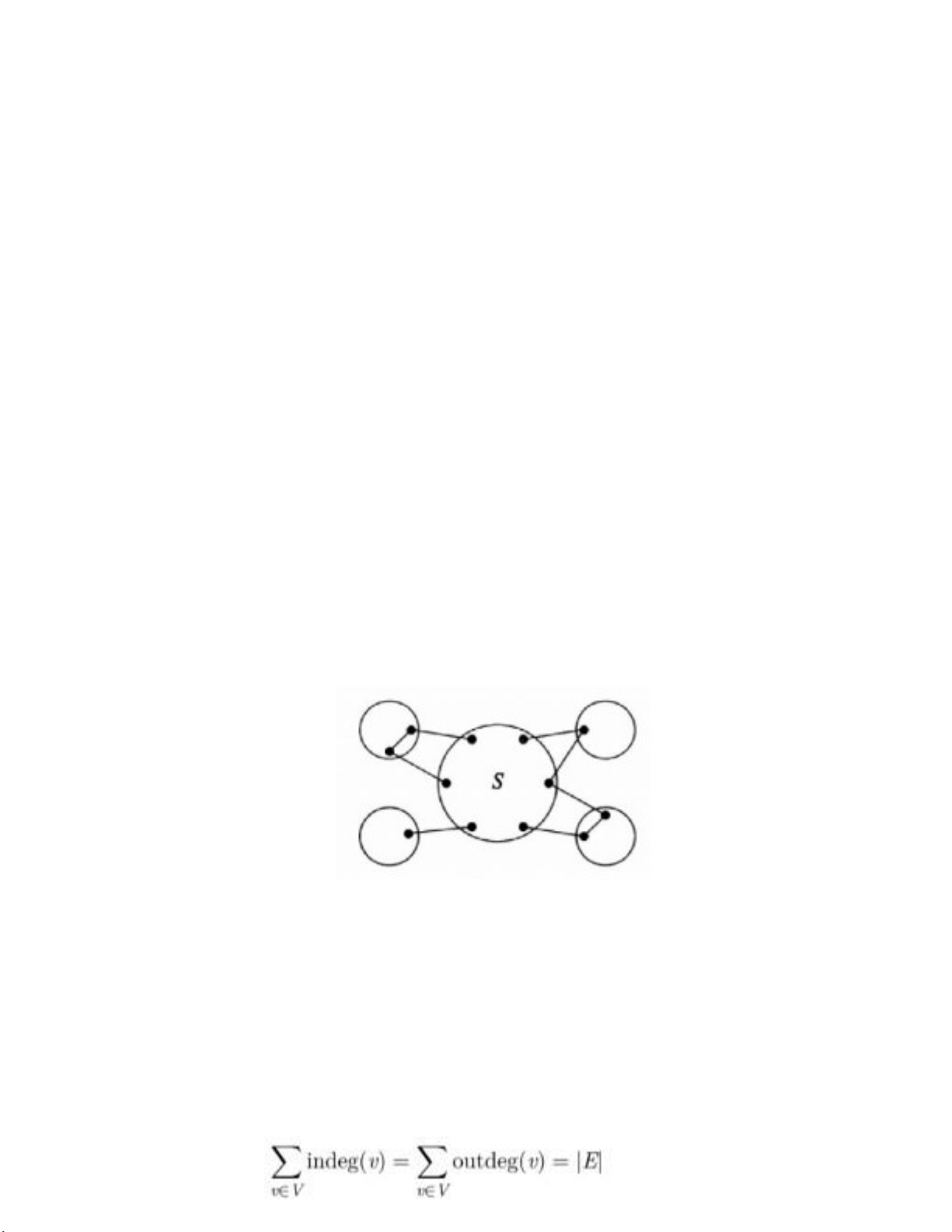
+ Nếu G = (V,E) có chu trình Hamilton, vậy thì với mọi tập đỉnh khác rỗng S,
đồ thị thu được từ G bằng cách xóa các đỉnh thuộc S chỉ có nhiều nhất |S| thành phần liên thông
- Định lý Ore : Giả sử G là một đơn đồ thị với n >= 3 đỉnh thoải mãn Với mọi
cặp đỉnh không liền kề u và v ta có degv + degu >= n khi đó G là đồ thị Hamilton
- Định lý Dirac : Nếu G là một đồ thị với n >= 3 thoải mãn
Bậc của mỗi đỉnh ít nhất bằng n/2, khi đó G là đồ thị Hamilton
6. Đồ thị có hướng
- Đồ thị có hướng là đồ thị trong đó các cạnh có hướng chỉ định một chiều từ
đỉnh xuất phát đến đỉnh đích
- Bậc vào của một đỉnh v là số cạnh có hướng với đỉnh kết thúc là đỉnh v,
tương tự với bậc ra.
- Công thức liên hệ giữa bậc vào và bậc ra
- Xét G(V,E) làDođwồnlothadị ecdóbyhhưuớ yenngthuvớ
(hiuynenđ2ỉ2n@hreVply=lo{ovp.1c,ovm2),v3,v4 . vn} và A là ma trận kề của G. Xét
là số hành trình có hướng từ vi tới vj, khi đó : + Ví dụ
- Một vài định nghĩa
+ Một đồ thị có hướng G = (V,E) là liên thông mạnh nếu với mọi đỉnh u và v
thuộc V, đều tồn tại một đường đi có hướng từ u tới v trong G
+ Một đồ thị có hướng G = (V,E) được gọi là phi chu trình(DAG) nếu nó
không chứa chu trình có hướng
- Một đồ thị định hướng của đồ thị (vô hướng) G = (V,E) là một đồ thị có
hướng thu được từ G bằng cách chọn một hướng
Cho mỗi cạnh xy của đồ thị
- Đồ thị thi đấu là một đồ thị định hướng của một đồ thị đầy đủ
+ Định lý : Mọi đồ thị thi đấu đều chứa một đường đi Hamilton
7. Tô màu đồ thị
- Tô màu đồ thị là quá trình gán màu cho mỗi đỉnh của đồ thị sao cho không có
hai đỉnh kề nhau có cùng màu.
- Sắc số của đồ thị là số nguyên k nhỏ nhất thỏa mãn có một cách tô màu cho G bằng k màu.
- Định lý : Nếu G là đồ thị với mọi đỉnh đều có bậc <= k, thì :
+ Sắc số <= k + 1
+ Nếu G liên thông và không chính quy thì Sắc số <= k
o Đồ thị chính quy là đồ thị có tất cả các đỉnh có cùng bậc
8. Đồ thị hai phần
- Đồ thị G là đồ thị hai phần khi Sắc số <= 2 - Định lý
+ G là đồ thị hai phần nếu và chỉ nếu nó không chứa chu trình độ dài lẻ 9. Cây
- Định nghĩa : Ta nói rằng một đồ thị T là một cây nếu nó thỏa mãn 2 tính chất + T liên thông + T không có chu trình
- Một số tính chất của cây T = (V,E)
+ T không chứa chu trình nhưng nếu thêm một cạnh nối 2 đỉnh không
kề nhau trong T thì đồ thị nhận được có đúng 1 chu trình + |E| = |V| - 1
+ T có ít nhất 2 đỉnh bậc 1
+ Nếu xóa 2 cạnh bất kì từ T thì thu được 2 đồ thị T1 và T2 đều là
cây - Rừng : tập hợp các cây T được gọi là một rừng
+ Nếu một từng chứa c cây thì ta có công thức |E| = |V| - c
- Cây gán nhãn : ta cố định các đỉnh của một cây, mỗi đỉnh được gán một nhãn
+ Định lý Cayley : Số cây gán nhãn với n đỉnh là n^(n-2)
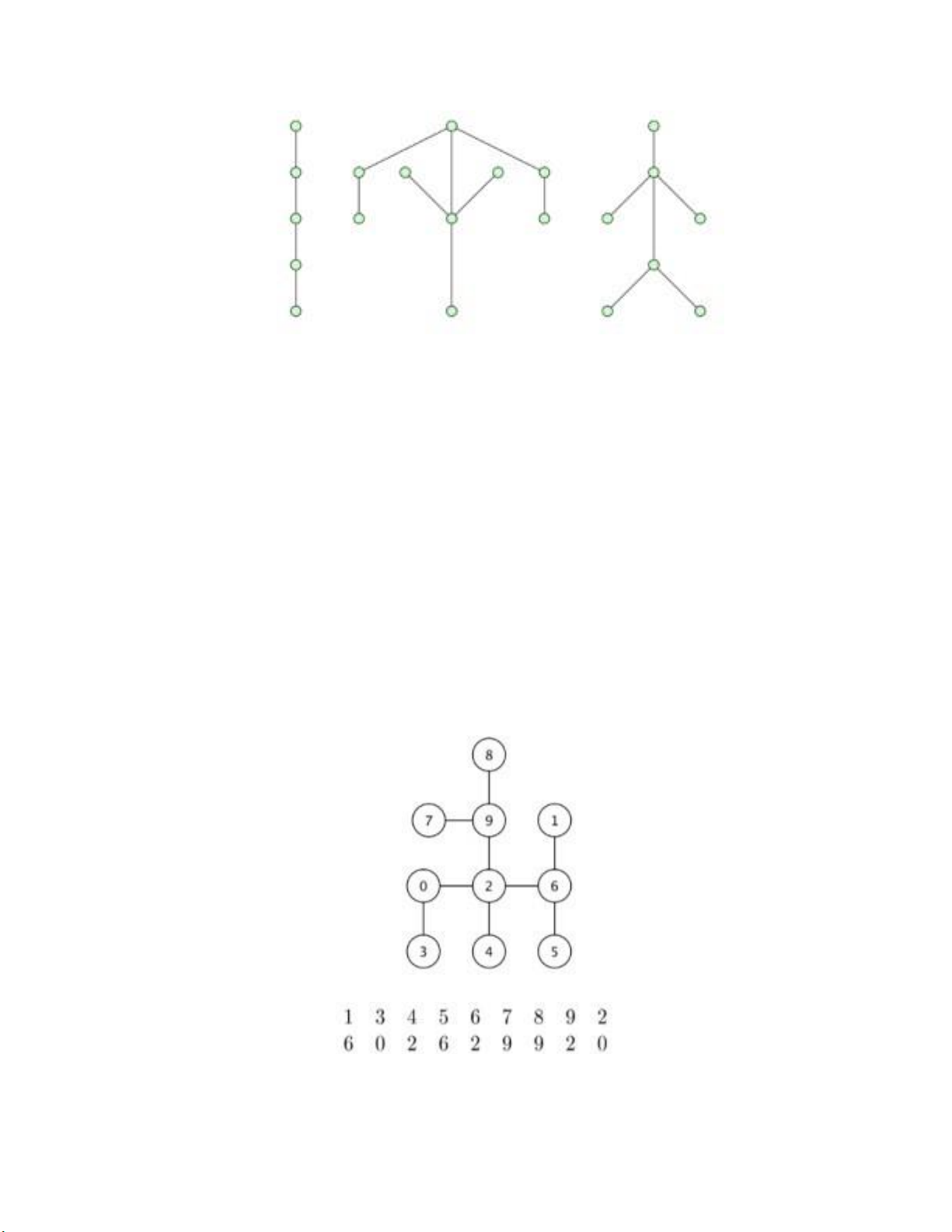
- Prufer code : được dùng để lưu trữ cây
Các bước tìm Prufer code :
+ Bước 1 : Tìm đỉnh có bậc nhỏ nhất và được đánh số nhỏ nhất trong cây,
xóa nỏ và in ra nhãn của đỉnh kề với nó
+ Bước 2 : Tính toán lại bậc của các đỉnh còn lại trong đồ thị
+ Bước 3 : Lặp lại bước 1 đến khi chỉ còn lại 2 đỉnh, đầu ra sẽ là một dãy
số gồm n -1 phần tử được gọi là Prufer code + Ví dụ : ⇒ 10. DFS
- Sắp xếp Topo (Topological Sorting) trong đồ thị là quá trình sắp xếp các
đỉnh sao cho mỗi cạnh chỉ đi từ đỉnh có thứ tự cao hơn đến đỉnh có thứ tự
thấp hơn. Nói cách khác, trong sắp xếp Topo, không có chu trình trong đồ thị.
+ Bước 1 : Duyệt qua tất cả các đỉnh chưa được sắp xếp, tìm đỉnh có bán
bậc vào nhỏ nhất, chọn đỉnh đó là đỉnh tiếp theo được sắp xếp.
+ Bước 2 : Duyệt qua tất cả các đỉnh mà đỉnh được chọn có cạnh hướng
đến đỉnh đó, giảm bán bậc vào của nó đi 1.
+ Bước 3 : Lặp lại Bước 1 và 2 cho đến khi đã sắp xếp tất cả các đỉnh
11. Bài toán tìm đường đi nhỏ nhất
- Thuật toán Dijkstra + Bước 1 :Khởi tạo:
o Đặt tất cả các đỉnh trong đồ thị có trạng thái "chưa xét" và khoảng
cách từ đỉnh xuất phát đến các đỉnh còn lại là vô cùng lớn (hoặc vô
cùng lớn tùy thuộc vào kiểu dữ liệu sử dụng).
o Đặt khoảng cách từ đỉnh xuất phát đến chính nó là 0.
+ Bước 3 : Bắt đầu từ đỉnh xuất phát và duyệt qua các đỉnh:
o Tại mỗi bước, chọn đỉnh có khoảng cách nhỏ nhất từ đỉnh xuất phát mà chưa được xét.
o Duyệt qua tất cả các đỉnh kề với đỉnh đó:
o Nếu khoảng cách từ đỉnh xuất phát tới đỉnh kề hiện tại lớn hơn
khoảng cách hiện tại và trọng số của cạnh giữa đỉnh đó và đỉnh kề
nhỏ hơn khoảng cách hiện tại, thì cập nhật khoảng cách mới.
o Đánh dấu đỉnh vừa xét là "đã xét".
+ Bước 3 : Lặp lại bước 2 cho đến khi tất cả các đỉnh đều đã được xét.
o Kết quả của thuật toán Dijkstra sẽ là khoảng cách ngắn nhất từ đỉnh
xuất phát đến tất cả các đỉnh còn lại trong đồ thị.
12. Bài toán cây khung nhỏ nhất
- Cây khung là một cây con của đồ thị gốc, bao gồm tất cả các đỉnh và một số
cạnh của đồ thị
- Thuật toán Kruskal:
+ Bước 1: Sắp xếp các cạnh của đồ thị theo trọng số tăng dần.
+ Bước 2: Duyệt qua từng cạnh đã được sắp xếp:
o Nếu việc thêm cạnh đó không tạo thành chu trình với các cạnh đã có
trong cây khung, thì thêm cạnh đó vào cây khung.
o Nếu việc thêm cạnh đó tạo thành chu trình, thì bỏ qua cạnh đó và tiếp
tục với cạnh tiếp theo.
+ Bước 3: Kết quả sẽ là cây khung nhỏ nhất của đồ thị. - Thuật toán Prim:
+ Bước 1: Chọn một đỉnh bất kỳ làm đỉnh xuất phát của cây khung.
+ Bước 2: Lặp cho đến khi tất cả các đỉnh đều đã được thêm vào cây khung:
o Tìm cạnh có trọng số nhỏ nhất mà một đỉnh nằm trong cây khung
và một đỉnh không nằm trong cây khung.
o Thêm cạnh đó vào cây khung và thêm đỉnh kề với cạnh đó vào tập hợp các đỉnh đã xét.
+ Bước 4: Kết quả sẽ là cây khung nhỏ nhất của đồ thị.
13. Luồng cực đại - Mô hình bài toán
+ Đồ thị có hướng mô tả hướng đi của dầu, trọng số
mỗi cạnh là lượng dầu tối đa mỗi ống có thể chuyển
+ Mục tiêu là tìm lưu lượng dầu tối đa có thể chuyển từ S sang T
- Lát cắt là một cách phân hoạch tập đỉnh thành hai phần L và R
- Khả năng thông qua của lát cắt là tổng khả năng thông
qua của các cạnh từ L tới R
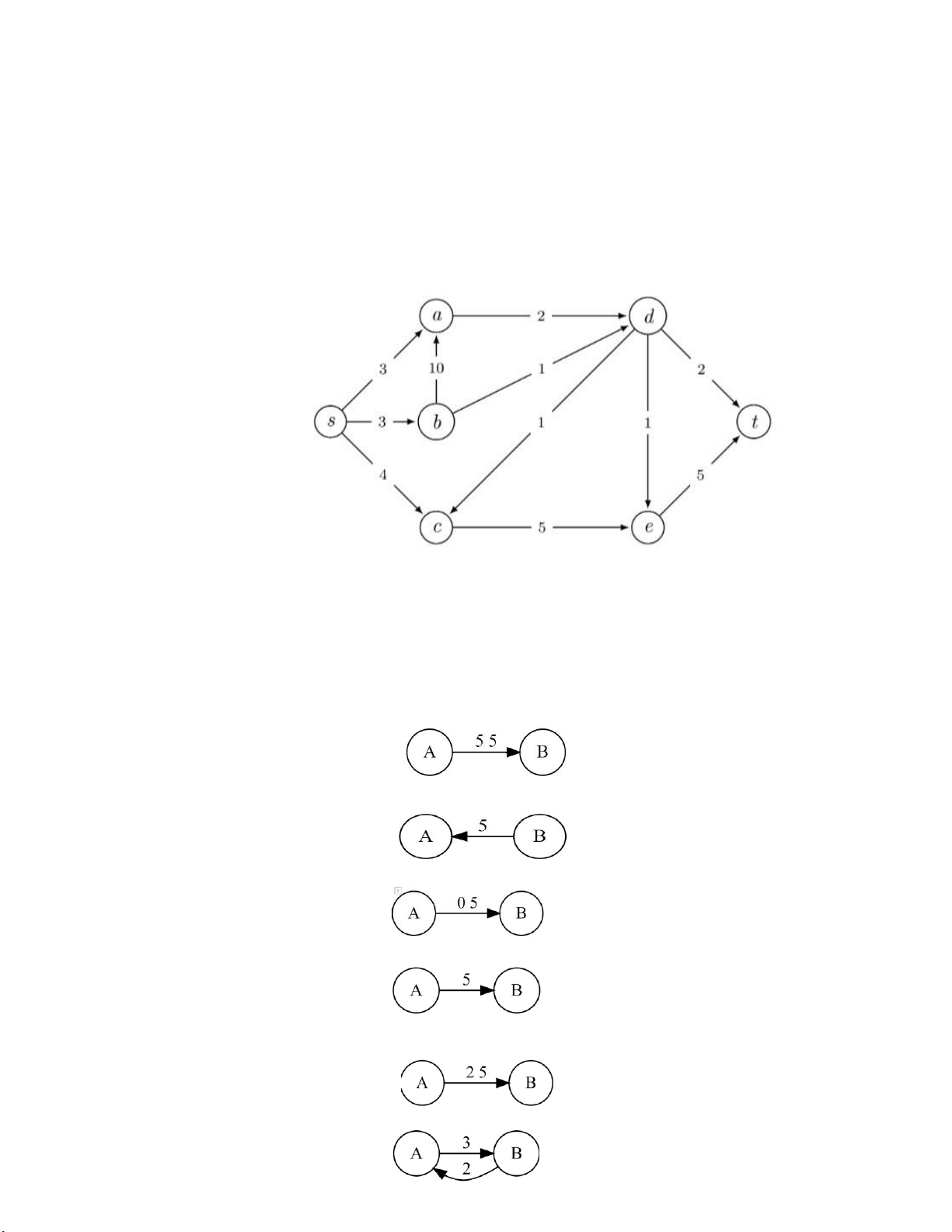
- Thuật toán Ford - Fulkerson
+ Bước 1 : Xây dựng đồ thị luồng từ đồ thị cho trước (đồ thị
G) ➢ f = c : Đảo chiều mũi tên và ghi lại giá trị luồng là f ⇒
➢ f = 0 : Giữ nguyên mũi tên và ghi giá trị luồng là c ⇒
➢ f < c : cạnh cũ = c - f cạnh mới = f ⇒
+ Bước 2 : Chọn một đường đi từ S tới T thông qua đồ thị luồng
+ Bước 3 : Chọn trọng số nhỏ nhất (k)trên đường đi vừa tìm được.
Nếu hướng của cạnh đó trong đồ thị G ban đầu cùng chiều với
đồ thị luồng thì tăng nó lên k, ngược lại thì giảm k
+ Bước 4 :Lặp lại các bước trên đến khi không thể tìm được đường đi từ S tới T trong đồ thị luồng
II. Đếm và tổ hợp 1. Hàm sinh
- Một vài hàm sinh hay gặp :
+ Hàm sinh của dãy (1,1,1,1,1 ... ) là 1/(1-x)
+ Hàm sinh của dãy (1,-1,1,-1, ..... ) là -1/(x + 1)
+ Hàm sinh của dãy (1,0,1,0, ..... ) là 1/(1-x^2)
+ Hàm sinh của dãy (1,2,3,4.....) là 1/(1-x)^2
+ Hàm sinh của dãy Fibonaci là x/(1-x-x^2)
2. Công thức truy hồi
- Định nghĩa : Công thức truy hồi đối với dãy số (An) là biểu biễn An qua một
hay nhiều số hạng đi trước của dãy
- Tìm Công thức truy hồi tuyến tính
Document Outline

• 1. Các đồ thị đặc biệt
• 2. Bậc của đồ thị vô hướng
• 3. Chu trình và đường đi
• 4. Đồ thị phẳng
• 5. Đồ thị Hamilton
• 6. Đồ thị có hướng
• 7. Tô màu đồ thị
  • + Sắc số <= k + 1
• 8. Đồ thị hai phần
• 9. Cây
  • - Một số tính chất của cây T = (V,E)
  • + |E| = |V| - 1
• 10. DFS
• 11. Bài toán tìm đường đi nhỏ nhất
• 12. Bài toán cây khung nhỏ nhất
  • - Thuật toán Kruskal:
  • - Thuật toán Prim:
• 13. Luồng cực đại
• - Thuật toán Ford - Fulkerson
• II. Đếm và tổ hợp
  • 1. Hàm sinh
  • 2. Công thức truy hồi