Đề cương ôn tập giữa học kì 2 môn Toán 11 sách Cánh diều

ĐỀ CƯƠNG ÔN TẬP GIỮA KỲ 2 MÔN TOÁN LỚP 11 CÁNH DIỀU
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất. 1
Câu 1. Rút gọn biểu thức 4 4 3
P  x  x với x  0 . 1 2
A. P  x B. 8 P  x C. 9 P  x D. 2 P  x Câu 2. Cho 5 2
a  3 ,b  3 và 6
c  3 mệnh đề nào dưới đây đúng
A. a  c  b .
B. a  b  c .
C. b  a  c .
D. c  a  b
Câu 3. Cho a  0 và a 1, khi đó log a bằng a A. 2 . B. -2 . C. 1  . D. 1 . 2 2
Câu 4. Cho log b  và log c  . Tính P   2 3 log b c . a  a 3 a 2 A. P 13 B. P  31 C. P  30 D. P 108
Câu 5. Tập xác định của hàm số 5x y  là A. R . B. 0;    . C. R   0 . D. 0;   .
Câu 6. Cho hàm số y  log x . Mệnh đề nào dưới đây là mệnh đề sai? 5
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định D  R   0 .
C. Đồ thị hàm số đã cho nằm bên phải trục tung.
D. Hàm số đã cho có tập giá trị là  .
Câu 7. Nghiệm của phương trình log 2x 1  2 là: 3   A. x  3. B. x  5. C. 9 x  . D. 7 x  . 2 2
Câu 8. Tập nghiệm của bất phương trình 2 x 1  x x9 5  5 là A.  2  ;4. B.  4  ;2. C.    ;2   4;    . D.    ;4   2;    .
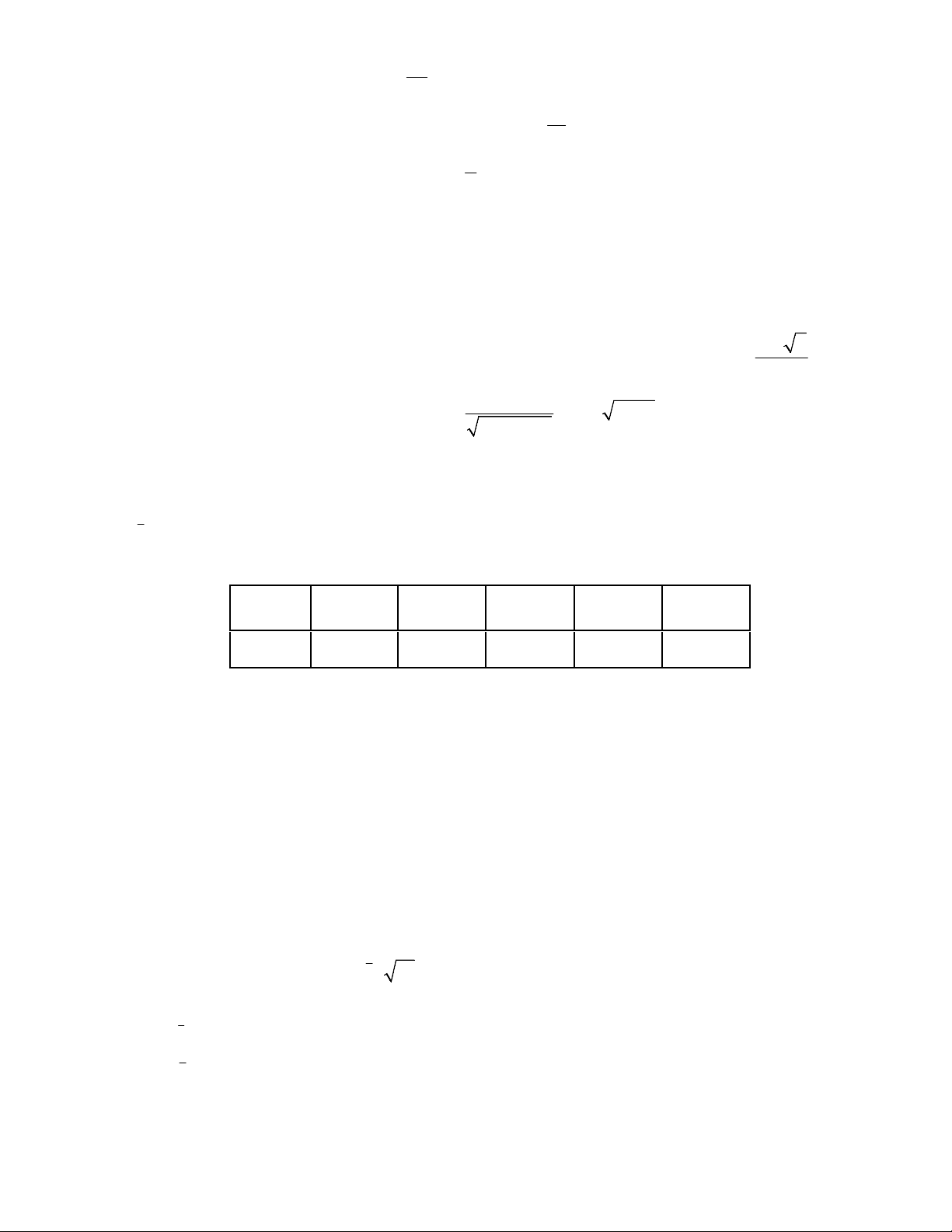
Câu 9. Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20 20;25 25;30 30;35 35;40 40;45 45;50 Số nhân 6 14 25 37 21 13 9 viên
Mẫu số liệu được chia thành bao nhiêu nhóm? A. 6 nhóm B. 5 nhóm C. 7 nhóm D. 8 nhóm
Câu 10. Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao 150;154 154;158 158;162 162;166 166;170 Số học sinh 25 50 200 175 50
Giá trị đại diện của nhóm 162;166 là A. 162 . B. 164 . C. 166 . D. 4 .
Câu 11. Hai xạ thủ bắn cung vào bia. Gọi X và X lần lượt là các biến cố "Xạ thủ thứ nhất bắn 1 2
trúng bia" và "Xạ thủ thứ hai bắn trúng bia". Hãy biểu diễn biến cố B theo hai biến cố X và X . 1 2
B : "Có đúng một trong hai xạ thủ bắn trúng bia".
A. B  X  X
B. B  X X  X X
C. B  X X  X X D. 1 2 1 2 1 2 1 2 1 2
B  X X  X X 1 2 1 2
Câu 12. Rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá. Tính xác suất của biến cố "Lá bài được chọn có
màu đen hoặc lá đó có số chia hết cho 3". A. 1 B. 4 C. 8 D. 1 2 9 13 4
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời tù câu 1 đến câu 4. Trong mối ý a), b), c), d) ở mồi câu, thí sinh chọn đúng hoặc sai b a Câu 1.   Cho các biểu thức sau: a b
A  a a log 3
 3 2b logb a với , 0  và
a  1,b  1
 log a  log b  log c  log a B
với a,b,c,d là các số dương. Khi đó: b c d d a) 3 4
A  a  b b) a B  b c) 3 2 7
A B a  a  b . c) 3 2 7
A B b  2 a  b .
Câu 2. Cho phương trình log x  6  log x 1 1 * . Khi đó: 3   3    
a) Điều kiện: x 1 2 b) Phương trình  
* có chung tập nghiệm với phương trình x 11x  9  0 x 1
c) Gọi x  a là nghiệm của phương trình   * , khi đó    x x a  5 lim 3 2
d) Nghiệm của phương trình  
* là hoành độ giao điểm của đường thẳng: d : 2x  y 8  0 1
với d : y  0 . 2
Câu 3. Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau: Khoảng điểm
6,5;7 7;7,5 7,5;8 8;8,5 8,5;9 9;9,5 9,5;10 Số học sinh 8 10 16 24 13 7 4
a) Cỡ mẫu của mẫu số liệu là n  80.
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: Q  7,58 . 1
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là: Q  8,15 . 2
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: Q  8,63 3
Câu 4. Một hộp đựng 30 tấm thẻ có đánh số từ 1 đến 30 , hai tấm thẻ khác nhau đánh hai số
khác nhau. Lấy ngẫu nhiên một tấm thẻ từ hộp, khi đó xác suất để lấy được:
a) Thẻ đánh số chia hết cho 3 bằng: 13
b) Thẻ đánh số chia hết cho 4 bằng: 11 30
c) Thẻ đánh số chia hết cho 3 và chia hết cho 4 bằng: 1 15
d) Thẻ đánh số chia hết cho 3 hoặc 4 bằng: 12
Phần 3. Câu trả lời ngắn.
Thí sinh trả lờ đáp án tù câu 1 đến câu 6.
Câu 1. Giả sử số tiền gốc là A , lãi suất là r% / kì hạn gửi (có thể là tháng, quý hay năm) thì
tồng số tiền nhận được cả gốc và lãi sau n kì hạn gửi là (1 )n A
r . Bà Hạnh gửi 100 triệu vào
tài khoản định kỳ tính lãi kép với lãi suất là 8% / năm. Tính số tiền lãi thu được sau 10 năm. 2   
Câu 2. Cho log b  và log c  với a; ;
b c  0;a  1. Tính giá trị của  log a b P a 4 a 3 a  3   c   
Câu 3. Tìm tất cả giá trị m để: Hàm số 1 y 
 log x  m xác định trên khoảng 3 2m 1 x 2;3
Câu 4. Giải bất phương trình sau:
log x  2  2 ; 1   4
Câu 5. Điều tra về số lượng học sinh khối 11 trong một lớp học, người ta thu được dữ liệu
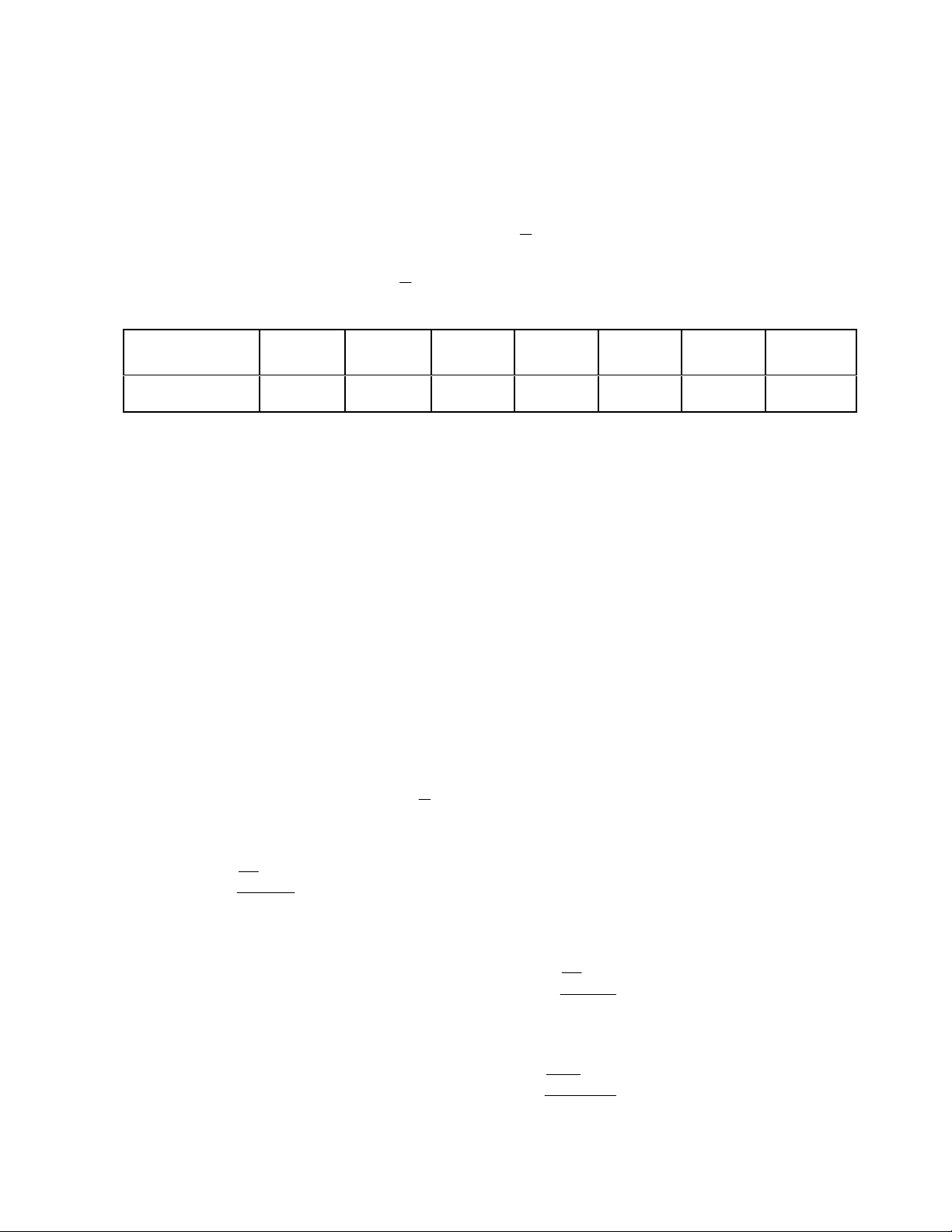
của 100 lớp học và có bảng phân phối tần số ghép nhóm sau: Nhóm
36;38 38;40 40;42 42;44 44;46 Tần số 9 15 25 30 21
Tìm trung vị của mẫu số liệu ghép nhóm trên.
Câu 6. Người ta thăm dò một số lượng người hâm mộ bóng đá tại một thành phố, nơi có hai
đội bóng đá X và Y cùng thi đấu giải vô địch quốc gia. Biết rằng số lượng người hâm mộ
đội bóng đá X là 22% , số lượng người hâm mộ đội bóng đá Y là 39%, trong số đó có 7%
người nói rằng họ hâm mộ cả hai đội bóng trên. Chọn ngẫu nhiên một người hâm mộ trong số
những người được hỏi, tính xác suất để chọn được người không hâm mộ đội nào trong hai đội
bóng đá X và Y . LỜI GIẢI CHI TIẾT
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất. 1
Câu 1. Rút gọn biểu thức 4 4 3
P  x  x với x  0 .
A. P  x1 B. 8 P  x 2 C. 9 P  x D. 2 P  x Chọn A Lời giải 1 1 3 1 3 Ta có:  4 4 3 4 4 4 4 1
P  x  x  x  x  x  x  x Câu 2. Cho 5 2
a  3 ,b  3 và 6
c  3 mệnh đề nào dưới đây đúng
A. a  c  b .
B. a  b  c .
C. b  a  c .
D. c  a  b Lời giải Chọn C  Ta có 5 2 4 6
a  3 ,b  3  3 ,c  3 và  4  5  6 
 b  a  c . 3  1
Câu 3. Cho a  0 và a 1, khi đó log a bằng a A. 2 . B. -2 . C. 1  . 2 D. 1 . 2 Chọn D Lời giải 1
Với a  0 và a 1, ta có: 1 1 2 log a  a  a  . a loga log 2 a 2
Câu 4. Cho log b  và log c  . Tính P   2 3 log b c . a  a 3 a 2 A. P 13 B. P  31 C. P  30 D. P 108 Chọn A Lời giải Ta có: b c  b  c    . a  2 3 log
 2loga 3loga 2.2 3.3 13
Câu 5. Tập xác định của hàm số 5x y  là A. R . B. 0;    . C. R   0 . D. 0;   . Lời giải Chọn A
Tập xác định của hàm số 5x y  là R
Câu 6. Cho hàm số y  log x . Mệnh đề nào dưới đây là mệnh đề sai? 5
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định D  R   0 .
C. Đồ thị hàm số đã cho nằm bên phải trục tung.
D. Hàm số đã cho có tập giá trị là  . Lời giải A. Đúng vì a>1
B. Ta có tập xác định của hàm số y  log x là D  0; 
 . Do đó đáp án B sai. 5
C. Đúng vì x  0 D. Đúng
Câu 7. Nghiệm của phương trình log 2x 1  2 là: 3   A. x  3. B. x  5. C. 9 x  . 2 D. 7 x  . 2 Chọn B Lời giải Điều kiện: 1
2x 1  0  x  2  1  1 Ta có x  x 
log 2x 1  2   2   2  x  5 . 3   2 2x 1 3 x  5
Vậy phương trình có nghiệm x  5.
Câu 8. Tập nghiệm của bất phương trình 2 x 1  x x9 5  5 là A.  2  ;4. B.  4  ;2. C.    ;2   4;    . D.    ;4   2;    . Lời giải Chọn A 2 x 1  x x9 2 2 5  5
 x 1  x  x 9  x  2x 8  0  2   x  4 .
Vậy Tập nghiệm của bất phương trình là  2  ;4.
Câu 9. Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các
nhân viên một công ty như sau: Thời gian
15;20 20;25 25;30 30;35 35;40 40;45 45;50 Số nhân 6 14 25 37 21 13 9 viên
Mẫu số liệu được chia thành bao nhiêu nhóm? A. 6 nhóm B. 5 nhóm C. 7 nhóm D. 8 nhóm Chọn C Lời giải
Mẫu số liệu được chia thành 7 nhóm
Câu 10. Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao
150;154 154;158 158;162 162;166 166;170 Số học sinh 25 50 200 175 50
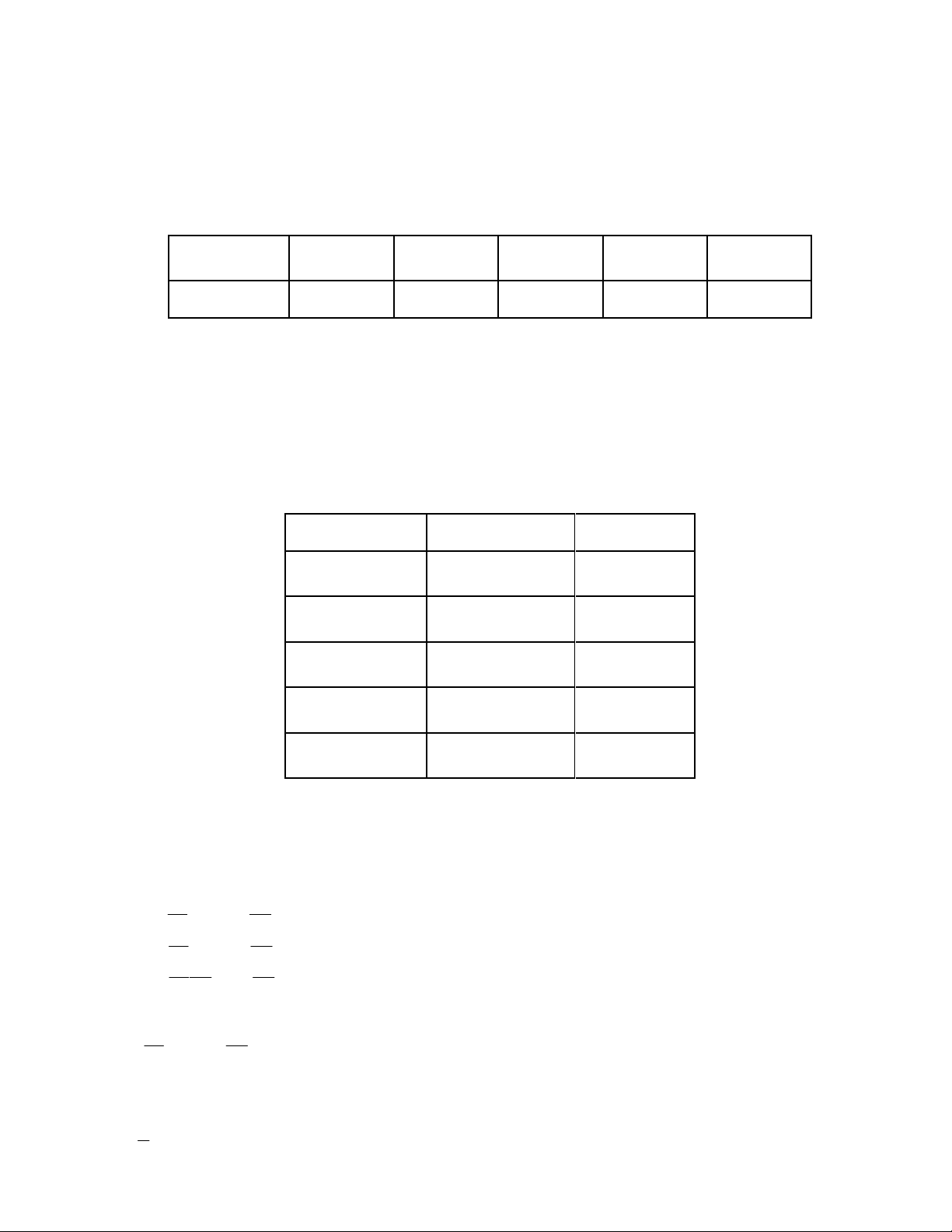
Giá trị đại diện của nhóm 162;166 là A. 162 . B. 164 . C. 166 . D. 4 . Lời giải Ta có bảng sau
Lớp chiều cao Giá trị đại diện Số học sinh 150;154 152 25 154;158 156 50 158;162 160 200 162;166 164 175 166;170 168 50
Câu 11. Hai xạ thủ bắn cung vào bia. Gọi X và X lần lượt là các biến cố "Xạ thủ thứ nhất 1 2
bắn trúng bia" và "Xạ thủ thứ hai bắn trúng bia". Hãy biểu diễn biến cố B theo hai biến cố
X và X  B : "Có đúng một trong hai xạ thủ bắn trúng bia". 1 2
A. B  X  X 1 2
B. B  X X  X X 1 2 1 2
C. B  X X  X X 1 2 1 2
D. B  X X  X X 1 2 1 2 Lời giải
B  X X  X X 1 2 1 2
Câu 12. Rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá. Tính xác suất của biến cố "Lá bài được
chọn có màu đen hoặc lá đó có số chia hết cho 3". A. 12 B. 49 C. 8 13 D. 14 Lời giải
Gọi A là biến cố "Lá bài được chọn có màu đen" và B biến cố "lá bài được chọn có số chia
hết cho 3" " Ta có P A B  P A  PB  P AB 1 12 1 12 8      . 2 52 2 52 13
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời tù câu 1 đến câu 4. Trong mỗ ý a ), b), c), d) ở mối câu, thí sinh chọn đúng hoặ sai b a Câu 1.   Cho các biểu thức sau: a b
A  a a log 3
 3 2b logb a với , 0  và
a  1,b  1
 log a  log b  log c  log a B
với a,b,c,d là các số dương. Khi đó: b c d d a) 3 4
A  a  b b) a B  b c) 3 2 7
A B a  a  b . c) 3 2 7
A B b  2 a  b . Lời giải a) Sai b) Sai c) Đúng d) Sai logab logba logab log 1 2 7 2 ba         Ta có: 3 2 3 2 3
A  a a   b   a   b         
  logab 72  logba a b 2 7 2 3 2 3 3 2 7
 b  a  a  b . Ta có:
log a b c  log a log a : a B        log1      0 .  b c d  d  d d 
Câu 2. Cho phương trình log x  6  log x 1 1 (*). Khi đó: 3   3  
a) Điều kiện: x 1 2 b) Phương trình  
* có chung tập nghiệm với phương trình x 11x  9  0 x 1
c) Gọi x  a là nghiệm của phương trình   * , khi đó    x x a  5 lim 3 2
d) Nghiệm của phương trình  
* là hoành độ giao điểm của đường thẳng: d : 2x  y 8  0 1
với d : y  0 . 2 Lời giải a) Đúng b) Đúng c) Sai d) Sai    Điều kiện: x 6 0   x  1. x 1  0
log x  6  log x 1 1 log x  6  log x 1  log 3 3   3   3   3   3 9
 log x  6  log 3 x 1  x  6  3 x 1  x  (thoả mãn điều kiện). 3   3     2
Vậy phương trình có nghiệm là 9 x  . 2
Câu 3. Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau: Khoảng điểm
6,5;7 7;7,5 7,5;8 8;8,5 8,5;9 9;9,5 9,5;10 Số học sinh 8 10 16 24 13 7 4
a) Cỡ mẫu của mẫu số liệu là n  80.
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: Q  7,58 . 1
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là: Q  8,15 . 2
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: Q  8,63 3 Lời giải a) Sai b) Đúng c) Đúng d) Đúng Gọi x ; x ; ;
 x lần lượt là điểm trung bình môn Toán của các học sinh sắp xếp theo thứ tự 1 2 82 không giảm. Ta có: x ; ;
 x  6,5;7 ; x ; ;
 x  7;7,5 ; x ; ;  x  8;8,5 ; 1 8   9 18   19 34   x ; ;
 x  8,5;9 ; x ; ;
 x  7;7,5 ; x ; ;  x  9,5;10 . 59 71   72 78   79 82  
Tứ phân vị thứ hai của mẫu số liệu là 1 x  x
mà x ; x  8;8,5 nên tứ phân vị thứ hai 41 42   41 42  2 của mẫu số 82 34 liệu là: 2 Q  8  8,58  8,15 . 2   24
Tứ phân vị thứ nhất của mẫu số liệu là x  7,5;8 . 21   82 18
Do đó tứ phân vị thứ nhất của mẫu số liệu là: 4 Q  7,5  8  7,5  7,58 . 1   16
Tứ phân vị thứ ba của mẫu số liệu là x  8,5;9 . 62   3.82 58
Do đó tứ phân vị thứ ba của mẫu số liệu là: 4 Q  8,5  9 8,5  8,63 . 3   13
Câu 4. Một hộp đựng 30 tấm thẻ có đánh số từ 1 đến 30 , hai tấm thẻ khác nhau đánh hai số
khác nhau. Lây ngẫu nhiên một tấm thẻ từ hộp, khi đó xác suất để lấy được:
a) Thẻ đánh số chia hết cho 3 bằng: 13
b) Thẻ đánh số chia hết cho 4 bằng: 11 30
c) Thẻ đánh số chia hết cho 3 và chia hết cho 4 bằng: 1 15
d) Thẻ đánh số chia hết cho 3 hoặc 4 bằng: 12 Lời giải a) Đúng b) Sai c) Đúng d) Đúng
a) Gọi A là biến cố: "Lấy được thẻ đánh số chia hết cho 3 ". Suy ra n A 10 và P A 10 1   30 3
b) Gọi B là biến cố "Lấy được thẻ đánh số chia hết cho 4 ". Suy ra nB  7 và PB 7  . 30
c) Ta có AB là biến cố: "Lây được thẻ đánh số chia hết cho 3 và chia hết cho 4 ". Suy ra AB  12;2 
4 ,n AB  2 và P AB 2 1   . 30 15
d) Xác suất để lấy được thẻ đánh số chia hết cho 3 hoặc 4 là:
P A B  P A  PB  P AB 1 7 1 1     3 30 15 2
Phần 3. Câu trả lời ngắn.
Thi sinh trả lờI đáp án từ câu 1 đến câu 6.
Câu 1. Giả sử số tiền gốc là A , lãi suất là r% / kì hạn gửi (có thể là tháng, quý hay năm) thì
tồng số tiền nhận được cả gốc và lãi sau n kì hạn gửi là (1 )n A
r . Bà Hạnh gửi 100 triệu vào
tài khoản định kỳ tính lãi kép với lãi suất là 8% / năm. Tính số tiền lãi thu được sau 10 năm. Lời giải
Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hạnh thu về là : n 10 (
A 1 r) 100(1 0,08)  215,892 triệu đồng.
Suy ra số tiền lãi bà Hạnh thu về sau 10 năm là 215,892 100 115,892 triệu đồng. 2   
Câu 2. Cho log b  và log c  với a; ;
b c  0;a  1. Tính giá trị của  log a b P a 4 a 3 a  3   c    Lời giải Ta có: 2 1  a  b  2 3 2 P  log    a  b  c   b  c a loga loga loga 2 loga 3log  3 a c    1 3 17 2 log b c         a 3loga 2 12 . 2 2 2
Câu 3. Tìm tất cả giá trị m để: Hàm số 1 y 
 log x  m xác định trên khoảng 3 2m 1 x 2;3 Lời giải    
Hàm số xác định trên khoảng  2m 1 x 0 2;3 khi và chỉ khi:  , x  2;3 x  m  0
x  2m 1       x    m 2 m 2 , 2;3      1 m  2 . x  m  2m 1  3 m  1
Câu 4. Giải bất phương trình sau:
log x  2  2 ; 1   4 Lời giải
Điều kiện: x  2  0  x  2.  * Khi đó, do cơ số 1
0  1 nên bất phương trình đã cho trở thành: 4 2  1  2 x  2 
 x  2  4  x     14 .  4 
Kết hợp với điều kiện  
* , ta được tập nghiệm của bất phương trình là: S   1  4;2.
Câu 5. Điều tra về số lượng học sinh khối 11 trong một lớp học, người ta thu được dữ liệu
của 100 lớp học và có bảng phân phối tần số ghép nhóm sau: Nhóm
36;38 38;40 40;42 42;44 44;46 Tần số 9 15 25 30 21
Tìm trung vị của mẫu số liệu ghép nhóm trên. Lời giải
Cỡ mẫu của mẫu số liệu là n 100 .
Gọi x , x , x , ,
 x là số học sinh trong một lớp học khối 11 được điều tra được sắp xếp theo 1 2 3 100 thứ tự không giảm.
Trung vị của mẫu số liệu là x  x 50 51 42;44 . 2 Ta có: n  C     u  u  . m 30;
9 15 25 49; m 42; m 44 1
Trung vị của mẫu số liệu ghép nhóm là: 100 49 2 M      e 42 44 42 631 42,07. 30 15
Câu 6. Người ta thăm dò một số lượng người hâm mộ bóng đá tại một thành phố, nơi có hai
đội bóng đá X và Y cùng thi đấu giải vô địch quốc gia. Biết rằng số lượng người hâm mộ
đội bóng đá X là 22% , số lượng người hâm mộ đội bóng đá Y là 39%, trong số đó có 7%
người nói rằng họ hâm mộ cả hai đội bóng trên. Chọn ngẫu nhiên một người hâm mộ trong số
những người được hỏi, tính xác suất để chọn được người không hâm mộ đội nào trong hai đội
bóng đá X và Y . Lời giải
Gọi A là biến cố: "Chọn được một người hâm mộ đội bóng đá X ", gọi B là biến cố: "Chọn
được một người hâm mộ đội bóng đá Y ".
Khi đó P A 22   PB 39   P AB 7 0,22, 0,39,   0,07 . 100 100 100
Suy ra: P A B  P A  PB  P AB  0,22 0,390,07  0,54 .
Xác suất để chọn được người không hâm mộ đội nào trong hai đội bóng đá X và Y là:
PA B 1 P A B  1 0,54  0,46 .