NỘ N N GIỮA HỌC KÌ I – TOÁN 7 I. ĐẠI SỐ A. ÓM Ắ LÝ H YẾ
1. Tập hợp Q các số hữu tỉ:
a) Khái niệm số hữu tỉ: a
- Số hữu tỉ là số viết được dưới dạng phân số
, với a, b , b  0 . b
- Tập hợp các số hữu tỉ ký hiệu là .
b) Số đối của một số hữu tỉ:
- Trên trục số, hai số hữu tỉ (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc
O và cách đều điểm gốc O được gọi là là số đối nhau.
- Số đối của số hữu tỉ a kí hiệu là a
- Số đối của 0 là 0
c) So sánh hai số hữu tỉ
- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a  b hay b  a
- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương
- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm
- Số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm
- Nếu a  b và b  c thì a  c
2. Cộng, trừ hai số hữu tỉ:
a) Quy tắc cộng, trừ hai số hữu tỉ:
Vì mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ
bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số. Tuy
nhiên, khi hai số hữu tỉ cùng viết ở dạng số thập phân thì ta có thể cộng trừ hai số đó
theo quy tắc cộng, trừ số thập phân.
b) Tính chất của phép cộng các số hữu tỉ:
- Phép cộng hai số hữu tỉ có các tính chất: Giao hoán, kết hợp, cộng với số 0, cộng với số đối.
- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng cho số đối của số hữu tỉ đó.
c) Quy tắc chuyển vế:
Khi chuyển một số hạng từ vế này sang vế kia, ta phải đổi dấu hạng tử đó:
x  y  z  x  z  y ;
x  y  z  x  z  . y
3. Nhân, chia hai số hữu tỉ:
a) Quy tắc nhân, chia hai số hữu tỉ:
Vì mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu
tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
Tuy nhiên, khi hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0
ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.
b) Tính chất của phép nhân các số hữu tỉ:
Phép nhân các số hữu tỉ có các tính chất: Giao hoán, kết hợp, nhân với 1, phân phối
của phép nhân đối với phép cộng và phép trừ.
4. Phép tính luỹ thừa với số mũ tự nhiên của một số hữu tỉ:
a) Phép tính luỹ thừa với số mũ tự nhiên:
Với n là một số tự nhiên lớn hơn 1 , luỹ thừa bậc n của một số hữu tỉ x , ký hiệu là n
x là tích của n thừa số x . n
x  x.x.x.. .
. ..x x , n , n   1 n thöøa soá x
Số x gọi là cơ số, n gọi là số mũ. Quy ước: 1 x  0
x, x 1 (x  0)
b) ích và thương của hai luỹ thừa cùng cơ số
- Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: m . n m n x x x  
- Khi chia hai luỹ thừa cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của luỹ thừa
bị chia trừ đi số mũ của luỹ thừa chia m : n mn x x  x
x  0, m  n
c) Luỹ thừa của luỹ thừa:
Khi tính luỹ thừa của một luỹ thừa, ta giữ nguyên cơ số và nhân các số mũ:  n m m.n x  x
d) Luỹ thừa của một tích: n
Với hai số hữu tỉ x và y , ta có:  .  n  . n x y x y
(Luỹ thừa của một tích, bằng tích các luỹ thừa)
e) Luỹ thừa của một thương: n n  x  x
Với hai số hữu tỉ x và y ( y  0 ), ta có:  y    n  0  y  y
(Luỹ thừa của một thương, bằng thương các luỹ thừa)
5. Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc.
a) Thứ tự thực hiện các phép tính:
- Đối với biểu thức không có ngoặc : luỹ thừa  nhân (chia)  cộng (trừ)
- Đối với biểu thức có ngoặc: ( )  [ ]   
b) Quy tắc dấu ngoặc:
- Khi bỏ dấu ngoặc có trước có dấu “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc
a  b  c  a  b  c
a  b c  a  b c
- Khi bỏ dấu ngoặc có trước có dấu “  ” đằng trước, ta giữ phải đổi dấu các số hạng
trong ngoặc: dấu “+” thành dấu “  ” và dấu “  ” thành dấu “+”
a b  c  a  b c
a b c  a  b  c
6. Biểu diễn thập phân của số hữu tỉ.
- Biểu diễn thập phân của số hữu tỉ: Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn. a
- Biểu diễn thập phân của số hữu tỉ r    b ( , , 0; a a b
b là phân số tối giản)
- Biểu diễn bằng số thập phân hữu hạn: Mẫu b không có ước nguyên tố khác 2 và 5
- Biểu diễn bằng số thập phân vô hạn tuần hoàn: Mẫu b có ước nguyên tố khác 2 và 5. B. BÀI T P
DẠNG 1: THỰC HIỆN PHÉP TÍNH
Bài 1. Thực hiện phép tính 2 1 5 1  2   1 a)  0, 4   b) 3   ( 0  ,5)   . 6 8 2  3  6
Bài 2. Thực hiện phép tính 8 4 1 2 a) 0,3  :  1  1   5 5 3     3 3 5 b) : (0,5) ( 6)    2  8 3  2 1   5 4   1 1  c) 2  4 :  ( 2  ,25)   d) 2 1 : 10 9      3 6   6 9   12 2 
Bài 3. Thực hiện phép tính 3  2 5  9 2 a)     :     . 2 1 4 3 b) 1  .  4  3 9  4      3 4   5 4   3 1  1     7  5 5  c)  6  5    d) 0,8 : 0, 2  8       5 3  3    48  24 16 
Bài 4. Tính một cách hợp lí 31  7 8   1 12 13   79 28  a)     b)         23  32 23   3 67 41  67 41  31  11 11 c) ( 3  0,75)   69,25  ( 6  ,9)   d) ( 34  ,5)  65,5 10  25 25
Bài 5. Chọn dấu "=", "  " thích hợp cho ? 25 25 25 a) 0,8  0,5 ? (0,8  0, ) 5 ; 12 12 12 37 37 37 b) : 5  :14 ? : (5 14) 63 63 63
Bài 6. Các phân số nào sau đây dưới dạng số thập phân hữu và vô hạn tuần hoàn. 1 8 11 5 12 43 7  12 36  153  63 ; ; ; ; ; ; ; ; ; ; 6 25 40 44 9 125 8 75 52 120 210
Bài 7. Viết các số thập phân sau đây dưới dạng phân số tối giản 0, (1) 0, (01) 1, (8) 0, (27) DẠNG 2: TÌM X
Bài 1. Tìm số hữu tỉ x, biết  3  5 5 1 5 2 a) . x     b) 3x   x  c)  : x  1  7  21 3 4 7 7 1 1 2 1 2 3 1 3 d) x   3 : e) x  x   1  0 f)  : x  2 2 7 3 5 7 7 14
Bài 2. Tìm các số nguyên n, m biết: m  1  1 1 8 a)    b) .27n 3n  c)  2  3  81 9 2n 3  2  1 d) 32 .
n 16n  1024 e) 1  n n 1 3 .3 5.3    162 f) n      3  27
DẠNG 3: TOÁN THỰC TẾ
Bài 1. Trong tháng 7 nhà bà Gấm dùng hết 340 số điện. Hỏi bà Gấm phải trả bao nhiêu tiền
điện, biết đơn giá điện như sau:
Giá tiền cho 50 số đầu tiên ( từ số 0 đến số 50) là 1678 đồng/số;
Giá tiền cho 50 số tiếp theo ( từ số 51 đến số 100) là 1734 đồng/số;
Giá tiền cho 100 số tiếp theo ( từ số 101 đến số 200) là 2014 đồng/số.
Giá tiền cho 100 số tiếp theo ( từ số 201 đến số 300) là 2536 đồng/số.
Giá tiền cho 100 số tiếp theo ( từ số 301 đến số 400) là 2834 đồng/số.
Bài 2. Một cửa hàng bán bánh Pizza niêm yết giá tiền như sau: Bánh Pizza iá tiền (đô la) Cỡ to 11,5 $ Cỡ trung bình 8,75 $ Cỡ nhỏ 6,25 $
($ là kí hiệu tền đô la của nước Mĩ, Pizza là món ăn thông dụng của người phương Tây)
Phillip muốn mua 3 cái pizza cỡ to, 2 cái pizza cỡ trung bình và 1 cái pizza cỡ nhỏ. Phillip đưa
cho người bán hàng 100 $. Hỏi người bán hàng phải trả lại cho Phillip bao nhiêu đô la?
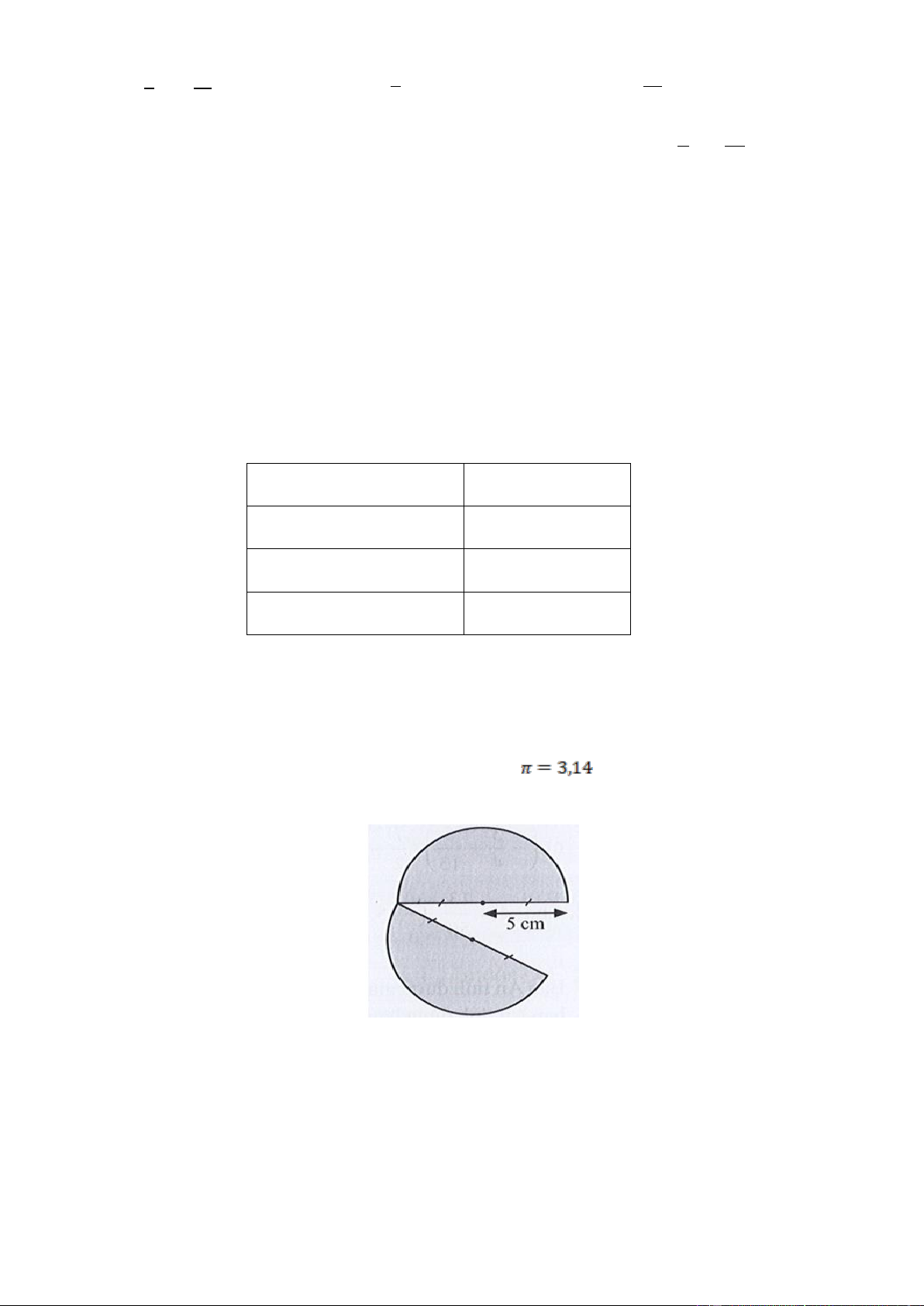
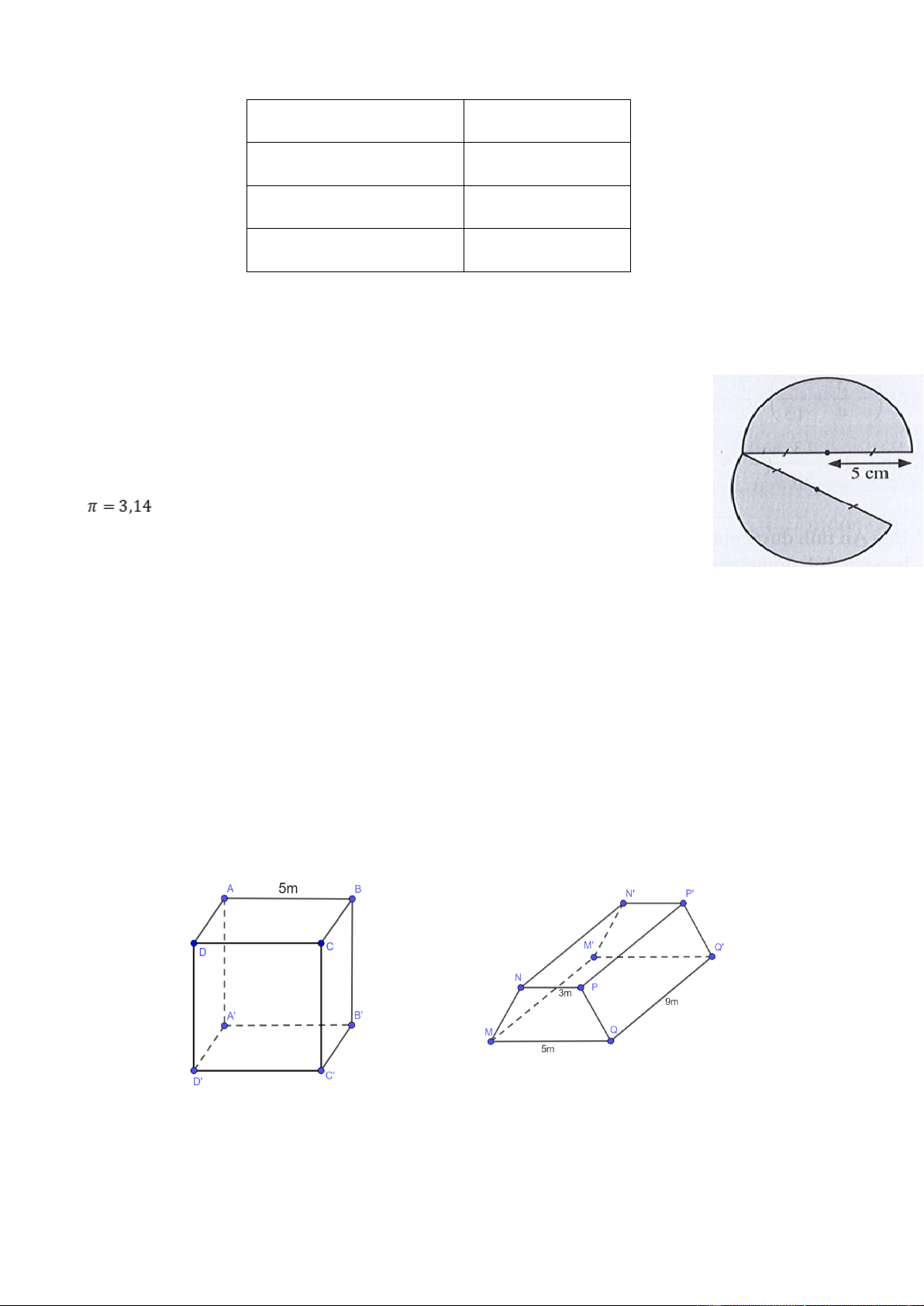
Bài 3. Người ta cắt một tấm tôn có dạng hình tròn bán kính 5cm thành hai phần bằng nhau như
hình dưới. Tính chu vi của tấm tôn sau khi bị cắt (lấy )
Bài 4. Một vườn trường có dạng hình chữ nhật với độ dài hai cạnh là 26 m và 14 m. Người ta
muốn rào xung quanh vườn, cứ cách 2 m đóng một cọc rào, mỗi góc vườn đều đóng một cọc
rào và chỉ để một cửa ra vào vườn rộng 4 m. Tính số cọc rào cần dùng, biết rằng hai cạnh bên
của cửa đồng thời là hai cọc rào.
Bài 5. Ông Phú gửi tiết kiệm 100 triệu đồng tại một ngân hàng với kì hạn một năm, lãi suất 5%
một năm. Hết thời hạn một năm, tiền lãi gộp vào số tiền gửi ban đầu và lại gửi theo thể thức
cũ. Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là bao nhiêu? BÀI T P NÂNG CAO
Bài 1. Tìm x 
để A và tìm giá trị đó x  3 1 2x a) A  b) B  x  2 x  3  Bài 2. Cho 42 x M 
. Tìm số nguyên x để M đạt giá trị nhỏ nhất. x 15 . HÌNH HỌC A. ÓM Ắ LÝ H YẾ
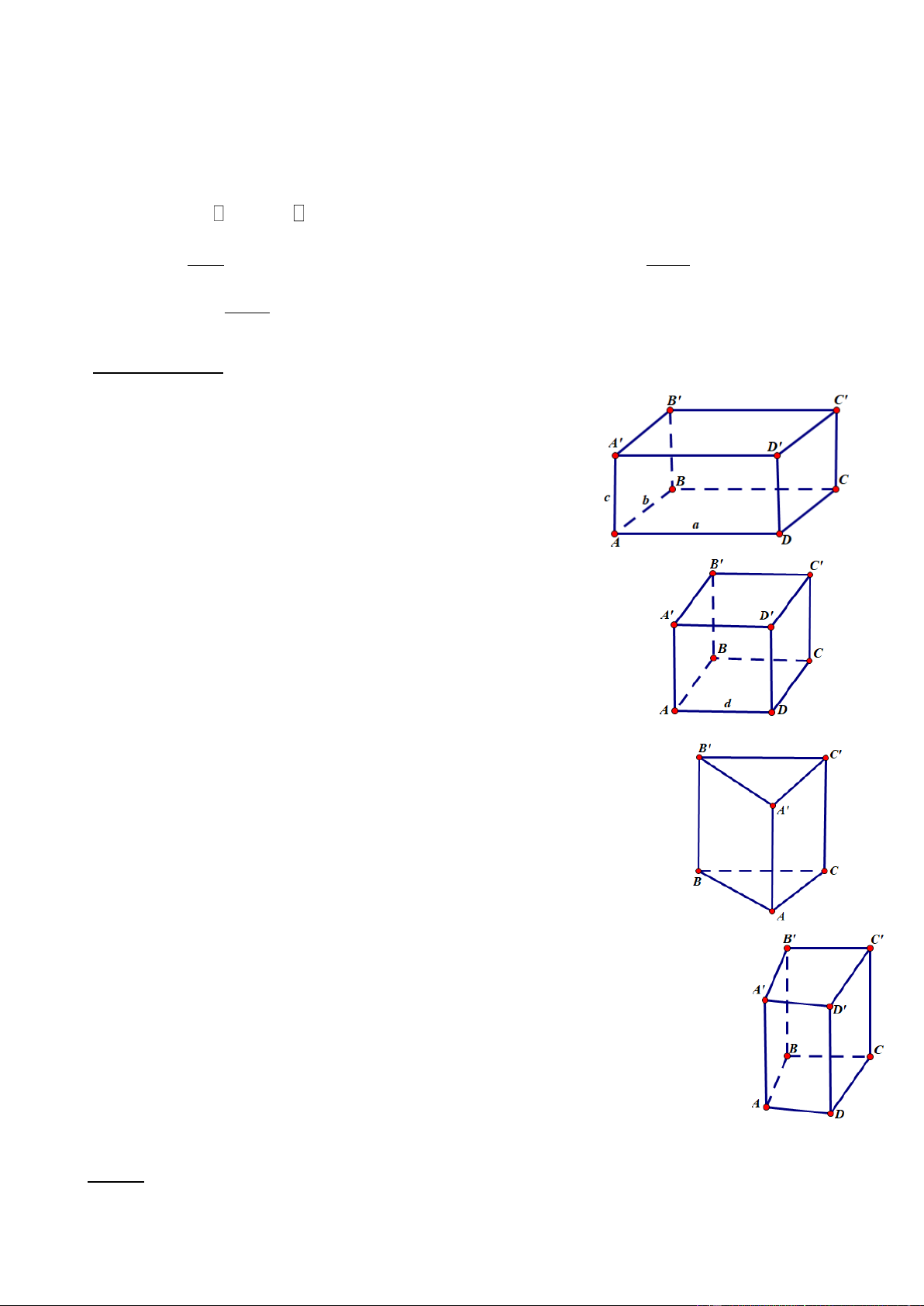
. Hình hộp chữ nhật
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Diện tích xung quanh: S
 2 a  b c xq  
- Thể tích: V  abc . Hình lập phương
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình vuông
- Các cạnh đều bằng nhau - Diện tích xung quanh: 2 S  4d xq - Thể tích: 3 V  d
. Hình lăng trụ đứng tam giác - Có 6 đỉnh
- Có 2 mặt đáy cùng là tam giác và song song với nhau, 3 mặt bên là các hình chữ nhật.
- Các cạnh bên bằng nhau
- Chiều cao là độ dài một cạnh bên.
V. Hình lăng trụ đứng tứ giác - Có 8 đỉnh
- Có 2 mặt đáy cùng là tứ giác và song song với nhau, 4 mặt bên là các hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao là độ dài một cạnh bên.
Chú ý: Hình hộp chữ nhật cũng là một hình lăng trụ đứng tứ giác
iện tích xung quanh. hể tích của hình lăng trụ:
Diện tích xung quanh = chu vi đáy . chiều cao
Thể tích = diện tích đáy . chiều cao
Chú ý: Diện tích toàn phần của hình lăng trụ đứng được tính bởi công thức: S  S  2S tp xq d B. BÀI T P
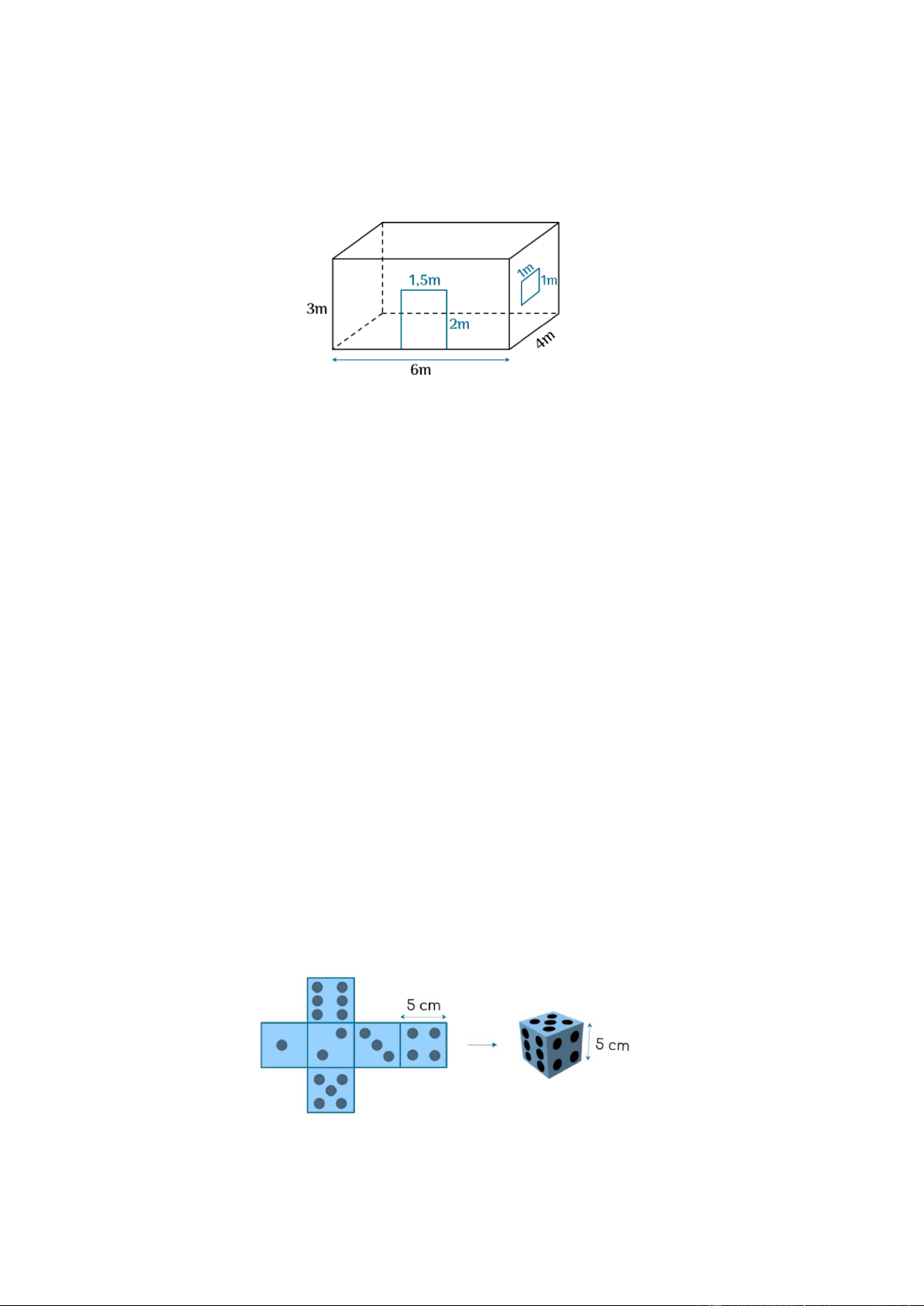
Bài 1: Căn phòng của anh Nam có một cửa lớn hình chữ nhật và một cửa sổ hình vuông với
kích thước như hình vẽ:
Anh Nam cần tốn bao nhiêu tiền để sơn bốn bức tường xung quanh của căn phòng này (không
sơn cửa)? Biết rằng để sơn mỗi mét vuông phải tốn 50 nghìn đồng. Lời giải
Diện tích xung quanh của căn phòng là: 2
2.(6  4).3  60 (m )
Diện tích của cửa lớn và cửa sổ là: 2
2.1,5  1.1  4 (m )
Diện tích cần phải sơn là: 2 60  4  56 (m )
Chi phí cần để sơn là:
56 . 50000  2800000 (đồng)
Bài 2. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có diện tích đáy 2 S
 24 cm và có thể tích ABCD 3
V  84 cm . Chiều cao của hình hộp chữ nhật có độ dài là?
Bài 3. Cho hình lập phương có diện tích một mặt bên là 2
81 cm . Tính thể tích của hình lập phương?
Bài 4. Cho hình lăng trụ đứng tam giác có độ dài ba cạnh đáy là 4 c , m 4 c ,
m 6 cm . Biết diện tích xung quanh bằng 2
98 cm . Tính chiều cao của hình lăng trụ?
Bài 5. Bạn Thục Anh làm một con xúc xắc hình lập phương từ tấm bìa có kích thước như hình vẽ.
Diện tích tấm bìa tạo thành con xúc xắc đó là bao nhiêu ? Lời giải
Diện tích tấm bìa tạo thành con xúc xắc đó là: 2 2 2 2
4.5  2.5  6.5  150 (cm ).
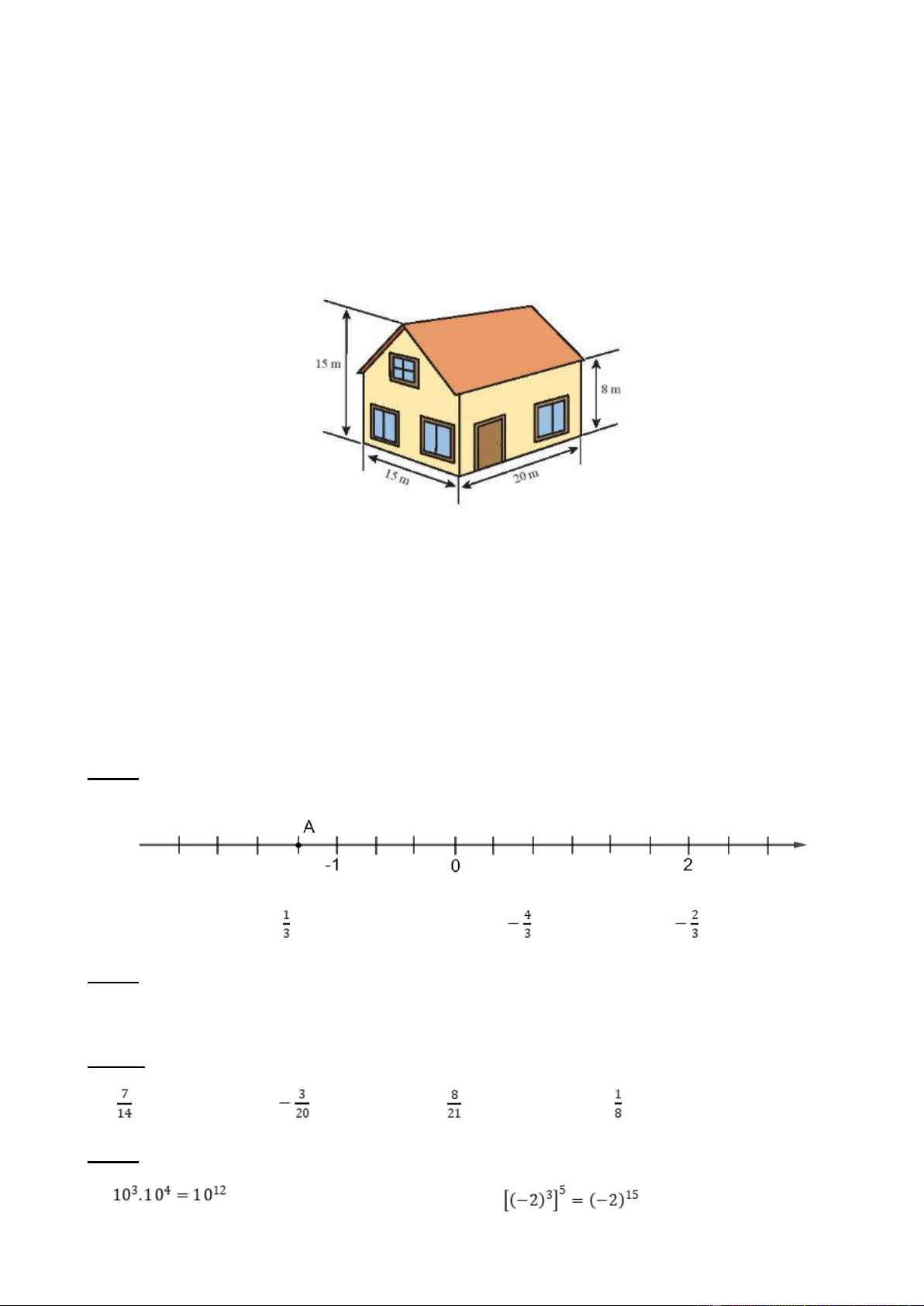
Bài 6. Một ngôi nhà có kích thước như hình vẽ.
a) Tính thể tích của ngôi nhà.
b) Biết rằng 1 l sơn bao phủ được 2
4 m tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn
phủ được tường mặt ngoài ngôi nhà? (không sơn cửa)? Biết tổng diện tích các cửa là 2 9 m .
III. BÀI T P THAM KHẢO A. TRẮC NGHIỆM
Hãy khoanh tròn vào chữ cái đứng trước câu trả lời đúng:
Câu 1: Trên trục số dưới đây, điểm A biểu diễn số hữu tỉ nào? A. 4. B. . C. D.
Câu 2: Với x là số hữu tỉ khác 0, tích x6.x2 bằng: A. x 12 B. x9 : x C. x6 + x2 D. x10 – x2
Câu 3: Phân số không viết được dưới dạng số thập phân hữu hạn là: A. B. C. D.
Câu 4: Trong các đẳng thức sau, đẳng thức nào là đúng? A. B. C. D.
Câu 5: Giá trị của thoả mãn A. B. C. D.
Câu 6: Bác Hà mua các loại rau của nhà hàng VIET TASTE để chuẩn bị nấu ăn liên hoan cuối
năm với bảng giá như sau: Số lượng Giá đơn vị STT Loại hàng (kg) (đồng/kg) 1 Bắp cải 1 8 000 2 Giá đỗ 1,5 25 000 3 Rau ngót 0,5 12 000 4 Rau muống 2,5 9 000
Hỏi bác Hà mua các loại rau hết bao nhiêu tiền? A. 74 000 đồng B. 74 500 đồng C. 63 500 đồng D. 51 500 đồng
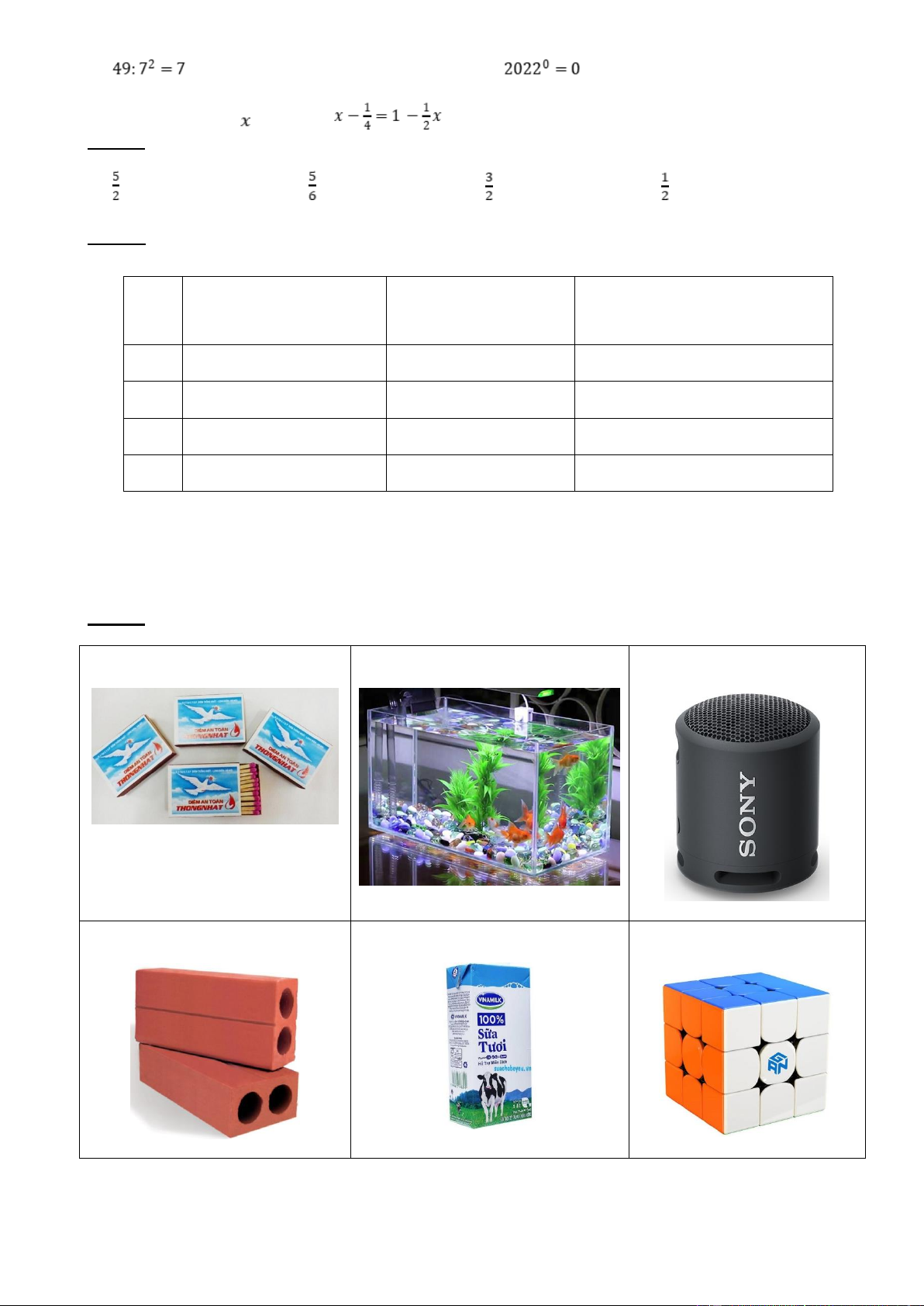
Câu 7: Quan sát các vật dưới đây. Đồ vật ở hình nào có dạng hình hộp chữ nhật? Hình 1 Hình 2 Hình 3 Hình 4 Hình 5 Hình 6 A. Hình 1; 2; 3; 4; 5 C. Hình 1; 2; 4; 5; 6 B. Hình 1; 2; 4; 5 D. Hình 6
Câu 8: Quan sát các vật dưới đây và cho biết đồ vật ở hình nào có dạng hình lăng trụ tam giác? Hình 1 Hình 2 Hình 3 Hình 4 Hình 5 Hình 6 A. Hình 1; 2; 4; 5 C. Hình 1; 2; 4; 5; 6 B. Hình 1; 4; 5 D. Hình 1; 4; 5; 6
Câu 9: Trong các khẳng định sau, khẳng định nào đúng?
A. Hình hộp chữ nhật có 6 mặt là hình chữ nhật, 4 đỉnh, 8 cạnh.
B. Hình lập phương có 6 mặt là hình vuông, 12 cạnh bằng nhau.
C. Hình lăng trụ đứng tam giác 6 mặt với mặt đáy là hình tam giác và 9 cạnh.
D. Hình lăng trụ đứng tứ giác có các mặt bên là hình chữ nhật, có 8 đỉnh và 8 cạnh.
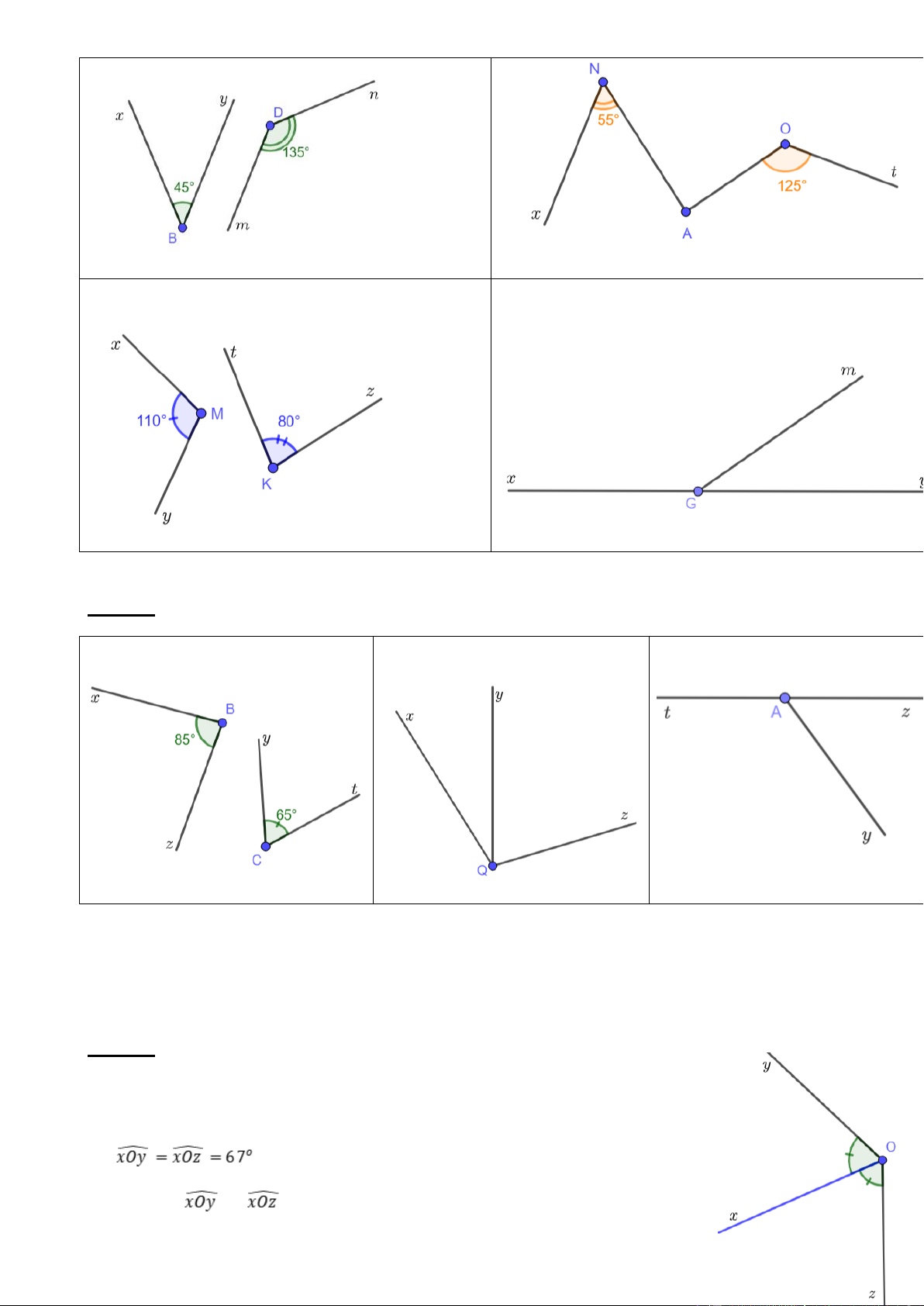
Câu 10: Hình nào dưới đây có 2 góc không bù nhau? A. B. C. D.
Câu 11: Hình nào dưới đây có 2 góc kề nhau nhưng không bù nhau? Hình a Hình b Hình c
A. Cả ba hình a, b, c B. Hình b C. Hình a D. Hình b và c
Câu 12: Cho góc yOz có số đo 1340 , biết Ox là tia phân giác của góc
yOz. Trong các khẳng định sau, khẳng định nào là sai ?
A. Tia Ox nằm trong góc yOz B. C. Hai góc và là hai góc kề nhau
D. Tia Oy là cạnh chung của hai góc kề nhau và B.Tự luận
Dạng 1: Thực hiện các phép tính
1. Tính giá trị của các biểu thức sau:  1 2 12   5  1  12 5 1  2 1 1 a) A  2          ; b) B  .  .  .12 ;  5 7 13   7 13  17 7 17 7 17.7 c) d) e)
2. Tính giá trị của các biểu thức sau: 3 2 40 29  2    2   2 .3 a) C  :  .     b) 13 15  3   3  8 .9 Dạng 2: Tìm x
3. Tìm số hữu tỉ x, biết  3  5 5 1 5 2 g) . x     h) 3x   x  i)  : x  1  7  21 3 4 7 7 1 1 2 1 2 3 1 3 j) x   3 :
k) x   x   1  0 l)  : x  2 2 7 3 5 7 7 14
4. Tìm các số nguyên n, m biết: m  1  1 1 8 g)    h) .27n 3n  i)  2  3  81 9 2n 3  2  1 j) 32 .
n 16n  1024 k) 1  n n 1 3 .3 5.3    162 l) n      3  27
5. Tìm số tự nhiên n sao cho: a) b) c)
Dạng 3. Toán thực tế.
Bài 1. Trong tháng 7 nhà bà Gấm dùng hết 340 số điện. Hỏi bà Gấm phải trả bao nhiêu tiền
điện, biết đơn giá điện như sau:
Giá tiền cho 50 số đầu tiên ( từ số 0 đến số 50) là 1678 đồng/số;
Giá tiền cho 50 số tiếp theo ( từ số 51 đến số 100) là 1734 đồng/số;
Giá tiền cho 100 số tiếp theo ( từ số 101 đến số 200) là 2014 đồng/số.
Giá tiền cho 100 số tiếp theo ( từ số 201 đến số 300) là 2536 đồng/số.
Giá tiền cho 100 số tiếp theo ( từ số 301 đến số 400) là 2834 đồng/số.
Bài 2. Một cửa hàng bán bánh Pizza niêm yết giá tiền như sau: Bánh Pizza Giá tiền Cỡ to 11,5 $ Cỡ trung bình 8,75 $ Cỡ nhỏ 6,25 $
($ là kí hiệu tền đô la của nước Mĩ, Pizza là món ăn thông dụng của người phương Tây)
Phillip muốn mua 3 cái pizza cỡ to, 2 cái pizza cỡ trung bình và 1 cái pizza
cỡ nhỏ. Phillip đưa cho người bán hàng 100 $. Hỏi người bán hàng phải trả
lại cho Phillip bao nhiêu đô la?
Bài 3. Người ta cắt một tấm tôn có dạng hình tròn bán kính 5cm thành hai
phần bằng nhau như hình dưới. Tính chu vi của tấm tôn sau khi bị cắt (lấy )
Bài 4. Một vườn trường có dạng hình chữ nhật với độ dài hai cạnh là 26 m
và 14 m. Người ta muốn rào xung quanh vườn, cứ cách 2 m đóng một cọc
rào, mỗi góc vườn đều đóng một cọc rào và chỉ để một cửa ra vào vườn rộng 4 m. Tính số cọc
rào cần dùng, biết rằng hai cạnh bên của cửa đồng thời là hai cọc rào.
Bài 5. Ông Phú gửi tiết kiệm 100 triệu đồng tại một ngân hàng với kì hạn một năm, lãi suất 5%
một năm. Hết thời hạn một năm, tiền lãi gộp vào số tiền gửi ban đầu và lại gửi theo thể thức
cũ. Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là bao nhiêu?
Dạng 5: Hình học
16. Cho các hình dưới đây với các kích thước ghi trên hình vẽ. Tính diện tích xung quanh và thể tích của
a) Hình lập phương ABCD.A’B’C’D’
b) Hình lăng trụ đứng tứ giác MNPQ.M’N’P’Q’. Biết đáy MNPQ là hình thang cân có độ dài 2
cạnh MQ=5m, NP=3m và chiều cao hình thang là 2,83m.
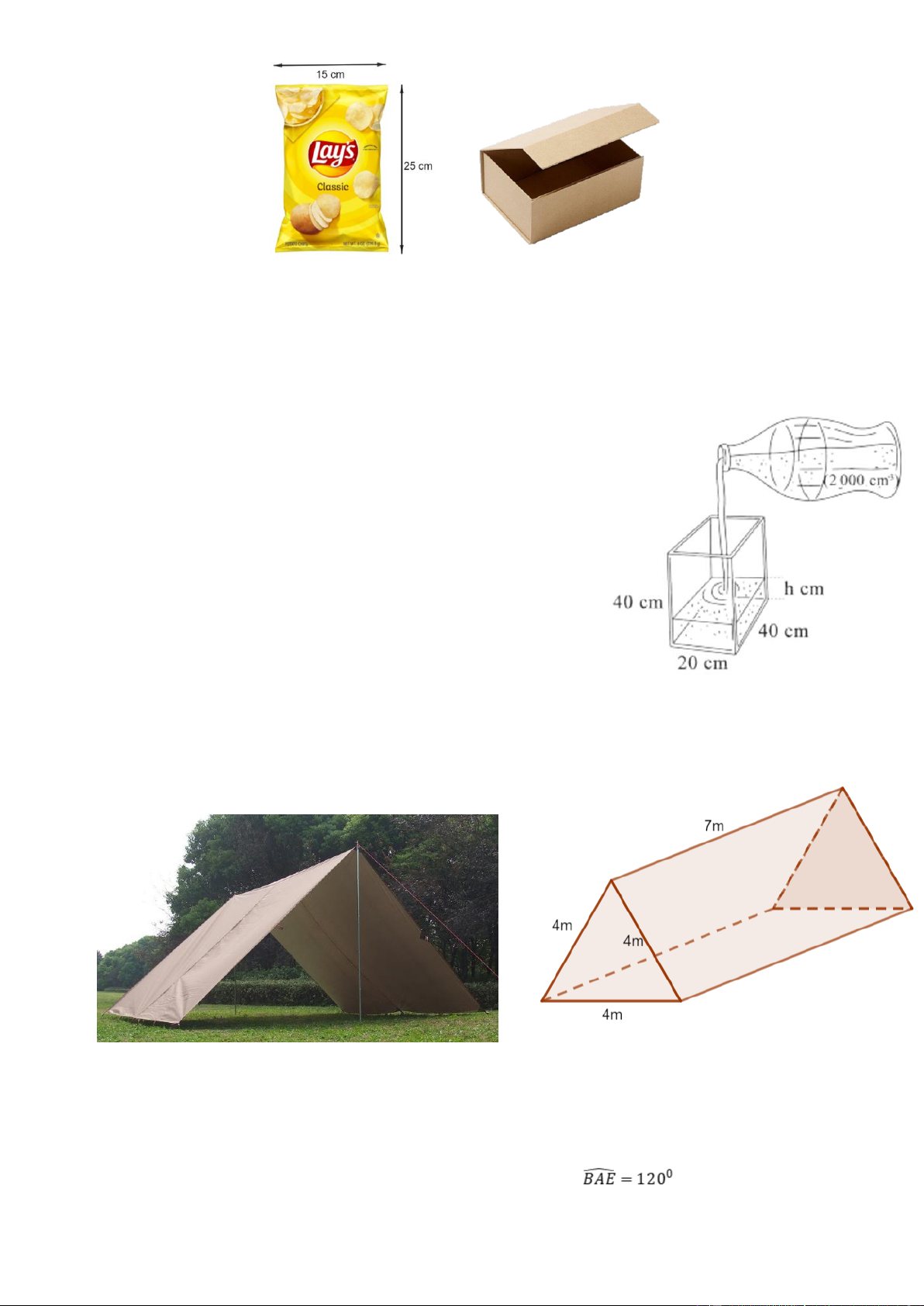
17. Nam mua một gói bimbim Lays vị truyền thống với bao bì có kích thước như hình vẽ dưới đây:
Hỏi nếu Nam làm một hộp (dạng hình hộp chữ nhật, có nắp) để đựng các gói bimbim hằng ngày, thì
a) Kích thước (chiều dài, chiều rộng, chiều cao) của chiếc hộp là bao nhiêu?
b) Diện tích giấy bìa để làm hộp là bao nhiêu? (các mép bìa dính vào nhau coi như không đáng kể)
c) Thể tích của chiếc hộp là bao nhiêu?
18. Một cái bể hình hộp chữ nhật và một cái chai có kích
thước và thể tích như hình bên.
a) Tính thể tích của bể
b) Tính chiều cao mực nước khi rót hết một chai nước vào bể
c) Nếu rót đầy bể thì cần bao nhiêu chai nước?
d) Biết giá kính làm bể cá là 95 320 đồng/1 m2. Hỏi bác Hà
mua bể cá hết bao nhiêu tiền? (bể cá không có nắp đậy)
19. Trong buổi học kỹ năng sống ở Sóc Sơn, các bạn lớp 7A đã được hướng dẫn cách dựng lều
chữ A (dạng hình lăng trụ đứng có đáy là tam giác đều) từ một tấm vải bạt cho trước.
a) Tính diện tích vải bạt cần sử dụng để làm hai mái và trải đáy của lều, biết kích thước lều như sau:
b) Nếu giáo viên lớp chuẩn bị được tấm vải bạt dài 15m rộng 7m thì tấm vải bạt cần thêm diện
tích là bao nhiêu đủ để làm hai mái và trải đáy của lều?
20. Hai đường thẳng BD và CE cắt nhau tại A, tạo thành góc như hình vẽ sau: Quan sát hình vẽ và hãy
a) Kể tên các góc kề nhau, bù nhau, phụ nhau.
b) Kể tên các góc đối đỉnh. c) Tính số đo góc của .
d) Vẽ tia phân giác Am của . Hỏi tia AE
có phải tia phân giác của không? Vì sao?