Đề cương ôn tập hóa 12 (trắc nghiệm và trả lời ngắn có đáp án)

Dạng 1. Câu hỏi trắc nghiệm nhiều lựa chọn
Câu 1: Loại đường nào sau đây có nhiều trong các loại nước tăng lực ? A. fructose. B. cellulose. C. glucose. D. saccharose. Đáp án: C. glucose.
Vì Glucose là một loại đường đơn giản, dễ hấp thụ và cung cấp năng lượng nhanh chóng, do đó
nó thường được sử dụng trong các loại nước tăng lực để cung cấp năng lượng tức thời.
Câu 2: Hợp chất nào sau đây chiếm thành phần nhiều nhất trong mật ong ? A. glucose. B. fructose. C. cellulose. D. saccharose. Đáp án: B. fructose.
Vì Fructose (đường фруктоза) là một loại đường tự nhiên có nhiều trong trái cây và mật ong.
Mật ong chứa chủ yếu là fructose và glucose, nhưng fructose thường chiếm tỷ lệ cao hơn, tạo
nên vị ngọt đậm của mật ong.
Câu 3: Mô tả nào dưới đây không đúng với glucose ?
A. Chất rắn, khó tan trong nước và có vị ngọt.
B. Có mặt trong hầu hết các bộ phận của cây, nhất là trong quả chín.
C. Còn có tên gọi là đường nho.
D Có 80-130mg/dL trong máu người trưởng thành, khỏe mạnh và lúc đói.
Đáp án: A. Chất rắn, khó tan trong nước và có vị ngọt. (Glucose thực tế dễ tan trong nước).
Vì Glucose là chất rắn, tan tốt trong nước và có vị ngọt. Nó có mặt trong hầu hết các bộ phận
của cây, đặc biệt là trong quả chín, và còn được gọi là đường nho. Nồng độ glucose trong máu
người trưởng thành khỏe mạnh dao động từ 80-130mg/dL khi đói. Vì vậy, mô tả "chất rắn, khó
tan trong nước" là không chính xác. 𝑎𝑠𝑚𝑡
Câu 4: Phương trình: 6𝑛𝐶𝑂2 + 5𝑛𝐻2𝑂𝑐ℎ𝑟𝑜𝑙𝑜𝑝ℎ𝑦 𝐼𝐼 (𝐶6𝐻10𝑂5)𝑛 + 6𝑛𝑂2 là phản ứng hoá học
chính của quá trình nào sau đây?
A. quá trình hô hấp.
B. quá trình quang hợp. C. quá trình khử.
D. quá trình oxi hoá.
Đáp án: B. quá trình quang hợp.
Vì phương trình hóa học cho thấy quá trình quang hợp, trong đó cây xanh sử dụng năng lượng
ánh sáng (asmt) và chất diệp lục (chlorophyll) để chuyển đổi carbon dioxide và nước thành
carbohydrate (tinh bột) và oxygen.
Câu 5. Công dụng quan trọng nhất của xà phòng là A. làm nhiên liệu. B. tẩy rửa. C. làm đẹp. D. chất phụ gia. Đáp án: B. tẩy rửa.
Vì công dụng quan trọng nhất của xà phòng là tẩy rửa, nhờ khả năng làm giảm sức căng bề mặt
của nước, giúp loại bỏ bụi bẩn và dầu mỡ. 2
Câu 6. Trong cơ thể chất béo bị oxygen hóa thành các chất nào sau đây ? A. NH3 và CO2. B. H2O và CO2. C. NH3 và H2O. D. NH3, CO2 và H2O. Đáp án: B. H2O và CO2
Trong cơ thể lipit bị oxi hóa thành H2O và CO2
Nhờ những phản ứng sinh hóa phức tạp, chất béo bị oxi hóa chậm tạo thành CO2, H2O và
cung cấp năng lượng cho cơ thể. Chất béo chưa sử dụng đến được tích lũy trong các mô mỡ.
Câu 7. Dầu mỡ (thực phẩm) để lâu bị ôi thiu là do
A. chất béo bị vữa ra.
B. chất béo bị thủy phân với nước trong không khí.
C. bị vi khuẩn tấn công.
D. chất béo bị oxi hóa chậm bởi oxygen không khí
Dấu mỡ bị ôi là do nối đôi C=C trong gốc axit của chất béo bị oxi hóa chậm bởi oxi không
khí tạo thành peoxit, chất này sẽ bị phân hủy thành các anđehit có mùi khó chịu
Câu 8. Không nên dùng xô, chậu bằng nhôm (aluminium) để đựng quần áo ngâm xà phòng vì
A. quần áo bị mục nhanh.
B. quần áo bị bạc màu nhanh.
C. quần áo không sạch.
D. xô chậu nhanh hỏng do trong xà phòng có base.
Đáp án: D. Xô chậu nhanh hỏng do trong xà phòng có base.
Vì xà phòng thường có tính base. Nhôm (aluminium) có thể phản ứng với base, dẫn đến việc xô
chậu bị ăn mòn và nhanh hỏng. Do đó, không nên dùng xô chậu nhôm để đựng quần áo ngâm xà phòng
Câu 9: Chất có nhiều trong khói thuốc lá gây hại cho sức khoẻ con người là A. cocaine. B. nicotine C. heroine D. cafein. Đáp án: B. Nicotine
Vì Nicotine là một chất gây nghiện có trong thuốc lá, được hấp thụ vào máu và ảnh hưởng đến
não bộ trong khoảng 10 giây sau khi hút vào. Sau mỗi lần hít một hơi thuốc lá, Nicotine gây
tăng nhịp đập của tim, co thắt mạch máu ở tim, tăng mạch và huyết áp.
Câu 10. Khi nấu canh cua thì thấy các mảng "riêu cua" nổi lên là do
A. phản ứng thủy phân của protein.
B. sự đông tụ của protein bởi nhiệt độ.
C. phản ứng màu của protein.
D. sự động tụ của lipid.
Đáp án: B. Sự đông tụ của protein bởi nhiệt độ.
Khi nấu canh cua, riêu cua nổi lên là do protein trong thịt cua bị đông tụ bởi nhiệt độ. Quá
trình này làm cho các protein kết lại với nhau, tạo thành mảng riêu
Câu 11. Một người thợ xây trong buổi sáng kéo được 500kg vật liệu xây dựng lên tầng
cao 10m. Để bù vào năng lượng đã tiêu hao, người đó cần uống cốc nước hoàn tan m
gam glucose. Biết nhiệt lượng tỏa ra khi oxi hóa hoàn toàn glucose C6H12O6 thành CO2
và H2O là 2804,8 kJ.. Giá trị của m là 3 A. 31,20 B. 3,15 C. 0,32 D. 314,7 Đáp án: B. 3,15 Giải
- Năng lượng mà người thợ xây đã tiêu hao: E  mgh  500.9,8.10  49000 J   49kJ
- Biết rằng nhiệt lượng tỏa ra khi oxi hóa hoàn toàn glucose là 2804,8 kJ. Vậy, để bù đắp
năng lượng đã tiêu hao (49 kJ), ta cầ 49
n một lượng glucose là m  .180  3,15 g  2804,8
Câu 12. Để giải thích hiện tượng khi nhúng chiếc đũa vào cốc nước thì thấy đũa như bị
gãy ở mặt nước, sử dụng kiến thức liên quan đến lĩnh vực nào? A. Hóa học B. Vật lí C. Sinh học D. Khoa học Trái Đất
Đáp án: B. Vật lí (hiện tượng khúc xạ ánh sáng).
Hiện tượng chiếc đũa bị "gãy" khi nhúng vào nước là do khúc xạ ánh sáng. Ánh sáng truyền từ
môi trường này sang môi trường khác bị thay đổi hướng, gây ra ảo giác về sự gãy khúc
Câu 13. Việc sản xuất xe máy điện là ứng dụng thuộc lĩnh vực nào của khoa học tự nhiên? A. Vật lý và Hóa học B. Sinh học C. Thiên văn học D. Khoa học Trái Đất
Đáp án: A. Vật lý và Hóa học.
Sản xuất xe máy điện liên quan đến cả vật lý (động cơ điện, điện từ trường, cơ học) và hóa học
(pin, vật liệu chế tạo)
Câu 14 . Ai là người phát triển thuyết tiến hóa bằng chọn lọc tự nhiên, đánh dấu bước
ngoặt trong sinh học hiện đại? 4 A. Mendel B. Darwin C. Linnaeus D. Pasteur Đáp án: B. Darwin
Thuyết tiến hóa của Charles Darwin được công bố lần đầu tiên vào năm 1859 trong cuốn sách
nổi tiếng mang tên Nguồn gốc các loài (On the Origin of Species). Trong cuốn sách này, Darwin
giới thiệu khái niệm chọn lọc tự nhiên, giải thích cách mà các loài phát triển và thích ứng qua
thời gian dựa trên biến thể tự nhiên.
Câu 15. Thành tựu nào trong khoa học tự nhiên cổ đại đã giúp con người dự đoán thời tiết và mùa vụ?
A. Định luật vạn vật hấp dẫn B. Lịch thiên văn C. Thuyết nguyên tử D. Máy hơi nước
Đáp án: B. Lịch thiên văn
Lịch thiên văn giúp con người dự đoán thời tiết và mùa vụ thông qua việc quan sát và ghi chép
các hiện tượng thiên văn, từ đó tìm ra quy luật và dự báo. Dưới đây là một số cách thức chính:
 Quan sát chu kỳ của Mặt Trời, Mặt Trăng và các hành tinh:
o Mặt Trời: Vị trí của Mặt Trời trên bầu trời trong năm (ví dụ: điểm phân, điểm chí) liên
quan trực tiếp đến sự thay đổi của các mùa. Bằng cách theo dõi chu kỳ này, người xưa
có thể biết được thời điểm bắt đầu và kết thúc của các mùa, từ đó dự đoán thời tiết.
o Mặt Trăng: Các pha của Mặt Trăng (trăng non, trăng lưỡi liềm, trăng tròn, v.v.) cũng
liên quan đến chu kỳ thời tiết. Một số nền văn hóa cổ đại sử dụng chu kỳ Mặt Trăng để
xác định thời điểm gieo trồng và thu hoạch.
o Các hành tinh: Mặc dù ít được sử dụng hơn, vị trí của các hành tinh đôi khi được cho là
có ảnh hưởng đến thời tiết. Ví dụ, sự liên kết của các hành tinh có thể được sử dụng để
dự đoán các hiện tượng thời tiết bất thường.
 Xác định các dấu hiệu thời tiết:
o Dấu hiệu trên bầu trời: Màu sắc của bầu trời, sự xuất hiện của cầu vồng, quầng mặt trời,
vầng hào quang quanh Mặt Trăng, v.v. đều có thể là dấu hiệu của thời tiết sắp tới.
o Dấu hiệu từ động vật và thực vật: Hành vi của động vật (ví dụ, chim di cư, kiến làm tổ),
sự nở hoa của thực vật, sự thay đổi màu sắc của lá cây, v.v. cũng có thể được sử dụng
để dự đoán thời tiết.
 Xây dựng lịch nông nghiệp:
o Bằng cách kết hợp các quan sát thiên văn với các dấu hiệu thời tiết, người xưa đã xây
dựng các lịch nông nghiệp. Những lịch này chia năm thành các khoảng thời gian khác
nhau (ví dụ: 24 tiết khí ở Việt Nam) và chỉ ra thời điểm thích hợp cho các hoạt động
nông nghiệp khác nhau (gieo trồng, chăm sóc, thu hoạch).
Ví dụ, ở Việt Nam, lịch 24 tiết khí dựa trên chuyển động của Mặt Trời trong năm. Mỗi tiết khí
(ví dụ: Lập Xuân, Vũ Thủy, Thanh Minh, v.v.) đại diện cho một giai đoạn thời tiết và ảnh hưởng
đến các hoạt động sản xuất nông nghiệp. Người nông dân sử dụng lịch này để xác định thời
điểm gieo trồng, bón phân, và thu hoạch các loại cây trồng.
Câu 17. Thời kỳ nào đánh dấu sự chuyển đổi từ triết lý tự nhiên sang khoa học tự nhiên
hiện đại dựa trên thực nghiệm?
A. Thời cổ đại Hy Lạp B. Trung cổ C. Phục Hưng
D. Cách mạng Công nghiệp Đáp án: C. Phục Hưng
Lý do:,Thời kỳ Phục Hưng (thế kỷ XIV-XVII) là giai đoạn lịch sử quan trọng, khi những nhà 5
khoa học bắt đầu áp dụng các phương pháp quan sát và thực nghiệm để tìm hiểu tự nhiên, thay
vì dựa vào tư duy triết học suy diễn.
Câu 18. Nhà khoa học là:
A. Người sử dụng các sản phẩm ứng dụng của nghiên cứu khoa học
B. Người thực hiện nghiên cứu khoa học
C. Người ứng dụng nghiên cứu khoa học
D. Cả ba đáp án trên đều đúng
Đáp án: D. Cả ba đáp án trên đều đúng
Lý do: Nhà khoa học không chỉ giới hạn là người nghiên cứu, mà còn là người ứng dụng kết quả
nghiên cứu và tạo ra sản phẩm khoa học.
Câu 19. Mô hình toán học nào thường được sử dụng để mô tả sự tăng trưởng của quần
thể vi khuẩn trong môi trường có giới hạn tài nguyên? A. Mô hình tuyến tính B. Mô hình lũy thừa
C. Mô hình logistic D. Mô hình bậc hai
Đáp án: B. Mô hình lũy thừa
Lý do: Sự tăng trưởng của quần thể vi khuẩn trong môi trường tài nguyên hạn chế thường được
mô tả bằng mô hình lũy thừa (thể hiện sự phát triển theo cấp số nhân trong giai đoạn đầu).
Câu 20. Khoa học tự nhiên bao gôm những lĩnh vực chính nào?
A. Vật lí, Sinh học, Thiên văn học, Hóa học, Văn học.
B. Vật lí, Sinh học, Thiên văn học, Khoa học Trái Đất, Hóa học.
C. Vật lí, Sinh học, Toán học, Hóa học, Tiếng anh.
D. Hóa học, Sinh học, Khoa học Trái Đất, Toán học, Lịch sử.
Đáp án: B. Vật lí, Sinh học, Thiên văn học, Khoa học Trái Đất, Hóa học
Lý do: Đây là các lĩnh vực chính cấu thành khoa học tự nhiên, mang tính đặc thù về nghiên cứu
hiện tượng trong tự nhiên.
Câu 21. Theo em việc sử dụng năng lượng gió để sản xuất điện thể hiện vai trò nào
dưới đây của khoa học tự nhiên?
A. Hoạt động nghiên cứu khoa học.
B. Nâng cao nhận thức của con người về thế giới tự nhiên.
C. ứng dụng công nghệ vào cuộc sống, sản xuất, kinh doanh.
D. Chăm sóc sức khỏe con người.
Đáp án: C. Ứng dụng công nghệ vào cuộc sống, sản xuất, kinh doanh.
Lý do: Sử dụng năng lượng gió để sản xuất điện là một ứng dụng sản xuất dựa trên những tiến
bộ khoa học, phục vụ đời sống con người.
Câu 22. Mô hình tăng trưởng chiều cao của một cây cho thấy cây cao thêm 0,25 m mỗi
năm. Nếu ban đầu cây cao 1 m, sau 3 năm chiều cao là bao nhiêu? A. 1,25 m B. 1,5 m C. 1,75 m D. 2,0 m Đáp án: C. 1,75 m Lý do:
 Tăng trưởng: 0,25×3=0,75 m
 Tổng chiều cao: 1+0,75=1,75 m
Câu 23. Ai được mệnh danh là “cha đẻ” của phương pháp thực nghiệm vật lí. A. Newton. B. Aristotle. C. Galilei. D. Einstein. Đáp án: A. Newton 6
Lý do: Có một số lý do chính khiến Isaac Newton được mệnh danh là "cha đẻ" của phương
pháp thực nghiệm vật lý:
 Kết hợp lý thuyết và thực nghiệm: Trước Newton, nhiều nhà khoa học có xu hướng tập
trung vào lý thuyết hoặc thực nghiệm một cách riêng rẽ. Newton đã kết hợp cả hai một cách
chặt chẽ, sử dụng thí nghiệm để kiểm chứng và phát triển các lý thuyết của mình, đồng thời
sử dụng lý thuyết để giải thích các kết quả thí nghiệm.
 Định lượng và toán học hóa: Newton đã sử dụng toán học để mô tả và phân tích các hiện
tượng vật lý một cách chính xác và định lượng. Điều này cho phép ông đưa ra các dự đoán
có thể kiểm chứng bằng thí nghiệm, một đặc điểm quan trọng của phương pháp khoa học hiện đại.
 Các thí nghiệm có hệ thống và kiểm soát: Newton đã thiết kế và thực hiện các thí nghiệm
một cách có hệ thống và kiểm soát, thay đổi các biến số một cách cẩn thận và ghi lại kết quả
một cách chi tiết. Điều này giúp ông xác định các mối quan hệ nhân quả giữa các hiện tượng.
 Ảnh hưởng to lớn: Các công trình của Newton, đặc biệt là Philosophiæ Naturalis Principia
Mathematica (Các nguyên lý toán học của triết học tự nhiên), đã có ảnh hưởng to lớn đến sự
phát triển của vật lý và khoa học nói chung. Phương pháp luận của ông đã trở thành tiêu
chuẩn cho các nhà khoa học sau này.
Mặc dù Newton không phải là người đầu tiên sử dụng thực nghiệm trong khoa học, nhưng
ông đã hệ thống hóa và hoàn thiện phương pháp này, đồng thời chứng minh sức mạnh của nó
thông qua các khám phá vĩ đại của mình. Vì vậy, việc ông được mệnh danh là "cha đẻ" của
phương pháp thực nghiệm vật lý là hoàn toàn xứng đáng .
Câu 24. Sự kiện nào sau đây là cở sở cho cuộc cách mạng công nghiệp lần thứ nhất?
A. Galilei làm thí nghiệm tại tháp nghiên Pisa. B. Joule tìm ra các định luật nhiệt động lực học.
C. Faraday tìm ra hiện tượng cảm ứng điện từ. D. Einstein xây dựng thuyết tương đối.
Đáp án: B. Joule tìm ra các định luật nhiệt động lực học.
Lý do: Các phát minh về nhiệt động lực học và năng lượng là nền tảng cho sự phát triển
máy móc trong cuộc cách mạng công nghiệp.
Câu 25. Kiến thức về từ trường Trái Đất được dùng để giải thích đặc điểm nào của loài chim di trú?
A. Xác định hướng bay. B. Làm tổ. C. Sinh sản. D. Kiếm ăn.
Đáp án: A. Xác định hướng bay.
Lý do: Nhiều loài chim sử dụng từ trường Trái Đất để định hướng trong hành trình di trú.
Câu 26. Thành tựu Vật lí nào sau đây gắn với giai đoạn Vật lí cổ điển?
A. Planck xây dựng thuyết lượng tử năm 1900. 7
B. Einstein xây dựng thuyết tương đối năm 1905.
C. Năm 350 TCN, Aristotle dựa vào quan sát cho rằng vật nặng rơi nhanh hơn vật nhẹ.
D. Năm 1687, Newton công bố các nguyên lý Toán học của Triết học tự nhiên.
Đáp án: D. Năm 1687, Newton công bố các nguyên lí Toán học của Triết học tự nhiên.
Lý do: Đây là tác phẩm nổi tiếng đánh dấu nền móng của vật lí cổ điển
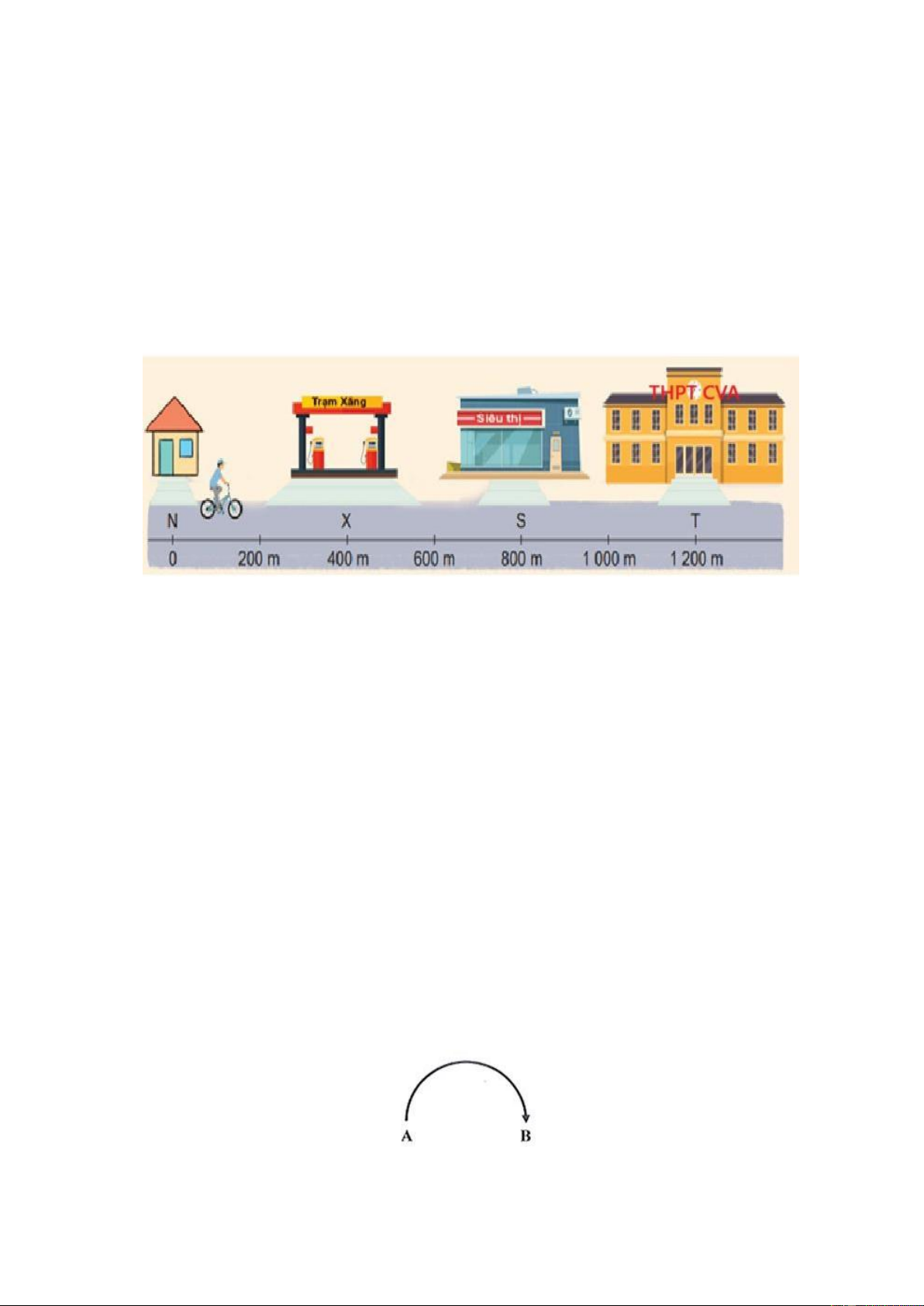
Câu 27. Bạn A đi xe đạp từ nhà qua trạm xăng, tới siêu thị mua đồ rồi quay về nhà cất
đồ, sau đó đi xe đến trường.
Quãng đường đi được từ trạm xăng đến nhà rồi đến siêu thị là A. 2800 m B. 2000 m C. 750 m D. 1200 m Đáp án: D. 1200 m Lý do:  Tính từ sơ đồ:
 Từ trạm xăng đến nhà: 400m
 Từ nhà đến siêu thị: 800 m
 Tổng: 400 + 800 = 1200 m
Câu 28. Một người đi theo nửa đường tròn có bán kính 50 m, từ A đến B như hình vẽ.
Quãng đường đã đi là: 8 A. 157 m B. 314m C. 100m D. 214m Đáp án: B. 314 m Lý do:
 Chu vi toàn phần của đường tròn: 2πr =2π×50 = 314 m
 Nửa đường tròn: π×50=157 m
Câu 29. Trái Đất quay quanh Mặt Trời một vòng trong thời gian một năm (trung bình là
365 ngày). Biết vận tốc quay của Trái Đất bằng 108000 km/h. Lấy π ≈ 3,14 thì giá trị
trung bình bán kính quỹ đạo của Trái Đất quanh Mặt Trời là: A. 145 000 000 km B. 150 000 000 km C. 150 649 682 km D. 149 300 000 Km Lời giải: Tính: Đổi 365 ngày = 8760 giờ C=108000⋅ 8760=946080000 km
Quỹ đạo có dạng hình tròn, bán kính trung bình R được tính bằng công thức: C = 2πR 108000.8760 R  150000000km 2.3,14 Đáp số: B. 150 000 000 km
Câu 30: Trong đêm tối từ lúc thấy tia chớp lóe sáng đến khi nghe thấy tiếng bom nổ
khoảng 15 giây. Hỏi chỗ bom nổ cách người quan sát bao xa? Biết vận tốc truyền âm
trong không khí bằng 340 m/s. A. 5100 m B. 5000 m C. 5200 m D. 5300 m Lời giải:
Thời gian để âm thanh truyền đến tai người là t =15s Vận tốc âm thanh trong không khí v=340 m/s
Công thức tính quãng đường: s=v⋅t Tính: s = 340⋅15 = 5100 m Đáp án: A. 5100 m
Câu 31: Cho biết người chị bên phải có trọng lượng 300 N, khoảng cách d1 = 2 m, còn
người em có trọng lượng 200 N. Để bập bênh cân bằng nằm ngang thì khoảng cách d1 bằng 9 A. 6 m. B. 4,5 m. C. 1,5 m. D. 3 m. Lời giải:
Để bập bênh cân bằng, tổng mô-men lực của hai người đối với trục quay phải bằng nhau. Công thức: M1=M2 ⟹ F1⋅d1=F2⋅d2 Trong đó:  F1=300 N, d1=2 M.  F2=200 N, cần tìm d2. Thay số: 300⋅2 = 200⋅d2 ⟹ d2= 3m Đáp án: D. 3 m
Câu 32. Một kĩ sư xây dựng nặng 75 kg trèo lên một chiếc thang dài 2,75 m.
Thang được dựa vào bức tường thẳng đứng và tạo một góc 600 với mặt phẳng
ngang như hình. Lấy g = 9,8 m/s2. Công của trọng lực tác dụng lên kĩ sư khi
người này leo từ chân đến đỉnh thang có giá trị A.1750,45 J. B. – 1750,45 J. C. 1010,63 J. D. –1010,63 J. Đáp số B. Lời giải: – 1750,45 J.
Công của trọng lực tác dụng vào kĩ sư khi trèo lên hết thang:
A = -m.g.l.cosα = -75.9,8.2,75.cos30 = -1750,45J
Câu 33. Trong một khán phòng có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền
sau nhiều hơn dãy trước đó 4 ghế, hỏi khán phòng đó có tất cả bao nhiêu ghế? A. 2190. B. 2560. C. 1236. D. 3214. Đáp số: A. 2190 Lời giải: N = 30, U1=15, d = 4 30 S 
2.15  30 1 .4  2190 30     2
Câu 34. Ai là người tiên phong trong việc sử dụng kính hiển vi để quan sát vi sinh vật? A. Antonie van Leeuwenhoek B. Galileo Galilei C. Louis Pasteur D. James Maxwell
Đáp án: A. Antonie van Leeuwenhoek 1 0
Câu 35. Người sáng lập ra World Wide Web (WWW) là ai? A. Alan Turing B. Bill Gates C. Steve Jobs D. Tim Berners-Lee Đáp án: D. Tim Berners-Lee
Câu 36. Ngành Vật lý bắt đầu phát triển từ thời kỳ nào trong lịch sử? A. Trung đại B. Hiện đại C. Cổ đại D. Thế kỷ XIX Đáp án: C. Cổ đại
Câu 37. Ai là người được coi là đặt nền móng cho ngành Vật lý cổ điển? A. Galileo Galilei B. Archimedes C. Isaac Newton D. Albert Einstein Đáp án: A. Galileo Galilei 1 1
Câu 38. Nhà khoa học nào đã mở đầu cho cuộc cách mạng khoa học hiện đại trong Vật lý? A. James Clerk Maxwell B. Galileo Galilei C. Niels Bohr D. Johannes Kepler Đáp án: B. Galileo Galilei
Câu 39. Trong phân tích thống kê, độ lệch chuẩn (standard deviation) cho biết:
A. Giá trị trung bình của dãy số liệu
B. Sai số tuyệt đối của phép đo
C. Mức độ phân tán của các số liệu quanh giá trị trung bình
D. Số lần đo trong một thí nghiệm
Đáp án: C. Mức độ phân tán của các số liệu quanh giá trị trung bình
Giải thích: Độ lệch chuẩn đo lường mức độ biến động của một tập hợp dữ liệu so với giá trị trung bình của nó.
Câu 40. Một nhà nghiên cứu đo nồng độ chất X trong 5 lần và thu được kết quả gần như
giống nhau, nhưng khác xa giá trị thực. Hiện tượng này thể hiện:
A. Độ chính xác cao, độ đúng thấp
B. Độ chính xác thấp, độ đúng cao
C. Độ chính xác và độ đúng đều cao
D. Độ chính xác và độ đúng đều thấp
Đáp án: B. Độ chính xác thấp, độ đúng cao
Giải thích: Độ chính xác biểu thị mức độ giống nhau của các phép đo, còn độ đúng biểu thị sự
gần đúng với giá trị thực. Trong trường hợp trên, kết quả có độ chính xác cao nhưng không
đúng với giá trị thực. *&*
Dạng 2. Câu hỏi trả lời ngắn
Câu 1. Một quần thể vi khuẩn tăng gấp đôi sau mỗi 30 phút. Nếu quần thể ban đầu có
100 vi khuẩn, sau 1 giờ sẽ có bao nhiêu vi khuẩn?  Giải:
 Sau 30 phút: 100 vi khuẩn * 2 = 200 vi khuẩn
 Sau 60 phút (1 giờ): 200 vi khuẩn * 2 = 400 vi khuẩn  Đáp án: 400 vi khuẩn
Câu 2. Một quần thể cây trồng tăng trưởng tuyến tính với tốc độ 20 cây mỗi năm. Nếu
ban đầu có 50 cây, sau 1 thập kỉ số cây là bao nhiêu, với tỉ lệ các cây sinh ra sống sót là 80%?  Giải:
 Số cây tăng thêm sau 1 thập kỷ (10 năm): 20 cây/năm * 10 năm = 200 cây
 Số cây sống sót sau 1 thập kỷ: 200 cây * 80% = 160 cây
 Tổng số cây sau 1 thập kỷ: 50 cây + 160 cây = 210 cây  Đáp án: 210 cây
Câu 3. Có 6 đường thẳng song song và 12 đường thẳng song song khác cắt 6 đường 1 2
thẳng song song đã cho. Hỏi có bao nhiêu hình bình hành được tạo thành. Giải:
 Để tạo thành một hình bình hành, cần chọn 2 đường thẳng từ nhóm 6 đường thẳng
song song và 2 đường thẳng từ nhóm 12 đường thẳng song song. 6!
 Số cách chọn 2 đường thẳng từ 6 đường thẳng song song: 2 C  15 6 2  ! 6  2! 12!
 Số cách chọn 2 đường thẳng từ 12 đường thẳng song song: 2 C   66 12 2  ! 12  2!
 Tổng số hình bình hành được tạo thành: 15 * 66 = 990
 Đáp án: 990 hình bình hành
Câu 4. Một năm đối xứng là năm mà viết xuôi hay ngược đều như nhau, ví dụ 2002 là
năm đối xứng. Hỏi từ năm 10 sau công nguyên đến năm 2025 có bao nhiêu năm đối xứng? Giải:
Trường hợp 1: Năm 2 chữ số (10–99)
Dạng đối xứng: aa → Có 9 năm: 11, 22, ..., 99
Trường hợp 2: Năm 3 chữ số (100–999)
Dạng đối xứng: aba
→ a∈{1,...,9}, b∈{0,...,9}
→ Có 9×10=90 năm đối xứng
Trường hợp 3: Năm 4 chữ số (1000–2025)
Dạng đối xứng: abba
→ a∈{1,2} (vì năm tối đa là 2025 nên chỉ các năm bắt đầu bằng 1 hoặc 2) Với a= 1
→ năm có dạng: 1bb1
→ b∈{0,...,9} ⇒ Có 10 năm: 1001, 1111, ..., 1991 Với a= 2
→ năm có dạng: 2bb2
→ b∈{0,...,0} vì chỉ có 2002 ≤ 2025 Tổng: 10+1= 11 năm Tổng kết:
 2 chữ số: 9 năm
 3 chữ số: 90 năm
 4 chữ số: 11 năm
Vậy tổng số năm đối xứng từ năm 10 đến 2025 là: 9+90+11=110 năm
Câu 5. Cho đa giác lồi có 40 cạnh. Mỗi đoạn thẳng đi qua hai đỉnh bất kì của nó mà
không phải là cạnh được gọi là một đường chéo của nó. Số giao điểm nằm bên trong đa
giác (không trùng với đỉnh) được tạo ra do các đường chéo của nó cắt nhau nhiều nhất là bao nhiêu?  Giải:
 Số đường chéo của đa giác lồi 40 cạnh là 2 C  40  740 40
 Số giao điểm tối đa của các đường chéo trong đa giác lồi 40 cạnh là 4 C  91390 40  Đáp án: 91390
Câu 6. Có 10 chiếc tất xanh và 10 chiếc tất đỏ ở trong hộp. Hỏi phải lấy ra ít nhất bao 1 3
nhiêu chiếc tất để chắc chắn có một đôi tất cùng màu?  Giải:
 Trường hợp xấu nhất là bạn lấy ra 1 chiếc tất xanh và 1 chiếc tất đỏ.
 Khi bạn lấy chiếc tất thứ ba, nó chắc chắn phải là màu xanh hoặc màu đỏ, tạo
thành một đôi với một trong hai chiếc tất bạn đã lấy trước đó.  Đáp án: 3 chiếc
Câu 7. Khi hai phần thi của khoa Toán kết thúc cũng vừa lúc hai kim đồng hồ (kim giờ,
kim phút) đã đổi chỗ cho nhau. Hỏi hai phần thi hết bao nhiêu giờ. Giải
Khi kim phút và kim giờ trùng nhau, thì thời gian trôi qua là:
Khoảng cách giữa hai kim đồng hồ chính là 5. 12 = 60 phút (1 giờ = 60 phút).
Do vậy, hết bao nhiêu giờ phần toán học kết thúc thì đồng hồ quay đúng 12 giờ. Đáp án là: 12 giờ.
Câu 8. Một nhà đầu tư dự định sử dụng 1 tỉ đồng để đầu tư vào ba loại trái phiếu: ngắn
hạn, trung hạn và dài hạn. Biết lãi suất của ba loại trái phiếu ngắn hạn, trung hạn, dài hạn
mỗi năm lần lượt là 3%, 4%, 5%. Người đó dự định sẽ đầu tư số tiền vào trái phiếu trung
hạn gấp đôi số tiền đầu tư vào trái phiếu ngắn hạn với mong muốn nhận được 1 4
tổng tiền lãi trong năm đầu tiên là 4,2% số tiền đầu tư. Người đó nên đầu tư vào mỗi loại
trái phiếu bao nhiêu tiền để đáp ứng được mong muốn của mình? Giải
Gọi số tiền đầu tư vào trái phiếu ngắn hạn là x, trung hạn là 2x, và dài hạn là y. Ta có hệ phương trình:
 x + 2x + y = 1,000,000,000 (Tổng số tiền đầu tư là 1 tỉ đồng)
 0.03x + 0.04(2x) + 0.05y = 0.042 * 1,000,000,000 (Tổng tiền lãi là 4,2% của 1 tỉ đồng)
 3x  y 1000000000
Giải hệ phương trình này, ta có: 
0,11x  0,05y  42000000
Vậy x = 200,000,000 (200 triệu đồng)
 Số tiền đầu tư vào trái phiếu ngắn hạn: 200,000,000 đồng
 Số tiền đầu tư vào trái phiếu trung hạn: 2 * 200,000,000 = 400,000,000 đồng
 Số tiền đầu tư vào trái phiếu dài hạn: 1,000,000,000 - 200,000,000 - 400,000,000 = 400,000,000 đồng
Câu 9. Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái
thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là
45𝑐𝑚,43𝑐𝑚, 41𝑐𝑚,…,31𝑐𝑚. Cái thang đó có bao nhiêu bậc? Giải
Ta có công thức số hạng tổng quát: an = a1 + (n−1)d
31 = 45 + (n-1)(-2) suy ra n = 8
Vậy, cái thang đó có 8 bậc.
Câu 10. Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15 . Chọn ngẫu nhiên 6 tấm thẻ
trong hộp. Có bao nhiêu cách chọn để tổng các số ghi trên 6 tấm thẻ là một số lẻ? Giải
Để tổng của 6 số là lẻ, ta cần có một số lẻ các số lẻ trong 6 tấm thẻ được chọn (1, 3 hoặc
5 số lẻ). Trong 15 tấm thẻ, có 8 số lẻ và 7 số chẵn. Ta có các trường hợp sau:
 1 số lẻ và 5 số chẵn: C(8,1)×C(7,5)=8×21 = 168
 3 số lẻ và 3 số chẵn: C(8,3)×C(7,3)=56×35 =1960
 5 số lẻ và 1 số chẵn: C(8,5)×C(7,1)=56×7 =392
Tổng số cách chọn: 168 + 1960 + 392 = 2520
Vậy, có 2520 cách chọn để tổng các số ghi trên 6 tấm thẻ là một số lẻ.
Câu 11. Lớp toán A có 50 học sinh biết rằng có 30 bạn thích chơi bóng đá 40 bạn thích
chơi bóng chuyền, 5 bạn không thích chơi môn nào. Hỏi có bao nhiêu bạn biết chơi cả hai môn Giải
 Số học sinh thích ít nhất một trong hai môn: 50 - 5 = 45
 Tổng số học sinh thích bóng đá hoặc bóng chuyền (hoặc cả hai): 30 + 40 = 70
 Số học sinh thích cả hai môn: 70 - 45 = 25
Vậy, có 25 bạn thích chơi cả hai môn.
Câu 12. Một vận động viên chạy bộ với tốc độ trung bình 12 km/h trong 30 phút. Trong
suốt quá trình này, cơ thể người cần tiêu thụ trung bình 0,035 mol oxy/phút để duy trì
hoạt động trao đổi chất. 1 5
a) Tính quãng đường vận động viên đã chạy được.
b) Tính tổng lượng mol khí O₂ mà cơ thể đã sử dụng trong suốt thời gian chạy.
c) Biết 1 mol O₂ có thể tạo ra khoảng 286 kJ năng lượng qua quá trình hô hấp tế
bào, hãy tính tổng năng lượng được sinh ra.
d) Nếu 25% năng lượng này được chuyển thành công cơ học để giúp người chạy di
chuyển, hãy tính công hữu ích mà người đó đã sinh ra.
e) Biết trọng lượng người đó là 60 kg, hãy ước lượng lực kéo trung bình cơ thể cần
tác động lên mặt đất (bỏ qua lực cản không khí và ma sát). Giải
(a) Tính quãng đường vận động viên đã chạy được.
 Thời gian chạy: 30 phút = 0.5 giờ
 Quãng đường: 12 km/h * 0.5 h = 6 km
Vậy, quãng đường vận động viên đã chạy được là 6 km.
(b) Tính tổng lượng mol khí O2 mà cơ thể đã sử dụng trong suốt thời gian chạy.
 Tổng lượng mol khí O2: 0.035 mol/phút * 30 phút = 1.05 mol
Vậy, tổng lượng mol khí O2 mà cơ thể đã sử dụng là 1.05 mol.
(c) Biết 1 mol O2 có thể tạo ra khoảng 286 kJ năng lượng qua quá trình hô hấp tế
bào, hãy tính tổng năng lượng được sinh ra.
 Tổng năng lượng: 1.05 mol * 286 kJ/mol = 300.3 kJ
Vậy, tổng năng lượng được sinh ra là 300.3 kJ.
(d) Nếu 25% năng lượng này được chuyển thành công cơ học để giúp người chạy di
chuyển, hãy tính công hữu ích mà người đó đã sinh ra.
 Công hữu ích: 300.3 kJ * 25% = 75.075 kJ
Vậy, công hữu ích mà người đó đã sinh ra là 75.075 kJ.
(e) Biết trọng lượng người đó là 60 kg, hãy ước lượng lực kéo trung bình cơ thể cần
tác động lên mặt đất (bỏ qua lực cản không khí và ma sát). F = ma Trong đó:
 F là lực kéo trung bình
 m là khối lượng của người (60 kg)
 a là gia tốc trung bình
Để ước lượng gia tốc trung bình, ta có thể chia vận tốc cuối cho thời gian:
a ≈ v/t = 3.33 m/s / 30 phút = 3.33 m/s / 1800 s ≈ 0.00185 m/s²
Vậy, lực kéo trung bình:
F = 60 kg * 0.00185 m/s² ≈ 0.111 N *&*