ĐỀ CƯƠNG ÔN TẬP HỌC PHẦN TOÁN RỜI RẠC | Đại học Kinh tế Kỹ thuật Công nghiệp

lOMoAR cPSD| 40190299
ĐỀ CƯƠNG ÔN TẬP HỌC PHẦN TOÁN RỜI RẠC
1. Phần 1 (2 điểm) 1.1. Bài toán đếm
- Hoán vị, Hoán vị lặp
- Chỉnh hợp không lặp, Chỉnh hợp lặp
- Tổ hợp, Tổ hợp lặp - Nguyên lý cộng - Nguyên lý nhân
- Nguyên lý bù trừ
- Công thức truy hồi 1.2.
Bài toán tồn tại
- Phương pháp chứng minh phản chứng - Nguyên lý Dirichlet 1.3. Bài toán liệt kê - Phương pháp sinh
- Phương pháp quay lui
2. Phần 2 (3 điểm)
2.1. Thuật toán nhánh cận giải bài toán người du lịch
2.2. Thuật toán nhánh cận giải bài toán cái túi
2.3. Bài toán lập lịch gia công chi tiết máy
3. Phần 3 (2 điểm)
3.1. Khái niệm đồ thị, đồ thị đẳng cấu, các loại đồ thị đặc biệt, cách biểu diễn đồ thị.
3.2. Đồ thị Euler
3.3. Đồ thị Hamilton.
4. Phần 4 (3 điểm)
4.1. Thuật toán tìm kiếm sâu (DFS), rộng (BFS)
4.2. Thuật toán Prim tìm cây khung cực tiểu
4.3. Thuật toán Dijkstra tìm đường đi ngắn nhất lOMoAR cPSD| 40190299 BÀI TẬP 1. Phần 1 1.1. Bài toán đếm
1. Trong các số nguyên từ 1 đến 1000 có bao nhiêu số không chia hết cho bất cứ
số nào trong các số 4 và 7?
2. Có bao nhiêu dãy nhị phân độ dài 8 được bắt đầu bởi 01 hoặc kết thúc bởi 11?
3. Có 6 người xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp mà A luôn
đứng phía trước B?
4. Có 6 người xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp mà A không
đứng cạnh B?
5. Một tổ học sinh có 8 em trong đó có 4 em nam, 4 em nữ. Hỏi có bao nhiêu
cách xếp tổ đứng thành một hàng ngang sao cho các em nam và các em nữ
đứng xen kẽ nhau.
6. Một cuộc họp có 8 người dự. Trong buổi họp mỗi người dự phát biểu 1 lần.
Hỏi có bao nhiêu cách bố trí thứ tự phát biểu sao cho A phát biểu sau B.
7. Cho các chữ số: 1, 2, 3, 4, 5. Hỏi có thể lập được bao nhiêu số có 3 chữ số từ các
chữ số đã cho với điều kiện: trong mỗi số này các chữ số không được lặp lại.
8. Có 7 người xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp mà A luôn
đứng phía sau B?
9. Một người khoá xe đạp bằng khoá số gồm 5 chữ số. Anh ta quên mất số đã
khoá mà chỉ còn nhớ trong số đã khoá có số 15 và 60. Hỏi để mở được khoá
anh ta phải thử nhiểu nhất bao nhiêu số?
10. Trên mặt phẳng cho n điểm (n>3) trong đó có k điểm thẳng hàng (3<=k<=n).
Hỏi có thể tạo được bao nhiêu tam giác có các đỉnh thuộc n điểm đã cho?
11. Trong phát hành sổ số mỗi vé số có một mã số gồm 2 phần: phần đầu gồm 2
chữ cái lấy từ A đến Z (26 chữ cái), phần sau gồm 4 chữ số lấy từ 0 đến 9 (10
chữ số). Hỏi có thể phát hành được nhiều nhất bao nhiêu vé số?
12. Một đội gồm 8 em đi thi học sinh giỏi. Đề thi gồm 3 bài. Biết 5 em làm được bài
1, 4 em làm được bài 2, 6 em làm được bài 3. Ngoài ra biết rằng em nào cũng
làm được ít nhất một bài. Hỏi nhiều nhất có bao nhiêu em làm được cả 3 bài.
13. Có bao nhiêu xâu nhị phân độ dài 10 được bắt đầu bằng 11 hoặc được kết
thúc bằng 00?
14. Trong các số từ 1 đến 500 có bao nhiêu số không chia hết cho bất cứ số nào
trong các số 3, 4 và 5?
15. Có 7 người xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp mà A luôn
đứng phía bên trái B? lOMoAR cPSD| 40190299
16. Tìm số giao điểm tối đa của:
a) 10 đường thẳng phân biệt
b) 10 đường tròn phân biệt
17. Có bao nhiêu cách may một lá cờ gồm 13 dải nối tiếp nhau, mỗi dải có một
trong 3 màu: xanh, đỏ hoặc vàng sao cho hai dải cạnh nhau có màu khác nhau.
18. Trong một lớp học có 50 sinh viên trong đó có 26 sinh viên đạt yêu cầu môn thi
thứ nhất, 21 sinh viên đạt yêu cầu môn thi thứ hai và 17 sinh viên không đạt yêu
cầu cả hai môn thi. Hỏi có bao nhiêu sinh viên đạt yêu cầu cả hai môn thi?
19. Một tổ học sinh có 9 em trong đó có 5 nam và 4 nữ. Cần thành lập một nhóm
gồm 5 em của tổ trong đó có 3 nam và 2 nữ. Hỏi có bao nhiêu cách thành lập
nhóm sao cho không đồng thời có em nam A và em nữ B?
20. Một tổ học sinh có 9 em trong đó có 6 nam và 3 nữ. Có bao nhiêu cách xếp tổ
đứng thành một hàng ngang sao cho không có 2 em nữ nào đứng cạnh nhau?
21. Một tổ học sinh có 10 em trong đó có 6 nam và 4 nữ. Cần thành lập một
nhóm gồm 5 em của tổ. Hỏi có bao nhiêu cách thành lập nhóm sao cho trong
nhóm có ít nhất 3 nam?
22. Phương trình x1+ x2 + x3 = 15 có bao nhiêu nghiệm nguyên không âm?
23. Phương trình x1 + x2 + x3 + x4 + x5 = 21 có bao nhiêu nghiệm nguyên không âm?
24. Tìm số nghiệm nguyên của phương trình: x1+ x2 + x3 + x4 = 20 với x1>=6,
x2>=3, x3>=9, x4>=-2
25. Tìm số nghiệm nguyên của phương trình: x+y+z=10 với 0<=x<=2, 0<=y<=4, 0<=z<=6.
26. Có thể nhận được bao nhiêu xâu khác nhau bằng cách sắp xếp lại các chữ cái
của từ SUCCESS?
27. Có bao nhiêu cách chia những xấp bài 5 quân cho mỗi một trong 4 người chơi
từ một cỗ bài chuẩn 52 quân?
28. Tìm nghiệm của các hệ thức truy hồi:
a) A = 5A − 6A
(n  2) có A = 0, A = 1 N N −1 N −2 0 1 b) A
= 7A −12A (n  2) có A = 1, A = 5 N N −1 N −2 1 2 c) A = 2A
+ 5A − 6A (n  3) có A = 0, A = −4, A = 8 N N −1 N − 2 N −3 0 1 2 d) A = 6A
− 9A (n  2) có A = 1, A = 6 N N −1 N −2 0 1
e) an = 6an-1- 11an-2 + 6an-3 (n>=3) với a0 = 2, a1 = 5, a2 = 15.
f) fn = fn-1 + fn-2, n  2 và f0 = f1 = 1
g) an = an-1 + 6an-2 với n  2, a0 = 3, a1 = 6 lOMoAR cPSD| 40190299
h) an =7an-1- 10an-2 với n  2, a0 = 2, a1 = 1
i) an =2an-1+ an-2- 2 an-3 với n  3, a0 = 3, a1 = 6, a2 = 0
j) an =7an-2+ 6 an-3 với n  3, a0 = 9, a1 = 10, a2 = 32
29. Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn văn, 20 em thích
môn toán, 18 em thích môn sử, 6 em ko thích môn nào, 5 em thích cả 3 môn.
Hỏi có bao nhiêu em chỉ thích hai môn trong ba môn trên.
1.2. Bài toán tồn tại
1. Một đề thi gồm 8 câu hỏi, với mỗi câu hỏi người dự thi chỉ cần trả lời đúng
hoặc sai. Hỏi phải có ít nhất bao nhiêu người dự thi để chắc chắn có 2 người
làm bài giống nhau.
2. Một nhóm gồm 9 học sinh. Chứng tỏ rằng trong nhóm có ít nhất 5 nam hoặc ít
nhất 5 nữ.
3. Một cuộc họp có n người dự. Chứng tỏ rằng luôn tìm được hai người trong
họ có số người quen bằng nhau (trong những người đến dự họp)
4. Chứng tỏ rằng trong 5 số bất kỳ được lấy ra từ 8 số nguyên dương đầu tiên
luôn tìm được hai số có tổng bằng 9
5. Giả sử điểm thi môn Toán rời rạc là một số nguyên từ 0 đến 10. Hỏi phải có ít nhất
bao nhiêu sinh viên dự thi để chắc chắn có 5 sinh viên được điểm bằng nhau.
6. Trên mặt phẳng cho n điểm. Mỗi điểm có thể nối với k điểm khác (0<=k<=n-1)
bằng các đoạn thẳng. Chứng tỏ rằng luôn tìm được 2 điểm có cùng số điểm nối.
7. Chứng tỏ rằng trong 7 số bất kỳ được lấy ra từ 10 số nguyên dương đầu tiên
luôn tìm được hai cặp số mỗi cặp có tổng bằng 11.
8. Chứng minh rằng trong n+1 số nguyên dương khác nhau luôn tìm được hai
số có cùng số dư khi chia cho n.
9. Một tổ gồm 10 sinh viên quê ở các tỉnh Thái Bình, Hà Nam và Thanh Hoá.
Chứng tỏ rằng có ít nhất 4 sinh viên của tổ cùng tỉnh.
10. Một đề thi gồm 6 câu hỏi, với mỗi câu hỏi có 3 phương án lựa chọn A, B, C.
Hỏi phải có ít nhất bao nhiêu người dự thi để chắc chắn có 3 người làm bài giống nhau.
11. Có 16 cầu thủ, số áo của mỗi người được đánh từ 1 đến 16 đứng thành một
vòng tròn theo thứ tự bất kỳ. Chứng minh rằng luôn tìm được 3 cầu thủ đứng
liền nhau có tổng các số áo ít nhất là 25.
12. Có 20 thành phố, giữa các thành phố có thể có các đường giao thông nối trực
tiếp với nhau hoặc không. Chứng tỏ rằng có ít nhất hai thành phố có số thành
phố khác nối trực tiếp với chúng là như nhau. lOMoAR cPSD| 40190299
13. Một bảng có 8 đội bóng thi đấu theo thể thức vòng tròn một lượt (hai đội bất kỳ thi
đấu với nhau một trận). Chứng tỏ rằng tại bất cứ thời điểm nào cũng tìm được
2 đội có số trận đã đấu bằng nhau.
14. Chứng tỏ rằng trong n+1 số nguyên dương không vượt quá 2n luôn tồn tại 2
số mà số này là bội của số kia.
15. Trong một tháng 30 ngày một công nhân làm việc liên tục và mỗi ngày làm
được ít nhất 1 sản phẩm, nhưng cả tháng làm được nhiều nhất 45 sản phẩm.
Chứng tỏ rằng luôn tìm được một số ngày liên tục trong tháng mà trong những
ngày này người công nhân làm được đúng 14 sản phẩm.
16. Trong không gian tọa độ Đề các cho 9 điểm có toạ độ nguyên. Chứng tỏ rằng luôn
tìm được 2 điểm trong 9 điểm này mà toạ độ trung điểm của đoạn thẳng nối
2 điểm đó cũng là nguyên.
17. Một đề thi gồm 5 câu hỏi, với mỗi câu hỏi có 4 phương án lựa chọn A, B, C,
D. Hỏi phải có ít nhất bao nhiêu người dự thi để chắc chắn có 2 người làm
bài giống nhau.
1.3. Bài toán liệt kê
Liệt kê cấu hình tổ hợp tiếp theo bằng phương pháp sinh
1. Sinh dãy nhị phân a) 10100111111 b) 11001111111
2. Sinh hoán vị của các số 1,2,3,4,5,6 a) 146325 b) 341256
3. Sinh tập con 4 phần tử của tập 6 phần tử {1,2,3,4,5,6} a) 1256 b) 1652 lOMoAR cPSD| 40190299 2. Phần 2
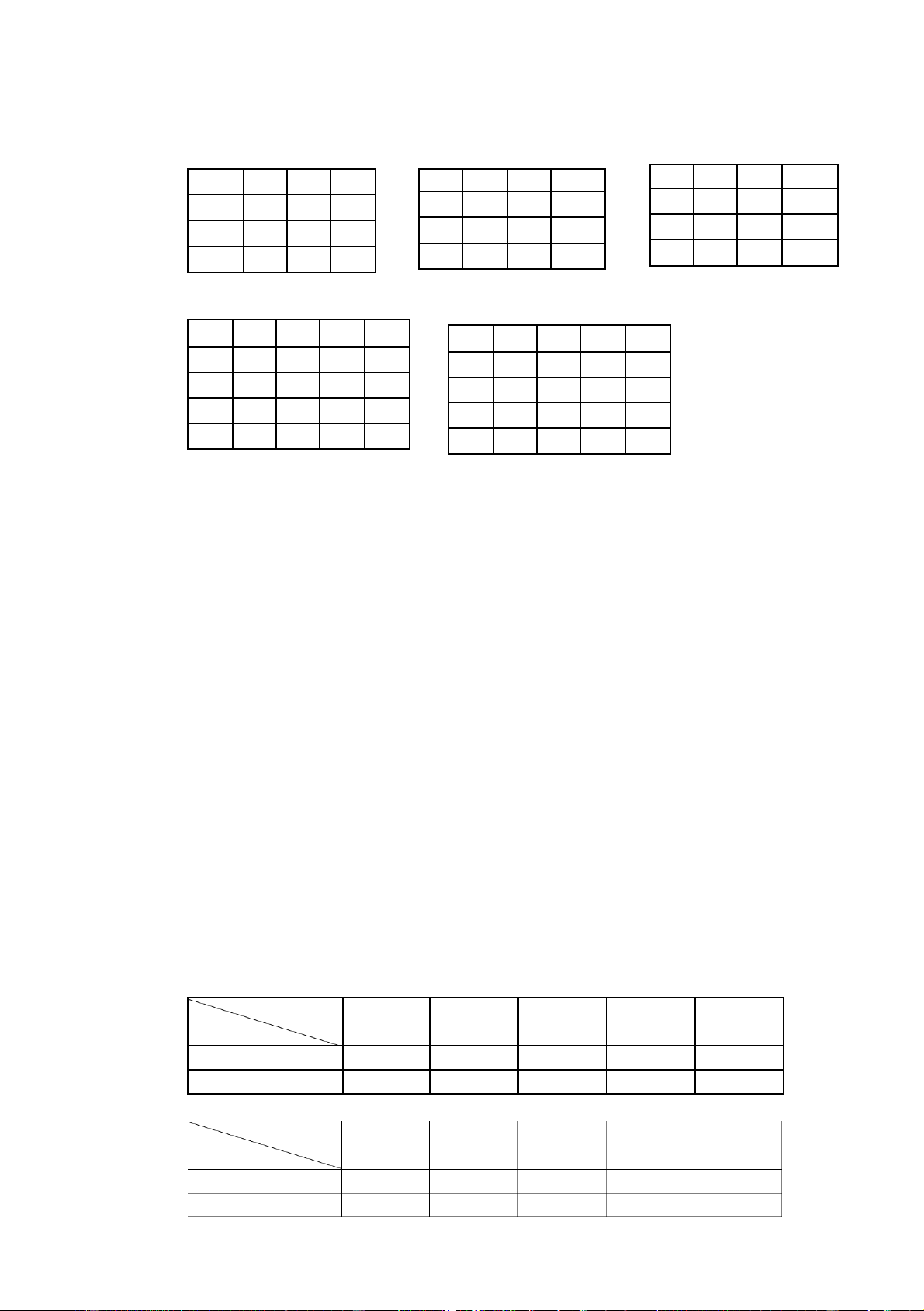
2.1. Áp dụng thuật toán nhánh cận giải bài toán người du lịch với ma trận chi phí sau:  9 12 30  34 12 22  50 20 27 40  22 17 23  17 50 34  18 45 15 23  10 31 28  14 27 24  25 9 35 27  45 19 27  19 37 38  (a) (b) (c)  10 15 22 17  27 9 13 14 23  26 13 15 12  15 28 16 15 29  14 12 17 12  24 22 9 35 27  16 12 15 30  26 23 16 18 19  22 28 16 17  (d) (e)
2.2. Áp dụng thuật toán nhánh cận giải bài toán cái túi sau, chỉ rõ kết quả mỗi bước:
a) 5 X + 3 + 8 + 6 → max 1 X2 X3 X4
với x1,x2,x3,x4 nhận các giá trị 0,1 4X + + +  1
5X2 6X3 3X4 7 2 + + + → b) X 7 5 6 max 1 X2 X3 X4
với x1,x2,x3,x4 nhận các giá trị là số tự nhiên 3X + + +  1
6X2 3X3 5X4 8
c) 4 X + 7 + 3 + 5 → max 1 X2 X3 X4
với x1,x2,x3,x4 nhận các giá trị 0,1 4X + + +  1
8X2 2X3 4X4 8 + + + + → d) 2 X 7 5 6 4 max 1 X2 X3 X4 X5
với x1,x2,x3,x4,x5 nhận các giá trị là số 0,1 3X + + + +  1
6X2 3X3 5X4 3X5 8 e) 4 X + + + + → 1
7 X2 5 X3 6 X4 4 X5 max với x1,x2,x3,x4,x5 nhận các giá trị là số tự 3X + + + +  1
6X2 3X3 5X4 3X5 8 nhiên 2.3.
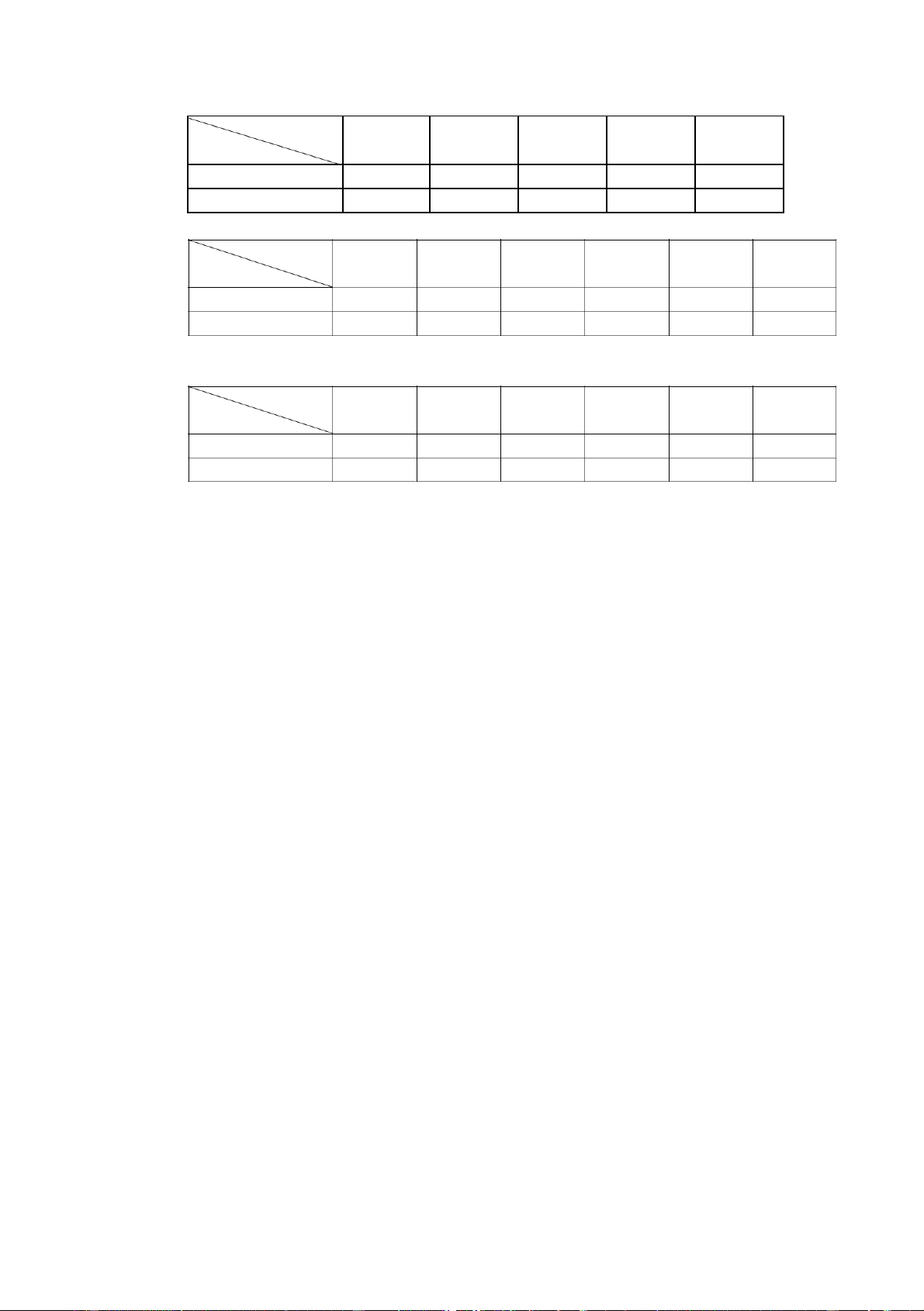
1) Cho thời gian gia công các chi tiết trên 2 máy A và B trong bảng sau. Hãy
lập lịch gia công cho các chi ti ết này sao cho thời gian gia công là ít nhất. Vẽ
sơ đồ Gantt cho lịch gia công tối ưu: a) Chi tiết D1 D2 D3 D4 D5 Máy A 5 3 7 6 2 B 4 6 3 2 5 b) Chi tiết D1 D2 D3 D4 D5 Máy A 4 6 7 3 2 B 8 2 4 7 5 lOMoAR cPSD| 40190299 c) Chi tiết D1 D2 D3 D4 D5 Máy A 4 6 7 3 2 B 8 2 4 5 3 d) Chi tiết D1 D2 D3 D4 D5 D6 Máy A 4 8 5 3 2 7 B 4 3 7 5 5 4 e) Chi tiết D1 D2 D3 D4 D5 D6 Máy A 3 8 5 3 2 7 B 4 5 6 3 5 4 lOMoAR cPSD| 40190299 Phần 3
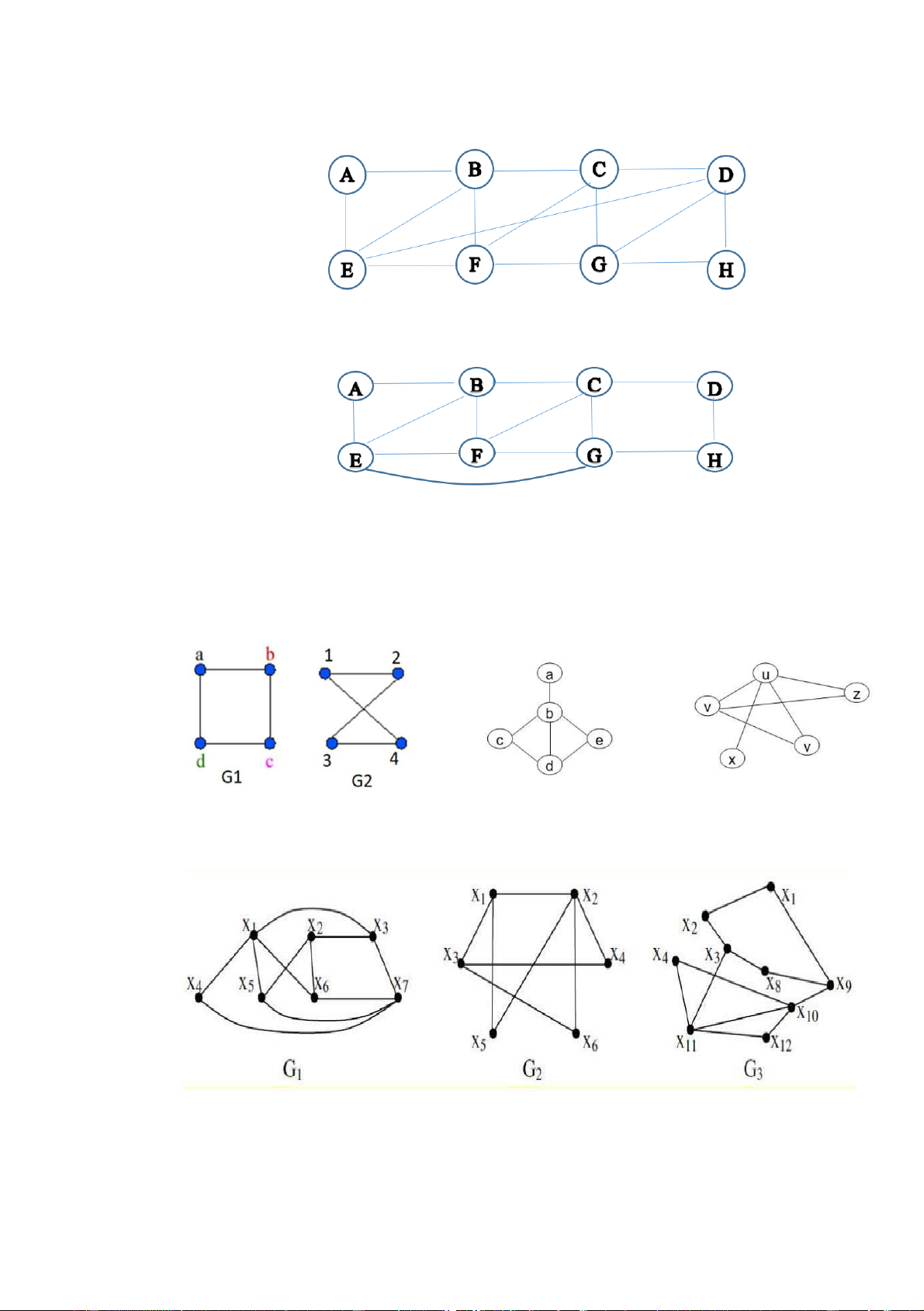
3.1. Cho đồ thị sau:
1. Lập ma trận kề, danh sách cạnh, danh sách kề biểu diễn đồ thị trên
2. Đồ thị trên có chu trình Euler không? Nếu có hãy tìm chu trình Euler (nếu có).
3.2. Cho đồ thị:
1. Lập ma trận kề, danh sách cạnh, danh sách kề biểu diễn đồ thị trên
2. Đồ thị trên có chu trình Euler không? Nếu có hãy tìm chu trình Euler (nếu có).
3. Đồ thị trên có chu trình Hamilton không? Nếu có hãy tìm chu trình Hamilton (nếu có).
3.3. Các cặp đồ thị sau có đẳng cấu với nhau không? tại sao? G1 G2
3.4. Các đồ thị trong hình dưới đây, đồ thị nào là đồ thị phân đôi? Nếu là đồ thị
phân đôi hãy phân hoạch tập đỉnh thành 2 tập thuộc 2 phía và vẽ lại đồ thị đó? lOMoAR cPSD| 40190299 Phần 4
4.1. Cho đồ thị
1. Duyệt chiều sâu (DFS) theo đồ
thị bắt đầu từ đỉnh 3
2. Duyệt chiều sâu (DFS) theo đồ
thị bắt đầu từ đỉnh 8
3. Duyệt chiều rộng (BFS) theo đồ
thị bắt đầu từ đỉnh 5
4. Duyệt chiều rộng (DFS) theo
đồ thị bắt đầu từ đỉnh 2
5. Tìm cây khung cực tiểu bắt đầu từ đỉnh 3
6. Tìm đường đi ngắn nhất từ đỉnh 7 đến tất cả các đỉnh khác của đồ thị
4.2. Cho đồ thị
1. Duyệt chiều sâu (DFS) theo đồ
thị bắt đầu từ đỉnh 2
2. Duyệt chiều sâu (DFS) theo đồ
thị bắt đầu từ đỉnh 8
3. Duyệt chiều rộng (BFS) theo đồ
thị bắt đầu từ đỉnh 7
4. Duyệt chiều rộng (DFS) theo
đồ thị bắt đầu từ đỉnh 5
5. Tìm cây khung cực tiểu bắt đầu từ đỉnh 6
6. Tìm đường đi ngắn nhất từ đỉnh 4 đến tất cả các đỉnh khác của đồ thị
4.3. Cho đồ thị
1. Duyệt chiều sâu (DFS) theo đồ thị
bắt đầu từ đỉnh 6
2. Duyệt chiều sâu (DFS) theo đồ thị bắt
đầu từ đỉnh 7
3. Duyệt chiều rộng (BFS) theo đồ thị bắt
đầu từ đỉnh 4
4. Duyệt chiều rộng (DFS) theo đồ thị
bắt đầu từ đỉnh 3
5. Tìm cây khung cực tiểu bắt đầu từ đỉnh 8
6. Tìm đường đi ngắn nhất từ đỉnh 2 đến tất cả các đỉnh khác của đồ thị
4.4. Cho đồ thị lOMoAR cPSD| 40190299
1. Duyệt chiều sâu (DFS) theo đồ thị bắt
đầu từ đỉnh 1
2. Duyệt chiều rộng (DFS) theo đồ thị bắt
đầu từ đỉnh 3
3. Tìm đường đi ngắn nhất từ đỉnh 2 đến tất
cả các đỉnh khác của đồ thị
4.5. Cho đồ thị
1. Duyệt chiều sâu (DFS) theo đồ thị bắt
đầu từ đỉnh 5
2. Duyệt chiều rộng (DFS) theo đồ thị bắt
đầu từ đỉnh 10
3. Tìm đường đi ngắn nhất từ đỉnh 6 đến tất
cả các đỉnh khác của đồ thị lOMoAR cPSD| 40190299
BÀI TẬP TỔNG HỢP BÀI 1
Câu 1 (2 điểm) Giải các hệ thức truy hồi với các điều kiện đầu sau: A
N = AN −1 +11AN −2 với n≥2 và điều kiện đầu a0=2, a1=3
Câu 2 (3 điểm)
Cho thời gian gia công các chi ti ết trên 2 máy A và B trong b ảng sau. Hãy lập
lịch gia công cho các chi ti ết này sao cho thời gian gia công là ít nhất. Vẽ sơ đồ
Gantt cho lịch gia công tối ưu: Chi tiết D1 D2 D3 D4 D5 Máy A 6 3 7 5 2 B 4 5 3 2 4
Câu 3: (2 điểm) Cho đồ thị sau:
1. Lập ma trận kề biểu diễn đồ thị trên?
2. Định nghĩa đồ thị Euler, đồ thị nửa Euler?
3. Đồ thị trên có chu trình Euler không?
Vì sao? Nếu có hãy tìm chu trình Euler đó?
Câu 4: (3 điểm) Cho đồ thị sau
1. Duyệt đồ thị trên theo phương pháp Duyệt theo chiều rộng – BFS
(Đỉnh bắt đầu là đỉnh 4)
2. Dùng thuật toán Dijkstra tìm đường đi ngắn nhất từ đỉnh 7 đến tất
cả các đỉnh còn lại của đồ thị. lOMoAR cPSD| 40190299 BÀI 2
Câu 1 (2 điểm) Trong tổng số 2504 sinh viên của một khoa công nghệ thông tin,
có 1876 theo học môn ngôn ngữ lập trình Pascal, 999 học môn ngôn ngữ Fortran
và 345 học ngôn ngữ C. Ngoài ra còn biết 876 sinh viên học cả Pascal và Fortran,
232 học cả Fortran và C, 290 học cả Pascal và C. Nếu 189 sinh viên học cả 3
môn Pascal, Fortran và C thì trong trường hợp đó có bao nhiêu sinh viên
không học môn nào trong 3 môn ngôn ngữ lập trình kể trên.
Câu 2 (3 điểm) Áp dụng thuật toán nhánh cận giải bài toán người du lịch
với ma trận chi phí như sau:  20 16 12 5  7 21 14 19  10 6 1721
Câu 3: (2 điểm) Cho đồ thị sau:
1. Lập ma trận kề biểu diễn đồ thị trên?
2. Định nghĩa đồ thị Hamilton, đồ thị nửa Hamilton?
3. Đồ thị trên có chu trình Hamilton không? Vì sao? Nếu có hãy tìm chu
trình Hamilton đó?
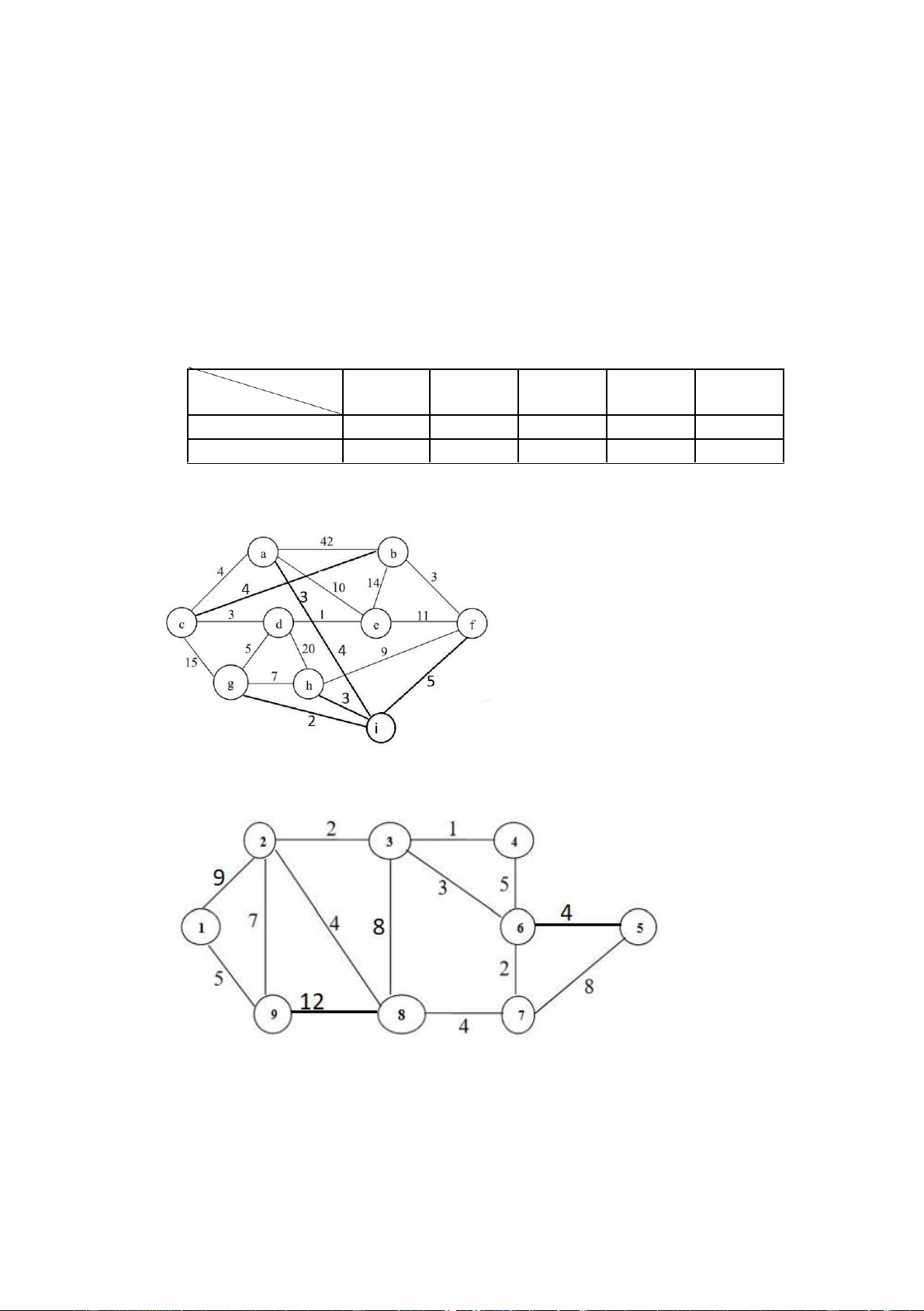
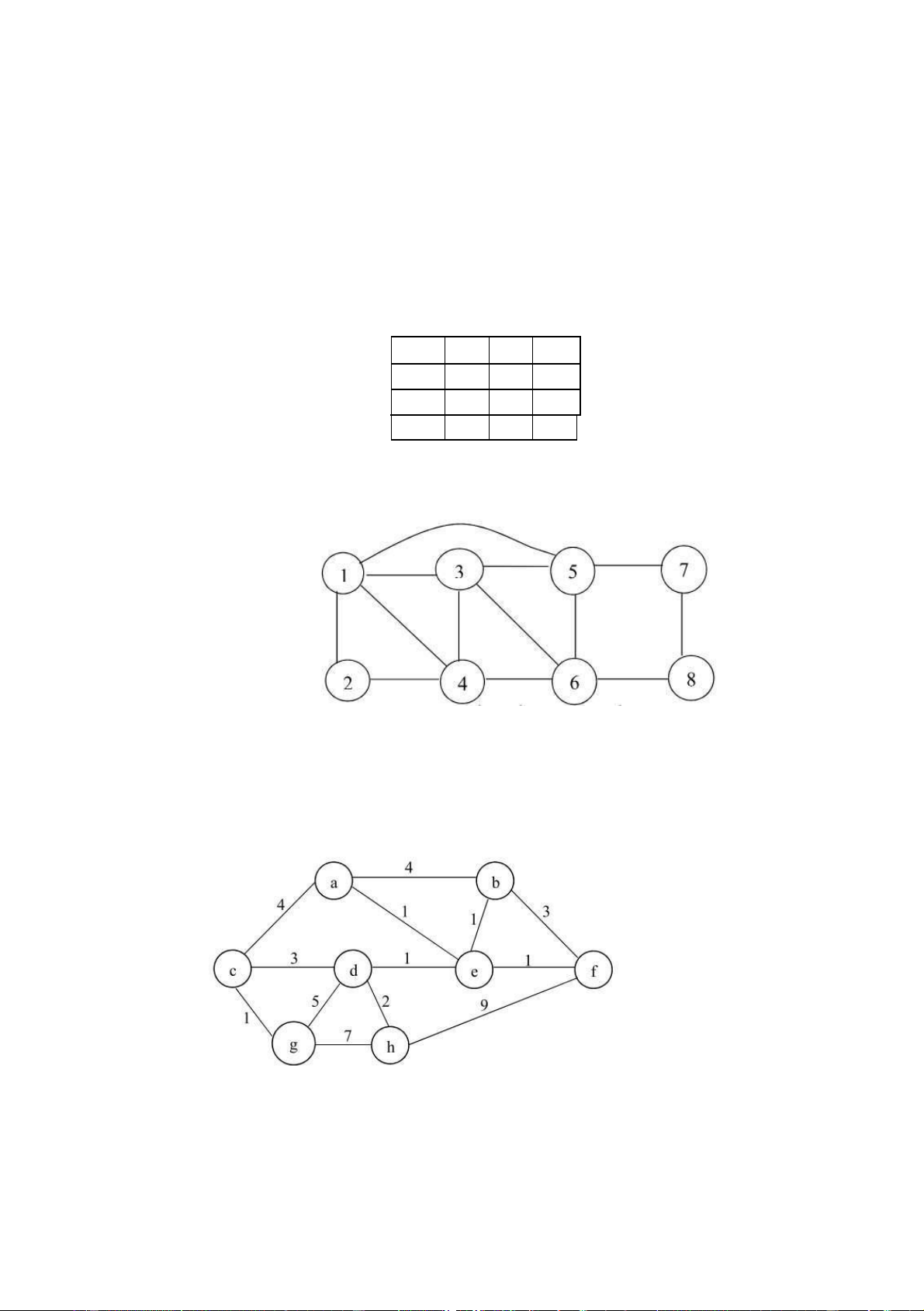
Câu 4: (3 điểm) Cho đồ thị sau
1. Duyệt đồ thị trên theo phương pháp Duyệt theo chiều sâu – DFS
(Đỉnh bắt đầu là đỉnh e)
2. Tìm cây khung cực tiểu của đồ thị từ đỉnh d.