1/2/2012 Chương 3 LÝ THUYẾT VỀ HÀNH VI CỦA NGƯỜI TIÊU DÙNG 1 Giả định chung
Mô hình này dựa trên giả định về
hành vi của người tiêu dùng là: người
tiêu dùng sẽ chọn nhóm hàng có khả
năng mang lại cho họ sự thỏa mãn tối đa. 2 I HỮU DỤNG
� Hữu dụng được dùng để chỉ mức độ thỏa
mãn của con người sau khi tiêu dùng một
hàng hóa, dịch vụ nào đó.
� Ba giả thuyết cơ bản về thị hiếu con người:
� Người tiêu dùng có thể so sánh, xếp hạng các
tập hợp hàng hóa theo sự ưa thích hay tính
hữu dụng mà chúng đem lại.
� Thị hiếu có tính "bắc cầu".
� Người tiêu dùng thích nhiều hàng hóa hơn ít. 3 1 1/2/2012 II.1 Tổng hữu dụng
� Trong trường hợp lý tưởng, chúng ta giả
sử hữu dụng có thể được đo lường bằng
số và đơn vị của phép đo lường này là đơn vị hữu dụng (đvhd).
� Tổng hữu dụng là toàn bộ lượng thỏa mãn
đạt được do tiêu dùng một số lượng hàng
hóa hay một tập hợp các hàng hóa, dịch vụ
nào đó hay tham gia một hoạt động nào đó
trong một khoảng thời gian nhất định. 4
Bảng 3.1 Tổng hữu dụng và hữu dụng biên
khi sử dụng một hàng hóa X
Lượng tiêu dùng Tổng hữu dụng Hữu dụng biên (X) U(X) MU(X) (1) (2) (3) 0 0 - 1 4 4 2 7 3 3 9 2 4 10 1 5 10 0 6 9 -1 7 7 -2 5 II.1 TỔNG HỮU DỤNG
� Như vậy, mức hữu dụng mà một cá
nhân có được từ việc tiêu dùng phụ
thuộc vào số lượng hàng hóa, dịch vụ
mà cá nhân đó tiêu dùng.
� Hàm hữu dụng biểu diễn mối liên hệ
giữa số lượng hàng hóa, dịch vụ được
tiêu dùng và mức hữu dụng mà một cá
nhân đạt được từ việc tiêu dùng số
lượng hàng hóa, dịch vụ đó. 6 2 1/2/2012 Hàm hữu dụng
� Nếu một cá nhân tiêu dùng một loại hàng hóa X
thì hàm hữu dụng có dạng: U = U(X) (3.1)
trong đó: U là tổng hữu dụng và X là số lượng
hàng hóa được tiêu dùng. Lưu ý: X vừa được
dùng để chỉ tên của hàng hóa và cũng đồng
thời là số lượng hàng hóa được tiêu dùng.
� Nếu một cá nhân tiêu dùng một tập hợp hai hay
nhiều hàng hóa: X, Y, Z,... thì hàm tổng hữu dụng có dạng: U = U(X, Y, Z, ...) (3.2) 7 II.2 HỮU DỤNG BIÊN
� Hữu dụng biên là phần thay đổi trong
tổng số hữu dụng do sử dụng thêm hay
bớt một đơn vị sản phẩm hay hàng hóa nào đó. � Theo định nghĩa: � MU = U dU � (3.3) �X dX
Vậy, hữu dụng biên chính là đạo hàm của
tổng hữu dụng theo số lượng hàng hóa. 8 II.2 HỮU DỤNG BIÊN
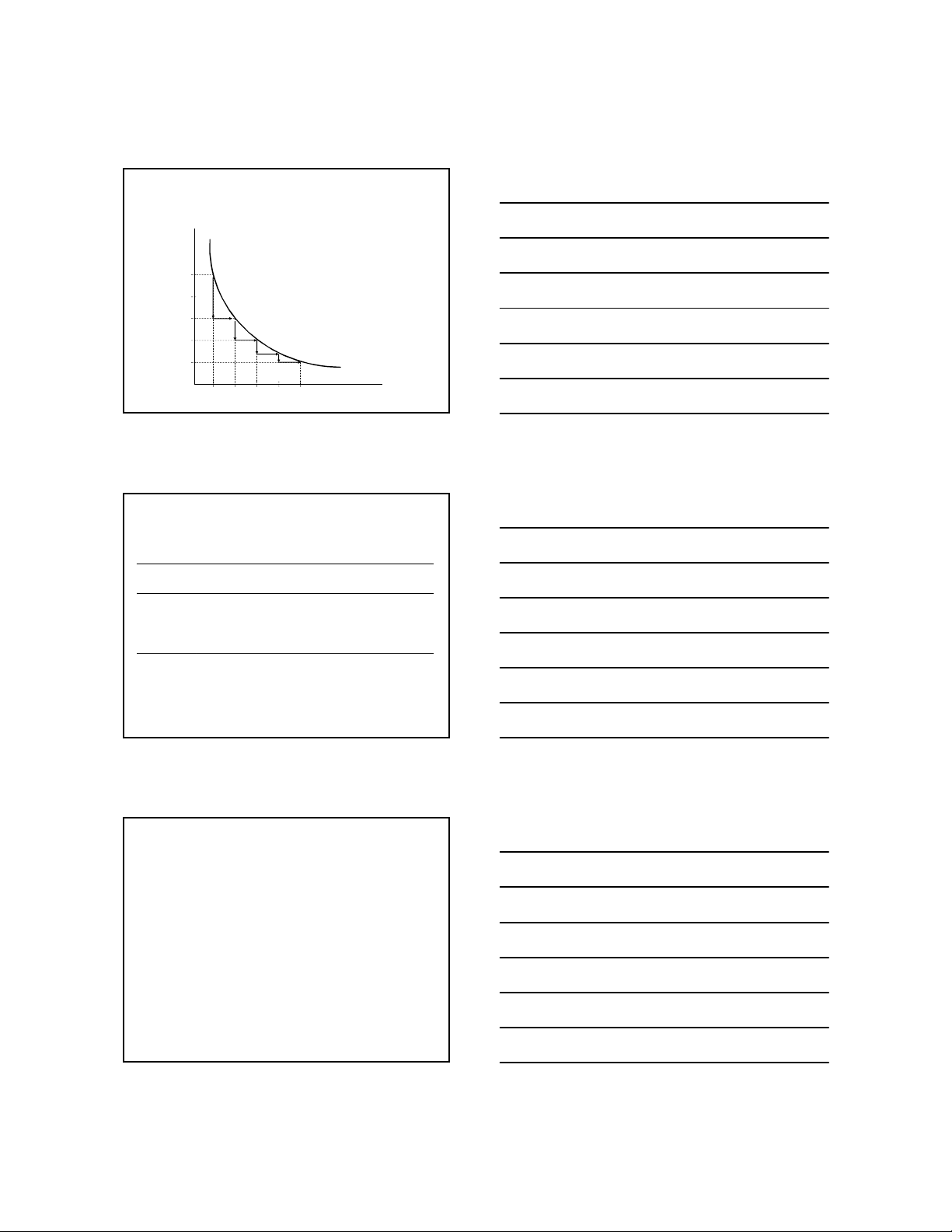
• Hữu dụng biên có xu hướng giảm dần khi số
lượng hàng hóa, dịch vụ được tiêu thụ tăng lên.
• Thông thường, một cá nhân chỉ tiêu dùng thêm
hàng hóa, dịch vụ khi hữu dụng biên vẫn còn giá
trị dương bởi vì một người chỉ tiêu dùng khi cần
thỏa mãn thêm từ hàng hóa, dịch vụ.
• Do đó, các hàm số (3.1), (3.2) được giả định là
các hàm số liên tục và có đạo hàm riêng theo các
biến X, Y, Z, ... là các hàm số liên tục và có giá trị dương giảm dần. 9 3 1/2/2012 II ĐƯỜNG CONG BÀNG QUAN VỀ HỮU DỤNG II.1 ĐƯỜNG CONG BÀNG QUAN
Đường cong bàng quan (về hữu dụng) là
đường tập hợp các phối hợp khác nhau
về mặt số lượng của hai hay nhiều loại
hàng hóa, dịch vụ tạo ra một mức hữu
dụng như nhau cho người tiêu dùng. 10 phim Vùng ưa thích hơn n xem � D ố lầ S � C ? A YA � � B Vùng kém � ? ưa thích E XA Số bữa ăn
Hình 3.1 Xếp hạng các tập hợp hàng hóa 11
Bảng 3.2 Các tập hợp hàng hóa tạo ra
cùng một mức hữu dụng Tập hợp Số bữa ăn Số lần Hữu (X) xem phim dụng (Y) (U) A 1 5 10 B 2 3 10 C 3 2 10 D 5 1 10 12 4 1/2/2012
• Một mức hữu dụng hay mức thỏa mãn
cụ thể có thể được tạo ra từ nhiều tập hợp hàng hóa khác nhau.
• Giả sử một cá nhân tiêu dùng hai loại
hàng hóa X và Y. Phương trình của
đường bàng quan đối với hai loại hàng
hóa X và Y sẽ có dạng: U0 = U(X, Y) (3.5)
Trong đó: U0 không đổi, chỉ có số lượng
X và Y thay đổi để đạt hữu dụng U0. 13
Hình 3.2. Đường cong bàng quan Hướng tăng lên của hữu dụng vé phim ố �C S A YA � U2 U1 YB �B U0 XA XB Số bữa ăn 14
Đặc điểm của đường cong bàng quan
�Tất cả những phối hợp nằm trên cùng một
đường cong mang lại một mức hữu dụng như nhau.
�Tất cả những phối hợp nằm trên đường cong
bàng quan phía trên (phía dưới) đem lại hữu dụng cao hơn (thấp hơn).
�Đường cong bàng quan thường dốc xuống
về hướng bên phải và lồi về phía gốc tọa độ.
�Những đường cong bàng quan không bao giờ cắt nhau. 15 5 1/2/2012 Y �B C � � A U' U X
Hình 3.3 Các đường cong bàng quan không thể cắt nhau 16
II.2 TỶ LỆ THAY THẾ BIÊN (MRS) �
Khi di chuyển dọc theo đường cong
U0, số bữa ăn của cá nhân tăng lên,
trong khi số lần xem phim giảm xuống để
các điểm vẫn còn nằm trên đường cong. �
Sự tiêu dùng của cá nhân biểu hiện
sự đánh đổi giữa hai hàng hóa X và Y để
giữ mức hữu dụng không đổi. 17
II.2 TỶ LỆ THAY THẾ BIÊN (MRS)
Tỷ lệ thay thế biên của hàng hóa X cho hàng
hóa Y là số lượng hàng hóa Y mà cá nhân
phải bớt đi để tăng thêm một đơn vị hàng
hóa X mà không làm thay đổi hữu dụng. Công thức: �Y dY MRS � � � � X � dX U � 0 U U � 0 U
Vậy, nghịch dấu với độ dốc của đường cong bàng
quan tại một điểm nào đó chính là tỷ lệ thay thế
biên giữa hai sản phẩm Y và X tại điểm đó. 18 6 1/2/2012
Hình 3.4 Tỷ lệ thay thế biên Y �A -2 +1 �B -1 �C -2/3 D � U0 X 19
Bảng 3.3 Tỷ lệ thay thế biên của các tập hợp
hàng hóa nằm trên một đường bàng quan
Tập hợp Bữa ăn (X) Xem phim Tỷ lệ thay thế (Y) biên (MRS) A 1 5 2 B 2 3 1 C 3 2 1/2 D 5 1 20
Sở thích của người tiêu dùng cho thấy
một tỷ lệ thay thế biên giảm dần: để
giữ mức hữu dụng không đổi, cần
phải hy sinh một khối lượng giảm dần
của một mặt hàng để sau đó đạt được
một sự gia tăng tương ứng trong khối
lượng của mặt hàng khác. 21 7 1/2/2012
II.3 Mối quan hệ giữa hữu dụng biên và tỷ lệ thay thế biên
� Khi giảm tiêu dùng một số lượng của hàng hóa
Y, làm cá nhân kém thỏa mãn hơn một lượng MU � Y Y .
� Lượng giảm sút của hữu dụng này sẽ được
thay thế bằng việc tăng tiêu dùng hàng hóa X.
Lượng hữu dụng tăng thêm từ việc tăng X (MU � X
X) phải bù đắp vừa đủ lượng hữu dụng
mất đi từ việc giảm Y. Do vậy: 22 MU � � Y Y + MUX X = 0
� MUX�X � -MUY�Y �Y MUX MUX � - � hay MRS � �X MUY MUY
Vì vậy, tỷ lệ thay thế biên của X cho Y bằng
với tỷ số của hữu dụng biên của X và Y. 23 Ví dụ.
Giả sử một cá nhân nào đó có phương
trình hữu dụng như sau: U = XY .
Hãy thiết lập biểu thức tính MRS.
Ta có hai cách tìm ra tỷ lệ thay thế biên:
Cách 1: ta thiết lập hàm số của Y theo
X và tính đạo hàm của Y theo X. 24 8 1/2/2012 Cách 1: U � XY U 2 � Y � X dY U 2 U 2 Y � � � � � � � dX X 2 X.X X dY Y � MRS � - � dX X 25
Cách 2: tính hữu dụng biên của X và Y và lập tỷ số: �U Y MU X � � �X 2 XY �U X MU Y � � �Y 2 XY MU X Y � � MU Y X Y � MRS � X
Nhận xét: khi số lượng hàng hóa X mà cá nhân tiêu
dùng tăng dần, tỷ lệ thay thế biên của nó giảm dần. 26
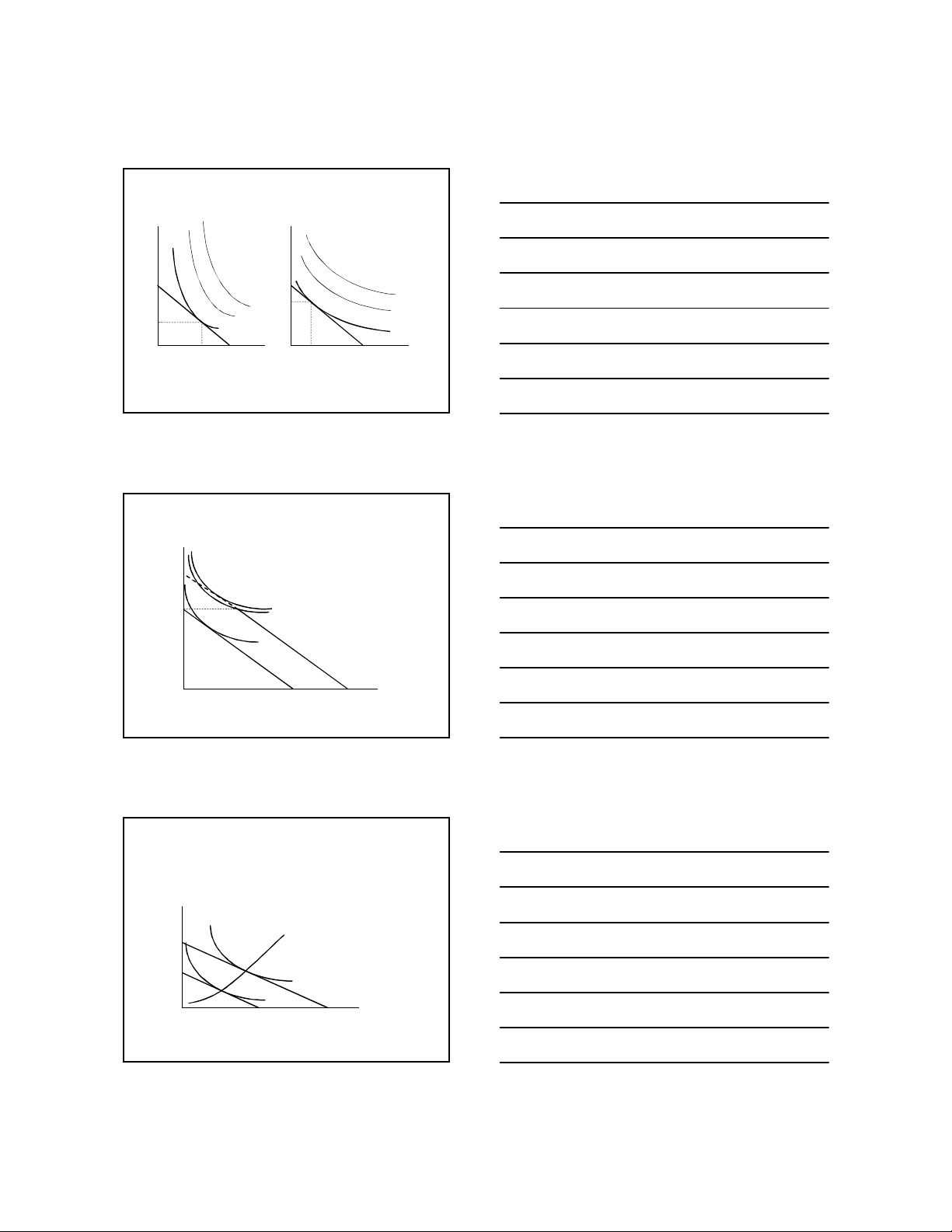
II.4 ĐƯỜNG CONG BÀNG QUAN ĐỐI VỚI CÁC SỞ THÍCH KHÁC NHAU Số vé phim Số vé phim �A U3 B U2 � �A U3 �B U U U2 1 1 Số bữa ăn Số bữa ăn
Đồ thị 3.5.a Người háu ăn
Đồ thị 3.5.b Người thích xem phim 27 9 1/2/2012
� Để giữ mức hữu dụng không đổi, một
người háu ăn sẽ hy sinh một số lượng lớn
các lần xem phim để có thêm một bữa ăn:
tỷ lệ thay thế biên của bữa ăn rất lớn. Do
vậy, đường cong bàng quan của người này dốc hơn.
� Ngược lại, một người thích xem phim sẽ hy
sinh nhiều bữa ăn để có thêm một vé xem
phim. Tỷ lệ thay thế biên của bữa ăn rất
thấp. Do vậy, đường cong bàng quan của
người này phẳng hơn so với người kia. 28 III. ĐƯỜNG NGÂN SÁCH
(ĐƯỜNG GIỚI HẠN TIÊU DÙNG) III. 1 ĐƯỜNG NGÂN SÁCH
Giả sử cá nhân này có 50 đơn vị tiền và
giá của một lần xem phim là 10 đơn vị
tiền và của một bữa ăn là 5 đơn vị tiền.
Cá nhân này có thể mua được một trong
những tập hợp hàng hóa như trình bày trong bảng 3.4. 29
Bảng 3.4 Những tập hợp hàng hóa có thể mua Tập Số Số tiền Số lần Số tiền chi Tổng hợp bữa chi xem cho xem số tiền ăn cho bữa phim phim ăn A 0 0 5 50 50 B 2 10 4 40 50 C 4 20 3 30 50 D 6 30 2 20 50 E 8 40 1 10 50 F 10 50 0 0 50 30 10 1/2/2012 Khái niệm
Đường ngân sách hay giới hạn tiêu dùng là
đường thể hiện các phối hợp có thể có giữa
hai hay nhiều sản phẩm mà người tiêu dùng
có thể mua vào một thời điểm nhất định với
mức giá và thu nhập bằng tiền nhất định của người tiêu dùng đó.
Giả sử một cá nhân có số tiền là I, dùng chi tiêu
cho hai hàng hóa là X và Y có giá lần lượt là PX và
PY. Những tập hợp X và Y mà cá nhân mua được
phải thỏa mãn phương trình:
I = XPX + YPY hay Y = I/PY + PX/PY X (3.9)31
Hình 3.7 Đường ngân sách Y Đường ngân sách E I/P � Y I = XPX + YPY C Điểm không thể � đạt được YA A � �D �B YB F � XA XB I/PX X 32
Sự đánh đổi giữa X và Y
� Trượt dọc theo đường ngân sách, cá nhân thể
hiện sự đánh đổi giữa hai hàng hóa: nếu cá nhân
muốn mua nhiều bữa ăn hơn thì phải giảm bớt số
lần xem phim. Mỗi lần tăng thêm hai bữa ăn, cá
nhân phải đánh đổi hết một lần xem phim.
� Độ lớn của sự đánh đổi bằng với tỷ giá của bữa ăn
và vé xem phim (5/10= 0,5).
� Tỷ giá của hai hàng hóa X và Y cũng chính là độ
dốc của đường ngân sách. Độ dốc I/ Y P X P S � � I/ X P Y P 33 11 1/2/2012 III. 2 TÁC ĐỘNG CỦA SỰ THAY
ĐỔI VỀ THU NHẬP VÀ GIÁ CẢ ĐỐI VỚI ĐƯỜNG NGÂN SÁCH
III.2.1 Sự thay đổi của thu nhập
Chúng ta sẽ xem xét tác động của thu nhập
bằng việc vẽ các đường ngân sách của cá
nhân ứng với các mức thu nhập là 50; 30 và
80 và của vé phim là 10 và của bữa ăn là 5. 34 10 im ph 5 em X I = 80 I = 50 0 I = 30 0 5 10 15 20 Bæîa àn
Hình 3.9 Tác động của sự thay đổi thu nhập đối với đường ngân sách 35 3
III.2.1 Sự thay đổi của thu nhập
Vậy, khi thu nhập thay đổi đường ngân sách sẽ tịnh tiến.
� Nếu thu nhập tăng, đường ngân sách
dịch chuyển sang phía phải, cá nhân có
thể mua được nhiều hàng hóa hơn.
� Nếu thu nhập giảm, đường ngân sách
dịch chuyển sang phía trái, cá nhân
mua được ít hàng hóa hơn. 36 12 1/2/2012
III.2.2 Sự thay đổi của giá cả
� Khi tỷ giá của các hàng hóa thay đổi sẽ
làm cho độ dốc của đường ngân sách thay đổi.
� Chúng ta sẽ xem xét tác động của giá
cả bằng việc vẽ các đường ngân sách
của cá nhân ứng với các mức giá của
bữa ăn là 5; 10 và 2 và của vé phim là
10. Cá nhân có mức thu nhập chung là 50 đvt. 37 6 A' A 4 phim em 2 X 0 F' F F' 0 5 10 15 20 25 30 Bæîa àn
Hình 3.10 Tác động của sự thay đổi giá cả đối với đường ngân sách 38
III.2.2 Sự thay đổi của giá cả �
Vậy, khi giá của bữa ăn tăng lên, đường
ngân sách sẽ quay quanh điểm A vào phía
trong. Cá nhân mua được ít bữa ăn hơn. �
Khi giá của bữa ăn giảm, đường ngân
sách sẽ quay quanh điểm A ra phía ngòai.
Cá nhân mua được nhiều bữa ăn hơn. �
Tương tự, khi giá vé xem phim thay đổi
đường ngân sách sẽ quay dọc trục tung. 39 13 1/2/2012
IV NGUYÊN TẮC TỐI ĐA HÓA HỮU DỤNG
IV.1 NGUYÊN TẮC TỐI ĐA HÓA HỮU DỤNG
Tập hợp hàng hóa mang lại hữu dụng tối đa
phải thỏa mãn 2 điều kiện:
� Tập hợp hàng hóa phải nằm trên đường ngân sách.
� Tập hợp hàng hóa phải mang lại mức hữu
dụng cao nhất cho cá nhân. 40
Hình 3.11. Nguyên tắc tối đa hóa hữu dụng Y 5 A � C U Y � 3 C U2 B U1 � O XC 10 X 41 Nguyên tắc
Để tối đa hóa hữu dụng, ứng với một số tiền
nhất định nào đó, một cá nhân sẽ mua số
lượng hàng hóa X và Y với tổng số tiền đó
và tại đó tỷ lệ thay thế biên (MRS) bằng với
tỷ giá của hai loại hàng hóa đó.
Vậy: một tập hợp hàng hóa X và Y tối đa
hóa hữu dụng phải thỏa mãn 2 phương trình sau: I = XPX + YPY (1) X P M X U X P MR S � hay � (2) 42 Y P M Y U Y P 14 1/2/2012 Ví dụ 1
Giả sử một cá nhân có hàm tổng hữu
dụng khi tiêu dùng hai hàng hóa X và Y như sau: U = X0,5Y0,5.
Đơn giá của hàng hóa X Y là 0,25 đvt,
của hàng hóa là 1 đvt. Một cá nhân có 2
đơn vị tiền để tiêu xài. Cá nhân sẽ có
sự lựa chọn như thế nào?
Giải: Phương trình đường ngân sách: 2 = 0,25X + Y (1) 43 Ví dụ 1
Hữu dụng biên của X và Y: U � -0,5 0,5 X MU � � 0,5X Y X � U � 0,5 -0,5 Y MU � � 0,5X Y Y �
Để tối đa hóa hữu dụng, thì: MUX PX 0,5X -0,5Y 0,5 0,25 � � � MUY PY 0,5X 0,5Y -0,5 1 Y �
� 0,25 � Y � 0,25X (2) X 44 Ví dụ 1
Giải hệ (1) và (2), ta được: X = 4 Y = 1
Khi đó hữu dụng tối đa đạt được là: U = 40,510,5 = 2 Số tiền chi cho X là: IX = 4x0,25 = 1đvt Số tiền chi cho Y là: IY = 1x1 = 1đvt 45 15 1/2/2012
Ví dụ 2: Thiết kế xe gắn máy mới iểu dáng iểu dáng K K 10 10 U U3 3 � 7 U U2 2 3 � U1 U1 7 10 Hiệu năng 3 10 Hiệu năng
HÌnh 3.12.a Nhóm thích hiệu Hình 3.12.b Nhóm thích kiểu năng dáng 46
Ví dụ 3: Trợ cấp bằng tiền hay hiện vật? phim A�' em X E' � U A� � 1 E B � U2 U0 F F' � � 10 14 Bữa ăn 47
V ẢNH HƯỞNG CỦA THU NHẬP ĐẾN SỰ LỰA CHỌN CỦA NGƯỜI TIÊU DÙNG Xem phim Đường mở rộng A' thu nhập C' A � U1 C� U0 F F' Bữa ăn
Hình 3.13 Ảnh hưởng của sự gia tăng thu nhập 48 16 1/2/2012 Xem phim Đường mở rộng thu nhập C' � U3 C' � U C 2 � U1 X X Bữa ăn 1 3 X2
Hình 3.14 Thu nhập tăng làm giảm cầu của hàng thứ cấp 49 Đường Engel
� Đường Engel biểu diễn mối quan hệ giữa
lượng hàng hóa tiêu dùng và thu nhập.
� Đối với hàng bình thường, khi thu nhập
tăng, tiêu dùng hàng hóa này tăng nên đường Engel dốc lên.
� Đường Engel của hàng thứ cấp có một
khoảng quay vòng ra phía sau do tiêu
dùng giảm khi thu nhập tăng. 50 Thu Đường Đường Thu nhập Engel Engel nhập C' Hàng I3 C' � thứ � C' cấp I2 � C'� C I � Hàng 1 C bình � thường X X X X 1 2 X3 a) Hàng bình thường b) Hàng thứ cấp
Hình 3.15 Đường Engel đối với hàng bình thường và hàng thứ cấp 51 17 1/2/2012
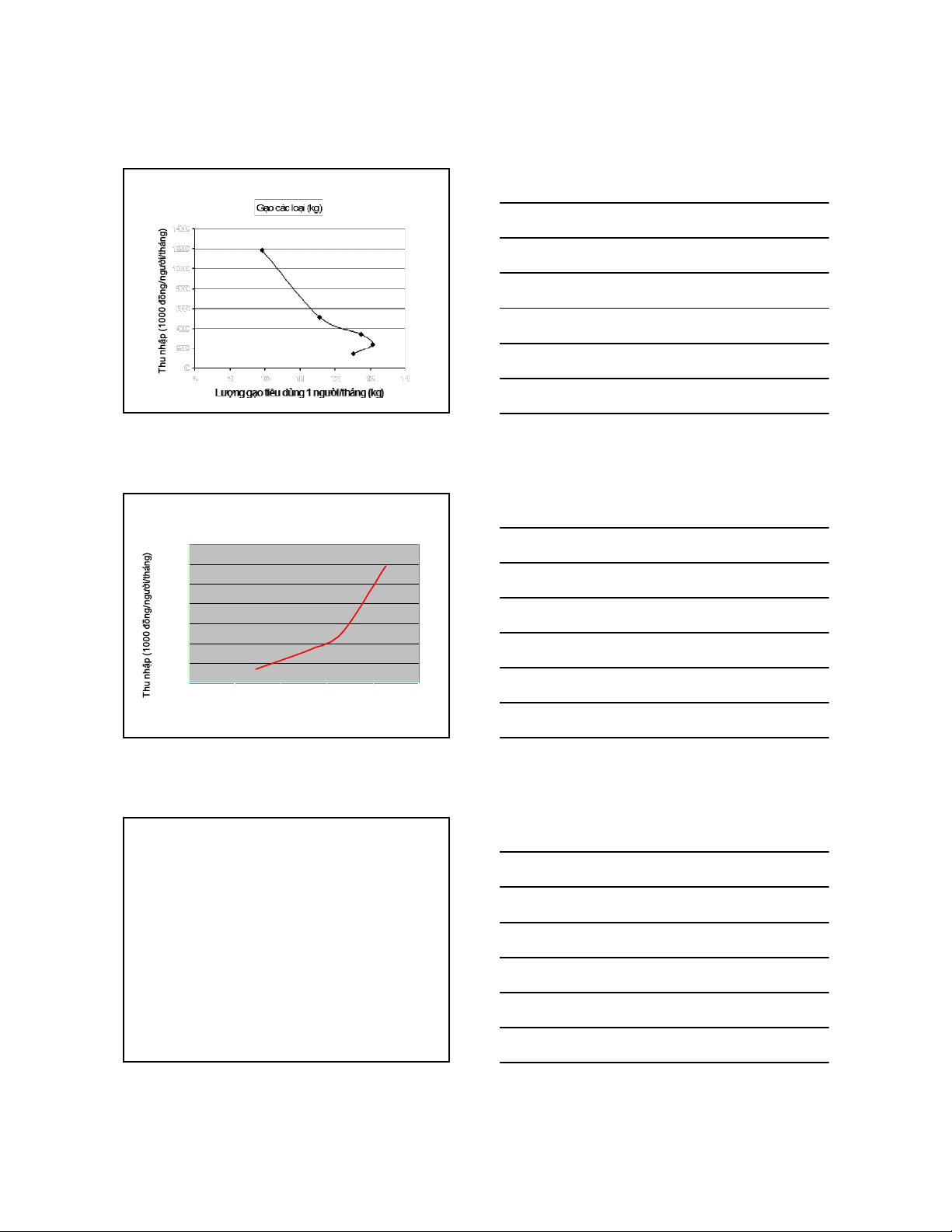
Đường Engel đối với gạo (năm 2004) 52
Đường Engel đối với thịt (năm 2004) 1400 1200 1000 800 600 400 200 0 0 0.5 1 1.5 2 2.5
Lượng thịt tiêu dùng 1 người/tháng (kg) 53
VI ĐƯỜNG CẦU CÁ NHÂN
• Giả sử một cá nhân có khoản thu nhập I
để chi cho hai hàng hóa X và Y, có giá
lần lượt là PX và PY.
• Chúng ta khảo sát việc tối đa hóa hữu
dụng của một cá nhân qua 3 mức giá khác nhau của X (P 1 2 3
X >PX >PX ) , trong
khi giá của hàng hóa Y là PY và thu nhập không đổi. 54 18 1/2/2012 Y U
Hình 3.15. Đường cầu 1 U2 U3 cá nhân Y1 � Y2 C �C’ �C’ Y3 I1 I2 I3 X1 X2 X3 X P X P C X1 � P C’ X2 � C’ PX3 � DX X1 X2 X3 X 55 Đường cầu cá nhân
� Đường cầu cá nhân của một người tiêu dùng
đối với một hàng hóa nào đó được xác định
bởi số lượng hàng hóa người đó mua ứng với
các mức giá khác nhau.
� Đường cầu cá nhân có độ dốc đi xuống về
phía phải. Đường cầu này có hai đặc tính quan trọng:
� Độ hữu dụng đạt được thay đổi khi di chuyển dọc
theo đường cầu. Giá sản phẩm càng thấp, độ hữu
dụng đạt được càng cao.
� Tại mỗi điểm trên đường cầu, cá nhân đều tối đa hóa hữu dụng. 56 Ví dụ
Một cá nhân có hàm hữu dụng đối với hai hàng hóa X và Y như sau: U = 2 - 1/X - 1/Y
trong đó X và Y � 1. Hãy thiết lập hàm số cầu
của cá nhân này đối với X và Y. Giải:
Phương trình đường ngân sách: I = XPX + YPY (1)
Hữu dụng biên của X và Y: MUX = 1/X2 MUY = 1/Y2 57 19 1/2/2012
Để tối đa hóa hữu dụng thì: 2 M X U X P 1/X PX � � � 2 M Y U Y P 1/Y PY 2 Y PX � � 2 X PY X P � Y � X Y P (2)
Thế (2) vào (1), ta được: X P I � X X P � X Y P � X X P � X X P Y P Y P 58 I � X � X P � X P Y P và I Y � Y P � X P Y P
Biểu thức của X và Y trên là các hàm số cầu
của cá nhân đối với X và Y. Ta thấy:
• X và Y nghịch biến với giá của chúng.
• Khi giá của Y tăng thì cá nhân sẽ mua X giảm
và khi giá của X tăng thì Y giảm nên X và Y là cặp hàng bổ sung. 59
VII ĐƯỜNG CẦU THỊ TRƯỜNG
• Mỗi cá nhân trên thị trường có sở thích
khác nhau về một hàng hóa X nào đó
nên hàm số cầu của mỗi cá nhân đối với X sẽ khác nhau.
• Giả sử trên thị trường chỉ có hai người
tiêu dùng hàng hóa X. Giả sử hàm số
cầu của người tiêu dùng thứ nhất được
ký hiệu là X1 và của người thứ hai là X2.
• Như thế, hàm số cầu của thị trường là: X = X1 + X2 60 20