Đề cương ôn tập lý thuyết thi cuối kỳ môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

TỔNG HỢP LÝ THUYẾT THI TỰ LUẬN CUỐI KỲ PHÀN 1: ĐIỆN
Câu 1. Phát biểu định luật Coulomb. Định nghĩa điện trường. Nêu đặc điểm của
véctơ cường độ điện trường. Phát biểu nguyên lý chồng chất điện trường. Giải:
• Phát biểu định luật Coulomb:
Lực tương tác tĩnh điện giữa hai điện tích điểm q1và q2đặt cách nhau một khoảng r:
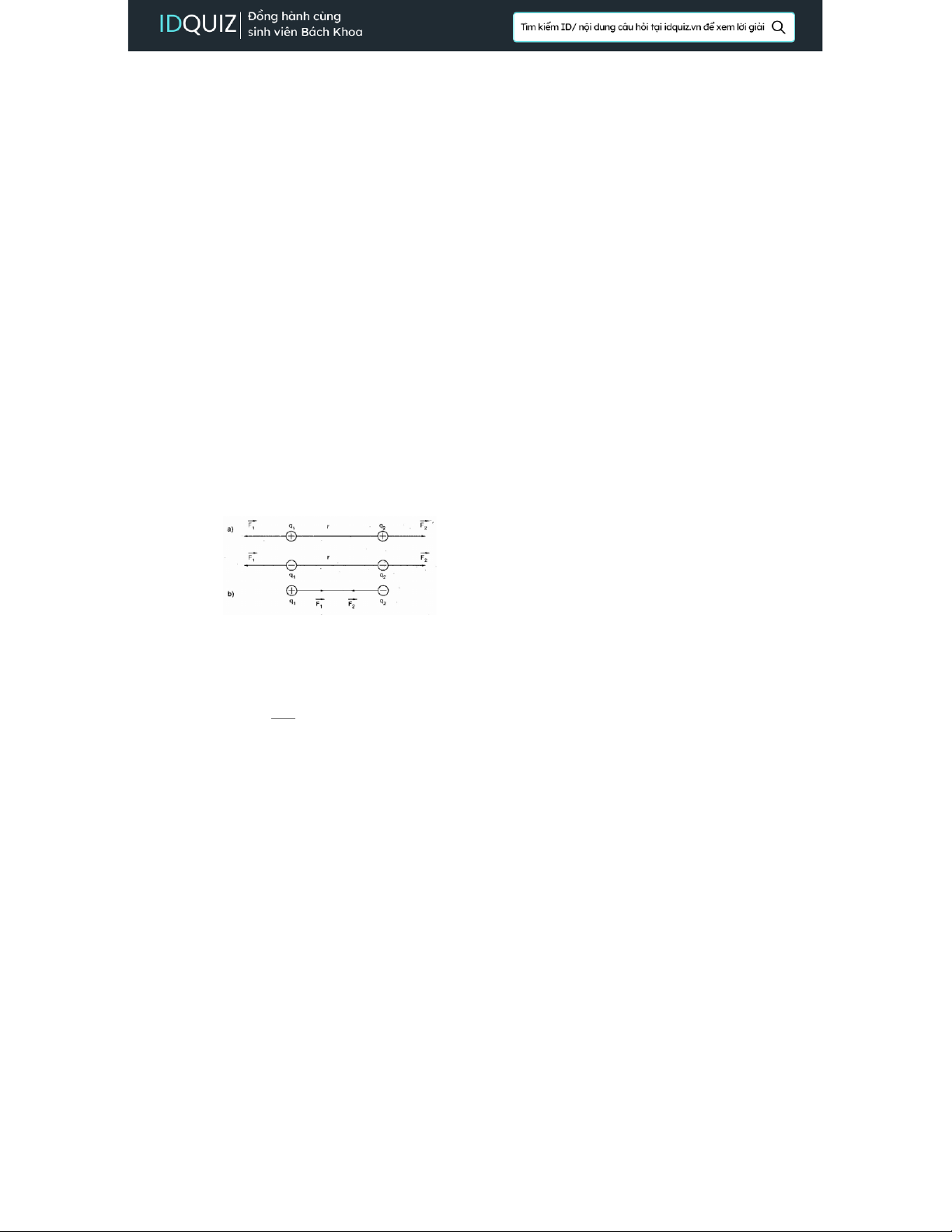
• Có phương nằm trên đường thẳng nối q1và q2
• Có chiều như hình 1.1 a khi q1, q2cùng dấu, hoặc có chiều như hình 1.1 b khi q q2trái dấu
• Có độ lớn tỷ lệ thuận với tích các độ lớn của hai điện tích và tỷ lệ nghịch với phương khoảng cách r
• Phụ thuộc vào môi trường xung quanh ε Hinh 1.1
• Công thức tính độ lớn lực tương tác giữa 2 điện tích:
F=k·q1q2εr2với k=9.109hằng số Coulomb Nm2/C2  
• Định nghĩa điện trường:
• Điện trường là một dạng vật chất tồn tại trong không gian xung quanh điện tích
và gắn liền với điện tích. Đặc trưng của điện trường là gây ra lực điện tác dụn
lên mọi vật tích điện khác đặt trong khoảng không gian có điện trường.
• Đặc điểm của vecto Cường độ điện trường (tĩnh):
• Điểm đặt: VectơEcó điểm đặt tại vị trí mà ta xét cường độ điện trường.
• Phương: Vectơ cường độ điện trường tại một điểm có phương trùng với phương
của lực điện tác dụng lên một điện tích dương thử qqq đặt tại điểm đó. • Chiều: • vectơ 
Ecó chiều hướng ra xa Q nếu Q >0. • vectơ 
Ecó chiều hướng về phía Q nếu Q <0. • Độ lớn: E=k·|Q| εr2 Trong đó:
• E: độ lớn cường độ điện trường (V/m), +k= 9×109hằng số Coulomb Nm2/C2  
+Q : điện tích tạo ra điện trường (C)
+r : khoảng cách từ điện tích Q đến điểm cần xét (m) +ε: hằng số điện môi
• Nguyên lý chồng chất điện trường: Vectơ điện trường tại Mdo một hệ điện tích
điểm gây ra bằng tổng hợp các vectơ điện trường do từng điện tích điểm gây r tại M .  E= − → X Eı i
Câu 2. Nêu cách xác định véctơ cường độ điện trường của điện tích điểm, hệ
điện tích điểm phân bố gián đoạn và hệ điện tích phân bố liên tục. Áp dụng cho
lưỡng cực điện, dây dẫn thẳng dài (vô hạn), vành tròn, đĩa tròn tích điện đều. Giải:
• Cách xác định véctơ cường độ điện trường của điện tích điểm: • Điểm đặt: Vectơ 
Ecó điểm đặt tại vị trí mà ta xét cường độ điện trường.
• Phương: Vectơ cường độ điện trường tại một điểm có phương trùng với phương
của lực điện tác dụng lên một điện tích dương thử q đặt tại điểm đó. • Chiều: • vectơ 
Ecó chiều hướng ra xa Q nếu Q >0. εr2=1 4πεε0|Q| • vectơ 
Ecó chiều hướng về phía Q nếu Q <0. • Độ lớn: E=k·|Q| εr2
• Cách xác định vectơ cường độ điện trường của hệ điện tích điểm phân bố gián đoạn:
• Vecto cường độ điện trường do hệ điện tích điểm tác động lên một vật chính bằng
tổng vecto cường độ điện trường của từng điện tích điểm tác dụng lên điểm ấy E=− →E1+− → E2+· · · =X  − → El i
• Cách xác định vectơ cường độ điện trường của hệ điện tích điểm phân bố liên tục:
• Ta chia nhỏ vật thành nhiều phần nhỏ chứa điện tích dq. Vật mang điện được coi
là hệ gồm vô số điện tích điểm r2·r E= toan bo vat dE = toan bo vat Z Z 1  −→ dq 4πεε0 r
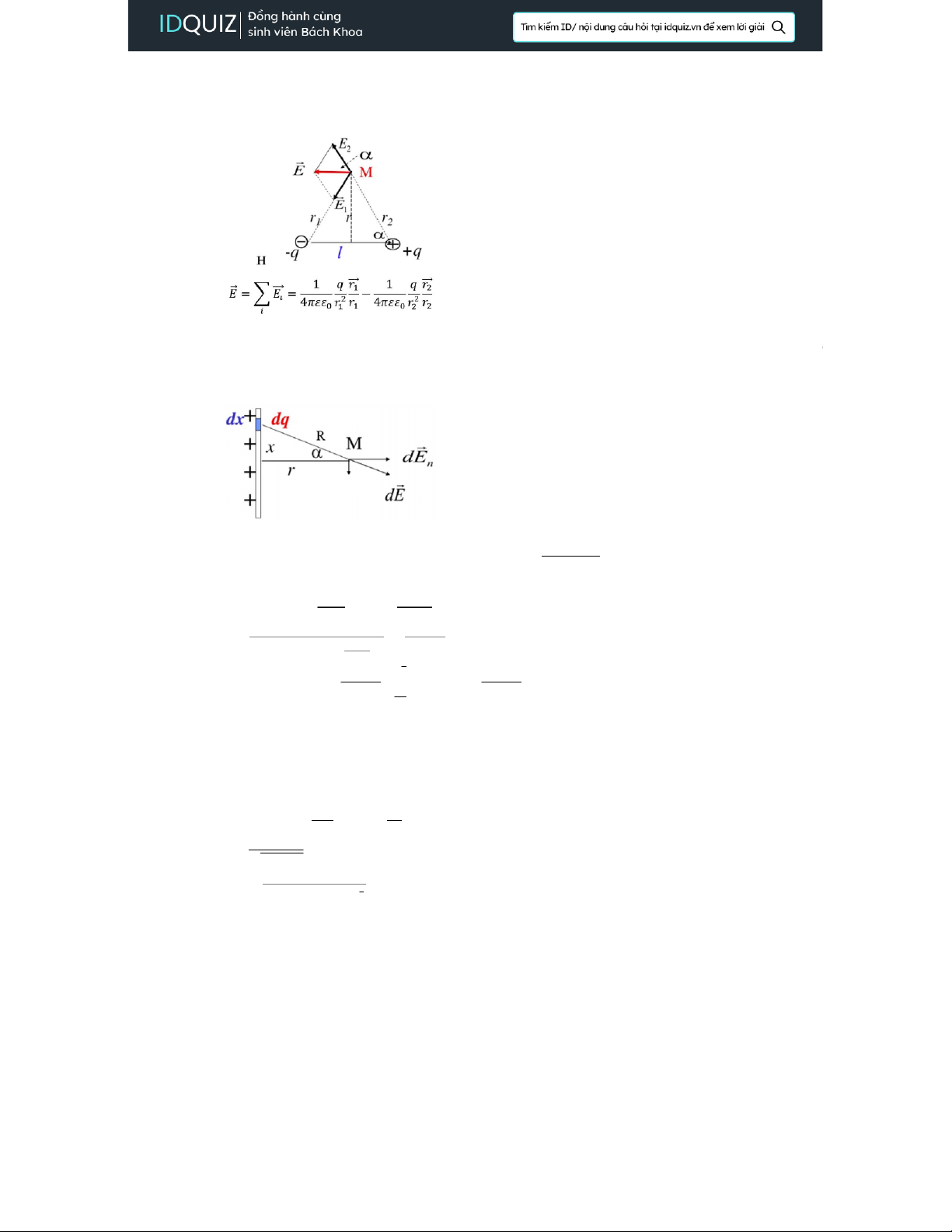
• Áp dụng cho lưỡng cực điện: lưỡng cực điện là một hệ gồm 2 điện tích trái dấ
cùng độ lớn, cách nhau một khoảng lrất nhỏ so với khoảng cách từ điểm cần
xét đến lưỡng cực điện
• Áp dụng cho dây dẫn thẳng dài (vô hạn) tích điện đều: Xét một đoạn dây dẫn c
chiều dài rất nhỏ có cường độ điện trường dE tại một điểm cách dây một khoả r Do −→
Exđối xứng từng đôi ⇒dE =dEy =dE ·cos α=dq ·cos α 4πεεoR2
Mà dq =λdx với λlà mật độ điện dài của dây dẫn x=rtan α⇒dx =rdα co2α;R=r cos α ⇒dE =λ·rdα cos α 2=λ  4πεεordα cos2α·4πεεo r  4πεεor π ⇒E= dE ·cos α=λ Z 2 cos αdα =λ Z π 2πεεor − 2
• Áp dụng cho vành tròn tích điện đều: Chia vành tròn thành những đoạn nhỏ ma điện tích dq. Do −→
Exđối xứng từng đôi ⇒dEy=dE ·cos φ
Mà dq =λ·rdφ =q2πr ·rdφ =q2π·dφ cos φ=h√r2+h2 => dEy=q·hdφ 3 8π2εεo(r2+h2) 2 ⇒E= dE 2 2π y=q.h Z dφ =q.h Z 3 3 8π2εεo(r2+h2) 0 4πεo(r2+h2) 2
• Áp dụng cho đĩa tròn tích điện đều: Chia đĩa tròn thành các vành tròn như hình vẽ. Ta có: dE =dq ·h 3 4πεεo(r2+h2) 2 Mặt khác:
dS =π(r+dr)2−πr2=2πrdr →dq =σdS =σ.2πrdr →dE =σ.2πhrdr 3 4πεεo(r2+h2) 2 2εεo  →E= r  Z σ·2πhrdr =σ 1−1  3 1+  0 4πεεo(r2+h2) r 2 2 q h2
Câu 3. Khảo sát trường hợp hạt tích điện đứng yên và chuyển động trong điện
trường đều. Nguyên tắc cấu tạo và hoạt động của ống tia âm cực. Giải:
• Hạt tích điện đứng yên trong điện trường đều
• Khi đặt hạt tích điện q , khối lượng m đứng yên vào điện trường đều E thì điệ
tích đó sẽ chịu tác dụng của lực điện F
• Lực điện F này có đặc điểm:
• Phương: Trùng với phương của điện trườn Eg 
• Chiều: Cùng chiều với E 
nếu q >0và ngược chiều  Enếu q <0 • Độ lớn: F=|q|E • Gia tốc của hạt: a=F m=|q|E m
→Kết quả là hậ điện tích sẽ chuyển động với gia tốc a=|q|E mdọc theo đường
sức điện trường nếu q >0và ngược chiều đường sức điện nếu q <0
• Hạt tích điện chuyển động trong điện trường đều
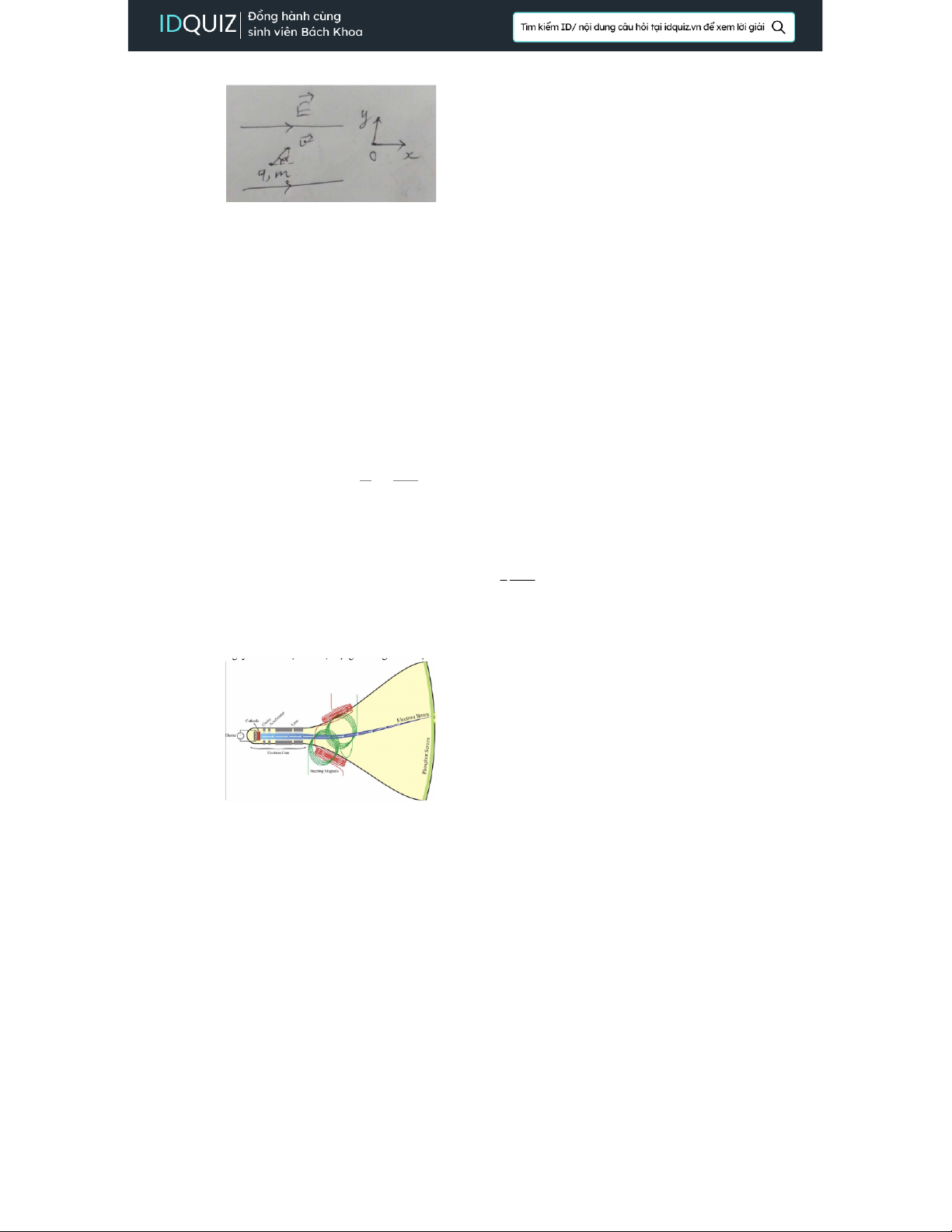
• Khi đặt hạt tích điện q , khối lượng m đang chuyển động với vận tốc v hợp vớ
đường sức điện một góc αvào điện trường đều E thì điện tích đó sẽ chịu tác dụng của lực điện F
• Lực điện F này có đặc điểm:
• Phương: Trùng với phương của điện trườn Eg 
• Chiều: Cùng chiều với E 
nếu q >0và ngược chiều  Enếu q <0 • Độ lớn: F=|q|E • Gia tốc của hạt: a=F m=|q|E m
• Phương trình chuyển động: x=vcos α.t +12|q|E mt2 y=vsin α.t
• Nguyên tắc cấu tạo và hoạt động của ống tia âm cực • Cấu tạo gồm:
• Hai bản kim loại phẳng tích điện trái dấu là catot và anot • Lưới điều khiển • Phiến lệch hướng • Màn hình
• Nguyên tắc hoạt động:
Khi hai phiến kim loại được nối với nhau tới nguồn có hiệu điện thế cao:
• Cực âm ca-tot được nung nóng và phát ra electron tự do
• Điện trường giữa catốt và anot tạo gia tốc cho electron chuyển động
• Các điện trường lệch hướng hoặc từ trường làm thay đổi hướng của tia electron
• Tia electron đập vào màn huỳnh quang làm phát sáng tại điểm va chạm
Câu 4. Phát biểu và chứng minh định lý Ostrogradski-Gauss (Định luật Gauss).
Áp dụng cho trường hợp mặt cầu mang điện đều, mặt phẳng vô hạn mang điện
đều, hai mặt phẳng mang điện tích đối nhau, mặt trụ thẳng dài vô hạn mang điện đều. Giải:
• Phát biểu định lý O −G:Điện thông qua một mặt kín bằng tổng đại số các điện
tích chứa trong mặt kín ấy. ϕe= (S) I  D·dS=X qi i
• Chứng minh định lý O −G cho trường hợp: dϕe= D·dS
=D·ds ·cos α(với αlà góc tạo bởi 
Dvà vecto pháp tuyến n )
=Dn.ds (Dnlà hình chiếu củaD trên n )
Xét một mặt kín là một mặt cầu tâm O, bán kính Rcó: ϕe = S Dnds =q Z 4πr2.4πr2=q
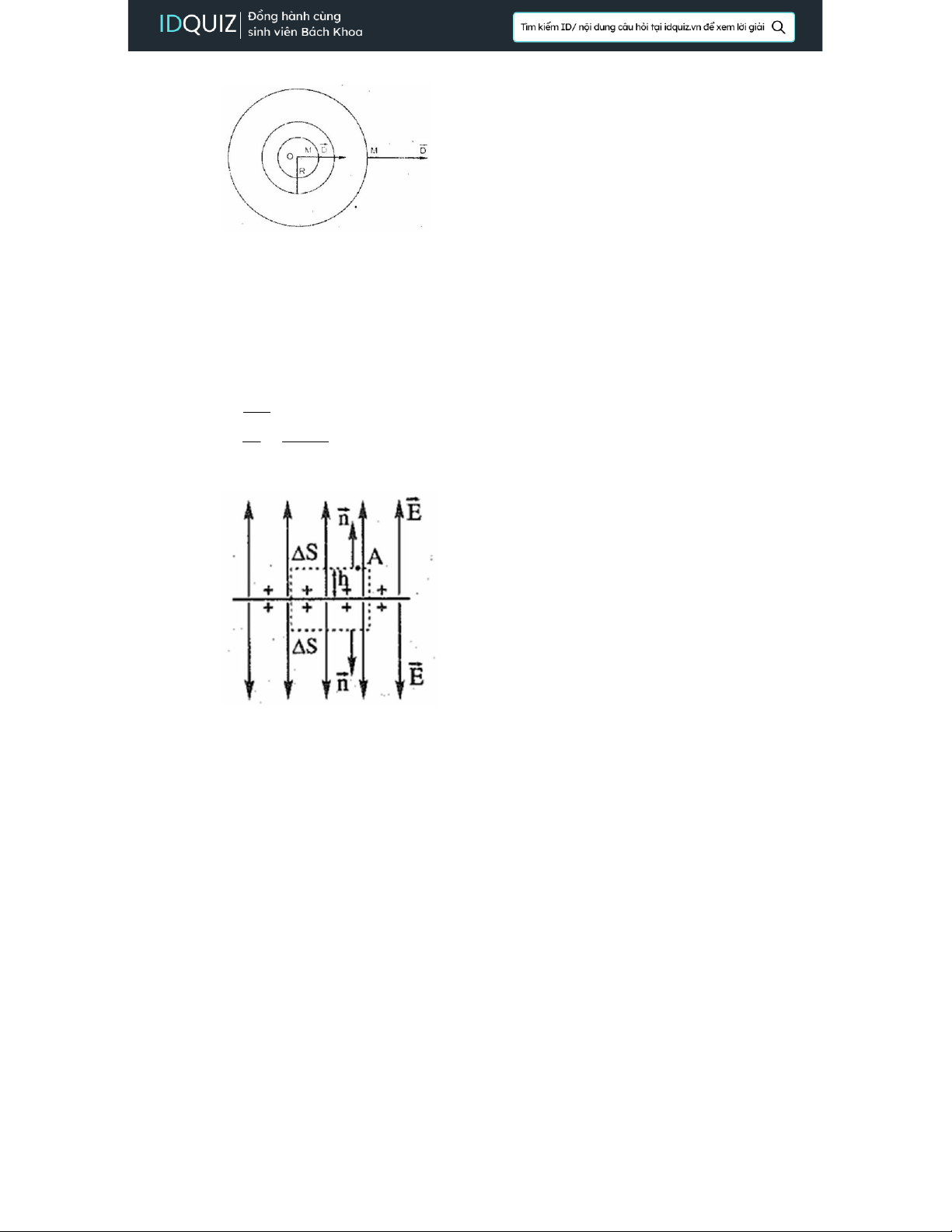
• Áp dụng cho mặt cầu mang điện đều
Điện trường ở đây có tính chất đối xứng cầu: vectơ điện cảm tại M có phương nằm
theo OM và có cường độ chỉ phụ thuộc r. Vẽ mặt cầu S(O,r), điện thông qua S cho bởi: ϕe= (S) S= (S) Z  D·d Z D·dS ·cos 0◦=D (S) Z dS =DS =D4πr2=q →D=q 4πr2 →E=D =q εεo 4πεεor2
• Áp dụng cho mặt phẳng vô hạn mang điện đều
Ta chọn mặt kín S là mặt của một hình trụ (biểu diễn bằng đường nét đứt) có đườ
sinh vuông góc với mặt phẳng, hai đáy song song (đáy trên chứa điểm A ) cách mặ
phẳng một khoảng h và có diện tích ∆S. Chọn chiều dương của pháp tuyến n hướn ra mặt ngoài S .
Điện thông toàn phần qua mặt Schỉ cong bằng điện thông qua hai đáy và có giá trị ϕ=2D·∆S·cos α=2D·∆S=q →D=q 2∆S=σ.∆ 2 S ∆S=σ 2 →E=D =σ εεo 2εεo
• Áp dụng cho hai mặt phẳng mang điện tích đối nhau
Chọn mặt kín S là mặt trụ, có hai đáy song song diện tích ∆S cách đều mặt phẳng
mặt xung quanh hình trụ vuông góc với mặt phẳng. Như vậy điện thông ϕqua toàn
bộ mặt Schỉ còn bằng điện thông qua hai mặt đáy.
Đối với mặt kín S3thì tổng đại số các điện tích bên trong mặt kín là: q=σ.∆S+(−σ.∆S)=0 X
Áp dụng định lý O-G ta được: ϕ= q=0 X
• Áp dụng cho mặt trụ thẳng dài vô hạn mang điện đều
Điện trường ở đây có tính chất đối xứng trụ xung quanh trục z. Vẽ mặt trụ kín S t
z đi qua M , có độ dài bằng l, điện thông qua mặt kín S bằng: Φe=điện thông qua
đáy + điện thông qua mặt bên; trong đó điện thông qua hai đáy bằng 0D (/v/ì vectơ 
mặt đáy), còn điện thông qua mặt bên =2πrlD. →Φ=2πrlD =q. →D=q 2πrl =λ. 2 lπrl =λ 2πr →E=D =λ εεo 2πεε r o
Câu 5. Tính công của lực tĩnh điện. Từ đó chứng tỏ trường tĩnh điện là một trường thế. Giải:
• Công của lực tĩnh điện: Giả sử q, q0>0.
• Công của lực tĩnh điện khi dịch chuyển điện tích điểm q0trong điện trường của điện tích điểm q.
Công của lực tĩnh điện trong chuyển dời vô cùngSn . hỏ d dA = S=q F·dS=q 0·q
0· E·dS=q0·q 4π·ε·ε0·r3·r ·d 4π·ε·ε0r3·dS ·cos α 
Elà véctơ cường độ điện trường gây bởi điện tích q tại q0. α: góc giữa v và d S . dS ·cos α=dr →dA =q 4·q π 0 ·ε·ε0·dr r2
Công chuyển dời q0từ M →N là: AMN= M S= K rN N . Z 4π·ε·ε0 1 q Z 4 q π ··q ε 0
·ε0·dr r2=q·q04π·ε·ε0· −1 r =q·q0 rM−1 rN 0·E·d       N K  M rM
• Chứng tỏ trường tĩnh điện là một trường thế
Trường hợp tổng quát, nếu ta dịch chuyển điện tích q0trong điện trường bất kì thì ta
coi điện trường này như vô số điện tích điểm.
Xét hệ điện tích điểm a1,a2, . . . , an n X
→Lực tĩnh điện tác dụng lên q0 F : =  Fl i=1 →A n n n MN= N i=1 N Z q . Z X  0· 4 a π i F X X i=1
·ε·ε0·riM−q0·ai 4π·ε·ε0·riN l·dS=  Fl·d S=   M i=1 M
Vậy công của lực tĩnh điện trong sự dịch chuyển một điện tích q0trong một điện trườ
bất kì không phụ thuộc vào dạng đường cong dịch chuyển mà chỉ phụ thuộc vào đi đầu và điểm cuối.
→Công của lực tĩnh điện khi dịch chuyển q0theo một đường cong kín bất kì bằng 0
→Trường tĩnh điện là một trường thế: A= q0·  I E·dS=0 hay I E·dS=0.
Câu 6. Dẫn ra công thức tính thế năng của điện tích trong điện trường. Nêu địn
nghĩa, ý nghĩa của điện thế và hiệu điện thế. Nêu định nghĩa và các tính chất của mặt đẳng thế. Giải:
• Công thức tính thế năng của điện tích trong điện trường
• Xét điện tích q đứng yên tạo ra điện trườ E. ng 
• Điện tích q0dịch chuyển từ M→N
⇒qochịu tác dụng của lực tĩnh điện F:F=qo· E Ta có Công: F·− → dA =dl =qo·E·− →dl =qo·E·l·cos ϕ Hay dA =q 4 0 π qεε0·dr r2 Công dA = A rb rb 1 MN= (M N) Z q 4 o π q εoε·dr 2=qoq4πεoεZ d rr 2=qoq4πεoε r  a−1 rb Z ra ra
• Mà công của lực tĩnh điện tác dụng lên điện tích chuyển động trong điện trường
bằng độ giảm thế năng W của điện tích đó trong điện trường. dA =−dW ⇔AMN= N dA = N Z Z M−dW =WM−WN M ⇔WM−WN=qoq 4πε ε o ra−qoq 4πε ε o rb
Vậy biểu thức thể năng của điện tích điểm qo đặt trong điện trường của điện tích
điểm qvà cách điện tích này một đoạn r. W=qoq4πεoεr +C
với C là hằng số tùy ý, W là thế năng tương tác của hệ điện tích qovà q . • Điện thế:
• Định nghĩa điện thế: Điện thế tại một điểm không phụ thuộc vào độ lớn của điệ
tích qomà chỉ phụ thuộc vào các điện tích gây ra điện trường và vào vị trí của
điểm đang xét trong điện trường: V=W = ∞ Z  E·ds qo M
• Ý nghĩa của điện thế: Điện thế tại một điểm trong điện trường là đại lượng có
trị bằng công của lực tĩnh điện trong sự dịch chuyển một đơn vị điện tích dươn
từ điểm đó ra xa vô cùng. • Hiệu điện thế:
• Định nghĩa: Hiệu điện thế giữa hai điểm M và N được tính bằng tỷ số giữa côn
của lực tĩnh điện trong sự dịch chuyển điện tích điểm qotừ điểm M tới điểm N đ
trong điện trường với điện tích qo.
• Ý nghĩa: Hiệu điện thế giữa hai điểm M và N trong điện trường là đại lượng có
trị bằng công của lực tĩnh điện trong sự dịch chuyển một đơn vị điện tích dươn
từ điểm M tới điểm N . • Mặt đẳng thế:
• Định nghĩa: Mặt đẳng thế là quỹ tích những điểm có cùng điện thế.
• Các tính chất của mặt đẳng thế:
• Các mặt đẳng thế không cắt nhau, vì tại mỗi điểm có một giá trị xác định của thế.
• Công của lực điện trong sự dịch chuyển điện tích qotrên một mặt đẳng thế bằng 0 .
• Vectơ điện trường tại một điểm luôn trực giao với mặt đẳng thế đi qua điểm ấy
• Xét 2 mặt đẳng thế gần nhau, Vectơ điện trường có phương trực giao với các
mặt đẳng thế, có chiều là chiều giảm điện thế và có độ lớn bằng độ giảm điện
thế trên đơn vị độ dài dọc theo đường sức.
Câu 7. Trình bày về mối liên hệ giữa cường độ điện trường và điện thế. Áp dụ
cho hai mặt phẳng song song vô hạn mang điện đều, trái dấu; mặt cầu mang
điện đều; mặt trụ thẳng dài vô hạn mang điện đều. Giải:
• Liên hệ giữa cường độ điện trường và điện thế.
• Xét q0di chuyển từ M →N=dℓ Tại   M:V (dV > 0)  N:V+dV
• Có dAMN=F·dℓ=q0Edℓ Mà dAMN=q0[VM−VN]=−q0dV ⇒Edℓ=−dV P
⇔Edℓ cos φ=−dV ⇒cos φ < 0⇒φlà góc tù
⇒Eluôn hướng về phía điện thế giảm (∗)
Chiếu lên phương dịch chuyển ⇒Eℓ=−dV dℓ
• Nếu xét trong hệ Oxyz , có thế viết:  Ex=−∂V ∂x , Ey=−∂V y , Ez=−∂V   ∂z  E=− → Ex+− → Ey+− →
Ez=−ı∂V∂x −ȷ∂V k∂V ∂z = ∂y −−−−−→  − grad V 
Chiếu theo pháp tuyến ⇒E=En=−∂V dn .
• Áp dụng cho 2 mặt phẳng song song vô hạn mang điện đều, trái dấu: E=−dVdr ⇔dV =Edr ⇔ V2V1−dV = d Z Z Edr 0 ⇔V1−V2=Ed
• Áp dụng cho mặt cầu mang điện đều
Điện thế tại điểm M cách tâm O của quả cầu một đoạn r cho bởi công thức:  V=q 4πεoεr nếu r > R  V=q 
4πεoεR =const nếu r < R
Áp dụng công thức: E=−dV ds , ta được:  E=q  4πε ε o r2nếu r > R  E=0 nếu r < R
• Áp dụng cho mặt trụu thẳng dài vô hạn tích điện đều
Giả sử λ > 0. Ta tính điện thế VA−VBgiữa hai điểm A và B cùng nằm trên đường O
vuông góc với dây (OA =rA;OB =гв ) VA−VB= (AB) E·ds = (AB) E·dr = rB Z  Z E·ds v` u Z Edr rA Với E=λ 2πεε r o VA−VB= rB rB Z λ dr r=λ 2πεεoZ dr 2πεε r r o A rA VA−VB=λ ln 1 rA−λ ln 1 2πεεo 2πεεo rB
Từ đây có thể suy ra điện thế tại A và tại B : VA=λ ln 1 +C 2πεεo rA VB=λ ln 1 +C 2πεεo rB
Vậy điện thế tại một điểm M cách dây một khoảng r: V=λ ln 1 r+C 2πεεo
Câu 8. Nêu điều kiện cân bằng tĩnh điện và tính chất của vật dẫn tích điện. Nêu
định nghĩa và công thức tính điện dung của vật dẫn cô lập.
• Điều kiện cân bằng tĩnh điện của một vật dẫn mang điện:
• Véctơ cường độ điện trường tại mọi điểm bên trong vật dẫn phải bằng 0:−→ Etr=0.
• Thành phần tiếp tuyến − →
Etcủa véctơ cường độ điện trường tại mọi điểm trên bề
mặt vật dẫn bằng 0 . Nói cách khác, tại mọi điểm trên mặtEv pậ htảidẫ v n u ,ô  ng góc với vật dẫn: Et − → =0; E=− → En.
• Tính chất của vật dẫn tích điện:
• Vật dẫn tích điện cân bằng là một khối đẳng thế
• Khi vật dẫn tích điện cân bằng, điện tích chỉ phân bố trên bề mặt của vật dẫn
• Nếu trong vật dẫn tích điện cân bằng có những lỗ rỗng thì lý luận tương tự nh
trên ta kết luận được rằng:
• Điện trường trong lố rỗng và ở thành lỗ rỗng bằng 0
• Không có điện tích trong lỗ rỗng và trên thành lỗ rỗng
• Một vật dẫn rỗng hay đặc nếu được giữ ở trạng thái có điện thế luôn không đổ
(chẳng hạn bằng cách nối vật ấy với đất) thì cũng có thể coi là ở trạng thái tíc Etrong =
điện cân bằng, và khi đó: −−−− g → radV  =− → 0.
• Điện dung của vật dẫn cô lập:
• Định nghĩa: Tỷ số không đổi giữa điện tích và điện thế của một vật dẫn có lập
được gọi là điện dung của vật dẫn ấy. • Công thức tính:
Điện dung của vật dẫn được ký hiệu là C :C=q V
Trong hệ SI, điện dung C tính ra đơn vị fara (F).
Câu 9. Định nghĩa hiện tượng điện hưởng. Thế nào là điện hưởng một phần,
điện hưởng toàn phần? Định nghĩa tụ điện. Tính điện dung của tụ phẳng, tụ trụ và tụ cầu. Giải:
• Định nghĩa hiện tượng điện hưởng
• Hiện tượng điện hưởng là hiện tượng các điện tích cảm ứng xuất hiện trên vật
dẫn (lúc đầu không mang điện) khi đặt trong điện trường ngoài.
• Điện hưởng một phần và toàn phần:
• Gọi q và q′lần lượt là điện tích tổng cộng trên vật mang điện A và độ lớn điện
tích cảm ứng xuất hiện trên vật dẫn (BC).
• Nếu chỉ có một số phần đường cảm ứng điện xuất phát từ A tới tận cùng trên
dẫn (BC), còn một số đường cảm ứng điện khác lại đi ra vô cùng.
Hiện tượng này được gọi là điện hưởng 1 phần (độ lớn điện tích cảm ứng nhỏ hơn
độ lớn điện tích trên vật mang điện).
• Nếu vật dẫn (BC) bao bọc hoàn toàn vật mang điện A ; toàn bộ đường cảm ứn
điện xuất phát từ A đèu tận cùng trên vật dẫn (BC)ta có hiện tượng điện hưởng toàn phần.
Trong trường hợp điện hưởng toàn phần, độ lớn của điện tích cảm ứng bằng độ lớn
điện tích trên vật mang điện.
• Định nghĩa tụ điện
• Tụ điện là một hệ hai vật dẫn A,B sao cho vật dẫn B bao bọc hoàn toàn vật d
A ( A,B được gọi là hai bản của tụ điện)
• Điện dung của tụ điện phẳng:
• Hai bản tụ song song, cách nhau một khoảng d.
Nếu d« kích thước mỗi bản, ta coi điện trường giữa hai bản tụ như điện trường gây
ra bởi hai mặt phẳng song song vô
hạn mang điện có mật độ điện mặt như nhau, trái dấu. Ta có: C=Q U.
Mặt khác, hiệu điện thế giữa hai mặt phẳng V vô hạn tích điện đều: U=V1−V2=dσ =dQ ε·ε0·S;σ=Q S:mật độ điện mặt ε·ε0 ε: hằng số điện môi ⇒C=ε·ε0·Sd.
• Điện dung của tụ điện trụ:
Áp dụng định luật Gauss, ta chọn một mặt Gauss là một hình trụ đồng trục với hai
bản tụ, bán kính r, ta có: E·(2πrl)= Q ε=> E =Q 2πεrl
Khi đó, hiệu điện thế của hai bản tụ là: V= R2 Edr = R2 R2 Z Z 2 Q πεrl dr =Q 2πεl Z dr r=Q 2πεl ·ln R2 R R1 1 R1 R1 Mặt khác, C=Q U ⇒C=2πεl ln R2 R1
• Điện dung của tụ điện cầu:
Trong tụ điện cầu, hai bản tụ là hai mặt cầu kim loại đồng tâm bán kính R1, R2bao bọc lẫn nhau: R1< R2.
Hiệu điện thế giữa hai điểm trong điện trường của một mặt cầu mang điện đều - U giữa hai bản. V1−V2=q 4π, ε, ε0 1 =q  R1−1 R2 4π·ε, ε0·R1−R2 . R1R2
Điện dung của tụ điện cầu: C= U Q =4π·ε.ε0·R1R2 . R2−R1
Nếu R1−R2=d≪R1(R2≈R1):C=π·ε.ε0R2 q=ε 1 ·ε0S q.
Câu 10. Chứng minh công thức tính năng lượng tương tác điện của hệ điện
tích điểm, vật dẫn cô lập tích điện, năng lượng tụ điện phẳng và năng lượng điện trường.
• Chứng minh công thức tính năng lượng tương tác điện của hệ điện tích điểm
Năng lượng tương tác của hai điện tích điểm q1và q2đặt cách nhau một khoảng r ch bởi: W=1 q1q r 2 =1 2 q1 1 q 1 q  2 1 r r+q  2 4πε ε o 4πεoε 4πε ε o Trong đó: 1 q2
r=V1là điện thế do q2gây ra tại vị trí q1 4πε0ε 1 q1
r=V2là điện thế do q1gây ra tại vị trí q2 4πε0ε ⇒W=1 2(q1V1+q2V2)
Mở rộng cho hệ n điện tích điểm, ta được: n ⇒W=1 X qiVi 2 i=1
• Chứng minh công thức tính năng lượng của vật dẫn cô lập tích điện
Xét một vật dẫn (cô lập) tích điện và có điện thế V ( V là điện thế chung của mọi
trong vật dẫn). Ta chia vật dẫn thành những phần tử điện tích nhỏ dq: năng lượng
của vật dẫn là năng lượng của hệ các phần tử điện tích dq đó:
W=1 2 V dq (lấy tổng cho cả vật dẫn) X
=12V dq (V không đổi cho cả vật dẫn) X Hay W=12V Q =CV 2 2=1 Q2 2 C
• Chứng minh công thức tính năng tụ điện
Tụ điện là hệ hai vật dẫn ở trạng thái điện hưởng toàn phần, tích điện +Qvà -Q ,
điện thế lần lượt là V1và V2.
Năng lượng của tụ điện cho bởi:
W=1 2V1Q+1 2V2(−Q)= 12Q(V1−V2)
Trong đó Q=C(V1−V2)với C là điện dung của tụ điện Vậy:
W=1 2Q(V1−V2)= 1 2C(V1−V2)2=1 Q2 2 C
• Chứng minh công thức tính năng điện trường
Trong biểu thức tính năng lượng tụ điện: W=1 2C(V1−V2)2
Mà điện dung C cho bởi: C=εoεS
dcòn hiệu điện thế giữa hai bản V1−V2liên hệ với
cường độ điện trường giữa hai bản bởi: E=V1−V2 d=> V1−V2=Ed Vậy W=1 εoεdS E2d2= 1 2εoεE2 Sd = 12ε ∆V    oεE2 2
trong đó ∆V=thế tích khoảng không gian giữa hai bạn tụ điện = bằng thể tích khoản không gian điện trường.
Câu 11. Dùng phương pháp ảnh điện để xác định lực tác dụng giữa một điện
tích điểm và một mặt phẳng kim loại vô hạn, tính điện dung của một dây dẫn hình trụ. Giải:
• Dùng phương pháp ảnh điện để xác định lực tác dụng giữa một điện tích điểm
và một mặt phẳng kim loại vô hạn
• Ta lấy điện tích q′=−qđặt tại vị trí O′đối xứng với O qua mặt phẳng (P). • Lực điện 
Fdo vật dẫn (C)trong miền (D) tác dụng lên (q) cũng là lực do q′tác dụng lên q: F=1 4πεoε|qq′| OO′2 OO′=2a   F=1 q2 4πε ε o 4a2
• Tính điện dung của một dây dẫn hình trụ