Đề cương Thống kê kinh doanh (có đáp án) | Học viện Ngân hàng

ĐỀ CƯƠNG THỐNG KÊ KINH DOANH
Chương 1: Tổng quan về thống kê và thu thập dữ liệu.
NHẬN ĐỊNH ĐÚNG /SAI VÀ GIẢI THÍCH
1. Đối tượng nghiên cứu của thống kê học là các hiện tượng về quá trình tái sản xuất xã hội.
2. Tiêu thức thống kê là một bộ phận của tổng thể.
3. Tổng thể đồng chất bao gồm các đơn vị có nhiều đặc điểm chủ yếu khác nhau
liên quan đến mục đích nghiên cứu.
4. Chỉ tiêu thống kê phản ánh mặt lượng của hiện tượng kinh tế xã hội trong điều
kiện thời gian và địa điểm cụ thể.
5. Thang đo khoảng là thang đo thứ bậc có các khoảng cách đều nhau có điểm gốc là 0.
6. Dữ liệu định tính gồm các giá trị bằng con số cụ thể.
7. Chỉ tiêu thống kê phản ánh đặc điểm của đơn vị thống kê
8. Thang đo định danh là việc đánh số các biểu hiện cùng loại của một tiêu thức,
giữa các biểu hiện có quan hệ hơn kém.
9. Dân số của Việt Nam vào 0h ngày 1/7/2019 là khoảng 76 triệu người là một chỉ tiêu thống kê.
10. Yêu cầu của điều tra thống kê là đầy đủ về nội dung và số lượng đơn vị điều tra.
11. Xây dựng hệ thống chỉ tiêu thống kê là nêu ra những chỉ tiêu thống kê để phân tích. KEY.
1. Sai. Đối tượng nghiên cứu của thống kê là môn khoa học xã hội nghiên cứu
mặt lượng gắn liền với mặt chất của hiện tượng kinh tế xã hội số lớn trong
thời gian và địa điểm cụ thể.
2. Sai. Tiêu thức thống kê là một số đặc điểm của đơn vị tổng thể được chọn ra để nghiên cứu.
3. Sai. Tổng thể đồng chất bao gồm các đơn vị giống nhau về một số đặc điểm
chủ yếu có liên quan đến mục đích nghiên cứu.
4. Sai. Chỉ tiêu thống kê phản ánh mặt lượng gắn với mặt chất của các hiện
tượng và quá trình kinh tế trong điều kiện thời gian và địa điểm cụ thể. 1
5. Sai. Thang đo khoảng là thang đo thứ bậc có các khoảng cách đều nhau nhưng
không có điểm gốc là 0.
6. Sai. Dữ liệu định tính gồm các nhãn hay tên được sử dụng để xác định đặc
điểm của mỗi phần tử.
7. Sai. Chỉ tiêu thống kê phản ánh đặc điểm của số lớn đơn vị tổng thể hoặc cả tổng thể
8. Sai. Thang đo định danh là việc đánh số các biểu hiện cùng loại của một tiêu
thức, được dùng với các tiêu thức thuộc tính.
9. Sai. Chưa khẳng định được chắc chắn
Chỉ tiêu thống kê là các mức độ phản ánh lượng gần với chất của các mặt và
các tính chất cơ bản của hiện tượng kinh tế xã hội số lớn trong điều kiện thời
gian và địa điểm cụ thể
Xét trong toàn bộ nền kinh tế thì đố chỉ là một tiêu thức thống kê nhưng để
đánh giá tính chất của hiện tượng kinh tế xã hội thì còn có thu nhập bình quân, tuổi thọ,...
10. Đúng. Yêu cầu của điều tra thống kê bao gồm đầy đủ về nội dung và số lượng
đơn vị điều tra chính xác kịp thời, đảm bảo tính khả thi, hiệu quả và tiết kiệm.
11. Sai. Xây dựng hệ thống chỉ tiêu thống kê, muốn nên ra chỉ tiêu thống kê phải
căn cứ vào mục đích nghiên cứu, tính chất đặc điểm của đối tượng nghiên
cứu,... Sau đó phân tích xong thì chúng ta phải đánh giá xem xét nó có chính
xác, kịp thời, cụ thể và tiết kiệm hay không. 2
Chương 2: Phương pháp trình bày và mô tả dữ liệu.
NHẬN ĐỊNH ĐÚNG /SAI VÀ GIẢI THÍCH
1. Khi trình bày dữ liệu định lượng, chỉ có thể dùng bảng phân bổ tần số.
2. Phân tổ thống kê có thể vừa nghiên cứu mối quan hệ giữa thiêu thức nguyên
nhân và tiêu thức kết quả, vừa nghiên cứu mối quan hệ giữa nhiều tiêu thức
nguyên nhân và 1 tiêu thức kết quả
3. Tần số thu được sau khi phân tổ biểu hiện bằng một số tuyệt đối
4. Không thể cộng các số tuyệt đối thời kỳ liền nhau đề có số tuyệt đối của thời kỳ dài hơn.
5. Số sinh viên nam bằng 90% số sinh viên nữ trong cùng lớp. Đây là số tương đối không gian.
6. Có thể cùng lúc phân tổ thống kê thành nhiều tiêu thức khác nhau.
7. Số trung bình cộng gia quyền là một dạng của số trung bình cộng giản đơn.
8. Tổng thể nào cũng tính ra số trung bình.
9. Công thức tính chỉ số tổng hợp giá là số bình quân cộng giản đơn.
10. Trung vị là lượng biến tiêu thức của đơn vị đứng ở vị trí chính giữa trong dãy số lượng biến.
11. Số trung vị phụ thuộc vào tất cả lượng biến
12. Không phải tổng thể nào cũng có mốt.
13. Mốt không chịu ảnh hưởng của lượng biến đột xuất.
14. Biểu đồ box plot không cho phép nhận biết dữ liệu đột xuất.
15. Số trung vị san bằng chênh lệch giữa các lượng biến. KEY.
1. Sai. Có thể dùng bảng phân bổ tần số, sơ đồ thân lá và đồ thị phân bổ dữ liệu.
2. Sai. Chưa đủ. Phân tổ thống kê ngoài vừa nghiên cứu mối quan hệ giữa thiêu
thức nguyên nhân và tiêu thức kết quả, vừa nghiên cứu mối quan hệ giữa nhiều
tiêu thức nguyên nhân và 1 tiêu thức kết quả thì nó còn nghiên cứu quan hệ
giữa nhiều tiêu thức thống kê và nhiều tiêu thức kết quả.
3. Đúng. Tần số là số lần xuất hiện của lượng biến nên luôn luôn là số tuyệt đối.
4. Sai. Có thể cộng các số tuyệt đối thời kỳ liền nhau đề có số tuyệt đối của thời kỳ dài hơn.
Ví dụ : Doanh thu của doanh nghiệp X năm 2010 là 120 tỷ đồng. 3
Nhiều chỉ tiêu khác như: chi phí sản xuất, lượng hàng hoá tiêu thụ ... đều là
số tuyệt đối thời kỳ, vì đó là kết quả tổng hợp mặt lượng của hiện tượng trong
một độ dài thời gian nhất định. Các số tuyệt đối thời kỳ của cùng một chỉ tiêu
có thể cộng được với nhau, thời kỳ càng dài thì trị số của nó càng lớn.
5. Sai. Số tương đối biểu hiện sự so sánh giữa các bộ phận khác nhau trong cùng
một tổng thể nên đây là số tương đối so sánh. 6. Đúng.
7. Sai. Số trung bình cộng giản đơn là dạng đặc biệt của số trung bình cộng gia
quyền. (các tần số bằng nhau và bằng 1).
8. Sai. Số trung bình chỉ được tính ra từ một tổng thể đồng chất.
9. Sai. Công thức tính chỉ số tổng hợp giá là số bình quân cộng gia quyền.
10. Đúng. Số trung vị là lượng biến tiêu thức của đơn vị đứng ở vị trí chính giữa
trong một dãy số lượng biến. Số trung vị phân chia dãy số lượng biến thành
hai phần (từ số trung vị trở lên và từ trung vị trở xuống), mỗi phần có số đơn
vị tổng thể bằng nhau.
11. Sai. Trung vị là lượng biến của đơn vị ở vị trí chính giữa dãy số phân phối vì
vậy không phụ thuộc vào các biến còn lại.
12. Đúng. Tổng thể có các lượng biến đều có tần số bằng 1 không xác định được mốt.
13. Đúng. Mốt nói lên mức độ phổ biến nhất của hiện tượng, là lượng biến có tần
số lớn nhất trong dãy số, vì vậy không chịu ảnh hưởng bởi sự bằng nhau hay
xấp xỉ của tần số các lượng biến. 14. Sai.
=> Tác dụng của hộp ria mèo (box plot)
+ Nhận biết vị trí của bộ dữ liệu trên cơ sở Me
+ Nhận biết sự dàn trải của dữ liệu trên cơ sở độ dài của hộp (khoảng tứ phân
vị Ro) và độ dài của ria mèo
+ Nhận biết độ lệch phân phối của dữ liệu
+ So sánh 2 hay nhiều bộ dữ liệu với cùng 1 thước đo
+ Nhận biết lượng biến đột xuất (outliers) và nghi ngờ có thể là lượng biến đột xuất
15. Sai. Số trung vị là lượng biến đứng ở vị trí chính giữa ở dãy số. 4 BÀI TẬP.
1. Một số công thức cần nhớ 1.1.
Số trung bình cộng:
- Số trung bình cộng giản đơn: ∑n �� x̅ = i=1 n
- Số trung bình cộng gia quyền: ∑ ���� � �̅ = �=1 � ∑ � �= � 1
- Số trung bình điều hòa (vận dụng khi không biết fi): ∑� �� �̅ = �=1 ∑� �� �=1 �� 1.2. Số trung bình nhân
- Số trung bình nhân đơn giản: �̅ = √∏ � � = �� 1
- Số trung bình nhân gia quyền: ∑ �� � �=1 √∏ �̅ = � � � � � � =1 1.3. Số trung vị
- Nếu dữ liệu không phân tổ: �+1
+ Số liệu lẻ: Me là lượng biến đứng ở vị trí 2 �
+ Số liệu chẵn: Me là số trung bình của 2 lượng biến đứng vị trí thứ và thứ 2 � + 1 2
- Nếu dữ liệu phân tổ ∑ ��+1
+ Không có khoảng cách tổ: M
e là lượng biến có tần số tích lũy bằng 2 + Có khoảng cách tổ ∑ �� − � � 2 ��−1 � = + ℎ�� � ��� ��(���) 5 Trong đó:
���(���): giới hạn dưới của tổ có trung vị
ℎ�� : trị số của khoảng cách tổ có trung vị
∑ �� : tổng các tần số của dãy số lượng biến
���−1 : tổng các tần số của các tổ đứng trước tổ có số trung vị
��� : tần số của tổ có số trung vị 1.4. Mốt
- Tìm tổ có chứa Mo (tổ có tần số lớn nhất) - Tính Mo � − � � �� ��−1 0 = + ℎ �� � (��� − − ���−1) + (��� ���+1) ��(���) Trong đó:
���(���) : giới hạn dưới của tổ có mốt
ℎ�� : trị số khoảng cách tổ có mốt
��� : tần số tổ có mốt
���−1 : tần số của tổ đứng liền trước
���+1 : tần số của tổ đứng liền sau 1.5.
Phương sai và độ lệch tiêu chuẩn - Phương sai giản đơn: ∑� (�� − �̅)2 �2 = �=1 � − 1 - Phương sai gia quyền ∑� (�� − �̅)2�� �2 = �=1 � ∑ � − � 1 = � 1
- Độ lệch tiêu chuẩn là căn bậc 2 của phương sai 1.6.
Hệ số biến thiên
- Tham số đo độ biến thiên tương đối và được tính bằng cách so sánh độ lệch
tiêu chuẩn và số trung bình cộng � � = � 100(%) � ̅
Dùng để so sánh độ biến thiên của các hiện tượng cùng loiaj nhưng số trung
bình không bằng nhau hoặc so sánh các hiện tượng khác loại 6
2. Bài tập vận dụng
Bài 1: Có tài liệu về số phụ nữ trong độ tuổi sinh đẻ tại một địa phương năm 2010 như sau: Nhóm tuổi 15-18 18-25 25-30 30-40 40-49 Số phụ nữ 90 158 172 130 115 Hãy tính: a. Khoảng biến thiên b. Nhóm tuổi trung bình
c. Phương sai và độ lệch tiêu chuẩn d. Hệ số biến thiên Giải: xi fi Tần số tích lũy 16.5 90 90 21.5 158 248 27.5 172 420 35 130 550 44.5 115 665 a. Khoảng biến thiên: � = ���� −
���� = 49 − 15 = 34 b. Nhóm tuổi trung bình: ∑5 ���� �̅ = �=1 = 28 5 ∑ � �= � c. Phương sai 1 ∑� (�� − �̅)2�� �2 = �=1 = 83,68 � ∑ � − � 1 = � Độ lệch tiêu chuẩn: 1 � = √�2 = 9,148 d. Hệ số biến thiên � 9,148 � = � �̅ . 100 = 100 = 31.55% 28 7
Bài 2: Có dãy số liệu về giá trị xuất khẩu của 10 doanh nghiệp năm 2009 như
sau. (Đ/v tính: triệu USD) 45 50 72 50 48 51 50 54 80 52 Xác định:
a/ Giá trị xuất khẩu bình quân một doanh nghiệp
b/ Mốt, trung vị về giá trị xuất khẩu.
c/ Khoảng biến thiên, độ lệch tiêu chuẩn về giá trị xuất khẩu.
d/ Hệ số biến thiên về giá trị xuất khẩu Giải: Viết lại theo thứ tự: 45 48 50 50 50 51 52 54 72 80
a. Giá trị xuất khẩu bình quân: ∑10 �� x ̅ = i=1 = 55,2 10
b. Lượng biến 50 xuất hiện 3 lần trong dãy số, do đó Mo=50 Trung vị: 50 + 51 �� = = 50,5 2
c. Khoảng biến thiên: � = ���� −
���� = 80 − 45 = 35 ∑10 (��−�̅)2
Độ lệch tiêu chuẩn: � = √�2 = �=1 10−1 = 11,307
d. Hệ số biến thiên về giá trị xuất khẩu � 11,307 � = �̅ . 100 = . 100 = 20,483% 55,2
Bài 3: Có tài liệu về doanh thu hang năm của 21 công ty dược phẩm(tỉ đồng) như sau 84,08 36,53 74,78 64,52 88,79 24,59 114,13 6,08 13,74 57,94 40,19 18,50 28,18 13.56 104,98 141,38 18,72 83,05 43,41 7,39 21.27
a. Hãy xác định giá trị nhỏ nhất, giá trị tứ phân vị thứ nhất, trung vị, giá trị tứ
phân vị thứ 3 và giá trị lớn nhất của toàn bộ số liệu trên
b. Tính giới hạn dưới và dưới hạn trên 8
c. Doanh thu lớn nhất trong 21 công ty ở trên là 141,38 tỷ đồng. Giả sử do sai
sót của người nhập dữ liệu, số liệu được ghi là 411,39 tỷ đồng. Sử dụng
phương pháp dữ liệu đột biến để tìm ra lỗi sai trên Giải: Viết lại theo thứ tự 1 6.08 2 7.39 3 13.56 4 13.74 5 18.5 6 18.72 7 21.27 8 24.59 9 28.18 10 36.53 11 40.19 12 43.41 13 57.94 14 64.52 15 74.78 16 83.05 17 84.08 18 88.79 19 104.98 20 114.13 21 141.38
a. Giá trị nhỏ nhất xmin=6,08 Vị 1
trí tứ phân vị thứ nhất Q (� + 1)=5,5 1= 4
Giá trị tứ phân vị thứ nhất: �1 = 18,5 + 0,25(18,72 − 18,5) = 18,56
Trung vị: Me= ��+1 = �11 = 40,19 2 Vị 3
trí tứ phân vị thứ 3: Q3= (� + 1) = 16,5 4
Giá trị tứ phân vị thứ 3: �3 = 83.05 + 0,75(84,08 − 83,05) = 83,82
Giá trị lớn nhất xmax = 141,38 b. IQR= Q3-Q1 = 65,27
Giới hạn trên = Q3+3IQR=279,63
Giới hạn dưới = Q1-3IQR= -177,25
c. Phương pháp dữ liệu đột xuất có phát hiện được sai sót vì 411.38 tỷ đ > 279.63(Giới hạn trên) 9
Chương 3: Ước lượng.
NHẬN ĐỊNH ĐÚNG /SAI VÀ GIẢI THÍCH
1. Mức ý nghĩa α là xác suất đề tham số của tổng thể chung rơi vào trong khoảng tin cậy.
2. Phương pháp tổ chức chọn mẫu không làm ảnh hưởng tới cỡ mẫu điều tra.
3. Phương sai của lượng biến lớn chứng tỏ lượng biến thay đổi nhiều. KEY.
1. Sai. α là xác suất để tham số của tổng thể chung không rơi vào trong khoảng tin cậy.
2. Sai. Phương pháp tổ chức chọn mẫu là một trong các yếu tố làm ảnh hưởng tới cỡ mẫu điều tra.
3. Đúng. Theo công thức BÀI TẬP
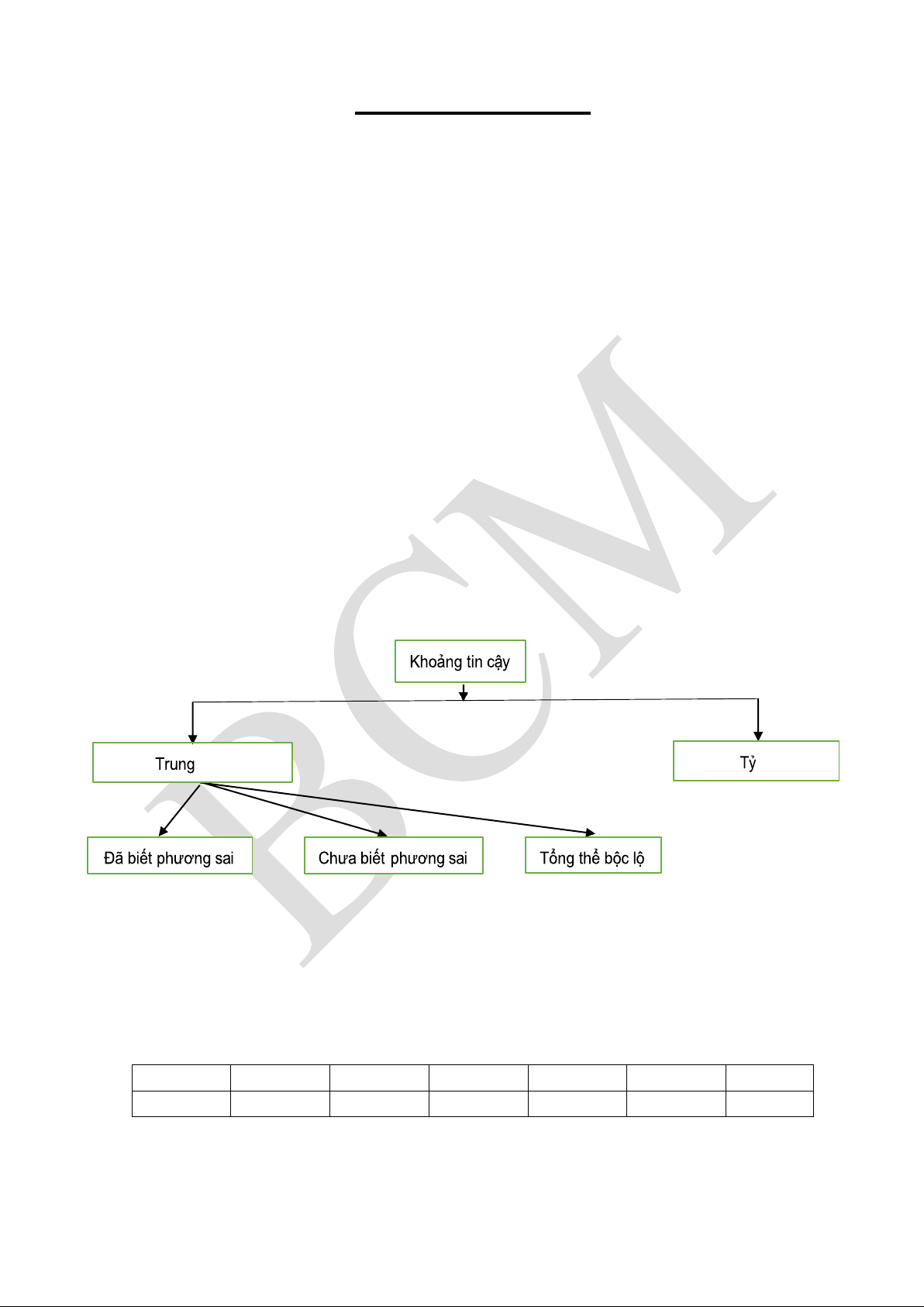
I. Ước lượng của tổng thế chung bình lệ
Dạng 1: Ước lượng trung bình đã biết phương sai
Điều tra thu nhập (triệu/năm) hàng năm của 25 hộ gia đình trong vùng ta có bảng số liệu: Thu nhập 11,5 11,6 11,7 11,8 11,9 12 Số hộ 5 8 4 6 1 1
Hãy ước lượng mức thu nhập trung bình trong vùng với độ tin cậy 95%, biết
rằng thu nhập là biến ngẫu nhiên có phân phối chuẩn với độ lệch chuẩn σ = 0,2 Giải: 10
Gọi X là biến ngẫu nhiên thu nhập hộ gia đình trong vùng, ta có: X ~ N (μ; 0,22) �
Có x̅ =11,672, độ tin cậy = 95% hay � = 0,05 => = 0,025 2 ��/2 = �0.025 = 1,96
Vậy khoảng ước lượng của thu nhập trung bình μ là: σ σ x̅ − �� ≤ /2 . μ ≤ x̅ + � √� �/2 . √� Thay số ta có kết quả 0,2 0,2 11,672 − 1.96. ≤ μ ≤ 11,672 + 1.96.  11,594 ≤ μ ≤ √25 √25 11,75
Vậy với độ tin cậy 95%, thu nhập trung bình của vùng nằm trong khoảng (11,594; 11,75) triệu/ năm
Dạng 2: Ước lượng trung bình chưa biết phương sai
Điều tra thu nhập (triệu/năm) hàng năm của 25 hộ gia đình trong vùng ta có bảng số liệu: Thu nhập 11,5 11,6 11,7 11,8 11,9 12 Số hộ 5 8 4 6 1 1
Hãy ước lượng mức thu nhập trung bình trong vùng với độ tin cậy 95%, biết
rằng thu nhập là biến ngẫu nhiên có phân phối chuẩn Giải:
Gọi X là biến ngẫu nhiên thu nhập hộ gia đình trong vùng, ta có:
X ~ N (μ; σ 2)Ta có: x̅ = 11,672, s = 0,137 �
Với độ tin cậy 95%  � = 0,05 = 0,025 = > 2  ��−1=�24 =2.06 �/2 0.025
Khoảng ước lượng cho thu nhập trung bình là: s s x ̅ - ��−1. ≤ μ ≤ x̅ + ��−1. � /2 √� �/2 √�
Thay số vào ta có kết quả 0.137 0.137
11,672 - 2.06. ≤ μ ≤ 11,672 + 2.06. √25 √25 11,6156≤ μ ≤ 11,7284
Vậy với độ tin cậy 95%, thu nhập trung bình của vùng nằm trong khoảng (11,62; 11,72) triệu/ năm 11
Dạng 3 Trường hợp tổng thể chung có giới hạn
Có kết quả điều tra sản lượng lúa thu hoạch của 100 hộ gia đình trong tổng số
1000 họ tjai xã A theo phương pháp chọn 1 lần(chọn không lặp) như sau Sản lượng(kg) Số hộ(hộ) 5200-5400 25 5400-5600 20 5600-5800 40 5800-6000 15
Tính khoảng tin cậy cho sản lượng lúa thu hoạch trung bình một hộ gia đình
trong toàn xã A với độ tin cậy 95% Giải: � 100 Ta có =
=0.1 > 0.5 => sử dụng công thức tổng thể chung để tính khoảng tin � 1000
cậy cho sản lượng lúa thu hoạch trung bình một hộ gia đình trong toàn xã A s s x ̅ - ��−1. � � . √1 − ≤ μ ≤ x̅ + ��−1. . √1 − �/2 √� � � / √� � 2 �
Với độ tin cậy 95%  � = 0,05 = 0,025 = > 2  ��−1=�24 =2.06 �/2 0.025 Thay số vào ta có 0.137 100 100 11,672 - 2.06. . √1 −
≤ μ ≤ 11,672 + 2.06. 0.137 . √1 − √25 1000 √25 1000  11.6284 ≤ μ ≤ 11,7255
Vậy với độ tin cậy 95%, thu nhập trung bình của vùng nằm trong khoảng
(11.6284, 11,7255) triệu/ năm
Dạng 4 Ước lượng tỷ lệ
Một mẫu ngẫu nhiên gồm 400 cử tri, trong đó có 32 người bầu cử cho ứng cử
viên A. Ước lượng tỷ lệ p cho tổng thể chung với độ tin cậy 95% Giải: 32 f= =0.8 400 độ �
tin cậy = 95% hay � = 0,05 => = 0,025 2 ��/2 = �0.025 = 1,96
Tỷ lệ p cho tổng thể chung với độ tin cậy 95% là 12 f - .√�.(1−� ≤ p ≤ f + .√�.(1−�) � ) � � � /2 � �/2
0.8 – 1.96 .√0.8.(1−0.8)
≤ p ≤ 0.8 – 1.96 .√0.8.(1−0.8) 400 400 0.053 ≤ p ≤ 0.107
Vậy với độ tin cậy 95%, tỷ lệ p cho tổng thể chung nằm trong khoảng (0.053,0.107) 13