Đề luyện tập giữa kỳ 1 môn Toán 10 chuyên

ĐỀ LUYỆN TẬP GKI MÔN TOÁN 10 CHUYÊN Câu 1 (2,0 điểm).
a) Cho tập hợp A =  5 − ;− 2; 1
− ; 2 và B =x ( 2 x − )( 3 | 2 x + ) 1 = 
0 . Tìm tập hợp A  B . 1  b) Cho ánh xạ f : ;+ → 
 xác định bởi công thức f ( x) 2
= x − 2 . Xét tính song ánh của ánh xạ f . 4   
Câu 1. (1,5 điểm) Cho hàm số bậc hai 2
y = x − 3x + 4 .
a) Lập bảng biến thiên của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = x − 3x + 4 trên −2;  3 .
Câu 3 (1,5 điểm). Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết.
Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ đề vẽ một tấm thiệp loại lớn có giá 20
nghìn đồng. Học sinh chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm thiệp. Gọi x
là số tấm thiệp loại nhỏ và y là số tấm thiệp loại lớn với x, y   . Hãy cho biết số tiền lớn nhất học sinh có
thể thu được là bao nhiêu?
Câu 4 (1,5 điểm). Trong hệ tọa độ Oxy , cho các điểm A(1;0), B(2;3);G (3;0) .
a) Tìm điểm C sao cho G là trọng tâm tam giác ABC .
b) Tìm tọa độ các điểm M trên Oy sao cho tam giác ABM vuông tại M .
Câu 5 (2,0 điểm). Cho tam giác ABC nhọn, không cân, AB  AC và có hai đường phân giác trong, phân
giác ngoài đỉnh A lần lượt là AD, AE . a) Chứng minh rằng ( ; ED CB) = 1 − bằng định nghĩa.
b) Gọi K là trung điểm của DE , đường tròn đường kính DE cắt BA tại N ( N  A) . Chứng minh rằng tứ
giác ACKN nội tiếp.
Câu 6 (1,5 điểm). Cho tam giác ABC nhọn, hai đường cao BE,CF (E  ;
CA F  AB) cắt nhau tại H .
Đường thẳng qua H song song với BC cắt C ,
A AB lần lượt tại S,T . Đường tròn đường kính BS,CT cắt
nhau tại điểm K ở ngoài tam giác ABC .
a) Chứng minh AF.AT = AE.AS .
b) Chứng minh AK ⊥ BC .
-----------------Hết--------------- SỞ GD-ĐT LẠNG SƠN
KIỂM TRA CUỐI HỌC KÌ I LỚP 10 CHUYÊN TRƯỜNG THPT CHUYÊN
NĂM HỌC 2024 - 2025 CHU VĂN AN MÔN: TOÁN
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
Đề thi gồm có 01 trang, 6 câu Mã đề 142 Câu 1 (2,0 điểm).  1  a) Cho tập hợp 3
A = − ;− 3;1 và B = x ( 2 x − x − )( 3 | 2 1 x + 3) = 
0 . Tìm tập hợp A  B .  2  1  b) Cho ánh xạ f : ;+ → 
 xác định bởi công thức f ( x) 2
= x + 2 . Xét tính song ánh của ánh xạ f . 3   
Câu 2. (1,5 điểm) Cho hàm số bậc hai 2
y = x − 5x + 6 .
a) Lập bảng biến thiên của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = x − 5x + 6 trên −1;  3 .
Câu 3 (1,5 điểm). Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết.
Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ đề vẽ một tấm thiệp loại lớn có giá 20
nghìn đồng. Học sinh chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm thiệp. Gọi x
là số tấm thiệp loại nhỏ và y là số tấm thiệp loại lớn với x, y   . Hãy cho biết số tiền lớn nhất học sinh có
thể thu được là bao nhiêu?
Câu 4 (1,5 điểm). Trong hệ tọa độ Oxy , cho các điểm A(1;0), B(2; 3 − );G(3;0) .
a) Tìm điểm C sao cho G là trọng tâm tam giác ABC .
b) Tìm tọa độ các điểm N trên Oy sao cho tam giác ABN vuông tại N .
Câu 5 (2,0 điểm). Cho tam giác ABC nhọn, không cân, AB  AC và có hai đường phân giác trong, phân
giác ngoài đỉnh A lần lượt là AD, AE . a) Chứng minh rằng ( ; ED BC ) = 1 − .
b) Gọi I là trung điểm của DE , đường tròn đường kính DE cắt CA tại M (M  A) . Chứng minh rằng tứ
giác ABIM nội tiếp.
Câu 6 (1,5 điểm). Cho tam giác ABC nhọn, hai đường cao BE,CF (E  ;
CA F  AB) cắt nhau tại H .
Đường thẳng qua H song song với BC cắt C ,
A AB lần lượt tại S,T . Đường tròn đường kính BS,CT cắt
nhau tại điểm K ở ngoài tam giác ABC .
a) Chứng minh AF.AT = AE.AS .
b) Chứng minh AK ⊥ BC .
-----------------Hết---------------
Hướng dẫn chấm mã 141: Mọi cách giải khác đúng cho điểm tối đa. Câu Nội dung Điểm
a) Cho tập hợp A =  5 − ;− 2; 1
− ; 2 và B =x ( 2 x − )( 3 | 2 x + ) 1 =  0 . Tìm tập hợp A  B . 1  b) Cho ánh xạ f : ;+ → 
 xác định bởi công thức f ( x) 2
= x − 2 . Xét tính song ánh của 4    ánh xạ f . a) Xét phương trình a x = 2 ( x − = x =  x − 2)(x + ) 2 2 2 0 2 2 3 1 = 0      x = − 2 . 0,5 3 3 x +1 = 0 x = 1 − x = 1 −  − Câu
Do x   nên B =   1 . 0,5 1
Khi đó: A  B = −  1 . (2,0 điểm) b 1 
Với mọi x ; x 
;+ khi đó f ( x = x − 2 và f ( x = x − 2 . 2 ) 2 1 ) 2 1 2   4  1 2
Xét f ( x ) = f ( x ) 2 2
 x − 2 = x − 2 1 2 1 2 0,5 2 2  x = x 1 2
 (x − x x + x = 0 1 2 ) ( 1 2 ) 1  1 1 1 Vì x ; x 
;+ nên x + x  + =  0 . 1 2   4  1 2 4 4 2
Suy ra x = x . Từ đó ta có f đơn ánh. 1 2 0,5 1 
Lấy −5  , không tồn tại x  ;+ 
 để f ( x) = 5
− . Do đó f không toàn ánh. 4 
Vậy f không song ánh. Cho hàm số bậc hai 2
y = x − 3x + 4 .
a) Lập bảng biến thiên của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = x − 3x + 4 trên −2;  3 .
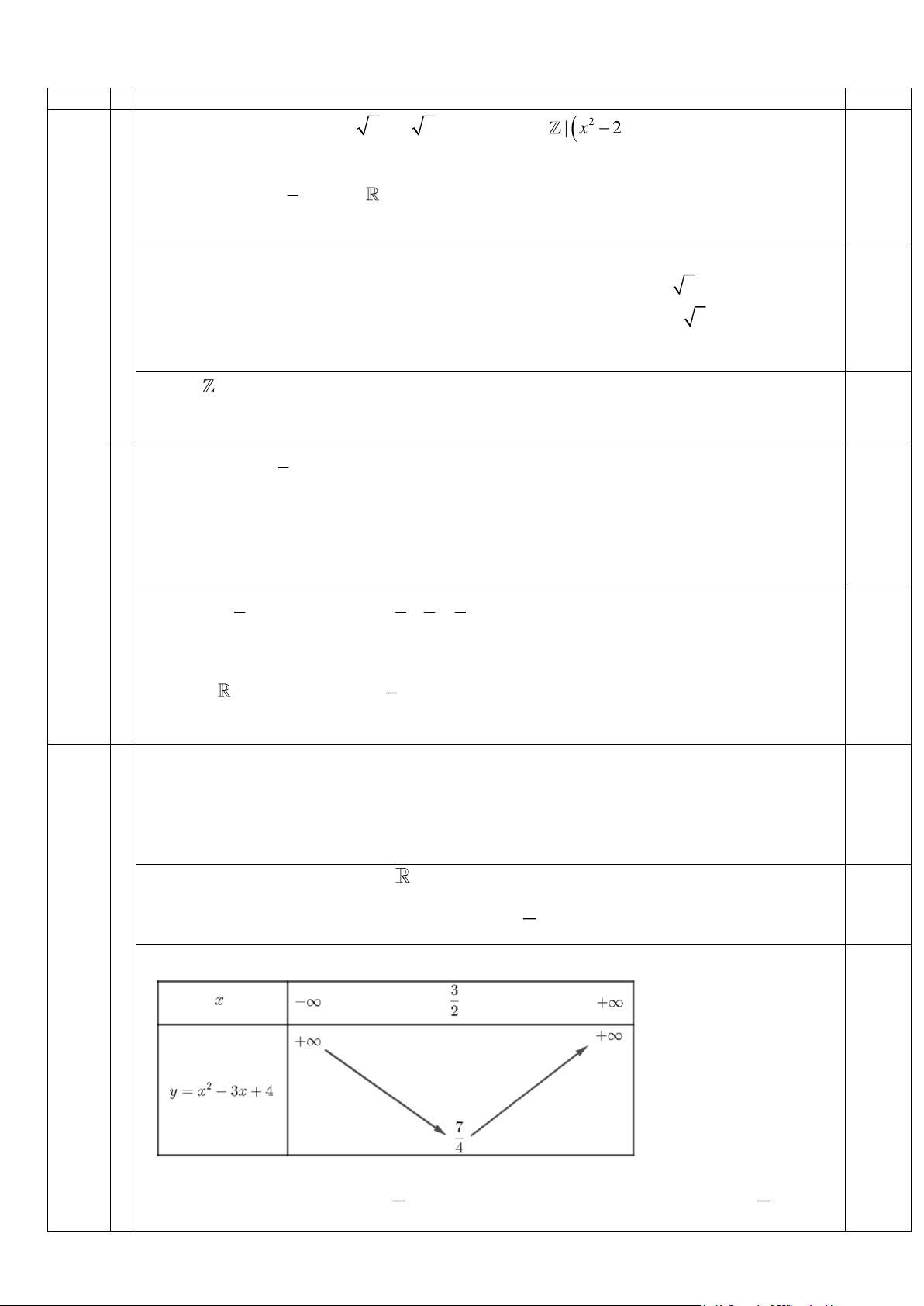
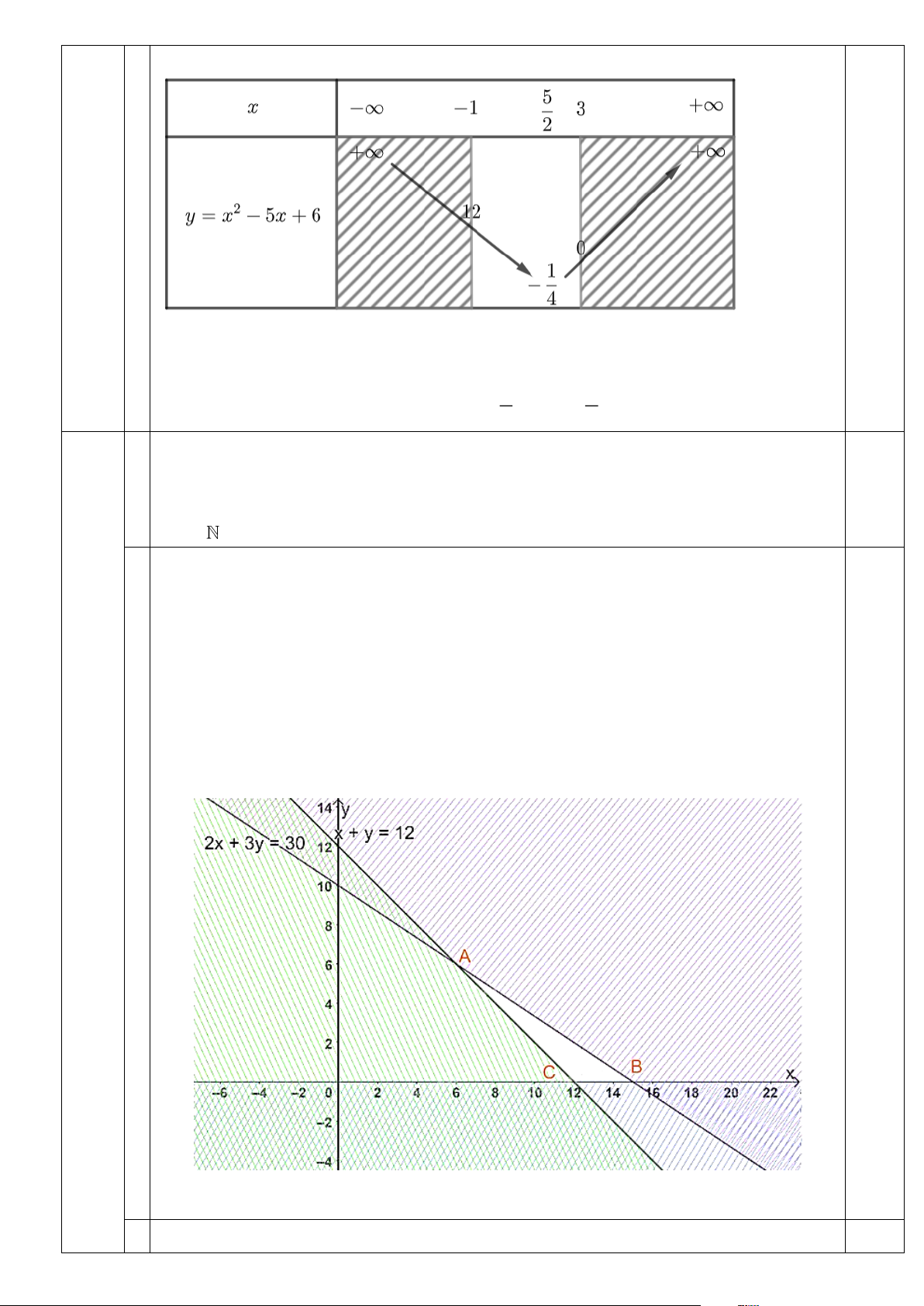
a) Tập xác định của hàm số D =  . 0,5 3
Ta có a = 1  0 và trục đối xứng của hàm số x = . 2 Câu
Khi đó ta có bảng biến thiên: 0,5 2 (1,5 điểm)  3   3 
Hàm số đồng biến trên khoảng ;+ 
 ; hàm số nghịch biến trên khoảng ; −   .  2   2 
Dựa vào bảng biến thiên ta có: 0,5 Vậy:
Giá trị lớn nhất của hàm số trên −2; 
3 là 14 khi x = −2 . 7 3
Giá trị nhỏ nhất của hàm số trên −2;  3 là khi x = . 4 2 Câu
Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 3
2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ đề vẽ một tấm thiệp loại lớn 0.5 (1,5
có giá 20 nghìn đồng. Học sinh chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít điểm)
nhất 12 tấm thiệp. Gọi x là số tấm thiệp loại nhỏ và y là số tấm thiệp loại lớn với x, y   .
Hãy cho biết số tiền lớn nhất học sinh có thể thu được là bao nhiêu?
Ta có các điều kiện ràng buộc đối với x và y như sau:
- Hiển nhiên x  0, y  0 .
- Tổng số giờ vẽ không quá 30 giờ nên 2x + 3y  30 .
- Số tấm thiệp tối thiểu là 12 tấm nên x + y  12 .
x  0, y  0 
Từ đó ta có hệ bất phương trình:
2x + 3y  30 .  x + y  12 
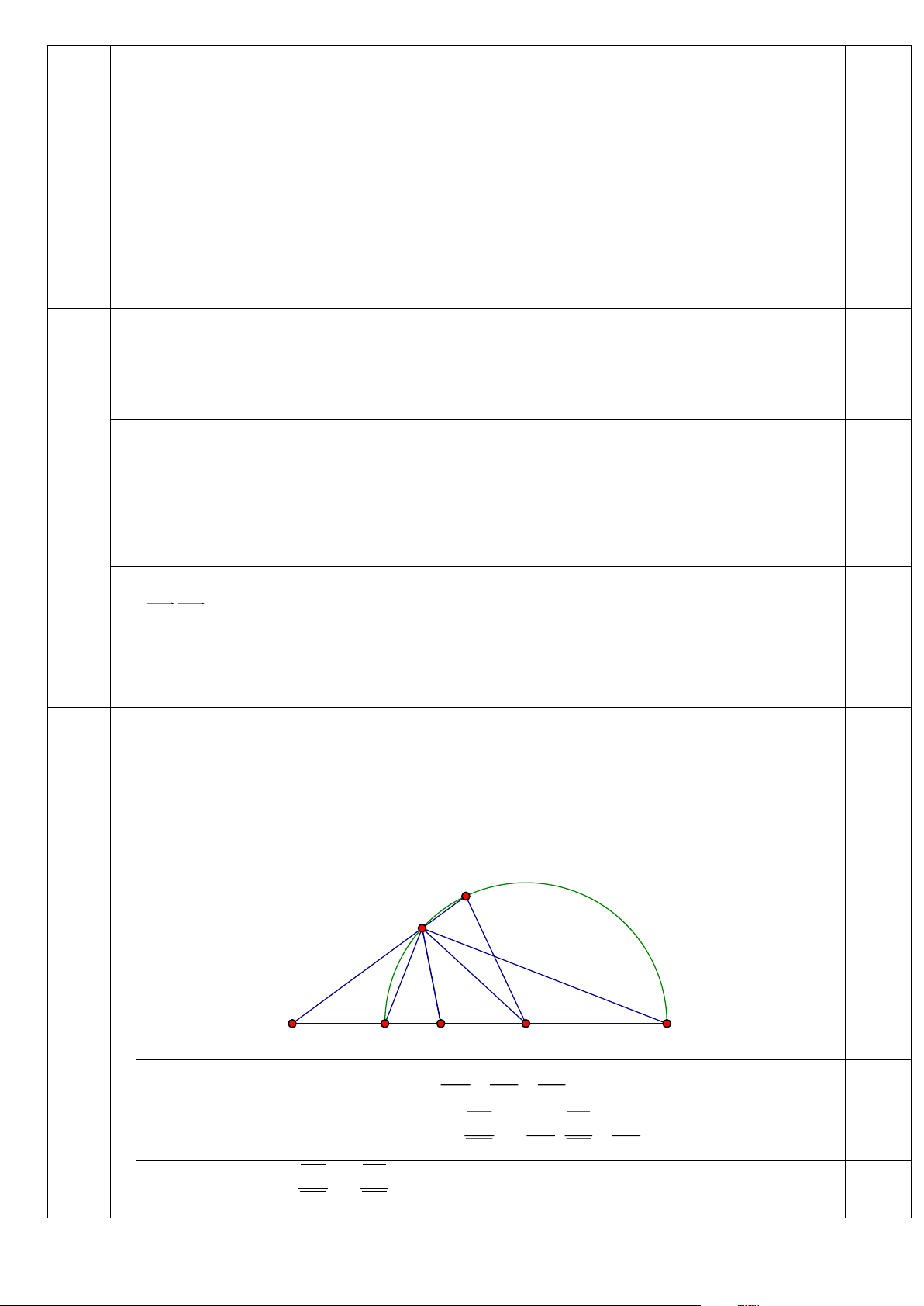
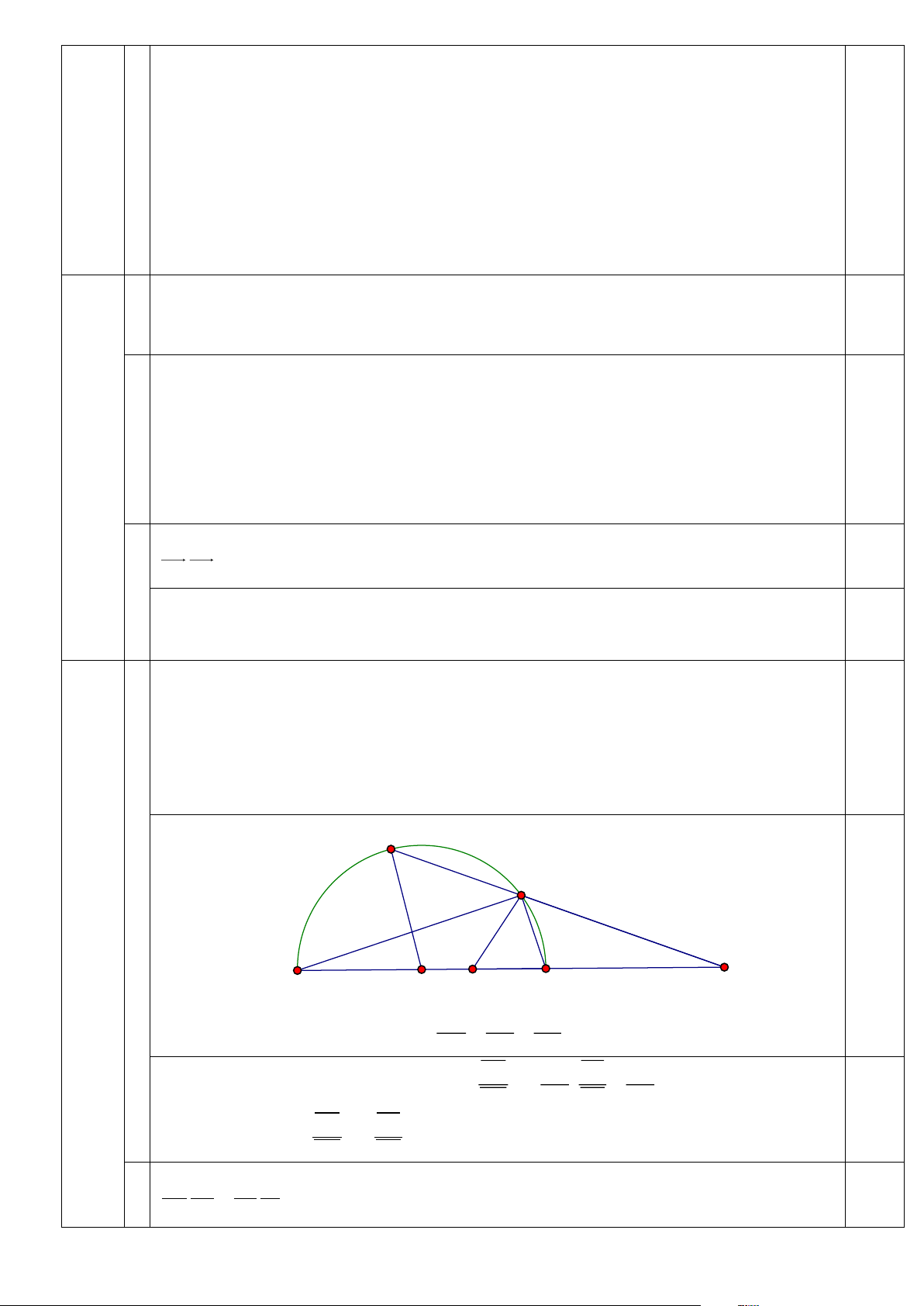
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như hình dưới. 1,0
Miền không gạch chéo (miền tam giác ABC , bao gồm cả các cạnh) trong hình trên là phần
giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh A(6;6), B(15;0),C (12;0) . 0.5
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: F = 10x + 20 y
Tính giá trị của F tại các đỉnh của tam giác:
Tại A(6;6): F = 180.
Tại B (15;0) : F = 150.
Tại C (12;0) : F = 120.
F đạt giá trị lớn nhất bằng 180 tại A(6;6) .
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền
nhất. Khi đó P = 3.6 + 6 = 24 . Câu
Trong hệ tọa độ Oxy , cho các điểm A(1;0), B(2;3);G (3;0) . 4 (1,5
a) Tìm điểm C sao cho G là trọng tâm tam giác ABC . điểm)
b) Tìm tọa độ các điểm M trên Oy sao cho tam giác ABM vuông tại M . Lời giải: a a/ Gọi C ( ;
x y) , vì G là trọng tâm tam giác nên ta có 0,5
x + x + x = 3x 1  + 2 + x = 3.3 = 9 A B c G   
y + y + y = 3y  0 + 3+ y = 3.0 = 0 A B C G x = 6 Do đó,   C (6; 3 − ). y = 3 −
b b/ Gọi M (0; y) là điểm trên trục Oy , Vì MA ⊥ MB nên 0,5 
MA MB =  ( − ) ( − ) + y ( y − ) 2 . 0 0 1 . 0 2 .
3 = 0  y − 3y + 2 = 0 .
Giải ra ta được y = 1 hoặc y = 2 . Do đó, các điểm M thỏa mãn bài toán là M (0; ) 1 và 0,5 M (0;2) . Câu
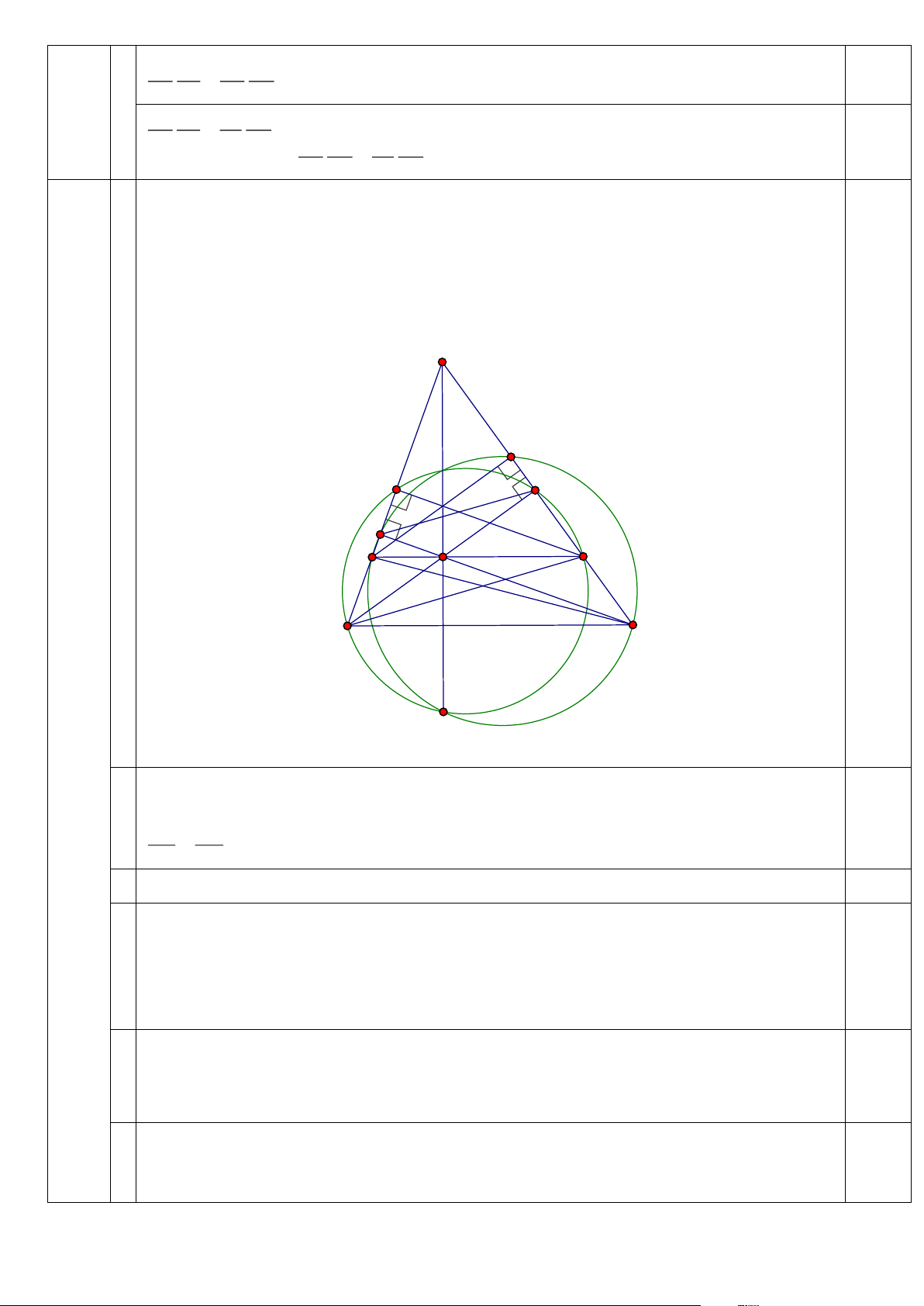
Cho tam giác ABC nhọn, không cân, AB  AC và có hai đường phân giác trong, phân giác 5
ngoài đỉnh A lần lượt là AD, AE . (2,0 a) Chứng minh rằng ( ; ED CB) = 1 − bằng định nghĩa. điểm)
b) Gọi K là trung điểm của DE , đường tròn đường kính DE cắt BA tại N ( N  A) . Chứng
minh rằng tứ giác ACKN nội tiếp. Lời giải: N A B D C K E DB AB EB 0,5
a/ a/ Vì AD , AE là các phân giác nên = = ( ) 1 . DC AC EC DB AB EB AB
Theo vị trí của D, E so với B,C thì ta có = − ; = (2). DC AC EC AC DB EB 0,5 Từ (1) và (2) suy ra = − tức là ( ; ED CB) = 1 − . DC EC
b/ Vì (ED : BC) = 1
− và K là trung điểm của DE nên theo hệ thức Maclaurin thì 0,5 B .
D BE = BC.BK (3).
Ta có AE ⊥ AD nên đường tròn đường kính DE có tâm là K và đi qua A , do đó 0,5 B . D BE = B . A BN (4).
Từ (3) và (4) suy ra BC.BK = B .
A BN , tức là ACKN nội tiếp. Câu
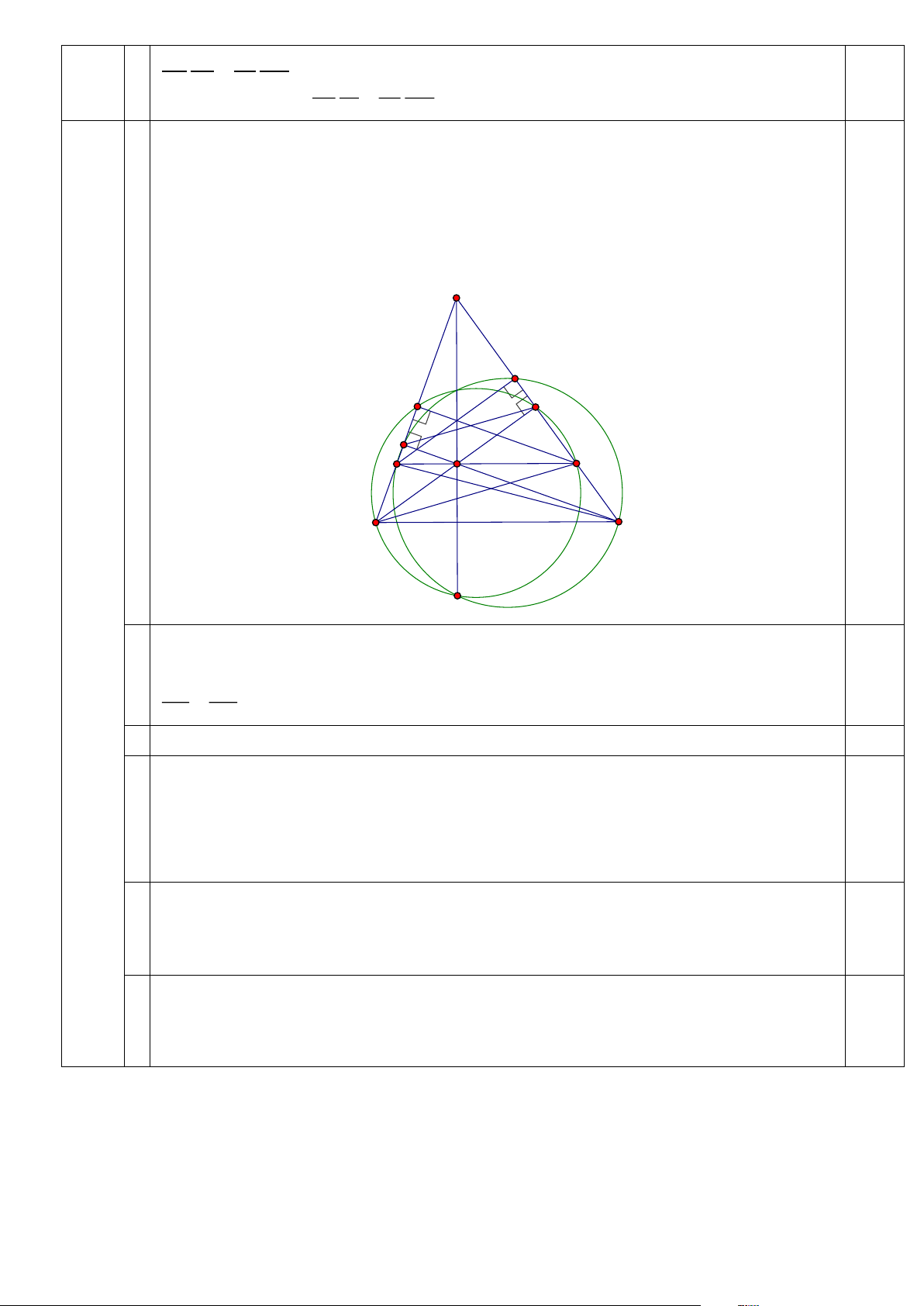
Cho tam giác ABC nhọn, hai đường cao BE,CF (E  ;
CA F  AB) cắt nhau tại H . Đường 6 (1,5
thẳng qua H song song với BC cắt C ,
A AB lần lượt tại S,T . Đường tròn đường kính điểm)
BS,CT cắt nhau tại điểm K ở ngoài tam giác ABC .
a) Chứng minh AF.AT = AE.AS .
b) Chứng minh AK ⊥ BC . A P Q E F H T S B C K Lời giải 0,25 a/ Vì   = = 90o BFC BEF
nên BFEC nội tiếp, suy ra AF.AB = AE.AC (1).Vì TS || BC nên AT AS =
 AT.AC = A . B AS (2). AB AC
Nhân (1) và (2) vế theo vế và rút gọn suy ra AF.AT = AE.AS . 0,25
b/ Gọi P,Q lần lượt là giao điểm của BS,CT  với AB, AC tương ứng, với kí hiệu 0,5
BS,CT là các đường tròn đường kính BS,CT tương ứng.
Thế thì BQ ⊥ QS và PT ⊥ PC . Do đó,  
TQS = TPS nên TQPS nội tiếp suy ra A . P AS = A . Q AT (3) .
Nhân (2) và (3) vế theo vế và rút gọn ta suy ra 0,25 A . P AC = A . Q AB  (  ; A BS) = (  ;
A CT ) (4).
Vì BFEC nội tiếp nên H .
B HE = HC.HF  (
 H;(BS)) = (
 H;CT ) (5).
Từ (4) và (5) thì AH là trục đẳng phương của BS,CT , hơn nữa K là giao điểm của hai 0,25
đường tròn này nên cũng có cùng phương tích với hai đường tròn, suy ra ,
A H , K thẳng
hàng. Hơn nữa AH ⊥ BC , do đó AK ⊥ BC .
Hướng dẫn làm tròn điểm toàn bài: 0,25
-----------------Hết---------------
Hướng dẫn chấm mã 142: Mọi cách giải khác đúng cho điểm tối đa. Câu Nội dung Điểm  1  a) Cho tập hợp 3
A = − ;− 3;1 và B = x ( 2 x − x − )( 3 | 2 1 x + 3) =  0 . Tìm tập hợp  2  A  B . 1  b) Cho ánh xạ f : ;+ → 
 xác định bởi công thức f ( x) 2
= x + 2 . Xét tính song ánh 3    của ánh xạ f .  1 x = −  2 a
2x − x −1 = 0 
a) Xét phương trình (2x − x − ) 1 (x + 3) 2 2 3 = 0    x =1  . 0.5 3 x + 3 = 0  3 x = − 3   Câu
Do x   nên B =   1 . 1
Khi đó: A  B =   1 . 0,5 (2,0 điểm) 1 
b) Với mọi x ; x 
;+ khi đó f ( x = x + 2 và f ( x = x + 2. 2 ) 2 1 ) 2 1 2   3  1 2
Xét f ( x ) = f ( x ) 2 2
 x + 2 = x + 2 1 2 1 2 2 2  x = x 0,5 1 2
 (x − x x + x = 0 1 2 ) ( 1 2 ) 1  1 1 2 Vì x ; x 
;+ nên x + x  + =  0 . 1 2   3  1 2 3 3 3
Suy ra x = x . Từ đó ta có f đơn ánh. 1 2 1 
Lấy 0   , không tồn tại x  ;+ 
 để f ( x) = 0 . Do đó f không toàn ánh. 0,5 3 
Vậy f không song ánh. Cho hàm số bậc hai 2
y = x − 5x + 6 .
a) Lập bảng biến thiên của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = x − 5x + 6 trên −1;  3 .
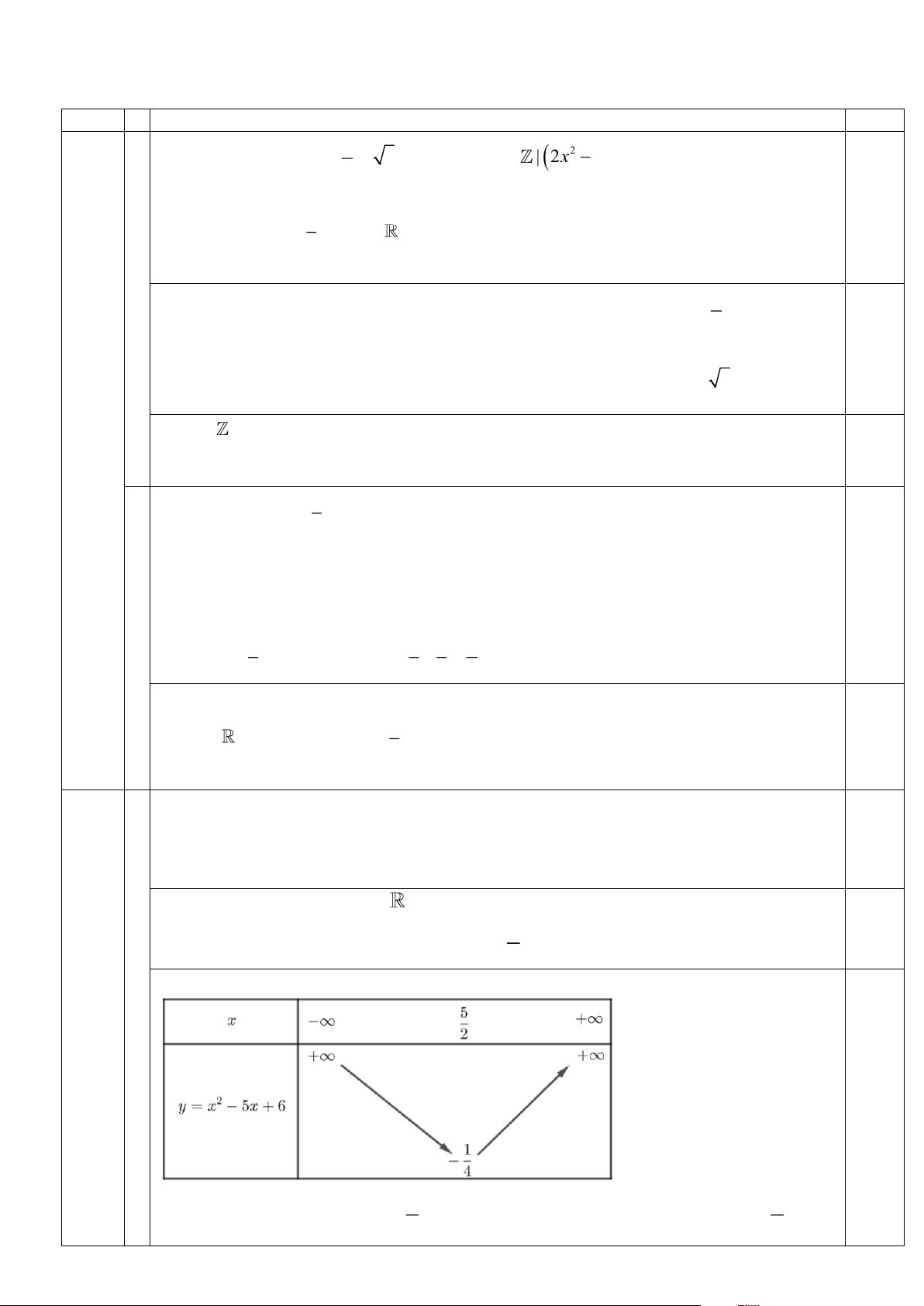
Tập xác định của hàm số D =  . 0,5 5
Ta có a = 1  0 và điểm uốn của hàm số x = . 2 Câu
Khi đó ta có bảng biến thiên: 2 0,5 (1,5 điểm)  5   5 
Hàm số đồng biến trên khoảng ;+ 
 ; hàm số nghịch biến trên khoảng ; −   .  2   2 
Dựa vào bảng biến thiên ta có: 0,5 Vậy:
Giá trị lớn nhất của hàm số trên −1;  3 là 12 khi x = −1. 1 5
Giá trị nhỏ nhất của hàm số trên −1;  3 là − khi x = . 4 2 Câu
Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 3
2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ đề vẽ một tấm thiệp loại (1,5
lớn có giá 20 nghìn đồng. Học sinh chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải điểm)
vẽ ít nhất 12 tấm thiệp. Gọi x là số tấm thiệp loại nhỏ và y là số tấm thiệp loại lớn với
x, y   . Hãy cho biết số tiền lớn nhất học sinh có thể thu được là bao nhiêu?
Ta có các điều kiện ràng buộc đối với x và y như sau:
- Hiển nhiên x  0, y  0 . 1,0
- Tổng số giờ vẽ không quá 30 giờ nên 2x + 3y  30 .
- Số tấm thiệp tối thiểu là 12 tấm nên x + y  12 .
x  0, y  0 
Từ đó ta có hệ bất phương trình: 2x + 3y  30 . x + y 12 
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như hình dưới.
Miền không gạch chéo (miền tam giác ABC , bao gồm cả các cạnh) trong hình trên là phần
giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh A(6;6), B(15;0),C (12;0) . 0,5
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: F = 10x + 20 y
Tính giá trị của F tại các đỉnh của tam giác:
Tại A(6;6): F = 180.
Tại B (15;0) : F = 150.
Tại C (12;0) : F = 120.
F đạt giá trị lớn nhất bằng 180 tại A(6;6) .
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền
nhất. Khi đó P = 2.6 + 6 = 18 . Câu
Câu 3 (1,5 điểm). Trong hệ tọa độ Oxy , cho các điểm A(1;0), B(2; 3 − );G(3;0) . 4
a) Tìm điểm C sao cho G là trọng tâm tam giác ABC . (1,5
b) Tìm tọa độ các điểm N trên điểm)
Oy sao cho tam giác ABN vuông tại N . Lời giải: 0,5 a/ Gọi C ( ;
x y) , vì G là trọng tâm tam giác nên ta có
x + x + x = 3x 1  + 2 + x = 3.3 = 9 A B c G    .
y + y + y = 3y  0 − 3+ y = 3.0 = 0 A B C G x = 6 Do đó,   C (6;3) . y = 3
b/ Gọi N (0; y) là điểm trên trục Oy , Vì NA ⊥ NB nên  0.5
NA NB =  ( − ) ( − ) + y ( y + ) 2 . 0 0 1 . 0 2 .
3 = 0  y + 3y + 2 = 0 .
Giải ra ta được y = −1 hoặc y = −2 . Do đó, các điểm N thỏa mãn bài toán là N (0;− ) 1 và 0,5 N (0; 2 − ) . Câu
Cho tam giác ABC nhọn, không cân, AB  AC và có hai đường phân giác trong, phân giác 5
ngoài đỉnh A lần lượt là AD, AE . (2,0 a) Chứng minh rằng ( ; ED BC ) = 1 − . điểm)
b) Gọi I là trung điểm của DE , đường tròn đường kính DE cắt CA tại M (M  A) .
Chứng minh rằng ABIM nội tiếp. Lời giải: M A 0,5 E I B D C a/ DB AB EB
a/ Vì AD , AE là các phân giác nên = = ( ) 1 . DC AC EC DB AB EB AB
Theo vị trí của D, E so với B,C thì ta có = − ; = (2). DC AC EC AC 0,5 DB EB Từ (1) và (2) suy ra = − tức là ( ; ED BC ) = 1 − . DC EC
b/ Vì (ED : BC ) = 1
− và I là trung điểm của DE nên theo hệ thức Maclaurin thì 0,5 . CD CE = . CB CI (3).
Ta có AE ⊥ AD nên đường tròn đường kính DE có tâm là I và đi qua A , do đó 0,5 . CD CE = . CA CM (4). Từ (3) và (4) suy ra . CB CI = .
CA CM , tức là ABMI nội tiếp. Câu
Cho tam giác ABC nhọn, hai đường cao BE,CF (E  ;
CA F  AB) cắt nhau tại H . Đường 6 (1,5
thẳng qua H song song với BC cắt C ,
A AB lần lượt tại S,T . Đường tròn đường kính điểm)
BS,CT cắt nhau tại điểm K ở ngoài tam giác ABC .
a) Chứng minh AF.AT = AE.AS .
b) Chứng minh AK ⊥ BC . A P Q E F H T S B C K Lời giải 0,25 a/ Vì   = = 90o BFC BEF
nên BFEC nội tiếp, suy ra AF.AB = AE.AC (1).Vì TS || BC nên AT AS =
 AT.AC = A . B AS (2). AB AC
Nhân (1) và (2) vế theo vế và rút gọn suy ra AF.AT = AE.AS . 0,25
b/ Gọi P,Q lần lượt là giao điểm của BS,CT  với AB, AC tương ứng, với kí hiệu 0,5
BS,CT là các đường tròn đường kính BS,CT tương ứng.
Thế thì BQ ⊥ QS và PT ⊥ PC . Do đó,  
TQS = TPS nên TQPS nội tiếp suy ra A . P AS = A . Q AT (3) .
Nhân (2) và (3) vế theo vế và rút gọn ta suy ra 0,25 A . P AC = A . Q AB  (  ; A BS) = (  ;
A CT ) (4).
Vì BFEC nội tiếp nên H .
B HE = HC.HF  (
 H;(BS)) = (
 H;CT ) (5).
Từ (4) và (5) thì AH là trục đẳng phương của BS,CT , hơn nữa K là giao điểm của 0,25
hai đường tròn này nên cũng có cùng phương tích với hai đường tròn, suy ra , A H , K
thẳng hàng. Hơn nữa AH ⊥ BC , do đó AK ⊥ BC .
Hướng dẫn làm tròn điểm toàn bài: 0,25
-----------------Hết---------------