Đề giao lưu HSG Toán 6 lần 2 năm 2023 – 2024 cụm CM số 6 Nga Sơn – Thanh Hóa
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 6 đề thi giao lưu học sinh giỏi môn Toán 6 lần 2 năm học 2023 – 2024 cụm chuyên môn số 6 huyện Nga Sơn, tỉnh Thanh Hóa; kỳ thi được diễn ra vào ngày 18 tháng 01 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm.
Preview text:
PHÒNG GD&ĐT NGA SƠN ĐỀ THI GIAO LƯU HỌC SINH GIỎI LỚP 6,7,8 LẦN 2
CỤM CHUYÊN MÔN SỐ 6 NĂM HỌC 2023-2024 Môn: Toán 6
(Đề thi gồm có 01 trang)
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 18 tháng 01 năm 2024
Câu 1(4,0 điểm). Tính hợp lí
a) 21.72 - 11.72 + 990.72 + 49.125.16 b) (169 - 42).(169 - 52) … (169 - 132) 2 2 2 2 − + + + + + 15 9 20 9 200 3 ... c) 5.4 .9 − 4.3 .8 3 4 5 100 d) 9 19 29 6 5.2 .6 − 7.2 .27 1 2 3 99 ... + + + + 2 3 4 100
Câu 2(3 điểm). Tìm x, biết: a) ( 2 + ) =( − )2 2
19x 2.5 :14 13 8 − 4 b) 52x - 3 – 2.52 = 52.3 1 2 7 3 75 , 3 : + 2 . ,125 − . 8 , 0 − ,12 : c) 4 5 2 2 = 64 1 1 + 75 , 0 x 2
Câu 3(5 điểm):
a) Tìm số nguyên x và y, biết : xy - x + 2y = 3.
b) Tìm 2 số tự nhiên biết tổng của 2 số bằng 432 và ƯCLN của chúng là 36.
c) Tìm tất cả các số nguyên tố p, q sao cho 7p + q; pq + 11đều là số nguyên tố.
Câu 4(6,0 điểm).
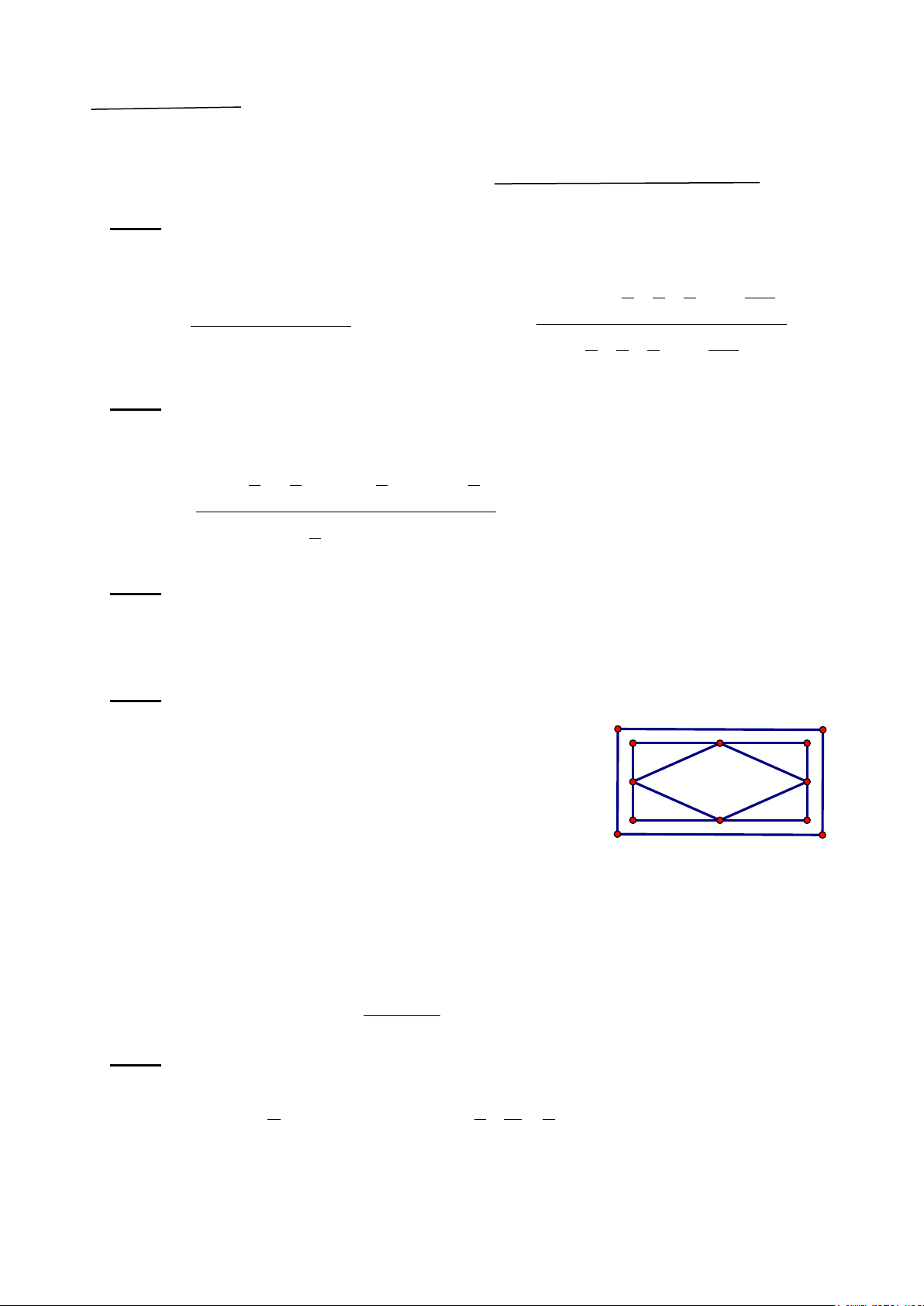
1. Một mảnh sân chơi hình chữ nhật có chiều dài và chiều Lối đi
rộng lần lượt là 40m và 25m. Người ta làm một lối đi xung
quanh sân (thuộc phần đất của sân) rộng 1m, phần còn lại Trồng hoa Hồng
của sân trồng hai loại hoa là hoa Cúc và hoa Hồng. Phần đất
trồng hoa Hồng có dạng hình thoi (như hình vẽ bên). Biết Lối đi
mỗi mét vuông giống cây hoa Cúc có giá là 25000 đồng.
Tính số tiền mua giống cây hoa Cúc để trồng.
2. Cho hai tia đối nhau Ax, Ay. Trên tia Ax lấy hai điểm B và C sao cho B nằm giữa A và C và AC = 8c ;
m AB = 6cm .
a) Tính độ dài đoạn thẳng BC .
b) Trên tia Ay lấy điểm M , gọi K là trung điểm của đoạn thẳng AM . Chứng minh: BA + BM BK = 2
Câu 5(2,0 điểm):
a) Cho tổng A = 1 + 32 + 34 + 36 +…+ 32008 .Tính giá trị biểu thức: B = 8A - 32010
b)T×m ph©n sè a tho¶ m·n ®iÒu kiÖn: 4 a 2 < < vµ 7a + 4b = 1994 b 7 b 3
HƯỚNG DÃN CHẤM GIAO LƯU HỌC SINH GIỎI Câu Nội dung Điểm
a) 21.72 - 11.72 + 990.72 + 49.125.16 = 72(21 – 11 + 990) + 49.125.16 0.5đ
= 49. 1000 + 49. 2000 = 49.3000 = 147000 0.5đ
b) = (169 - 42).(169 - 52) … (169 - 169)
= (169 - 42).(169 - 52) … 0 = 0 0.5đ 15 9 20 9 5.4 .9 − 4.3 .8 30 18 2 20 27 0.5đ c) = 5.2 .3 − 2 .3 .2 9 19 29 6 5.2 .6 − 7.2 .27 9 19 19 29 18 5 .2 .2 .3 − 7.2 .3 1 29 18 2 = 2 .3 (5.2 −3 ) = 2 28 18 2 .3 (5.3− 7.2) d) ta cã 2 2 2 2 200 3 ... − + + + + + 3 4 5 100 1 2 2 2 2 2
(4,0đ) = 200 − 2 + + + + +...+ 2 3 4 5 100 (
) 2 2 2 2 2 2 2 2 2 ... 2 = − + − + − + − + + − 2 3 4 100 4 6 198 = 0 +1+ + +...+ 3 4 100 1 1 2 3 99 2 ... = + + + + 2 3 4 100 2 2 2 2 200 3 ... − + + + + + 1 2 3 99 2 + + + ...+ 3 4 5 100 ⇒ D = 2 3 4 100 = = 2 1 2 3 99 1 2 3 99 ... ... + + + + + + + + 2 3 4 100 2 3 4 100 a) ( 2 + ) =( − )2 2 19x 2.5 :14 13 8 − 4 (19x+50) :14=9 2 ⇒ x = 4 .Vậy x = 4 1.0đ
(3,0đ) b) 52x - 3 – 2.52 = 52.3 ⇒52x - 3 = 52.3 + 2.52 1,0đ
⇒ 52x - 3 = 52.5 ⇒ 52x - 3 = 53
⇒ 2x - 3 = 3 ⇒ 2x = 6 ⇒ x = 3. Vậy x = 3 15 12 5 7 4 6 2 4 . − . − . − . c) 4 5 4 2 5 5 3 9 1 = 64 ⇒ 16 = . 64 9 x ⇒ x = 4 9 1.0đ x 4
a) Tìm số nguyên x và y, biết : xy - x + 2y = 3.
xy - x + 2y = 3 ⇒ ( xy – x) + (2y – 2) = 1
⇒ x( y – 1) + 2( y – 1) = 1 ⇒(y – 1)( x + 2) = 1 0.75đ y −1 =1 y = 2 *) ⇒ x 2 1 + = x = 1 − y −1 = 1 − y = 0 *) ⇒ x 2 1 + = − x = 3 −
Vậy x = - 1 ; y = 2 hoặc x = -3 ; y = 0 0.75đ
b)Gọi 2 số tự nhiên cần tìm là a; b ( * a,b∈ N ). 0.5đ Ta có: a + b = 432 Giả sử a < b . a = 36m b = 36n Vì Vì UCLN(a,b) = 36 ⇒ (m,n) =1 0.5đ m < n Ta có: 36m + 36n = 432 ⇔ 36(m+ n) = 432 3 ⇔ m+ n = 432 : 36 (5,0đ) ⇔ m+ n =12 Ta có bảng giá trị sau: m n a b 0.5đ 1 11 36 396 5 7 180 252 Vậy (a,b)∈{(36;369);(180; } 352)
c)Ta có p, q là số nguyên tố nên pq +11 là số nguyên tố lớn hơn 11
⇒ pq + 11 là số lẻ nên pq là số chẵn
Do 7p + q là số nguyên tố lớn hơn 7 nên p, q không thể cùng chẵn
*)Th1: p = 2 7p+ q =14 +q. Ta thấy 14 chia 3 dư 2 0.5đ
+)Nếu q chia hết cho 3, do q nguyên tố nên q = 3 7p+ q = 17;
pq +11=17 đều nguyên tố ( thỏa mãn).
+)Nếu q chia cho 3 dư 1⇒ 14+q chia hết cho 37p+ q là hợp số ( loại)
+)Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 pq + 11 chia hết cho 3 nên pq 0.75đ +11 là hợp số 0.25đ
*)Th2: q = 2 7p + q= 7p+2 và pq + 11 = 2p +11
+)Nếu p chia hết cho 3 thì p = 3 khi đó 7p + q= 7p+2 = 23 và pq + 11 = 2p +11
= 17 đều nguyên tố ( thỏa mãn)
+)Nếu p chia 3 dư 1 thì 7p chia 3 dư 1 nên 7p + 2 chia hết cho 3 nên
7p + 2 là hợp số (loại)
+)Nếu p chia cho 3 dư 2 thì 2p chia 3 dư 1 ⇒ suy ra 2p + 11 chia hết cho 3 nên pq +11là hợp số ( loại) 0.5đ
Vậy ( p, q) là (2 ; 3) hoặc ( 3; 2)
1/Tính được diện tích trồng hoa Hồng: − − = ( 2 (40 2).(25 2) : 2 437 m )
Tính được diện tích vườn hình chữ nhật để trồng hoa:( − ) ( − ) = ( 2 40 2 . 25 2 874 m )
Tính được diện tích trồng hoa Cúc: − = ( 2 874 437 437 m ) 2đ
Tính được số tiền mua giống hoa Cúc: 437.25 000 =10 925 000 (đồng) 2/ 4 a)
Ta có: Điểm B nằm giữa hai điểm A và C
(6.0đ) Nên AB+ BC = AC mà AC = 8c ; m AB = 6cm Suy ra: 6 + BC = 8 1.5đ BC = 8− 6 BC = 2 cm Vậy BC = 2cm
b) Vì Ax và Ay là hai tia đối nhau. Điểm M thuộc tia Ay và B thuộc tia Ax .
⇒ Điểm A nằm giữa 2 điểm B và M
⇒ AM + AB = BM 2.5đ
⇒ AM = BM − AB AM BM − AB
Mặt khác, K là trung điểm của AM nên AK = = 2 2
Vì hai tia AB và AM đối nhau, mà điểm K là trung điểm của AM nên hai tia AB và AK đối nhau
⇒ Điểm A nằm giữa hai điểm B và K ⇒
BM − AB 2BA + BM − AB BA + BM
BK = BA + AK = BA + = = 2 2 2 Vậy BA + BM BK = 2
a)A = 1 + 32 + 34 + 36 +…+ 32008
9A = 32 + 34 + 36 + 38 +… + 32010 1.0đ 9A- A = 8A = 32010 - 1
B = 8A - 32010 = 32010 - 1 - 32010 = -1. b) 1.0đ 5 (2.0đ) Chú ý:
1. Thí sinh có thể làm bài bằng cách khác, nếu đúng vẫn được điểm tối đa.
2. Nếu thí sinh chứng minh bài hình mà không vẽ hình thì không chấm điểm bài hình.
3. Chấm và cho điểm từng phần, điểm của toàn bài là tổng các điểm thành phần không làm tròn.