Đề giữa học kì 1 Toán 11 năm 2025 – 2026 trường THPT Nhữ Văn Lan – Hải Phòng

SỞ GIÁO DỤC - ĐÀO TẠO HẢI PHÒNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THPT NHỮ VĂN LAN
NĂM HỌC 2025 – 2026 MÔN : Toán 11
Thời gian làm bài 90 phút – Không kể giao đề
Họ và tên ………………………………………………… Lớp …… Mã đề 101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Một công ty may quần áo đồng phục học sinh cho biết cỡ áo theo chiều cao của học sinh được tính như sau: Chiều cao (cm) 150 [ ;160) 160 [ ;167) 167 [ ;170) 170 [ ;175) 175 [ ;180) Cỡ áo S M L XL XXL
Công ty muốn ước lượng tỉ lệ các cỡ áo khi may cho học sinh lớp 11 đã đo chiều cao của 36 học
sinh khối 11 của một trường và thu được mẫu số liệu sau (đơn vị là cm)
160; 161; 161; 162; 162; 162; 163; 163; 163;
164; 164; 164; 164; 165; 165; 165; 165; 165;
166; 166; 166; 166; 167; 167; 168; 168; 168;
168; 169; 169; 170; 171; 171; 172; 172; 174 .
Số học sinh có chiều cao vừa vặn với size XL là bao nhiêu? A. 7 B. 6 C. 5 D. 8
Câu 2. Số đo theo đơn vị rađian của góc 135° là A. 4π . B. 6π . C. 3π . D. 5π . 5 7 4 6
Câu 3. Tập nghiệm của phương trình sin x = 0 là A. π  π S   kπ |k  = +
∈. B. S = − + k2π | k ∈. C.  2   2  π S  k2π | k  = + ∈.
D. S = {kπ |k ∈ }  .  2 
Câu 4. Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 12 răng là: A. 0 30 . B. 0 40 . C. 0 60 . D. 0 50 .
Câu 5. Bốn số x, − 4, y, 8 theo thứ tự đó lập thành một cấp số cộng. Khẳng định nào sau đây đúng? A. x = 6; − y = 3 − . B. x = 6; − y = 2 − . C. x = 1 − 0; y = 2 . D. x = 8; − y = 3 .
Câu 6. Cho cấp số nhân (u với u = 4 và u =16 . Công bội của cấp số nhân đã cho bằng n ) 2 3 A. 12. B. 1 . C. 4 . D. 12 − . 4
Câu 7. Hàm số y = tan x tuần hoàn với chu kỳ bằng bao nhiêu?
A. T = 4π . B. π T = .
C. T = 2π . D. T = π . 2
Câu 8. Khẳng định nào dưới đây là đúng?
A. Hàm số y = cos x là hàm số lẻ.
B. Hàm số y = sin x là hàm số chẵn.
C. Hàm số y = tan x là hàm số lẻ.
D. Hàm số y = cot x là hàm số chẵn.
Câu 9. Cho dãy số  2n
u , biết u =
. Ba số hạng đầu tiên của dãy số đó là n n 2n + 1 A. 4 2 3 ; ; . B. 1 3 4 ; ; . C. 2 4 2 ; ; . D. 1 1 1 ; ; . 5 3 4 2 4 5 3 5 3 2 4 8
GK1 Toán11 Mã đề 101 Trang 1/4
Câu 10. Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau: Điểm [20;30) 30 [ ; 40) [40;50) 50 [ ;60) [60;70) [70;80) 80 [ ;90) 90 [ ;100] Số thí sinh 4 6 15 12 10 6 4 3
Có bao nhiêu học sinh thi đỗ môn Toán? Biết rằng thí sinh đạt từ 50 điểm trở nên thì tính là đỗ. A. 37 B. 36 C. 35 D. 34
Câu 11. Cho cấp số cộng (u với u = 3 và u = 7 . Công sai của cấp số cộng đã cho bằng n ) 4 5 A. 4 . B. 3 . C. 7 . D. 4 − . 7 3
Câu 12. Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 2,4,6,8,16,32,. .. B. 2, − − 3, 4, − − 5, 6, − − 7,. ..
C. 1,3,9,27,81,243,.... D. 2,2,4,8,16,32,. ..
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Chiều sâu của mực nước cao nhất là 17m .
a) Cho 0 < <     
. Xét được dấu của biểu thức A = cos  + >   0 . 2  2  b) Cho 4
cos x = và 3 < x < 2 . Khi đó, 7 cos 2x = − . 5 2 25
c) Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian   
t (giờ) được cho bởi công thức ( ) = 2sin t h t  + +   15 .  4 6  d) Góc có số đo π o 270 đổi ra radian là 3 . 2
Câu 2. Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau: Điện lượng (Nghìn mAh) [0,9;0,95) [0,95;1,0) 1 [ ,0;1,05) 1 [ ,05;1,1) 1 [ ,1;1 1 , 5) Số pin 10 20 35 15 5 Khi đó:
a) Số pin có điện lượng từ 1,05 đến dưới 1,1 nghìn mAh là 15 viên.
b) Số trung bình của dãy số liệu là 1,016.
c) Độ dài của các nhóm là 0,05.
d) Hãng cần dừng sản xuất 50% pin có điện lượng thấp nhất. Điện lượng của pin không vượt quá 1,03
nghìn mAh bị dừng sản xuất.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
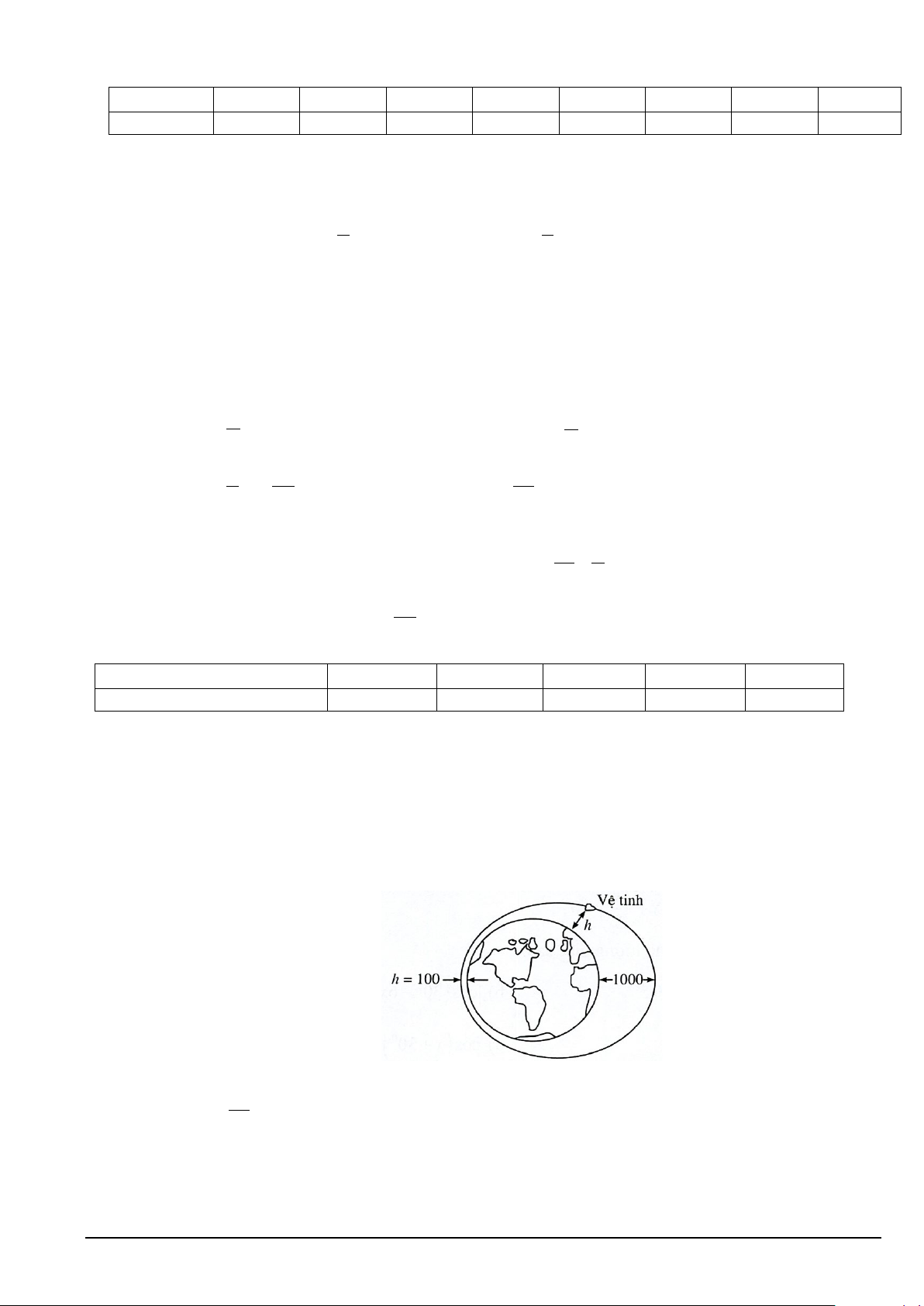
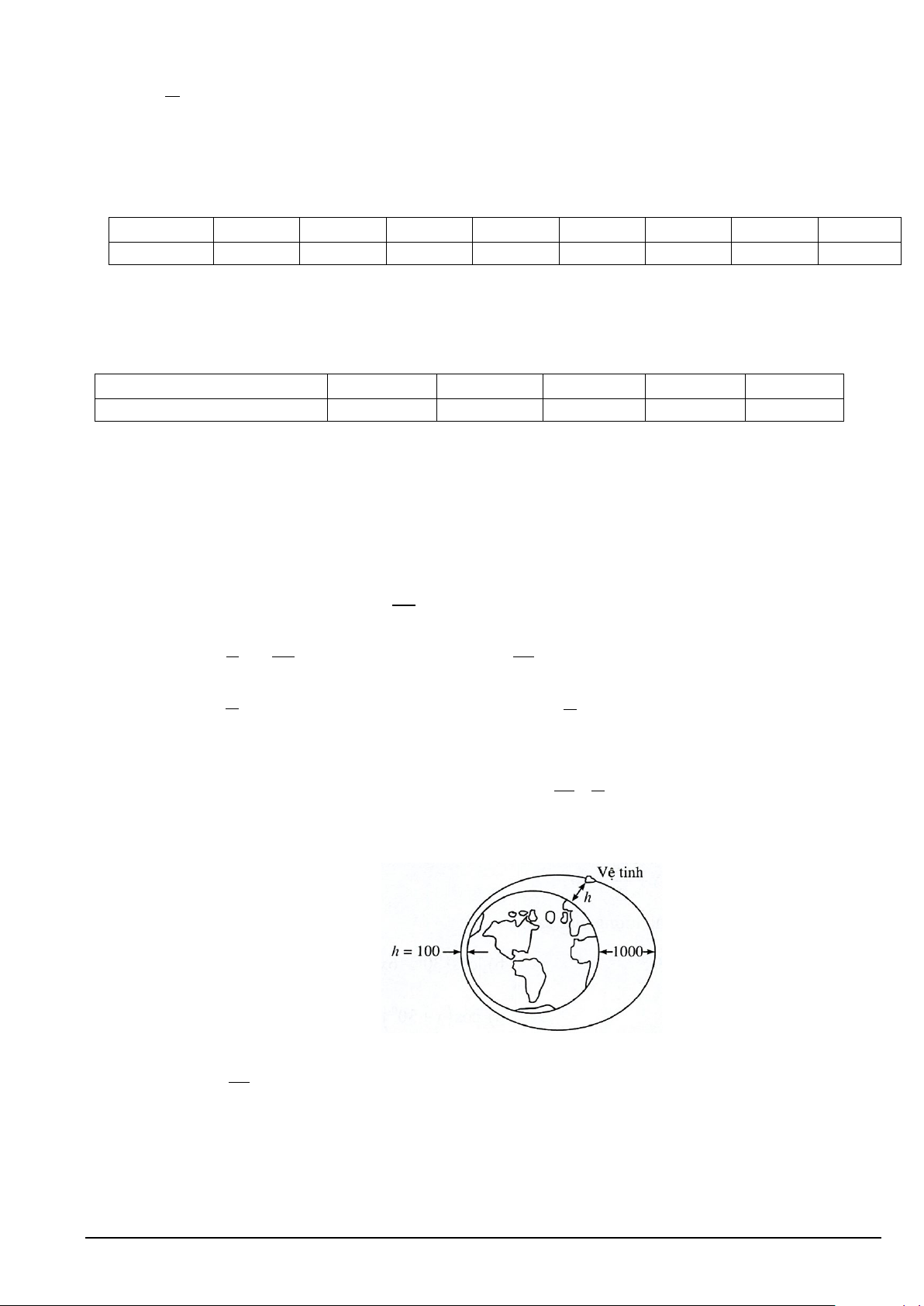
Câu 1. Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ)
Độ cao h (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức
h = 550 + 600⋅cos  t . Trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người 50
ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất 250 km . Trong khoảng 60 phút đầu
tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm t để có thể thực hiện thí nghiệm đó? (kết quả
làm tròn đến chữ số thập phân thứ nhất).?
GK1 Toán11 Mã đề 101 Trang 2/4
Câu 2. Chiều cao (đơn vị: m ) của 41 cây bạch đàn được cho ở bảng sau
Số đo chiều cao (m) [6,5;7) [7;7,5) [7,5;8) 8 [ ;8,5) 8 [ ,5;9) Số cây 9 10 15 5 2
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên. Kết quả làm tròn đến hàng phần mười?
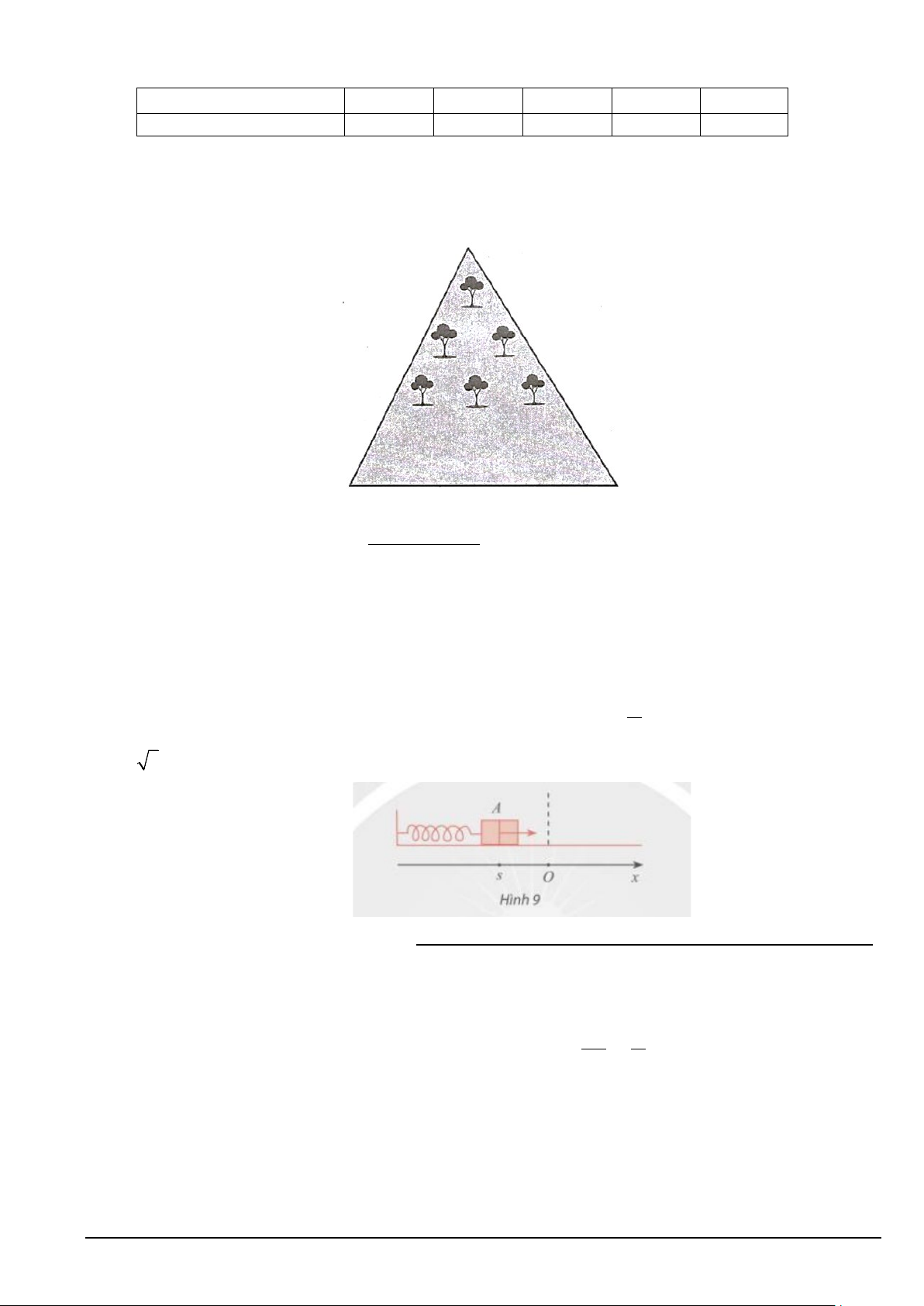
Câu 3. Người ta trồng 1275 cây trong một khu vườn hình tam giác theo cách sau: Hàng thứ nhất có 1 cây,
hàng thứ hai có 2 cây, và cứ như thế mỗi hàng sau sẽ có nhiều hơn hàng ngay trước đó 1 cây. Hỏi tổng số
hàng cây trong khu vườn bằng bao nhiêu?
Câu 4. Viết thêm sáu số vào giữa hai số 160 và 5 để được một cấp số nhân gồm tám số hạng. Tìm tổng tất
cả các số hạng của cấp số nhân đó ( Làm tròn đến hàng đơn vị)?
PHẦN IV. Tự luận. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1: Biến đổi thành tích biểu thức cos7a + cos5a ; cos7a − cos5a
u + u = 540 −
Câu 2: Cho cấp số nhân (u có 4 6 . Tính S . n )  u + u =  180 21 3 5
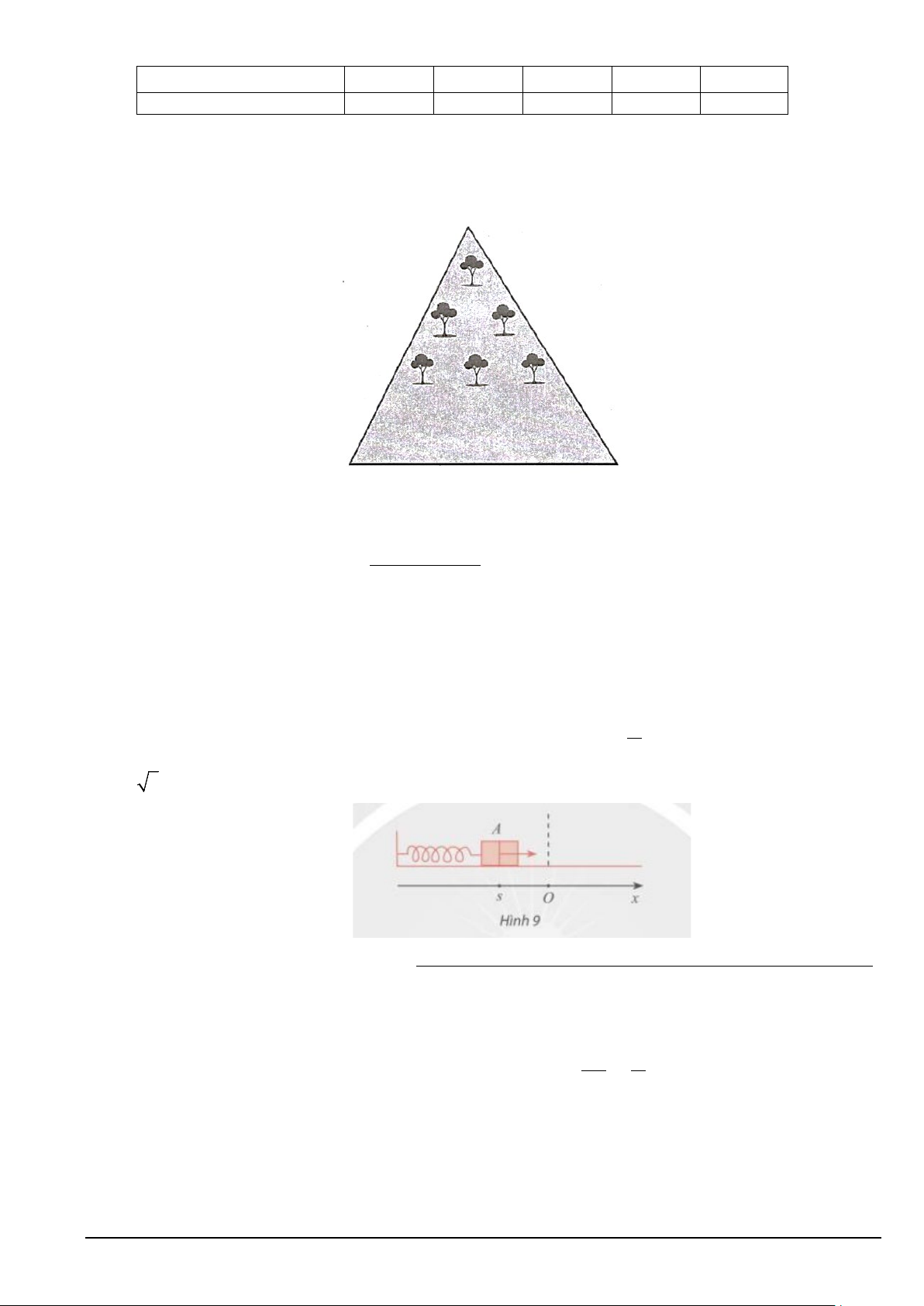
Câu 3: Trong Hình 9, khi được kéo ra khơi vị trí cân bằng ờ điểm O và buông tay, lực đàn hồi của lò xo
khiến vật A gắn ở đầu của lò xo dao động quanh O . Toạ độ s( cm) của A trên trục Ox vào thời điểm π
t (giây) sau khi buông tay được xác định bởi công thức s 10sin 10  = t + 
. Tìm thời điểm sớm nhất để 2    s = 5
− 3 cm ( làm tròn đến hàng phần trăm)?
(Theo https://www.britannica.com/science/simple-harmonic-motion)
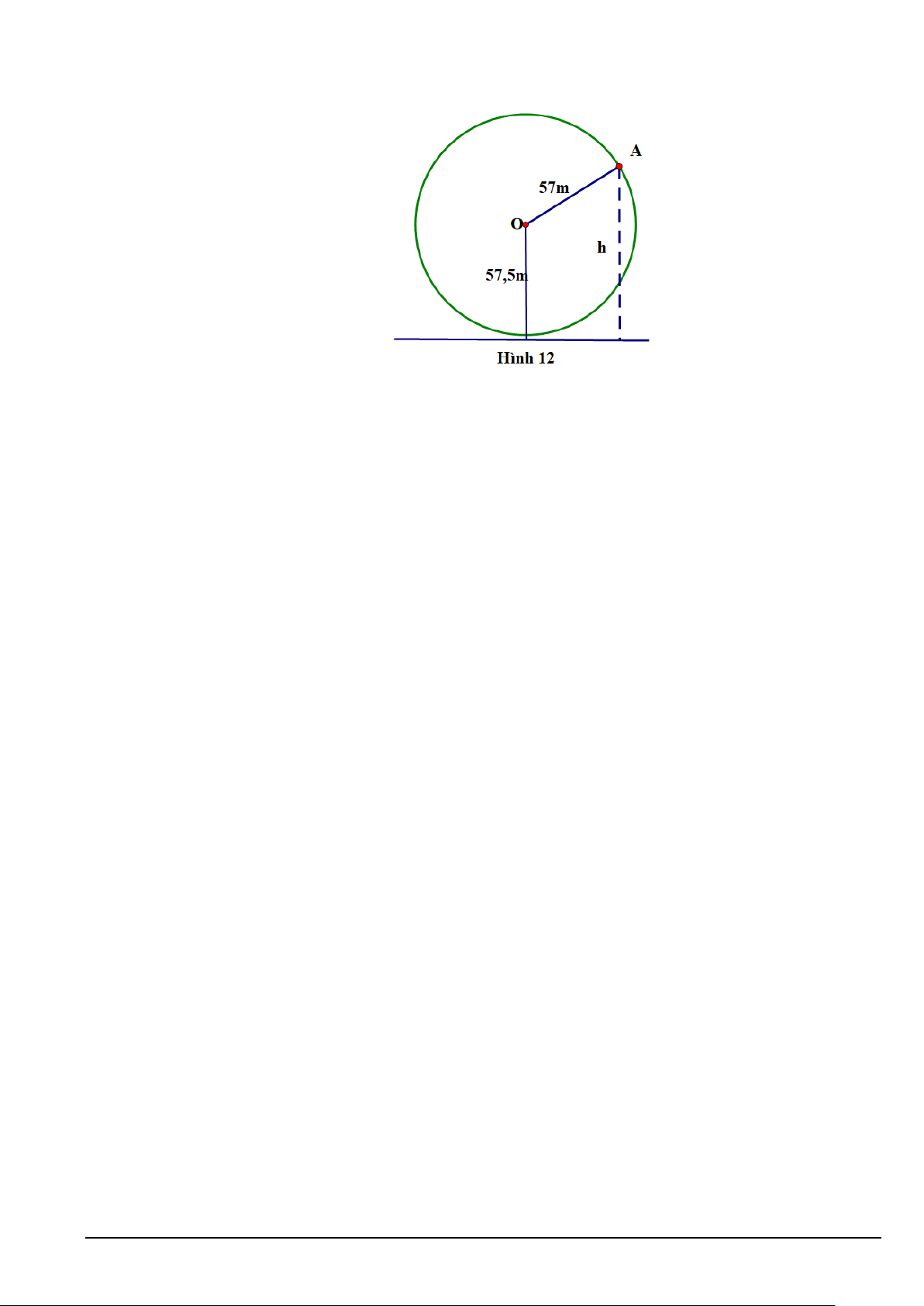
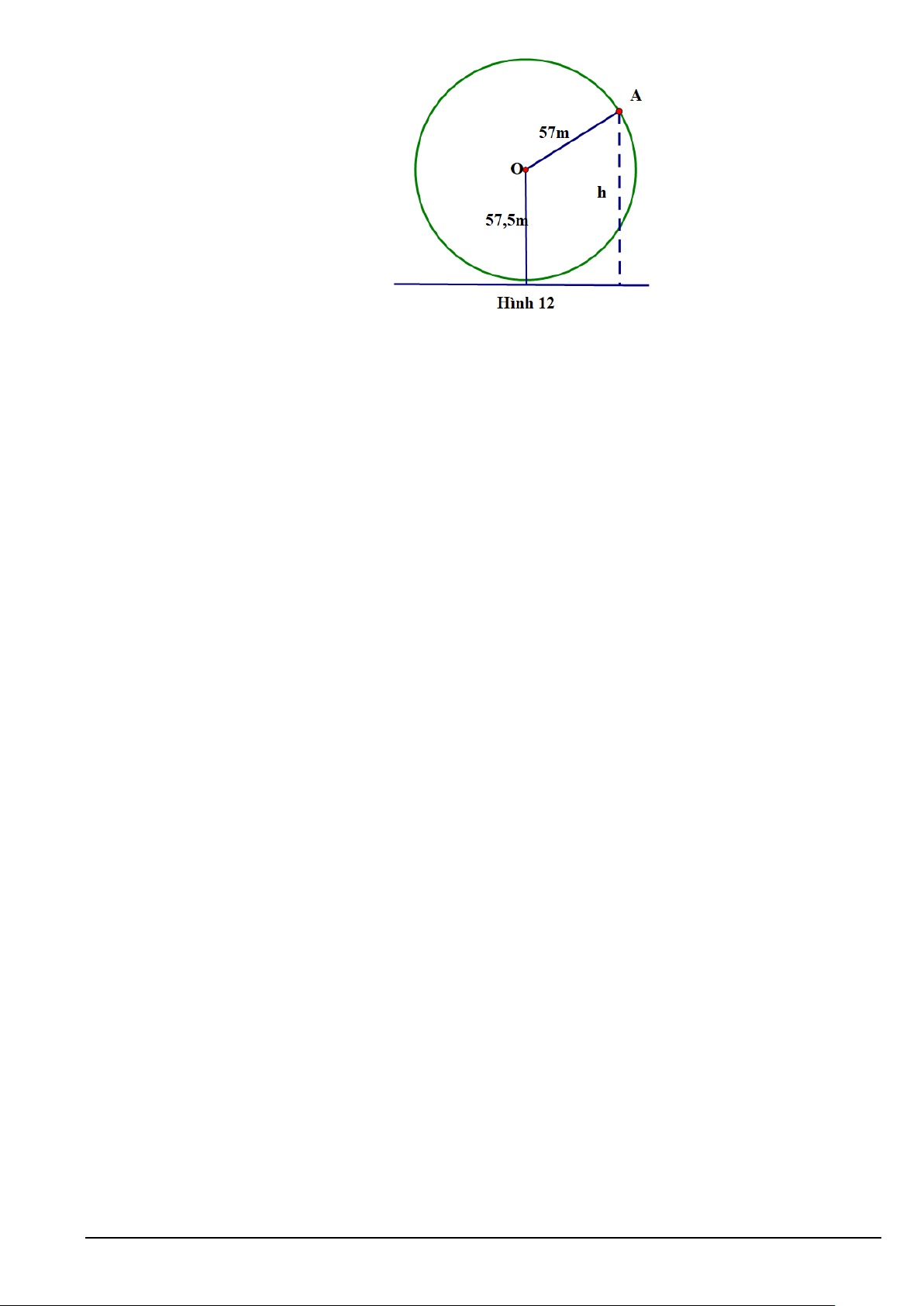
Câu 4: Một vòng quay trò chơi có bán kính 57 m , trục quay cách mặt đất 57,5 m , quay đều mỗi vòng hết
15 phút. Khi vòng quay quay đều, khoảng cách h( m) từ một cabin gắn tại điểm A của vòng  π π
quay đến mặt đất được tính bởi công thức: h(t) 2 57sin t  = − + 
 57,5 với t là thời gian quay  15 2 
của vòng quay tính bằng phút (t ≥ 0)Hình 12.
a) Tính chu kì của hàm số h(t)?
b) Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?
GK1 Toán11 Mã đề 101 Trang 3/4
c) Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì
cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m ?
------ HẾT ------
GK1 Toán11 Mã đề 101 Trang 4/4
SỞ GIÁO DỤC - ĐÀO TẠO HẢI PHÒNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THPT NHỮ VĂN LAN
NĂM HỌC 2025 – 2026 MÔN : Toán 11
Thời gian làm bài 90 phút – Không kể giao đề
Họ và tên ………………………………………………… Lớp …… Mã đề 102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Khẳng định nào dưới đây là đúng?
A. Hàm số y = sin x là hàm số chẵn.
B. Hàm số y = cot x là hàm số chẵn.
C. Hàm số y = tan x là hàm số lẻ.
D. Hàm số y = cos x là hàm số lẻ.
Câu 2. Cho dãy số  2n
u , biết u =
. Ba số hạng đầu tiên của dãy số đó là n n 2n + 1 A. 4 2 3 ; ; . B. 1 1 1 ; ; . C. 1 3 4 ; ; . D. 2 4 2 ; ; . 5 3 4 2 4 8 2 4 5 3 5 3
Câu 3. Số đo theo đơn vị rađian của góc 135° là A. 4π . B. 5π . C. 3π . D. 6π . 5 6 4 7
Câu 4. Trong các dãy số sau, dãy số nào là một cấp số nhân? A. 2, − − 3, 4, − − 5, 6, − − 7,. .. B. 2,2,4,8,16,32,. ..
C. 2,4,6,8,16,32,. ..
D. 1,3,9,27,81,243,....
Câu 5. Một công ty may quần áo đồng phục học sinh cho biết cỡ áo theo chiều cao của học sinh được tính như sau: Chiều cao (cm) 150 [ ;160) 160 [ ;167) 167 [ ;170) 170 [ ;175) 175 [ ;180) Cỡ áo S M L XL XXL
Công ty muốn ước lượng tỉ lệ các cỡ áo khi may cho học sinh lớp 11 đã đo chiều cao của 36 học
sinh khối 11 của một trường và thu được mẫu số liệu sau (đơn vị là cm)
160; 161; 161; 162; 162; 162; 163; 163; 163;
164; 164; 164; 164; 165; 165; 165; 165; 165;
166; 166; 166; 166; 167; 167; 168; 168; 168;
168; 169; 169; 170; 171; 171; 172; 172; 174 .
Số học sinh có chiều cao vừa vặn với size XL là bao nhiêu? A. 7 B. 8 C. 6 D. 5
Câu 6. Cho cấp số cộng (u với u = 3 và u = 7 . Công sai của cấp số cộng đã cho bằng n ) 4 5 A. 4 . B. 7 . C. 3 . D. 4 − . 3 7
Câu 7. Cho cấp số nhân (u với u = 4 và u =16 . Công bội của cấp số nhân đã cho bằng n ) 2 3 A. 4 . B. 12 − . C. 1 . D. 12. 4
Câu 8. Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 12 răng là: A. 0 60 . B. 0 50 . C. 0 30 . D. 0 40 .
Câu 9. Tập nghiệm của phương trình sin x = 0 là A. S π  π = {kπ |k ∈ }  . B. S   kπ |k  = +
∈. C. S = − + k2π | k ∈. D.  2   2  π S  k2π | k  = + ∈.  2 
GK1 Toán 11 Mã đề 102 Trang 1/4
Câu 10. Hàm số y = tan x tuần hoàn với chu kỳ bằng bao nhiêu? A. π T = .
B. T = 4π .
C. T = π . D. T = 2π . 2
Câu 11. Bốn số x, − 4, y, 8 theo thứ tự đó lập thành một cấp số cộng. Khẳng định nào sau đây đúng? A. x = 8; − y = 3 . B. x = 6; − y = 2 − . C. x = 6; − y = 3 − . D. x = 1 − 0; y = 2 .
Câu 12. Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau: Điểm [20;30) 30 [ ; 40) [40;50) 50 [ ;60) [60;70) [70;80) 80 [ ;90) 90 [ ;100] Số thí sinh 4 6 15 12 10 6 4 3
Có bao nhiêu học sinh thi đỗ môn Toán? Biết rằng thí sinh đạt từ 50 điểm trở nên thì tính là đỗ. A. 36 B. 34 C. 35 D. 37
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau: Điện lượng (Nghìn mAh) [0,9;0,95) [0,95;1,0) 1 [ ,0;1,05) 1 [ ,05;1,1) 1 [ 1 , ;1 1 , 5) Số pin 10 20 35 15 5 Khi đó:
a) Hãng cần dừng sản xuất 50% pin có điện lượng thấp nhất. Điện lượng của pin không vượt quá 1,03
nghìn mAh bị dừng sản xuất.
b) Số trung bình của dãy số liệu là 1,016.
c) Số pin có điện lượng từ 1,05 đến dưới 1,1 nghìn mAh là 15 viên.
d) Độ dài của các nhóm là 0,05.
Câu 2. Chiều sâu của mực nước cao nhất là 17m . a) Góc có số đo π o 270 đổi ra radian là 3 . 2 b) Cho 4
cos x = và 3 < x < 2 . Khi đó, 7 cos 2x = − . 5 2 25
c) Cho 0 < <     
. Xét được dấu của biểu thức A = cos  + >   0 . 2  2 
d) Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh
tính theo thời gian t (giờ) được cho bởi công thức ( ) 2    = sin t h t  + +   15 .  4 6 
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 1. Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ)
Độ cao h (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức
h = 550 + 600⋅cos  t . Trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người 50
ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất 250 km . Trong khoảng 60 phút đầu
tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm t để có thể thực hiện thí nghiệm đó? (kết quả
làm tròn đến chữ số thập phân thứ nhất).?
Câu 2. Viết thêm sáu số vào giữa hai số 160 và 5 để được một cấp số nhân gồm tám số hạng. Tìm tổng tất
cả các số hạng của cấp số nhân đó ( Làm tròn đến hàng đơn vị)?
GK1 Toán 11 Mã đề 102 Trang 2/4
Câu 3. Chiều cao (đơn vị: m ) của 41 cây bạch đàn được cho ở bảng sau
Số đo chiều cao (m) [6,5;7) [7;7,5) [7,5;8) 8 [ ;8,5) 8 [ ,5;9) Số cây 9 10 15 5 2
Hãy tìm trung vị của mẫu số liệu ghép nhóm trên. Kết quả làm tròn đến hàng phần mười?
Câu 4. Người ta trồng 1275 cây trong một khu vườn hình tam giác theo cách sau: Hàng thứ nhất có 1 cây,
hàng thứ hai có 2 cây, và cứ như thế mỗi hàng sau sẽ có nhiều hơn hàng ngay trước đó 1 cây. Hỏi tổng số
hàng cây trong khu vườn bằng bao nhiêu?
PHẦN IV. Tự luận. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1 :Biến đổi thành tích biểu thức cos7a + cos5a ; cos7a − cos5a
u + u = 540 −
Câu 2: Cho cấp số nhân (u có 4 6 . Tính S . n )  u + u =  180 21 3 5
Câu 3: Trong Hình 9, khi được kéo ra khơi vị trí cân bằng ờ điểm O và buông tay, lực đàn hồi của lò xo
khiến vật A gắn ở đầu của lò xo dao động quanh O . Toạ độ s( cm) của A trên trục Ox vào thời điểm π
t (giây) sau khi buông tay được xác định bởi công thức s 10sin 10  = t + 
. Tìm thời điểm sớm nhất để 2    s = 5
− 3 cm ( làm tròn đến hàng phần trăm)?
(Theo https://www.britannica.com/science/simple-harmonic-motion)
Câu 4: Một vòng quay trò chơi có bán kính 57 m , trục quay cách mặt đất 57,5 m , quay đều mỗi vòng hết
15 phút. Khi vòng quay quay đều, khoảng cách h( m) từ một cabin gắn tại điểm A của vòng  π π
quay đến mặt đất được tính bởi công thức: h(t) 2 57sin t  = − + 
 57,5 với t là thời gian quay  15 2 
của vòng quay tính bằng phút (t ≥ 0)Hình 12.
a) Tính chu kì của hàm số h(t)?
b) Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?
c) Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì
cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m ?
GK1 Toán 11 Mã đề 102 Trang 3/4
------ HẾT ------
GK1 Toán 11 Mã đề 102 Trang 4/4 Đề\câu 1 2 3 4 5 6 7 8
9 10 11 12 1a 1b 1c 1d 2a 2b 2c 2d 000 C A D C C B A C B C C D S D S D D D D S 101 B C D C C C D C C C A C S S D D D D D S 102 C D C D C A A A A C D C S D D D D S S D 103
C D A D C A A C D A D A S D D D S D S D 104
D D A C A B C D D C D D D D S S D S D D 1 2 3 4 729 7,6 33,3 50 33,3 7,6 50 729 33,3 729 7,6 50 7,6 729 50 33,3 50 33,3 729 7,6
ĐÁP ÁN ĐỀ THI GIỮA HỌC KÌ 1 – LỚP 11 (năm 2025-2026)
PHẦN 4. Tự luận ( 3 điểm)
Câu 19: Biến đổi thành tích biểu thức cos7a + cos5a ; cos7a − cos5a Lời giải
Ta có: cos7a + cos5a 2cos6a cos a =
= − tan 6a tan a . ( 0,5đ) cos7a − cos5a 2 − sin 6asin a
u + u = 540 −
Câu 20: Cho cấp số nhân (u có 4 6 . Tính S . n )  u + u =  180 21 3 5 Lời giải
Ta có u + u = 540 −
⇔ (u + u q = 540 − .( 0,25đ) 3 5 ) 4 6
Kết hợp với phương trình thứ hai trong hệ, ta tìm được q = 3
− . Lại có u + u =180 3 5 ⇔ u ( 2 4
q + q =180.( 0,25đ) 1 ) u ( 21 1− q 1 ) 1 Vì q = 3
− nên u = 2. Suy ra S = = ( 21 3 +1 .( 0,25đ) 21 ) 1 1− q 2
Câu 21: Trong Hình 9, khi được kéo ra khơi vị trí cân bằng ờ điểm O và buông tay, lực đàn hồi của lò xo khiến
vật A gắn ở đầu của lò xo dao động quanh O . Toạ độ s( cm) của A trên trục Ox vào thời điểm t (giây) sau khi π
buông tay được xác định bởi công thức s 10sin 10  = t + 
. Tìm thời điểm sớm nhất để s = 5 − 3 cm ( làm tròn 2    đến hàng phần trăm)?
(Theo https://www.britannica.com/science/simple-harmonic-motion) Lời giải Xét phương trình: π 10sin 10  t + = 5 −   3  2   π  3 ⇔ sin 10t + = −  2    2 π π sin 10  t  sin   ⇔ + = −  2  3      π π π π 10  t k2  + = − + π t = − +  k 2 3  12 5 ⇔  ,k ∈ ⇔  ,k ∈  π 4π π π 10t k2  + = + π t = +  k  2 3  12 5 π Vậy 7 t = . ( 0,75đ) 60
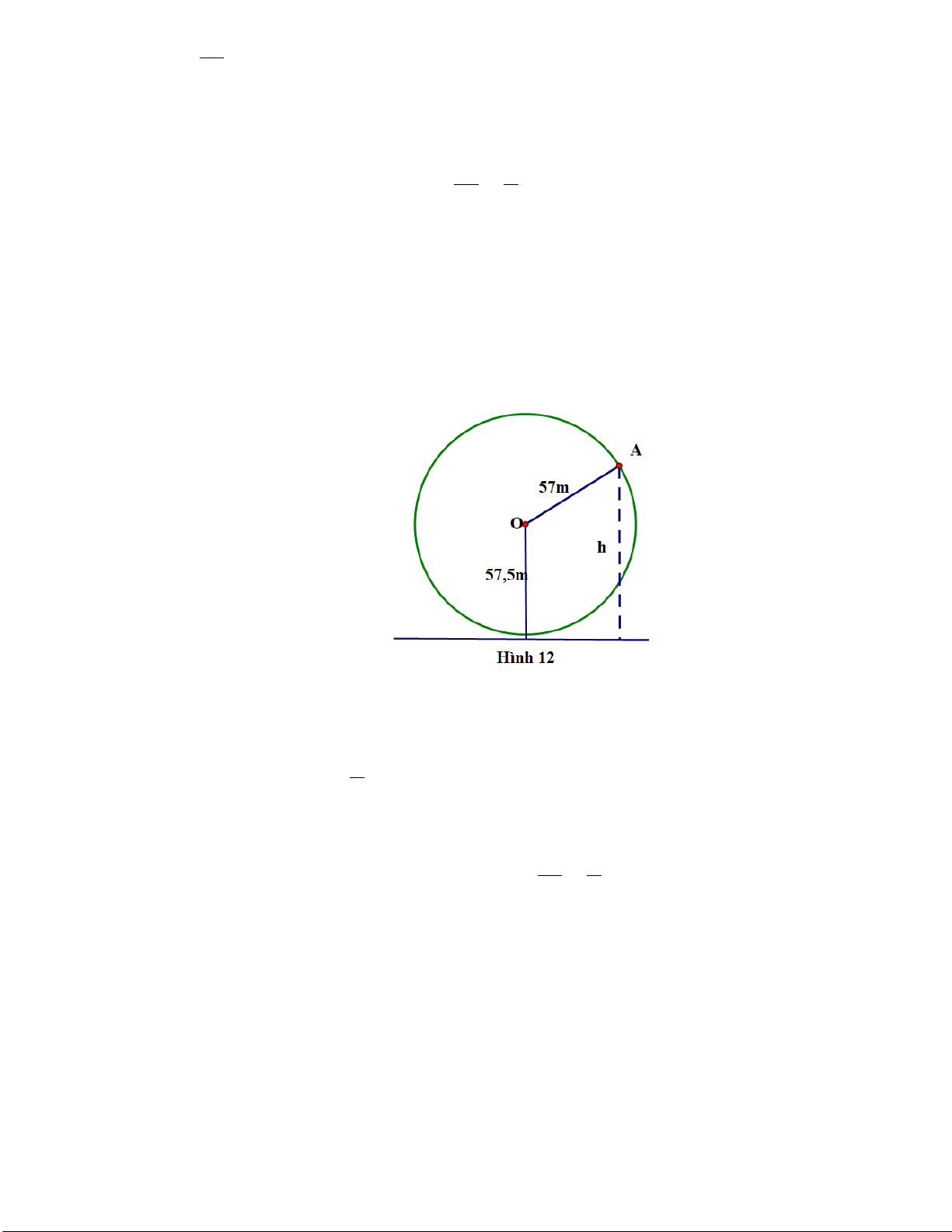
Câu 22: Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m , quay đều mỗi vòng hết 15
phút. Khi vòng quay quay đều, khoảng cách h( m) từ một cabin gắn tại điểm A của vòng quay đến mặt  π π
đất được tính bởi công thức: h(t) 2 57sin t  = − + 
 57,5 với t là thời gian quay của vòng quay tính  15 2 
bằng phút (t ≥ 0) Hình 12.
a) Tính chu kì của hàm số h(t)?
b) Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?
c) Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị
trí cao nhất? Ở vị trí đạt được chiều cao là 86 m ? Lời giải
a) Vì vòng quay trò chơi quay mỗi vòng hết 15 phút nên chu kì của hàm số h(t) bằng 15 phút. ( 0,25đ)  π b) Khi 
t = 0 thì h = 57sin − + 57,5 =  
0,5( m) . Vậy khi đó khoảng cách từ cabin đến mặt đất bằng  2  0,5 m .( 0,25đ)  π π
c) Khi quay một vòng, cabin ở vị trí cao nhất khi 2 sin t  − = 
 1 hay t = 7,5 (phút); cabin đạt được  15 2 
chiều cao là 86 m lần đầu tiên khi t = 5 (phút). ( 0,5đ)
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 11
https://toanmath.com/de-thi-giua-hk1-toan-11
Document Outline

• Ma_de_101
• Ma_de_102
• Dap_an_excel_TN
  • Sheet1
• đáp án phần tự luận- T11-GK1
• XEM THEM - GIUA KY 1 - TOAN 11